第五章 系统的稳定性2
机械工程控制基础第五章系统稳定性分析

9/88
5.3 代数稳定性判据 劳斯判据
Logo
同时,如果劳斯阵列中第一 列所有项均为正号,则系统 一定稳定。
劳斯阵列为
sn a0 a2 a4 a6 s n1 a1 a3 a5 a7 s n2 b1 b2 b3 b4 s n3 c1 c2 c3 c4
由劳斯阵列的第一列看出:第一列中系数符号全为正
值,所以控制系统稳定。
16/88
Logo
5.3 代数稳定性判据 劳斯判据
例2 设控制系统的特征方程式为
s4 2s3 3s2 4s 3 0
试应用劳斯稳定判据判断系统的稳定性。
解:首先,由方程系数可知已满足稳定的必要条件。其次,排劳
阵列
s4 1 3 3
2/88
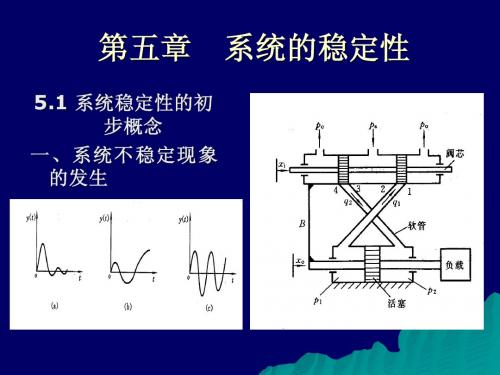
5.1 系统稳定性的基本概念
d
o
F
Logo
b
c
M
o
稳定性的定义:若控制系统在任何足够小的初始偏差的 作用下,其过渡过程随着时间的推移,逐渐衰减并趋于 零,具有恢复到原来状态的性能,则该系统是稳定的, 否则,该系统为不稳定。
3/88
Logo
5.2 系统稳定的充要条件
N(s)
X i s
+
G1 s
➢ 劳斯判据还说明:实部为正的特征 根数,等于劳斯阵列中第一列的系 数符号改变的次数。
12/88
5.3 代数稳定性判据 劳斯判据
Logo
劳斯判据的表述:
1.系统闭环传递函数特征方程式的系数没有为0的, 同时都是正数。(必要条件,要想系统稳定必 须满足这个条件)
2.劳斯阵列的第一列全部为正。(充分条件)
第五章 系统的稳定性
0
0
S0
2
0
0
例3
S4 1 S3 5 S2 4.8
s + 5s + 8s + 16 s + 20 = 0
4 3 2
8 16
5 × 8 − 1× 16 24 = = 4 .8 5 5
4.8 × 16 − 5 × 20 = − 4.83 4 .8
20 0 0 0 0
20 0 0
S1 –4.83 S0 20
解:系统的开环传递函数为 系统的闭环传递函数为 特征方程为
s3 s2
1
2 ωn ( s + K ) X 0 ( s) Gk = = 2 E (s) s ( s + 2ξωn )
2 X 0 (s) ωn ( s + K ) GB = = 3 2 2 X i ( s ) s + 2ξωn s 2 + ωn s + kωn
s s0
2、 Routh稳定判据 、 稳定判据 Routh表中第一列各元符号改变的次数等于 表中第一列各元符号改变的次数等于 系统特征方程具有正实部特征根的个数。 系统特征方程具有正实部特征根的个数。 因此,系统稳定的充要条件是, 因此,系统稳定的充要条件是,Routh表中 表中 第一列各元符号均为正 且值不为零。 符号均为正, 第一列各元符号均为正,且值不为零。
an − 2 an − 3 A2 B2 ⋮ D2
an − 4 an −5 A3 B3 ⋮
an − 6 ⋯ an − 7 A4 B4 ⋮
s n −1 s n −2 s
n −3
⋮ s
2 1
⋮ ⋮
A1an −3 − an −1 A2 B1 = A1 A1an −5 − an −1 A3 B1 = A1 ⋮
1习题集第五章系统稳定性

【解】 由特征方程列劳斯表如下:
S4
1
T 100
S3
2
10
S 2 T 5 100
S1 10(T 5) 200
S0
100
T 50 由劳斯判据,系统稳定,则
10(T 5) 200 0 解得: T 25
5-8 已知系统特征方程如下,试求系统在 s 右平面的根数及虚根值. (1) s5 3s4 12s3 24s2 32s 48 0
1.5K 0
解得: 0 K 5 3 5
5-12 试确定如下图所示系统的稳定性.
【解】 由系统方框图可得系统的闭环传递函数为:
10(10s 1)
(s)
特征方程为: s(s 1) 10(10s 1) 0
s(s 1) 10(10s 1)
即: s2 101s 10 0
5-3 设单位反馈系统的开环传递函数分别为
K (s 1) G(s)
s (s 1) (s 5)
1 K * (s 1) 【解】 G(s) 5
1 s(s 1)( s 1)
5
所以开环增益 K 1 K * 5
由开环传递函数可得系统的闭环传递函数为:
K (s 1) (s)
1 s(s 1)( s 1) K (s 1)
,试用对数频率特性判别系统的稳定性。
【解】画出开环频率特性,并依系统中有两个积分环节做出辅助线如图所示:
在 L() 0范围内,N N 0 ,故 P 2N ,则系统闭环稳定。
10
0.1K A 0
0.1K A (0.09 0.2K A ) 0.1K A 0
第五章第五节 生态系统的稳定性

恢复力稳定性高的生态系统特征:
① 生物种类较少,物种扩张受到的制约较小。
恢复力强
恢复力弱
恢复力稳定性高的生态系统特征:
②、生物个体小,繁殖快。能以休眠方式渡 过不利时期或产生适应新环境的变异。
6、在草原上人工种草,为了防止鸟把草籽吃掉, 用网把试验区罩上,后来发现,草的叶子几乎被 虫吃光,而没加网罩的草地反而长得较好。造成 这种现象的原因是( C ) A.植被破坏 B.环境污染 C.食物链被破坏 D.缺水干旱 7、生态系统能够保持稳定的原因主要是( A.相对稳定的物质循环 B.缺水干旱 C.自动调节能力 D.食物链被破坏
丁 甲 乙 丙 甲 乙
丙
甲 乙 丁
丙 甲
丁
乙 丁 丙
A
B
C
D
6、某生态学家以“保护和利用草原生态系统”为课题, 对某草原进行了几项专题研究,并绘制了如下两图。其 中:甲图表示一个鼠群迁入一个新的生态系统后的种群 增长曲线;乙图表示单位面积的放牧量与生产者的净生 产量的关系,图中的虚线代表未放牧时,草原中生产者 的净生产量,请据图分析并回答下列问题:
负反馈调节 兔与植物的关系
兔的数量增加 兔吃大量植物 兔因饥饿死亡
兔吃少量植物 植物减少
兔的食物增加
植物增加
结果:抑制或减弱了最初发生的变化,使 生态系统达到或保持稳定。 范围:生物群落内部、 生物群落与无机环境之间
正反馈
生态系统中某一成分 的变化所引起的其它 一系列的变化,反过 来加速最初发生变化 的成分所发生的变化。
恢复力强
恢复力较弱
3、抵抗力稳定性与恢复力稳定性的关系
第五章系统的稳定性-机械工程控制基础-教案

Chp.5系统稳定性基本要求1.了解系统稳定性的定义、系统稳定的条件;2.掌握Routh判据的必要条件和充要条件,学会应用Routh判据判定系统是否稳定,对于不稳定系统,能够指出系统包含不稳定的特征根的个数;3.掌握Nyquist 判据;4.理解Nyquist 图和Bode 图之间的关系;5.掌握Bode 判据;6.理解系统相对稳定性的概念,会求相位裕度和幅值裕度,并能够在Nyquist 图和Bode 图上加以表示。
重点与难点本章重点1.Routh 判据、Nyquist 判据和Bode 判据的应用;2.系统相对稳定性;相位裕度和幅值裕度求法及其在Nyquist图和Bode 图的表示法。
本章难点Nyquist 判据及其应用。
§1 概念示例:振摆1、稳定性定义:若系统在初始条件影响下,其过渡过程随时间的推移逐渐衰减并趋于0,则系统稳定;反之,系统过渡过程随时间的推移而发散,则系统不稳定。
(图5.1.2)讨论:①线性系统稳定性只取决于系统内部结构和参数,是一种自身恢复能力。
与输入量种类、性质无关。
②系统不稳定必伴有反馈作用。
(图5.1.3)若x0(t)收敛,系统稳定;若x0(t)发散,则系统不稳定。
将X0(s)反馈到输入端,若反馈削弱E(s) →稳定若反馈加强E(s) →不稳定③稳定性是自由振荡下的定义。
即x i(t)=0时,仅存在x i(0-)或x i(0+)在x i(t)作用下的强迫运动而系统是否稳定不属于讨论范围。
2、系统稳定的条件:对[a n p n+a n-1p n-1+…a1p+a0]x0(t)=[b m p m+b m-1p m-1+…b1p+b0]x i(t)令B(s)= a n p n+a n-1p n-1+…a1p+a0 A(s)= b m p m+b m-1p m-1+…b1p+b0初始条件:B0(s) A0(s)则B(s)X0(s)- B0(s)= A(s)X i(s)- B0(s)X i(s)=0,由初始条件引起的输出:L-1变换根据稳定性定义,若系统稳定须满足,即z i为负值。
第五章第五节生态系统的稳定性

生物圈Ⅱ号的启示
人类应保持对自然的敬畏,不 满300万岁的人类想对45亿高龄的 地球指手划脚当家作主,为时尚早 。人类要避免对自然环境的种种自 作聪明,否则,人们很可能不会再 有下一个五千年文明。
第五节生态系统稳定性
少量砍伐森林中的树木,森林的 结构功能不会破坏。
草原上适量放养牲畜,草原不至 于破坏。
பைடு நூலகம்
丙
7、如图是某温带草原生态系统中一个食物网简图。请据图 回答: (1)在生态系统稳定性方面,该生态系统 恢复力稳定性 _____________ 比森林生态系统要强。 捕食、竞争 (3)猫头鹰和蛇的关系属于 _________。该生态系统成分 中未表示的成分有 非生物物质和能量、分解者 。
8.根据下列材料,回答问题: 材料一 红树林是生长在热带、亚热带海岸潮间带 特有的植被,具有丰富的动植物资源。广东是我国红树 林资源最丰富的省份之一,其中雷州半岛和深圳湾的红 树林分布区被列为国家级红树林自然保护区,红树林的 保护和发展也被列为广东建设林业生态省的八大工程之 一。 材料二 2004年12月,印度洋地震引起的海啸导致 死亡十多万人,几百万人无家可归。但因为有茂密的红 树林,印度泰米尔纳德邦一个渔村里的172户人家在这次 海啸中幸免遇难。
课题:设计并制作生态缸,观察其稳定性
阅读后思考:在制作生态缸时,有哪些制作要求?
课题:设计并制作生态缸,观察其稳定性
设计要求 相关分析 小生态瓶中所形成的生态系统, 防止外界生物或非生物因素的 必须是封闭的 干扰 投放的生物,必须具有很强的生 要能够进行物质循环和能量流 活力,成分齐全。 动,以免破坏食物链。 让里面的植物见光,又便于学生 小生态瓶必须是透明的 进行观察。 生态瓶宜小不宜大,瓶中的水 便于操作;缸内储备一定量的 量应为容器的4/5。 空气
线性系统理论(第五章)系统运动的稳定性

的一个状态 。
t [t0,)
如果 xe 不在坐标原点,可以通过非奇异线性变换,使 xe 0,
因此,平衡状态的稳定性问题都可以归结为原点的稳定性问题。
对线性定常系统:x Ax 其平衡状态 Axe 0
A 非奇异,只存在一个位于状态空间原点的平衡状态。
主要内容为: •外部稳定性和内部稳定性 李亚普诺夫意义下稳定性的一些基本概念 •李亚普诺夫第一法 •李亚普诺夫第二法 •性连续系统的稳定性 •线性定常离散系统的稳定性
§5.1 外部稳定性和内部稳定性
一、外部稳定性
外部稳定性:称一个因果系统为外部稳定(BIBO)是指对任何
一个有界输入u(t), ‖u(t)‖≤β1<∞ t [t0, ) 的任意输入u(t),对应的输出y(t)均为有界,即
§5.2 李亚普诺夫意义下运动稳定性的一些基本概念
一、李亚普诺夫第一方法和第二方法 李亚普诺夫第一方法也称李亚普诺夫间接法,属于小范围 稳定性分析方法。是求出线性化以后的常微分方程的解, 从而分析原系统的稳定性。
李亚普诺夫第二方法也称李亚普诺夫直接法,不需要求解 微分方程的解,就能够提供系统稳定性的信息。
x2 x2
fx22
可见,只有在 x2 0 时,d E / dt 0 。在其他各处均有d E / dt 0 ,
这表明系统总能量是衰减的,因此系统是稳定的。
Lyapunov第二法是研究系统平衡状态稳定性的。
二、自治系统、平衡状态和受扰运动
1、自治系统:没有输入作用的一类动态系统
x f (x,t) x(t0) x0 t [t0,)
A 奇异,存在无穷多个平衡状态。
3、受扰运动:动态系统的受扰运动定义为其自治系统由初始 状态扰动 x0 引起的一类动态运动,即系统的状态零输入响 应。
生态系统的稳定性

第五章第五节生态系统的稳定性(第2课时)小鱼死了3条,有2条在水面上浮头,思考:病死还是饿死?接着又往缸内加了5只小虾,同时加了100 mL的剑水蚤作为食物,结果这5只小青虾也未能逃出死亡,改进:加绿藻的数量的同时,适量增加剑水蚤的数量,结果藻类亮绿,小虾、小鱼活动自如。
当堂达标:1.为观察不同水质对生态系统稳定性的影响,设计并制作了小生态瓶。
其与自然生态系统相比的特殊性表现在()A.不输入太阳能B.因封闭而不开放C.缺少分解者D.不进行物质循环2. 观察自我制作的小生态瓶不包括()A.观察植物的生存状况B.观察水质的变化情况C.观察动物的生存状况D.观察分解者的生存状况3. 下列关于小生态瓶制作的说法正确的是()A.生态瓶的密封性越差,其生物死亡就越快B.生态瓶中放入河水和小鱼,不放沙子也可构成一个微型生态系统C.生态瓶中的生物间最好不要有捕食关系,否则稳定性就差D.生态瓶制作完成后,一般要避光存放4. 下列四个一样大小的玻璃缸中均饲养了相同数目的蝌蚪,哪个玻璃缸中的蝌蚪最容易因缺O2而死亡()A.放有水草,放在阳光下B.没有水草,放在阳光下C.放有水草,放在黑暗中D.没有水草,放在黑暗中5.上图是一个密封的养鱼缸,它是一个自我平衡的生态系统,请分析在一定时间内能够保持动态平衡的原理:(1)有稳定的________来源。
(2)各类生物数量____________。
(3)植物的光合作用能为____________________。
(4)动物生命活动过程中产生的________能供___________________ 。
(5)微生物能利用__________________ __ 转化无机物为____________________。
当堂达标答案:1—4 BDBC5. (1)能量(2)相对稳定(3)动物生活提供氧气和养料(4)CO2 植物进行光合作用合成有机物和碳元素来源(5)动物粪便和动植物残体植物生活提供营养物质教学反思:本实验以小组为单位进行,着重培养学生的团队协作意识和严谨的科学态度,让学生在实践中体验成功的喜悦,总结失败的教训。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Nyquist图上单位圆对应Bode图上0分贝线; Nyquist图上负实轴对应Bode图上-1800线。
[GH]
1
(−1, j 0)
Im
4
ω = +∞
ω=0
20lgGH
1
2
ωc
3
4
ω
2
31
ωg 2
ω
Nyquist轨迹与单位圆交点的频率,即对数幅频特性曲线 与横轴交点的频率,即输入与输出幅值相等时的频率,称 为剪切频率或幅值穿越频率、幅值交界频率,记为ωc。 Nyquist轨迹与负实轴交点的频率,即对数相频特性曲线 与横轴交点的频率,称为相位穿越频率或相位交界频率, 记为ωg。
ω1=1, ω2=5。20lgK = 20lg2 = 6dB。
画出对数幅频特性曲线
21
L(ω )(dB)
ωc
ωc′
ω
由图可知
− 40(lg ω c − lg ω1 ) = 0 − 20 lg K 40 lg(ω c ω1 ) = 20 lg K = 20 lg 2
所以K1=10时,剪切频率为 ωc = 2 = 1.414
8
10 已知系统开环传递函数 G(s)H(s) = s(0.1s +1) 试用对数判据判别闭环稳定性。
解:绘制系统开环对数频率特性如图
P=0, ωc<ωg 闭环稳定。
9
L(ω )(dB)
系统开环传递函数为
K G ( s) H ( s) = s (Ts + 1)
ω
ω = 1/ T
试用对数稳定判据判 断其稳定性 。
22
所以K1=10时,相角裕度为
γ = 180° + ϕ (ωc ) = 180° − 90° − arctgωc − arctg(ωc 5) = 19.5°
书中求法:
2.84(dB)
−40 1
ωc
当ω=1时, 实际值为:
10 20 lg G ( jω ) H ( jω ) = 20 lg = 2.84dB 1× 2 × 1.04
L(ω )(dB) L(ω )(dB)
ω
ω
ϕ (ω )(°)
ϕ (ω )(°)
ω ω
在图 (c)中,对数幅频特性还可上移Kg,即开环系统的增益 增加Kg倍,则闭环系统达到稳定的临界状态。 17
在乃氏图中,乃氏曲线与负实轴的交点到原点的距离即为 1/Kg ,它代表在频率ωg处开环频率特性的模。 对于稳定系统,1/Kg<1,如图(a) 所示; 对于不稳定系统有1/Kg>1,如图 (b) 所示。
令
tan(a + b) =
cos(a + b) cos a cos b − sin a sin b = =0 sin(a + b) sin a cos b + cos a sin b
分子分母同除以 cos a cos b 得:
cos a cos b − sin a sin b 1 − tan a tan b = =0 sin a cos b + cos a sin b tan a + tan b
3
2 穿越的概念
[GH]
1
(−1, j 0)
Im
ω = +∞
ω=0
20lgGH
1
2
ωc
3
4
ω
2
3
0
Re
0
ωc
-1800
ω g1
ωg 2
ω
¾开环Nyquist轨迹在点(-1,j0)以左穿过负实轴称为“穿越”。
¾若沿频率ω增加的方向,开环轨迹自上而下(相位增加) 穿过点 (-1,j0)以左的负实轴称为正穿越;反之称为负穿越。 ¾若沿 ω 增加的方向,开环轨迹自点 (-1,j0)以左的负实轴 开始向下称为半次正穿越;反之称为半次负穿越。
50 100
ω
−
π
2
ω
− π
3 π − 2
γ =55D
ω g
若开环对数幅频特性对横轴有多个剪切频率,则取其 最大者来判别系统稳定性。
7
Bode判据与Nyquist判据相比较具有的优点: ①Bode图容易绘制; ②用Bode图上的渐近线可粗略判断系统稳定性; ③用Bode图可找出系统各环节中引起不稳定产生的 主要因素并可合理选择其中参数进行校正; ④调整开环增益K时,对应系统 Bode 图会产生上下 平移,故容易找出系统稳定所需的增益值。
ϕ (ω )(°)
ω
伯德图
解:系统的开环传递函数在s平面右半部没有极点, 即P=0,而在L(ω)≥0的频段内,相频特性ϕ(ω)不穿 越-180°线,故闭环系统必然稳定。
10
第五章
系统的稳定性
系统稳定性的概念 Routh稳定判据 Nyquist稳定判剧 Bode稳定判剧 系统的相对稳定性
1 Kg
jY (ω )
jY (ω )
γ
γ
ϕ
X (ω )
ϕ
X (ω )
1 Kg
18
几点说明: ① 对于 — 个稳定的最小相位系统,其相角裕度应为正 值,增益裕度应大于1 ; ② 严格地讲,应当同时给出相角裕度和增益裕度,才能 确定系统的相对稳定性。但在粗略估计系统的暂态响 应指标时,主要对相角裕度提出要求。 ③ 为使系统有满意的稳定储备,以及得到较满意的暂态 响应,在工程实践中,一般希望
ωc′ = 20 = 4.472
′ ) = 180° − 90° − arctgωc ′ − arctg(ωc ′ 5) = −29.2° γ = 180° + ϕ (ωc
25
欲 求 增 益 裕 度 , 则 须 先 求 出 ωg , 这 里 给 出 MATLAB计算的值。 sys=tf([10],conv(conv([1 0],[1 1]),[1 5])); margin(sys); figure sys=tf([100],conv(conv([1 0],[1 1]),[1 5])); margin(sys);
6
( 1 )若对数幅频曲线 穿越零分贝线时的相角大 于 -1800 , 系 统 稳 定 。 反 之,系统不稳定。 (2)若相频曲线穿越1800线时的对数幅频特性 的值为负则系统稳定。反 之,系统不稳定。此时的 对数幅频特性值的负值即 为幅值裕量。
20
dB 16 ω c =7 5 10
1
1 5 d B
γ = 30° ~ 60°
Kg ≥ 2
K g ≥ 6dB
19
④ 对于最小相位系统,开环幅频特性和相频特性之间 存在唯一的对应关系。上述相角裕度意味着,系统 开 环 对 数 幅 频 特 性 在 剪 切 频 率处的斜率应大于- 40dB/dec,且有一定宽度。在实际中常取-20dB/dec。 ⑤ 在闭环稳定条件下,稳定裕度越大,反映系统稳定 程度越高。稳定裕度也间接反映了系统动态过程的 平稳性,裕度大意味着超调小、振荡弱,阻尼大。
12
1. 相角裕度γ 在频率特性上对应于幅值 A(ω) = 1( 即 L(ω)=0)的角频 率称为剪切频率(截止频率),以ωc表示。 在剪切频率处,相频特性距-180°线的相位差γ叫做 相角裕度。即
γ = ϕ (ωc ) − ( −180°) = 180° + ϕ (ωc )
具有正相角裕度的系统不仅稳定,而且还有相当的稳 定储备,它可以在ωc的频率下,允许相角再增加(迟 后)γ度才达到临界稳定状态。 相角裕度也叫相位稳定性储备。
代入得
1 − 0.2ω g 2 = 0
ω g = 5s −1
24
所以K1=10时,相角裕度为
γ = 180° + ϕ (ωc ) = 180° − 90° − arctgωc − arctg(ωc 5) = 19.5°
当K1从10变到100时,幅频特性上移20dB,如上图中虚 线所示,此时
′ ω1 ) = 20 lg K ′ = 20 lg 20 40 lg(ωc
K g = 1 A(ω g )
在Bode图上,增益裕度改以分贝(dB)表示
K g = − 20 lg A (ω g ) = − L (ω g )
16
对于稳定的系统,L(ωg )必在Bode图0dB线以下,这时称 为正增益裕度,如图 (c) 所示。 对于不稳定系统, L(ωg )必在0dB线以上,这时称为负增 益裕度,如图 (d) 所示。
20
单位反馈系统开环传递函数为
K1 G ( s) = s ( s + 1)( s + 5)
分别求取K1= 10及K1= 100时的相角裕度和增益裕度 。 解:相角裕度可通过对数幅频特性用图解法求出。 K1=10时
K1 2 G (s) = = 5s (1 + s )(1 + s 5) s (1 + s )(1 + s 5)
ω
14
相应地,在乃氏图中,γ 即为乃氏曲线与单位圆的交点A 对负 实轴的相位差值。 对于稳定系统,A点必在负实轴以下。如图(a) 所示。 对于不稳定系统,A点必在负实轴以上,如图 (b) 所示。
1 Kg
jY (ω )
jY (ω )
γ
ϕ
X (ω )
γ
ϕ
X (ω )
1 Kg
15
2. 增益裕度Kg 在相频特性等于-180°的频率ωg (穿越频率) 处,开环幅频特性A(ωg)的倒数,称为增益裕 度,记做Kg 。即
26
27
routh判据 系统闭环 传递函数 特征方程
奈氏判据
对数判据
代数判据
几何判据
系统开环 传递函数
频率特性
奈氏图 稳定性判据 绝对稳定性 博德图 系统稳定性 系统闭环传递 函数无右极点 相角裕量 相对稳定性 幅值裕量
