多元回归分析案例
多元线性回归分析范例

多元线性回归分析范例多元线性回归是一种用于预测因变量和多个自变量之间关系的统计分析方法。
它假设因变量与自变量之间存在线性关系,并通过拟合一个多元线性模型来估计因变量的值。
在本文中,我们将使用一个实际的数据集来进行多元线性回归分析的范例。
数据集介绍:我们选取的数据集是一份汽车销售数据,包括了汽车的价格(因变量)和多个与汽车相关的特征(自变量),如车龄、行驶里程、汽车品牌等。
我们的目标是通过这些特征来预测汽车的价格。
数据集包括了100个样本。
数据集的构成如下:车龄(年),行驶里程(万公里),品牌,价格(万元)----------------------------------------5,10,A,153,5,B,207,12,C,10...,...,...,...建立多元线性回归模型:我们首先需要将数据集划分为自变量矩阵X和因变量向量y。
其中,自变量矩阵X包括了车龄、行驶里程和品牌等特征,因变量向量y包括了价格。
在Python中,我们可以使用NumPy和Pandas库来处理和分析数据。
我们可以使用Pandas的DataFrame来存储数据集,并使用NumPy的polyfit函数来拟合多元线性模型。
首先,我们导入所需的库并读取数据集:```pythonimport pandas as pdimport numpy as np#读取数据集data = pd.read_csv('car_sales.csv')```然后,我们将数据集划分为自变量矩阵X和因变量向量y:```python#划分自变量矩阵X和因变量向量yX = data[['车龄', '行驶里程', '品牌']]y = data['价格']```接下来,我们使用polyfit函数来拟合多元线性模型。
我们将自变量矩阵X和因变量向量y作为输入,并指定多项式的次数(线性模型的次数为1):```python#拟合多元线性模型coefficients = np.polyfit(X, y, deg=1)```最后,我们可以使用拟合得到的模型参数来预测新的样本。
SPSS多元回归分析实例
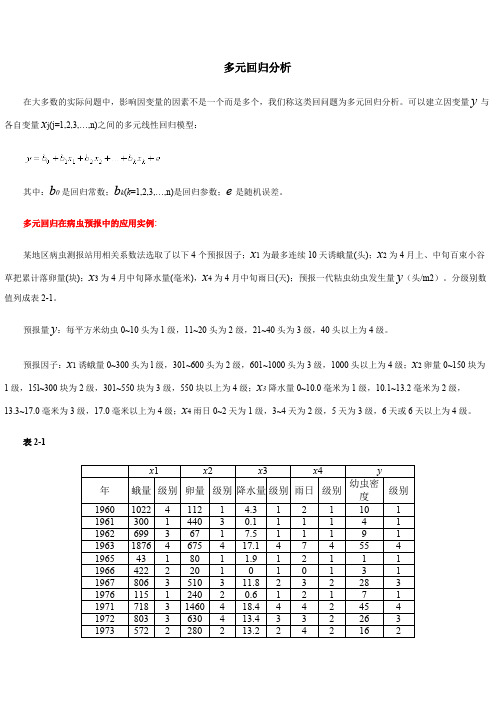
t i e an dl l t 多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y 与各自变量x j (j=1,2,3,…,n)之间的多元线性回归模型:其中:b 0是回归常数;b k (k =1,2,3,…,n)是回归参数;e 是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x 1为最多连续10天诱蛾量(头);x 2为4月上、中旬百束小谷草把累计落卵量(块);x 3为4月中旬降水量(毫米),x 4为4月中旬雨日(天);预报一代粘虫幼虫发生量y (头/m2)。
分级别数值列成表2-1。
预报量y :每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x 1诱蛾量0~300头为l 级,301~600头为2级,601~1000头为3级,1000头以上为4级;x 2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x 3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x 4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x 1x 2x 3x 4y 年 蛾量 级别 卵量 级别 降水量 级别 雨日 级别 幼虫密度级别1960102241121 4.31211011961300144030.111141196269936717.511191196318764675417.14745541965431801 1.9121111966422220101013119678063510311.82322831976115124020.612171197171831460418.444245419728033630413.433226319735722280213.224216219742641330342.243219219751981165271.84532331976461214017.515328319777693640444.7432444197825516510101112数据保存在“DATA6-5.SAV”文件中。
多元回归分析案例

多元回归分析案例下面以一个实际案例来说明多元回归分析的应用。
假设我们是一家电商公司,希望了解哪些因素会影响网站用户购买商品的金额。
为了回答这个问题,我们收集了以下数据:每位用户购买的商品金额(因变量),用户的年龄、性别和收入水平(自变量)。
首先,我们需要构建一个多元回归模型。
由于因变量是连续型变量,我们可以选择使用线性回归模型。
模型的形式可以表示为:购买金额=β0+β1×年龄+β2×性别+β3×收入水平+ε其中,β0是截距,β1、β2和β3是自变量的系数,ε是误差项。
接下来,我们需要对数据进行预处理。
首先,将性别变量转换为虚拟变量,比如用0表示男性,1表示女性。
然后,我们可以使用逐步回归方法,逐步选择自变量,以确定哪些变量对因变量的解释最显著。
在实际操作中,我们可以使用统计软件,比如SPSS或R来进行多元回归分析。
下面是一个用R进行多元回归分析的示例代码:```R#导入数据data <- read.csv("data.csv")#转换性别变量为虚拟变量data$gender <- as.factor(data$gender)#构建多元回归模型model <- lm(购买金额 ~ 年龄 + 性别 + 收入水平, data=data)#执行逐步回归step_model <- step(model)#显示结果summary(step_model)```通过运行这段代码,我们可以得到每个自变量的系数估计值、显著性水平、拟合优度等统计结果。
这些结果可以帮助我们理解各个自变量对于购买金额的影响程度以及它们之间的相对重要性。
在实际应用中,多元回归分析可以帮助我们识别哪些因素对于一些特定的因变量具有显著影响。
通过控制其他自变量,我们可以解释每个自变量对因变量的独立贡献,并用于预测因变量的值。
总之,多元回归分析是一种强大的统计工具,可以应用于各个领域,帮助我们理解和预测自变量对因变量的影响。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析案例。
在统计学中,多元回归分析是一种用于探究多个自变量与因变量之间关系的方法。
通过多元回归分析,我们可以了解不同自变量对因变量的影响程度,以及它们之间的相互作用情况。
在本篇文档中,我将通过一个实际案例来介绍如何使用SPSS软件进行多元回归分析。
案例背景:假设我们是一家电子产品公司的市场营销团队,在推出新产品之前,我们希望了解不同因素对产品销量的影响。
我们收集了一些数据,包括产品的售价、广告投入、竞争对手的售价、季节等因素,以及产品的销量作为因变量。
数据准备:首先,我们需要将数据录入SPSS软件中。
在SPSS中,我们可以通过导入Excel文件的方式将数据导入到软件中,并进行必要的数据清洗和处理。
确保数据的准确性和完整性对于后续的多元回归分析非常重要。
模型建立:接下来,我们需要建立多元回归模型。
在SPSS中,我们可以通过依次选择“分析”-“回归”-“线性回归”来进行多元回归分析。
在“因变量”栏中输入销量,然后将所有自变量依次输入到“自变量”栏中。
在建立模型之前,我们还需要考虑是否需要进行变量转换或交互项的添加,以更好地拟合数据。
模型诊断:建立模型后,我们需要对模型进行诊断,以确保模型的准确性和有效性。
在SPSS中,我们可以通过查看残差的正态性、异方差性以及自相关性来进行模型诊断。
如果模型存在严重的偏差或违反了多元回归分析的假设,我们需要进行相应的修正或改进。
模型解释:最后,我们需要解释多元回归模型的结果。
在SPSS的输出结果中,我们可以看到各个自变量的系数、显著性水平、调整R方等统计指标。
通过这些指标,我们可以了解不同自变量对销量的影响程度,以及它们之间的相互作用情况。
同时,我们还可以进行各种假设检验,来验证模型的有效性和可靠性。
结论:通过以上多元回归分析,我们可以得出不同自变量对产品销量的影响程度,以及它们之间的相互作用情况。
这些结果对于我们制定产品的定价策略、广告投放策略以及市场营销策略都具有重要的指导意义。
商务统计学课件-多元线性回归分析实例应用

6.80
13.65
14.25
27
8.27
6.50
13.70
13.65
28
7.67
5.75
13.75
13.75
29
7.93
5.80
13.80
13.85
30
9.26
6.80
13.70
14.25
销售周期
1
销售价格/元
其他公司平均销售价格
/元
多元线性回归分析应用
多元线性回归分析应用
解
Y 表示牙膏销售量,X 1 表示广告费用,X 2表示销售价格, X 3
个自变量之间的线性相关程度很高,回归方程的拟合效果较好。
一元线性回归分析应用
解
广告费用的回归系数检验 t1 3.981 ,对应的 P 0.000491 0.05
销售价格的回归系数检验 t2 3.696 ,对应的 P 0.001028 0.05
其它公司平均销售价格的回归系数检验
…
14
1551.3
125.0
45.8
29.1
15
1601.2
137.8
51.7
24.6
16
2311.7
175.6
67.2
27.5
17
2126.7
155.2
65.0
26.5
18
2256.5
174.3
65.4
26.8
万元
表示其他公司平均销售价格。建立销售额的样本线性回归方程如
下:
Yˆi 15.044 0.501X 1i 2.358 X 2i 1.612 X 3i
一元线性回归分析应用
多元线性回归实例分析

SPSS--回归—多元线性回归模型案例解析!(一)多元线性回归,主要是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程为:毫无疑问,多元线性回归方程应该为:上图中的x1, x2, xp分别代表“自变量”Xp截止,代表有P个自变量,如果有“N组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示:那么,多元线性回归方程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:无偏性假设,即指:期望值为03:同共方差性假设,即指,所有的随机误差变量方差都相等4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释.今天跟大家一起讨论一下,SPSS—-—多元线性回归的具体操作过程,下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型.数据如下图所示:点击“分析”——回归——线性——进入如下图所示的界面:将“销售量”作为“因变量"拖入因变量框内,将“车长,车宽,耗油率,车净重等10个自变量拖入自变量框内,如上图所示,在“方法”旁边,选择“逐步”,当然,你也可以选择其它的方式,如果你选择“进入”默认的方式,在分析结果中,将会得到如下图所示的结果:(所有的自变量,都会强行进入)如果你选择“逐步”这个方法,将会得到如下图所示的结果:(将会根据预先设定的“F统计量的概率值进行筛选,最先进入回归方程的“自变量”应该是跟“因变量”关系最为密切,贡献最大的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于0.05,当概率值大于等于0.1时将会被剔除)“选择变量(E)" 框内,我并没有输入数据,如果你需要对某个“自变量”进行条件筛选,可以将那个自变量,移入“选择变量框”内,有一个前提就是:该变量从未在另一个目标列表中出现!,再点击“规则”设定相应的“筛选条件”即可,如下图所示:点击“统计量"弹出如下所示的框,如下所示:在“回归系数”下面勾选“估计,在右侧勾选”模型拟合度“ 和”共线性诊断“ 两个选项,再勾选“个案诊断”再点击“离群值”一般默认值为“3",(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
多元回归分析SPSS案例
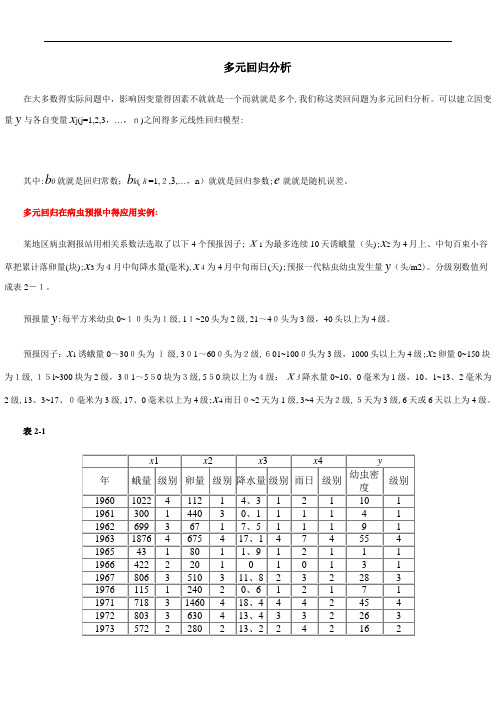
多元回归分析在大多数得实际问题中,影响因变量得因素不就就是一个而就就是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间得多元线性回归模型:其中:b0就就是回归常数;b k(k=1,2,3,…,n)就就是回归参数;e就就是随机误差。
多元回归在病虫预报中得应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10、0毫米为1级,10、1~13、2毫米为2级,13、3~17、0毫米为3级,17、0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1数据保存在“DATA6-5、SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”与“幼虫密度”变量,并输入数据。
再创建蛾量、卵量、降水量、雨日与幼虫密度得分级变量“x1”、“x2”、“x3”、“x4”与“y”,它们对应得分级数值可以在SPSS数据编辑窗口中通过计算产生。
编辑后得数据显示如图2-1。
图2-1或者打开已存在得数据文件“DATA6-5、SAV”。
2)启动线性回归过程单击SPSS主菜单得“Analyze”下得“Regression”中“Linear”项,将打开如图2-2所示得线性回归过程窗口。
多元回归模型分析案例

多元回归模型分析案例多元回归模型分析是一种重要的数据分析技术,它可用于解决一系列实际问题,如预测商品消费量、预测股票市场行情等。
本文将以一个简单的案例来说明如何利用多元回归模型来分析数据,以便发现有用的信息,并更好地了解因果关系。
假设一家商店想要预测它的销售额,并且想了解它的销售额与其他变量之间的关系。
接下来,我们以该商店的历史销售数据建立一个多元回归模型,预测未来销售额,并分析它与其他变量之间的关系。
首先,需要收集有关商店历史销售数据的所有信息,包括产品的价格、促销活动的有效性等。
然后,使用统计软件将这些数据分析成矩阵,并将这些变量作为自变量,而销售额作为因变量。
然后,使用多元线性回归的算法,对收集的数据进行分析和处理,并建立一个具有最佳拟合度的多元回归模型。
回归模型中,各变量之间的关系可以通过相关系数来衡量,其中正相关系数表示两个变量增大时,另一变量也会增大;反之,负相关系数表示两个变量增大时,另一变量则下降。
根据统计分析,可以得出每一个变量与销售额之间的相关性。
通过观察变量与销售额之间的关系,我们可以清楚地了解到每一个变量对销售额影响的程度,以及它们之间的因果关系。
此外,建立的多元回归模型还可用于预测未来的销售情况。
将未来的变量值带入模型,即可得出推测的未来销售额,方便商店更好地制定销售计划和预算。
当然,预测的准确程度取决于多元回归模型的准确性。
本文以一个简单的案例介绍了如何使用多元回归模型来分析数据,以更好地了解因果关系,以及用于预测未来销售情况。
多元回归模型分析是一种重要的数据分析技术,被广泛用于现实生活中的实际问题的解决。
但要记住,多元回归分析的结果仅供参考,最后的决策仍应根据实际情况,由实际决策者综合评估。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元回归分析案例计量经济学案例分析多元回归分析案例学院: 数理学院班级: 数学092班学号: 094131230姓名: 徐冬梅摘要:为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,用Eviews软件对相关数据进行了多元回归分析,得出了相关结论关键词:多元回归分析 ,Evicews软件, 中国人口自然增长;一、建立模型为了全面反映中国“人口自然增长率”的全貌,选择人口自然增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
国名总收入,居民消费价格指数增长率,人均GDP作为解释变量暂不考虑文化程度及人口分布的影响。
通过对表1的数据进行分析,建立模型。
其模型表达式为:(i=1,2,,3) Y,,,,X,,X,,X,ui11i22i33ii其中Y表示人口自然增长率,X 表示国名总收入,X表示居民消费价格指12 数增长率,X表示人均GDP,根据以往经验和对调查资料的初步分析可知,Y与3X,X,X3呈线性关系,因此建立上述三元线性总体回归模型。
Xi则表示各解12释变量对税收增长的贡献。
µi表示随机误差项。
通过上式,我们可以了解到,每个解释变量增长,亿元,粮食总产值会如何变化,从而进行财政收入预测。
相关数据: 表1国民总收居民消费价人口自然增人均GDP年份入(亿元)格指数增长长率(%。
)Y (元)X3 X1 率(CPI)%X21988 15.73 15037 18.8 13661989 15.04 17001 18 15191990 14.39 18718 3.1 16441991 12.98 21826 3.4 18931992 11.6 26937 6.4 23111993 11.45 35260 14.7 29981994 11.21 48108 24.1 40441995 10.55 59811 17.1 50461996 10.42 70142 8.3 58461997 10.06 78061 2.8 64201998 9.14 83024 -0.8 67961999 8.18 88479 -1.4 71592000 7.58 98000 0.4 78582001 6.95 108068 0.7 86222002 6.45 119096 -0.8 93982003 6.01 135174 1.2 105422004 5.87 159587 3.9 123362005 5.89 184089 1.8 140402006 5.38 213132 1.5 160242007 5.24 235367 1.7 175352008 5.45 277654 1.9 19264二、参数估计利用上表中的数据,运用eview软件,采用最小二乘法,对表中的数据进行线性回归,对所建模型进行估计,估计结果见下图。
从估计结果可得模型:ˆY,15.77177,0.000392X,0.050364X,0.005881X 123Y关于X的散点图: 1 可以看出Y和X成线性相关关系 1Y关于X的散点图: 2可以看出Y和X成线性相关关系 2Y关于X的散点图: 3可以看出Y和X成线性相关关系 3回归结果三、模型检验:1、经济意义检验模型估计结果说明,在假定其它变量不变的情况下,当年国民总收入每增长1亿元,人口增长率增长0.000392%;在假定其它变量不变的情况下,当年居民消费价格指数增长率每增长 1%,人口增长率增长0.050364%;在假定其它变量不变的情况下,当年人均GDP没增加一元,人口增长率就会降低0.005881%。
这与理论分析和经验判断相一致。
2、统计检验(1)、拟合优度检验,22,,,TSSYYnY,, 由于, ESSXYnY,,,ESSn,1222 所以 =0.941625, =0.930680, R,RR,,,1(1)TSSnk,,1可见模型在整体上拟合得非常好。
(2)、F 检验由于 RSSTSSESS,,ESSk/F, 所以 =86.02977 , RSSnk/(1),,,,0.05针对,给定显著性水平,在F分布表中查出自H:,,,,,,00123由度为k-1=3和n-k-1=16的临界值。
由表3.4中得到F(3,16),3.24,F=86.02977 ,由于F=86.02977 >应拒绝原假设F(3,16),3.24,,说明回归方程显著,即“国民总收入”、“居民消费价格指H:,,,,,,00123 数增长率”、“人均GDP”等变量联合起来确实对“人口自然增长率”有显著影响。
(3)、t 检验2;eee:,i2,,,, 由于0.780038 n,k,1n,k,1:::S,S,S, 且0.830371,8.89415E-05 ,0.03196669,,,,012:S,0.00121009 , ,3当, HH:0,:0,,,,0010:,0:t,, 18.99364 ,0:S,0t,,0.05在时, (16)=2.120因为t=18.99364>2.120,所以在95%的置信, 2度下拒绝原假设,说明截距项对回归方程影响显著。
当 HH:0,:0,,,,0111 :,1: 4.407392 ,,t,1:S,10在时,t(16)=2.120因为t=4.407392>2.120所以在95%的置信度,,0.05,2下拒绝原假设,说明X1变量对Y影响显著。
当 HH:0,:0,,,,0212:,2:,,1.575515 t,2:S,2在时,t(16)=2.120因为t=1.575515<2.120,所以在95%的置信度,,0.05, 2下接受原假设,说明X2变量对Y影响不显著。
当 HH:0,:0,,,,0313:,3:t,, - 4.859971 ,3:S,3t在时,(16)=2.120因为t=- 4.859971<2.120,所以在95%的置信,,0.05, 2度下接受原假设,说明X3变量对Y影响不显著。
(4)、的置信区间 ,,,,,,,,,,,012345,,的置信区间为:,计算得: tStS,,,,,,,,,,0,,000,,2200(14.01138,17.53216); ,,0,,的置信区间为:,计算得: tStS,,,,,,,,,,1,,111,,2211(0.000203,0.000581); ,,1,,的置信区间为:tStS,计算得: ,,,,,,,,,,2,,222,,2222(-0.01741,0.118133); ,,2,,的置信区间为:tStS,计算得:; ,,,,,,,,,,3,,333,,2233,,(-0.00845,-0.00332) 3综上所述,模型通过各种检验,符合要求。
四、方差分析(新增解释变量对被解释变量边际贡献显著性的分析)2R引入不同解释变量的ESS,RSS,首先做Y对的回归,得到样本回归方程为 X1:Y,13.65401-0.0000457 X1(24.45422) (-9.131990)2=175.8443, 37.95517,=0.822473; RESSRSS,1112由t检验可知,对Y有显著影响。
=0.822473表明,对于各种人口自然增RX11长率Y来说,国民总收入(亿元)只解释了Y的总离差的82%,还有18%没有X1 解释。
引入第二个解释变量后,样本回归方程为: X2ˆY=-12.55023-0.0000399+0.092504 XX212=182.8952, 30.90454,=0.855451; RESSRSS,121212新引入的方差分析表 X2变差来源平方和自由度 F统计量1 对回归 =175.8443 XESS112 对和回归 XX=182.8952 ESS21121 F=50.30362 对和回归,XX-=7.050958 ESSESS2112120-3=17 新增的部分对X2和回归的残=974550.4 XRSSX2231差对于给定的显著性水平=0.05,查F分布表可得临界值,F(1,17)4.45,,0.05由于F=50.30362>4.45,所以新引入的解释变量是显著的,的引入可以显XX22 2R著的提高对Y的解释程度,即的边际贡献较大,因此从0.822473提高到X20.855451,RSS从=37.95517降低到30.90454 再引入第三个解释变量: X3ˆY=15.77177+0.000392+0.050364-0.005881 XXX3212R=201.3198, 12.48060,=0.941625; ESSRSS,123123123新引入的方差分析表 X3变差来源平方和自由度 F统计量2 对和回归 XX30.90454, RSS,21123 对,和回=201.3198 XXESSX123231归1 F=86.02977 对,和回-=470399 XXESSXESS1232311220-4=16 归,由新增的X3部分对,和12.48060 XRSS,X12321回归的残差 X3查F分布表可得临界值=4.49,F=86.02977>4.49,所以新引入的解释F(1,16)0.052R变量显著,即的边际贡献较大,因此从0.855451提高到0.941625,RSSXX33从30.90454下降到12.48060,因此应该引入。
X3只引入一个解释变量,或;引入两个解释变量和,和或XXXXXXXX23232111 2R和;以及引入三个变量的ESS,RSS和的结果如表 XXXX32312R引入不同解释变量时的ESS,RSS,引入解释变量回归平方和ESS 残差平方和RSS 判定系数2 X=175.8443 37.95517, ESSRSS,=0.822473 R11112 X=87.21383 RSS=126.5859 ESS=0.407923 R22222 X=180.1995 =33.60087 ESSRSSR=0.842840 33332, XX=182.8952 30.90454 ESSRSS,=0.855451 R211212122, =199.3845 14.41684 XESSRSS,XR=0.932569 131331132, =186.1663 =27.63290 XXESSRSSR=0.870753 232323232 XXX=201.3198 12.48060 ESSRSS,R=0.941625 231123123123由Eviews可得,只引入一个解释变量,,时的F统计量分别为XXX231=83.39325,=12.40147,=96.53269,由,和都大于临界值FFFFFF232311,所以如果单独用,或作解释变量都显著,如果引入F(1,18)4.41,XXX0.05234 两个解释变量,显然引入,的结果最好,如果引入三个解释变量XXXXX32311无论最后引入哪个解释变量结果都显著,因此最后确定引入三个解释变量,相应的回顾方程为 :ˆY =15.77177+0.000392+0.050364-0.005881 XXX32122R=0.941625 =0.930680 R模型预测设2009年国民总收入为295267亿元,居民消费价格指数增长率为2.1%,人均GDP为21427元,将值代入样本回归方程,得到1998年的各项税收总量预测值ˆ的点估计值: Y1998:15.77177+0.000392*295267+0.050364*0.021-0.005881*21427 Y,2009(亿元),实际人口自然增长率为5.51%。
