自动控制原理第13讲(奈氏稳定判据)
合集下载
(第13讲) 第五章 乃魁斯特(Nyquist)稳定性判据

在控制系统应用中,由
F (s) 1 G (s)H (s)
很容易确定
的P数。因此,如果, F (s )
的轨迹图中确定了R,则s平面上封闭曲线内的零点数
很容易确定。
开环传递函数与闭环传递函数的关系:
06-7-20
控制系统系统的稳定性分析
14
R(s)
C(s) G (s )
G (s)
B1 ( s ) A1 ( s )
06-7-20
控制系统系统的稳定性分析
3
奈奎斯特稳定判据(Nyquist Stability Criterion) 闭环传递函数
C (s) R (s) G (s)
R(s) G (s )
C(s)
H(s )
1 H ( s )G ( s )
图5-4-1 闭环系统 结构图
1 H ( s )G ( s ) 0
例如:考虑下列开环传递函数:
06-7-20 控制系统系统的稳定性分析 6
G (s)H (s)
6 ( s 1)( s 2 )
其特征方程为:
6
F (s) 1 G (s)H (s) 1
( s 1)( s 2 )
( s 1 . 5 j 2 . 4 )( s 1 . 5 j 2 . 4 ) ( s 1)( s 2 )
控制系统系统的稳定性分析 11
如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…),
即包围的零点数与极点数相同,则在 F ( s ) 平面上,
相应的封闭曲线不包围
F (s)
平面上的原点。
上述讨论是映射定理的图解说明,奈奎斯特稳 定判据正是建立在映射定理的基础上。
自动控制原理第13讲(奈氏稳定判据)

精选.
奈氏曲线图
10
Im
0 -1 0
(c)由于ν=2,从 0 点逆时针
=0 补画半径为无穷大的半园。
Re
P=0, N=-1
Z=2
该闭环不系统稳定。
0
Im
K Gc(S)S2(TS1)
Gd
(S)
10 S(TS1)
(d)ν=1,从 0 点逆时针
?
补画半径为无穷大的1/4园。
0
=0
Z P R P 2N
GH( j )
K*
K 180
(s p1 )(s p2 )(s p3 ) 0 270
R: s 绕奈氏路径一周时,F(j)包围[F]平面(0, j0)点的圈数
N: 开环幅相曲线精G选.H(j)包围[G]平面(-1, j0)点的圈数
5
N的确定方法
开环幅相曲线包围(-1,j0)点的圈数,仅仅与幅相曲线
C
B
-1 A
0
Re
c
10 20 40
c
lg
100 200 400 01000
rad s
ZP2N
NN N
-90
-180
c
b
-270
精选.
a
lg rad
s
12
P205 5.12 Ti 0,K0, 判断闭环系统是否
题 开环 号 极点
穿越负实轴次数
奈氏判据 闭环极点
闭环 系统
(1) P=0 (2) P=0 (3) P=0 (4) P=0 (5) P=0 (6) P=0 (7) P=0 (8) P=1 (9) P=1 (10) P=1
精选.
8
(2)开环传递函数含ν 个积分环节 ν型系统
奈氏曲线图
10
Im
0 -1 0
(c)由于ν=2,从 0 点逆时针
=0 补画半径为无穷大的半园。
Re
P=0, N=-1
Z=2
该闭环不系统稳定。
0
Im
K Gc(S)S2(TS1)
Gd
(S)
10 S(TS1)
(d)ν=1,从 0 点逆时针
?
补画半径为无穷大的1/4园。
0
=0
Z P R P 2N
GH( j )
K*
K 180
(s p1 )(s p2 )(s p3 ) 0 270
R: s 绕奈氏路径一周时,F(j)包围[F]平面(0, j0)点的圈数
N: 开环幅相曲线精G选.H(j)包围[G]平面(-1, j0)点的圈数
5
N的确定方法
开环幅相曲线包围(-1,j0)点的圈数,仅仅与幅相曲线
C
B
-1 A
0
Re
c
10 20 40
c
lg
100 200 400 01000
rad s
ZP2N
NN N
-90
-180
c
b
-270
精选.
a
lg rad
s
12
P205 5.12 Ti 0,K0, 判断闭环系统是否
题 开环 号 极点
穿越负实轴次数
奈氏判据 闭环极点
闭环 系统
(1) P=0 (2) P=0 (3) P=0 (4) P=0 (5) P=0 (6) P=0 (7) P=0 (8) P=1 (9) P=1 (10) P=1
精选.
8
(2)开环传递函数含ν 个积分环节 ν型系统
bode判据

开环稳定性和闭环稳定性是两个概念,二者 不容混淆。
22
5.3 奈氏稳定性判据
例4、 ( s ) K (T2 s 1) G 2
s (T1s 1)
j
j
ω
(-1,j0)
ω=∞
ω ω=0
(-1,j0)
ω=∞
T1<T2
T1=T2
闭环系统稳定
闭环系统临界稳定
23
5.3 奈氏稳定性判据
j
ω ω =0
Ts 1 K 0
20
T 0 1 K 0 K 1
5.3 奈氏稳定性判据
例3、已知 P=2
(-1,j0)
j
奈氏曲线逆时针包围
(1, j 0) 点一圈,N=1
闭环稳定的充要条件
P 2 N 1 2 2
故闭环稳定
21
5.3 奈氏稳定性判据
可见: 系统开环稳定,但各个部件及其受控对象的参数匹配不当, 很可能闭环系统不稳定 。 开环不稳定,只要合理地选择控制装置,完全能调出稳定 的闭环系统。
另外,实际系统的参数在工作过程中会发生 波动,故系统必须有一定的稳定裕度。
5.5 控制系统的相对稳定性
j
c(t)
(-1,j0)
t
j
c(t)
(-1,j0)
t
结论:离 (1, j 0) 点远一些好。
5.5 控制系统的相对稳定性
j
在幅相平面上画一个以原点为圆心, 1为半径的圆。
5.3 奈氏稳定性判据
[ F ( j )] 平面的坐标原点相当于[G( j ) H ( j )] 平面的(1, j 0 ) 点,则 F ( j ) 1 G( j ) H ( j ) 向量对其原点的转角相当于
奈氏稳定判据课件

0
F
F (s)平面
8
1 、 奈氏判据数学基础…
j
z1
s
p1
0
z2
p2
s平面
s F(s) 映射
j F(s)
F(s)
0
F
F (s)平面
幅角原理: R=P-Z Z — s平面闭合曲线Γ包围F(s)的零点个数 P — s平面闭合曲线Γ包围F(s)的极点个数 R — 当s沿Γ顺时针运动一周,F(s)平面上闭合曲线гF 逆时针包围原点的圈数。
G( j0 )H( j0 )
14
1 、 奈氏判据数学基础…
3)G(S)H(S)含等幅振荡环节:
G(s)H (s)
(s2
1
2 n
)1
G1 ( s)
G(s)H (s) s jn e j
1
(2 jne j 2e2 j )1
G1( jn
e j )
j
jn
e j
e j( 90o )v1
(2n )v1
G1(
z1 )( s p1 )( s
z2 ) p2 )
F (s) s z1 s z2 s p1 s p2
F (s) s z1 s z2 s p1 s p2
2 0 (2 ) (2 ) 2
j
j
F(s)
z1
s
p1
0
z2
p2
s平面
s F(s) 映射
F(s)
重点回顾
幅相曲线绘制三要素
(1)开环幅相曲线的起点( 0)和终点( )
(2)开环幅相曲线与实轴的交点
交点处的频率 x -------穿越频率
x : Im[G( jx )H ( jx )] 0 或 (x ) G( jx )H ( jx ) k , k 0,1,2 交点处坐标 Re[G( jx )H ( jx )]
F
F (s)平面
8
1 、 奈氏判据数学基础…
j
z1
s
p1
0
z2
p2
s平面
s F(s) 映射
j F(s)
F(s)
0
F
F (s)平面
幅角原理: R=P-Z Z — s平面闭合曲线Γ包围F(s)的零点个数 P — s平面闭合曲线Γ包围F(s)的极点个数 R — 当s沿Γ顺时针运动一周,F(s)平面上闭合曲线гF 逆时针包围原点的圈数。
G( j0 )H( j0 )
14
1 、 奈氏判据数学基础…
3)G(S)H(S)含等幅振荡环节:
G(s)H (s)
(s2
1
2 n
)1
G1 ( s)
G(s)H (s) s jn e j
1
(2 jne j 2e2 j )1
G1( jn
e j )
j
jn
e j
e j( 90o )v1
(2n )v1
G1(
z1 )( s p1 )( s
z2 ) p2 )
F (s) s z1 s z2 s p1 s p2
F (s) s z1 s z2 s p1 s p2
2 0 (2 ) (2 ) 2
j
j
F(s)
z1
s
p1
0
z2
p2
s平面
s F(s) 映射
F(s)
重点回顾
幅相曲线绘制三要素
(1)开环幅相曲线的起点( 0)和终点( )
(2)开环幅相曲线与实轴的交点
交点处的频率 x -------穿越频率
x : Im[G( jx )H ( jx )] 0 或 (x ) G( jx )H ( jx ) k , k 0,1,2 交点处坐标 Re[G( jx )H ( jx )]
《工程控制基础》频域:奈氏 判据

24
例:已知某系统G(jω)H(jω)轨迹,有2个开环极点分
布在s的右半平面,试判别系统的稳定性。
解:系统有2个开环极点分布在s的右半平面(P=2),
G(jω)H(jω)轨迹在点(-1, j0)以左的负实轴有1次正穿越,
2次负穿越,
N 2(N N ) 1 2 2
求得:Z=P+N=2-2=0 所以系统是稳定系统。
K=1时,奈氏曲线穿过 (-1, j0) 点两次,系统临界稳定。
(a)P=0 0
Im P0
0
R
Re (b)P=1
0
P 1 Im
R
K
0
Re
26
例5-12
(b)若b>1, N= 2(N+ - N–)=2(2-1)=2,且 P=1,所以 Z=P+N=3 系统不稳定。
若b<1<a, N= 2(N+ - N–)=2(1-1)=0,且 P=1,所以 Z=P+N=1 系统不稳定。
(1, j0)
_
0
0
Re
G( j )H ( j )
G( j )H ( j )
23
如果G(jω)H(jω)按顺时针方向绕(-1, j0) 一周,则必正穿越一次。反之,若按逆时针方 向包围点 (-1, j0) 一周,则必负穿越一次。 这种正负穿越之和即为G(jω)H(jω)包围的圈 数。
N=2(N+-N-) 注意:这里对应的ω变化范围 0 。
3
5.3.2 幅角原理
1.映射
复数s
s平面
s=σ+jω.
F(s)
F(s) 复平面
F(s)= u+jv.
在s平面上除了F(s)零点和极点外的任意点si ,经过复变函 数F(s)的映射,均可在F(s)平面上可以找到对应的点
例:已知某系统G(jω)H(jω)轨迹,有2个开环极点分
布在s的右半平面,试判别系统的稳定性。
解:系统有2个开环极点分布在s的右半平面(P=2),
G(jω)H(jω)轨迹在点(-1, j0)以左的负实轴有1次正穿越,
2次负穿越,
N 2(N N ) 1 2 2
求得:Z=P+N=2-2=0 所以系统是稳定系统。
K=1时,奈氏曲线穿过 (-1, j0) 点两次,系统临界稳定。
(a)P=0 0
Im P0
0
R
Re (b)P=1
0
P 1 Im
R
K
0
Re
26
例5-12
(b)若b>1, N= 2(N+ - N–)=2(2-1)=2,且 P=1,所以 Z=P+N=3 系统不稳定。
若b<1<a, N= 2(N+ - N–)=2(1-1)=0,且 P=1,所以 Z=P+N=1 系统不稳定。
(1, j0)
_
0
0
Re
G( j )H ( j )
G( j )H ( j )
23
如果G(jω)H(jω)按顺时针方向绕(-1, j0) 一周,则必正穿越一次。反之,若按逆时针方 向包围点 (-1, j0) 一周,则必负穿越一次。 这种正负穿越之和即为G(jω)H(jω)包围的圈 数。
N=2(N+-N-) 注意:这里对应的ω变化范围 0 。
3
5.3.2 幅角原理
1.映射
复数s
s平面
s=σ+jω.
F(s)
F(s) 复平面
F(s)= u+jv.
在s平面上除了F(s)零点和极点外的任意点si ,经过复变函 数F(s)的映射,均可在F(s)平面上可以找到对应的点
自动控制原理-5.4奈氏判据
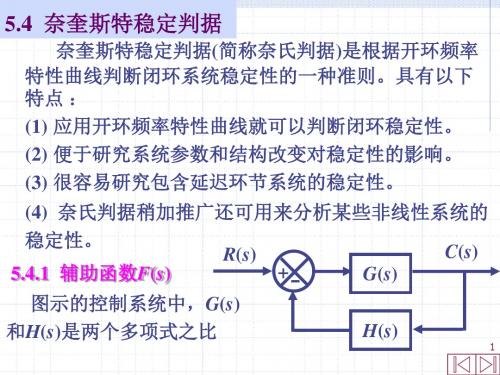
稳定性。
5.4.1 辅助函数F(s)
R(s)
+﹣
图示的控制系统中,G(s)
C(s) G(s)
和H(s)是两个多项式之比
H(s)
1
G(s) M1(s)
N 开环传递函数为:
1
(
s)
H(s) M2(s) N2(s)
Gk (s) G(s)H(s) 闭环传递函数为:
M1(s)M2(s) N1(s)N2(s)
(1)0型系统(开环没有串联积分 0 环节的系统)
s为包s围平虚面轴s 和整个右映半射平面。F(s)
正虚轴 j (:0)
F(j) ( : 0)
s
负虚轴 j (: 0)
F(j) ( : 0)
半径的半圆
( 1, j0)点
5
F(j)和G(j)H(j)只相差常数1。 F(j)包围原点就 是G(j)H(j)包围(-1,j0)点。
R=2 z = p R = 2
kT1T2
T1 T2
1
∴ 闭环系统是不稳定的 。
当 kT1T2 > 1 T1 T2
R=0
z = p R= 0
=0+
∴ 闭环系统是稳定的 。
Im
0
Re
增补线
16
(3) 由奈氏判据判稳的实际方法
用奈氏判据判断系统稳定性时,一般只须绘制从
j 1
F(s)曲线从B点开始,绕原点顺时针方向转了一圈。 4
幅角原理:如果封闭曲线内有Z个F(s)的零点, P个F(s)
的极点 ,则s 沿封闭曲线s 顺时针方向转一圈时,在F(s)
平面上,曲线F(s)绕其原点逆时针转过的圈数R为P和Z之
自动控制原理Nyquist稳定判据

(N = m - n , 若N≥ 1,n不会为负值,则必有m ≥1)
3.4,Nyquist稳定判据
例3.15已知开环传递函数 判断系统稳定性
G0 (
j
)
( T1
j
k 1 )( T2
j
1)
Nyquist图画法(示意图)
Im
G0( j ) G0( j )G0( j )
0 180 0
j
(1)特殊点
面上的Nyuist图顺时针包围原点N次。 n>m时
多数情况,当s从0 ± j∞ 时, G0(s) 0, F(s) = 1+G0(s) 0
3.4,Nyquist稳定判据
N=m― n
DC(s)=0的根 闭环极点
D0(s)的根 开环极点
(3)开环频率特性G0(jω )和Nyuist图
开环传递函数G0(s),令s = jω ,即开环频率特性G0(jω )
3.4,Nyquist稳定判据
利用柯西复角原理判稳定的思路:
(1)使F(s)与系统传递函数相联系 (2)封闭曲线域为右半平面(或左半平面) (3)使封闭曲线为虚轴,与频率特性相联系
3.4,Nyquist稳定判据
2,D形围线和Nyquist图:
+
G(s)
-
H(s)
开环传递函数
G0( s ) G( s )H ( s )
例3.17 G0 (
j )( T1j来自1)( T2k( T01 j 1 )( T01 j 1 ) j 1)( T3 j 1)( T4 j 1)( T5
j 1)
T1 ,T2 ,T3 T01 ,T02 T4 ,T5
Im
-1
k Re
0
Nyquist判据: N=0,n=0,所以m=0 系统稳定
3.4,Nyquist稳定判据
例3.15已知开环传递函数 判断系统稳定性
G0 (
j
)
( T1
j
k 1 )( T2
j
1)
Nyquist图画法(示意图)
Im
G0( j ) G0( j )G0( j )
0 180 0
j
(1)特殊点
面上的Nyuist图顺时针包围原点N次。 n>m时
多数情况,当s从0 ± j∞ 时, G0(s) 0, F(s) = 1+G0(s) 0
3.4,Nyquist稳定判据
N=m― n
DC(s)=0的根 闭环极点
D0(s)的根 开环极点
(3)开环频率特性G0(jω )和Nyuist图
开环传递函数G0(s),令s = jω ,即开环频率特性G0(jω )
3.4,Nyquist稳定判据
利用柯西复角原理判稳定的思路:
(1)使F(s)与系统传递函数相联系 (2)封闭曲线域为右半平面(或左半平面) (3)使封闭曲线为虚轴,与频率特性相联系
3.4,Nyquist稳定判据
2,D形围线和Nyquist图:
+
G(s)
-
H(s)
开环传递函数
G0( s ) G( s )H ( s )
例3.17 G0 (
j )( T1j来自1)( T2k( T01 j 1 )( T01 j 1 ) j 1)( T3 j 1)( T4 j 1)( T5
j 1)
T1 ,T2 ,T3 T01 ,T02 T4 ,T5
Im
-1
k Re
0
Nyquist判据: N=0,n=0,所以m=0 系统稳定
奈氏判据

P 2
S2
Z2
P 1
0
0
F (S1 )ຫໍສະໝຸດ ReS3Ls
(a )
(b)
LF
图4-36
S 和 F(s) 的映射关系
8
设 F (s) 在S平面上,除有限个奇点外,为单值的连续函 数,若在S平面上任选一封闭曲线 Ls ,并使 Ls不通过 F (s) 的奇点,则S平面上的封闭曲线 Ls映射到F(s)平面 上也是一条封闭曲线 LF 。当解析点s按顺时针方向沿 Ls 变化一周时,则在 F (s) 平面上,LF 曲线按逆时针方 向旋转的周数N(每旋转2弧度为一周),或 LF 按逆 时针方向包围 F(s)平面原点的次数,等于封闭曲线 Ls 内包含F(s)的极点数P与零点数Z之差。即
Im
GH
0 0
Im
1 0
GH
0
Im
GH
0 0
1
0
Re
Re 0
1
0
Re
T
(b)
T
(c )
T
稳定
图4-42 系统的奈氏曲线
1
0
(1)
F ( j)
LGH
G( j ) H ( j )
Ls
LF
(a)s平面的Nyquist轨迹 (b)[F]平面的奈氏曲线 (c)[GH]平面的奈氏曲线
图4-37
12
奈氏轨迹 Ls在GH平面上的映射LGH称为奈奎斯特曲线或奈氏曲线.
三、奈奎斯特稳定判据 闭环系统稳定的充分必要条件是,GH 平面上的奈奎斯
第四节
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D(s) (s 1 )(s 2 )(s 3 )
N (s) (s p1 )(s p2 )(s p3 )
(s) G(s) 1GH(s)
F(s)的特点
① F(s)的
零点 i : 闭环极点 极点 pi : 开环极点
个数相同
② F ( j ) 1 GH( j )
§5.3.1
奈奎斯特稳定判据 (3)
非最小相位系统 NNN该闭环系统不稳定。 11
3 在对数坐标图上应用奈奎斯特稳定性判据
Im
L() 20lg GH dB
40
20
0 0.1
0.4
-20
-40
j ()0
0
1
2
4
G ( j )H ( j ) 1 G ( j )H ( j ) 1
C
B
-1 A
0
Re
c
10 20 40
c
lg
100 200 400 01000
7
Im
0
-1
(b)
K Gb(S)(T1S1)T(2S1)T(3S1)
0
K Re
P=0, NN N 01 1
Z=P-2N=2
闭环系统不稳定。
Im
0 0
K -1
Re
(c)
Gc(S)
K (TS1)
P=1, NN N 1 201 2
Z=P-2N=0
奈氏曲线图
闭环系统稳定。 8
(2)开环传递函数含ν 个积分环节 ν型系统
Z P R P 2N
GH( j )
K*
K 180
(s p1 )(s p2 )(s p3 ) 0 270
R: s 绕奈氏路径一周时,F(j)包围[F]平面(0, j0)点的圈数
N: 开环幅相曲线GH(j)包围[G]平面(-1, j0)点的圈数
N的确定方法
开环幅相曲线包围(-1,j0)点的圈数,仅仅与幅相曲线
自动控制原理
§5.3 频域稳定判据
§5.3
频域稳定判据
§5.3 频域稳定判据
系统稳定的充要条件 — 全部闭环极点均具有负的实部 代数稳定判据 — Ruoth判据
由闭环特征多项式系数(不解根)判定系统稳定性
不能用于研究如何调整系统结构参数来改善系统稳定性及 性能的问题
频域稳定判据 —
Nyquist 判据 对数稳定判据
0
奈氏曲线图
9
例2 给出含有两个积分环节的开环系统 幅相曲线,试判断系统的稳定性。
(b)由于ν=2,从 0 点逆时针
补画半径为无穷大的半园。
P=0, N=0 Z=0
-1
所以,闭环系统稳定。 0
Im
0
0
Re
Gb(S)K(TS2S1)
奈氏曲线图
10
Im
0 -1 0
(c)由于ν=2,从 0 点逆时针
设F(s)在右半s平面有
Z个零点 (闭环极点) Z=2 P个极点 (开环极点) P=1
F ( j )
(
2
s 1
)(
s
2
2
)(
s
0
3
)
( s2p1
)( s
0
p2
)( s
0
p3
)
s 绕奈氏路径转过一周,
F(j)绕[F]平面原点转过的角度jF()为
F ( j) 2 ( Z P ) 2 ( P Z ) 2 R
=0 补画半径为无穷大的半园。
Re
P=0, N=-1
Z=2
该闭环不系统稳定。
0
Im
Gc(S)
K S2(TS1)
Gd
(S)
10 S(TS1)
(d)ν=1,从 0 点逆时针
?
补画半径为无穷大的1/4园。
0
=0
Re
虚线的终端落在负实轴上
P=1, N=-1/2, Z=1-2(-1/2)=2
奈氏曲线图
由开环频率特性直接判定闭环系统的稳定性
可研究如何调整系统结构参数改善系统稳定性及性能问题
§5.3.1
奈奎斯特稳定判据 (1)
§5.3.1 奈奎斯特稳定判据
解释 设
说明 设
Z P 2N
K G(s)
( T1s 1) (T2s 1)(T3s 1)
K
K1 K2
Z P 2N 1 2 0 1 不稳定 Z P 2N 1 2 ( 1) 2 不稳定
区间的正负穿越如图所示
6
稳定性分析举例
(1)开环传递函数不含积分环节(0型系统) 直接采用Z=P-2N的稳定性判
例1 据给出三个开环传递函数不含有积分环节的
奈氏曲线,试判断系统的稳定性。
Ga(S)(T1S1)KT (2S1)
Im 0 0
P=0, N=0
-1
)P=0 奈氏曲线
rad s
ZP2N
NN N
-90
-180
c
b
-270
a
lg rad
s
12
P205 5.12 Ti 0,K0, 判断闭环系统是否
题 开环 号 极点
穿越负实轴次数
奈氏判据 闭环极点
闭环 系统
(1) P=0 NN N 01 1 Z=P-2N=2 不稳定
(2) P=0 N N N 000 Z=P-2N=0 稳定 (3) P=0 N N N 0 1 1Z=P-2N=2 不稳定 (4) P=0 N N N 000 Z=P-2N=0 稳定 (5) P=0 N N N 0 1 1Z=P-2N=2 不稳定 (6) P=0 N N N 1 10Z=P-2N=0 稳定 (7) P=0 N N N 1 10Z=P-2N=0 稳定 (8) P=1 N N N 1 2 01 2 Z=P-2N=0 稳定 (9) P=1 N N N 0 00Z=P-2N=1 不稳定 (10) P=1 N N N 0 1 2 1 2 Z=P-2N=2 不稳定 13
2
系统结构图如图所示
K*M(s) GH(s)
K*
N(s) (s p1 )(s p2 )(s p3 )
(s) G(s) 1GH(s)
§5.3.1
奈奎斯特稳定判据 (2)
构造辅助函数 F(s)
F(s)1G(H s)
K*M (s) N(s)K*M (s)
1
N(s)
N(s)
(s p1 )(s p2 )(s p3 ) K *M (s) (s p1 )(s p2 )(s p3 )
绘制开环幅相曲线后,应从频率0+对应的点 开始,逆时针补画ν/4个半径无穷大的圆。 -900ν
例2 给出含有1个积分环节的开环系统幅相曲线,
试判断系统的稳定性。
Im
(a)ν=1,从 0 点逆时针
补画半径为无穷大的1/4园。 -1
0
0 Re
P=0, N=0
Z=0
所以,闭环系统稳定。
K Ga(S) S(TS1)
穿越实轴区间(-,-1)的次数有关。 把自上向下(逆时针)穿越这个区间的次数表示为 N
把自下向上(顺时针)穿越这个区间的次数表示为 N
注意:若穿越时从这个区间的实轴上开始时Im
记为半次正(半次负)穿越。
右图中 N 2 N 2
NNN220
- +- + -1 0
Re
幅相曲线在负实轴(-.-1)
N (s) (s p1 )(s p2 )(s p3 )
(s) G(s) 1GH(s)
F(s)的特点
① F(s)的
零点 i : 闭环极点 极点 pi : 开环极点
个数相同
② F ( j ) 1 GH( j )
§5.3.1
奈奎斯特稳定判据 (3)
非最小相位系统 NNN该闭环系统不稳定。 11
3 在对数坐标图上应用奈奎斯特稳定性判据
Im
L() 20lg GH dB
40
20
0 0.1
0.4
-20
-40
j ()0
0
1
2
4
G ( j )H ( j ) 1 G ( j )H ( j ) 1
C
B
-1 A
0
Re
c
10 20 40
c
lg
100 200 400 01000
7
Im
0
-1
(b)
K Gb(S)(T1S1)T(2S1)T(3S1)
0
K Re
P=0, NN N 01 1
Z=P-2N=2
闭环系统不稳定。
Im
0 0
K -1
Re
(c)
Gc(S)
K (TS1)
P=1, NN N 1 201 2
Z=P-2N=0
奈氏曲线图
闭环系统稳定。 8
(2)开环传递函数含ν 个积分环节 ν型系统
Z P R P 2N
GH( j )
K*
K 180
(s p1 )(s p2 )(s p3 ) 0 270
R: s 绕奈氏路径一周时,F(j)包围[F]平面(0, j0)点的圈数
N: 开环幅相曲线GH(j)包围[G]平面(-1, j0)点的圈数
N的确定方法
开环幅相曲线包围(-1,j0)点的圈数,仅仅与幅相曲线
自动控制原理
§5.3 频域稳定判据
§5.3
频域稳定判据
§5.3 频域稳定判据
系统稳定的充要条件 — 全部闭环极点均具有负的实部 代数稳定判据 — Ruoth判据
由闭环特征多项式系数(不解根)判定系统稳定性
不能用于研究如何调整系统结构参数来改善系统稳定性及 性能的问题
频域稳定判据 —
Nyquist 判据 对数稳定判据
0
奈氏曲线图
9
例2 给出含有两个积分环节的开环系统 幅相曲线,试判断系统的稳定性。
(b)由于ν=2,从 0 点逆时针
补画半径为无穷大的半园。
P=0, N=0 Z=0
-1
所以,闭环系统稳定。 0
Im
0
0
Re
Gb(S)K(TS2S1)
奈氏曲线图
10
Im
0 -1 0
(c)由于ν=2,从 0 点逆时针
设F(s)在右半s平面有
Z个零点 (闭环极点) Z=2 P个极点 (开环极点) P=1
F ( j )
(
2
s 1
)(
s
2
2
)(
s
0
3
)
( s2p1
)( s
0
p2
)( s
0
p3
)
s 绕奈氏路径转过一周,
F(j)绕[F]平面原点转过的角度jF()为
F ( j) 2 ( Z P ) 2 ( P Z ) 2 R
=0 补画半径为无穷大的半园。
Re
P=0, N=-1
Z=2
该闭环不系统稳定。
0
Im
Gc(S)
K S2(TS1)
Gd
(S)
10 S(TS1)
(d)ν=1,从 0 点逆时针
?
补画半径为无穷大的1/4园。
0
=0
Re
虚线的终端落在负实轴上
P=1, N=-1/2, Z=1-2(-1/2)=2
奈氏曲线图
由开环频率特性直接判定闭环系统的稳定性
可研究如何调整系统结构参数改善系统稳定性及性能问题
§5.3.1
奈奎斯特稳定判据 (1)
§5.3.1 奈奎斯特稳定判据
解释 设
说明 设
Z P 2N
K G(s)
( T1s 1) (T2s 1)(T3s 1)
K
K1 K2
Z P 2N 1 2 0 1 不稳定 Z P 2N 1 2 ( 1) 2 不稳定
区间的正负穿越如图所示
6
稳定性分析举例
(1)开环传递函数不含积分环节(0型系统) 直接采用Z=P-2N的稳定性判
例1 据给出三个开环传递函数不含有积分环节的
奈氏曲线,试判断系统的稳定性。
Ga(S)(T1S1)KT (2S1)
Im 0 0
P=0, N=0
-1
)P=0 奈氏曲线
rad s
ZP2N
NN N
-90
-180
c
b
-270
a
lg rad
s
12
P205 5.12 Ti 0,K0, 判断闭环系统是否
题 开环 号 极点
穿越负实轴次数
奈氏判据 闭环极点
闭环 系统
(1) P=0 NN N 01 1 Z=P-2N=2 不稳定
(2) P=0 N N N 000 Z=P-2N=0 稳定 (3) P=0 N N N 0 1 1Z=P-2N=2 不稳定 (4) P=0 N N N 000 Z=P-2N=0 稳定 (5) P=0 N N N 0 1 1Z=P-2N=2 不稳定 (6) P=0 N N N 1 10Z=P-2N=0 稳定 (7) P=0 N N N 1 10Z=P-2N=0 稳定 (8) P=1 N N N 1 2 01 2 Z=P-2N=0 稳定 (9) P=1 N N N 0 00Z=P-2N=1 不稳定 (10) P=1 N N N 0 1 2 1 2 Z=P-2N=2 不稳定 13
2
系统结构图如图所示
K*M(s) GH(s)
K*
N(s) (s p1 )(s p2 )(s p3 )
(s) G(s) 1GH(s)
§5.3.1
奈奎斯特稳定判据 (2)
构造辅助函数 F(s)
F(s)1G(H s)
K*M (s) N(s)K*M (s)
1
N(s)
N(s)
(s p1 )(s p2 )(s p3 ) K *M (s) (s p1 )(s p2 )(s p3 )
绘制开环幅相曲线后,应从频率0+对应的点 开始,逆时针补画ν/4个半径无穷大的圆。 -900ν
例2 给出含有1个积分环节的开环系统幅相曲线,
试判断系统的稳定性。
Im
(a)ν=1,从 0 点逆时针
补画半径为无穷大的1/4园。 -1
0
0 Re
P=0, N=0
Z=0
所以,闭环系统稳定。
K Ga(S) S(TS1)
穿越实轴区间(-,-1)的次数有关。 把自上向下(逆时针)穿越这个区间的次数表示为 N
把自下向上(顺时针)穿越这个区间的次数表示为 N
注意:若穿越时从这个区间的实轴上开始时Im
记为半次正(半次负)穿越。
右图中 N 2 N 2
NNN220
- +- + -1 0
Re
幅相曲线在负实轴(-.-1)
