初二数学课件平方根立方根3
合集下载
北师大版八年级数学上册 2.3 立方根 课件 (共15张PPT)
19
2
3 1 - = _____3_____;
27
( 2 ) ( x - 1)3 = 27 , 求 x ; x 求 x ;
x=-5 4
( 4 ) 若 a + 8 + (b - 27)2 = 0 , 求 3 a - 3 b 的值. -5
课堂小结
1.什么叫一个数的立方根？怎样用符号表示数a的立方根？
立方根的个数的性质可以概括为立方根的唯一性， 即一个数的立方根是唯一的.
注意： ①求立方根用到立方运算； ②负数的立方根注意符号.
探究新知
( 1 ) 3 5 表示 5的立方根，由立方根定义我们知道，x3 = a , x 是 a 的立方根， 那么（ 3 5 ）3 = 5 .
再如（： 3 -2 ）3 = ___-_2____. 类推得到（ 3 a )3 = ___a_____. ( 2 ) 因为a 是 a3的立方根 ，所以 3 a3 = ____a_____.
如：1 000的立方根是10，0的立方根是0．
探究新知
做一做 （1）2的立方等于多少？是否有其他的数，它的立 方也是8？ （2）-3的立方等于多少？是否有其他的数，它的 立方也是-27？ 议一议 （1）正数有几个立方根？是正是负？为什么？ （2）是否任何负数都有立方根？若有，有几个？ 是正是负？ （3）0的立方根是什么？
即（： 3 a )3 = a ,
3 a3 = a .
探究新知
例２ 求下列各式的值:
( 1 ) 3 27; ( 2 ) 3 -64;
27
(3) 3-
.
1 000
解：（1）3 27 = 3
（2） 3 -64 = -4
（3）3 - 27 = - 3 1 000 10
八年级上数学实数平方根与立方根
6.1平方根立方根一、知识要点：1、平方根的意义：如果一个数的平方等于a，这个数就叫做a的平方根（或二次方根）。
注意：这样的数常常有两个。
2、平方根的性质：(1)一个正数有两个平方根,它们互为相反数;如9的平方根是±3。
(2)0的平方根是0本身；(3)负数没有平方根。
3.平方根的表示方法:正数a的平方根表示为“± ”4.算术平方根:正数a的正的平方根也叫做a的算术平方根。
记作。
0的平方根0,也叫做0的算术平方根。
5. ≥0（当 a<0时, 无意义）。
到此为止,我们已学完三个非负数:|a|、a2和(a≥0)。
6.立方根和开立方同平方根开平方的概念类似。
二.易犯错误：1.算术平方根与平方根混淆，例如出现100的平方根等于10的错误．2. 表示的正数a的平方根。
蕴含条件a≥0。
三.例题分析:例1.求下列各数的平方根,算术平方根:(1)121 (2)0.0049 (3) (4)4 (5)|a|2解:(1)∵(±11)2=121∴121的平方根是±11,算术平方根是11；即± =±11, =11。
(2)∵(±0.07)2=0.0049 ∴0.0049的平方根是±0.07,算术平方根是0.07,即,±=±0.07, =0.07。
(3)∵(± )2= ∴ 的平方根是± ,算术平方根是, 即±=± , = 。
(4)要先把带分数化成假分数,即4∵(± )2= ∴4 的平方根为± ，算术平方根为。
即,± 。
(5) ∵(±|a|)2=|a|2,而±|a|=±a。
∴|a|2的平方根是±a,算术平方根为|a|。
说明:通过例1,我们看到必须熟记1-20的平方数,和1-10的立方数,才能很好地做这部分习题。
例2.求下列各式的值:(1)3 =3× = (2)± =± (3)=8(4)± =± (5)- (带分数要先化成假分数)(6)3× =3×7=21(7)(8) ×0.6+ ×0.9=0.3+0.3=0.6(9) (a<b)= ∵a<b，∴原式=-(a-b)=b-a。
冀教版初二数学上册《14.5 用计算器求平方根与立方根》课件
（来自《点拨》）
冀教版八年级数学上册
知1－练
解：设正方形的边长为x m，由题意，得x2＝81. 因为x＞0，所以x＝9. 所以正方形周长＝4×9＝36(m)． 设圆的半径为r m，由题意，知πr2＝81， 81 81 2 则r ＝ .因为r＞0，所以r＝ . π π
81 所以圆周长＝2π· ≈31.90(m)． π
(2)按键顺序：2ndF
3
1 2 0
（来自《教材》）
显示结果：4.932 424 149，所以 3 120 ≈4.932.
冀教版八年级数学上册
知1－讲
解：(3)按键顺序： 2ndF
3
5 ab c 8
显示结果：－0.854 987 973，
5 所以 ≈－0.855. 8
3
(4)按键顺序：
（来自《教材》）
冀教版八年级数学上册
知1－讲
总 结
在实际问题中，要根据实际情况取近似值.
冀教版八年级数学上册
知1－练
1 学校要建一个面积是81 m2的草坪，草坪周围用
铁栅栏围绕，有两种方案．有人建议建成正方 形的，也有人说要建成圆形的，如果从节省铁 栅栏费用的角度考虑，你选择哪种？请说明理 由．(π≈3.14)
（来自《教材》）
冀教版八年级数学上册
知1－讲
3m 4 3 3 . 解：由公式m＝ πr ρ，得r＝ 3 4πρ
因为m＝400 kg，ρ＝2 600 kg/m3，π＝3.14， 所以r＝
3
3m 3 400 3 4πρ 4 3.14 2 600
≈0.332 460 015≈0.33(m). 答：这个大理石球的半径约为0.33m.
（来自《点拨》）
优秀课件八年级数学上册《4.2立方根》课件 (共15张PPT)
请举例说明
a的平方根怎样表示? a
类似的请同学们想一想a的立方根怎样表示？
立方根的表示方法：
数a的立方根用 a表示
3
2.开立方. 求一个数的立方根的运算，叫做开立方.开立方 与立方也是互为逆运算，因此求一个数的立方根可 以通过立方运算来求.
你会区别下列的数吗？
a ， a ， a a 表示a的算术平方根 a 表示a的平方根或a的二次方根 3 a 表示a的立方根或a的三次方根
a
3
a
a
3
(
3
a) a
课堂练习1： 下列说法对不对？
2、 1的立方根是±1。
1 1 3、 的立方根是 6 36
（ ×）
（ ×） （ （
4、 64的立方根是+4 5、64的算术平方根是8
×
1、 -4没有立方根。
（
）
√）
√）
例2、求下列各式的值：
（1 ） 3
125
（2）
10 2 27
3
(3)
3
- 64 16
解： （1）3 125 5
（2） 3
10 64 4 3 2 27 27 3
(3) 3 - 64 16 4 4 0
课堂练习2：
2.你能求出下列各式中的未知数x吗？ （1） x3＝-64 （2）（x－1）3＝125 （ 3） 3
解:
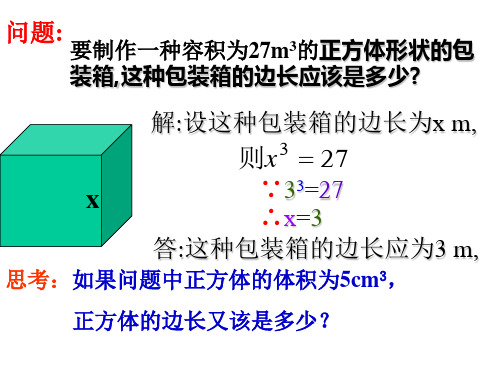
问题:
要制作一种容积为27m3的正方体形状的包 装箱,这种包装箱的边长应该是多少?
x
解:设这种包装箱的边长为x m, 3 则x 27 ∵33=27 ∴x=3 答:这种包装箱的边长应为3 m,
思考：如果问题中正方体的体积为5cm3， 正方体的边长又该是多少？
3.2 立方根(课件)湘教版数学八年级上册
负数 a 的算术平方根而非 a的立方根 .
◆任何数都可以开立方，即在
任意数 .
a 中， a可以是
知1－讲
2. 开立方： 求一个数的立方根的运算，叫作开立方 .
特别解读：立方 根与开立方的关系：立方 根是一个数，是
开立方的结果；而开立方是求一个数的立方根的运算 .
知1－练
例1 [母题 教材 P113 例 1 ]求下列各数的立方根：
∴4a－6b＋3＝－4＋3＝－1.
感悟新知
知识点 3 用计算器求一个数的立方根
知3－讲
用计算器可Байду номын сангаас求一个数的立方 根或它的近似值，按键顺序为
先按
2ndF
键，再按数字键，最后按 = 键，根据显
示结果写出立方根或它的近似值 .
知3－讲
特别说明
不同型号的计算器按键可能不同，使用计算器
时，一定要按说明书操作 .
x=6，
联立方程组，得ቊ
解得ቊ
y=10.
x － y+4 =0，
∴ x+y=16. ∴ x+y 的算术平方根是 4.
知2－练
感悟新知
知2－练
4-1.已知 3 2a+1和3 1－3b互为相反数，求4a － 6b ＋ 3 的值．
解：依题意得2a＋1＋1－3b＝0，
∴2a－3b＝－2.
∴4a－6b＝－4.
(2)
(－15) 3 =－
1－0.973 ；
1－0.973 =
15 3 = － 15.
0.027 =
0.33 =0.3.
知2－练
1
(3) － －8 ÷ 2 + (－1) 100.
最新八年级上册数学精品课件第11章 数的开方
第11章 数的开方
11.1 平方根与立方根
知识点 平方根
平方根节是数学爱好者的节日,这一天的月份和日期的数字正 好是当年年份最后两位数字的算术平方根,例如2009年的3月3 日,2016年的4月4日.
知识点 平方根
√ + a 是求非负数a的平方根,因为没有一个数的平方等于负数,所以负
数没有平方根.
知识点 实数的性质
存在两个和为零的无理数,所以互为相反数的两个实数可都为 无理数.
知识点 实数的大小比较
边长为a的正方形的面积是5,下图三个小伙伴的两次站队的位 置完美诠释了边长a的整数部分的确定方法. 第一次:
第二次:
知识点 实数的运算
某丝巾的形状是等腰钝角三角形.
知识点 实数的运算
某厂在下图所示的方格纸中设计出面积最大的丝巾,求出三边 的长的过程就是实数运算的过程.
知识点 利用计算器求一个数的立方根
利用科学计算器可以求出一个数的立方根.
第11章 数的开方
11.2 实 数
知识点 无理数的概念
公元前500年,希伯索斯发现了一个惊人的事实,一个正方形的 对角线与其一边的长度是不可公度的(若正方形的边长为1,则对 角线的长不是一个有理数),这一不可公度性与毕氏学派的“万 物皆为数”(指有理数)的哲理大相径庭.人们为了纪念希伯索斯 这位为真理而献身的可敬学者,就把不可通约的量取名“无理 数”——这就是无理数的由来.
知识点 开平方
开平方时,被开方数a必须是非负数.
知识点 利用计算器求一个正数的算术平方根(了解)
知识点 立方根
两个正方体的对话完美诠释了立方根的概念及其求法.
知识点 立方根
知识点 开立方
4阶魔方,又称“魔方的复仇”,由四层完全相同的64个小正方 体组成,求体积为64的4阶魔方的边长的过程就是开立方运算.
11.1 平方根与立方根
知识点 平方根
平方根节是数学爱好者的节日,这一天的月份和日期的数字正 好是当年年份最后两位数字的算术平方根,例如2009年的3月3 日,2016年的4月4日.
知识点 平方根
√ + a 是求非负数a的平方根,因为没有一个数的平方等于负数,所以负
数没有平方根.
知识点 实数的性质
存在两个和为零的无理数,所以互为相反数的两个实数可都为 无理数.
知识点 实数的大小比较
边长为a的正方形的面积是5,下图三个小伙伴的两次站队的位 置完美诠释了边长a的整数部分的确定方法. 第一次:
第二次:
知识点 实数的运算
某丝巾的形状是等腰钝角三角形.
知识点 实数的运算
某厂在下图所示的方格纸中设计出面积最大的丝巾,求出三边 的长的过程就是实数运算的过程.
知识点 利用计算器求一个数的立方根
利用科学计算器可以求出一个数的立方根.
第11章 数的开方
11.2 实 数
知识点 无理数的概念
公元前500年,希伯索斯发现了一个惊人的事实,一个正方形的 对角线与其一边的长度是不可公度的(若正方形的边长为1,则对 角线的长不是一个有理数),这一不可公度性与毕氏学派的“万 物皆为数”(指有理数)的哲理大相径庭.人们为了纪念希伯索斯 这位为真理而献身的可敬学者,就把不可通约的量取名“无理 数”——这就是无理数的由来.
知识点 开平方
开平方时,被开方数a必须是非负数.
知识点 利用计算器求一个正数的算术平方根(了解)
知识点 立方根
两个正方体的对话完美诠释了立方根的概念及其求法.
知识点 立方根
知识点 开立方
4阶魔方,又称“魔方的复仇”,由四层完全相同的64个小正方 体组成,求体积为64的4阶魔方的边长的过程就是开立方运算.
立方根课件
开立方——求一个数的立方根的运算． 3的立方是___, 27的立方根是___.
3
27 3
3
( 27) 27
3 3
3
注意：(1) 开立方与立方互为逆运算．
(2)
( a) a
例题 求下列各数的立方根
（1）64
8 （2） 125
（3）9
小结一:
(1)立方运算与开立方运算互为逆运算,故熟记一些 常用的立方数对开立方运算是十分有益的; (2)
3
a中
当a为某个有理数的立方时,a的开立方结果不带三 次根号; 当a不是某个有理数的立方时, a的开立方结果带三 次根号; (3)学习了立方根的表示方法后,解题中用符号表示 比用语言叙述简便得多.
例二: 求下列各式的值
“平方根”与“立方根”的比 较
知识延伸：
１． ２．
3
+2,-2 的平方根是＿＿＿. 64
64
2 的立方根是＿＿＿＿＿.
３．平方根等于它本身的数的个数为ａ， 立方根等于它本身的数的个数为ｂ，算 术平方根等于它本身的数的个数为ｃ， 则ａ＋ｂ＋ｃ的立方根是＿＿． 3 6
这节课的收获是……பைடு நூலகம்
问题与思考:
某种植物细胞可近似看作是 棱长是1 的正方体，它的体积增大一倍时，这个正 方体的棱长多少？ 棱长为1时，正方体的体积是多少？
设棱长为x,根据题意，得 X3 =2
X 为多少呢?
2.4 立 方 根
定义 一般地，如果一个数x的立方等于a，即x3＝a, 那么这个数x就叫做a的立方根. (也叫做三次方根) . 比如: 23 =8， 所以2叫做8的立方根;
(-２)3＝-８，所以-２叫做-8的立方根; ０3＝０， 表示方法
平方根与算术平方根立方根无理数PPT课件
根”。
（2）个数不同：一个正数有两个平方根，而一个
正数的算术平方根只有一个。
（3）表示方法不同：正数a的算术平方根表示
第9页/共32页
立方根：
1. 定义:
一般地，如果一个数x的立方等于a，即x3=a， 那么这个数x就叫做a的立方根．(也叫做三次方 根) 。
2.表示方法：
第10页/共32页
什么叫做开平方？那开立方呢？
无理数： 无限不循环小数
含有 ～ 的数
有规律但不循环的数
第25页/共32页
按性质分类： 实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
负实数
正实数
0
第26页/共32页
你能在数轴上找到表示 的点吗？
2
小结：
有理数可以用数轴上的点表示，无理数也可以用数轴上的点 表示.
每一个无理数都能在数轴上表示出来. 数轴上的点有些表示有理数，有些表示无理数. 每一个实数都可以用数轴上的一个点来表示；反过来， 数轴上的每一点都表示一个实数。即实数和数轴上的 点是一一对应的。
第21页/共32页
思考：
2 介于哪两个整数之间？你是根据什么考虑的？
A
1
2
B 4D
1
2
2C
1.42 __<__( 2)2 __<__1.52
1.4 ___<_ 2 __<__1.5
1.412 _<___( 2)2 __<__1.42 2
1.41 ___<_ 2 __<__1.42
1.414 2 _<___( 2)2 _<___1.415 2
第28页/共32页
（2）个数不同：一个正数有两个平方根，而一个
正数的算术平方根只有一个。
（3）表示方法不同：正数a的算术平方根表示
第9页/共32页
立方根：
1. 定义:
一般地，如果一个数x的立方等于a，即x3=a， 那么这个数x就叫做a的立方根．(也叫做三次方 根) 。
2.表示方法：
第10页/共32页
什么叫做开平方？那开立方呢？
无理数： 无限不循环小数
含有 ～ 的数
有规律但不循环的数
第25页/共32页
按性质分类： 实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
负实数
正实数
0
第26页/共32页
你能在数轴上找到表示 的点吗？
2
小结：
有理数可以用数轴上的点表示，无理数也可以用数轴上的点 表示.
每一个无理数都能在数轴上表示出来. 数轴上的点有些表示有理数，有些表示无理数. 每一个实数都可以用数轴上的一个点来表示；反过来， 数轴上的每一点都表示一个实数。即实数和数轴上的 点是一一对应的。
第21页/共32页
思考：
2 介于哪两个整数之间？你是根据什么考虑的？
A
1
2
B 4D
1
2
2C
1.42 __<__( 2)2 __<__1.52
1.4 ___<_ 2 __<__1.5
1.412 _<___( 2)2 __<__1.42 2
1.41 ___<_ 2 __<__1.42
1.414 2 _<___( 2)2 _<___1.415 2
第28页/共32页
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§16.1
平方根与立方根
第二课时 算术平方根
备用知识
平方根的意义、性质和求法。
学习过程
一、双基讲练
算术平方根的意义 讲解点1： 一个正数a有两个平方根，其中正数a的正的平 方根，叫做a的算术平方根。记作 a ，读作 “根号a”。0的算术平方根是0，即 0 =0；例 如：4的算术平方根记作 4 =2。 注意：（1）当a≥0时， a 表示a的算术平方根，± a 表示a的平方根；（2）由于一个正数a有两个平方根且 互为相反数，因此当已知a的算术平方根为 a 时，可以写 出它的另一个平方根是- a 。所以，要求一个非负数的平 方根，可以先求这个数的算术平方根。
如何求一个数a的算术平方根？ 关键：还是把求算术平方根转化为平方运算
[典例] 求下列各数的平方根及算术平方根
（1）16；（2）0；（3）（-3）2 解：（1）∵(±4)2=16；∴16的平方根是±4，算术平 方根为4，即± 16 =±4， 16 =4 （2）∵02=0；∴0的平方根和算术平方根都是0， 即± 0 =0， 0 =0 （3）∵(±3)2=（-3）2；∴ （-3）2 的平方根是 ±3，算术平方根为3，即± 3 =±3， 3 =3 评析：求一个非负数a的平方根及的方法是：（1） 先求出某个数的平方等于a；（2）再求出a的算术平 方根；（3）最后求出a的平方根。
第二课时作业
课标王P1，1——14 有困难的同学只做“基础研究”。 “开放实践”题有余力的同学做。
2 n n 的整数部分。
五、小结
1. 算术平方根的意义 非负数a的正的平方根。 2．算术平方根的性质 （1）正数a的算术平方根是一个正数；（2）0的算 术平方根是0；（3）负数没有算术平方根。 3．算术平方根的表示法 一个非负数a的平方根用符号表示为： a 读作：“根号a”，其中a叫做被开方数 4. 求法 与求平方根方法一样，还是利用平方运算来求。 5. 注意平方根和算术平方根的区别与联系。
（D）
1
的平方根是
1 4
：
1 16
=
1 4
16
4.填空：
1
1Leabharlann （1）9 的平方是 （2）-9的平方是 （3） 6
1 4
； 9 的平方根是 ；-9的算术平方根 。 。 。 。
。 。
的算术平方根是
2
（4）当x=4时， ( x 8) = （5） 16 的算术平方根是 （6） (3 ) 2 的算术平方根是 思考题：当n是正整数时，求出
算术平方根的性质 （1）正数a的算术平方根是一个正数；（2）0的算 术平方根是0；（3）负数没有算术平方根。 由此看出算术平方根 a 具有双重非负性：一是被开 放数a≥0；二是算术平方根 a ≥0。即已知 a ， 则a≥0， a ≥0。 [典例] X为何值时，下列各式有意义？
讲解点2：
2 2x x x 1 x 1 （1） ；（2） ；（3） ；（4） ； （5） 1 x x 请记录解答过程（见黑板）
评析：这类题目中的式子，都是被开方数的算术平方根， 因此其根号下的被开方数必须是非负数式子才有意义， 当被开方数为负数时，式子无意义，因此解这类题目的 一般方法是利用被开方数的非负性列不等式（组）解题。
讲解点3： 平方根与算术平方根的区别和联系
（1）除定义有所区别外，还有如下不同：①表示不 同。一个是 ± a ，一个是 a ；②个数不同。任 何正数的平方根都有两个，且互为相反数；任何正数 只有一个算术平方根。特别地，0的平方根和算术平 方根的个数是一样的；③取值范围不同。平方根的值 可以是正数、负数或者0；算术平方根的值只能是正 数和0，不可能是负数。 （2）联系：①算术平方根是平方根中正的平方根， 所以平方根包含算术平方根；②只有在被开方数 为非负数的条件下，才有平方根和算术平方根；③0 的平方根和算术平方根都是0。
1.求下列各数的算术平方根
2；（3）1 9 （1）196；（2）（-5）
16
2. 若 x 3 3 x 有意义，求x的值。 3. 下列语句，写成数学式子正确的是：（ （A）9是81的平方根：± 81 =9 ）
（B）5是（-5）2的算术平方根： (5) 2=5 （C）±6是36的平方根： 36 =±6
[典例]
求下列各式的值：
（2）± 1.96 （3） (2) 2 解：（1） 25 表示求25的算术平方根，即 25 =5 （2）± 1.96表示求1.96的平方根，即± 1.96 =±1.4
（3） (2) 表示求-2的平方后，再求这个平方数的算术平
2
（1） 25
方根，即
(2)
2
= 4 =2
[练习]
平方根与立方根
第二课时 算术平方根
备用知识
平方根的意义、性质和求法。
学习过程
一、双基讲练
算术平方根的意义 讲解点1： 一个正数a有两个平方根，其中正数a的正的平 方根，叫做a的算术平方根。记作 a ，读作 “根号a”。0的算术平方根是0，即 0 =0；例 如：4的算术平方根记作 4 =2。 注意：（1）当a≥0时， a 表示a的算术平方根，± a 表示a的平方根；（2）由于一个正数a有两个平方根且 互为相反数，因此当已知a的算术平方根为 a 时，可以写 出它的另一个平方根是- a 。所以，要求一个非负数的平 方根，可以先求这个数的算术平方根。
如何求一个数a的算术平方根？ 关键：还是把求算术平方根转化为平方运算
[典例] 求下列各数的平方根及算术平方根
（1）16；（2）0；（3）（-3）2 解：（1）∵(±4)2=16；∴16的平方根是±4，算术平 方根为4，即± 16 =±4， 16 =4 （2）∵02=0；∴0的平方根和算术平方根都是0， 即± 0 =0， 0 =0 （3）∵(±3)2=（-3）2；∴ （-3）2 的平方根是 ±3，算术平方根为3，即± 3 =±3， 3 =3 评析：求一个非负数a的平方根及的方法是：（1） 先求出某个数的平方等于a；（2）再求出a的算术平 方根；（3）最后求出a的平方根。
第二课时作业
课标王P1，1——14 有困难的同学只做“基础研究”。 “开放实践”题有余力的同学做。
2 n n 的整数部分。
五、小结
1. 算术平方根的意义 非负数a的正的平方根。 2．算术平方根的性质 （1）正数a的算术平方根是一个正数；（2）0的算 术平方根是0；（3）负数没有算术平方根。 3．算术平方根的表示法 一个非负数a的平方根用符号表示为： a 读作：“根号a”，其中a叫做被开方数 4. 求法 与求平方根方法一样，还是利用平方运算来求。 5. 注意平方根和算术平方根的区别与联系。
（D）
1
的平方根是
1 4
：
1 16
=
1 4
16
4.填空：
1
1Leabharlann （1）9 的平方是 （2）-9的平方是 （3） 6
1 4
； 9 的平方根是 ；-9的算术平方根 。 。 。 。
。 。
的算术平方根是
2
（4）当x=4时， ( x 8) = （5） 16 的算术平方根是 （6） (3 ) 2 的算术平方根是 思考题：当n是正整数时，求出
算术平方根的性质 （1）正数a的算术平方根是一个正数；（2）0的算 术平方根是0；（3）负数没有算术平方根。 由此看出算术平方根 a 具有双重非负性：一是被开 放数a≥0；二是算术平方根 a ≥0。即已知 a ， 则a≥0， a ≥0。 [典例] X为何值时，下列各式有意义？
讲解点2：
2 2x x x 1 x 1 （1） ；（2） ；（3） ；（4） ； （5） 1 x x 请记录解答过程（见黑板）
评析：这类题目中的式子，都是被开方数的算术平方根， 因此其根号下的被开方数必须是非负数式子才有意义， 当被开方数为负数时，式子无意义，因此解这类题目的 一般方法是利用被开方数的非负性列不等式（组）解题。
讲解点3： 平方根与算术平方根的区别和联系
（1）除定义有所区别外，还有如下不同：①表示不 同。一个是 ± a ，一个是 a ；②个数不同。任 何正数的平方根都有两个，且互为相反数；任何正数 只有一个算术平方根。特别地，0的平方根和算术平 方根的个数是一样的；③取值范围不同。平方根的值 可以是正数、负数或者0；算术平方根的值只能是正 数和0，不可能是负数。 （2）联系：①算术平方根是平方根中正的平方根， 所以平方根包含算术平方根；②只有在被开方数 为非负数的条件下，才有平方根和算术平方根；③0 的平方根和算术平方根都是0。
1.求下列各数的算术平方根
2；（3）1 9 （1）196；（2）（-5）
16
2. 若 x 3 3 x 有意义，求x的值。 3. 下列语句，写成数学式子正确的是：（ （A）9是81的平方根：± 81 =9 ）
（B）5是（-5）2的算术平方根： (5) 2=5 （C）±6是36的平方根： 36 =±6
[典例]
求下列各式的值：
（2）± 1.96 （3） (2) 2 解：（1） 25 表示求25的算术平方根，即 25 =5 （2）± 1.96表示求1.96的平方根，即± 1.96 =±1.4
（3） (2) 表示求-2的平方后，再求这个平方数的算术平
2
（1） 25
方根，即
(2)
2
= 4 =2
[练习]