“等价关系”部分习题参考答案
抽象代数等价关系习题答案

抽象代数等价关系习题答案抽象代数等价关系习题答案抽象代数是数学中的一个重要分支,研究的是代数结构的一般性质和规律。
在抽象代数中,等价关系是一个基本概念,它描述了两个元素之间的相等性。
在本文中,我将为大家提供一些抽象代数中等价关系习题的答案,希望能对大家的学习有所帮助。
1. 设A是一个非空集合,R是A上的一个等价关系。
证明:对于任意的a ∈ A,[a] = A。
解答:根据等价关系的定义,[a]是由所有与a等价的元素组成的集合。
而等价关系具有自反性,即对于任意的元素a,a与自身等价。
因此,a ∈ [a],即a属于[a]中的元素。
又因为R是等价关系,所以对于任意的b ∈ A,若a与b等价,则b与a也等价。
因此,[a]中的任意元素与a都等价,即[a]包含了A中的所有元素。
综上所述,[a] = A。
2. 设A是一个非空集合,R是A上的一个等价关系。
证明:对于任意的a, b ∈ A,若a与b等价,则[a] = [b]。
解答:假设a与b等价,即(a, b) ∈ R。
根据等价关系的定义,对于任意的c ∈ [a],都有(c, a) ∈ R。
由于(a, b) ∈ R,根据等价关系的传递性,对于任意的c ∈ [a],都有(c, b) ∈ R。
因此,[a]的任意元素与b都等价,即[b] ⊆ [a]。
同理可证,[a] ⊆ [b]。
综上所述,[a] = [b]。
3. 设A是一个非空集合,R是A上的一个等价关系。
证明:对于任意的a, b ∈ A,若[a] ∩ [b] ≠ ∅,则[a] = [b]。
解答:假设[a] ∩ [b] ≠ ∅,即存在一个元素c,使得c ∈ [a] 且c ∈ [b]。
根据等价关系的定义,对于任意的d ∈ [a],都有(d, a) ∈ R。
由于c ∈ [a],根据等价关系的传递性,对于任意的d ∈ [a],都有(d, c) ∈ R。
同理可证,对于任意的d ∈ [b],都有(d, c) ∈ R。
因此,[a]和[b]中的任意元素与c都等价,即[a] ⊆[b] 且 [b] ⊆ [a]。
等价关系证明题

等价关系证明题【原创实用版】目录1.等价关系证明题的概念和分类2.等价关系证明题的解题方法3.等价关系证明题的例题解析4.总结与展望正文一、等价关系证明题的概念和分类等价关系证明题是数学中一种常见的题型,主要涉及到集合、方程、不等式等数学概念的等价关系的证明。
等价关系证明题可以分为以下几类:集合相等、集合包含关系、方程根的等价关系、不等式解集的等价关系等。
二、等价关系证明题的解题方法1.集合相等关系的证明:通常采用元素与集合关系的互证方法,即证明两个集合的元素具有一一对应的关系。
2.集合包含关系的证明:可以采用直接证明和反证法两种方法。
直接证明是证明集合 A 中的任意元素都属于集合 B;反证法是假设集合 A中有元素不属于集合 B,然后推导出矛盾。
3.方程根的等价关系证明:通常采用代数方法,将方程的根与等价条件建立起代数关系,然后证明这个代数关系成立。
4.不等式解集的等价关系证明:可以采用代数方法、几何方法等多种方法,关键是将不等式的解集与等价条件建立起代数关系或几何关系。
三、等价关系证明题的例题解析例题:证明集合 A={x|x^2-3x+2=0}与集合 B={1,2}是相等关系。
解析:首先解出集合 A 中的元素,得到 A={1,2},然后证明 A 与 B 的元素具有一一对应的关系,即 A 中的任意元素都属于 B,B 中的任意元素都属于 A。
因此,集合 A 与集合 B 是相等关系。
四、总结与展望等价关系证明题是数学中常见的题型,涉及到多种数学概念的等价关系的证明。
解决这类问题需要掌握一定的数学方法和技巧,如元素与集合关系的互证方法、直接证明与反证法、代数方法等。
在实际解题过程中,还需要灵活运用这些方法和技巧,提高解题效率。
【大学课程】近世代数教材习题答案

§1.1 集合1、 设A B ⊆ ,证明:A B A = ,A B B = .证明:由A B ⊆,可知A 的所有元素都属于B ,既A 的所有元素,都是A 和B 的共同元, 则由交集定义可知 A A B ⊆ . 又A B A ⊆ ,所以A B A = .由并集定义知,A B 的所有元素,都属于A 或B ; 又A B ⊆,所以A B 的所有元素都属于B ,即A B B ⊆. 又B A B ⊆,故A B B =2、 设B ,()i A i I ∈ 均为集合Ω 的子集,试证:()1 ()i i i I i I B A B A ∈∈⎛⎫=⎪⎝⎭ ()2 ()i i i I i IBA B A ∈∈⎛⎫=⎪⎝⎭ 证明:()1 由定义i i Ix B A ∈⎛⎫∈⎪⎝⎭当且仅当x B ∈且x 属于某一i A ;当且仅当x 属于某一i B A ;当且仅当()i i Ix B A ∈∈.()2 由定义i i I x BA ∈⎛⎫∈⎪⎝⎭当且仅当x 属于B ,或x 属于任一i A ,i I ∈;当且仅当x 属于任一i B A ,i I ∈;当且仅当()i i Ix B A ∈∈.§1.2 等价关系1、设为整数集,问以下各关系是否为M 的等价关系?1)0aRb ab ⇔≥ 2)4aRb a b ⇔+ 3)aRb a b ⇔= 4)220aRb a b ⇔+≥ 解:1)不是,因为不满足传递性2)不是,不满足反身性和传递性 3)是 4)是2、试指出上题中等价关系所决定的分类.解:3)每个元素是一个类 4)整个整数集作成一个类 3、找出下列证明中的错误:若S 的关系R 有对称性和传递性,则必有反身性.这是因为,对任意的a S ∈ ,由对称性,如果aRb ,则bRa .再由传递性,得aRa ,所以R 有反身性.解:以上证明过程中只考虑了当aRb 成立的情况,但是当对于元素a ,不存在b 使aRb 成立时,aRa 就不能得到.4、在复数集中,规定关系"" :a b a b ⇔=. (1)证明:是的一个等价关系;(2)试确定相应的商集,并给出每个等价类的一个代表元素.(1)证明:设a ,b ,c ∈ ,则()a 因为aa =,所以a a ,于是 是有反身性;()b 若ab ,则a b =,于是b a =,从而b a ,说明是具有对称性;()c 若ab ,bc ,则a b =,b c =,于是a c =,从而a c ,从而具有传递性.所以是的一个等价关系.(2)解:相应的商集[]{}0r r R r =∈≥且,其中[]{}()[]{}cos sin 0,2r x x r r i θθθπ=∈==+∈对任意的c ∈ ,等价是[]c :代表元素可取作c .§1.31、{}1,2,,100S = ,找一个A A ⨯到A 的映射.解:设(),a b 表示A A ⨯的任意元素,,a b A ∈ ,则作映射:f A A A ⨯→ ,()(),f a b b = .f 是一个A A ⨯到A 的映射.2、设A ,B 是两个有限集合,则(1)A 到B 的不同映射共有多少?(2)A 到B 的单射共有多少个?解:(1)设A n = , B m =,则A 到B 的映射有n m 个 (2)设A n = , B m =,若n >m ,则A 到B 没有单射; 若n m ≤,则A 到B 有()!!m m n - 个单射. 3、设x 是数域F 上全体n (n >1)阶方阵作成的集合.问::A A ϕ→是否为x 到F 的一个映射?其中A 为A 的行列式,是否为满射或单射?解:ϕ 是映射,且是满射,但不是单射4、设:f A B →为双射,则f 的逆映射1:f B A -→也是一个双射且()11f f --=.证明:设()() ,f x y x A y B =∈∈ ,则1:f y x -→,即()1f y x -=, 因f 是A B →的双射, 所以1f -是B 到A 的双射, 且1f -的逆映射就是f ,即()11ff --=.5、设:f A B →,:g B C →为两个双射到:g f A C → 也是双射且()111g f f g ---= .证明:()()11111B C g f f g g g ---⋅⋅==,()()111111B A fg gf f f ----==,故g f 也是双射,且()111gf f g ---= .§1.41、设A 是一个有限集合,则A 上不同的二元运算共有多少个?解:设A n = ,则2A A n ⨯= ,故A A ⨯到A 有2n n 个不同的映射. 即A 上有2n n 个不同的二元运算.2、{},,A a b c = ,规定A 的两个不同的代数运算.解:()a 第一个代数运算() , ,R x y a xRy x y A →=∀∈ ()b 第二个代数运算() , ,R x y y xRy x y A →=∀∈3、设M 为整数集,问()22 ,a b a b a b M =+∀∈是否满足结合律和交换律.解:交换律满足,但结合律不满足.例如()1104=,()1102= 4、设M 为实数集,问:23a b a b =+ (),a b M ∀∈是否满足结合律和交换律.解:都不满足.例()1004=,()1002=,故()()100100≠,又102=,013=,故1001≠.5、数域F 上全体非零多项式的集合对于()()()()(),f x g x f x g x =是否满足结合律和交换律?其中()()(),f x g x 表示()f x 与()g x 的首项函数为1的最大公因式.解:显然是代数运算且满足交换律.又结合律也满足,因为根据最大公因式的性质知:())()(()()(),,,,f g h f g h f g h f g h ===§2.11、有限群中每个元素的阶都是有限的。
等价关系-函数自测题原稿

集合论--等价关系、函数部分自测题(答案)一、选择题1、设R和S是集合A上的等价关系,则R∪S的对称性( )(1)一定满足;(2)一定不满足;(3)不一定满足;(4)不可能满足.答案:〔(1)〕.2、设R1和R2是非空集A上的等价关系,下述各式哪个是等价关系( )(1)(A×A)-R1;(2)R21;(3)R1-R2;(4)r(R1-R2).答案:〔(2)〕.3、设集合A中有4个元素,则A上的不同的等价关系的个数为( )(1)11个; (2)14个;(3)15个; (4)17个.答案:〔(3)〕.4、对任何a∈A,形成的A上的等价关系R的等价关系(a)R为( )(1)空集; (2)非空集(3)是空集也可为非空集(4){x|x∈A}.答案:〔(2)〕.5、集合A上的等价关系R,其等价类集合{〔a〕R|a∈A}称为( )(1)A与R的并集,记作A∪R(2)A与R的交集,记作A∩R(3)A关于R的商集,记作A/R(4)A与R的差集,记作A-R.答案:〔(3)〕.6、集合A上的等关系R,决定了A的一个划分,该划分就是( )(1)并集A∪R; (2)交集A∩R;(3)差集A-R; (4)商集A/R答案:〔(4)〕.7、设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为( )(1)2+3个; (2)23个;(3)2×3个;(4)32个.答案:〔(2)〕.8、 52张扑克牌分配给4个桥牌比赛者进行比赛,扑克牌集合A到桥牌比赛者集合B的函数f:A→B为( )(1)单射函数; (2)双射函数;(3)满射函数; (4)一个映射.答案:〔(3)〕.9、集合R上的函数“…是取…的平方”为R→R的( )(1)映射; (2)单射;(3)满射; (4)双射.答案:〔(1)〕.10、若f、g都是满射的,则复合函数fog必是( )(1)映射; (2)入射;(3)满射; (4)双射.答案:〔(3)〕.11、映射的复合运算满足( )(1)交换律; (2)结合律;(3)幂等律; (4)分配律.答案:〔(2)〕.12、设f和g都是从A到A的双射函数,则(fog)-1为( )(1)f-1og-1;(2)fog-1;(3)(gof)-1;(4)g-1of-1答案:〔(4)〕.二、填空题1、设R为集合A上的等价关系,对任何a∈A,集合〔a〕R= ,称为元素a形成的R等价类;〔a〕R≠φ,因 .答案:〔{x|x∈A,aRx};至少有a∈〔a〕R〕2、集合A上的等价关系R,其等价类集合称作A关于R的商集,记作 .答案:〔{a}R|a∈A;A/R〕.3、设10人集合E={赵茵,赵小滨,孙丽春,赵萍,钱洁,李靖华,李秀娟,钱钰,李惠芝,李莉}上的同姓关系为R,则等价类赵·= ,钱·= ,孙·= ,李·= ,而商集E/R= .答案:〔{赵茵,赵萍};{钱小滨,钱洁,钱钰};{孙丽春};{李靖华,李秀娟,李惠芝,李莉};{赵·,钱·,孙·,李·}〕4、根据集合A上的等价关系R与划分之间的关系,推知R可确定,A的一个划分可确定 .答案:〔A的一个划分;A的一个等价关系〕.5、设f:a称b为父亲,g:b称c为父亲,则fog: .答案:答案:〔a称c为祖父〕.6、设f:a称b为母亲,b:b称c为父亲,则fog: .答案:答案:〔a称c为外祖父〕.7、设f:a称b为父亲或母亲,f1:b称c为子或女,则fof1 .答案:〔a是c的兄弟或姐妹,或者a和c是同一个人〕..8、设函数f:A→B有逆函数f-1:B→A,则f-1of= ,fof-1= .答案:〔I B; I A〕.9、设gof是一个复合函数.(1)若g和f是满射的,则gof为 .(2)若g和f是入射的,则gof为 .(3)若g和f是双射的,则gof为 .答案:〔满射的;入射的;双射的〕.10、设映射f:A→B,g:B→C,且g和f是满射,则fog为;若g和f是双射,则fog为且(fog)-1= .答案:〔满射;双射;g-1of-1〕.三、判断题1、平面上直线间的平行关系||是等价关系.答案:〔y〕.2、数集A上的不等关系≠可确定A的一个划分.答案:〔N〕.3、某妇人的子女构成的集合A中,关系R:……与……姐妹,能得到A的一个划分.答案:〔N〕.4、数集A中的整除关系|,能得到A的一个划分.答案:〔N〕.5、一个关系,如果它的图示的始集A的每个点能作一条矢线且仅作一条矢线到终集B 的一个点,称这个关系为函数.对吗?答案:〔y〕.6、若有f(A)=B的映射f:A→B,则称此f为满射.答案:〔y〕.7、映射f:A→B,当值域B*=B时,为满射.答案:〔y〕.8、映射f:A→B,若B中的点至多只有一条f的矢线可以到达,则称f为单射.答案:〔y〕.9、映射f:A→B,若对每一个a∈A,b∈A,有a≠b f(a)≠f(b),则称f为单射.答案:〔y〕.10、对于映射f:A→B,当f-1:B→A也是映射时,则称此f为双射.答案:〔y〕.11、映射f:A→B是双射的充分必要条件是,从A的每一点有且仅有一条矢线可引出,在B的每一点有且仅有一条矢线到达.答案:〔y〕.12、双射函数就是满射函数.答案:〔N〕.13、双射是一一对应的,它的逆不一定一一对应.答案:〔N〕.14、函数f、g、h可以复合,但fo(goh)≠(fog)oh答案:〔N〕.15、若f:A→B,g: B→C是双射函数,则(gof)-1=g-1of-1.答案:〔N〕.16、若f:Z→N,则f(i)=|3i|+1是双射函数i∈Z.答案:〔N〕.17、关于f={<n,m>|m∈N,n+m<10}是函数.答案:〔N〕.18、函数f:N→R,f(n)=lgn是满射的.答案:〔N〕.19、函数f:R→R,f(x)=x2,它存在逆函数f-1.答案:〔N〕.20、函数f:R→R,f(x)=x3+2,则f-1(x)=x-2.答案:〔N〕.。
离散数学课后习题答案(第三章)

R1={<a,b>,<b,a>,<b,c>,<c,b>,<a,c>,<c,a>,<a,a>,<b,b>,<c,c>}
R2={<a,a>,<b,b>,<c,c>,<b,c>,<c,b>}
R1-R2={<a,b>,<b,a>,<a,c>,<c,a>}
所以R1和R2是A上等价关系,但R1-R2不是A上等价关系。
r(R1-R2)=(R1-R2)∪IA
={<a,b>,<b,a>,<a,c>,<c,a>,<a,a>,<b,b>,<c,c>}
不是A上的等价关系。
3-10.8设C*是实数部分非零的全体复数组成的集合,C*上的关系R定义为:(a+bi)R(c+di)ac>0,证明R是等价关系,并给出关系R的等价类的几何说明。
c)若R1是A上等价关系,则
<a,a>∈R1<a,a>∈R1○R1
所以R12是A上自反的。
若<a,b>∈R12则存在c,使得<a, c>∈R1∧<c,b>∈R1。因R1对称,故有
<b, c>∈R1∧<c,a>∈R1<b, a>∈R12
即R12是对称的。
若<a,b>∈R12∧<b, c>∈R12,则有
a)(A×A)-R1;
b)R1-R2;
c)R12;
d) r(R1-R2)(即R1-R2的自反闭包)。
解a)(A×A)-R1不是A上等价关系。例如:
A={a,b},R1={<a,a>,<b,b>}
A×A={<a,a>,<a,b>,<b,a>,<b,b>}
(A×A)-R1={<a,b>,<b,a>}
所以(A×A)-R1不是A上等价关系。
即R是对称的。
3设任意<x,y>∈A,<u,v>∈A,<w,s>∈A,对
等价类+因果图习题及答案

2)((x==4)||(y<5))设计测试用例 x=4, y=3;
3)((x!=4)||(y>5)),设计测试用例 x=2,y=6;
4)((x!=4)||(y<5)),设计测试用例x=2,y=3;
由于x=4第一个条件已经考虑,所以上面1)2)合成x=2,y=6;
2->7->8->9
路径覆盖
x=4, y=6, z=5
x=2, y=6, z=15
x=5, y=5, z=5
x=2, y=5, z=5
2->4,5->7->8->9
2->7->8->9
2->4,5->7->9
2->7->9
2、使用逻辑覆盖测试方法测试以下程序段
void Do(int X,int A,int B)
{
1 int k=0,j=0;
2 if((x>3)&&(z<10))
3 {
4 k=x*y-1;
5 j=sqrt(k);
6 }
7 if((x==4)||(y>5))
8 j=x*y+10;
9 j=j%3;
}
要求(1)画出程序段的控制流图
(2)分别以条件覆盖,路径覆盖方法设计测试用例
答:(1)
(2)条件覆盖:
(2)如果三条件边相等,则程序输出为“等边三角形”;
(3)如果恰好有两条边相等,则程序输出为“等腰三角形”;
(4)如果三条边都不相等,则程序输出为“一般三角形”
等价关系证明题

等价关系证明题摘要:1.等价关系证明题的概述2.等价关系的基本性质3.证明等价关系的方法4.举例说明等价关系证明题的解法正文:一、等价关系证明题的概述等价关系证明题是数学中一种常见的题目类型,主要考察学生对等价关系的理解和应用。
等价关系是指两个数学表达式在某些特定条件下具有相同的值,通过证明等价关系,可以加深对数学概念的理解,提高解题能力。
二、等价关系的基本性质等价关系具有以下几个基本性质:1.自反性:对于任意的x,x 与x 等价。
2.对称性:如果a 与b 等价,那么b 与a 也等价。
3.传递性:如果a 与b 等价,b 与c 等价,那么a 与c 也等价。
三、证明等价关系的方法证明等价关系的方法主要有以下几种:1.代入法:将等价关系的一个表达式代入另一个表达式,证明它们的值相等。
2.恒等变形法:对等价关系的两个表达式进行恒等变形,最终证明它们的值相等。
3.反证法:假设等价关系的两个表达式的值不相等,然后通过推理证明这个假设是错误的。
四、举例说明等价关系证明题的解法例如,证明以下等价关系:x^2 + 2x + 1 = (x + 1)^2解法:1.代入法:将x^2 + 2x + 1 代入(x + 1)^2,得到:(x + 1)^2 = (x + 1) * (x + 1) = x^2 + 2x + 1因此,x^2 + 2x + 1 与(x + 1)^2 等价。
2.恒等变形法:对x^2 + 2x + 1 和(x + 1)^2 进行恒等变形,得到:x^2 + 2x + 1 = x^2 + 2x + 1(x + 1)^2 = x^2 + 2x + 1因此,x^2 + 2x + 1 与(x + 1)^2 等价。
通过以上证明,我们可以得出结论:x^2 + 2x + 1 与(x + 1)^2 是等价关系。
总之,掌握等价关系的基本性质和证明方法,可以帮助我们更好地解决等价关系证明题。
七等价关系与等价类
因为 i. 对aA, a与a在同一分块中,故有aRa,即R是自反的; ii. 对a,bA,若aRb ,则a与b在同一分块中,故b与a也必在同一 分块中,则bRa,故R是对称的; iii. 对a,b,cA,若aRb,bRc即a与b在同一分块中,b与c在同一分块 中,因为Si∩Sj=(i≠j),所以b属于且仅属于一个分块,故a与c必 在同一分块中,故有aRc,即R是传递的;
例题
例 空集上的任何二元关系R都是等价关系,因为 i. (x)(x∈→xRx) ii. (x)(y)(x∈∧y∈∧xRy→yRx) iii.(x)(y)(z)(x∈∧y∈∧z∈∧ xRy∧yRz→xRz ) 都恒为真,所以R是等价关系。
另外:集合A上的全域关系R=A × A也是等价关系。
2. 等价类 定义 设R为集合A上的等价关系,对a∈A,集合
例题
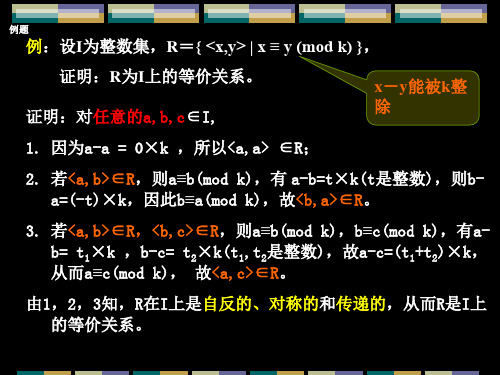
例:设I为整数集,R={ <x,y> | x ≡ y (mod k) },
证明:R为I上的等价关系。 证明:对任意的a,b,c∈I,
x-y能被k整 除
1. 因为a-a = 0×k ,所以<a,a> ∈R;
2. 若<a,b>∈R,则a≡b(mod k),有 a-b=t×k(t是整数),则ba=(-t)×k,因此b≡a(mod k),故<b,a>∈R。
定理1
定理1 设给定集合A上的等价关系R,对于a,b ∈A
证明
aRb iff [a]R=[b]R
1)充分性 若[a]R=[b]R,因为a ∈[a]R ,故a ∈[b]R ,即bRa,又R 是对称的,故aRb.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《二元关系》部分习题参考答案
3.5 等价关系和划分(P129)
第2题
证明:∀x∈A,<x,x>∈R;∀<x,y>∈R,<y,x>∈R;∀<x,y>∈R,<y,z>∈R,则有<x,z>∈R,所以R是自反的、对称的、传递的,因而R 是等价关系。
第3题
解:(1)A上最大等价关系是全域关系,故其元素个数为n2个。
(2)A上最大等价关系的秩是1。
(3)A上最小等价关系是相等关系,故其元素个数为n个。
(4)A上最小等价关系的秩为n。
第5题
解:(a)不是等价关系。
因为A⨯A-R1不具有自反性。
(b)也不是等价关系。
也不具有自反性。
(c)是等价关系。
(d)不是等价关系。
(e)不是等价关系。
第7题
解:(a)R=“<”不是等价关系,因为<不具有自反性和对称性。
R诱导的等价关系全域关系。
(b)它不是等价关系。
因为<0,0>∉R,所以不具有自反性。
R诱导的等价关系是R⋃<0,0>。
(c)它不是等价关系。
因为<0,0>∉R,故它不具有自反性,有<0,1>∈R,但<1,0>∉R,故它不具有对称性。
R诱导的等价关系是:
{<a,b>|(a≥0∧b≥0)∨(a≤0∧b≤0)}
(d)它不是等价关系。
因为<0,0>∉R,所以不具有自反性。
(e) 它不是等价关系。
因为R不具有对称性。
R诱导的等价关系为I上的全域关系。
第10题
解:A的所有划分如下:
π1={{a,b,c}} π2={{a},{b,c}}
π3={{b},{a,c}} π4={{c},{a,b}} π5={{a},{b},{c}}
<P,细分>的哈斯图为:
第11题
解:(a) π1所诱导的等价关系的序偶为:
R1={<a,a>,<a,b>,<a,c>,<b,a>,<b,b>,<b,c>,<c,a>,<c,b>,<c,c>,<d,d>} (b) π2和π3诱导的等价关系分别是:
R2={<a,a>,<b,b>,<c,c>,<d,d>}
R3=A⨯A
(c){{ π1, π2, π3},细分}的哈斯图为:
第12题
解:(a)如果π1=π2,则π1⋃π2是A的划分,其他情况不是A的划分。
(b)如果π1=π2,则π1⋂π2是A的划分,其他情况不是A的划分。
(c) 如果π1⋂π2=∅,则π1-π2是A的划分,其他情况不是A的划分。
(d)因为[π1⋂π2-π1]⋃π1=π1,所以是A的划分。
第16题
解:(a)其哈斯图为:
(b)(A/R1)∙(A/R2)诱导的等价关系为R4:aR4b⇔a≡b(mod 15)其秩为15。
(A/R1)∙(A/R3)诱导的等价关系为R3,其秩为6。
(A/R1)+(A/R2)诱导的等价关系为I⨯I,即全域关系,其秩为1。
(A/R1)+(A/R3)诱导的等价关系为R1,其秩为3。
