人教版六年级下册《比例的意义和基本性质》课件
合集下载
小学数学课件《比例的意义和基本性质》
4.5∶2.7 ＝ 10∶6
表示两个比相等的式子叫做比例。
例题
一辆汽车第一次2小时行驶80千米，第二次5小时 行驶200千米．列表如下：
时间（时）
2
路程（千米）
80
第一次行驶的路程和时间的比是： 第二次行驶的路程和时间的比是：
5 200
80∶2 200∶5
80∶2＝40 200∶5＝40
比值相等
202X
比例的意义和 基本性质
单击此处添加文本具体内容，简明扼要地阐述 你的观点
01 复习1
02 什么叫做比？
03
什么叫做比值？ ○ 两个数相除又叫做两个数的比． ○ 比的前项除以比的后项所得商，叫做比值．
复习2
3、求下面各比的比值：
12∶16 ＝ 12 ÷ 16 ＝ 0.75
∶ ＝÷ ＝
4.5∶2.7 = 4.5÷ 2.7＝ 10∶6 ＝ 10÷ 6＝
(例)6∶9 和 9∶12
比例的意义：
比例的基本性质：
因为： 6 ∶ 9 ＝
因为： 6 × 12 ＝ 72
9∶12 =
9 × 9 ＝ 81
≠ 所以： 6∶9 和 9∶12
不能组成比例．
72 ≠ 81 所以： 6∶9 和 9∶12
不能组成比例．
1.4∶2 和 7∶10
∶
和∶
0.75:0.1 和 7.5:1
验证： 6:10=9:15
∶
= 6 ∶4
外项积是： 80 × 5 ＝ 400 内项积是： 2 × 200＝400
2 × 200＝ 80 × 5
＝
2 × 200＝ 80 × 5
在比例里，两个外项的积等于两个内项的积．
这叫做比例的基本性质．
表示两个比相等的式子叫做比例。
例题
一辆汽车第一次2小时行驶80千米，第二次5小时 行驶200千米．列表如下：
时间（时）
2
路程（千米）
80
第一次行驶的路程和时间的比是： 第二次行驶的路程和时间的比是：
5 200
80∶2 200∶5
80∶2＝40 200∶5＝40
比值相等
202X
比例的意义和 基本性质
单击此处添加文本具体内容，简明扼要地阐述 你的观点
01 复习1
02 什么叫做比？
03
什么叫做比值？ ○ 两个数相除又叫做两个数的比． ○ 比的前项除以比的后项所得商，叫做比值．
复习2
3、求下面各比的比值：
12∶16 ＝ 12 ÷ 16 ＝ 0.75
∶ ＝÷ ＝
4.5∶2.7 = 4.5÷ 2.7＝ 10∶6 ＝ 10÷ 6＝
(例)6∶9 和 9∶12
比例的意义：
比例的基本性质：
因为： 6 ∶ 9 ＝
因为： 6 × 12 ＝ 72
9∶12 =
9 × 9 ＝ 81
≠ 所以： 6∶9 和 9∶12
不能组成比例．
72 ≠ 81 所以： 6∶9 和 9∶12
不能组成比例．
1.4∶2 和 7∶10
∶
和∶
0.75:0.1 和 7.5:1
验证： 6:10=9:15
∶
= 6 ∶4
外项积是： 80 × 5 ＝ 400 内项积是： 2 × 200＝400
2 × 200＝ 80 × 5
＝
2 × 200＝ 80 × 5
在比例里，两个外项的积等于两个内项的积．
这叫做比例的基本性质．
六年级下册数学_比例的意义和基本性质人教新课标ppt(荐)(18张)精品课件
课堂导入
国旗长2.4m，宽1.6m。 国旗长60cm，宽40cm。
这三幅图都是什么地方的场景？有什么共同点？
新知探究
比例的意义
图中操场上和教室里的两面国旗长和宽的比值有什么关系？
国旗长2.4m，宽1.6m。
操场上的国旗：2.4:1.6＝
国旗长60cm，宽40cm。
教室里的国旗： 60:40＝
新知探究
欣欣文具店采购一批不同型号的彩色卡纸。
感悟数学知识的内在联系，培养初步的数学辩证思想。
（1）写出卡纸长度和宽度的比，填在上表中。
像这样表示两个比相等的式子叫作比例。
每种型号卡纸的长度和宽度如下表：
所以2.4:1.6=60:40 这三面国旗的长与宽的比都可以组成比例，所有国旗的长与宽的比都是3:2。
想一想，在上图的三面国旗的尺寸中，
0.6：0.2＝3
课堂练习
2 用图中的4个数据可以组成多少个比例？
3:1.5＝4:2
3:4＝1.5:2
2:1.5＝4:3
2:4＝1.5:3
1.5:3＝2:4
1.5:2＝3:4
4:3＝2:1.5
4:2＝3:1.5
如果四个不同的数能组成比例，就能写出八个形式不同 的比例。图中只要是相对应的边的比就能组成比例。
下面各表中相对应的两个量的比能否组成比例？如果能，把组成的比例写出来。
像这样表示两个比相等的式子叫作比例。
观察下面的比值，你发现了什么？
人教版 数学 六年级 下册
时间/时 所以，20:5和1:4不能组成比例。
（1）6:10和9:15
2
3
这三面国旗的长与宽的比都可以组成比例，所有国旗的长与宽的比都是3:2。
课堂练习
人教版六年级下册比例的意义和基本性质ppt课件
应用比例的意义判断下面的 比例是否正确：
1.
20 ：5 = 1 ：4 (错)
2.
1 2
：1 3
= 6 ：4
(对)
3.
0.6 ：0.2 = 3 ：1 44
(对)
4.
6 ：10 = 9 ：15 (对)
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
＝ 2.4︰1.6 60︰40
外项
内项
＝ 2.4
60
1.6
40
内项
外项
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
6∶9 和 9∶12
比例的意义： 因为： 6 ∶ 9 ＝ 2
3 9∶12 = 3
4 2 ≠3 34
比例的基本性质： 因为： 6 × 12 ＝ 72
9 × 9 ＝ 81
72 ≠ 81
所以： 6∶9 和 9∶12
所以： 6∶9 和 9∶12
不能组成比例。
不能组成比例。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1.
20 ：5 = 1 ：4 (错)
2.
1 2
：1 3
= 6 ：4
(对)
3.
0.6 ：0.2 = 3 ：1 44
(对)
4.
6 ：10 = 9 ：15 (对)
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
＝ 2.4︰1.6 60︰40
外项
内项
＝ 2.4
60
1.6
40
内项
外项
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
6∶9 和 9∶12
比例的意义： 因为： 6 ∶ 9 ＝ 2
3 9∶12 = 3
4 2 ≠3 34
比例的基本性质： 因为： 6 × 12 ＝ 72
9 × 9 ＝ 81
72 ≠ 81
所以： 6∶9 和 9∶12
所以： 6∶9 和 9∶12
不能组成比例。
不能组成比例。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
六年级数学下册课件- 4.1 比例的意义和基本性质 -人教新课标(共19张PPT)
（二）按要求写比例
你能从1、2、3、4、6，这5个数 中找出4个组成比例吗？（要求： 一个比例中不重复使用同一个数）
在比例里，两个外项的 积等于两个内项的积。这叫 做比例的基本性质
你能用字母表示这个性质吗？
分组练习
应用比例的基本性质，判断下面每组 中的两个比能否组成比例？
(1) 6 ：3 和 8 ：5
六年级数学下册第四单元
五星红旗是中国的 国旗，是现在中国在世 界的标志和象征！他的 本意是：红色象征革命 ；五星呈黄色，有象征 中国人为黄种人之意。
大星代表中国共产党，四颗小星代表人民 群众，四颗小星环拱于大星之右，并各有 一个角尖正对大星的中心点，象征中国共 产党领导下的革命人民大团结和人民对党 的拥护。
国旗长5m，宽 10 m。
3
国旗长2.4m，宽1.6m。
写出每面国旗的长与宽 的比，并计算比值？
国旗长60cm，宽40cm。
国旗长5m，宽 10 m。国旗长2.4m，宽1.6m。国旗长60cm，宽40cm。
3
5：130
=
3 2
2.4:1.6=
3 2
60:40=
3 2
通过计算你发现了什么？
国旗长5m，宽 10 m。国旗长2.4m，宽1.6m。国旗长60cm，宽40cm。
:1 3
和6:4
因为
1: 1＝ 3 23 2
（4）0.6:0.2和
3 4
:
1 4
因为 0.6:0.2＝3
6:4 ＝
3 2
= 3
3
2
2
所以，1 : 1 23
＝ 6:4 可以组
成比例。
3 4
:
1 4
＝3
比例的意义和基本性质 (课件
课件名
做一做
人教版六年级下册第四单元第1课比例的意义和基本性质
3cm 1.5cm
2、用图中的4个 数据可以组成多少 个比例？
2cm 4cm
3∶1.5 = 4∶2 3∶4 = 1.5∶2
1.5∶3 = 2∶4 4∶3 = 2∶1.5
课件名
2.4
人教版六年级下册第四单元第1课比例的意义和基本性质
＝ ︰1.6 60 ︰ 40
1∶ 1
36
和
1 ∶1
24
1.2∶ 3
4和54∶5课件名人教版六年级下册第四单元第1课比例的意义和基本性质
我是小法官，对错我来判判。
（1）比例是由任意两个比组成的。 （ ）
（2）在比例里，两个内项的积与两个外项的 积的差是0。 （ ）
（3）比例式中有四个外项，四个内项。（ ）
比的前项除以比的后项所得的商，叫做 比值。 3、什么叫做比的基本性质？
比的前项和后项同时乘或者除以相同 的数（0 除外），比值不变。
课件名
人教版六年级下册第四单元第1课比例的意义和基本性质
长5m,宽10 m 3
长2.4m,宽1.6m 长60cm,宽40cm
课件名
尝试计算，展开讨论
操场上的国旗
人教版六年级下册第四单元第1课比例的意义和基本性质
在比例里，两个外项的积等于两个 内项的积。这叫做比例的基本性质。
比例的基 本性质
＝ 2.4
60
1.6
40
交叉相乘
2.4×40＝96 1.6×60=96
课件名
人教版六年级下册第四单元第1课比例的意义和基本性质
做一做
应用比例的基本性质，判断下面哪组中的两个比 可以组成比例。
人教版六年级数学下《比例的意义和基本性质 比例的意义》公开课课件_19
教学目标：1、理解比例的意义，理解比例各部分名称；理解比例的基本性质。
2、能根据比例的意义和基本性质，准确判断两个比能否组成比例。
3、在探究、观察比较中，培养学生分析、概括水平和勇于探索的精神。
教学重点：理解比例的意义和基本性质，能准确判断两个比能否组成比例。
教学难点：探究发现比例的基本性质。
教学准备：多媒体课件。
教学过程：一、复习导入么？（比）是的，上学期我们已经学过了比的相关知识，说说你对比已经有了哪些了解？（生答：比的意义、各部分名称、基本性质等。
）二、探究新知（一）教学比例的意义1．出示情境图（四幅），渗透《国旗法》，实行爱国主义教育。
师：这四幅图中都有什么呀？（国旗）对，五星红旗是我们每一个中国人的骄傲，每当看到国旗冉冉升起的时候，一种自豪感便油不过生，同学们你们知道吗？国家还专门制定了一部法律——《中华人民共和国国旗法》，《国旗法》中规定（课件出示）：中华人民共和国国旗是中华人民共和国的象征和标志。
每个公民和组织，都理应尊重和爱护国旗。
而我们要怎样尊重和爱护国旗呢？现阶段最需要做的就是在每周的升旗仪式上自觉保持绝对安静，不交头接耳、嬉戏打闹，相信同学生一定能做到。
关于《国旗法》中的其他要求和规定，同学们课下能够查阅资料了解一下。
师：同学们，观察四幅图中的国旗，你们发现了吗？在不同的场合，国旗的大小一样吗？（不一样）课件出示：四幅国旗的长与宽。
这面国旗长5M，宽10/3M；学校里举行升旗仪式使用的国旗长2.4M，宽1.6M；悬挂在教师上方的国旗它的长是60CM，宽40CM；当我们国家的企业、单位等实行外事交流活动时，也要摆放国旗，这面国旗它的长是15CM，宽是10CM。
2．写出四面国旗长与宽的比，并求比值。
其实在制作国旗的尺寸当中，也存有着有趣的比，不相信同学们能够写出这四面国旗的长与宽之比，并求出比值。
开始~3．学生汇报。
（课件同时出示）5:10/3=3/2 2.4:1.6=3/2 60:40=3/2 15:10=3/2从这里，你有什么发现呢？（生答：我发现这四面国旗的长宽之比的比值都是相等的，比值都是3/2。
比例的意义和基本性质教学PPT课件
因为： 6 ∶ 9 ＝ 2 3
9∶12
=
3 4
2≠3 34
所以： 6∶9 和 9∶12
比例的基本性质： 因为： 6 × 12 ＝ 72
9 × 9 ＝ 81
72 ≠ 81 所以： 6∶9 和 9∶12
不能组成比例。
不能组成比例。
第16页/共25页
比和比例有什么区别？
意义 构成
比 两现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
4、求下面各比的比值：
12∶16 = 12 ÷ 16 = 0.75
3∶1 = 3÷ 1= 6 48 4 8
4.5∶2.7 = 4.5÷
2.7= 1 2
3
第1页/共25页
1 3
︰2
和
1 ︰4 6
第8页/共25页
6∶10 和 9∶15
因为
6∶10 ＝
3 5
9∶15
=
3 5
3 5
=
3 5
所以 6∶10 和 9∶15 能组成比例．
1 ︰2 3
和
1 6
︰
4
因为
1 3
︰2
=
1 6
1 6 ︰4
=
1 24
1 6
≠
1 24
所以 1 ︰ 2 3
和
1 6
︰
4
不能组成比例。
第9页/共25页
第11页/共25页
指出下面比例的外项和内项。
4.5 ∶ 2.7 = 10 ∶ 6
内项 外项
1∶1 23
=
6∶4
内项
外项
仔细观察，你 发现了什么？
第12页/共25页
比例的基本性质(新人教版)(共23张PPT)
24: 6 = 8 :2
6、运用比例的根本性质，判断下面两个比能不能组成比 例。
0.2∶2.5 和 4∶50
因为 0.2 × 50 ＝ 10
2.5 × 4 ＝ 10
10 = 10
所以 0.2∶2.5 和 4∶50 能组成比例。
1.2∶3
4
和
4 5
∶5
因为 1.2 × 5 ＝ 6
3 4
4
×5
3 ＝5
1 2
×
4
=
2
1
内项积：3 × 6 = 2
31
0.6 ∶0.2= 4 ∶4
外项积：0.6 ×14 = 0.15
3
内项积： 0.2 ×4 = 0.15
如果把比例改成分数形式呢？如：
3 9， 5 15
3×15=5×9。等号两边的分子和分母分别交叉
相乘,所得的积相等。
这个规律叫做比例的根本 性质。
验证:是不是其他的比例都有这样的规律？
观察组成比例的两个内项和两个外项，并探究它 们的关系。同学们小组内交流。
32 : 320 = 1 : 10
内项 外项
外项积是： 32×10 内项积是： 320× 1
32 ×10＝ 320× 1
组成比例的两个 内项的积和两个 外项的积相等Leabharlann 验证其他的比例有没有这个规律.
11
2 ∶3 = 6 ∶4
外项积：
外项
两端的两项叫做比例的 外项，
中间的两项叫做比例的内 项。
2.4:1.6＝60:40
内项
外项
上面的比例还可以写成分数形式：
2.4 1.6
＝
60 40
2.4和40仍然是外项，1.6和60仍然是内项。
6、运用比例的根本性质，判断下面两个比能不能组成比 例。
0.2∶2.5 和 4∶50
因为 0.2 × 50 ＝ 10
2.5 × 4 ＝ 10
10 = 10
所以 0.2∶2.5 和 4∶50 能组成比例。
1.2∶3
4
和
4 5
∶5
因为 1.2 × 5 ＝ 6
3 4
4
×5
3 ＝5
1 2
×
4
=
2
1
内项积：3 × 6 = 2
31
0.6 ∶0.2= 4 ∶4
外项积：0.6 ×14 = 0.15
3
内项积： 0.2 ×4 = 0.15
如果把比例改成分数形式呢？如：
3 9， 5 15
3×15=5×9。等号两边的分子和分母分别交叉
相乘,所得的积相等。
这个规律叫做比例的根本 性质。
验证:是不是其他的比例都有这样的规律？
观察组成比例的两个内项和两个外项，并探究它 们的关系。同学们小组内交流。
32 : 320 = 1 : 10
内项 外项
外项积是： 32×10 内项积是： 320× 1
32 ×10＝ 320× 1
组成比例的两个 内项的积和两个 外项的积相等Leabharlann 验证其他的比例有没有这个规律.
11
2 ∶3 = 6 ∶4
外项积：
外项
两端的两项叫做比例的 外项，
中间的两项叫做比例的内 项。
2.4:1.6＝60:40
内项
外项
上面的比例还可以写成分数形式：
2.4 1.6
＝
60 40
2.4和40仍然是外项，1.6和60仍然是内项。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
比。
式子叫做比例。
构成
由两个数组成，分别叫比的 前项和后项。
由四个数组成，两 端的两项叫做比例 的外项，中间的两 项叫做比例的内项。
基本 比的前项和后项同时乘或除 在比例里，两个外
性质 以相同的数（0除外），比 项的积等于两个内
值不变。
项的积。
思考？ 3 ∶ 2 = 9 ∶6
内项 外项 (1):交换两个外项的位置,比例还成立吗? (2):交换两个内项的位置,比例还成立吗? (3):交换其中一个外项和一个内项的位置,比例还成 立吗? (4):把两个外项和两个内项分别交换位置,比例还成 立吗?
(错)
(2)0.2 ：2.5 = 4 ：50 (对)
(3)2：3 = 1 ：1 23
(错)
(4)1.2 ：0.6 = 10 ：5 (对)
试一试 应用比例的意义或者基本性质，判断
下面的两个比能不能组成比例。
6∶9 和 9∶12
比例的意义：
因为：
6
∶
9
＝
2 3
比例的基本性质： 因为： 6 × 12 ＝ 72
内项
外项
1 2
∶1 3
=
6 ∶4
内项 外项
＝ 2.4 ︰1.6
60 ︰ 40
内项 外项
＝ 2.4 ︰1.6
60 ︰ 40
内项 外项
外项积是：2.4 × 40 ＝ 96
内项积是：1.6 × 60 ＝96
× ＝×
＝ 2.4 ︰ 1.6 60 ︰ 40
内项 外项
在比例里，两个外项的积等于 两个内项的积。
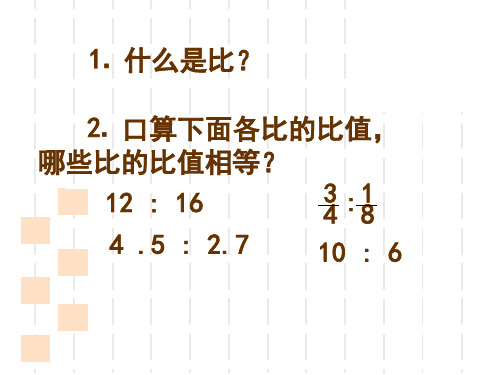
⒈ 什么是比？
⒉ 口算下面各比的比值，
哪些比的比值相等？
12 : 16
3 4
:
1 8
4 .5 : 2.7
10 : 6
表示两个比相等的式子叫做比例。
应用比例的意义判断下面的 比例是否正确：
1.
20 ：5 = 1 ：4 (错)
2.
1 2
：1 3
= 6 ：4
(对)
3.
0.6 ：0.2 = 3 ：1 44
2.4×40 ＝ 1.6×60
＝ 2.4︰1.6 60︰40
外项
内项
＝ 2.4
60
1.6
40
内项
外项
交叉相乘
2.4×40 ＝ 1.6×60
2.4︰1.6 ＝60︰40
内项 外项
在比例里，两个外项的积等于两个 内项的积,这叫做比例的基本性质。
巩固练习
1、应用比例的基本性质判断下面的比例是否正
确：(1)6 ：3 = 8 ：5
9∶12
=
3 4
9 × 9 ＝ 81
2 ≠3
3
4
72 ≠ 81
所以： 6∶9 和 9∶12
所以： 6∶9 和 9∶12
பைடு நூலகம்
不能组成比例。
不能组成比例。
下面这个算式可以组成哪些比 例，把组成的比例写出来。
3 × 40 = 8 × 15
如果把3、40看作外项
3∶8＝15 ∶40 3∶15 ＝8∶40 40∶8＝15 ∶3 40∶15 ＝8∶3
如果把3、40看作内项
8∶3＝40∶15 8∶40＝3∶15 15∶3＝40∶8 15∶40＝3∶8
4.填空：
（1）在比例里，两个内项的积是18，
其中一个外项是2，另一个外项是（9）。
（2）如果5a=3b，那么，ab
=
（3） ， （5）
b a
=
（5） （3）
。
比和比例有什么区别？
比
比例
意义 两个数相除又叫做两个数的 表示两个比相等的
(对)
4.
6 ：10 = 9 ：15 (对)
＝ 2.4 ︰ 1.6 60 ︰ 40
内项
外项
组成比例的四个数，叫做比例的项， 中间的两项叫做比例的内项， 两端的两项叫做比例的外项。
＝ 2.4︰1.6 60︰40
外项
内项
＝ 2.4
60
1.6
40
内项
外项
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6