计算方法习题集及答案(总结版)
《结构力学》习题集及答案(下册)第十章结构弹性稳定计算
第十章 结构弹性稳定计算一、判断题:1、稳定方程即是根据稳定平衡状态建立的平衡方程。
2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。
3、在稳定分析中,有n 个稳定自由度的结构具有n 个临界荷载。
4、两类稳定问题的主要区别是:荷载—位移曲线上是否出现分支点。
5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。
6、能量法确定临界荷载的依据是势能驻值原理。
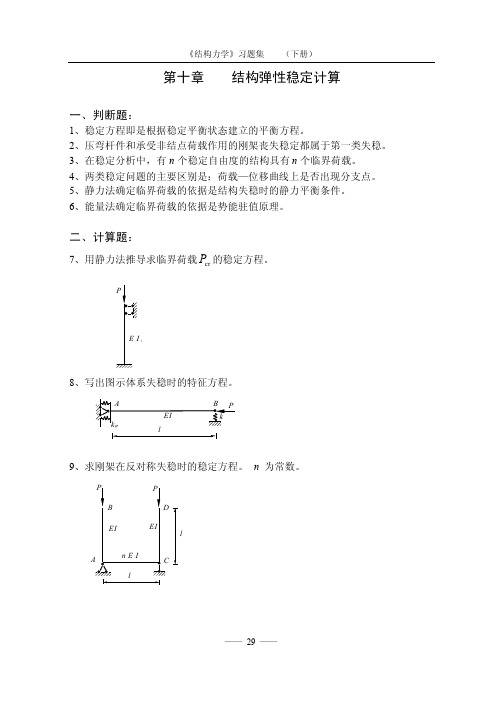
二、计算题:7、用静力法推导求临界荷载cr P 的稳定方程。
PE I ,l8、写出图示体系失稳时的特征方程。
k lEIk AB P9、求刚架在反对称失稳时的稳定方程。
n 为常数。
l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。
转动刚度kl k r 2=,k 为弹簧刚度。
P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。
已知弹簧刚度l EI k 33= 。
PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。
PEI l13、用静力法求图示结构的临界荷载cr P ,欲使B 铰不发生水平移动,求弹性支承的最小刚度k 值。
PlEI A Bk14、用静力法确定图示具有下端固定铰,上端滑动支承压杆的临界荷载crP。
P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。
设失稳时两柱的变形曲线均为余弦曲线:yxh=-δπ(cos).12提示:cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。
PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆,AB段失稳时变形曲线设为:()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。
l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ,设变形曲线为正弦曲线。
计算方法习题集及解答(总结版)

左边 ( )- 右边 证明:当 m=0 时
∑∞
= T0 h
T=
∆ i
h
2i
=
i=1
设 时等式成立,即 ( )- m=k
Tk h
∑∞
T=
∆ h (k ) 2k +2i i
i =1
当 时 m=k+1
∑ ∑ Tk+(1 h)-T=
4k
+1Tk
(
h 2
)
−
Tk
(h)
4k +1 −1
−T=
4k +1[T
+
∞ i =1
0
1
2
3
4
5
6
7
8
1.5 1.44444 1.47929 1.456976 1.47108 1.46209 1.46779 1.4416 1.46647
9 1.4650
10
11
1.46593 1.4653
x* ≈ 1.466
迭代公式(2):
k
0
xk
1.5
12 1.46572
13 1.46548
14 1.46563
xk +1
=
ln(4 − xk ln 2
)
k
0
1
2
3
4
5
6
7
8
9
10
2
xk 1.5 1.322 1.421 1.367 1.397 1.380 1.390 1.384 1.387 1.386 1.386
x* ≈ 1.386
2. 方程 x3 − x2 −1 = 0 在 x = 1.5附近有根,把方程写成三种不同的等价形式:
结构力学习题集(下)_结构的动力计算习题与答案

结构⼒学习题集(下)_结构的动⼒计算习题与答案第九章结构的动⼒计算⼀、判断题:1、结构计算中,⼤⼩、⽅向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复⼒作⽤下的振动称为⾃由振动。
3、单⾃由度体系其它参数不变,只有刚度EI 增⼤到原来的2倍,则周期⽐原来的周期减⼩1/2。
4、结构在动⼒荷载作⽤下,其动内⼒与动位移仅与动⼒荷载的变化规律有关。
5、图⽰刚架不计分布质量和直杆轴向变形,图a 刚架的振动⾃由度为2,图b 刚架的振动⾃由度也为2。
6、图⽰组合结构,不计杆件的质量,其动⼒⾃由度为5个。
7、忽略直杆的轴向变形,图⽰结构的动⼒⾃由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同⼀体系在不考虑阻尼和考虑阻尼时的⾃振频率,ω与ωD 的关系为ωω=D 。
⼆、计算题:10、图⽰梁⾃重不计,求⾃振频率ω。
l l /411、图⽰梁⾃重不计,杆件⽆弯曲变形,弹性⽀座刚度为k ,求⾃振频率ω。
12、求图⽰体系的⾃振频率ω。
l l0.5l 0.513、求图⽰体系的⾃振频率ω。
EI = 常数。
ll 0.514、求图⽰结构的⾃振频率ω。
l l15、求图⽰体系的⾃振频率ω。
EI =常数,杆长均为l 。
16、求图⽰体系的⾃振频率ω。
杆长均为l 。
17、求图⽰结构的⾃振频率和振型。
l /218、图⽰梁⾃重不计,W EI ==??2002104kN kN m 2,,求⾃振圆频率ω。
B2m2m19、图⽰排架重量W 集中于横梁上,横梁EA =∞,求⾃振周期ω。
EIEIW20、图⽰刚架横梁∞=EI 且重量W 集中于横梁上。
求⾃振周期T 。
EIEIWEI 221、求图⽰体系的⾃振频率ω。
各杆EI = 常数。
a aa22、图⽰两种⽀承情况的梁,不计梁的⾃重。
求图a 与图b的⾃振频率之⽐。
l /2/2(a)l /2l /2(b)23、图⽰桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求⽔平⾃振周期T 。
结构力学习题集(下)矩阵位移法习题及答案
第八章 矩阵位移法一、(O) 二、(X) 3、(O) 4、(X) 五、(X) 六、(O) 7、(O) 八、(X) 九、(O) 10、(O) 1一、(A)一、判定题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
二、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
五、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应知足的变形条件。
6、图示结构用矩阵位移法计算时(计轴向变形)未知量数量为8个。
7、在直接刚度法的先处置法中,定位向量的物理意义是变形持续条件和位移边界条件。
8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
九、矩阵位移法中,等效结点荷载的“等效原那么”是指与非结点荷载的结点位移相等。
10、矩阵位移法既能计算超静定结构,也能计算静定结构。
11、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采纳先处置法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234( )二、计算题:12、用先处置法计算图示结构刚度矩阵的元素133322,,K K K 。
123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI13、用先处置法计算图示刚架结构刚度矩阵的元素153422,,K K K 。
EI ,EA 均为常数。
l14、计算图示结构整体刚度矩阵的元素665544,,K K K 。
E 为常数。
l l1342A , I AA /222A I , 2A1五、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。
代数式求值-初中数学习题集含答案

代数式求值(北京习题集)(教师版)一.选择题(共6小题)1.(2019秋•海淀区校级期中)历史上,数学家欧拉最先把关于x 的多项式用记号()f x 来表示,把x 等于某数a 时的多项式的值用f (a )来表示,例如2x =-时,多项式2()56f x x x =+-的值记为(2)f -,那么(2)f -等于( ) A .8B .12-C .20-D .02.(2018秋•平谷区期末)如果23x y -=,那么代数式42x y -+的值为( ) A .1-B .4C .4-D .13.(2019秋•海淀区校级期中)已知当2x =时,代数式33ax bx -+的值为5,则当2x =-时,33ax bx -+的值为() A .5B .5-C .1D .1-4.(2018秋•房山区期末)按下面的程序计算,若开始输入的值x 为正数,最后输出的结果为283,则满足条件的x 不同值最多有( )A .6个B .5个C .4个D .3个5.(2018秋•西城区期末)如果2220x x --=,那么2631x x --的值等于( ) A .5B .3C .7-D .9-6.(2018秋•海淀区期末)若2x =时42x mx n +-的值为6,则当2x =-时42x mx n +-的值为( ) A .6-B .0C .6D .26二.填空题(共4小题)7.(2019秋•门头沟区期末)如图,这是一个运算的流程图,输入正整数x 的值,按流程图进行操作并输出y 的值.如果输出3y =,那么输入的x 的值为 .8.(2019秋•北京期中)已知250x x +-=,则代数式2331x x ++的值为 .9.(2019秋•海淀区校级期中)已知2x y +=,则322x y --的值是 . 10.(2018秋•滨海县期末)已知222x x +=,则多项式2243x x +-的值为 . 三.解答题(共5小题)11.(2018秋•海淀区校级期中)已知关于x 的多项式32ax bx cx d +++,其中a ,b .c 为互为互不相等的整数,且4abc =-(1)则a b c ++的值为 .(2)若a b c <<,当1x =时,这个多项式的值为5,求d 的值. 12.(2018秋•海淀区校级期中)间读材料:为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算.将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表. 北京市居民用水阶梯水价表 单位:元/立方米(1)若小明家去年第一,二,三,四季度用水量分别是50,60,90,50立方米,则小明家第三季度应缴纳的水费为 .(2)截至9月底,小明家今年共纳水费935元,则小明家共用水 立方米.(3)若小明家明年预计用水x 立方米,且总量不超过240立方米,则应缴纳的水费多少元?(用含x 的代数式表示) 13.(2018秋•延庆区期中)定义:任意两个数a ,b ,按规则ac a b b=-+得到一个新数c ,称所得的新数c 为数a ,b 的“机智数”. (1)若1a =,2b =,直接写出a ,b 的“机智数” c ;(2)如果,221a m m =++,2b m m =+,求a ,b 的“机智数” c ; (3)若(2)中的c 值为一个整数,则m 的整数值是多少?14.(2017秋•西城区校级期中)当2x =时,代数式31ax bx -+的值等于17-,求:当1x =-时,代数式31235ax bx --的值.15.(2017秋•海淀区校级期中)关于x 的多项式322(1)43k k x kx x x ++++-是关于x 的二次多项式. (1)求k 的值.(2)若该多项式的值2,且[]a 表示不超过a 的最大整数,例如[2.3]2=,请在此规定下求21[20172]2k x x --的值.代数式求值(北京习题集)(教师版)参考答案与试题解析一.选择题(共6小题)1.(2019秋•海淀区校级期中)历史上,数学家欧拉最先把关于x 的多项式用记号()f x 来表示,把x 等于某数a 时的多项式的值用f (a )来表示,例如2x =-时,多项式2()56f x x x =+-的值记为(2)f -,那么(2)f -等于( ) A .8B .12-C .20-D .0【分析】把2x =-代入256x x +-,求出(2)f -等于多少即可. 【解答】解:当2x =-时,2()56f x x x =+- 2(2)5(2)6=-+⨯-- 4106=--12=-故选:B .【点评】此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.2.(2018秋•平谷区期末)如果23x y -=,那么代数式42x y -+的值为( ) A .1-B .4C .4-D .1【分析】将2x y -的值整体代入到424(2)x y x y -+=--即可. 【解答】解:当23x y -=时, 424(2)431x y x y -+=--=-=,故选:D .【点评】本题主要考查代数式的求值,运用整体代入思想是解题的关键.3.(2019秋•海淀区校级期中)已知当2x =时,代数式33ax bx -+的值为5,则当2x =-时,33ax bx -+的值为() A .5B .5-C .1D .1-【分析】首先根据当2x =时,代数式33ax bx -+的值为5,求出82a b -的值是多少;然后应用代入法,求出当2x =-时,33ax bx -+的值为多少即可.【解答】解:当2x =时,代数式33ax bx -+的值为5,822a b ∴-=,当2x =-时, 33ax bx -+ 823a b =-++(82)3a b =--+ 23=-+1=故选:C .【点评】此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.4.(2018秋•房山区期末)按下面的程序计算,若开始输入的值x 为正数,最后输出的结果为283,则满足条件的x 不同值最多有( )A .6个B .5个C .4个D .3个【分析】根据程序框图,得出满足题意x 的值即可. 【解答】解:把23x =代入得:313x +=; 把3x =代入得:3110x +=; 把10x =代入得:3131x +=; 把31x =代入得:3194x +=; 把94x =代入得:31283200x +=>, 则满足条件的x 不同值为23,3,10,31,94,共5个. 故选:B .【点评】此题考查了代数式求值,弄清题中的程序框图是解本题的关键. 5.(2018秋•西城区期末)如果2220x x --=,那么2631x x --的值等于( ) A .5B .3C .7-D .9-【分析】由2220x x --=得222x x -=,将其代入226313(2)1x x x x --=--计算可得. 【解答】解:2220x x --=,则226313(2)1x x x x --=-- 321=⨯- 61=- 5=,故选:A .【点评】本题考查了求代数式的值的应用,能整体代入是解此题的关键.6.(2018秋•海淀区期末)若2x =时42x mx n +-的值为6,则当2x =-时42x mx n +-的值为( ) A .6-B .0C .6D .26【分析】把2x =代入求出4m n -的值,再将2x =-代入计算即可求出所求. 【解答】解:把2x =代入得:1646m n +-=, 解得:410m n -=-,则当2x =-时,原式16416106m n =+-=-=, 故选:C .【点评】此题考查了代数式求值,熟练掌握运算法则是解本题的关键. 二.填空题(共4小题)7.(2019秋•门头沟区期末)如图,这是一个运算的流程图,输入正整数x 的值,按流程图进行操作并输出y 的值.如果输出3y =,那么输入的x 的值为 5或6 .【分析】x 的取值可分为两种情况,偶数或者奇数,分别列出这两种情况下的等式再计算即可. 【解答】解: ①当x 是偶数,32x=,解得6x = ②当x 是奇数,132x +=,解得5x = 所以,x 的值是5或6. 故答案为5或6.【点评】本题考查有理数的运算,结合编程的流程图出题,题目新颖,并且运用到了分类讨论这一重要数学思想.熟练掌握有理数的运算法则是解题的关键.8.(2019秋•北京期中)已知250x x +-=,则代数式2331x x ++的值为 16 .【分析】由250x x +-=得到:25x x +=,将25x x +=整体代入所求的式子即可求出答案. 【解答】解:由250x x +-=得到:25x x +=, 则223313()135116x x x x ++=++=⨯+=, 故答案为:16.【点评】本题考查代数式求值,解题的关键是将25x x +=整体代入,本题属于基础题型. 9.(2019秋•海淀区校级期中)已知2x y +=,则322x y --的值是 1- . 【分析】将要求大V 代数式变形,再将2x y +=整体代入求值即可. 【解答】解:2x y +=32232()x y x y ∴--=-+ 322=-⨯ 34=-1=-故答案为:1-.【点评】本题考查了代数式的求值,正确变形并整体代入,是解题的关键. 10.(2018秋•滨海县期末)已知222x x +=,则多项式2243x x +-的值为 1 . 【分析】先变形,再整体代入求出即可. 【解答】解:222x x +=,222432(2)32231x x x x ∴+-=+-=⨯-=, 故答案为:1.【点评】本题考查了求代数式的值,能够整体代入是解此题的关键. 三.解答题(共5小题)11.(2018秋•海淀区校级期中)已知关于x 的多项式32ax bx cx d +++,其中a ,b .c 为互为互不相等的整数,且4abc =-(1)则a b c ++的值为 1或4 .(2)若a b c <<,当1x =时,这个多项式的值为5,求d 的值.【分析】(1)根据题中的条件确定出a ,b ,c 组成的三个整数,确定出a b c ++的值即可;(2)根据a ,b ,c 的大小确定出各自的值,代入多项式,把1x =代入使其代数式的值为5,即可求出d 的值. 【解答】解:(1)关于x 的多项式32ax bx cx d +++,其中a ,b .c 为互为互不相等的整数,且4abc =-,∴这三个数由2-,1,2组成或1-,1,4组成,则1a b c ++=或4; (2)a b c <<,2a ∴=-,1b =,2c =,多项式为3222x x x d -+++,把1x =代入得:2125d -+++=, 解得:4d =.【点评】此题考查了代数式求值,以及多项式,熟练掌握运算法则是解本题的关键. 12.(2018秋•海淀区校级期中)间读材料:为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算.将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表. 北京市居民用水阶梯水价表 单位:元/立方米(1)若小明家去年第一,二,三,四季度用水量分别是50,60,90,50立方米,则小明家第三季度应缴纳的水费为 550元 .(2)截至9月底,小明家今年共纳水费935元,则小明家共用水 立方米.(3)若小明家明年预计用水x 立方米,且总量不超过240立方米,则应缴纳的水费多少元?(用含x 的代数式表示) 【分析】(1)小明家第三季度用水量90立方米,应缴纳的水费为905450⨯=(元); (2)(3)根据阶梯收费的意义正确列出代数式即可. 【解答】解:(1)小明家第三季度用水量90立方米,第一阶梯水量150506040--=(立方米),第二阶梯用水量904050-=(立方米) 应缴纳的水费为405507550⨯+⨯=(元). 故答案为550;(2)设小明家共用水x 立方米, 15057(260151)935⨯+⨯->,∴小明家用水少于260立方米,15057(150)935x ∴⨯+-=,解得176x ≈(立方米) 故答案为176;(3)当150x 时,应缴纳的水费为5x ,当151240x 时,应缴纳的水费为15057(150)7300x x ⨯+-=-.【点评】本题考查了列代数式与代数式求值,正确理解阶梯收费的意义是解题的关键. 13.(2018秋•延庆区期中)定义:任意两个数a ,b ,按规则ac a b b=-+得到一个新数c ,称所得的新数c 为数a ,b 的“机智数”. (1)若1a =,2b =,直接写出a ,b 的“机智数” c ;(2)如果,221a m m =++,2b m m =+,求a ,b 的“机智数” c ; (3)若(2)中的c 值为一个整数,则m 的整数值是多少? 【分析】(1)根据题意和a 、b 的值可以求得“机智数” c ;(2)根据题意,可以求得221a m m =++,2b m m =+时的“机智数” c ; (3)根据(2)中的结论和分式有意义的条件可以求得m 的值. 【解答】解:(1)1a =,2b =,ac a b b=-+, 131222c ∴=-+=, 即a ,b 的“机智数” c 是32; (2)221a m m =++,2b m m =+,ac a b b =-+, 2222211(21)()m m c m m m m m m m m++∴=-++++=-+; (3)2222211(21)()m m c m m m m m m m m ++=-++++=-+,1c m m=-为一个整数, 1m ∴=或1m =-(舍去), 即m 的整数值是1.【点评】本题考查代数式求值,解答本题的关键是明确题意,利用因式分解的方法解答.14.(2017秋•西城区校级期中)当2x =时,代数式31ax bx -+的值等于17-,求:当1x =-时,代数式31235ax bx --的值.【分析】先代入求出49a b -=-,再把1x =-代入,变形后再代入,即可求出答案. 【解答】解:当2x =时,代数式31ax bx -+的值等于17-,∴代入得:82117a b -+=-,即49a b -=-, 当1x =-时,31235ax bx -- 1235a b =-+-3(4)5a b =--- 3(9)5=-⨯-+ 32=.【点评】本题考查了求代数式的值,能够整体代入是解此题的关键.15.(2017秋•海淀区校级期中)关于x 的多项式322(1)43k k x kx x x ++++-是关于x 的二次多项式. (1)求k 的值.(2)若该多项式的值2,且[]a 表示不超过a 的最大整数,例如[2.3]2=,请在此规定下求21[20172]2k x x --的值.【分析】(1)由多项式是关于x 的二次多项式知三次项系数为0、二次项系数不为0,据此求得k 的值; (2)由多项式的值为2知245x x +=,结合(1)中0k =及新定义计算可得. 【解答】解:(1)是关于x 的二次多项式, (1)0k k ∴+=, 0k ∴=或1k =-,当1k =-时,220kx x +=,此时变为x 的一次多项式, 1k ∴=-不合题意,舍去, 0k ∴=.(2)多项式的值为2, 2432x x ∴+-=, 245x x ∴+=,由(1)0k =,∴22211115[20172][02][(4)][5][]322222k x x x x x x --=--=-+=-⨯=-=-. 【点评】本题主要考查代数式的求值,解题的关键是掌握多项式的定义及代数式的求值、整体思想的运用.。
计算方法习题集及答案第四版

解:
y次迭代公式
k
0
1
2
3
3.5
3.64
3.63
3.63
6. 试证用牛顿法求方程在[1,3]内的根是线性收敛的。 解:
令
y次迭代公式 故
从而 ,时, 故, 故牛顿迭代公式是线性收敛的 7. 应用牛顿法于方程, 导出求立方根的迭代公式,并讨论其收敛
性。
解:
相应的牛顿迭代公式为 迭代函数,, 则,
习题1.1
1. 什么叫数值方法?数值方法的基本思想及其优劣的评价标准如 何?
数值方法是利用计算机求解数学问题近似解的方法 2. 试证明 及
证明: (1)令
即 又 即 ⑵ 设,不妨设, 令 即对任意非零,有 下面证明存在向量,使得, 设,取向量。其中。 显然且任意分量为, 故有即证。 3. 古代数学家祖冲之曾以作为圆周率的近似值,问此近似值具有
解: (1)迭代公式,公式收敛
k
0
1
2
3
0
(2),, 局部收敛 k0 1 2 3
0.25
0.25098 0.25098
456789
1.5 1.322 1.421 1.367 1.397 1.380 1.390 1.384 1.387 1.386
2. 方程在附近有根,把方程写成三种不同的等价形式:
(1),对应迭代公式;
9
10
11
12
13
14
15
16
1.4650 1.46593 1.4653 1.46572 1.46548 1.46563 1.465534 1.465595
迭代公式(2):
k
0
1
2
3
计算机网络应用基础习题集(含答案)

《计算机网络应用基础》课程习题集【说明】:本课程《计算机网络应用基础》(编号为03009)共有单选题,判断改错题,简答题,计算题1,计算题2, 填空题等多种试题类型,其中,本习题集中有[简答题]等试题类型未进入。
一、单选题1.计算机网络中可以共享的资源包括( )A.硬件、软件、数据B.主机、外设、软件C.硬件、程序、数据D.主机、程序、数据2.在TCP/IP体系结构中,与OSI参考模型的网络层对应的是( )A.网络接口层B.互联层C.传输层D.应用层3.完成路径选择功能是在OSI模型的( )A.物理层B.数据链路层C.网络层D.运输层4.在以太网中,冲突( )A.是由于介质访问控制方法的错误使用造成的B.是由于网络管理员的失误造成的C.是一种正常现象D.是一种不正常现象5.下面关于以太网的描述哪个是正确的( )A.数据是以广播方式发送的。
B.所有节点可以同时发送和接受数据。
C.两个节点相互通信时,第3个节点不检测总线上的信号。
D.网络中有一个控制中心,用于控制所有节点的发送和接受。
6.为局域网上各工作站提供完整数据、目录等信息共享的服务器是()服务器。
A.磁盘 B.终端C.打印 D.文件7.接收端发现有差错时,设法通知发送端重发,直到正确的码字收到为止,这种差错控制方法称为()。
A.前向纠错 B.自动请求重发C.冗余检验 D.混合差错控制8. HDLC是()。
A.面向字符型的同步协议 B.面向比特型的同步协议C.异步协议 D.面向字计数的同步协议9.一般认为决定局域网特性的主要技术有三个,它们是()。
A.传输媒体、差错检测方法和网络操作系统B.通信方式、同步方式和拓朴结构C.传输媒体、拓扑结构和媒体访问控制方法D.数据编码技术、媒体访问控制方法和数据交换技术10.字符问的同步定时是指()。
A.字符问问隔任意 B.字符问比特凤间隔任意C.字符间间隔固定 D.字符内比特间间隔固定11. FDDI标准规定网络的传输介质采用( )A.非屏蔽双绞线B.屏蔽双绞线C.光纤D.同轴电缆12.在计算机网络中,所有的计算机均连接到一条公共的通信传输线路上,这种连接结构被称为( )A.总线结构B.环型结构C.星型结构D.网状结构13.下面不属于网卡功能的是( )A.实现介质访问控制B.实现数据链路层的功能C.实现物理层的功能D.实现调制和解调功能14.对于用集线器连接的共享式太网哪种描述是错误的( )A.集线器可以放大所接收的信号。
(完整版)基础工程习题集与参考答案

( 基础工程习题集与参照答案)一、选择题1、依据《建筑地基基础设计规范》的规定,计算地基承载力设计值时一定用内摩擦角的什么值来查表求承载力系数?A 设计值B标准值C均匀值2、砌体承重结构的地基同意变形值是由以下哪个值来控制的?A 沉降量B沉降差C局部倾斜3、在进行浅基础内力计算时,应采纳下述何种基底压力?A 基底净反力B基底总压力C基底附带压力4、当建筑物长度较大时,,或建筑物荷载有较大差异时,设置沉降缝,其原理是?A 减少地基沉降的举措B一种施工举措C减少不均匀沉降的建筑举措5、以下何种结构对地基的不均匀沉降最敏感?A框架结构B排架结构C筒体结构6、框架结构的地基同意变形值由以下何种性质的值控制?A 均匀沉降B沉降差C局部倾斜7 、高耸结构物的地基同意变形值除了要控制绝对沉降量外,还要由以下何种性质控制?A 均匀沉降B沉降差C倾斜8、当基底压力比较大、地基土比较脆弱而基础的埋置深度又受限制时,不可以采纳?A 筏板基础B刚性基础C扩展式基础9 、沉降计算时所采纳的基底压力与地基承载力计算时所采纳的基底压力的主要差异是?A荷载效应组合不一样及荷载性质(设计值或标准值)不一样B荷载性质不一样及基底压力性质不一样(总应力或附带应力)C荷载效应、荷载性质及基底压力性质都不一样10、防备不均匀沉降的举措中,设置圈梁是属于A 建筑举措B 结构举措C 施工举措11、刚性基础往常是指A 箱形基础B 钢筋混凝土基础C 无筋扩展基础12、砖石条形基础是属于哪一类基础?A 刚性基础B 柔性基础C 轻型基础13、沉降缝与伸缩缝的差异在于A 伸缩缝比沉降缝宽B 伸缩缝不可以填实 C 沉降缝一定从基础处断开14、赔偿基础是经过改变以下哪一个值来减小建筑物的沉降的?A 基底的总压力B 基底的附带压力C 基底的自重压力15 、对于上部结构为框架结构的箱形基础进行内力剖析时,应按下述何种状况来计算?A 局部曲折B 整体曲折C 同时考虑局部曲折和整体曲折16、全赔偿基础地基中不产生附带应力,所以,地基中.A 不会产生沉降B也会产生沉绛C会产生很大沉降17、依照建筑《地基基础设计规范》规定,需作地基承载力验算的建筑物的范围是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
雅克比法:
3 10 12 5
3 (k ) 2 (k ) x1( k +1) = − 5 x2 − 5 x3 −
,x
( k +1) 2
(k ) 1 (k ) =1 4 x1 − 2 x 3 + 5
18 i
,x
( k +1) 3 −4
(k ) 3 =−1 + 10 x (2 k ) + 5 x1
取初始向量 x
(2) x (3) x
3
= 1+ x2 =
,对应迭代公式 x 对应迭代公式 x
0
k +1
= 3 1 + x k2 ;
2
1 , x −1
k
+1 =
1 xk − 1
。
0
判断以上三种迭代公式在 x 解: (1) ϕ ( x) = 1 + x1
2
= 1 .5
的收敛性,选一种收敛公式求出 x
2 x3
−
2 3
= 1 .5
5
习题 3
1.
设有方程组
5 x1 + 2 x 2 + x3 = −12 − x1 + 4 x 2 + 2 x3 = 20 2 x − 3x + 10 x = 3 2 3 1
( k +1) (k )
∞
(1)
考察用 Jacobi 法,Gauss-Seidal 法解此方程组的收敛性; −x (2) 用 Jacobi 法及 Gauss-Seidal 法解方程组,要求当 x
1.
x
k +1 k k
'
<1
公式收敛
3 0.25098
k
0 0
1 0.25
2 0.25098
xk
x* ≈ 0.25098
− x) (2) ϕ ( x) = ln(4 ,x ln 2 xk +1 =
k 0
0
= 1.5
, ϕ (x )
0
'
<1
局部收敛
6 7 8 9 10
ln(4 − xk ) ln 2
1 2 3 4 5
355 = 0.266 ×10 −6 ≤ 0.5 × 101−7 113
该近似值具Байду номын сангаас 7 为有效数字。
1
4.
若 T(h)逼近其精确值 T 的截断误差为
R (T ) : = T (h) − T = ∑ Ai h 2i
i =1 ∞
其中,系数 A 与 h 无关。试证明由
i
T0 (h) = T (h) h 4 m Tm −1 ( ) − Tm−1 (h) 2 Tm(h) = , m = 1,2,L 4m − 1
y
次迭代公式 x
k +1
k +1
= xk −
( xk − 2)( xk + 3) 3 xk + 4
故e
= x* − xk +1 = 2 − xk −
( xk − 2)( xk + 3) ( xk − 2)(2 xk + 1) = 3 xk + 4 3xk + 4
4
ek = x* − xk = xk − 2
1
,迭代 18 次有 x − x < 10 (i=1,2,3) x = −3.999996 , x = 2.999974 , x = 2.000000 高斯-塞德尔法: 12 = x − x +5, x x =− x − x − ,x =− x + 5 取初始向量 x = x = x = 0 ,迭代 8 次有 x − x < 10 (i=1,2,3) x = −4.000033 , x = 2.999983 , x = 2.000002
2
xk
1.5
1.322
1.421
1.367
1.397
1.380
1.390
1.384
1.387
1.386
1.386
x* ≈ 1.386
2.
方程 x
3
− x2 −1 = 0
在 x = 1.5 附近有根,把方程写成三种不同的等价形式:
k
(1) x = 1 + x1 ,对应迭代公式 x
2
+1 = 1+
1 ; 2 xk
∞
k
(k ) i
h 2 k + 2i
当 m=k+1 时
k +1
i =1
∞ ∞ k +1 ( k ) h 2 k + 2i h 4 [ T + ∆ ( ) ] − [ T + ∆i( k ) (h) 2 k + 2 i ] 4 Tk ( ) − Tk (h) ∑ ∑ i 2 i =1 i =1 2 Tk + ( −T = −T 1 h)-T= 4k +1 − 1 4 k +1 − 1 ∞
证明: (1)令 x
x
j =1
r
= max xi
1≤i ≤ n
∞
= lim(∑ xi )1/ p = lim xr [∑ (
p p →∞ i =1 p →∞ i =1
n
n
xi xr
) p ]1/ p ≤ lim xr [∑ (
p →∞ i =1
n
xr xr
) p ]1/ p = lim xr ⋅ n1/ p = xr
1 + x2
ϕ ' ( x) = − x(1 + x 2 )
1 2
−
2 3
1 x −1
2 1.47929 11 1.4653
ϕ ' ( x) = − ( x − 1)
3 1.456976 12 1.46572
4 1.47108 13 1.46548
5 1.46209
6 1.46779 14 1.46563
p →∞
即x
∞
≤ xr
n p 1/ p
又 lim(∑ x
p →∞ i =1
i
)
≥ lim(∑ xr )1/ p = xr
p p →∞ i =1
n
即x ≥x x =x ⑵ 设 x = ( x ,...x ) ≠ 0 ,不妨设 A ≠ 0 ,
∞ r ∞ r
1 n
令 µ = max ∑ a
n 1≤i ≤ n j =1
n j =1 i0 j
0
≠0
,使得
0
∞ ∞
=µ
,
j
设 µ = ∑ a ,取向量 x 显然 x
0 ∞
= ( x1 ,...xn )T
n
。其中 x
n i =1
= sign( ai0 j )( j = 1, 2,..., n)
。
=1
且 Ax 任意分量为 ∑ a
0 i =1 n n i i =1 j =1
i0 j
5.
3 2
k +1
= ϕ ( xk )
是有局部收敛性。 在[3,4]中的根的近似值(精确到小数点后两位) 。
3
− 2x 2 − 4x − 7 = 0
f ' ( x) = 3x 2 − 4 x − 4
y
次迭代公式 x
k +1 = xk −
3 2 xk − 2 xk − 4 xk − 7 2 3 xk − 4 xk − 4
习题一 1. 什么叫数值方法?数值方法的基本思想及其优劣的评价标准如何? 数值方法是利用计算机求解数学问题近似解的方法 2. 试证明 x = max x , x = ( x , x , L x ) ∈ R 及 A = max ∑ a
n
T
n
∞
1≤i ≤ n
i
1
2
n
∞
1≤ i ≤ n
ij
, A = (aij ) ∈ R n×n .
k
0 3.5
1 3.64
2 3.63
3 3.63
xk
x* ≈ 3.63
试证用牛顿法求方程 ( x − 2) ( x + 3) = 0 在[1,3]内的根 x 解: 令 f ( x) = ( x − 2) ( x + 3)
6.
2
2
*
=2
是线性收敛的。
f ' ( x) = 3 x 2 − 2 x − 8 = ( x − 2)(3 x + 4)
附近的根到 4 位有效数字。
ϕ ' ( x) = −
2 3
ϕ ( x0 ) ' < 1 ϕ ( x0 ) ' < 1 ϕ ( x0 ) ' > 1
局部收敛 局部收敛 不是局部收敛
(2) ϕ ( x) = (3) ϕ ( x) = 迭代公式(1) :
0 1.5 9 1.4650 1 1.44444 10 1.46593
x j = ∑ ai0 j
,
故有 Ax
3.
0 ∞
= max
∑ aij x j = ∑ ai0 j = µ
即证。
355 古代数学家祖冲之曾以 113 作为圆周率 π 的近似值,问此近似值具有多少位有效数字? 325 解: x = 133 = & 0.314159292 ×10
1
x − x∗ = π −
从而
ek +1 2 xk + 1 = ek 3xk + 4
, k → ∞ 时, x
k
→2
故 k → ∞ , ee
