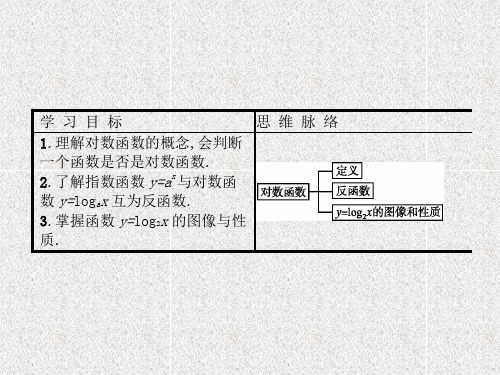
新人教A版必修一课件：第四章 4.4.1 对数函数的概念
合集下载
4.4.1 对数函数的概念 课件 高一数学同步精讲课件(人教A版2019必修第一册)原创精品
2
则方程
ax2-2x+2=4
1
即存在x∈[ ,2], 使得 a
2
2
成立.
1
1
令t= , 则t∈[ ,2],
2
1
在区间[ ,2]上有解,
2
2
= 2
所以
1 2 1
a=2(t+ ) 2
2
3
∈[ ,12]
2
1
4.已知集合P=[ ,2],函数y=log2(ax2-2x+2)的定义域
2
转
化
与
化
归
为Q .
函数图象必需与轴有公共点的问题.
1
2.设函数f(x)=f( )lgx+1,求f(10)的值.
对
偶
思
想
+
方
程
思
想
1
解析：用 替代原方程中的x，得
1
f( )=-f(x)lgx+1
,与原方程联立，
1+
解得：f(x)=
1+2
所以 f(10)=1
方法：结构造对偶式，联立两函数方程，可解出函
(1)若P∩Q≠，求实数a的取值范围；
1
2
(2)若方程log2(ax -2x+2)=2在[ ,2]内有解，求实
2
数a的取值范围.
方法总结：
(1)不等式在区间内有解问题，通过分离参数，转化
为求有关函数的最值问题;
(2)方程在区间内有解问题，通过分离参数，转化为
求有关函数的值域问题.
课堂小结
一、本节课学习的新知识
2
转
化
则方程
ax2-2x+2=4
1
即存在x∈[ ,2], 使得 a
2
2
成立.
1
1
令t= , 则t∈[ ,2],
2
1
在区间[ ,2]上有解,
2
2
= 2
所以
1 2 1
a=2(t+ ) 2
2
3
∈[ ,12]
2
1
4.已知集合P=[ ,2],函数y=log2(ax2-2x+2)的定义域
2
转
化
与
化
归
为Q .
函数图象必需与轴有公共点的问题.
1
2.设函数f(x)=f( )lgx+1,求f(10)的值.
对
偶
思
想
+
方
程
思
想
1
解析：用 替代原方程中的x，得
1
f( )=-f(x)lgx+1
,与原方程联立，
1+
解得：f(x)=
1+2
所以 f(10)=1
方法：结构造对偶式，联立两函数方程，可解出函
(1)若P∩Q≠，求实数a的取值范围；
1
2
(2)若方程log2(ax -2x+2)=2在[ ,2]内有解，求实
2
数a的取值范围.
方法总结：
(1)不等式在区间内有解问题，通过分离参数，转化
为求有关函数的最值问题;
(2)方程在区间内有解问题，通过分离参数，转化为
求有关函数的值域问题.
课堂小结
一、本节课学习的新知识
2
转
化
【课件】4.4.1、4.4.2 对数函数的概念、图象和性质(课件)(新教材人教版必修第一册)
解：(1)对数函数 y＝log2x， 因为它的底数 2>1， 所以它在(0，＋∞)上是增函数． 又 3.4＜8.5，于是 log23.4<log28.5. (2)对数函数 y＝log0.3x， 因为它的底数 0<0.3<1， 所以它在(0，＋∞)上是减函数． 又 1.8＜2.7，于是 log0.31.8>log0.32.7.
1．比较对数值大小的注意点 (1)比较两个同底数的对数大小首先要根据对数的底数来判断对 数函数的单调性，然后比较真数大小，再利用对数函数的单调性判 断两个对数值的大小．
(2)底数中含有参数时，需要对底数进行讨论． (3)对于不同底的对数，可以估算范围，如 log22<log23<log24，即 1<log23<2，从而借助中间值比较大小． 2．求 y＝logaf(x)型函数的值域的注意点 (1)先求定义域，进而确定 f(x)的取值范围； (2)利用对数函数 y＝logax 的单调性求出 logaf(x)的取值范围．
x∈[1，＋∞)时，y∈ 的特点
_[_0_，__＋__∞_)__
x∈[1，＋∞)时，y∈_(_－__∞_，__0_]_
对称性 函数 y＝logax 与 y＝ x 的图象关于_x_轴__对称
预习验收 衔接课堂
1．下列函数是对数函数的是( D ) A．y＝2＋log3x B．y＝loga(2a)(a>0，且 a≠1) C．y＝logax2(a>0，且 a≠1) D．y＝ln x
2．函数 y＝lgxx－＋11的定义域是( C ) A．(－1，＋∞) B．[－1，＋∞) C．(－1,1)∪(1，＋∞) D．[－1,1)∪(1，＋∞)
3．已知 f(x)＝log3x，则 f 95＋f(15)＝_3_. 4.若函数 f(x)＝loga(2x－3)(a>0，且 a≠1)的图象恒过定点 P，则 P 点的坐标是__(2_,_0_)_．
高一数学新人教版(A版)必修第1册《4.3.1 对数的概念》精品课件
概念辨析
1．思考辨析 (1)logaN 是 loga 与 N 的乘积．( ) (2)(－2)3＝－8 可化为 log(－2)(－8)＝3.( ) (3)对数运算的实质是求幂指数．( )
[答案] (1)× (2)× (3)√
2．若 a2＝M(a>0 且 a≠1)，则有( )
A．log2M＝a
B．logaM＝2
例 3 设 5log5(2x－1)＝25，则 x 的值等于( )
A．10
B．13
C．100
D．±100
(2)若 log3(lg x)＝0，则 x 的值等于________.
思路探究：(1)利用对数恒等式alogaN＝N求解；
(1)B (2)10
(2)利用logaa＝1，loga1＝0求解．
(1)由 5log5(2x－1)＝25 得 2x－1＝25，所以 x＝13，故选 B.
1
C．log39＝2 与 92＝3 D．log55＝1 与 51＝5
【答案】C [C 不正确，由 log39＝2 可得 32＝9.]
3．若 log2(logx9)＝1，则 x＝________. 【答案】3 [由 log2(logx9)＝1 可知 logx9＝2，即 x2＝9，∴x＝3(x＝－3 舍去)．] 4． log33＋3log32＝________. 【答案】3 [log33＋3log32＝1＋2＝3.]
上述问题实际上就是从2=1.11x ，3=1.11x ， 4=1.11x ，… 中分别求出x，即已知底数和幂的值，求指数．这是本节要学习 的对数．
对数的发明
对数
对数的创始人是苏格兰数学家纳皮尔（Napier，1550年 ~1617年）。他发明了供天文计算作参考的对数，并于1614 年在爱丁堡出版了《奇妙的对数定律说明书》，公布了他的 发明。恩格斯把对数的发明与解析几何的创始，微积分的建 立并称为17世纪数学的三大成就。
4.4.1对数函数的概念说课(教学课件)-高中数学人教A版(2019)必修第一册
设计意图
分层设计是为了让每 位同学都有获得感 ，增强 学习动力；基于因材施教 的原则 ，让不同的学生有 不同的发展；促使本节课 的教学目标在课后继续落 实.
再次体验类比方法的 实用性 ，为后续学习做好 铺垫.
板书设计
电子 屏幕
例1： （师生互动） 例2： （师生互动）
练习1：（学生板演）
谢聆 谢听
人民教育出版社A版 普通高中教科书 《数学》必修第一册
4.4.1 对数函数的概念
目录
1
【教材分析】
2 【学情分析学策略】
6 【教学过程】
教材分析
教材分析
逻辑论证依据 方法和过程 知识基础
背景 概念 图象和性质 应用
教材分析
更强调对数函数概念的建构和动态生成； 本节课通过挖掘函数定义的本质进行演绎
推理，抽象概括出对数函数的定义.
学情分析
知识 基础
对函数的认知已经由“变量说”转换为了“集合-对 应说” ，掌握了逻辑论证的依据.还学习了指数函数的相 关知识，能进行指数与对数的运算.
形高一 学生
能力 基础
经历了幂函数、指数函数学习方法和过程，体 会了研究一般函数的方法，具备了一定类比、数
结合的数学思想，积累了从具体到抽象、从特殊到 一般的数学活动经验.
设计意图
从多个层面进行回顾 ， 起到了梳理、提炼、升华 ， 检验的效果 ，也启发学生 要关注知识生成与发展的 过程 ，利用结构框图建构 单元学习意识、启示下一 节课学习的任务 ，提高学 生对本节课的整体认识.
教学过程 分层作业 巩固发展
基础作业
课本131页 练习第3题
提升作业
探究作业
类比幂函数、指数函数的研究方 法探究对数函数的图象和性质.
新教材2024版高中数学第四章指数函数与对数函数4.1指数课件新人教A版必修第一册
指数幂及其运算性质
1．分数指数幂的意义
正分数指数幂
m
规定：an
＝__n__a_m___(a＞0，m，n∈N*，且
n＞1)
分数 指数
1
负分数指数幂
规定：a－mn
＝
1
m
＝___n _a_m___(a＞0，m，n∈N*，且
an
幂
n＞1)
0 的分数 0 的正分数指数幂等于___0_____，0 的负分数指数
(1)a±2a12
1
b2
＋b＝ a ±b ；
1 2
1 2
2
(2)a－b＝ a ＋b a －b ； 1
1 1
1
2
2
2
2
3
(3)a2
＋b23
＝ a ＋b (a－a 1
1
1
2
2
2
1
b2
＋b)；
3
(4)a2
－b23
＝ a －b (a＋a 1
1
1
2
2
2
1
b2
＋b)．
易错警示 忽视条件限制致误 已知 x∈[1，2]，化简：(4 x－1)4＋6 (x2－4x＋4)3＝________．
1．(题型 2)下列运算结果中，正确的是
A．a2a3＝a5
B．(－a2)3＝(－a3)2
C．( a－1)0＝1
D．(－a2)3＝a6
()
【答案】A 【解析】a2a3＝a2+3＝a5，(－a2)3＝－a6≠(－a3)2＝a6，( a－1)0＝1， 若成立，需要满足 a≠1，(－a2)3＝－a6，故正确的是 A．故选 A．
第四章 指数函数与对数函数
4.1 指数
人教A版高中数学必修第一册第4章4-3-1对数的概念课件
第四章 指数函数与对数函数
4.3 对数 4.3.1 对数的概念
1．理解对数的概念，掌握对数的基本性质．(数学抽象) 学习
2．掌握指数式与对数式的互化，能应用对数的定义和性质解 任务
方程．(数学运算)
01
必备知识·情境导学探新知
某种细胞分裂时，由1个分裂成2个，2个分裂成4个，…． 问题 依次类推，那么1个这样的细胞分裂
表达式
ax＝N x＝logaN
a 底数 底数
名称 x
指数 对数
N 幂值 真数
知识点2 对数的基本性质 (1)负数和0没__有__对数； (2)loga1＝0_(a>0，且a≠1)； (3)logaa＝1_(a>0，且a≠1)．
填空： (1)ln e＝____1____；(2)lg 10＝____1____； (3)ln 1＝____0____；(4)lg 1＝___基础
1．下列选项中，可以求对数的是( )
A．0
B．－5 √C．π
D．－x2
C [根据对数的定义，得0和负数没有对数，所以选项A，B不可以 求对数，又－x2≤0，所以选项D没有对数，因为π>0，所以选项C可 以求对数．]
1234
√
1234
3．已知logx16＝2，则x等于( )
提醒 对数运算是指数运算的逆运算
思考 1．x＝logaN中为什么规定N>0? [提示] x＝logaN是由ax＝N(a>0，且a≠1)变形而来的，由于正数的 任意次幂都是正数，即ax＝N>0，所以要规定N>0．
思考 2．在指数式与对数式中，a，x，N这三个量有何异同？ [提示]
类别
指数式 对数式
x次得到细胞个数N是多少？分裂多少次得到细 胞个数为8个，256个呢？如果已知细胞分裂后 的个数N，如何求分裂次数呢？
4.3 对数 4.3.1 对数的概念
1．理解对数的概念，掌握对数的基本性质．(数学抽象) 学习
2．掌握指数式与对数式的互化，能应用对数的定义和性质解 任务
方程．(数学运算)
01
必备知识·情境导学探新知
某种细胞分裂时，由1个分裂成2个，2个分裂成4个，…． 问题 依次类推，那么1个这样的细胞分裂
表达式
ax＝N x＝logaN
a 底数 底数
名称 x
指数 对数
N 幂值 真数
知识点2 对数的基本性质 (1)负数和0没__有__对数； (2)loga1＝0_(a>0，且a≠1)； (3)logaa＝1_(a>0，且a≠1)．
填空： (1)ln e＝____1____；(2)lg 10＝____1____； (3)ln 1＝____0____；(4)lg 1＝___基础
1．下列选项中，可以求对数的是( )
A．0
B．－5 √C．π
D．－x2
C [根据对数的定义，得0和负数没有对数，所以选项A，B不可以 求对数，又－x2≤0，所以选项D没有对数，因为π>0，所以选项C可 以求对数．]
1234
√
1234
3．已知logx16＝2，则x等于( )
提醒 对数运算是指数运算的逆运算
思考 1．x＝logaN中为什么规定N>0? [提示] x＝logaN是由ax＝N(a>0，且a≠1)变形而来的，由于正数的 任意次幂都是正数，即ax＝N>0，所以要规定N>0．
思考 2．在指数式与对数式中，a，x，N这三个量有何异同？ [提示]
类别
指数式 对数式
x次得到细胞个数N是多少？分裂多少次得到细 胞个数为8个，256个呢？如果已知细胞分裂后 的个数N，如何求分裂次数呢？
4.4.1对数函数的概念课件(人教版)
∴
1－x＞0， x＜1，
∴－1＜x＜1.∴该函数的定义域为(－1,1)．
5－x＞0， (2)要使函数式有意义，需 x－2＞0，
x－2≠1，
x＜5， ∴ x＞2，
x≠3，
∴2＜x＜5，且 x≠3.
∴该函数的定义域为(2,3)∪(3,5).
20
4.4.1 对数函数的概念 课堂小结
1. 对数函数概念 2. 对数函数的特征
4.4.1 对数函数的概念 变式训练
2、点A(8,-3)和B(n,2)在同一个对数函数图象上,则
—14
n=______.
解：设对数函数为f(x)=logax(a>0,且a≠1).
则由题意可得f(8)=-3,即loga8=-3,所以a-3=8,
则a=
8-
1 3
1 2
17
4.4.1 对数函数的概念 典型例题——对数函数型的定义域
10
4.4.1 对数函数的概念 情景导入 阅读课本130-131页，思考并完成以下问题 1. 对数函数的概念是什么？ 2. 对数函数解析式的特征？
11
4.4.1 对数函数的概念 研探新知 知识点一 对数函数的概念 函数y＝logax(a＞0，且a≠1)叫做对数函数， 其中x是自变量，函数的定义域是(0，＋∞)．
2
①求f(x)的解析式;
②解方程f(x)=2.
解：
①由题意设f(x)=logax(a>0,且a≠1),由函数图象过点（ 可得f(4)= 1
4，1 ） 2
即loga4=
1 2
2
1
,所以4=a2 ,解得a=16,故f(x)=log16x.
②方程f(x)=2,即log16x=2
所以x=162=256.
新人教A版必修一对数函数的概念对数函数图像和性质课件(22张)
;
(2)下列函数中,是对数函数的是
.(填序号)
①y=log4x;②y=log2(3x);③y=logx2;④y=log3(x-1);⑤y=log2x2;
1
⑥y= 2 log3x.
探究一
探究二
探究三
易错辨析
解析:(1)设 f(x)=logax(a>0,且 a≠1),
1
依题意有 loga4=-1,故 a=4,
探究三
易错辨析
对于含有偶次根式中被开方式为对数式时,要注意被开方的代数
式为非负,还要顾及对数式中本身的真数大于0这一隐含信息,错解
中显然忘记了真数大于0这一隐含条件.
1
2
3
4
5
6
1.下列函数中,是对数函数的是(
A.y=log2x-1
B.y=logx3x
C.y= log 1 x
D.y=3log5x
2
探究一
探究二
探究三
易错辨析
变式训练2函数f(x)=3x(0<x≤2)的反函数的定义域为(
A.(0,+∞)
B.(1,9]
C.(0,1)
D.[9,+∞)
解析:∵ 0<x≤2,∴1<3x≤9,
即函数f(x)的值域为(1,9].
故函数f(x)的反函数的定义域为(1,9].
答案:B
)
探究一
探究二
探究三
易错辨析
C.
2
D.x2
解析:由题意,知 f(x)=logax.∵f(x)的图像过点(√,a),
1
∴a=loga√.∴a=2.∴f(x)=log 1 x.故选 B.
2
答案:B
函数y=logax(a>0,且a≠1)的反函数是y=ax(a>0,且a≠1);函数
(2)下列函数中,是对数函数的是
.(填序号)
①y=log4x;②y=log2(3x);③y=logx2;④y=log3(x-1);⑤y=log2x2;
1
⑥y= 2 log3x.
探究一
探究二
探究三
易错辨析
解析:(1)设 f(x)=logax(a>0,且 a≠1),
1
依题意有 loga4=-1,故 a=4,
探究三
易错辨析
对于含有偶次根式中被开方式为对数式时,要注意被开方的代数
式为非负,还要顾及对数式中本身的真数大于0这一隐含信息,错解
中显然忘记了真数大于0这一隐含条件.
1
2
3
4
5
6
1.下列函数中,是对数函数的是(
A.y=log2x-1
B.y=logx3x
C.y= log 1 x
D.y=3log5x
2
探究一
探究二
探究三
易错辨析
变式训练2函数f(x)=3x(0<x≤2)的反函数的定义域为(
A.(0,+∞)
B.(1,9]
C.(0,1)
D.[9,+∞)
解析:∵ 0<x≤2,∴1<3x≤9,
即函数f(x)的值域为(1,9].
故函数f(x)的反函数的定义域为(1,9].
答案:B
)
探究一
探究二
探究三
易错辨析
C.
2
D.x2
解析:由题意,知 f(x)=logax.∵f(x)的图像过点(√,a),
1
∴a=loga√.∴a=2.∴f(x)=log 1 x.故选 B.
2
答案:B
函数y=logax(a>0,且a≠1)的反函数是y=ax(a>0,且a≠1);函数
新教材人教A版第四章4.4.1对数函数的概念课件(30张)
B．2
C．1
D．0
a2＋a－5＝1， 【解析】选 B.因为函数 f(x)＝(a2＋a－5)logax 为对数函数，所以a>0，
a≠1，
解得 a＝2.
2．对数函数的图象过点 M(16，4)，则此对数函数的解析式为( )
A．y＝log4x
B．y＝log1 x
4
C．y＝log1 x
2
D．y＝log2x
【解析】选 D.设对数函数的解析式为 y＝loga x(a>0，且 a≠1)，由于对数函数的图
【解析】(1)由题意得，x＝(1＋8%) y， 即 x＝1.08y，y∈[0，＋∞) . 可得 y＝log1.08x，x∈[1，＋∞) .
(2)令 x＝43 ，得 y＝log1.0843 ＝2lglg21－.0l8g 3 ＝0.6002.－0303.477 ≈3.79.则该企业全年投入的研发资金开始超过43 的年份是 2024 年．
象过点 M(16，4)，
所以 4＝loga16，得 a＝2.所以对数函数的解析式为 y＝log2x.
3．函数 f(x)＝ln (1－x)的定义域是( ) A．(0，1) B．[0，1) C．(1，＋∞)
D．(－∞，1)
【解析】选 D.由 1－x>0 得 x<1.
4．已知对数函数
f(x)的图象过点(8，3)，则
函数 f(x)＝ln (2x－4)的定义域是( ) A．(0，2) B．(0，2] C．[2，＋∞)
D．(2，＋∞)
【解析】选 D.要使 f(x)有意义，则：2x－4>0，所以 x>2.所以 f(x)的定义域为(2， ＋∞).
素养发展·创新应用
应用类型 实际问题中的对数函数(数学建模) 【典例】某企业 2020 年全年投入研发资金为 1，为激励创新，该企业计划今后每 年投入的研发资金比上年增长 8%，该企业 y 年后全年投入的研发资金为 x， (1)求 y 关于 x 的函数关系式． (2)求该企业全年投入的研发资金开始超过43 的年份是哪一年？ (参考数据：lg 1.08≈0.033，lg 2≈0.301，lg 3≈0.477)
高中数学人教A版必修第一册第四章4.4.1对数函数的概念课件
引入新知 y loga x (a 0,且a 1)
思考：(1)定义中为什么规定 a 0且a 1 呢？
（2）如何根据对数函数的定义判断一个 函数是否为一个对数函数呢？
①底数a为大于0且不等于1的常数． ②自变量x在真数的位置上，且x的系数是1. ③logax系数是1.
练习：判断以下函数是对数函数的是
8.已知函数f
(x)
loga
x 1(a x 1
0, 且a
1).
(1)求f (x)的定义域；
(2)判断函数的奇偶性.
解：(1) x 1 0, (x 1)(x 1) 0 x 1
x 1或x 1, 定义域为{x | x 1或x 1}
(2)由(1)知定义域为{x | x 1或x 1}关于原点对称
f
(x)
loga
x 1 x 1
loga
x 1 x 1
log
a
x 11
x 1
loga
x 1 x 1
f
(x)
f (x)为奇函数
作业
课本P140页A组第1题
由a a
2 2a 8 0 1 0且a 1
, 0
得a 4
巩固新知 金版P91【跟踪训练】
1.若函数f (x) log(a1) x a2 2a 8是对数函数，则a _4___
由a a
2 2a 8 0 1 0且a 1
, 0
得a 4
2.若对数函数的图象经过点M (8,3)，则f 1 ___-1____
4.4.1 对数函数的概念
BUSINESS
REPORT
复习
计算下列各式的值：
log2 1 0
log2 2 1
log2 4 2 log2 8 3
数学人教A版必修第一册4.4.1对数函数的概念课件
答案：1
4．已知对数函数 f(x)的图象过点 P(8,3)，则
1
f32＝________.
解析：设对数函数 f(x)＝logax(a>0，且 a≠1)，
∵f(x)的图象过点 P(8,3)，
∴3＝loga8，∴a3＝8，a＝2.
1
1
∴f(x)＝log2x.f32＝log2 ＝log22－5＝－5.
物价x
年数y
1
0
2
3
4
5
6
7
8
解: (1)由题意可知，经过y年后物价x为
x= (1+5%)y,
即 x= 1.05y (y∈[0，+∞)) .
由指数与对数的关系，可得
y= log1.05x (x∈[1，+∞)) . 当 x= 2时, y ≈ 14 .
所以，该地区的物价经过14年后会翻一番 .
9
10
例2 (2)填写下表，并根据表中的数据，说明该地物价的
【变式】某公司制定了一个激励销售人员的嘉奖方案：当销售利润不超过10万
元时，按销售利润的15%进行嘉奖；当销售利润超过10万元时，若超出A万元，
则超出部分按25 ( + 1)进行嘉奖.记奖金为(单位：万元).
(1)写出奖金关于销售利润的关系式；
解:(1)由题意知 = 0.15，0 ≤ ≤ 10，
1.5 + 25 ( − 9)， > 10.
【变式】某公司制定了一个激励销售人员的嘉奖方案：当销售利润不超过10万
元时，按销售利润的15%进行嘉奖；当销售利润超过10万元时，若超出A万元，
则超出部分按25 ( + 1)进行嘉奖.记奖金为(单位：万元).
4．已知对数函数 f(x)的图象过点 P(8,3)，则
1
f32＝________.
解析：设对数函数 f(x)＝logax(a>0，且 a≠1)，
∵f(x)的图象过点 P(8,3)，
∴3＝loga8，∴a3＝8，a＝2.
1
1
∴f(x)＝log2x.f32＝log2 ＝log22－5＝－5.
物价x
年数y
1
0
2
3
4
5
6
7
8
解: (1)由题意可知，经过y年后物价x为
x= (1+5%)y,
即 x= 1.05y (y∈[0，+∞)) .
由指数与对数的关系，可得
y= log1.05x (x∈[1，+∞)) . 当 x= 2时, y ≈ 14 .
所以，该地区的物价经过14年后会翻一番 .
9
10
例2 (2)填写下表，并根据表中的数据，说明该地物价的
【变式】某公司制定了一个激励销售人员的嘉奖方案：当销售利润不超过10万
元时，按销售利润的15%进行嘉奖；当销售利润超过10万元时，若超出A万元，
则超出部分按25 ( + 1)进行嘉奖.记奖金为(单位：万元).
(1)写出奖金关于销售利润的关系式；
解:(1)由题意知 = 0.15，0 ≤ ≤ 10，
1.5 + 25 ( − 9)， > 10.
【变式】某公司制定了一个激励销售人员的嘉奖方案：当销售利润不超过10万
元时，按销售利润的15%进行嘉奖；当销售利润超过10万元时，若超出A万元，
则超出部分按25 ( + 1)进行嘉奖.记奖金为(单位：万元).
对数函数的概念课件-高一数学人教A版(2019)必修第一册
D
A. B. C. D.
[解析] 由题意得 解得 ，所以函数 的定义域是 .故选D.
探究点二 求与对数函数有关的函数的定义域
（3）若函数 的定义域为 ，则 ( )
B
A.1 B. C.2 D.无法确定
[解析] 由函数 的定义域为 ，得 的解集为 ，即 且 的根为 ，故 .故选B.
4.4.1 对数函数的概念
1.理解对数函数的概念.2.会求与对数函数有关的函数定义域.3.了解对数函数在生产实际中的简单应用.
01
新课导入
问题1：拉面师傅在做兰州拉面时，从1根拉扯成2根，2根拉扯成4根，4根拉扯成8根……若已知师傅拉面了x次，如何表示面条根数y？若已知一碗面条根数是y，又如何表示拉面次数x？
a>0，且a≠1
1
自变 x
归纳小结
【思考1】对数的概念中，真数N需满足什么条件？为什么？
提示：N>0.因为0和负数没有对数.
【思考2】对数函数的概念中，自变量x的取值范围是什么？对数型函数需要满足什么条件呢？
提示：x>0.对数型函数需要满足的真数部分大于0，底数部分大于0且不等于1.
对数函数的定义域
探究点一 对数函数的概念及应用
例2（1） 已知函数 的定义域为 ,函数 的定义域为 ，则 ( )
D
A. B. C. D.
[解析] 由 得 , .由 得 ，故 , .故选D.
探究点二 求与对数函数有关的函数的定义域
（2）[2023·广西南宁三中高一月考] 函数 的定义域是( )
03
当堂检测
探究点一 对数函数的概念及应用
例1（1） 给出下列函数： ； ； ； .其中是对数函数的为______.（填序号）
A. B. C. D.
[解析] 由题意得 解得 ，所以函数 的定义域是 .故选D.
探究点二 求与对数函数有关的函数的定义域
（3）若函数 的定义域为 ，则 ( )
B
A.1 B. C.2 D.无法确定
[解析] 由函数 的定义域为 ，得 的解集为 ，即 且 的根为 ，故 .故选B.
4.4.1 对数函数的概念
1.理解对数函数的概念.2.会求与对数函数有关的函数定义域.3.了解对数函数在生产实际中的简单应用.
01
新课导入
问题1：拉面师傅在做兰州拉面时，从1根拉扯成2根，2根拉扯成4根，4根拉扯成8根……若已知师傅拉面了x次，如何表示面条根数y？若已知一碗面条根数是y，又如何表示拉面次数x？
a>0，且a≠1
1
自变 x
归纳小结
【思考1】对数的概念中，真数N需满足什么条件？为什么？
提示：N>0.因为0和负数没有对数.
【思考2】对数函数的概念中，自变量x的取值范围是什么？对数型函数需要满足什么条件呢？
提示：x>0.对数型函数需要满足的真数部分大于0，底数部分大于0且不等于1.
对数函数的定义域
探究点一 对数函数的概念及应用
例2（1） 已知函数 的定义域为 ,函数 的定义域为 ，则 ( )
D
A. B. C. D.
[解析] 由 得 , .由 得 ，故 , .故选D.
探究点二 求与对数函数有关的函数的定义域
（2）[2023·广西南宁三中高一月考] 函数 的定义域是( )
03
当堂检测
探究点一 对数函数的概念及应用
例1（1） 给出下列函数： ； ； ； .其中是对数函数的为______.（填序号）
4.4.1 对数函数的概念与对数函数的图象和性质课件ppt
4
定义域为( ,1).
5
探究三
指数函数与对数函数关系的应用
例3(2020四川宜宾高一检测)已知函数f(x)=log2x,若函数g(x)是f(x)的反函数,
则f(g(2))=(
A.1
B.2
)
C.3
D.4
答案 B
解析 ∵g(x)是f(x)的反函数,∴g(x)=2x.
∵g(2)=22=4,∴f(g(2))=f(4)=log24=2.
单调递增.
图1
(2)∵f(x)=log5|x|,∴f(x)是偶函数,其图象如图2所示.其定义域为
(-∞,0)∪(0,+∞),值域为R,函数的单调递增区间为(0,+∞),单调递减区间为
(-∞,0).
图2
探究五
对数型复合函数的单调性问题
(1)求函数f(x)=
log2)若函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,求实数a的取值范围.
2
∴-1≤2log 1 x≤1,即
2
2
1 -1
1 1
1
log 1 (2) ≤2log 1 x≤log 1 (2) ,化简可得2≤x2≤2.
2
2
2
2
再由 x>0 可得 2 ≤x≤ 2,故函数 f(x)的定义域为[ 2 , 2].
反思感悟 求解与对数函数有关的函数的定义域的方法
(1)求与对数函数有关的函数的定义域时,除遵循前面已学过的求函数定义
y=log 1 x,即 f(x)=log 1 x,所以
2
2
1
1
g
f(4x-1)=lo (4x-1),其定义域满足 4x-1>0,即 x>4.故定义域为
定义域为( ,1).
5
探究三
指数函数与对数函数关系的应用
例3(2020四川宜宾高一检测)已知函数f(x)=log2x,若函数g(x)是f(x)的反函数,
则f(g(2))=(
A.1
B.2
)
C.3
D.4
答案 B
解析 ∵g(x)是f(x)的反函数,∴g(x)=2x.
∵g(2)=22=4,∴f(g(2))=f(4)=log24=2.
单调递增.
图1
(2)∵f(x)=log5|x|,∴f(x)是偶函数,其图象如图2所示.其定义域为
(-∞,0)∪(0,+∞),值域为R,函数的单调递增区间为(0,+∞),单调递减区间为
(-∞,0).
图2
探究五
对数型复合函数的单调性问题
(1)求函数f(x)=
log2)若函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,求实数a的取值范围.
2
∴-1≤2log 1 x≤1,即
2
2
1 -1
1 1
1
log 1 (2) ≤2log 1 x≤log 1 (2) ,化简可得2≤x2≤2.
2
2
2
2
再由 x>0 可得 2 ≤x≤ 2,故函数 f(x)的定义域为[ 2 , 2].
反思感悟 求解与对数函数有关的函数的定义域的方法
(1)求与对数函数有关的函数的定义域时,除遵循前面已学过的求函数定义
y=log 1 x,即 f(x)=log 1 x,所以
2
2
1
1
g
f(4x-1)=lo (4x-1),其定义域满足 4x-1>0,即 x>4.故定义域为
对数函数的概念-高一数学课件(人教A版2019必修第一册)
（5） =
解：（1）定义域：{ ∣ ＜}
（4）定义域： ≠
（2）定义域：{ ∣
＜＜，或＞}
（3）定义域：{ ∣ ＜ }
（5）定义域：
≥
小结
（1）对数函数的概念
（2）对数函数的定义域
函数 = > 且 ≠ 叫做对数函数
4
5
6
7
8
9
10
0
14
23
28
33
37
40
43
45
47
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增
加1倍所需的时间在逐渐缩小.
当堂练习
求下列函数的定义域：（1） = −
（2） =
−
（3） =
（4） = ( > , 且 ≠ )
第四章指数函数与对数函数
4.4.1对数函数的概念
课程标准
通过具体实例，了解对数函数的概念。
能用描点法或借助计算工具画出具体对数函数的图象，
探索并了解对数函数的单调性与特殊点。
复习回顾
回顾1 什么是函数？
函数的概念:一般地， 设、是非空的数集，如果按照某个确定的对应关系
，使对于集合中的任意一个数，在集合中都有唯一确定的数和它对应，
因为 − > ,即 < ,
所以函数 = ( − )的定义域是{| < }.
例题讲解
例2 假设某地初始物价为,每年以%的增长率递增,经过年后的
物价为.
(1)该地的物价经过几年后会翻一番？
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
解：（1）定义域：{ ∣ ＜}
（4）定义域： ≠
（2）定义域：{ ∣
＜＜，或＞}
（3）定义域：{ ∣ ＜ }
（5）定义域：
≥
小结
（1）对数函数的概念
（2）对数函数的定义域
函数 = > 且 ≠ 叫做对数函数
4
5
6
7
8
9
10
0
14
23
28
33
37
40
43
45
47
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增
加1倍所需的时间在逐渐缩小.
当堂练习
求下列函数的定义域：（1） = −
（2） =
−
（3） =
（4） = ( > , 且 ≠ )
第四章指数函数与对数函数
4.4.1对数函数的概念
课程标准
通过具体实例，了解对数函数的概念。
能用描点法或借助计算工具画出具体对数函数的图象，
探索并了解对数函数的单调性与特殊点。
复习回顾
回顾1 什么是函数？
函数的概念:一般地， 设、是非空的数集，如果按照某个确定的对应关系
，使对于集合中的任意一个数，在集合中都有唯一确定的数和它对应，
因为 − > ,即 < ,
所以函数 = ( − )的定义域是{| < }.
例题讲解
例2 假设某地初始物价为,每年以%的增长率递增,经过年后的
物价为.
(1)该地的物价经过几年后会翻一番？
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
人教版(新教材)高中数学第一册(必修1)精品课件：4.4.1 对数函数的概念
2 题型探究
PART TWO
一、对数函数的概念及应用
例1 (1)下列给出的函数：
①y＝log5x＋1；②y＝logax2(a>0，且a≠1)；③ y
log (
3 1)
x; ④ y＝log32x；⑤y＝logx
3
(x>0，且x≠1)；⑥ y log 2 x. 其中是对数函数的为
π
A.③④⑤
B.②④⑥
解析
a2－2a－3＝0， 依题意有a>0，
a≠1，
解得 a＝3.
12345
课堂小结
KE TANG XIAO JIE
1.知识清单： (1)对数函数的定义. (2)对数函数的定义域. 2.方法归纳：待定系数法. 3.常见误区：易忽视对数函数底数有限制条件.
跟踪训练1 (1)下列函数表达式中，是对数函数的有
①y＝logx2；②y＝logax(a∈R)；③y＝log8x；④y＝ln x；⑤y＝logx(x＋2)；
⑥y＝log2(x＋1).
A.1个
√B.2个
C.3个
D.4个
(2)若对数函数f(x)的图象过点(4，－2)，则f(8)＝__－__3____.
二、与对数函数有关的定义域
例2 求下列函数的定义域. (1)y＝loga(3－x)＋loga(3＋x)；
解 由33＋－xx>>00，， 得－3<x<3， ∴函数的定义域是(－3,3).
(2)y＝log2(16－4x)；
解 由16－4x>0，得4x<16＝42， 由指数函数的单调性得x<2， ∴函数y＝log2(16－4x)的定义域为(－∞，2).
解析 设f(x)＝logax(a>0，且a≠1)， 由图象过点M(8,3)，则有3＝loga8， 解得a＝2. 所以对数函数的解析式为f(x)＝log2x， 所以 f 12＝log212＝－1.
人教A版高中同步学案数学必修第一册精品课件 第四章 对数函数-4.4.1 对数函数的概念
1
2
解要使函数式有意义,需ቊ
解得 > ,且 ≠ .所以函数 = log (3−1) 5的定
3
3
3 − 1 ≠ 1,
1
3
2
3
义域是{| > , 且 ≠ }.
（2） =
ln(4−)
.
−3
4 − > 0,
解要使函数式有意义,需ቊ
解得 < 4,且 ≠ 3.所以函数
− 3 ≠ 0,
第四章
4.4 对数函数
4.4.1 对数函数的概念
A级 必备知识基础练
1.下列函数,其中为对数函数的是( C
A. = log 1 (−)B. = 2 log 4 (1 − )
)
2
C. = ln D. = log (2+)
2.下列函数相等的是( C
)
A. = log 3 2 与 = 2 log 3 B. = lg 10 与 = 10lg
=
ln(4−)
的定义域是{|
−3
< 4,且 ≠ 3}.
B级 关键能力提升练
12.每年红嘴鸥都要从西伯利亚飞越数千公里来到美丽的昆明过冬,科学家经过测量发
现候鸟的飞行速度可以表示为函数 =
1
log 3
2
100
− lg 0 ,单位是km/min,其中表示候
鸟每分钟耗氧量的单位数,常数0 表示测量过程中候鸟每分钟的耗氧偏差.（结果保留
[0,1)
7.函数 = ln(1 − )的定义域为______.
8.已知函数() = log 2 ( 2 + ).若(3) = 1,则 =
−7
____.
9.“每天进步一点点”可以用数学来诠释,假如你今天的数学水平是1,以后每天比前一天
2
解要使函数式有意义,需ቊ
解得 > ,且 ≠ .所以函数 = log (3−1) 5的定
3
3
3 − 1 ≠ 1,
1
3
2
3
义域是{| > , 且 ≠ }.
（2） =
ln(4−)
.
−3
4 − > 0,
解要使函数式有意义,需ቊ
解得 < 4,且 ≠ 3.所以函数
− 3 ≠ 0,
第四章
4.4 对数函数
4.4.1 对数函数的概念
A级 必备知识基础练
1.下列函数,其中为对数函数的是( C
A. = log 1 (−)B. = 2 log 4 (1 − )
)
2
C. = ln D. = log (2+)
2.下列函数相等的是( C
)
A. = log 3 2 与 = 2 log 3 B. = lg 10 与 = 10lg
=
ln(4−)
的定义域是{|
−3
< 4,且 ≠ 3}.
B级 关键能力提升练
12.每年红嘴鸥都要从西伯利亚飞越数千公里来到美丽的昆明过冬,科学家经过测量发
现候鸟的飞行速度可以表示为函数 =
1
log 3
2
100
− lg 0 ,单位是km/min,其中表示候
鸟每分钟耗氧量的单位数,常数0 表示测量过程中候鸟每分钟的耗氧偏差.（结果保留
[0,1)
7.函数 = ln(1 − )的定义域为______.
8.已知函数() = log 2 ( 2 + ).若(3) = 1,则 =
−7
____.
9.“每天进步一点点”可以用数学来诠释,假如你今天的数学水平是1,以后每天比前一天
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解析 设f(x)＝logax(a>0，且a≠1)， 由图象过点M(8,3)，则有3＝loga8， 解得a＝2. 所以对数函数的解析式为f(x)＝log2x， 所以 f 12＝log212＝－1.
反思
感悟 判断一个函数是否为对数函数的方法 对数函数必须是形如y＝logax(a>0，且a≠1)的形式，即必须满足以下条件： (1)对数式系数为1. (2)底数为大于0且不等于1的常数. (3)对数的真数仅有自变量x.
二、与对数函数有关的定义域
例2 求下列函数的定义域. (1)y＝loga(3－x)＋loga(3＋x)；
解 由33＋－xx>>00，， 得－3<x<3， ∴函数的定义域是(－3,3).
(2)y＝log2(16－4x)；
解 由16－4x>0，得4x<16＝42， 由指数函数的单调性得x<2， ∴函数y＝log2(16－4x)的定义域为(－∞，2).
2 题型探究
PART TWO
一、对数函数的概念及应用
例1 (1)下列给出的函数：
①y＝log5x＋1；②y＝logax2(a>0，且a≠1)；③ y
log (
31)
x;
④ y＝log32x；⑤y＝logx
3
(x>0，且x≠1)；⑥ y log 2 x. 其中是对数函数的为
π
A.③④⑤
B.②④⑥
三、对数函数模型的应用
例3 大西洋鲑鱼每年都要逆流而上，游回产地产卵，经研究发现鲑鱼的游速可以
表示为函数v＝
1θ 2log3100
，单位是m/s，θ是表示鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是900个单位时，它的游速是多少？
解 由 v＝12log310θ0可知， 当 θ＝900 时，v＝12log3910000＝12log39＝1(m/s). 所以当一条鲑鱼的耗氧量是900个单位时，它的游速是1 m/s.
4.对数函数 f(x)过点(9,2)，则 f 13＝___－__1___. 解析 设f(x)＝logax(a>0且a≠1)，loga9＝2， ∴a2＝9，∴a＝3(舍a＝－3)， ∴f(x)＝log3x，∴f 13＝log313＝－1.
12345
5.函数f(x)＝logax＋a2－2a－3为对数函数，则a＝____3____.
C.①③⑤⑥
√D.③⑥
解析 ①中对数式后面加1，所以不是对数函数； ②中真数不是自变量x，所以不是对数函数； ③和⑥符合对数函数概念的三个特征，是对数函数； ④不是对数函数； ⑤中底数是自变量x，而非常数a，所以不是对数函数，故③⑥正确.
(2)已知对数函数的图象过点 M(8,3)，则 f 12＝__－__1____.
思考 函数y＝logπx，y＝log23x 是对数函数吗？ 答案 y＝logπx是对数函数，y＝log23x 不是对数函数.
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.由y＝logax，得x＝ay，所以x>0.( √ ) 2.y＝log2x2是对数函数.( × ) 3.若对数函数y＝logax，则a>0.( √ ) 4.函数y＝loga(x－1)的定义域为(0，＋∞).( × )
跟踪训练1 (1)下列函数表达式中，是对数函数的有
①y＝logx2；②y＝logax(a∈R)；③y＝log8x；④y＝ln x；⑤y＝logx(x＋2)；
⑥y＝log2(x＋1).
A.1个
√B.2个
C.3个
D.4个
(2)若对数函数f(x)的图象过点(4，－2)，则f(8)＝__－__3____.
x2－4≥0， 解 要使函数有意义，需x＋3>0，
x＋3≠1，
即xx≤ >－－32，或x≥2， x≠－2，
即－3<x<－2 或 x≥2，
故所求函数的定义域为(－3，－2)∪[2，＋∞).
(2)y＝ 21－x＋ln(x＋1). 解 要使函数有意义，需x2＋－1x>>00，， 即xx><－2，1， ∴－1<x<2. 故所求函数的定义域为(－1,2).
D.y＝2logax(a>0且a≠1)
12345
2.函数y＝log2(x－2)的定义域是
A.(0，＋∞)
√C.(2，＋∞)
B.(1，＋∞) D.[4，＋∞)
12345
3.函数 f(x)＝ 3－x＋lg(x＋1)的定义域为
A.[－1,3)
√C.(－1,3]
B.(－1,3) D.[－1,3]
12345
第四章 4.4 对数函数
学习目标
XUEXIMUBIAO
1.理解对数函数的概念. 2.会求简单对数函数的定义域. 3.了解对数函数在生产实际中的简UOYIN
知识梳理 题型探究 随堂演练
1 知识梳理
PART ONE
知识点 对数函数的概念
一般地，函数 y＝logax(a>0，且a≠1) 叫做对数函数，其中x是自变量，函数的定义域 是 (0，＋∞) .
(1)依题意，找出或建立数学模型.
(2)依实际情况确定解析式中的参数.
(3)依题设数据解决数学问题.
(4)得出结论.
3 随堂演练
PART THREE
1.下列函数为对数函数的是 A.y＝logax＋1(a>0且a≠1) B.y＝loga(2x)(a>0且a≠1)
√C.y＝log(a－1)x(a>1且a≠2)
解析
a2－2a－3＝0， 依题意有a>0，
a≠1，
解得 a＝3.
12345
课堂小结
KE TANG XIAO JIE
1.知识清单： (1)对数函数的定义. (2)对数函数的定义域. 2.方法归纳：待定系数法. 3.常见误区：易忽视对数函数底数有限制条件.
(2)某条鲑鱼想把游速提高1 m/s，那么它的耗氧量的单位数是原来的多少倍？
解 设鲑鱼原来的游速、耗氧量为v1，θ1，提速后的游速、耗氧量为v2，θ2. 由 v2－v1＝1，即12log31θ020－12log31θ010＝1，得θθ21＝9. 所以耗氧量的单位数为原来的9倍.
反思 感悟
对数函数应用题的解题思路
(3)y＝log1－x5. 解 依题意知11－－xx≠>01，， 得 x<1 且 x≠0， ∴定义域为(－∞，0)∪(0,1).
反思
感悟 求含对数式的函数定义域关键是真数大于0，底数大于0且不为1.如需对
函数式变形，需注意真数、底数的取值范围是否改变.
跟踪训练2 求下列函数的定义域.
(1)y＝lgxx2＋－34；
反思
感悟 判断一个函数是否为对数函数的方法 对数函数必须是形如y＝logax(a>0，且a≠1)的形式，即必须满足以下条件： (1)对数式系数为1. (2)底数为大于0且不等于1的常数. (3)对数的真数仅有自变量x.
二、与对数函数有关的定义域
例2 求下列函数的定义域. (1)y＝loga(3－x)＋loga(3＋x)；
解 由33＋－xx>>00，， 得－3<x<3， ∴函数的定义域是(－3,3).
(2)y＝log2(16－4x)；
解 由16－4x>0，得4x<16＝42， 由指数函数的单调性得x<2， ∴函数y＝log2(16－4x)的定义域为(－∞，2).
2 题型探究
PART TWO
一、对数函数的概念及应用
例1 (1)下列给出的函数：
①y＝log5x＋1；②y＝logax2(a>0，且a≠1)；③ y
log (
31)
x;
④ y＝log32x；⑤y＝logx
3
(x>0，且x≠1)；⑥ y log 2 x. 其中是对数函数的为
π
A.③④⑤
B.②④⑥
三、对数函数模型的应用
例3 大西洋鲑鱼每年都要逆流而上，游回产地产卵，经研究发现鲑鱼的游速可以
表示为函数v＝
1θ 2log3100
，单位是m/s，θ是表示鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是900个单位时，它的游速是多少？
解 由 v＝12log310θ0可知， 当 θ＝900 时，v＝12log3910000＝12log39＝1(m/s). 所以当一条鲑鱼的耗氧量是900个单位时，它的游速是1 m/s.
4.对数函数 f(x)过点(9,2)，则 f 13＝___－__1___. 解析 设f(x)＝logax(a>0且a≠1)，loga9＝2， ∴a2＝9，∴a＝3(舍a＝－3)， ∴f(x)＝log3x，∴f 13＝log313＝－1.
12345
5.函数f(x)＝logax＋a2－2a－3为对数函数，则a＝____3____.
C.①③⑤⑥
√D.③⑥
解析 ①中对数式后面加1，所以不是对数函数； ②中真数不是自变量x，所以不是对数函数； ③和⑥符合对数函数概念的三个特征，是对数函数； ④不是对数函数； ⑤中底数是自变量x，而非常数a，所以不是对数函数，故③⑥正确.
(2)已知对数函数的图象过点 M(8,3)，则 f 12＝__－__1____.
思考 函数y＝logπx，y＝log23x 是对数函数吗？ 答案 y＝logπx是对数函数，y＝log23x 不是对数函数.
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.由y＝logax，得x＝ay，所以x>0.( √ ) 2.y＝log2x2是对数函数.( × ) 3.若对数函数y＝logax，则a>0.( √ ) 4.函数y＝loga(x－1)的定义域为(0，＋∞).( × )
跟踪训练1 (1)下列函数表达式中，是对数函数的有
①y＝logx2；②y＝logax(a∈R)；③y＝log8x；④y＝ln x；⑤y＝logx(x＋2)；
⑥y＝log2(x＋1).
A.1个
√B.2个
C.3个
D.4个
(2)若对数函数f(x)的图象过点(4，－2)，则f(8)＝__－__3____.
x2－4≥0， 解 要使函数有意义，需x＋3>0，
x＋3≠1，
即xx≤ >－－32，或x≥2， x≠－2，
即－3<x<－2 或 x≥2，
故所求函数的定义域为(－3，－2)∪[2，＋∞).
(2)y＝ 21－x＋ln(x＋1). 解 要使函数有意义，需x2＋－1x>>00，， 即xx><－2，1， ∴－1<x<2. 故所求函数的定义域为(－1,2).
D.y＝2logax(a>0且a≠1)
12345
2.函数y＝log2(x－2)的定义域是
A.(0，＋∞)
√C.(2，＋∞)
B.(1，＋∞) D.[4，＋∞)
12345
3.函数 f(x)＝ 3－x＋lg(x＋1)的定义域为
A.[－1,3)
√C.(－1,3]
B.(－1,3) D.[－1,3]
12345
第四章 4.4 对数函数
学习目标
XUEXIMUBIAO
1.理解对数函数的概念. 2.会求简单对数函数的定义域. 3.了解对数函数在生产实际中的简UOYIN
知识梳理 题型探究 随堂演练
1 知识梳理
PART ONE
知识点 对数函数的概念
一般地，函数 y＝logax(a>0，且a≠1) 叫做对数函数，其中x是自变量，函数的定义域 是 (0，＋∞) .
(1)依题意，找出或建立数学模型.
(2)依实际情况确定解析式中的参数.
(3)依题设数据解决数学问题.
(4)得出结论.
3 随堂演练
PART THREE
1.下列函数为对数函数的是 A.y＝logax＋1(a>0且a≠1) B.y＝loga(2x)(a>0且a≠1)
√C.y＝log(a－1)x(a>1且a≠2)
解析
a2－2a－3＝0， 依题意有a>0，
a≠1，
解得 a＝3.
12345
课堂小结
KE TANG XIAO JIE
1.知识清单： (1)对数函数的定义. (2)对数函数的定义域. 2.方法归纳：待定系数法. 3.常见误区：易忽视对数函数底数有限制条件.
(2)某条鲑鱼想把游速提高1 m/s，那么它的耗氧量的单位数是原来的多少倍？
解 设鲑鱼原来的游速、耗氧量为v1，θ1，提速后的游速、耗氧量为v2，θ2. 由 v2－v1＝1，即12log31θ020－12log31θ010＝1，得θθ21＝9. 所以耗氧量的单位数为原来的9倍.
反思 感悟
对数函数应用题的解题思路
(3)y＝log1－x5. 解 依题意知11－－xx≠>01，， 得 x<1 且 x≠0， ∴定义域为(－∞，0)∪(0,1).
反思
感悟 求含对数式的函数定义域关键是真数大于0，底数大于0且不为1.如需对
函数式变形，需注意真数、底数的取值范围是否改变.
跟踪训练2 求下列函数的定义域.
(1)y＝lgxx2＋－34；