圆柱的体积优秀课件
合集下载
《圆柱和圆锥——圆柱的体积》数学教学PPT课件(3篇)

V=sh
S h
教学新知
教学新知
试一试:一个圆柱形零件,底面半径是5厘米,高是8厘米。 这个零件的体积是多少立方厘米?
V=sh=5²π×8=628(cm³)
教学新知
练一练:
1.计算圆柱的体积。(单位:cm)
V=sh=4²π×8=401.92(cm³) V=sh=3²π×6=169.56(cm³)
V=sh=1.5²π×0.5×2=7.065(m³)
8.两个底面积相等的圆柱,一个高是4.5分米,体积是81立方分米。另 一个高是3分米,它的体积是多少立方分米?
s=V1÷h1=81÷4.5=18(dm²) V2=sh2=18×3=54(m³)
课堂练习
9.把3个高相等、底面半径都是10厘米的圆柱形盒子叠放在 一起,如图 所示,拿走1个盒子,表面积就减少314平方厘米。每个盒子的体积是 多少立方厘米?
个近似的长方体。拼成的长方体的底面积等于圆柱的(底面积), 高就是圆柱的( 高 )。 (2)用字母V表示圆柱的体积,S表示圆柱的底面积,h表示圆柱的高, 圆柱的体积公式可以写成(V=sh)。 (3)一个圆柱的底面积是0.6平方分米,高是3.5分米,体积是(2.1)立 方分米。
课后习题
2.—根木料如图所示,求这根木料的体积。(单位:m)
2.一根圆柱形木料,底面周长是62.8厘米,高是50厘米。这根木料的体 积是多少?
r=C÷2π=62.8÷6.28=10(cm) V=sh=10²π×50=15700(cm³)
教学新知
例一:完成下面的表格。
底面积/m2
高/m
体积/m3
圆 柱
0.6
1.2
0.25
3
0.72 0.75
《圆柱的体积》优秀ppt课件

新知导入
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平, 无水部分高10cm,内直径是6cm。小明喝了多少水?
3.14 × (6 ÷2 )2 ×10 =3.14×9 ×10 =282.6( cm3 ) = 282.6( mL ) 答:小明喝了282.6 mL 水。
课堂练习
哪根木料的体积大?
新知导入
把圆柱切开,拼成 一个近似的长方形。
把圆柱的底面分 成许多相等的扇形。
新知导入
把圆柱底面平均分的份数越多, 拼成的立体图形越接近长方体。
新知导入
底面积 高
高
长方体的体积=底面积 × 高
圆柱的体积 = 底面积 × 高
V=Sh
新知导入
同桌交流
(1)已知圆的半径和高,怎样求圆柱的体积? V=∏r2h
容积是指容器所能容纳物体的体积
杯子的底面积: 3.14 ×(8÷2)2 =3.14 ×16 =50.24(cm3)
杯子的容积: 50.24 ×10 =502.4( cm3 ) = 502.4(mL) 50.24 mL >498 mL 答:杯子能装下这袋牛奶。
新知导入
一根圆柱形木料底面直径是0.4m,长5m。 如果做一张课桌用去木料0.02m3 这根木 料最多能做多少张课桌?
(2)已知圆的直径和高,怎样求圆柱的体积? V=∏(d ÷2 )2h
(3)已知圆的周长和高,怎样求圆柱的体积? V=∏(C÷d÷2 )2h
新知导入
1.一根圆柱形形木料,底面 积是75 cm2 ,长90cm。它
的体积是多少?
2.一口圆柱形水井,地面以
下的井深10m,底面直径为 1m。挖出的土有多少m3?
杯子的底面积: 3.14 ×(8÷2)2 =3.14 ×16 =50.24(cm3)
六下《圆柱的体积》ppt课件4

• 如果用V表示圆柱的体积,用S表示圆 柱的底面积,用h表示圆柱的高,圆柱 的体积公式用字母表示为: •
1、反馈练习: 底面积是10平方米,高是2米,体积 是( ) 底面积是3平方分米,高是4分米, 体积是( )
2、运用新知,尝试解答实际问题.
一根圆柱形钢材,底面积是50平方厘米 高是2.1米,它的体积是多少?
四、全课总结 问:这节课里我们学到了哪些知识?
五、学生作业: 1、练习七的第l 题完成在书上。
2、课本26页试一试。 3、一个圆柱的石柱子底面的周长18.84分 米,高是20分米, 体积是多少?(选做)
教学目标
1.理解圆柱体体积公式的推导过程,掌握计算公 式,会运用公式计算圆柱的体积,并能解决一些 实际问题。 2.通过公式的推导,学生的分析推理能力得到提 高。 3. 渗透转化思想,感悟数学知识的魅力,提高审 美意识。
请大家想一想:在学习圆的面积时, 我们是怎样把圆转化成已学的图形, 来推导圆面积的计算公式的.
把圆等分切割,拼成一个近似的长方形, 找出圆与所拼成的长方形之间的关系,进 而推导出圆面积的计算公式.
1 2 3 4 5 6 7 8 7 1 8 16 9 10 15 1413 12 11 4 5 6 3 2 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 16 15 14 13 12 11 10 9
高8厘米。这个零件的体积是多少立方厘米?
(1)一个圆柱形水桶,从里面量底面直径是20厘米, 高是25厘米.这个水桶的容积是多少立方分米?
(2)一个圆柱的体积是62.8立方分米,高是 5分米,底面积是多少?
不会的可以向同学请教
4、拓展提高:
一个圆柱的石柱子底面的周长18.84 分米,高是20分米, 体积是多少?
圆柱的体积ppt课件
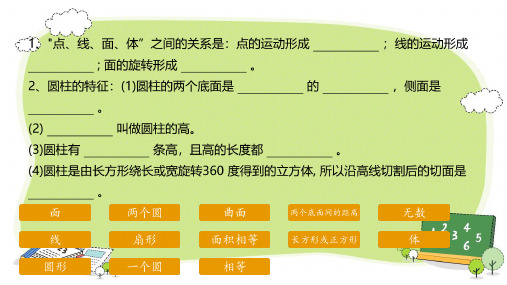
北师大版六年级数学下册第一单元《圆柱和圆锥》
圆柱的体积
第1课时
第2课时
教学目标
复习旧知
把左边的公式拖到右边相应的问题旁边
想一想,怎样计算圆柱的体积呢?
以前学习过哪些 图形的体积?
旧知识
新知识
?
这只是猜想, 还需要验证。
通过叠硬币,我们发现硬币的
( 底面)积是固定的,每增加
一(枚硬币),也(随之)增高就大增,加由一此些可,
V=πr×r× h
h
用长×宽×高能
不能推导圆柱体
积计算公式?
尝试解决下面的问题。
1.底面积 3.14×0.42=0.5024(m2) 2.体积 0.5024×5=2.5124(m3)
3.14×0.42×5 =3.14×0.8 =2.5124(m3)
答:柱子的体积是2.5124立方米。
尝试解决下面的问题。
答:这根金箍棒的体积是2512cm3。 如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒 重多少千克?
7.9×2512=19844.8(g)=19.8448(kg)
答:这根金箍棒重19.8448千克。
光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深4m。挖 出了多少立方米的土?
2cm
=157(cm3)
底面半径: 3.14÷3.14÷2=0.5(m)
体积: 3.14×0.52×4
=3.14×0.25×4
=3.14×0.25×4 =3.14(m3)
答:挖出了3.14立方米的土。
一个装满稻谷的圆柱形粮囤,底面面积为2m2,高为80cm。每立方 米稻谷约重600kg,这个粮囤存放的稻谷约重多少千克?
80cm=0.8m 2×0.8×600=960(kg)
圆柱的体积
第1课时
第2课时
教学目标
复习旧知
把左边的公式拖到右边相应的问题旁边
想一想,怎样计算圆柱的体积呢?
以前学习过哪些 图形的体积?
旧知识
新知识
?
这只是猜想, 还需要验证。
通过叠硬币,我们发现硬币的
( 底面)积是固定的,每增加
一(枚硬币),也(随之)增高就大增,加由一此些可,
V=πr×r× h
h
用长×宽×高能
不能推导圆柱体
积计算公式?
尝试解决下面的问题。
1.底面积 3.14×0.42=0.5024(m2) 2.体积 0.5024×5=2.5124(m3)
3.14×0.42×5 =3.14×0.8 =2.5124(m3)
答:柱子的体积是2.5124立方米。
尝试解决下面的问题。
答:这根金箍棒的体积是2512cm3。 如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒 重多少千克?
7.9×2512=19844.8(g)=19.8448(kg)
答:这根金箍棒重19.8448千克。
光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深4m。挖 出了多少立方米的土?
2cm
=157(cm3)
底面半径: 3.14÷3.14÷2=0.5(m)
体积: 3.14×0.52×4
=3.14×0.25×4
=3.14×0.25×4 =3.14(m3)
答:挖出了3.14立方米的土。
一个装满稻谷的圆柱形粮囤,底面面积为2m2,高为80cm。每立方 米稻谷约重600kg,这个粮囤存放的稻谷约重多少千克?
80cm=0.8m 2×0.8×600=960(kg)
人教版六年级数学下册《圆柱的体积》课件

的值。 3. 求方程的解的过程叫解方程。
(三)列方程解决问题 1、审题,弄清题意; 2、找出等量关系; 3、设出未知数,根据等量关系列出方程; 4、解方程,写出答句; 5、检验。
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高: V=∏(d2)2h
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
努 力 吧 !
判断正误,对的画“√”,错误的画“×”。
1. 圆柱体的底面积越大,它的体积越大。(×) 2. 圆柱体的高越长,它的体积越大。(×) 3.圆柱体的体积与长方体的体积相等。(×) 4.圆柱体的底面直径和高可以相等。(√ )
列方程解决下面的问题。
(1)果品商店购进20箱苹果。购进苹果的箱数
是橘子箱数的 4 。商店购进了多少箱橘子?
5
解:设商店购进了x箱橘子。
橘子箱数× 4 =苹果箱数
45x=20 5 x=20÷
x=25
4 5
答:商店购进了25箱橘子。
(2)妙想和乐乐一共收集了128枚邮票,妙
想收集的邮票数是乐乐的3倍。妙想、乐乐各
注意:
①在含有字母的式子里,数和字母中间的乘 号可以写作“•”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。 ③数与数之间的乘号不能省略。加号、减号、 除号都不能省略。
解下面的方程,并说一说你是怎么解的。
9x-1.8=5.4 解:
9x-1.8+1.8=5.4+1.8 9x=7.2
9x÷9=7.2÷9 x=0.8
a乘以4.5可以怎样写?s乘以h可以怎样写?
a 4.5或4.5a
s h或sh
用含有字母的式子表示下面的数量 1、一只青蛙每天吃a只害虫,100天吃掉(100a) 只害虫。
(三)列方程解决问题 1、审题,弄清题意; 2、找出等量关系; 3、设出未知数,根据等量关系列出方程; 4、解方程,写出答句; 5、检验。
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高: V=∏(d2)2h
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
努 力 吧 !
判断正误,对的画“√”,错误的画“×”。
1. 圆柱体的底面积越大,它的体积越大。(×) 2. 圆柱体的高越长,它的体积越大。(×) 3.圆柱体的体积与长方体的体积相等。(×) 4.圆柱体的底面直径和高可以相等。(√ )
列方程解决下面的问题。
(1)果品商店购进20箱苹果。购进苹果的箱数
是橘子箱数的 4 。商店购进了多少箱橘子?
5
解:设商店购进了x箱橘子。
橘子箱数× 4 =苹果箱数
45x=20 5 x=20÷
x=25
4 5
答:商店购进了25箱橘子。
(2)妙想和乐乐一共收集了128枚邮票,妙
想收集的邮票数是乐乐的3倍。妙想、乐乐各
注意:
①在含有字母的式子里,数和字母中间的乘 号可以写作“•”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。 ③数与数之间的乘号不能省略。加号、减号、 除号都不能省略。
解下面的方程,并说一说你是怎么解的。
9x-1.8=5.4 解:
9x-1.8+1.8=5.4+1.8 9x=7.2
9x÷9=7.2÷9 x=0.8
a乘以4.5可以怎样写?s乘以h可以怎样写?
a 4.5或4.5a
s h或sh
用含有字母的式子表示下面的数量 1、一只青蛙每天吃a只害虫,100天吃掉(100a) 只害虫。
《圆柱的体积》课件PPT

绿色圃中小学教育网
把一个长、宽、高分别是9cm、 7cm、3cm的长方体铁块和一个 棱长是5cm的正方体铁块,熔铸 成一个圆柱体。这个圆柱体的底 面直径是20cm,高是多少厘米?
绿色圃中小学教育网
将一个圆柱体沿着底面直径切成两个半 圆柱,表面积增加了40平方厘米,圆柱的 底面直径为4厘米,这个圆柱的体积是多 少立方厘米?
一桶油,用去了部分,你 能求出还剩多少升吗?
2分米
8分米
C=6.28米
绿色圃中小学教育网
将一个棱长10厘米的 正方体削成一个圆柱,如 果这想要个圆柱的体积最 大,要削去木块多少立方 厘米?
绿色圃中小学教育网
将一个棱长为6分米的正方体 钢材熔铸成底面半径为3分米的 圆柱体,这个圆柱有多长?
25.12 ÷6.28 =4(分米)
答:圆柱的高是4分米。
绿色圃中小学教育网
讨论
(1)已知圆的半径和高,怎样求圆柱的体积? (2)已知圆的直径和高,怎样求圆柱的体积? (3)已知圆的周长和高,怎样求圆柱的体积?
绿色圃中小学教育网
2 10 3.14 ×(10÷2)2×2=157(立方厘米)
绿色圃中小学教育网
4分米 10分米
0.8米
求各圆柱的 体积。
绿色圃中小学教育网
0.5分米ຫໍສະໝຸດ 一个圆柱的体积是25.12立 方分米,底面积是6.28平方分 米,求圆柱的高是多少分米?
这块石块的体积=圆柱的底面积×水面 变化的高度
绿色圃中小学教育网
绿色圃中小学教育网
绿色圃中小学教育网
绿色圃中小学教育网
绿色圃中小学教育网
绿色圃中小学教育网
绿色圃中小学教育网
一个无盖的圆柱形水桶,侧面积 是188.4平方分米,底面周长是 62.8分米。做这个水桶至少要多 少平方分米?这个水桶的体积是 多少立方分米?
圆柱体积PPT课件

r= d
2
S=∏r2 v=sh = ∏ r2 h
3.已知圆柱体的底面周长和高,怎样求体积 ?
r=c÷2∏
S=∏r2 v=sh = ∏ r2 h
一个圆柱,底面半径是2cm,高是5cm。 求它的体积?
r=2cm h=5cm S底=πr2 =2×2×3.14
=4×3.14 =12.56(cm2) V=Sh=5×12.56=62.8(cm3)
人教版小学六年级数学下册《圆柱的体积》
真 棒!
高 宽
长
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
v长=a b h
v正 =a 3
V=s底 h
圆的面积公式推导过程:
圆的面积公式推导过程:
S=π r 2
rHale Waihona Puke πrS=πr ×r =π r 2
圆面积计算公式的推导过程
()
圆
长方形
运用了什么数学思想?
一根圆柱形的钢材,底面积是50平方厘米, 高是2.1米。它的体积是多少?
2.1米=210厘米 50 ×210=10500(立方厘米) 答:它的体积是10500立方厘米。
50平方厘米=0.005平方米 0.005 ×2.1=0.0105(立方米) 答:它的体积是0.0105立方米。
看图列式,并写出相应的公式。
答:圆柱的表面积是62.8平方厘米。
计算右图圆柱是体积。(单位:dm)
d=10dm h=4dm S底=π(d÷2)2
=(10÷2)2×3.14 =25×3.14 =78.5(dm2) V=Sh=4×78.5=314(dm3)
1·0 4
一个圆柱,底面周长是94.2m,高是 100m。求它的体积?
圆柱的体积课件

16 15 14 13 12 11 10 9 16 15 14 13 12 11 10 9
真 棒!
高
长 宽 棱长
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
v =a b h
长
v =a 正
V=s底 h
பைடு நூலகம்
3
猜想:圆柱体积的大小跟
哪些条件有关?
观察:①甲乙两个圆柱有什么相同?什么不同? ②当高相等时,甲的体积为什么比乙的大? 圆柱的高相等,底面积大的体积就大。 真
6.28厘米
(2)
2 V=兀(d÷2)×h
(3)
2 3.14 ×(6.28÷3.14÷2) ×8 5厘米 2 V=兀(C÷兀÷2)×h
(4)
练习巩固 应用拓展
• 把一根长1.5分米的圆柱形钢材截成三段后, 如图,表面积比原来增加9.6平方分米,这 根钢材原来的体积是多少? (9.6÷3)×1.5= 4.8(立方分米) 答:这根钢材原来的 体积是4.8立方分米
将一个圆柱体沿着底面直径切成两个半 圆柱,表面积增加了40平方厘米,圆柱的 底面直径为4厘米,这个圆柱的体积是多 少立方厘米?
再见!
2、它的底面积变了吗?
∏r
1、拼成的长方体的体积与原来的圆柱体体积是否相等?
因为长方体的体积=底面积×高 所以圆柱的体积=底面积×高 V = S h
3、它的高变了吗?
V长方体 V=abh
=
V圆柱 V= 兀r2 × h
= 兀r ×r × h = 兀r 2 h ×
V=Sh
例4
一根圆柱形钢材,底面积 是50平方厘米,高是2.1米。 它的体积是多少?
V =s h
想 一 想
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱的体积
口头列式计算
求下面各圆的面积: (1)r=1厘米
3.14×12=3.14(平方厘米)
(2)d=4分米
3.14×(4÷2)2=12.56(平方分米)
(3)C=12.56米
3.14×(12.56÷3.14 ÷ 2)2=12.56(平方米)
口头列式计算
1、一个圆柱的底面周长是3.14厘米,高是3厘 米,这个圆柱的侧面积是多少?
4厘米
= 28.26××4
= 113.04(立方厘米)
求下面圆柱的体积。
半径:18.84÷3.14÷2
=6÷2
=3(分米)
高10分米
底面周长 18.84分米
体积:3.14×3×3×10
=3.14×90 =282.6(立方分米)
判断:
(1)圆柱体、长方体和正方体的体积都可以用底面积乘以
高的方法来计算。
正方体的体积=棱长×棱长×棱长 底面积
长方体或正方体的体积= 底面积×高
回忆一下:
在学习计算圆的面积时, 我们是怎样把圆变成已学过的 图形来计算面积的
转化
r ∏r
圆的面积S=∏r2
讨论:
能不能把圆柱 转化成我们已经学 过的形体来求出它 的体积?
怎样转化呢?
底面积
高
高
转化
讨 ①拼成的长方体的体积与原来圆柱体 的体 积是否相等?
3.14×3=9.42(平方厘米) 答:这个圆柱的侧面积是9.42平方厘米。
2、一个圆柱的底面直径是3分米,高是2分米, 这个圆柱的侧面积是多少?
3.14×3×2=18.84(平方分米) 答:这个圆柱的侧面积是18.84平方分米。
什么是物体的体积?
底面积Biblioteka 高高长宽
棱长
长方体的体积=长×宽×高 底面积
一个圆柱的体积是25.12立 方分米,底面积是6.28平方分 米,求圆柱的高是多少分米?
25.12 ÷6.28 =4(分米) 答:圆柱的高是4分米。
作 业:
10分米 0.5分米
求各圆柱的体积。
4分米
0.8米
√( )
× (2)圆柱的底面积扩大3倍,体积也扩大3倍 。 ( )
(3)一个长方体与一个圆柱体,底面积相等,
√ 高也相等,那么它们的体积也相等。 ( )
× (4) 两个圆柱体的侧面积相等,体积也一定相等。 ( )
(5)求圆柱的体积和圆柱的侧面积一样都
× 是用底面积乘高的方法来计算。 ( )
拓展练习
论 ②它的底面积变了吗? ③它的高变了吗? ④怎样计算圆柱体的体积呢?
底面积
高
高
转化
长方体体积=底面积×高
圆柱体积=底面积×高 V= s ×h V = ∏r2 × h
求下面圆柱的体积。
底面积4.5 平方厘米
高3厘米
4.5×3= 13.5(立方厘米)
求下面圆柱的体积。
3厘米 3.14×32×4
= 3.14×9××4
口头列式计算
求下面各圆的面积: (1)r=1厘米
3.14×12=3.14(平方厘米)
(2)d=4分米
3.14×(4÷2)2=12.56(平方分米)
(3)C=12.56米
3.14×(12.56÷3.14 ÷ 2)2=12.56(平方米)
口头列式计算
1、一个圆柱的底面周长是3.14厘米,高是3厘 米,这个圆柱的侧面积是多少?
4厘米
= 28.26××4
= 113.04(立方厘米)
求下面圆柱的体积。
半径:18.84÷3.14÷2
=6÷2
=3(分米)
高10分米
底面周长 18.84分米
体积:3.14×3×3×10
=3.14×90 =282.6(立方分米)
判断:
(1)圆柱体、长方体和正方体的体积都可以用底面积乘以
高的方法来计算。
正方体的体积=棱长×棱长×棱长 底面积
长方体或正方体的体积= 底面积×高
回忆一下:
在学习计算圆的面积时, 我们是怎样把圆变成已学过的 图形来计算面积的
转化
r ∏r
圆的面积S=∏r2
讨论:
能不能把圆柱 转化成我们已经学 过的形体来求出它 的体积?
怎样转化呢?
底面积
高
高
转化
讨 ①拼成的长方体的体积与原来圆柱体 的体 积是否相等?
3.14×3=9.42(平方厘米) 答:这个圆柱的侧面积是9.42平方厘米。
2、一个圆柱的底面直径是3分米,高是2分米, 这个圆柱的侧面积是多少?
3.14×3×2=18.84(平方分米) 答:这个圆柱的侧面积是18.84平方分米。
什么是物体的体积?
底面积Biblioteka 高高长宽
棱长
长方体的体积=长×宽×高 底面积
一个圆柱的体积是25.12立 方分米,底面积是6.28平方分 米,求圆柱的高是多少分米?
25.12 ÷6.28 =4(分米) 答:圆柱的高是4分米。
作 业:
10分米 0.5分米
求各圆柱的体积。
4分米
0.8米
√( )
× (2)圆柱的底面积扩大3倍,体积也扩大3倍 。 ( )
(3)一个长方体与一个圆柱体,底面积相等,
√ 高也相等,那么它们的体积也相等。 ( )
× (4) 两个圆柱体的侧面积相等,体积也一定相等。 ( )
(5)求圆柱的体积和圆柱的侧面积一样都
× 是用底面积乘高的方法来计算。 ( )
拓展练习
论 ②它的底面积变了吗? ③它的高变了吗? ④怎样计算圆柱体的体积呢?
底面积
高
高
转化
长方体体积=底面积×高
圆柱体积=底面积×高 V= s ×h V = ∏r2 × h
求下面圆柱的体积。
底面积4.5 平方厘米
高3厘米
4.5×3= 13.5(立方厘米)
求下面圆柱的体积。
3厘米 3.14×32×4
= 3.14×9××4
