小学数学《圆柱体积》PPT课件
合集下载
六年级数学下册课件3.1.3圆柱的体积人教版共20张PPT
答:这个圆柱的体积是785立方厘米
分享收获
这节课我收获 了……
这节课我知道 了……
0.9米=90厘米
V=Sh
=75×90 =6750(立方厘米) 答:它的体积是6750立方厘米。
解决问题
2、一根圆柱形的木料,横截面的半径是5厘米, 长是150厘米。这根木料的体积是多少立方厘米?
3.14×5²×150
=3.14×25×150
150cm
=78.5×150
=11775(cm³)
5cm
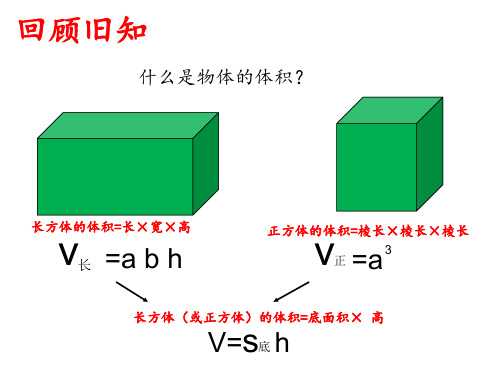
回顾旧知
什么是物体的体积?
长方体的体积=长×宽×高
v长 =a b h
正方体的体积=棱长×棱长×棱长
v正 =a3
长方体(或正方体)的体积=底面积× 高
V=s底 h
怎样求水泥 柱的体积呢?
下面长方体、正方体和圆柱的底面积都相等,高 也相等
想一想:谁和谁的体积相等?为什高么? 猜一猜:圆柱的体积和长方体、正方体的体积相等吗?
S=π r 2
r
πr
S=πr ×r =π r 2
自主探究
以小组为单位,结合手中的学具,探究圆柱的体 积
温馨提示: 1、圆柱体可以转化成已经学过的那种立体图形? 2、观察转化后的立体图形与原来的圆柱体有什么 关系?
如果把底面平均分的份数越多,结果会怎样呢?
把圆柱的底面平均分的份数越多,切拼 成的立体图形越接近长方体。
答:这根木料的体积是11775 cm³
解决问题
3、李家庄挖了一口圆柱形水井,地面 以下的井深10m,底面直径为1m。挖出 的土有多少立方米?
3.14 ×(1 ÷2)² ×10 =3.14 ×0.5² ×10 =3.14 ×0.25 ×10 =0.785 ×10 =7.85(m³)
分享收获
这节课我收获 了……
这节课我知道 了……
0.9米=90厘米
V=Sh
=75×90 =6750(立方厘米) 答:它的体积是6750立方厘米。
解决问题
2、一根圆柱形的木料,横截面的半径是5厘米, 长是150厘米。这根木料的体积是多少立方厘米?
3.14×5²×150
=3.14×25×150
150cm
=78.5×150
=11775(cm³)
5cm
回顾旧知
什么是物体的体积?
长方体的体积=长×宽×高
v长 =a b h
正方体的体积=棱长×棱长×棱长
v正 =a3
长方体(或正方体)的体积=底面积× 高
V=s底 h
怎样求水泥 柱的体积呢?
下面长方体、正方体和圆柱的底面积都相等,高 也相等
想一想:谁和谁的体积相等?为什高么? 猜一猜:圆柱的体积和长方体、正方体的体积相等吗?
S=π r 2
r
πr
S=πr ×r =π r 2
自主探究
以小组为单位,结合手中的学具,探究圆柱的体 积
温馨提示: 1、圆柱体可以转化成已经学过的那种立体图形? 2、观察转化后的立体图形与原来的圆柱体有什么 关系?
如果把底面平均分的份数越多,结果会怎样呢?
把圆柱的底面平均分的份数越多,切拼 成的立体图形越接近长方体。
答:这根木料的体积是11775 cm³
解决问题
3、李家庄挖了一口圆柱形水井,地面 以下的井深10m,底面直径为1m。挖出 的土有多少立方米?
3.14 ×(1 ÷2)² ×10 =3.14 ×0.5² ×10 =3.14 ×0.25 ×10 =0.785 ×10 =7.85(m³)
六年级数学下册课件- 3.1.3 圆柱的体积 人教版(共37张PPT)

人教教版六年级数学下册第二单元
体积:物体所占空间的大小
高
宽 长
长方体的体积=长×宽×高
ቤተ መጻሕፍቲ ባይዱ棱长
V=abh
正方体的体积=棱长×棱长×棱长
V=a³
底面积×高
圆柱体积的大小与哪些条件有关?
图1:
S甲>S乙
h甲 = h乙
v甲 > v 乙
圆柱体积的大小与圆柱的底面积有关
图2
将一个圆柱截成不相等的两段,哪个圆柱体积大?
V=sh
V=兀r 2h
1.
V=兀(d÷2) 2 h
V=兀(c÷2兀) 2 h
2.要区分清圆柱的体积计算公式和侧面积计算公式。
1、了解青蛙生长过程中几个不同阶段 的形体 变化, 知道它 是捉虫 能手, 懂得
2、能按问题的提示扩写句子,把句子 写具体 ,通过 选词填 空、连 句,了 解小蝌 蚪是怎 样变成 青蛙的 。 3、会分角色朗读课文,能背诵课文最 后两个 自然段 。应该 保护青 蛙
4、教学重点:学习生字新词,能分角 色有感 情地朗 读课文 ,懂得 青蛙是 捉害虫 的能手 ,懂得 保护青 蛙人人 有责。 5、教学难点:认识蝌蚪和青蛙,了解 青蛙生 长过程 以及在 不同阶 段的形 态变化 。
6、理解重点词句,了解作者从哪些方 面介绍 黄山奇 石,并 用自己 的话复 述。
S上=S下上 h上< h下
下
V上<V下
圆柱体积的大小与圆柱的高有关
圆柱体积的大小与 圆柱的底面积和高有关
圆面积公式的推导过程
圆面积公式的推导过程
r 圆的面积 S = 2
长方体的体积=底面积×高 圆柱体的体积 底面积
长方体的体积=底面积×高 圆柱体的体积 底面积
体积:物体所占空间的大小
高
宽 长
长方体的体积=长×宽×高
ቤተ መጻሕፍቲ ባይዱ棱长
V=abh
正方体的体积=棱长×棱长×棱长
V=a³
底面积×高
圆柱体积的大小与哪些条件有关?
图1:
S甲>S乙
h甲 = h乙
v甲 > v 乙
圆柱体积的大小与圆柱的底面积有关
图2
将一个圆柱截成不相等的两段,哪个圆柱体积大?
V=sh
V=兀r 2h
1.
V=兀(d÷2) 2 h
V=兀(c÷2兀) 2 h
2.要区分清圆柱的体积计算公式和侧面积计算公式。
1、了解青蛙生长过程中几个不同阶段 的形体 变化, 知道它 是捉虫 能手, 懂得
2、能按问题的提示扩写句子,把句子 写具体 ,通过 选词填 空、连 句,了 解小蝌 蚪是怎 样变成 青蛙的 。 3、会分角色朗读课文,能背诵课文最 后两个 自然段 。应该 保护青 蛙
4、教学重点:学习生字新词,能分角 色有感 情地朗 读课文 ,懂得 青蛙是 捉害虫 的能手 ,懂得 保护青 蛙人人 有责。 5、教学难点:认识蝌蚪和青蛙,了解 青蛙生 长过程 以及在 不同阶 段的形 态变化 。
6、理解重点词句,了解作者从哪些方 面介绍 黄山奇 石,并 用自己 的话复 述。
S上=S下上 h上< h下
下
V上<V下
圆柱体积的大小与圆柱的高有关
圆柱体积的大小与 圆柱的底面积和高有关
圆面积公式的推导过程
圆面积公式的推导过程
r 圆的面积 S = 2
长方体的体积=底面积×高 圆柱体的体积 底面积
长方体的体积=底面积×高 圆柱体的体积 底面积
人教版六年级数学下册3.1.3 圆柱的体积 (共41张PPT)

长方体体积=底面积×高
=
圆柱体积
V=Sh
32 返回
V=Sh
33 返回
智慧城堡
加油啊!
34 返回
闯关一
计算下面各圆柱的体积。
底面积
(平方米)
高
(米)
圆柱体积
(立方米)
15
3
45
6.4
4
25.6
35 返回
闯关二
火眼金睛判对错。
(1)圆柱体的底面积越大,它的体积越大。(× )
(2)长方体、正方体、圆柱体的体积都可以
圆的面积
近似长方形的面积
转化、推导是常用的数学研究方法。
9 返回
(1)你准备把圆柱体转化成什么立体图形? (2)你是怎样转化成这个立体图形的? (3)转化以后的立体图形和圆柱体之间有什么关 系?
10 返回
11 返回
12 返回
13 返回
14 返回
15 返回
16 返回
17 返回
18 返回
19 返回
20 返回
21 返回
22 返回
23 返回
24 返回
25 返回
26 返回
27 返回
单击此处编辑母版标题样式
28 返回
29 返回
30 返回
把圆柱的底面平均分的份数越多,切拼成的立体图 形越接近长方体。
31 返回
长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。
用底面积乘高的方法来计算。 ( √ )
(3)一个圆柱的底面积是10平方厘米,高是5米, 它的体积是10×5=50平方厘米( )
(1)5米=500厘米 (2)10×500=5000(立方厘米)
36 返回
=
圆柱体积
V=Sh
32 返回
V=Sh
33 返回
智慧城堡
加油啊!
34 返回
闯关一
计算下面各圆柱的体积。
底面积
(平方米)
高
(米)
圆柱体积
(立方米)
15
3
45
6.4
4
25.6
35 返回
闯关二
火眼金睛判对错。
(1)圆柱体的底面积越大,它的体积越大。(× )
(2)长方体、正方体、圆柱体的体积都可以
圆的面积
近似长方形的面积
转化、推导是常用的数学研究方法。
9 返回
(1)你准备把圆柱体转化成什么立体图形? (2)你是怎样转化成这个立体图形的? (3)转化以后的立体图形和圆柱体之间有什么关 系?
10 返回
11 返回
12 返回
13 返回
14 返回
15 返回
16 返回
17 返回
18 返回
19 返回
20 返回
21 返回
22 返回
23 返回
24 返回
25 返回
26 返回
27 返回
单击此处编辑母版标题样式
28 返回
29 返回
30 返回
把圆柱的底面平均分的份数越多,切拼成的立体图 形越接近长方体。
31 返回
长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。
用底面积乘高的方法来计算。 ( √ )
(3)一个圆柱的底面积是10平方厘米,高是5米, 它的体积是10×5=50平方厘米( )
(1)5米=500厘米 (2)10×500=5000(立方厘米)
36 返回
人教版六年级下册数学《圆柱的体积》课件

粮囤的容积
粮囤所装玉米
3.14×1.5²×2
14.13×750÷1000
=3.14×2.25×2
=10597.5÷1000
1.5m
=14.13 (m³ )
=10.5975(吨)
2m
答:这个粮囤能装10.5975吨。
花坛的底面积 3.14×(3÷2)2=3.14×1.5 2=7.065 (m2 )
两个花坛的体积 7.065×0.5×2=3.5325×2=7.065(m³)
练一练
已知底面直径和高求圆柱体积。
V=π(
d 2
)2h
= 3.14×(1÷2)2×10
= 7.85(立方米)
答:挖出的土有7.85立方米。
思考:
8cm
1.已知什么?
2.要求什么?
10cm
3.要注意什么?
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测
量得到的。)
8cm
10cm
杯子的容积。
杯子的底面积: 3.14 ×(8÷2)2
六 下数 学
目 1 温故知新 录 2 新知探究
3 课堂练习
4 课堂小结
013
学而时习之,不亦说乎
物体所占空间的大小是物体的体积。
高 宽
长方体的体积=长×宽×高
长
正方体的体积=棱长×棱长×棱长
棱长
r πr
S=πr2
学,然后知不足。
203
圆柱体积怎么计算?
小组讨论: 1.你准备把圆柱转化成什么立体图形? 2.你是怎样转化成这个立体图形的?
=3.14 ×16 =50.24(cm3)
杯子的容积: 50.24 ×10
=502.4( cm3 ) = 502.4(mL) 502.4 mL >498 mL 答:杯子能装下这袋牛奶。
人教版六年级数学下册《圆柱的体积》课件

的值。 3. 求方程的解的过程叫解方程。
(三)列方程解决问题 1、审题,弄清题意; 2、找出等量关系; 3、设出未知数,根据等量关系列出方程; 4、解方程,写出答句; 5、检验。
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高: V=∏(d2)2h
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
努 力 吧 !
判断正误,对的画“√”,错误的画“×”。
1. 圆柱体的底面积越大,它的体积越大。(×) 2. 圆柱体的高越长,它的体积越大。(×) 3.圆柱体的体积与长方体的体积相等。(×) 4.圆柱体的底面直径和高可以相等。(√ )
列方程解决下面的问题。
(1)果品商店购进20箱苹果。购进苹果的箱数
是橘子箱数的 4 。商店购进了多少箱橘子?
5
解:设商店购进了x箱橘子。
橘子箱数× 4 =苹果箱数
45x=20 5 x=20÷
x=25
4 5
答:商店购进了25箱橘子。
(2)妙想和乐乐一共收集了128枚邮票,妙
想收集的邮票数是乐乐的3倍。妙想、乐乐各
注意:
①在含有字母的式子里,数和字母中间的乘 号可以写作“•”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。 ③数与数之间的乘号不能省略。加号、减号、 除号都不能省略。
解下面的方程,并说一说你是怎么解的。
9x-1.8=5.4 解:
9x-1.8+1.8=5.4+1.8 9x=7.2
9x÷9=7.2÷9 x=0.8
a乘以4.5可以怎样写?s乘以h可以怎样写?
a 4.5或4.5a
s h或sh
用含有字母的式子表示下面的数量 1、一只青蛙每天吃a只害虫,100天吃掉(100a) 只害虫。
(三)列方程解决问题 1、审题,弄清题意; 2、找出等量关系; 3、设出未知数,根据等量关系列出方程; 4、解方程,写出答句; 5、检验。
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高: V=∏(d2)2h
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
努 力 吧 !
判断正误,对的画“√”,错误的画“×”。
1. 圆柱体的底面积越大,它的体积越大。(×) 2. 圆柱体的高越长,它的体积越大。(×) 3.圆柱体的体积与长方体的体积相等。(×) 4.圆柱体的底面直径和高可以相等。(√ )
列方程解决下面的问题。
(1)果品商店购进20箱苹果。购进苹果的箱数
是橘子箱数的 4 。商店购进了多少箱橘子?
5
解:设商店购进了x箱橘子。
橘子箱数× 4 =苹果箱数
45x=20 5 x=20÷
x=25
4 5
答:商店购进了25箱橘子。
(2)妙想和乐乐一共收集了128枚邮票,妙
想收集的邮票数是乐乐的3倍。妙想、乐乐各
注意:
①在含有字母的式子里,数和字母中间的乘 号可以写作“•”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。 ③数与数之间的乘号不能省略。加号、减号、 除号都不能省略。
解下面的方程,并说一说你是怎么解的。
9x-1.8=5.4 解:
9x-1.8+1.8=5.4+1.8 9x=7.2
9x÷9=7.2÷9 x=0.8
a乘以4.5可以怎样写?s乘以h可以怎样写?
a 4.5或4.5a
s h或sh
用含有字母的式子表示下面的数量 1、一只青蛙每天吃a只害虫,100天吃掉(100a) 只害虫。
《圆柱体的体积计算》PPT

冀教版六年级数学下册第三单元
圆柱体的体积计算
1、经历同桌合作,测量、计算圆柱物 体体积的过程。
2、会测量圆柱物体的有关数据,能根 据圆柱的高及直径或周长计算圆柱的体 积。
3、能找到解决问题的有效方法,能表 达解决问题的大致过程和结果。
同桌合作,测量自己准备的茶叶筒的 有关数据,计算出它的体积。
1.一个易拉罐(如下图),它的体积
找一找,哪些物体的形状是圆柱?
在生活中,你还见过哪些形状是 圆柱的物体?
圆柱的特点:
观察一个罐头盒。
指出它的底面、 侧面和高。
把下面罐头盒沿着它的一条高 剪开,再展开,看看商标是什么形 状。
1.长方形的长和宽分别与罐头盒的 什么有关系?
2.长方形的面积和罐头盒的侧面积 有什么关系?
怎样计算罐头盒的侧面积?
1.某工厂生产了侧面的商标纸,你 认为哪张纸比较适合?
2.求右面罐头盒商 标纸的面积。(接 缝处忽略不计) (单位:厘米)
3.求下面各圆柱的侧面积。
(1)d=8cm h=6cm
(2)r=3m h=1.5m
在自己家里找几个圆柱形的物体,测 量它们的直径和高,计算出它们的体积和 表面积。
冀教版六年级数学下册第三单元
圆柱和圆柱的侧面积
1、知识目标:理解圆柱体侧面积和表面积的含义。 2、能力目标:通过操作独立推导并掌握求圆柱的 侧面积的方法,并能运用到实际中解决问题。 3、情感目标:体验成功与失败的收获,体会合作 的愉悦。
是多少立方厘米? PPT模板:素材: PPT背景:图表: PPT下载:教程: 资料下载:范文下载: 试卷下载:教案下载: PPT论坛:课件: 语文课件:数学课件: 英语课件:美术课件: 科学课件:物理课件: 化学课件:生物课件: 地理课件:历史课件:
圆柱体的体积计算
1、经历同桌合作,测量、计算圆柱物 体体积的过程。
2、会测量圆柱物体的有关数据,能根 据圆柱的高及直径或周长计算圆柱的体 积。
3、能找到解决问题的有效方法,能表 达解决问题的大致过程和结果。
同桌合作,测量自己准备的茶叶筒的 有关数据,计算出它的体积。
1.一个易拉罐(如下图),它的体积
找一找,哪些物体的形状是圆柱?
在生活中,你还见过哪些形状是 圆柱的物体?
圆柱的特点:
观察一个罐头盒。
指出它的底面、 侧面和高。
把下面罐头盒沿着它的一条高 剪开,再展开,看看商标是什么形 状。
1.长方形的长和宽分别与罐头盒的 什么有关系?
2.长方形的面积和罐头盒的侧面积 有什么关系?
怎样计算罐头盒的侧面积?
1.某工厂生产了侧面的商标纸,你 认为哪张纸比较适合?
2.求右面罐头盒商 标纸的面积。(接 缝处忽略不计) (单位:厘米)
3.求下面各圆柱的侧面积。
(1)d=8cm h=6cm
(2)r=3m h=1.5m
在自己家里找几个圆柱形的物体,测 量它们的直径和高,计算出它们的体积和 表面积。
冀教版六年级数学下册第三单元
圆柱和圆柱的侧面积
1、知识目标:理解圆柱体侧面积和表面积的含义。 2、能力目标:通过操作独立推导并掌握求圆柱的 侧面积的方法,并能运用到实际中解决问题。 3、情感目标:体验成功与失败的收获,体会合作 的愉悦。
是多少立方厘米? PPT模板:素材: PPT背景:图表: PPT下载:教程: 资料下载:范文下载: 试卷下载:教案下载: PPT论坛:课件: 语文课件:数学课件: 英语课件:美术课件: 科学课件:物理课件: 化学课件:生物课件: 地理课件:历史课件:
圆柱体积PPT课件
r= d
2
S=∏r2 v=sh = ∏ r2 h
3.已知圆柱体的底面周长和高,怎样求体积 ?
r=c÷2∏
S=∏r2 v=sh = ∏ r2 h
一个圆柱,底面半径是2cm,高是5cm。 求它的体积?
r=2cm h=5cm S底=πr2 =2×2×3.14
=4×3.14 =12.56(cm2) V=Sh=5×12.56=62.8(cm3)
人教版小学六年级数学下册《圆柱的体积》
真 棒!
高 宽
长
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
v长=a b h
v正 =a 3
V=s底 h
圆的面积公式推导过程:
圆的面积公式推导过程:
S=π r 2
rHale Waihona Puke πrS=πr ×r =π r 2
圆面积计算公式的推导过程
()
圆
长方形
运用了什么数学思想?
一根圆柱形的钢材,底面积是50平方厘米, 高是2.1米。它的体积是多少?
2.1米=210厘米 50 ×210=10500(立方厘米) 答:它的体积是10500立方厘米。
50平方厘米=0.005平方米 0.005 ×2.1=0.0105(立方米) 答:它的体积是0.0105立方米。
看图列式,并写出相应的公式。
答:圆柱的表面积是62.8平方厘米。
计算右图圆柱是体积。(单位:dm)
d=10dm h=4dm S底=π(d÷2)2
=(10÷2)2×3.14 =25×3.14 =78.5(dm2) V=Sh=4×78.5=314(dm3)
1·0 4
一个圆柱,底面周长是94.2m,高是 100m。求它的体积?
圆柱的体积课件
16 15 14 13 12 11 10 9 16 15 14 13 12 11 10 9
真 棒!
高
长 宽 棱长
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
v =a b h
长
v =a 正
V=s底 h
பைடு நூலகம்
3
猜想:圆柱体积的大小跟
哪些条件有关?
观察:①甲乙两个圆柱有什么相同?什么不同? ②当高相等时,甲的体积为什么比乙的大? 圆柱的高相等,底面积大的体积就大。 真
6.28厘米
(2)
2 V=兀(d÷2)×h
(3)
2 3.14 ×(6.28÷3.14÷2) ×8 5厘米 2 V=兀(C÷兀÷2)×h
(4)
练习巩固 应用拓展
• 把一根长1.5分米的圆柱形钢材截成三段后, 如图,表面积比原来增加9.6平方分米,这 根钢材原来的体积是多少? (9.6÷3)×1.5= 4.8(立方分米) 答:这根钢材原来的 体积是4.8立方分米
将一个圆柱体沿着底面直径切成两个半 圆柱,表面积增加了40平方厘米,圆柱的 底面直径为4厘米,这个圆柱的体积是多 少立方厘米?
再见!
2、它的底面积变了吗?
∏r
1、拼成的长方体的体积与原来的圆柱体体积是否相等?
因为长方体的体积=底面积×高 所以圆柱的体积=底面积×高 V = S h
3、它的高变了吗?
V长方体 V=abh
=
V圆柱 V= 兀r2 × h
= 兀r ×r × h = 兀r 2 h ×
V=Sh
例4
一根圆柱形钢材,底面积 是50平方厘米,高是2.1米。 它的体积是多少?
V =s h
想 一 想
《圆柱的体积》PPT课件
面测量得到的。)
8cm
杯子的容积。
杯子的容积: 50.24 ×10 =502.4(cm3)
10cm
杯子的底面积: 3.14 ×(8÷2)2
=3.14 ×16 =50.24(cm2)
=502.4(mL) 牛奶的体积: 240×2=480(mL) 502.4>480 答:杯子能装下2袋这样的牛奶。
课堂练习
小明和妈妈出去游玩,带了一个圆柱形保温壶,从里 面量底面直径是8cm,高是15cm。如果两人游玩期间 要喝1L水,带这壶水够喝吗?
保温壶的底面积:
3.14×(8÷2)2 =3.14×16 =50.24(cm2)
保温壶的容积:
50.24×15=753.6(cm3) =0.7536(L)
1L>0.7536L
答:带这壶水不够喝。
课堂练习
一根圆柱形木料底面直径是0.4m,长5m。如果做一张 课桌用去木料0.02m3,这根木料最多能做多少张课桌?
木料的体积:
3.14×(0.4÷2)2×5 =3.14×0.2 =0.628(m3)
“退一”法。
0.628÷0.02=31.4(张)
答:这根木料最多能做31张课桌。
已知底面直径和高求圆柱体积。 V=π(d2 )2h =3.14×(1÷2)2×10 =7.85(立方米) 答:挖出的土有7.85立方米。
探究新知
下图的杯子能不能装下2袋这样的牛奶?(数据是从杯子 里面测量得到的。)
思考:
8cm
1.已知什么?
10cm
2.要求什么?
3.要注意什么?
探究新知
下图的杯子能不能装下2袋这样的牛奶?(数据是从杯子里
)
于土的高度有关。
两个花坛的体积
《圆柱:圆柱的体积》教学课件
05
生活中应用举例
建筑领域应用
建筑结构
圆柱体常被用作建筑的主要支撑结构, 如圆柱形的柱子,其体积计算对于确 定材料用量和承重能力至关重要。
建筑设计
在建筑设计中,圆柱体常被用于创造 独特的美感和空间感,体积计算有助 于实现精确的比例和平衡。
机械制造领域应用
机械零件
圆柱体是机械制造中常见的零件形状,如轴承、齿轮等,体积计算对于确定零件的尺寸和重量非常关 键。
液压和气压传动
圆柱体在液压和气压传动系统中用作活塞或气缸,体积计算有助于确定系统的传动效率和性能。
其他领域应用
容器设计
圆柱形的容器,如储水罐、油罐等,其体积计算对于确定容器的容量和形状优化至关重 要。
地理信息系统
在地理信息系统中,圆柱体模型常被用于地球表面的三维建模,体积计算有助于分析和 可视化地理数据。
《圆柱:圆柱的体积 》教学课件
目录
• 圆柱基本概念与性质 • 计算圆柱体积方法 • 拓展应用:不规则物体体积求解 • 实验操作:测量并计算圆柱体积 • 生活中应用举例 • 总结回顾与课堂互动环节
01 圆柱基本概念与性质
圆柱定义及特点
圆柱定义
圆柱是由两个平行且相等的圆面 以及连接这两个圆面的一个曲面 所围成的几何体。
分析误差原因
比较计算值与真实值的差异,分析 误差产生的原因,如测量工具精度、 操作规范等。
实验结果分析与讨论
结果展示
将实验数据以表格或图表形式展 示,包括测量值、计算值和误差
等。
结果分析
根据实验数据,分析圆柱体体积 与高度、半径之间的关系,以及
误差对实验结果的影响。
讨论与改进
针对实验过程中出现的问题和误 差原因进行讨论,提出改进措施 以提高实验精度和效果。例如, 改进测量工具、优化操作流程等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)3.14×(25.12÷3.14÷2)² ×2=100.48 ( 立方分米)
5深化练习
一个圆柱形钢管,底面周长是25.12分 米,高和直径相等,它的体积是多少?
(提示:先求底面积,最后求体积)
(4)圆柱体的底面直径和高可以相等。
(√ )
4、比一比,看谁的本领大。
求下面各圆柱的体积。
(1)底面半径是3厘米,高是5厘米。 (2)底面直径是8米,高是10米。 (3)底面周长是25.12分米,高是2 分米。
(1)3.14×3² ×5=141.3(立方厘米)
(2)3.14×(8÷2)² ×10=502.4 (立方米)
2、求圆柱的体积。(单位:厘米)
2 10
3.14 ×(10÷2)2×2=157(立方厘米)
答:它的体积是157立方厘米。
3、判断正误,对的画“√”,错 误 的画“×”。
(×)
(1)圆柱体的底面积越大,它的体积越大。
(2)圆柱体的高越长,它的体积越大。
(×)
பைடு நூலகம்
(3)圆柱体的体积与长方体的体积相等。
(×)
d 2 V=∏( ) h 2
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
下面这个杯子能不能装下这袋奶?(杯子
的数据是从里面测量得取的。)
8cm 498ml 10cm
杯子的底面积:3.14 ×(8÷2)2=50.24(cm)
杯子的容积: 50.24×10=502.4(ml)
答:502.4大于498,所以这个杯子能装下这袋 牛奶。
刘会宁
真 棒!
高
长 宽 棱长
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
v =a b h
长
v 正 =a
V=s底 h
3
把圆柱的底面平均分的份数越多,切拼成的立体图形越接 近长方体。
把圆柱的底面分成许多 相等的扇形,然后把圆柱 切开,对插,就拼成了一 个近似的长方体。
思考
1、拼成的长方体的体积与原来的圆柱体体积是否相等? 2、它的底面积变了吗? 3、它的高变了吗?
底面积 高
高
长方体体积=底面积×高 圆柱体积=底面积×高
V=sh
想一想、填一填:
把圆柱体切割拼成近似( 长方体 ), 体积 )相等。长方体的高就是圆柱 它们的( 体的( 高 ),长方体的底面积就是圆柱体的 底面积×高 ), ( 底面积),因为长方体的体积=( 所以圆柱体的体积=( 底面积×高 )。用 字母“V”表示( 体积 ),“S”表示 底面积 ( ),“ ),那么,圆 高 h”表示( 柱体体积用字母表示为( ) V=Sh
巩固练习
1、填表。
底面积 (平方米) 高 (米 )
圆柱体积
(立方米)
15
6.4
3 4
45 25.6
讨论
(1)已知圆的半径和高,怎样求圆柱的体积? (2)已知圆的直径和高,怎样求圆柱的体积? (3)已知圆的周长和高,怎样求圆柱的体积?
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高:
5深化练习
一个圆柱形钢管,底面周长是25.12分 米,高和直径相等,它的体积是多少?
(提示:先求底面积,最后求体积)
(4)圆柱体的底面直径和高可以相等。
(√ )
4、比一比,看谁的本领大。
求下面各圆柱的体积。
(1)底面半径是3厘米,高是5厘米。 (2)底面直径是8米,高是10米。 (3)底面周长是25.12分米,高是2 分米。
(1)3.14×3² ×5=141.3(立方厘米)
(2)3.14×(8÷2)² ×10=502.4 (立方米)
2、求圆柱的体积。(单位:厘米)
2 10
3.14 ×(10÷2)2×2=157(立方厘米)
答:它的体积是157立方厘米。
3、判断正误,对的画“√”,错 误 的画“×”。
(×)
(1)圆柱体的底面积越大,它的体积越大。
(2)圆柱体的高越长,它的体积越大。
(×)
பைடு நூலகம்
(3)圆柱体的体积与长方体的体积相等。
(×)
d 2 V=∏( ) h 2
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
下面这个杯子能不能装下这袋奶?(杯子
的数据是从里面测量得取的。)
8cm 498ml 10cm
杯子的底面积:3.14 ×(8÷2)2=50.24(cm)
杯子的容积: 50.24×10=502.4(ml)
答:502.4大于498,所以这个杯子能装下这袋 牛奶。
刘会宁
真 棒!
高
长 宽 棱长
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
v =a b h
长
v 正 =a
V=s底 h
3
把圆柱的底面平均分的份数越多,切拼成的立体图形越接 近长方体。
把圆柱的底面分成许多 相等的扇形,然后把圆柱 切开,对插,就拼成了一 个近似的长方体。
思考
1、拼成的长方体的体积与原来的圆柱体体积是否相等? 2、它的底面积变了吗? 3、它的高变了吗?
底面积 高
高
长方体体积=底面积×高 圆柱体积=底面积×高
V=sh
想一想、填一填:
把圆柱体切割拼成近似( 长方体 ), 体积 )相等。长方体的高就是圆柱 它们的( 体的( 高 ),长方体的底面积就是圆柱体的 底面积×高 ), ( 底面积),因为长方体的体积=( 所以圆柱体的体积=( 底面积×高 )。用 字母“V”表示( 体积 ),“S”表示 底面积 ( ),“ ),那么,圆 高 h”表示( 柱体体积用字母表示为( ) V=Sh
巩固练习
1、填表。
底面积 (平方米) 高 (米 )
圆柱体积
(立方米)
15
6.4
3 4
45 25.6
讨论
(1)已知圆的半径和高,怎样求圆柱的体积? (2)已知圆的直径和高,怎样求圆柱的体积? (3)已知圆的周长和高,怎样求圆柱的体积?
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高:
