2009年桂林测量考研试题
桂林理工大学工程测量学常考试题

桂林理工大学工程测量学常考试题(共11页)-本页仅作为预览文档封面,使用时请删除本页-第一章1.工程测量学定义:定义1. 研究各种工程在规划设计、施工建设和运营管理阶段进行测量工作的学科.( 大众化易于理解)定义2.研究工程、工业和城市建设以及资源开发各个阶段所进行的地形和有关信息的采和处理、施工放样、设备安装、变形监测分析和预测等的理论、方法和技术,以及对测量和有关的信息进行管理和使用的学科。
(更具体、准确、范围更大)定义3.工程测量学是研究地球空间(地面、地下、水下、空中)中具体几何实体的测量描绘抽象几何实体的测设实现的理论方法和技术的一门应用性学科.( 更加概括、抽象、严密和科学)(1)工程测量学主要包括以工程建筑为对象的工程测量和以机器设备为对象的工业测量两大部分。
(2)工程测量学按工程建设阶段划分其主要内容有哪些?答:工程测量按工程建设的规划设计、施工建设和运营管理三个阶段分为“工程勘测”、“施工测量”和“安全监测”,这三个阶段对测绘工作有不同的要求。
2.简述工程测量学的主要内容1)地形图测绘(测图)2)工程控制网布设(布网)3)施工放样技术和方法(放样)4)工程的变形监测分析和预报(监测)5)工程测量的仪器(仪器)6)工程测量学中的误差及测量平差理论(数据处理)7)大型精密设备的安装和调试测量,工业生产过程的质量检测和控制8)工程信息系统的建立与应用3. 工程测量的通用仪器:水准仪、经纬仪、陀螺经纬仪、全站仪和GPS接收机用途:测方向、角度、距离、高差、坐标差等几何量。
4.专用仪器:机械式、光电式及光机电(子)多传感器集成式仪器或测量系统。
主要特点是:高精度、自动化、遥测和持续观测基准线测量或准直测量仪器:有正锤、倒锤及垂线观测仪、引张线仪、各种激光准直仪、铅直仪(向下、向上)、自准直仪以及尼龙丝或金属丝准直测量系统等。
5工程建设规划设计阶段的测量工作有哪些?主要是提供各种比例尺的地形图,另外还要为工程,水文地质勘探以及水文测验等进行测量。
2009年上学期测量学试卷A参考答案

考试方式:闭卷、笔试
考试内容:
一、填空题(将正确的内容填写在相应的横线上,共25分)
1.在1:500比例尺的地形图上,围墙的符号是半依比例符号,水库的符号是依比例符号,路灯的符号是不依比例符号。(3分)
2.在1:5000比例尺的地形图上,某区域的图上面积为800平方毫米,则该区域的实地面积为20000m2。(2分)
3.已知A、B、C三点的坐标XA=2179.737m,YA=1655.636m;XB=2166.741m,YB=1757.266m;XC=2196.147m,YC=1775.437m,试求三角形ABC的三个内角的值(用度分秒的形式表示)。
解:
6.已知某经纬仪一个测回的测角中误差为±5″,今欲使某角度的测角精度达到±2″,则用该仪器至少需要观测7测回。(2分)
7.已知武昌某点的经纬度为L=114°17′E,B=30°31′N,则该点所在的1:100万比例尺图幅编号为H50,该图幅的经度范围是114°~120°E,纬度范围是28°~32°N。(3分)
4.用经纬仪瞄准同一竖面内不同高度的两个点,在竖盘上的读数差就是坚直角(×)
5.在测量过程中存在偶然误差,此种误差可以采用一定的观测方法或计算改正数的
方法加以消除。(×)
6.用同一钢尺在相同条件下丈量两条直线.丈量结果:一条长100m,另一条长200m,其相对误差均为1/3000,这说明该两条直线丈量精度相同。(√)
1.在已知水准点A、B间进行了图根附合水准路线测量,已知高程和观测成果列于下表,请完成相应的计算。
点号
测站数
高差(m)
高差改正数(mm)
改正后高差(m)
高程(m)
A
8
-0.127
2009考研数学(二)真题及参考答案

2009年研究生入学统一考试数学二试题与解析一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项是符合题目要求的.请将所选项前的字母填在答题纸指定位置上.(1)函数()3sin x x f x nx-=的可去间断点的个数为( )()A 1.()B 2. ()C 3.()D 无穷多个.(2)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则( )()A 11,6a b ==-.()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=(3)设函数(),z f x y =的全微分为dz xdx ydy =+,则点()0,0( )()A 不是(),f x y 的连续点. ()B 不是(),f x y 的极值点. ()C 是(),f x y 的极大值点. ()D 是(),f x y 的极小值点.(4)设函数(),f x y 连续,则()()222411,,yxydx f x y dy dy f x y dx -+=⎰⎰⎰⎰( )()A ()2411,xdx f x y dy -⎰⎰. ()B ()241,xxdx f x y dy -⎰⎰.()C ()2411,ydy f x y dx -⎰⎰.()D .()221,y dy f x y dx ⎰⎰(5)若()f x ''不变号,且曲线()y f x =在点()1,1上的曲率圆为222x y +=,则()f x 在区间()1,2内( )()A 有极值点,无零点. ()B 无极值点,有零点.()C 有极值点,有零点. ()D 无极值点,无零点.(6)设函数()y f x =在区间[]1,3-上的图形为1 ()f x -2 0 2 3x-1O则函数()()0xF x f t dt =⎰的图形为( )()A .()B .()C .()D .(7)设A ,B 均为2阶矩阵,**A B ,分别为A ,B 的伴随矩阵.若23A B ==,,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( )()A .**32O B A O ⎛⎫⎪⎝⎭()B .**23OB A O ⎛⎫⎪⎝⎭ ()C .**32O A BO ⎛⎫ ⎪⎝⎭()D .**23O A BO ⎛⎫⎪⎝⎭(8)设A P ,均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223P Q ααααααα==+(,,),(,,),则TQ AQ 为( ) ()A .210110002⎛⎫⎪⎪ ⎪⎝⎭()B .110120002⎛⎫⎪⎪ ⎪⎝⎭()f x 0 2 3x1 -2-11()f x 02 3x1 -1 1()f x 02 3x1 -2-11()f x 0 2 3x1 -2 -11()C .200010002⎛⎫⎪⎪ ⎪⎝⎭()D .100020002⎛⎫⎪⎪ ⎪⎝⎭二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.(9)曲线2221-x=0ln(2)u t e du y t t -⎧⎪⎨⎪=-⎩⎰在(0,0)处的切线方程为 . (10)已知+1k xe dx ∞=-∞⎰,则k = .(11)1n lime sin x nxdx -→∞=⎰.(12)设()y y x =是由方程xy 1ye x +=+确定的隐函数,则22x yx=∂=∂ .(13)函数2x y x =在区间(]01,上的最小值为 .(14)设αβ,为3维列向量,T β为β的转置,若矩阵T αβ相似于200000000⎛⎫⎪⎪ ⎪⎝⎭,则T =βα .三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求极限()[]401cos ln(1tan )limsin x x x x x→--+.(16)(本题满分10 分) 计算不定积分1ln(1)xdx x++⎰(0)x >. (17)(本题满分10分)设(),,z f x y x y xy =+-,其中f 具有2阶连续偏导数,求dz 与2z x y∂∂∂.(18)(本题满分10分)设非负函数()y y x = ()0x ≥满足微分方程20xy y '''-+=,当曲线()y y x = 过原点时,其与直线1x =及0y =围成平面区域D 的面积为2,求D 绕y 轴旋转所得旋转体体积. (19)(本题满分10分)计算二重积分()Dx y dxdy -⎰⎰,其中()()(){}22,112,D x y x y y x =-+-≤≥.(20)(本题满分12分)设()y y x =是区间-ππ(,)内过点-22ππ(,)的光滑曲线,当-0x π<<时,曲线上任一点处的法线都过原点,当0x π≤<时,函数()y x 满足0y y x ''++=.求()y x 的表达式. (21)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(),a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-;(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(22)(本题满分11分设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭. (Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ;(Ⅱ)对(Ⅰ)中的任一向量23,ξξ,证明:123,,ξξξ线性无关.(23)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值.2009年全国硕士研究生入学统一考试数学二试题答案一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项是符合题目要求的.请将所选项前的字母填在答题纸指定位置上.(1)函数()3sin x x f x nx-=的可去间断点的个数为( )()A 1.()B 2. ()C 3.()D 无穷多个.【答案】C 【解析】()3s i n x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=. 【答案】A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C . 另外201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排D .所以本题选A.(3)设函数(),z f x y =的全微分为dz xdx ydy =+,则点()0,0( )()A 不是(),f x y 的连续点. ()B 不是(),f x y 的极值点. ()C 是(),f x y 的极大值点. ()D 是(),f x y 的极小值点.【答案】 D【解析】因dz xdx ydy =+可得,z zx y x y∂∂==∂∂ 2222221,0,1z z z zA B C x x y y x y∂∂∂∂== === ==∂∂∂∂∂∂又在(0,0)处,0,0z zx y∂∂==∂∂ 210AC B -=>故(0,0)为函数(,)z f x y =的一个极小值点.(4)设函数(),f x y 连续,则()()222411,,yxydx f x y dy dy f x y dx -+=⎰⎰⎰⎰( )()A ()2411,xdx f x y dy -⎰⎰. ()B ()241,xxdx f x y dy -⎰⎰.()C ()2411,ydy f x y dx -⎰⎰.()D .()221,y dy f x y dx ⎰⎰【答案】C 【解析】222211(,)(,)xxdx f x y dy dy f x y dx +⎰⎰⎰⎰的积分区域为两部分:{}1(,)12,2D x y x x y =≤≤≤≤,{}2(,)12,4D x y y y x y =≤≤≤≤-将其写成一块{}(,)12,14D x y y x y =≤≤≤≤- 故二重积分可以表示为2411(,)ydy f x y dx -⎰⎰,故答案为C.(5)若()f x ''不变号,且曲线()y f x =在点()1,1上的曲率圆为222x y +=,则()f x 在区间()1,2内( )()A 有极值点,无零点. ()B 无极值点,有零点.()C 有极值点,有零点. ()D 无极值点,无零点.【答案】 B【解析】由题意可知,()f x 是一个凸函数,即''()0f x <,且在点(1,1)处的曲率322|''|12(1('))y y ρ==+,而'(1)1f =-,由此可得,''(1)2f =-在[1,2] 上,'()'(1)10f x f ≤=-<,即()f x 单调减少,没有极值点. 对于(2)(1)'()1(1,2)f f f ζζ-=<- , ∈ , (拉格朗日中值定理)(2)0f ∴ <而 (1)10f =>由零点定理知,在[1,2] 上,()f x 有零点. 故应选(B ). (6)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为( )1 ()f x -2 0 2 3x-1O()A .()B .()C .()D .【答案】D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征: ①[]0,1x ∈时,()0F x ≤,且单调递减. ②[]1,2x ∈时,()F x 单调递增. ③[]2,3x ∈时,()F x 为常函数.④[]1,0x ∈-时,()0F x ≤为线性函数,单调递增. ⑤由于F(x)为连续函数结合这些特点,可见正确选项为D .(7)设A ,B 均为2阶矩阵,**A B ,分别为A ,B 的伴随矩阵.若23A B ==,,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( )()A .**32O B A O ⎛⎫⎪⎝⎭()B .**23OB A O ⎛⎫⎪⎝⎭ ()C .**32O A BO ⎛⎫ ⎪⎝⎭()D .**23O A BO ⎛⎫⎪⎝⎭()f x 0 2 3x1 -2-11()f x 02 3x1 -1 1()f x 02 3x1 -2-11()f x 0 2 3x1 -2 -11【答案】 B【解析】根据CC C E *=若111,C C C CC C*--*==分块矩阵00A B ⎛⎫⎪⎝⎭的行列式22012360A AB B⨯=-=⨯=()即分块矩阵可逆 111100066000100B BA A AB B BBAA A**---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭10023613002BB AA ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭(8)设A P ,均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223P Q ααααααα==+(,,),(,,),则TQ AQ 为( ) ()A .210110002⎛⎫⎪⎪ ⎪⎝⎭()B .110120002⎛⎫⎪⎪ ⎪⎝⎭()C .200010002⎛⎫⎪⎪ ⎪⎝⎭()D .100020002⎛⎫⎪⎪ ⎪⎝⎭【答案】 A【解析】122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦,即:12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT T Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.(9)曲线2221-x=0ln(2)u t e du y t t -⎧⎪⎨⎪=-⎩⎰在(0,0)处的切线方程为 . 【答案】2y x =【解析】221222ln(2)22t dy t t t t dt t ==--⋅=--2(1)1(1)1t t dxe dt --==⋅-=- 所以 2dy dx= 所以 切线方程为2y x =.(10)已知+1k xe dx ∞=-∞⎰,则k = .【答案】2-【解析】1122lim bk xkxkxb e dx e dx e k +∞+∞-∞→+∞===⎰⎰因为极限存在所以0k <210k=-2k =-(11)1n lime sin x nxdx -→∞=⎰.【答案】0【解析】令sin sin cos x x xn I e nxdx e nx n e nxdx ---==-+⎰⎰2sin cos x xn e nx nenx n I --=---所以2cos sin 1xn n nx nx I e C n -+=-++即11020cos sin lim sin lim()1xx n n n nx nx e nxdx e n --→∞→∞+=-+⎰ 122cos sin lim()110n n n n ne n n -→∞+=-+++= (12)设()y y x =是由方程xy 1ye x +=+确定的隐函数,则22x yx=∂=∂ .【答案】3-【解析】对方程xy 1y e x +=+两边关于x 求导有''1y y xy y e ++=,得'1yyy x e -=+ 对''1y y xy y e ++=再次求导可得''''''22()0y y y xy y e y e +++=,得''2''2()yyy y e y x e +=-+ (*)当0x =时,0y =,'(0)0101y e -==,代入(*)得 ''20''032(0)((0))(0)(21)3(0)y y e y e +=-=-+=-+(13)函数2x y x =在区间(]01,上的最小值为 . 【答案】2ee-【解析】因为()22ln 2xy xx '=+,令0y '=得驻点为1x e =.又()22222ln 2xxy x x x x ''=++⋅,得21120e y e e -+⎛⎫''=> ⎪⎝⎭,故1x e=为2xy x =的极小值点,此时2e y e -=,又当10,x e ⎛⎫∈ ⎪⎝⎭时,()0y x '<;1,1x e ⎛⎤∈ ⎥⎝⎦时,()0y x '>,故y 在10,e ⎛⎫ ⎪⎝⎭上递减,在1,1e ⎛⎫ ⎪⎝⎭上递增.而()11y =,()()002022ln limlim11lim 222ln 00lim lim 1x x x xx x xx xxx x x y x e eee++→→+→++--+→→======,所以2xy x =在区间(]01,上的最小值为21ey e e -⎛⎫= ⎪⎝⎭.(14)设αβ,为3维列向量,T β为β的转置,若矩阵T αβ相似于200000000⎛⎫ ⎪⎪ ⎪⎝⎭,则T =βα .【答案】2【解析】因为T αβ相似于200000000⎛⎫⎪⎪ ⎪⎝⎭,根据相似矩阵有相同的特征值,得到T αβ得特征值是2,0,0而T βα是一个常数,是矩阵T αβ的对角元素之和,则T 2002βα=++=三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求极限()[]401cos ln(1tan )limsin x x x x x→--+.【解析】()[][]244001ln(1tan )1cos ln(1tan )2lim limsin sin x x x x x x x x x x→→-+--+= 22201ln(1tan )lim 2sin sin x x x x x x→-+=201ln(1tan )1lim 2sin 4x x x x →-+== (16)(本题满分10 分) 计算不定积分1ln(1)xdx x++⎰(0)x >. 【解析】 令1x t x+=得22212,1(1)tdtx dx t t -= =-- 22211ln(1)ln(1)1ln(1)11111x dx t d x t t dt t t t ++=+-+=---+⎰⎰⎰而22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以221ln(1)111ln(1)ln 1412(1)111ln(1)ln(1)2211111ln(1)ln(1)222x t t dx C x t t t x xx x x C x x x x x x x x x x C x ++++=+-+--++=++++-++++=+++++-++⎰ (17)(本题满分10分)设(),,z f x y x y xy =+-,其中f 具有2阶连续偏导数,求dz 与2zx y∂∂∂.【解析】123123zf f yf x zf f xf y∂'''=++∂∂'''=-+∂1231232111213212223331323331122331323()()1(1)1(1)[1(1)]()()z z dz dx dy x yf f yf dx f f xf dyzf f f x f f f x f y f f f x x yf f f xyf x y f x y f ∂∂∴=+∂∂''''''=+++-+∂'''''''''''''''''''=⋅+⋅-+⋅+⋅+⋅-+⋅++⋅+⋅-+⋅∂∂'''''''''''=+-++++-(18)(本题满分10分)设非负函数()y y x = ()0x ≥满足微分方程20xy y '''-+=,当曲线()y y x = 过原点时,其与直线1x =及0y =围成平面区域D 的面积为2,求D 绕y 轴旋转所得旋转体体积. 【解析】解微分方程20xy y '''-+=得其通解212122,y C x C x C C =++其中,为任意常数又因为()y y x =通过原点时与直线1x =及0y =围成平面区域的面积为2,于是可得10C =1112232220002()(2)()133C C y x dx x C x dx x x ==+=+=+⎰⎰从而23C =于是,所求非负函数223(0)y x x x =+ ≥又由223y x x =+ 可得,在第一象限曲线()y f x =表示为1131)3x y =+-(于是D 围绕y 轴旋转所得旋转体的体积为15V V π=-,其中552210051(131)9(23213)93918V x dy y dyy y dy ππππ==⋅+-=+-+=⎰⎰⎰395117518186V ππππ=-==. (19)(本题满分10分)计算二重积分()Dx y dxdy -⎰⎰,其中()()(){}22,112,D x y x y y x =-+-≤≥.【解析】由22(1)(1)2x y -+-≤得2(sin cos )r θθ≤+,32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰ 2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰ 3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-.(20)(本题满分12分)设()y y x =是区间-ππ(,)内过点-22ππ(,)的光滑曲线,当-0x π<<时,曲线上任一点处的法线都过原点,当0x π≤<时,函数()y x 满足0y y x ''++=.求()y x 的表达式.【解析】由题意,当0x π-<<时,'xy y =-,即ydy xdx =-,得22y x c =-+, 又()22y ππ-=代入22y x c =-+得2c π=,从而有222x y π+=当0x π≤<时,''0y y x ++=得 ''0y y += 的通解为*12cos sin y c x c x =+ 令解为1y Ax b =+,则有00Ax b x +++=,得1,0A b =-=, 故1y x =-,得''0y y x ++=的通解为12cos sin y c x c x x =+- 由于()y y x =是(,)ππ-内的光滑曲线,故y 在0x =处连续于是由1(0),(0)y y c π-=± += ,故1c π=±时,()y y x =在0x =处连续 又当 0x π-<<时,有22'0x y y +⋅=,得'(0)0xy y-=-=, 当0x π≤<时,有12'sin cos 1y c x c x =-+-,得2'(0)1y c +=- 由'(0)'(0)y y -+=得210c -=,即 21c =故 ()y y x =的表达式为22,0cos sin ,0x x y x x x x ππππ⎧⎪-- -<<=⎨-+-≤<⎪⎩或22,0cos sin ,0x x y x x x x ππππ⎧⎪- -<<=⎨+-≤<⎪⎩,又过点,22ππ⎛⎫- ⎪⎝⎭,所以22,0cos sin ,0x x y x x x x ππππ⎧⎪- -<<=⎨+-≤<⎪⎩.(21)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(),a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-;(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.【解析】(Ⅰ)作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----,易验证()x ϕ满足:()()a b ϕϕ=;()x ϕ在闭区间[],a b 上连续,在开区间(),a b 内可导,且''()()()()f b f a x f x b aϕ-=--.根据罗尔定理,可得在(),a b 内至少有一点ξ,使'()0ϕξ=,即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--(Ⅱ)任取0(0,)x δ∈,则函数()f x 满足;在闭区间[]00,x 上连续,开区间()00,x 内可导,从而有拉格朗日中值定理可得:存在()()000,0,x x ξδ∈⊂,使得()0'()(0)x f x f fx ξ-=-……()* 又由于()'lim x f x A +→=,对上式(*式)两边取00x +→时的极限可得:()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====- 故'(0)f +存在,且'(0)f A +=.(22)(本题满分11分设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ;(Ⅱ)对(Ⅰ)中的任一向量23,ξξ,证明:123,,ξξξ线性无关. 【解析】(Ⅰ)解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量,令32x =,由0Ax =解得,211,1x x =-= 求特解,令120x x ==,得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,其中1k 为任意常数解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭故有两个自由变量,令21x =-,由20A x =得131,0x x ==求特解21200η⎛⎫ ⎪ ⎪= ⎪ ⎪⎪⎝⎭故 321121000k ξ⎛⎫⎪⎛⎫ ⎪⎪=-+ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭ ,其中2k 为任意常数.(Ⅱ)证明:由于12121212122111121112(21)()2()(21)222210k k k k k k k k k k k k k -+--=+++-+-+-+102=≠ 故123,,ξξξ 线性无关.(23)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+- (Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. 【解析】(Ⅰ) 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+(Ⅱ) 若规范形为2212y y +,说明有两个特征值为正,一个为0.则 1) 若10a λ==,则 220λ=-< ,31λ= ,不符题意2) 若20λ= ,即2a =,则120λ=>,330λ=>,符合3) 若30λ= ,即1a =-,则110λ=-< ,230λ=-<,不符题意 综上所述,故2a =.。
自考_2009年10月全国高等教育自学考试工程测量真题

2021年10月全国高等教育自学考试工程测量真题一、单项选择题〔本大题共10小题,每题2分,共20分〕在每题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多项选择或未选均无分。
1.水准仪整平时,整平圆水准器用的是〔〕A.微倾螺旋B.脚螺旋C.水平微动螺旋2.1弧度约等于多少度?〔〕A.57.3B.360C.34383.钢尺精细量距时,丈量温度低于标准温度,如不加温度改正,那么所量距离符合以下哪条?〔〕A.小于实际距离C.大于实际距离4.根据需要,在图上表示的最小距离不大于实地0.5米,那么测图比例尺不应小于〔〕∶500∶1000∶2000∶50005.山脊与山谷的等高线在凸起局部与山脊线、山谷线〔〕A.重合B.平行C.正交6.建筑基线应平行或垂直于主要建筑物的轴线,长的一条基线尽可能布设在场地的〔〕A.西南角B.正北C.中央7.施工测量应首先建立施工控制网,测设建筑物的主轴线,然后根据主轴线测设建筑物的〔〕A.建筑基线B.细部点C.控制点∶1000地形图的比例尺精度是多少米?〔〕B.0.10C.0.209.水准管上多长的弧长所对的圆心角称为水准管分划值?〔〕A.2毫米B.4毫米C.6毫米10.关于磁偏角,描述正确的选项是〔〕A.大小是固定不变的C.只有周年变化没有周日变化三、填空题〔本大题共10小题,每题1分,共10分〕请在每题的空格中填上正确答案。
错填、不填均无分。
14.在目前的测量工作中,要求距离丈量的相对误差最高约为______。
15.水准尺倾斜时,读数将会变______。
16.竖直角的取值范围为______。
17.对于一般钢尺量距,拉力误差不超过______时,可以忽略拉力误差对距离的影响。
18.在高斯投影带中,高斯平面直角坐标系的纵轴处处与中央子午线______。
19.关于权,起作用的不是权的绝对值,而是权之间的______。
20.三角高程测量中,地球曲率和大气折光的合成影响称为______。
中国计量大学数学分析2009年考研初试真题

8.设函数 f x 在 0, 上连续可导, 且 f 0 0.试求
lim 1 f
t t0
4 V
x2 y2 z2 dxdydz ,
其中积分区域为V : x2 y2 z2 t2 .
9.讨论级数 1n sin x 的收敛性(包括条件收敛或绝对收敛).
f x A, x 0 , .
《数学分析》试卷 第 1 页 共 2 页
3.判断函数项级数在所示区间上的一致收敛性:
1
n1
1 n1
x2 n
, x
,
;
2 s i nnx n1 n
, x
0 ,2
.
4.证明函数 F y e xy2 dx 在 , 上连续. 0
f (xn y n )(xn1dx y n1dy) 0 ( n 正整数).
L
7 . 计 算 第 二 型 曲 面 积 分 : J y(x z)dydz x2dzdx y2 xz dxdy ,
S
其中 S 是曲面
z 5 x2 y2 上 z 1 的部分,并取外侧.
n1
n
二、(共 5 小题,每小题 12 分,共 60 分)
1.设 f x 在闭区间 a,b 上连续.证明在开区间 a,b 内至少存在一点 , 使
b
a
f
x
d x
f b . a
2.设函数 f 在 0, 上满足方程 f 2x f x, 且 lim f x A. 证明: x
中国计量学院 2009 年攻读硕士学位研究生入学试题
考试科目名称: 考试科目代码: 考 生 姓 名: 考 生 编 号:
09年第二学期工程测量考试范围及答案
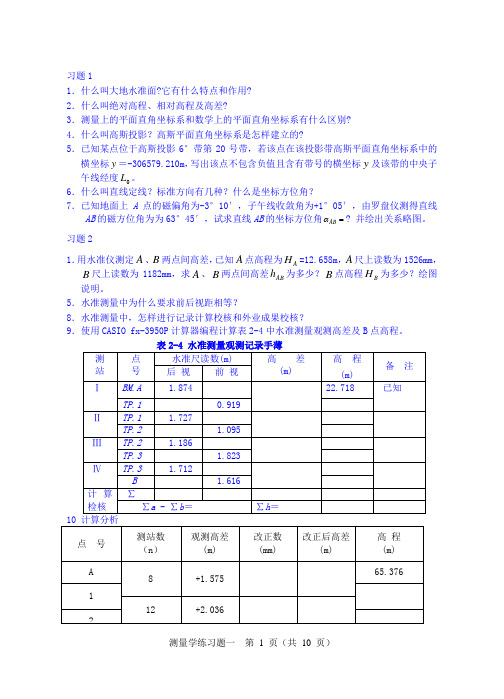
习题11.什么叫大地水准面?它有什么特点和作用? 2.什么叫绝对高程、相对高程及高差?3.测量上的平面直角坐标系和数学上的平面直角坐标系有什么区别? 4.什么叫高斯投影?高斯平面直角坐标系是怎样建立的?5.已知某点位于高斯投影6°带第20号带,若该点在该投影带高斯平面直角坐标系中的横坐标y =-306579.210m ,写出该点不包含负值且含有带号的横坐标y 及该带的中央子午线经度0L 。
6.什么叫直线定线?标准方向有几种?什么是坐标方位角?7.已知地面上A 点的磁偏角为-3°10′,子午线收敛角为+1°05′,由罗盘仪测得直线AB 的磁方位角为为63°45′,试求直线AB 的坐标方位角=AB α? 并绘出关系略图。
习题21.用水准仪测定A 、B 两点间高差,已知A 点高程为A H =12.658m ,A 尺上读数为1526mm ,B 尺上读数为1182mm ,求A 、B 两点间高差AB h 为多少?B 点高程B H 为多少?绘图说明。
5.水准测量中为什么要求前后视距相等?8.水准测量中,怎样进行记录计算校核和外业成果校核?9.使用CASIO fx-3950P 计算器编程计算表2-4中水准测量观测高差及B 点高程。
习题31. 何谓水平角?何谓竖直角?它们取值范围为多少?3. 经纬仪安置包括哪两个内容?怎样进行?目的何在?7. 测量水平角时,为什么要用盘左、盘右两个位置观测?8. 何谓竖盘指标差?如何消除竖盘指标差?9. 经纬仪有哪几条主要轴线?它们应满足什么条件?10. 用经纬仪瞄准同一竖直面内不同高度的两点,水平度盘上的读数是否相同?在竖直度盘上的两读数差是否就是竖直角?为什么?11. 用J6型光学经纬仪按测回法观测水平角,整理表3-7中水平角观测的各项计算。
12. 使用CASIO fx-3950P计算器编程计算表3-8竖直角观测的指标差和竖直角。
13. 用DJ6型光学经纬仪观测某一目标,盘左竖直度盘读数为7l°45′24″,该仪器竖盘(盘左)注记如l2题表3-8所示,测得竖盘指标差x=+24″,试求该目标正确的竖直角 为多少?15.某钢尺的尺长方程为l t=30m+0.006m+1.2×10-5×30m×(t -20°C),使用该钢尺丈量AB之间的长度为29.9358m,丈量时的温度t =12°C,使用拉力与检定时相同,AB两点间高差h AB=0.78m,试计算AB之间的实际水平距离?习题41.用钢尺丈量一条直线,往测丈量的长度为217.30m ,返测为217.38m ,今规定其相对误差不应大于l /2000,试问:(1)此测量成果是否满足精度要求?(2)按此规定,若丈量100m ,往返丈量最大可允许相差多少毫米? 3.选择测图控制点(导线点)应注意哪些问题?4.按表5-16的数据,计算闭合导线各点的坐标值。
2009年全国硕士研究生入学考试数学二真题及答案
y y x 0 。求 y(x)的表达式。
(21)(本题满分 11 分)(I)证明拉格朗日中值定理:若函数 f (x) 在[a,b]上连续,在(a,b)
可导,则存在 (a,b) ,使得 f (b) f (a) f ( )(b a) 。(II)证明:若函数 f (x) 在 x=0
阵
0 B
A 0
的伴随矩阵为()
(A)
0 2 A
3B
0
(B)
0 3 A
2B
0
பைடு நூலகம்(C)
0 2B
3A
0
(D)
0 3B
2 A
0
100
(8)设
A,P
均为
3
阶矩阵,
PT
为
P
的转置矩阵,且
1
x
1
y
A
2
dx
4x f x, y dy
1
1
C
2
dy
4y f x, y dx
1
1
B
2
dx
4x f x, y dy
1
x
D
2
1
2
dyy
f
x,
y dx
【答案】 C
2
2
2
2
【解析】 dx f (x, y)dy dy f (x, y)dx 的积分区域为两部分:
sin x
A 1 B 2 C 3 D 无穷多个
【答案】 C
【解析】由于 f x x x3 ,则当 x 取任何整数时, f x 均无意义.
2009年硕士研究生入学考试试题
2009年硕士研究生入学考试试题一:名词解释1:粗差2:系统误差3:偶然误差4水准测量的原理5:验潮站6:4D产品7:数字高程模型8:等高线3-8一定是,1,2好像有一个,不确定。
其它的就想不起来了。
二:简答题1:偶然误差的特性2:GPS测量中的误差来源3:光电测距仪测定的距离进行哪几方面的改正计算4:计算机中的坐标与实地中的坐标如何转换5:三角高程测量的方法1-4一定是,第5个就是两种情况之一三:论述题(5选2)1:各种坐标系的定义;原点,X轴,Y轴是如何规定的。
2:结合所学专业,论述本专业的现状和发展前景。
一、中国遥感技术应用现状1957年第一颗人造地球卫星升空标志着人类进入了太空时代,从此人类以崭新的角度开始重新认识自己赖以生存的地球。
空间信息技术是本世纪60年代发展起来的一门新兴的科学技术,遥感技术,包括地理信息系统和全球定位系统,则是对地观测的重要手段。
中国的遥感技术从70年代起步,经过十几年的艰苦努力,已发展到目前的实用化和国际化阶段,具体表现在具备了为国民经济建设服务的实用化能力和全方位地开展国际合作使其走向世界的国际化能力。
1为国民经济可持续发展提供科学的决策依据2具有对重大自然灾害灾情进行动态监测和评估的能力中国是自然灾害频繁且严重的国家,每年因灾害所造成的损失高达上千亿元人民币。
对重大灾害进行动态监测和灾情评估,减轻自然灾害所造成的损失是遥感技术应用的重要领域。
3利用遥感技术进行农作物估产和林业资源调查4地质矿产资源遥感调查此外,近年来发展起来的干涉测量雷达技术已经在三峡大坝等大型工程的环境监测和油气区地面沉降等应用领域显示出巨大的应用潜力。
二、中国遥感技术应用展望“九五”期间,中国国家科委已经把“遥感、地理信息系统及全球定位系统技术综合应用研究”列为“九五”国家科技攻关重中之重项目,至此遥感信息技术已连续四个五年计划被列入国家优先项目,说明了国家对遥感事业的重视。
可以预见,该项目的实施,可以有效地将这一高新技术广泛地应用于国民经济建设的各个方面,使其走上产业化发展的道路。
09年攻读硕士学位研究生入学试题B
游流速) 。若不计摩擦力,求水流对坎壁 AB 的作用力的大小及方向。(取动能动量校 正系数 β1 = β 2 = 1 )(20 分)
第6页
四、作图题 (共 20 分) 作图题
1、绘出图中密闭容器 AB 平面上的相对静水压强分布图,并标出力的方向。(8 分) 、
A h1 h2 B
A
h1 B (6 分) h2
2、判断下图中所绘水面曲线是否正确,试分析改正之。 、
第3页
郑 州 大 学 试 题 纸
N1 K N1 N2 i1<i k S2 N2 K i2<i k i1>i2 3、设管道长度为 L,水击波传播速度为 c ,不计阻力。当管道末端阀门突然关闭 、 时,试绘出水击波传播过程中离管道末端 x 距离处的水击压强水头 ∆p γ 随时间 t 的 变化过程图。 (6 分)
1、局部水头损失系数可用尼古拉兹的试验图来分析说明其变化规律。 、 2、重力与其它质量力同时作用时,等压面为水平面。 、 3、在恒定紊流中,瞬时流速不随时间变化。 、 4、明渠均匀流中,当底坡 i < ik (临界底坡) 时,则水深 h > hk。 、 5、时均压强减瞬时压强等于脉动压强。 、 6、缓流就是渐变流,急流就是急变流。 、 7、对于实用堰与宽顶堰,只要下游水位不超过堰顶时,就一定是自由出流。 、 8、上临界雷诺数 Re′ 是不定值,试验环境越安静, Re′ 越大。 、 k k 9、谢才公式 v = C RJ 只适用于明渠,不适用于管流。 、 10、在流场中,流网网格相对较密的地方,流速相对较小。
郑
州
大
学
2009 年攻读硕士学位研究生入学试题 B
学科、专业:水力学及河流动力学 研究方向:有压非恒定流理论与计算研究、工程水力学问题及数值模拟、河床演变机理等 考试科目(代码、名称) :
09春-桂林理工大学试卷样卷
位有效数字,0. 510mm有位有效数字。
3.测量误差分为、
和三类。
4.常用的数据处理方法有、
和等。
5.如图1所示,准确度为0.01mm的千分尺,
其读数为。
表二:
(五)三线摆实验
用三线扭摆法测刚体的转动惯量,实验装置如图
3所示,已知圆盘对 轴的转动惯量 ,式中的 为圆盘质量, 为圆盘振动周期, 。现将一质量为 的圆环放在圆盘上,且使圆环轴线与圆盘的轴线重合,扭摆周期为 。测量数据如表三所示,请计算圆环对其中心轴的转动惯量,正确表达圆环转动惯量测量结果。
2.系统处于稳定状态时加热盘温度为 ,散热盘温度为 ,测量散热盘温度随时间变化的数据如表四所示,计算散热盘处在稳态值 附近的温度变化率
表四
t/min
0
1
2
3
4
5
6
7
8
T/OC
59.8
58.6
57.3
56.0
54.7
53.5
52.5
51.4
50.3
(七)直流单臂电桥实验
1.画出直流单臂电桥测量电阻的原理电路图,写出 的计算式;说明用交换法( 与 互换位置)测量电阻的目的。
6.按照误差理论和有效数字的运算规则改正以下错误:
(1)L=(2900±80)mm改正为
(2)h=27.3×104±4000 (km)改正为
(3)d=2.345±0.435(m)改正为
(4)2m=2000mm改正为
(5) 改正为
7.推导下列间接测量量的误差传递公式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
桂林工学院2007年硕士研究生入学考试试题
考试科目代码:431
考试科目名称:测量学
(总分150分,三小时答完) 考生注意:1. 判断题、填空题需要写在答题纸上。
2. 考生自备计算器
一、 名词解释(每小题3分,共15分)
1.水准仪i 角误差:
2.系统误差:
3. 大地水准面:
4. 视差:
5. 危险圆:
二 、判断题(每小题2分,对的在括号里打“√”;错的打“×”;共20分)
1.对于微倾式光学水准仪,只要能够调节微倾螺旋使符合气泡居中,圆气泡是否居中对观
测结果无任何影响 。
( )
2.一幅大比例尺地形图的图号为45.00-65.00,则这幅图的西南角坐标为。
( )
3. 观测值之间权之比等于它们的中误差之比。
( )
4. 用一台测距精度为3mm+2ppm 全站仪测量一段长为1km 的距离,则这段距离测量的精度
为±5mm 。
( )
5. 在三角高程测量对向观测中,即使在往返测所得高差中没有加入球气差改正,其均值并
不受其影响。
( )
6. 在一个测区布设了若干条符合或闭合导线,只要每条导线的方位角闭合差、全长的相对
闭合差满足相应限差要求,则导线测量成果一定合格。
( )
7. 对于一条约13km 长的符合水准路线,可以采用按照四等水准测量的要求进行施测。
( )
8. 符合水准管气泡居中时,视准轴已处于水平。
( )
9. 相对于高级水准点而言,水准点的高程中误差均要求不大于±2cm ( )
10. 一付水准尺黑、红面刻划设计之差取4000、4100也是可以的。
( )
三、填空题(每小题1.5分,共30分)
1.水准面的特性是 。
2. 根据1956年黄海高程系算得P 点的高程为150.240米。
若改用1985年国家高程基准,
则A 点的高程为 米。
3. 设某地面点P 的经度为东经109 °25′ 42″,问该点位于6 投影带的带号是第
带,中央子午线的经度为 。
按3度投影带时的带号是 ; 其中央
子午线的经度为 。
4. 若在半径为6.37 KM 的范围内进行测量,并用水平面代替水准面 ,则地球曲率对水平距
离的最大影响为 ___________ ;对高差的影响为 cm 。
5. 地面是两点间的水平距离为88.355m ,则在1:500的地形图上,它的长度是 _____ cm 。
6. 已知A 点的坐标为3265.162,4631.338A A x y ==;B 点的坐标为2675.430,B x =
3675.430,B y =则AB 的坐标方位角为AB α=___________________。
7. 经纬仪竖直角观测时盘左读数为922318;''︒ 盘右读数为2673724''︒;则该方向的竖直
角指标差为_________ 秒;竖直角为 _______________ 。
设仪器高为1.515 m 、目标高为
2.000 m , 测距仪测得的斜距为637米,则两点之间点高差为 ___________ m 。
8. 在已知A 、B 两点之间内插等高线时,设98.35A H m =;107.68B H m =。
若等高距为1米,则在这两点之间共需要内插出 ______ 条计曲线和 ________ 条首曲线。
9. 水准测量时采用“后-前-前-后”的观测顺序,其目的是
_______________________________ ;测段之间采用偶数站观测的目的是
____________________________________ ; 通过限制前后视距差和距离累积差其目的是_____________________________; _________________________。
10. 一幅按标准分幅的1:1000比例尺地形图,其对应的实地面积为 __________ 亩。
四、简算(答)题(每小题6分,共36分)
1.丈量两段距离,一段往测为126.780m ,返测为126.762m ,另一段往、返测分别为357.230m 及357.256m ,试计算两距离的相对误差,问两段距离测量的最后结果是否具有相同的精度?
2. 什么叫多余观测,测量中多余观测有什么实际意义?
3. 衡量精度的指标有哪些?为什么常用中误差来衡量观测值的精度?它有何特点?
4. 在水准测量中,设每站观测高差的中误差均为5mm ,若从已知点推算待定点的高程,要求中误差不大于2cm ,问最多可设多少站?
5. 试简述水准仪进行i 角检验的方法,并推导出计算i 的公式。
6. 用你熟悉的计算机编程语言,写出用于坐标反算的程序模块
五、应用题(共49分)
1.用水准仪对A 、B 两点高差进行10次观测的结果如下:1.249, 1.253, 1.250,1.248,
1.252,1.247, 1.251,1.250,1.249,1.251,求算术平均值、观测值的中误差及算术平均值的中误差。
(9分)
2.简述导线测量中以下粗差的检定计算方法
(1)一个角度测量发生错误;(5分)
(2)一个边测量发生错误;(5分)
3.如图(1)所示,已知1341956AB α'''=︒,
3065542CD α'''=︒, 观测所得角度值如下:
1851424β'''=︒ ;21095942β'''=︒ ;3554636β'''=︒ ;41075300β'''=︒;5
β= 求BE
4. C H =。
