2009考研数学三真题及答案解析

2009考研数三真题

2009考研数三真题2009年考研数学三真题是一道经典的考题，它涉及到了数学分析、线性代数、复变函数等多个数学领域的知识。

这道题目的难度较大，需要考生具备扎实的数学基础和分析问题的能力。

下面我将从不同的角度对这道题目进行分析和解答。

首先，我们来看一下这道题目的具体内容。

题目要求证明函数序列f_n(x) = (1 + x/n)^n在区间[0,1]上一致收敛于e^x。

这道题目涉及到了数学分析中的函数极限和一致收敛的概念。

我们可以通过对函数序列的逐步分析来解答这道题目。

首先，我们可以考察函数序列f_n(x)的点wise收敛性。

对于每个固定的x∈[0,1]，当n趋向于无穷大时，(1 + x/n)^n趋向于e^x。

这是因为当n趋向于无穷大时，(1 + x/n)趋向于1，而e^x是一个固定的常数。

因此，对于每个固定的x∈[0,1]，函数序列f_n(x)是收敛的。

接下来，我们需要证明函数序列f_n(x)的一致收敛性。

一致收敛是指对于任意给定的ε>0，存在一个正整数N，使得当n>N时，对于所有的x∈[0,1]，有|f_n(x) - e^x|<ε。

为了证明一致收敛性，我们可以利用函数序列的导数来进行分析。

首先，我们计算函数序列f_n(x)的导数。

根据链式法则，我们有f_n'(x) = n(1 +x/n)^(n-1) * (1/n) = (1 + x/n)^(n-1)。

接下来，我们需要证明函数序列f_n'(x)在区间[0,1]上一致收敛于e^x的导数。

我们可以通过计算函数序列f_n'(x)的极限来证明一致收敛性。

当n趋向于无穷大时，(1 + x/n)^(n-1)趋向于e^x的导数。

这是因为当n趋向于无穷大时，(1 + x/n)趋向于1，而e^x的导数仍然是e^x。

因此，函数序列f_n'(x)在区间[0,1]上一致收敛于e^x的导数。

根据一致收敛的性质，我们知道如果一个函数序列在某个区间上一致收敛于一个函数，那么这个函数序列的极限函数也在这个区间上连续。

大学历年考研真题-2009年全国硕士研究生入学统一考试(数三)试题及答案

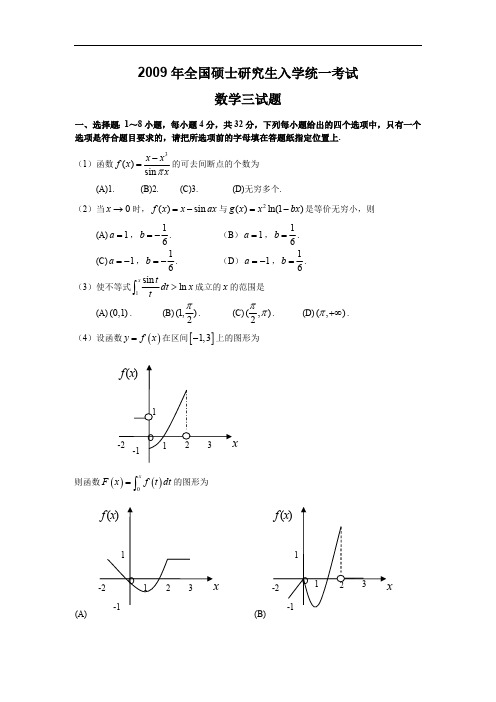
2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭.(B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.（7）设事件A 与事件B 互不相容，则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂ .（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . （12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)Tk β=，若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k = .(14) 设1X ，2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值. （16）（本题满分10 分）计算不定积分ln(1dx +⎰(0)x >. （17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=. （19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程.（20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.（Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值.（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x ；（Ⅱ）求条件概率{}11P X Y ≤≤. （23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.（Ⅰ）求{}10P X Z ==；（Ⅱ）求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题及答案解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

2009年考研数学三真题

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1.(B)2. (C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭.(B)**23OB A O ⎛⎫⎪⎝⎭.(C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，T P 为P 的转置矩阵，且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭.（7）设事件A 与事件B 互不相容，则(A)()0P AB =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z的间断点个数为 (A) 0. (B)1. (C)2 . (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos 0x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂ .（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . （12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k = .(14)设1X ，2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数()22(,)2ln f x y xy y y =++的极值.（16）（本题满分10 分）计算不定积分ln(1dx +⎰(0)x >. （17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥. （18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=.（19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程. （20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.（Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2211y y +，求a 的值.（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0x e y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x ；（Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. （Ⅰ）求10P X Z ⎡==⎤⎣⎦；（Ⅱ）求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题解析需要完整答案及试卷解析的同学请添加微信公众号：考研365天微信号：ky365t关注后聊天窗口回复“答案”（听说关注我们的同学都能顺利上研哦）1994-2016 年政治考研真题+答案解析1986-2016 年英语一/二考研真题+答案解析1987-2016 年数学一/二/三考研真题+答案解析。

数3--09真题答案

2009年考研数学(三)试卷答案速查一、选择题（1）C （2）A （3）A （4）D （5）B （6）A （7）D （8）B 二、填空题（9）3e 2 （10）2ln 21+ （11）1e（12）8000 （13）2 （14）2np 三、解答题（15）极小值11(0,)e ef =−．（16）1ln(12x C +++−+．（17）83−．（18）略．（19）230y x +−=．（20）（Ⅰ）21101021k −⎛⎫⎛⎫ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪−⎝⎭⎝⎭ξ （1k 为任意常数）． 323101/2100010k k −−⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ξ，（23,k k 为任意常数）．（Ⅱ）略．（21）（Ⅰ）特征值为1232,,1a a a λλλ=−==+．（Ⅱ）2a =．（22）（Ⅰ）10,()0,Y X y x f y x x ⎧, <<⎪=⎨⎪⎩其他. （Ⅱ）{}e 211e 1P X Y −=−．（23）（Ⅰ）4{10}P X Z ===. （Ⅱ）(,)X Y 的概率分布为2009年全国硕士研究生入学统一考试数学（三）参考答案一、选择题：1～8小题,每小题4分,共32分．下列每题给出的四个选项中,只有一个选项是符合题目要求的．请将所选项前的字母填在答题纸．．．指定位置上．（1）【答案】C ．【解答】当x 取任何整数时，sin π0x =，()f x 均无意义，所以()f x 的间断点有无穷多个，但可去间断点为极限存在的点．由30x x −=解得0,1,1x =−．因为3200131lim lim sin ππcos ππx x x x x x x →→−−==，3211132lim lim sin ππcos ππx x x x x x x →→−−==， 3211132lim lim sin ππcos ππx x x x x x x →−→−−−==，故可去间断点为3个，即0,1,1x =−．故选C ．（2）【答案】A ．【解答】222000()sin sin 1cos limlim lim lim 1()ln(1)()3x x x x f x x ax x ax a axg x x bx x bx bx →→→→−−−====−⋅−−，因为2lim(3)0x bx →−=，所以0lim(1cos )0x a ax →−=，从而 1.a =再有，2220001()1cos 12lim lim lim 1()336x x x x f x x g x bx bx b→→→−===−=−−，得16b =−．故选A ．（3）【答案】A ．【解答】令1sin ()d ln xtf x t x t=−⎰(0)x >，有sin 1()0x f x x−'=(0)x >，从而()f x 当0x >时单调减少．由(1)0f =知，当(0,1)x ∈时，()(1)0f x f >=，即1sin d ln x tt x t>⎰．故选A ．（4）【答案】D ．【解答】0()()d xF x f t t =⎰，0()F x 表示()y f x =与x 轴、y 轴及0x x =所围的图形的代数面积．由()y f x =的图形可知，①因为()y f x =只有有限个第一类间断点，所以()F x 连续．②当[]1,0x ∈−时，()0F x ． ③当[]0,1x ∈时()0F x ，且单调递减．④[]1,2x ∈时()F x 单调递增，且(1)0,(2)0F F <>．⑤[]2,3x ∈时，()F x 为常函数．故选D ．（5）【答案】B ．【解答】因为当A 可逆时，1*−=A A A ，所以112211*−−⨯−⎛⎫⎛⎫⎛⎫==− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（）O A O A O A O B A B B O B O B O AO 1123−**−**⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭OA B B OA B O B A B A O B A O A O ，故选B ．（6）【答案】A ．【解答】因为1223123100100(,,)(,,)110110001001⎛⎫⎛⎫ ⎪ ⎪=+== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭Q P ααααααα，所以 T TT T 100100100100110110110110001001001001110100100210010010110110.001002001002⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥ ⎪ ⎪ ⎪ ⎪==⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪ ⎪== ⎪⎪⎪ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭Q AQ P AP P AP 故选A ．（7）【答案】D ．【解答】因为,A B 互不相容，所以AB =∅，()0P AB =，从而()()1()1P A B P AB P AB ==−=，故选D ．（8）【答案】B ．【解答】由全概率公式，{}{}{}(),0,1Z F z P XY z P XY z Y P XY z Y ===+={}{}0,0,1P z Y P X z Y ==+=，因为X 与Y 相互独立，所以{}{}{}{}{}11()0010()22Z F z P z P Y P X z P Y P z z ==+==+Φ，当0z <时，1()()2Z F z z =Φ；当0z 时， 11()()22Z F z z =+Φ．所以0z =为间断点，故选B ．二、填空题：9～14小题,每小题4分,共24分．请将答案写在答题纸．．．指定位置上．（9）【答案】3e 2．【解答】原式cos 10x x −→=02e(1cos )lim13x x x→−=2021e 2lim 13x x x →⋅=3e 2=．（10）【答案】2ln 21+．【解答】因为z 对x 求偏导时，把y 当常数，所以不妨在(e )y xz x =+中令0y =，得(,0)(1)x z x x =+，于是d (1)(1)ln(1)d 1x x z x x x x x x ⎡⎤'⎡⎤=+=+++⎣⎦⎢⎥+⎣⎦，从而(1,0)1d d x z zx x=∂==∂2ln 21+．（11）【答案】1e．【解答】11211222e (1)e (1)(1)lim lim e,e (1)(1)e (1)n n n n n n n nn n n n n n ρ++++→∞→∞−−−−+==⋅=−−+−−所以该幂级数的收敛半径为11eR ρ==．（12）【答案】8000．【解答】因为d 0.2d p p Q Q p ε=−=，得d 0.2d p QQ p=−，收益函数()R pQ p =，边际收益d d d (1)(10.2)0.8d d d R Q p QQ p Q Q Q p p Q p=+=+=−=．当10000Q =时，d 8000d Rp=，即价格增加1元会使产品收益增加8000元．（13）【答案】2．【解答】因为T αβ相似于300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭，所以Tαβ的特征值为3,0,0，从而T T 1()3k tr =+==βααβ，2k =．（14）【答案】2np ．【解答】222()(1)ET E X S E X ES EX DX np np p np =−=−=−=−−=．三、解答题：15～23小题,共94分．解答应写出文字说明、证明过程或演算步骤．请将答案写在答题纸．．．指定位置上．（15）（本题满分9分）解：由22()2(2)0()210x y f x,y x y f x,y x y ln y ⎧'=+=⎪⎨'=++=⎪⎩解得10,e x y ==.而2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =，则1112(0,)(0,)(0,)eee12(2),0,e e xxxyyy A f B f C f ''''''==+====，因为20B AC −<而0A >，所以(,)f x y 有极小值11(0,)eef =−．（16）（本题满分10分）原式2221ln(1)11ln(1)d()d 1111t t t t t t t +=+=−−−−+⎰⎰ 22ln(1)111d 14(1)4(1)2(1)t t t t t t ⎛⎫+=−−− ⎪−−++⎝⎭⎰ 2ln(1)111ln 1412(1)t t C t t t ++=+−+−−+1ln(12x C =++−−+．（17）（本题满分10分）解：在极坐标系下积分区域可化为2(sin cos )r θθ+，则3π2(sin cos )4π04()d d d (cos sin )d Dx y x y r r r r θθθθθ+−=−⎰⎰⎰⎰3π34π48(cos sin )(sin cos )d 3θθθθθ=−+⎰3π34π48(sin cos )d(sin cos )3θθθθ=++⎰ 3π44π4818(sin cos ).343θθ=⋅+=−（18）（本题满分11分）证明：（Ⅰ）作辅助函数()()()()()()f b f a F x f x f a x a b a−=−−−−，有()()F a F b =，且()()()()f b f a F x f x b a−''=−−．由罗尔定理存在(,)a b ξ∈，使得()0F ξ'=，即()()()()f b f a F b a ξ'−=−，结论成立．（Ⅱ）由拉格朗日中值定理，得()000()0()(0)lim lim lim ()x x x f x f f xf f x xξξ++++→→→−'''===，0x ξ<<. 因为()0lim x f x A +→'=，所以0lim ()x f A ξ+→'=，故'(0)f +存在，且'(0)f A +=．（19）（本题满分10分）解：曲边梯形的面积为1()d tS f x x =⎰，旋转体的体积为21π()d tV f x x =⎰，由题，V tS π=，即211()d ()d tt f x x t f x x =⎰⎰，两边对t 求导可得21()()d ()tf t f x x tf t =+⎰， ①再对t 求导可得2()()2()()f t f t f t tf t ''=+，即(2())()2()f t t f t f t '−=，把t 当成函数，()y f t =当成自变量，上式变为d 11d 2t t y y+=，解一阶线性微分方程得通解23t y =+．在①式中令 1t =，得(1)1f =，代入通解得13C =，23t y =+．所以该曲线方程为：230y x =．（20）(本题满分11分)解：（Ⅰ）因为111111100(|)1111021104220000−−−⎛⎫⎛⎫ ⎪ ⎪=−→ ⎪ ⎪ ⎪ ⎪−−−⎝⎭⎝⎭A ξ，解得21101021k −⎛⎫⎛⎫⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪−⎝⎭⎝⎭ξ ，其中1k 为任意常数．因为2220220440⎛⎫ ⎪=−− ⎪ ⎪⎝⎭A ，有2122012201(|)2201000044020000−−⎛⎫⎛⎫⎪ ⎪=−−→ ⎪ ⎪ ⎪ ⎪−⎝⎭⎝⎭A ξ，解得3231102100010k k ⎛⎫−⎪−⎛⎫⎛⎫ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭ξ，其中23,k k 为任意常数．（Ⅱ）由于1212131121102221k k k k k k −−−−=−≠−−+，故123,,ξξξ线性无关．（21）(本题满分11分)解：（Ⅰ）二次型f 的矩阵为0101111a a a ⎛⎫ ⎪=− ⎪⎪−−⎝⎭A ，由01||01()(2)(1)111aa a a a a λλλλλλλ−−−=−=−−+−−−−+E A ，解得A 的特征值为1232,,1a a a λλλ=−==+．（Ⅱ）若二次型f 的规范形为2212y y +时，可知二次型相似于矩阵100010000⎛⎫⎪ ⎪ ⎪⎝⎭，则该二次型必有一个特征值为0，其余均大于0，故20a −=，2a =．（22）(本题满分11分) 解：（Ⅰ）边缘概率密度0e d e 0,()(,)d 0,0.xx x X y x x f x f x y y x −−+∞−∞⎧=, >⎪==⎨⎪⎩⎰⎰当0x >时，条件概率密度10,(,)()()0,Y X X y x f x y f y x xf x ⎧, <<⎪==⎨⎪⎩其他. （Ⅱ）{}111101,1(,)d d d e d 12e xx P X Y f x y x y x y −−−∞−∞===−⎰⎰⎰⎰，{}11101(,)d d d e d 1e x yP Y f x y x y y x +∞+∞−−−∞−∞===−⎰⎰⎰⎰，{}{}{}1,1e 2111e 1P X Y P X Y P Y −==−．（23）(本题满分11分)解：（Ⅰ）{}10P X Z ==表示在没有取到白球的条件下取了一次红球的概率，12113324{10}9C P X Z C C ====．（Ⅱ）,X Y 的可能取值为0,1,2，{}{}{}{}{}{}{}{}{}11133311116666112311116666121166112211661210,0,1,0,4611212,0,0,1,363211,1,2,10,910,2,1,20,2,20.9C C C P X Y P X Y C C C C C C P X Y P X Y C C C C C P X Y P X Y C C C C P X Y P X Y P X Y C C =================================综上，(,)X Y 的概率分布为。

考研数三2009真题答案

考研数三2009真题答案考研数学是每年数万考生必须面对的一道难题。

其中，数学三是考研数学中最为困难的一门科目之一。

为了帮助考生更好地备考，本文将针对2009年的考研数学三真题进行解析和答案讲解。

首先，我们来看一下2009年考研数学三的试卷结构。

该试卷共分为两个部分，第一部分是选择题，共有10道题，每道题都有4个选项，考生需要选择其中的一个正确答案。

第二部分是主观题，共有5道题，考生需要详细解答每道题目。

在解答选择题时，考生需要注意以下几点。

首先，要仔细阅读题目，理解题意。

其次，要运用所学的数学知识，分析并解决问题。

最后，要注意选项的排除法，排除明显错误的选项，从而找到正确答案。

接下来，我们来看一下2009年考研数学三选择题的答案解析。

1. 题目：已知函数f(x)满足f'(x)=2x+1，且f(0)=1，则f(1)的值为多少？答案：根据题目中的已知条件，我们可以通过积分得到f(x)的表达式为f(x)=x^2+x+C，其中C为常数。

代入f(0)=1，可以得到C=1。

因此，f(x)=x^2+x+1。

代入x=1，可以得到f(1)=3。

2. 题目：设函数f(x)在区间[a,b]上连续，且满足f(a)=f(b)=0，证明：存在ξ∈(a,b)，使得f(ξ)=ξf'(ξ)。

答案：根据题目中的已知条件，我们可以使用罗尔定理来证明。

由于f(x)在区间[a,b]上连续且在[a,b]的内部可导，根据罗尔定理，存在ξ∈(a,b)，使得f'(ξ)=0。

因此，f(ξ)=ξf'(ξ)。

3. 题目：设函数f(x)在区间[a,b]上连续，且在(a,b)内可导，证明：存在ξ∈(a,b)，使得f'(ξ)=(b-a)f(ξ)/(b-a+ξ-a)。

答案：根据题目中的已知条件，我们可以使用柯西中值定理来证明。

由于f(x)在区间[a,b]上连续且在(a,b)的内部可导，根据柯西中值定理，存在ξ∈(a,b)，使得f'(ξ)=(f(b)-f(a))/(b-a)=(0-0)/(b-a)=0。

2009考研数学三真题及答案解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为3()sin x x f x xπ-=(A)1.(B)2.(C)3.(D)无穷多个.（2）当时，与是等价无穷小，则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A)，. （B ），. 1a =16b =-1a =16b =(C)，. （D ），.1a =-16b =-1a =-16b =（3）使不等式成立的的范围是1sin ln x tdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞（4）设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭（6）设均为3阶矩阵，为的转置矩阵，且，,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若，则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭（7）设事件与事件B 互不相容，则A (A). (B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为X Y X (0,1)N Y ，记为随机变量的分布函数，则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z的间断点个数为(A)0.(B)1. (C)2.(D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）.0x →=（10）设，则.()y xz x e =+(1,0)zx ∂=∂（11）幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为()Q Q P =P 0.2p ξ=10000件时，价格增加1元会使产品收益增加元.（13）设,，若矩阵相似于，则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫⎪ ⎪ ⎪⎝⎭k = (14)设，,…,为来自二项分布总体的简单随机样本，和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差，记统计量，则.2T X S =-ET =三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数的极值.()22(,)2ln f x y xy y y =++（16）（本题满分10 分）计算不定积分 .ln(1dx +⎰(0)x >（17）（本题满分10 分）计算二重积分，其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则()f x [],a b (),a b ，得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-（Ⅱ）证明：若函数在处连续，在内可导，且()f x 0x =()0,,(0)σσ>，则存在，且.'0lim ()x f x A +→='(0)f +'(0)f A +=（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍，求该曲线的方程.t π（20）（本题满分11 分）设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭（Ⅰ）求满足，的所有向量，.21A ξξ=231Aξξ=2ξ3ξ（Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关.2ξ3ξ1ξ2ξ3ξ（21）（本题满分11 分）设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型的矩阵的所有特征值.f （Ⅱ）若二次型的规范形为，求的值.f 2211y y +a （22）（本题满分11 分）设二维随机变量的概率密度为(,)X Y 0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度；()Y X f y x （Ⅱ）求条件概率.11P X Y =⎡≤≤⎤⎣⎦（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z （Ⅰ）求；10P X Z ⎡==⎤⎣⎦（Ⅱ）求二维随机变量的概率分布.(,)X Y 2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为3()sin x x f x xπ-=(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】()3sin x x f x xπ-=则当取任何整数时，均无意义x ()f x 故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==故可去间断点为3个，即0,1±（2）当时，与是等价无穷小，则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A)，. （B ），. 1a =16b =-1a =16b =(C)，.（D ），.1a =-16b =-1a =-16b =【答案】A.【解析】为等价无穷小，则2()sin ,()(1)f x x ax g x x ln bx =-=-222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛故排除(B)、(C).230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-另外存在，蕴含了故排除(D).201cos lim3x a axbx →--1cos 0a ax -→()0x → 1.a =所以本题选(A).（3）使不等式成立的的范围是1sin ln xtdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞【答案】A.【解析】原问题可转化为求成立时的111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 取值范围，由，时，知当时，.故应选(A).1sin 0tt->()0,1t ∈()0,1x ∈()0f x >（4）设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由的图形可见，其图像与轴及轴、()y f x =x y 所围的图形的代数面积为所求函数，从而可得出几个方面的特征：0x x =()F x ①时，，且单调递减.[]0,1x ∈()0F x ≤②时，单调递增.[]1,2x ∈()F x ③时，为常函数.[]2,3x ∈()F x ④时，为线性函数，单调递增.[]1,0x ∈-()0F x ≤⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭【答案】B.【解析】根据，若CC C E *=111,C C C CC C*--*==分块矩阵的行列式，即分块矩阵可逆O A B O ⎛⎫ ⎪⎝⎭221236O A A B B O ⨯=-=⨯=（）1111661O B BO A O A O A O B B O B O B O AO A O A**---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B AO A O ****⎛⎫⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B).（6）设均为3阶矩阵，为的转置矩阵，且，,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若，则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【答案】A.【解析】，即：122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦（7）设事件与事件B 互不相容，则A (A).(B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=【答案】D.【解析】因为互不相容，所以,A B ()0P AB =(A)，因为不一定等于1，所以(A)不正确.()()1()P AB P A B P A B ==- ()P A B (B)当不为0时，(B)不成立，故排除.(),()P A P B (C)只有当互为对立事件的时候才成立，故排除.,A B(D)，故(D)正确.()()1()1P A B P AB P AB ==-= （8）设随机变量与相互独立，且服从标准正态分布，的概率分布为X Y X (0,1)N Y ，记为随机变量的分布函数，则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z 的间断点个数为（）(A)0.(B)1. (C)2.(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=独立,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤（1）若，则0z <1()()2Z F z z =Φ（2）当，则0z ≥1()(1())2Z F z z =+Φ为间断点，故选(B).0z ∴=二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）.0x →=【答案】.32e 【解析】.00x x →→=02(1cos )lim13x e x x→-=20212lim 13x e x x →⋅=32e =（10）设，则.()y xz x e =+(1,0)zx ∂=∂【答案】.2ln 21+【解析】由，故()xy z x e=+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦代入得，.1x =()ln 21,01ln 22ln 212z e x∂⎛⎫=+=+ ⎪∂⎝⎭（11）幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑【答案】.1e【解析】由题意知，()210nn n e a n--=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以，该幂级数的收敛半径为1e（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为()Q Q P =P 0.2p ξ=10000件时，价格增加1元会使产品收益增加元.【答案】8000.【解析】所求即为()QP Q P Q ''=+因为，所以0.2p Q PQξ'==-0.2Q P Q '=-所以()0.20.8QP Q Q Q '=-+=将代入有.10000Q =()8000QP '=（13）设,，若矩阵相似于，则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭k =【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦Tαβ3，0，0.而为矩阵的对角元素之和，，.TαβT αβ1300k ∴+=++2k ∴= (14)设，,…,为来自二项分布总体的简单随机样本，和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差，记统计量，则 .2T X S =-ET =【答案】2np 【解析】由.222()(1)ET E X S E X ES np np p np =-=-=--=三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数的极值.()22(,)2ln f x y xy y y =++【解析】，，故.2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =.2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =则，，.12(0,)12(2xxef e ''=+1(0,)0xyef ''=1(0,)yyef e ''=而0xxf ''> 2()0xy xx yy f f f ''''''-<二元函数存在极小值.∴11(0,)f e e=-（16）（本题满分10 分）计算不定积分 .ln(1dx+⎰(0)x >得t =22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t +=+-+=---+⎰⎰⎰而22111112(11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C +++=+-+--+=+++⎰（17）（本题满分10 分）计算二重积分，其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥【解析】由得，22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰.3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则()f x [],a b (),a b ，得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-（Ⅱ）证明：若函数在处连续，在内可导，且()f x 0x =()0,,(0)σσ>，则存在，且.'0lim ()x f x A +→='(0)f +'(0)f A +=【解析】（Ⅰ）作辅助函数，易验证满足：()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ；在闭区间上连续，在开区间内可导，且()()a b ϕϕ=()x ϕ[],a b (),a b .''()()()()f b f a x f x b aϕ-=--根据罗尔定理，可得在内至少有一点，使，即(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取，则函数满足：在闭区间上连续，开区间内可导，0(0,)x δ∈()f x []00,x ()00,x 从而有拉格朗日中值定理可得：存在，使得()()000,0,x x ξδ∈⊂……()0'00()(0)x f x f f x ξ-=-()*又由于，对上式（*式）两边取时的极限可得：()'lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故存在，且.'(0)f +'(0)f A +=（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍，求该曲线的方程.t π【解析】旋转体的体积为22()()11x x t t V f dx f dxππ==⎰⎰曲边梯形的面积为：，则由题可知()1x ts f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dxπππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得 22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰继续求导可得，化简可得''2()()()()()f t f t f t tf t f t --=，解之得'1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y-=⋅+在式中令，则，代入得 1t =2(1)(1)0,()0,(1)1f f f t f -=>∴= 1223t cyy -=+.11,2)33c t y =∴=所以该曲线方程为：.230y x +=（20）（本题满分11 分）设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭（Ⅰ）求满足，的所有向量，.21A ξξ=231Aξξ=2ξ3ξ（Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关.2ξ3ξ1ξ2ξ3ξ【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭故有一个自由变量，令，由解得，()2r A =32x =0Ax =211,1x x =-= 求特解，令，得120x x ==31x = 故，其中为任意常数21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k解方程231Aξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量，令，由得231,0x x =-=20A x =11x =令，由得230,1x x ==-20A x =10x =求得特解21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭故，其中为任意常数3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k （Ⅱ）证明：由于12121212122111121112(21)()2((21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故线性无关. 123,,ξξξ（21）（本题满分11 分）设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型的矩阵的所有特征值.f （Ⅱ）若二次型的规范形为，求的值.f 2211y y +a【解析】（Ⅰ） 0101111a A a a ⎛⎫ ⎪=- ⎪⎪--⎝⎭0110||01()1111111aa aE A a a a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--.123,2,1a a a λλλ∴==-=+（Ⅱ）若规范形为，说明有两个特征值为正，一个为0.则2212y y +1)若，则，，不符题意10a λ==220λ=-<31λ=2)若，即，则，，符合20λ=2a =120λ=>330λ=>3)若，即，则，，不符题意30λ=1a =-110λ=-<230λ=-<综上所述，故2a =（22）（本题满分11 分）设二维随机变量的概率密度为(,)X Y 0(,)0x e y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x （Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦【解析】（Ⅰ）由得其边缘密度函数0(,)0x y xe f x y -<<⎧= ⎨⎩其它()0xx x x f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== <<即|1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪⎩其它（Ⅱ）[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而11111[1,1](,)12xxx x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x yY yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰.11122[1|1]11e e P X Y e e ----∴ ≤≤==--（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z ①求.10P X Z ⎡==⎤⎣⎦②求二维随机变量的概率分布.(,)X Y 【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球.12113324(10)9C P X Z C C ⨯∴====⋅（Ⅱ）X ，Y 取值范围为0，1，2，故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======012 XY01/41/61/36 11/31/9021/900。

09真题考研数学真题解析--数三修订版

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.1. （09年，4分）函数()3sin x x f x xπ-=的可去间断点的个数为 ( )(A ) 1. (B ) 2. (C ) 3. (D ) 无穷多个.【考查分析】本题考查间断点的定义和分类，属于间断点计算与判别的基本题型【详解】由于()3sin x x f x xπ-=,则当x 取任何整数时,()f x 均无意义,故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±.320032113211131lim lim ,sin cos 132lim lim ,sin cos 132lim lim .sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即1,2,30,1x =±.选C【评注】此题有相当多的考生选择（D ），认为使sin 0x π=成立的点有无穷多个，同时审题不细，没有利用()f x 的极限值以确定可去间断点的个数，故错误率较高。

2.（09年，4分）当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A ) 11,6a b ==-. (B ) 11,6a b ==. (C ) 11,6a b =-=-. (D ) 11,6a b =-=.【考查分析】本题考查等价无穷小替换，洛比达法则的计算极限，属于极限计算基本题型【详解】方法1：()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bx a ax a b ax b →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛即36a b =-,故排除（B ）,（C ）.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选（A ）.方法2：由泰勒公式3331sin () (0)6ax ax a x x x ο=-+→ 3333001(1)()()6lim lim 1()111, 1 1, .66x x a x a x x f x g x bx a a b b ο→→-++⇒==-⇒=-=⇒==-因此选（A ）.【评注】求极限的问题是考试的热点和重点，洛比达法则和等价无穷小替换是常用的计算和简化的方法。

2009年考研数学三答案解析

2009年全国硕士研究生入学统一考试数学三试题及解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3s i n x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

另外201cos lim3x a axbx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排D 。

2009考研数学三真题

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1~8小题，每小题8分，共32分（1）函数3()sin x x f x nx-=的可去间断点的个数为（）（A ）1 （B ）2 （C ）3 （D ）无穷多个（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-等价无穷小，则（）（A ）11,6a b ==- （B ）11,6a b == （C ）11,6a b =-=- （D ）11,6a b =-=（3）使不等式1sin ln x xdt x t>⎰成立的x 的范围是（）（A ）（0，1）（B ）（1，2π）（C ）（2π，π）（D ）（π，+∞）（4）设函数()y f x =在区间[-1,3]上的图形为则函数0()()xF x f t dt =⎰为（）（5）设Ａ、B 均为2阶矩阵，,A B **分别为A 、B 的伴随矩阵。

若|A|=2，|B|=3，则分块矩阵00A B ⎛⎫⎪⎝⎭的伴随矩阵为（）（A ）0320B A **⎛⎫⎪⎝⎭ （B ）0230B A **⎛⎫⎪⎝⎭ （C ）0320A B **⎛⎫⎪⎝⎭ （D ）0230A B **⎛⎫⎪⎝⎭（6）设A ，P 均为3阶矩阵，T P 为P 的转置矩阵，且TP A Ｐ＝100010002 ⎛⎫ ⎪ ⎪ ⎪ ⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则T Q AQ 为（）（Ａ）2101 ⎛⎫ ⎪ 1 0 ⎪ ⎪0 0 2⎝⎭ （Ｂ）11012000 ⎛⎫ ⎪ ⎪ ⎪ 2⎝⎭ （Ｃ）20001 ⎛⎫ ⎪ 0 ⎪ ⎪0 0 2⎝⎭ （Ｄ）100020002 ⎛⎫⎪ ⎪ ⎪ ⎝⎭（7）设事件A 与事件B 互不相容，则（）（A ）()0P AB =（B ）()()()P AB P A P B = （C ）()1()P A P B =-（D ）()1P A B ⋃=（8）设随机变量 X 与 Y 相互独立，且 X 服从标准正态分布N(0,1),Y 的概率分布为 P{Y=0}=P{Y=1}=12，记()z F z 为随机变量Z=XY 的分布函数，则函数()z F z 的间断点个数为（）（A ）0（B ）1（C ）2（D ）3二、填空题：9-14 小题，每小题 4分，共 24 分（9）cos x x →=___________。

2009考研数学三真题及答案

2009考研数学三真题及答案一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是（） ()A .(0,1)()B .(1,)2π()C .(,)2ππ()D .(,)π+∞（4）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为（）()A .()B .()C .()D .（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==则分块矩阵00A B ⎛⎫⎪⎝⎭的伴随矩阵为（） ()A .**0320B A ⎛⎫⎪⎝⎭()B . **0230B A⎛⎫⎪⎝⎭()C .**0320A B ⎛⎫⎪⎝⎭()D .**0230A B ⎛⎫⎪⎝⎭（6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P AP ⎛⎫⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则T Q AQ 为（）()A .210110002⎛⎫⎪⎪ ⎪⎝⎭()B . 110120002⎛⎫⎪⎪ ⎪⎝⎭()C .200010002⎛⎫⎪⎪ ⎪⎝⎭()D .100020002⎛⎫ ⎪⎪ ⎪⎝⎭（7）设事件A 与事件B 互不相容，则（）()A .()0P AB =()B . ()()()P AB P A P B =()C .()1()P A P B =-()D .()1P A B ⋃=（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为（）()A .()B . 1 ()C .2()D . 3二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）cos x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k =(14)设1X ，2X ,…n X 是来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET =三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值。

考研数学三(微积分)历年真题试卷汇编32(题后含答案及解析)

考研数学三（微积分）历年真题试卷汇编32(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．(2009年)函数的可去间断点的个数为( )A．1．B．2．C．3．D．无穷多个．正确答案：C解析：当x=k(k=0，±1，±2，…)时，sinnx=0，则这些点都是f(x)的间断点．而当x=0，±1时，x—x3=0，又则x=0，x=±1为f(x)的可去间断点，其余均为无穷间断点．故应选C．2．(1995年)设f(x)为可导函数，且满足条件，则曲线y=f(x)在点(1，f(1))处的切线斜率为( )A．2B．－1C．D．－2正确答案：D解析：由得f(1)=一2．所以，应选D．3．(2006年)设函数f(x)在x=0处连续，，则( )A．f(0)=0且f－’(0)存在．B．f(0)=1且f－’(0)存在．C．f(0)=0且f+’(0)存在．D．f(0)=1且f+’(0)存在．正确答案：C解析：直接法故应选C．4．(2018年)下列函数中，在x=0处不可导的是( )A．f(x)=｜x｜sin｜x｜．B．C．f(x)=cos｜x｜正确答案：D解析：由导数定义知该极限不存在，则在x=0处不可导，故应选D．5．(2009年)设函数y=f(x)在区间[一1，3]上的图形为则函数F(x)=∫0xf(t)dt 的图形为( )A．B．C．D．正确答案：D解析：由题设知，当X∈(一1，0)时F’(x)=f(x)，而当x∈(一1，0)时f(x)≡1＞0，即F’(x)＞0，从而F(x)单调增．显然A选项是错误的，因为A选项中F(x)在(一1，0)中单调减．由于F(x)=∫0xf(t)dt，则F(0)=0，显然C选项错误．由于当x∈(2，3]时f( x)≡0，则当x∈(2，3]时F(x)=∫0xf(t)dt=∫02f(t)dt+∫2xf(t)dt=∫02f(t)dt+∫2x0dt=F(2) 则B是错误的，D是正确的．6．(1999年)设f(x，y)连续，且其中D是由y=0，y=x2，x=1所围区域，则f(x，y)等于( )A．xyB．2xyC．D．xy+1正确答案：C解析：令则f(x，y)=xy+A，将f(x，y)=xy+A代入(*)式得7．(2012年)已知级数条件收敛，则( )A．B．C．D．正确答案：D解析：又由条件收敛知0＜2一a≤1则1≤a＜2故应选填空题8．(2004年)若，则a=______，b=______．正确答案：应填a=1，b=一4．解析：当a=1时，又1—b=5，则b=—4．9．(1997年)设y=f(lnx)ef(x)，其中f可微，则dy=______．正确答案：应填解析：由y=f(lnx)ef(x)可知10．(2014年)设某商品的需求函数为Q=40—2p(p为商品的价格)，则该商品的边际收益为______．正确答案：应填20—Q．解析：由题设知收益函数为则边际收益为11．(2000年)=______。

考研数学题及答案-2009数学三--1

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b = 【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

另外201cos lim3x a axbx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除D 。

考研数学三真题(2009年)

0
f (x)
1 0 -1
f (x)
1
-2
1
2
3
x
-2
0 -1
1
2
3
x
A.
B .
第 1 页共 21 页
f (x)
1 0
f (x)
1
-1
1
2
3
x
-2
0 -1
1
2
3
x
C .Βιβλιοθήκη D .（5）设 A, B 均为 2 阶矩阵， A, B* 分别为 A, B 的伴随矩阵，若 | A | 2,| B | 3 则分块矩阵 0 B A 的伴随矩阵为（ 0 ） 0 3A
1
B . 2
C .
3
D .无穷多个
）
（2）当 x 0 时， f (x) x sin ax 与 g ( x ) x 2 ln(1 bx) 是等价无穷小，则（
A . a 1 ， b 1
6
C . a 1 ， b 1
（3）使不等式 1
x
6 sin t dt ln x 成立的 x 的范围是（ t
第 3 页共 21 页
（16）（本题满分 10 分）计算不定积分 ln(1
1 x )dx (x 0) x
（17）（本题满分 10 分）计算二重积分 (x y)dxdy ，其中 D (x, y) (x 1)2 ( y 1)2 2, y x .
2009 年全国硕士研究生入学统一考试真题试卷《数学三》试题
一、选择题：1～8 小题，每小题 4 分，共 32 分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）函数 f (x) x x3 的可去间断点的个数为：（ sinx ）

2009年考研数学一、二、三真题(含详解)

O
A
O
A O
A
1
O B1
B
O
B
O
B
O
6
A1
O
O
6
1 A
A
1 B
B
6
O
O
1 2
A
1 B 3 O
O 3A
6
6
(D) a 1,b 1 6
【解析】 f x x sin ax 与 g x x2 ln 1 bx 是 x 0 时的等价无穷小,则
lim
x0
f (x) g(x)
lim
x0
x sin ax x2 ln(1 bx)
lim
x0
x sin ax x2 (bx)
lim
x0
x
sin ax bx3
,且单调递减；
0
（定积分对应的图像位于 x 轴下方）
③ x 1, 2 时, F(x) x f (t)dt 0 单调递增； 0
④ x 2,3 时, F '(x) f (x) 0 为常函数；
⑤ F (x) 为连续函数. 结合这些特点,可见正确选项为(D)
(4)
设有两个数列
an
,
bn
,若
lim
n
则 max 1k 4
Ik
(
)
D1
D2
D4
-1
D3
1
x
(A) I1
(B) I2 (C) I3 (D) I4
-1
【答案】(A)
【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令 f (x, y) y cos x ,
D2, D4 两区域关于 x 轴对称, f (x, y) y cos x f (x, y) ,即被积函数是关于 y 的奇函数, 所以 I2 I4 0 ；

2009年考研数学三真题及答案解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1) 函数()3sin x x f x xπ-=的可去间断点的个数为 ( )(A) 1.(B) 2. (C) 3.(D) 无穷多个.(2) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(3) 使不等式1sin ln x tdt x t>⎰成立的x 的范围是 ( ) (A) (0,1).(B) (1,)2π. (C) (,)2ππ. (D) (,)π+∞.(4) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)(C) (D)(5) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B AO ⎛⎫⎪⎝⎭. (C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭. (6) 设,A P 均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭.若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为 ( )(A) 210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B) 110120002⎛⎫⎪⎪ ⎪⎝⎭.(C) 200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D) 100020002⎛⎫ ⎪⎪ ⎪⎝⎭.(7) 设事件A 与事件B 互不相容,则 ( )(A) ()0P AB =.(B) ()()()P AB P A P B =. (C) ()1()P A P B =-.(D) ()1P A B = .(8) 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 ( )(A) 0. (B) 1. (C) 2. (D) 3.二、填空题：9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.(9) cos 0x x →= .(10) 设()y x z x e =+,则(1,0)zx ∂=∂ _______ .(11) 幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 ______. (12) 设某产品的需求函数为()Q Q p =,其对价格p 的弹性0.2p ε=,则当需求量为10000件时,价格增加1元会使产品收益增加 _______ 元.(13) 设(1,1,1)T α=,(1,0,)T k β=.若矩阵T αβ相似于300000000⎛⎫⎪⎪ ⎪⎝⎭,则k = ____ .(14) 设12,,,m X X X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = _____.三、解答题：15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分10 分)计算不定积分ln 1dx ⎛+ ⎝⎰ (0)x >. (17)(本题满分10 分)计算二重积分()Dx y dxdy -⎰⎰,其中()()(){}22,112,D x y x y y x =-+-≤≥.(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理：若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明：若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线方程. (20)(本题满分11 分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ； (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明：123,,ξξξ线性无关. (21)(本题满分11 分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值；(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为,0,(,)0,x e y x f x y -⎧<<=⎨⎩其他. (I) 求条件概率密度()Y X f y x ； (II) 求条件概率{}11P X Y ≤≤.(23)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==；(Ⅱ)求二维随机变量(),X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)【答案】(C)【解析】由于()3sin x x f x xπ-=,则当x 取任何整数时,()f x 均无意义,故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±.320032113211131lim lim ,sin cos 132lim lim ,sin cos 132lim lim .sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即1,2,30,1x =±. (2) 【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bxa ax ab axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛即36a b =-,故排除B,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选A.(3) 【答案】(A)【解析】原问题可转化为求1sin ()ln 0xtf x dt x t=->⎰成立时x 的取值范围. 11111sin sin 1()ln sin 11sin 0.xx x x x tt f x dt x dt dt t tt t t dt dt t t =-=---==>⎰⎰⎰⎰⎰由()0,1t ∈时,1sin 0tt->,知当()0,1x ∈时,()0f x >.故应选(A). (4) 【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征：① []1,0x ∈-时,()0F x ≤为线性函数,单调递增； ② []0,1x ∈时,()0F x ≤,且单调递减； ③ []1,2x ∈时,()F x 单调递增； ④ []2,3x ∈时,()F x 为常函数； ⑤ ()F x 为连续函数. 结合这些特点,可见正确选项为(D). (5) 【答案】(B) 【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O⨯=-=⨯=（）,即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B).(6)【答案】(A)【解析】1223123100100(,,)(,,)110110001001Q P ααααααα⎛⎫⎛⎫ ⎪ ⎪=+== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,100100110110001001110100100210010010110110.001002001002TT Q AQ P A P ⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥⎢⎥⎪ ⎪=⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪ ⎪== ⎪⎪⎪ ⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(7) 【答案】(D)【解析】因为,A B 互不相容,所以()0P AB =.(A)()()1()P AB P A B P A B ==- ,因为()P A B 不一定等于1,所以(A)不正确； (B)当(),()P A P B 不为0时,()B 不成立,故排除； (C)只有当,A B 互为对立事件的时候才成立,故排除； (D)()()1()1P A B P AB P AB ==-= ,故()D 正确. (8) 【答案】(B) 【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤. (1) 当0z <时,1()()2Z F z z =Φ；(2) 当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题：9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上. (9) 【答案】32e 【解析】cos cos 10x x x x -→→= 200221(1cos )32lim lim 233x x e x e x e x x→→⋅-===.(10) 【答案】12ln 2+【解析】解法1：由于()xy z x e=+,故()(),01xz x x =+,()ln(1)ln(1)01ln(1)1x x x x x y z x x e e x xx ++=∂'⎡⎤'⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦∂+⎣⎦,代入1x =,得ln 2(1,0)1ln 22ln 212z e x ∂⎛⎫=+=+ ⎪∂⎝⎭.解法2：由于ln()()()ln()yx x e y xy x y y e x e z x x e x e x x x x e +⎡⎤∂⎡⎤∂+∂⎡⎤⎣⎦⎣⎦===+⋅++⎢⎥∂∂∂+⎣⎦, 故000(1,0)1(1)ln(1)2ln 211z e e x e ∂⎡⎤=+⋅++=+⎢⎥∂+⎣⎦. (11) 【答案】1e -【解析】由题意知,()210nn n e a n --=>,()()()()1121211221lim lim 1111lim ,111n n n nn n n nn n n n n e a n a n e e e n e n e e +++→∞→∞++→∞--=⋅+--⎡⎤⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦=⋅=⎡⎤+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以,该幂级数的收敛半径为1e -. (12) 【答案】8000【解析】所求即为()Qp Q p Q ''=+. 因为0.2p Q pQε'=-=,所以0.2Q p Q '=-,所以()0.20.8Qp Q Q Q '=-+=. 将10000Q =代入有()8000Qp '=. (13) 【答案】2【解析】T αβ相似于300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭,根据相似矩阵有相同的特征值,得到Tαβ的特征值为3,0,0.而Tαβ为矩阵T αβ的对角元素之和,1300k ∴+=++,2k ∴=.(14) 【答案】2np【解析】222()(1)ET E X S EX ES np np p np =-=-=--=.三、解答题：15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)【解析】 2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,)21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+= 所以 2212(2)0,B AC e e-=-+<且0A >. 从而1(0,)f e 是(,)f x y 的极小值,极小值为11(0,)f e e=-.(16)(本题满分10 分) 【解析】解法1t =,则21,1x t =-()()2221ln 1ln 11ln 111111dx t d t t dt t t t ⎛⎛⎫+=+ ⎪ -⎝⎭⎝+=-⋅--+⎰⎰⎰而()()()()()()2211112411111111ln 1ln 1,4421dt dt t t t t t t t C t ⎡⎤=--⎢⎥-+-++⎢⎥⎣⎦=--++++⎰⎰所以()()2ln1111ln1ln141211ln1ln41ln1ln211ln1ln.22t tdx Ct t tx Cx Cx x C ⎛+++=+-+--+⎝⎛=++⎝⎛=++⎝⎛=+++-⎝⎰解法21ln1ln11dx x x dx-'⎛⎛⎛=-⎝⎝⎝⎰⎰1ln112x dx⎛⎛⎫=+--⎪⎪⎝⎭⎰11ln122x x⎛=++-⎝⎰(2ln lnuduu C C=++=+分部即)11ln1ln1ln22dx x x C ⎛⎛+=++-+⎝⎝⎰1ln1ln211ln1ln.22x Cx x C⎛=++⎝⎛=++⎝(17)(本题满分10 分)【解析】解法1如右图所示,区域D的极坐标表示为302(sin cos),44rππθθθ≤≤+≤≤.132(sin cos )442(sin cos )33404334433443444()(cos sin )1(cos sin )38(cos sin )(sin cos )38(sin cos )(sin cos )3818(sin cos ).343Dr r x y dxdy d r r rdrr d d d θθππθθππππππππθθθθθθθθθθθθθθθθθ+=+=-=-⎡⎤=-⋅⎢⎥⎢⎥⎣⎦=-+=++=⨯+=-⎰⎰⎰⎰⎰⎰⎰解法2 将区域D 分成12,D D两部分(如右图),其中(){}(){}12,110,,12.D x y y x D x y x y x =-≤≤+-≤=≤≤+≤≤由二重积分的性质知()()()12DD D x y dxdy xy dxdy x y dxdy-=-+-⎰⎰⎰⎰⎰⎰,而()1111)D x y dxdyx y dy-=-⎰⎰⎰⎰103122,33x=-=-=-⎰()221020230)122(21242,23xD x y dxdy dx x y dyx dx -=-⎡=---⎣⎡⎤=-+=-⎢⎥⎢⎥⎣⎦⎰⎰⎰⎰⎰ 所以()()()1228233DD D x y dxdy x y dxdy x y dxdy -=-+-=--=-⎰⎰⎰⎰⎰⎰. (18)(本题满分11 分) 【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且()()()()()(),()()()()()().f b f a F a f a a a f a b af b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()000()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈. 由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10 分) 【解析】解法1 由题意知211()()t tf x dx t f x dx ππ=⎰⎰,两边对t 求导得21()()()tf t f x dx tf t =+⎰,代入1t =得 (1)1f =或(1)0f = (舍去). 再求导得 2()()2()()f t f t f t tf t ''=+,记()f t y =,则112dt t dy y+=, 因此, 111222()()dydyy y t eedy C y C --⎰⎰=+=+⎰132222()33y y C y -=+=+.代入1,1t y ==得13C =,从而23t y =+故所求曲线方程为23x y =+解法2 同解法1,得2()()2()(),(1)1f t f t f t tf t f ''=+=.整理得22dy ydt y t=-. 令y u t =,则 dy du u t dt dt=+, 原方程变成 23221du u u t dt u -=-, 分离变量得211(32)u du dt u u t-=-,即 114332dtdu u u t -⎛⎫+=⎪-⎝⎭, 积分得 21ln (32)ln 3u u Ct --=, 即 1233(32)u u Ct ---=.代入1,1t u ==,得1C =,所以231(32)u u t -=. 代入y u t =化简得2(32)1y t y -=,即23t y =.故所求曲线方程为23x y =(20)(本题满分11 分)【解析】(Ⅰ)对矩阵1()A ξ 施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ⎪---⎛⎫ ⎪⎪⎪=-→ ⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪⎝⎭可求得 2122122k kk ξ⎛⎫-+ ⎪ ⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ 施以初等行变换()211110220122201000044020000A ξ⎛⎫-⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭,可求得 312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1 由(Ⅰ)知12311122211,,102222ka ka kbξξξ--+--=-=-≠-, 所以123,,ξξξ线性无关.解法2 由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=, ①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=, ②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠，于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11 分) 【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111aE A aa a a a λλλλλλλ---=-=--+----+, 所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1 由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫ ⎪ ⎪ ⎪⎝⎭,其秩为2,故 1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意. 当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意. 当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +. 综上可知,2a =.解法2 由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零. 又21a a a -<<+,所以2a =.(22)(本题满分11 分)【解析】(I)X 的概率密度0,0,,0,()(,)0,0.0,0xx x X e dy x xe x f x f x y dy x x --+∞-∞⎧⎧>>⎪===⎨⎨≤⎩⎪≤⎩⎰⎰当0x >时,Y 的条件概率密度|1,0,(,)(|)()0,Y X X y x f x y f y x x f x ⎧<<⎪== ⎨⎪⎩其他.(II)Y 的概率密度,0,()(,)0,0.y Y e y f y f x y dx y -+∞-∞⎧>==⎨≤⎩⎰{}{}{}111111,11|11(,)2.11xx y P X Y P X Y P Y dx e dyf x y dxdye e e e dy--∞-∞--≤≤≤≤=≤-===--⎰⎰⎰⎰⎰(23)(本题满分11分)【解析】(Ⅰ) 12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========. (Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,0,0,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为。

2009考研数学三真题及答案解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为3()sin x x f x xπ-=(A)1.(B)2.(C)3.(D)无穷多个.（2）当时，与是等价无穷小，则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A)，. （B ），. 1a =16b =-1a =16b =(C)，. （D ），.1a =-16b =-1a =-16b =（3）使不等式成立的的范围是1sin ln x tdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞（4）设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭（6）设均为3阶矩阵，为的转置矩阵，且，,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若，则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭（7）设事件与事件B 互不相容，则A (A). (B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为X Y X (0,1)N Y ，记为随机变量的分布函数，则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z的间断点个数为(A)0.(B)1. (C)2.(D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）.0x →=（10）设，则.()y xz x e =+(1,0)zx ∂=∂（11）幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为()Q Q P =P 0.2p ξ=10000件时，价格增加1元会使产品收益增加元.（13）设,，若矩阵相似于，则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫⎪ ⎪ ⎪⎝⎭k = (14)设，,…,为来自二项分布总体的简单随机样本，和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差，记统计量，则.2T X S =-ET =三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数的极值.()22(,)2ln f x y xy y y =++（16）（本题满分10 分）计算不定积分 .ln(1dx +⎰(0)x >（17）（本题满分10 分）计算二重积分，其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则()f x [],a b (),a b ，得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-（Ⅱ）证明：若函数在处连续，在内可导，且()f x 0x =()0,,(0)σσ>，则存在，且.'0lim ()x f x A +→='(0)f +'(0)f A +=（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍，求该曲线的方程.t π（20）（本题满分11 分）设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭（Ⅰ）求满足，的所有向量，.21A ξξ=231Aξξ=2ξ3ξ（Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关.2ξ3ξ1ξ2ξ3ξ（21）（本题满分11 分）设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型的矩阵的所有特征值.f （Ⅱ）若二次型的规范形为，求的值.f 2211y y +a （22）（本题满分11 分）设二维随机变量的概率密度为(,)X Y 0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度；()Y X f y x （Ⅱ）求条件概率.11P X Y =⎡≤≤⎤⎣⎦（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z （Ⅰ）求；10P X Z ⎡==⎤⎣⎦（Ⅱ）求二维随机变量的概率分布.(,)X Y 2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为3()sin x x f x xπ-=(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】()3sin x x f x xπ-=则当取任何整数时，均无意义x ()f x 故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==故可去间断点为3个，即0,1±（2）当时，与是等价无穷小，则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A)，. （B ），. 1a =16b =-1a =16b =(C)，.（D ），.1a =-16b =-1a =-16b =【答案】A.【解析】为等价无穷小，则2()sin ,()(1)f x x ax g x x ln bx =-=-222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛故排除(B)、(C).230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-另外存在，蕴含了故排除(D).201cos lim3x a axbx →--1cos 0a ax -→()0x → 1.a =所以本题选(A).（3）使不等式成立的的范围是1sin ln xtdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞【答案】A.【解析】原问题可转化为求成立时的111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 取值范围，由，时，知当时，.故应选(A).1sin 0tt->()0,1t ∈()0,1x ∈()0f x >（4）设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由的图形可见，其图像与轴及轴、()y f x =x y 所围的图形的代数面积为所求函数，从而可得出几个方面的特征：0x x =()F x ①时，，且单调递减.[]0,1x ∈()0F x ≤②时，单调递增.[]1,2x ∈()F x ③时，为常函数.[]2,3x ∈()F x ④时，为线性函数，单调递增.[]1,0x ∈-()0F x ≤⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭【答案】B.【解析】根据，若CC C E *=111,C C C CC C*--*==分块矩阵的行列式，即分块矩阵可逆O A B O ⎛⎫ ⎪⎝⎭221236O A A B B O ⨯=-=⨯=（）1111661O B BO A O A O A O B B O B O B O AO A O A**---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B AO A O ****⎛⎫⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B).（6）设均为3阶矩阵，为的转置矩阵，且，,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若，则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【答案】A.【解析】，即：122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦（7）设事件与事件B 互不相容，则A (A).(B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=【答案】D.【解析】因为互不相容，所以,A B ()0P AB =(A)，因为不一定等于1，所以(A)不正确.()()1()P AB P A B P A B ==- ()P A B (B)当不为0时，(B)不成立，故排除.(),()P A P B (C)只有当互为对立事件的时候才成立，故排除.,A B(D)，故(D)正确.()()1()1P A B P AB P AB ==-= （8）设随机变量与相互独立，且服从标准正态分布，的概率分布为X Y X (0,1)N Y ，记为随机变量的分布函数，则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z 的间断点个数为（）(A)0.(B)1. (C)2.(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=独立,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤（1）若，则0z <1()()2Z F z z =Φ（2）当，则0z ≥1()(1())2Z F z z =+Φ为间断点，故选(B).0z ∴=二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）.0x →=【答案】.32e 【解析】.00x x →→=02(1cos )lim13x e x x→-=20212lim 13x e x x →⋅=32e =（10）设，则.()y xz x e =+(1,0)zx ∂=∂【答案】.2ln 21+【解析】由，故()xy z x e=+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦代入得，.1x =()ln 21,01ln 22ln 212z e x∂⎛⎫=+=+ ⎪∂⎝⎭（11）幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑【答案】.1e【解析】由题意知，()210nn n e a n--=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以，该幂级数的收敛半径为1e（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为()Q Q P =P 0.2p ξ=10000件时，价格增加1元会使产品收益增加元.【答案】8000.【解析】所求即为()QP Q P Q ''=+因为，所以0.2p Q PQξ'==-0.2Q P Q '=-所以()0.20.8QP Q Q Q '=-+=将代入有.10000Q =()8000QP '=（13）设,，若矩阵相似于，则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭k =【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦Tαβ3，0，0.而为矩阵的对角元素之和，，.TαβT αβ1300k ∴+=++2k ∴= (14)设，,…,为来自二项分布总体的简单随机样本，和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差，记统计量，则 .2T X S =-ET =【答案】2np 【解析】由.222()(1)ET E X S E X ES np np p np =-=-=--=三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数的极值.()22(,)2ln f x y xy y y =++【解析】，，故.2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =.2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =则，，.12(0,)12(2xxef e ''=+1(0,)0xyef ''=1(0,)yyef e ''=而0xxf ''> 2()0xy xx yy f f f ''''''-<二元函数存在极小值.∴11(0,)f e e=-（16）（本题满分10 分）计算不定积分 .ln(1dx+⎰(0)x >得t =22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t +=+-+=---+⎰⎰⎰而22111112(11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C +++=+-+--+=+++⎰（17）（本题满分10 分）计算二重积分，其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥【解析】由得，22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰.3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则()f x [],a b (),a b ，得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-（Ⅱ）证明：若函数在处连续，在内可导，且()f x 0x =()0,,(0)σσ>，则存在，且.'0lim ()x f x A +→='(0)f +'(0)f A +=【解析】（Ⅰ）作辅助函数，易验证满足：()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ；在闭区间上连续，在开区间内可导，且()()a b ϕϕ=()x ϕ[],a b (),a b .''()()()()f b f a x f x b aϕ-=--根据罗尔定理，可得在内至少有一点，使，即(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取，则函数满足：在闭区间上连续，开区间内可导，0(0,)x δ∈()f x []00,x ()00,x 从而有拉格朗日中值定理可得：存在，使得()()000,0,x x ξδ∈⊂……()0'00()(0)x f x f f x ξ-=-()*又由于，对上式（*式）两边取时的极限可得：()'lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故存在，且.'(0)f +'(0)f A +=（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍，求该曲线的方程.t π【解析】旋转体的体积为22()()11x x t t V f dx f dxππ==⎰⎰曲边梯形的面积为：，则由题可知()1x ts f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dxπππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得 22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰继续求导可得，化简可得''2()()()()()f t f t f t tf t f t --=，解之得'1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y-=⋅+在式中令，则，代入得 1t =2(1)(1)0,()0,(1)1f f f t f -=>∴= 1223t cyy -=+.11,2)33c t y =∴=所以该曲线方程为：.230y x +=（20）（本题满分11 分）设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭（Ⅰ）求满足，的所有向量，.21A ξξ=231Aξξ=2ξ3ξ（Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关.2ξ3ξ1ξ2ξ3ξ【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭故有一个自由变量，令，由解得，()2r A =32x =0Ax =211,1x x =-= 求特解，令，得120x x ==31x = 故，其中为任意常数21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k解方程231Aξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量，令，由得231,0x x =-=20A x =11x =令，由得230,1x x ==-20A x =10x =求得特解21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭故，其中为任意常数3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k （Ⅱ）证明：由于12121212122111121112(21)()2((21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故线性无关. 123,,ξξξ（21）（本题满分11 分）设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型的矩阵的所有特征值.f （Ⅱ）若二次型的规范形为，求的值.f 2211y y +a【解析】（Ⅰ） 0101111a A a a ⎛⎫ ⎪=- ⎪⎪--⎝⎭0110||01()1111111aa aE A a a a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--.123,2,1a a a λλλ∴==-=+（Ⅱ）若规范形为，说明有两个特征值为正，一个为0.则2212y y +1)若，则，，不符题意10a λ==220λ=-<31λ=2)若，即，则，，符合20λ=2a =120λ=>330λ=>3)若，即，则，，不符题意30λ=1a =-110λ=-<230λ=-<综上所述，故2a =（22）（本题满分11 分）设二维随机变量的概率密度为(,)X Y 0(,)0x e y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x （Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦【解析】（Ⅰ）由得其边缘密度函数0(,)0x y xe f x y -<<⎧= ⎨⎩其它()0xx x x f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== <<即|1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪⎩其它（Ⅱ）[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而11111[1,1](,)12xxx x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x yY yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰.11122[1|1]11e e P X Y e e ----∴ ≤≤==--（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z ①求.10P X Z ⎡==⎤⎣⎦②求二维随机变量的概率分布.(,)X Y 【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球.12113324(10)9C P X Z C C ⨯∴====⋅（Ⅱ）X ，Y 取值范围为0，1，2，故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======012 XY01/41/61/36 11/31/9021/900。

考研数三完整版(历年真题+答案详解)之-2009年真题1

(C)(D)〔5〕设均为2阶矩阵，分别为的伴随矩阵，假设，那么分块矩阵的伴随矩阵为(A). (B). (C). (D).〔6〕设均为3阶矩阵，为的转置矩阵，且，假设，那么为 (A). (B). (C). (D).〔7〕设事件与事件B 互不相容，那么(A). (B). (C). (D).(A) 0. (B)1. (C)2 . (D)3.二、填空题：9~14小题，每题4分，共24分，请将答案写在答题纸指定位置上. 〔9〕 . 〔10〕设，那么 .〔11〕幂级数的收敛半径为 . 元.〔13〕设,，假设矩阵相似于，那么 .(14)设，,…,为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，那么 .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解容许写出文字说明、证明过程或演算步骤. 〔15〕〔此题总分值9分〕〔16〕〔此题总分值10 分〕计算不定积分 . 〔17〕〔此题总分值10 分〕计算二重积分，其中. 〔18〕〔此题总分值11 分〕〔Ⅰ 〔Ⅱ 〔19〕〔此题总分值10 分〕〔20〕〔此题总分值11 分〕设,.〔Ⅰ〕求满足，的所有向量，.〔Ⅱ〕对〔Ⅰ〕中的任意向量,，证明,,线性无关.〔21〕〔此题总分值11 分〕设二次型.〔Ⅰ〕求二次型的矩阵的所有特征值.〔Ⅱ〕假设二次型的标准形为，求的值.〔22〕〔此题总分值11 分〕〔Ⅰ〔Ⅱ〕求条件概率.〔23〕〔此题总分值11分〕袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、、分别表示两次取球所取得的红、黑与白球的个数.〔Ⅰ〕求；〔Ⅱ〕求二维随机变量的概率分布.2021年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每题4分，共32分，以下每题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.(A)1. (B)2. (C)3. (D)无穷多个.【答案】C.【解析】那么当取任何整数时，均无意义故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解故可去间断点为3个，即〔2〕当时，与是等价无穷小，那么(A)，. 〔B〕，.(C)，. 〔D〕，.【答案】A.【解析】为等价无穷小，那么故排除(B)、(C).另外存在，蕴含了故排除(D).所以此题选(A).〔3〕使不等式成立的的范围是(A). (B). (C). (D).【答案】A.【解析】原问题可转化为求成立时的取值范围，由，时，知当时，.故应选(A).(A) (B)(C)(D)【答案】D.①时，，且单调递减.②时，单调递增.③④⑤结合这些特点，可见正确选项为(D).〔5〕设均为2阶矩阵，分别为的伴随矩阵，假设，那么分块矩阵的伴随矩阵为(A). (B).(C). (D).【答案】B.【解析】根据，假设分块矩阵的行列式，即分块矩阵可逆故答案为(B).〔6〕设均为3阶矩阵，为的转置矩阵，且，假设，那么为(A). (B).(C). (D).【答案】A.【解析】，即：〔7〕设事件与事件B互不相容，那么(A). (B).(C). (D).【答案】D.【解析】因为互不相容，所以(A)，因为不一定等于1，所以(A)不正确.(B)当不为0时，(B)不成立，故排除.(C)只有当互为对立事件的时候才成立，故排除.(D)，故(D)正确.〔〕(A) 0. (B)1. (C)2 . (D)3.【答案】B.【解析】独立〔1〕假设，那么〔2〕当，那么为间断点，应选(B).二、填空题：9~14小题，每题4分，共24分，请将答案写在答题纸指定位置上. 〔9〕.【答案】.【解析】.〔10〕设，那么.【答案】.【解析】由，故代入得，.〔11〕幂级数的收敛半径为.【答案】.【解析】由题意知，所以，该幂级数的收敛半径为元.【答案】8000.【解析】所求即为因为，所以所以将代入有.〔13〕设,，假设矩阵相似于，那么.【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为3，0，0.而为矩阵的对角元素之和，，.(14)设，,…,为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，那么.【答案】【解析】由.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解容许写出文字说明、证明过程或演算步骤.〔15〕〔此题总分值9分〕【解析】，，故..那么，，.而〔16〕〔此题总分值10 分〕计算不定积分.而所以〔17〕〔此题总分值10 分〕计算二重积分，其中.【解析】由得，.〔18〕〔此题总分值11 分〕〔Ⅰ〔Ⅱ【解析】〔Ⅰ；在闭区间上连续，在开区间内可导，且.根据罗尔定理，可得在内至少有一点，使，即〔Ⅱ……又由于，对上式〔*式〕两边取时的极限可得：故存在，且.〔19〕〔此题总分值10 分〕【解析】旋转体的体积为曲边梯形的面积为：，那么由题可知两边对t求导可得继续求导可得，化简可得，解之得所以该曲线方程为：.〔20〕〔此题总分值11 分〕设,.〔Ⅰ〕求满足，的所有向量，.〔Ⅱ〕对〔Ⅰ〕中的任意向量,，证明,,线性无关. 【解析】〔Ⅰ〕解方程故，其中为任意常数解方程求得特解故，其中为任意常数〔Ⅱ〕证明：由于故线性无关.〔21〕〔此题总分值11 分〕设二次型.〔Ⅰ〕求二次型的矩阵的所有特征值.〔Ⅱ〕假设二次型的标准形为，求的值.【解析】〔Ⅰ〕.〔Ⅱ〕假设标准形为，说明有两个特征值为正，一个为0.那么1)假设，那么，，不符题意2)假设，即，那么，，符合3)假设，即，那么，，不符题意综上所述，故〔22〕〔此题总分值11 分〕〔Ⅰ〔Ⅱ〕求条件概率【解析】〔Ⅰ故即〔Ⅱ〕而.〔23〕〔此题总分值11分〕袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、、分别表示两次取球所取得的红、黑与白球的个数.①求.②求二维随机变量的概率分布.【解析】〔Ⅰ〕在没有取白球的情况下取了一次红球，利用压缩样本空间那么相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球.〔Ⅱ〕X，Y取值范围为0，1，2，故。

2009年数学三试题答案、解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1~8小题，每小题8分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内。

（1）函数3()sin x x f x nx-=的可去间断点的个数为（）（A ）1 （B ）2 （C ）3 （D ）无穷多个【答案】C 【解析】3()sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±3200131lim lim sin cos x x x x x x x ππππ→→--== 3211132lim lim sin cos x x x x x x x ππππ→→--== 3211132lim lim sin cos x x x x x x x ππππ→-→---== 故可去间断点为3个，即0，±1（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-等价无穷小，则（）（A ）11,6a b ==- （B ）11,6a b ==（C ）11,6a b =-=-（D ）11,6a b =-=【解析与点评】考点：无穷小量比阶的概念与极限运算法则。

参见水木艾迪考研数学春季基础班教材《考研数学通用辅导讲义》（秦华大学出版社）例 4.67，强化班教材《大学数学强化 299》16、17 等例题。

【答案】A22220000sin sin 1cos sin lim lim lim limln(1)()36x x x x x ax x ax a x a axx bx x bx bx bx →→→→---===---- 230sin lim 166.x a ax a b b axa→==-=-36a b =-意味选项错误。

再由21cos lim 3x a axbx→-=-存在，故有1cos 0(0)a ax x -→→，故a=1，D 错误，所以选A 。

考研数学三(概率论与数理统计)历年真题试卷汇编16(题后含答案及解析)

考研数学三（概率论与数理统计）历年真题试卷汇编16(题后含答案及解析)题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．[2007年] 设随机变量(X，Y)服从二维正态分布，且X与Y不相关，fX(x)，fY(y)分别表示X，Y的概率密度，则在Y=y的条件下X的条件密度fX|Y(x|y)为( )．A．fX(x)B．fY(y)C．fX(x)fY(y)D．fX(x)／fY(y)正确答案：A解析：解一仅(A)入选．因(X，Y)服从二维正态分布，且X与Y不相关，故X与Y相互独立．设f(X，Y)为(X，Y)的联合概率密度，则f(X，Y)=fX(x)fY(y)．因Y服从正态分布，则对任意y有fY(y)＞0．故解二设(X，Y)服从二维正态分布N(μ1，μ2；σ12，σ22；ρ)，则概率密度为且X～N(μ1，σ12)，Y～N(μ2，σ22)，即又因X，Y不相关，则ρ=0，于是知识模块：概率论与数理统计2．[2009年] 设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布P(Y=0)=P(Y=1)=1／2．记FZ(z)为随机变量Z=XY的分布函数，则函数FZ(z)的间断点的个数为( )．A．0B．1C．2D．3正确答案：B解析：又X，Y相互独立，故当z＜0时，当z≥0时，综上所述，所以FZ(z)只有一个间断点z=0．仅(B)入选．知识模块：概率论与数理统计3．[2012年] 设随机变量X与Y相互独立，且都服从区间(0，1)内的均匀分布，则P{X2+Y2≤1}=( )．A．1／4B．1／2C．π／8D．π／4正确答案：D解析：由题设有因X与Y相互独立，故从而或知识模块：概率论与数理统计4．[2016年] 设随机变量X与Y相互独立，且X～N(1，2)，Y～N(1，4)，则D(XY)=( )．A．6B．8C．14D．15正确答案：C解析：解一直接利用命题3．4．1．1(1)求之．由X～N(1，2)得到E(X)=1，D(X)=2；由Y～N(1，4)得到E(Y)=1，D(Y)=4．故D(XY)=D(X)D(Y)+[E(X)]2D(Y)+[E(Y)]2D(X)=2×4+12×4+12×2=14．仅(C)入选．解二利用方差和期望的性质求之．D(XY)=E(XY)2－[E(XY)]2=E(X2Y2)=[E(XY)]2因X，Y相互独立，则E(X2Y2)=E(X2)E(Y2)，而E(X2)=D(X)+[E(X)]2=3，E(Y2)=D(Y)+[E(Y)]2=1+4=5，即E(X2Y2)=15，又E(XY)=E(X)E(Y)=1×1=1，故D(XY)=E(X2Y2)－[E(XY)]2=15－1=14．仅(C)入选．注：命题3．4．1．1 (1)设随机变量X，Y相互独立，则D(XY)=D(X)D(Y)+[E(X)]2D(Y)+[E(Y)]2D(X)≥D(X)D(Y)；知识模块：概率论与数理统计5．[2008年] 设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则( )．A．P(Y=－2X－1)=1B．P(Y=2X－1)=1C．P(Y=－2X+1)=1D．P(Y=2X+1)=1正确答案：D解析：解一因X～N(0，1)，Y～N(1，4)，故E(X)=0，D(X)=1，E(Y)=1，D(Y)=4．于是有又由ρXY=P(Y=aX+b)=1及命题3．4．2．3(4)得a＞0，故a=2．于是a=2,b=1．仅(D)入选．解二设Y=aX+b(a≠0)．由ρXY=1得a／|a|=1，因而a＞0．排除(A)、(C)．又因E(Y)=E(aX+b)=aE(X)+b=a·0+b=b=1．排除(B)．仅(D)入选．注：命题3．4．2．3 相关系数的常用性质有(4)当Y 与X有线性关系Y=aX+b(a≠0，b为常数)时，则X和Y的相关系数ρXY=a／|a|．因而当a＞0时，ρXY=1；当a＜0时，ρXY=－1；知识模块：概率论与数理统计6．[2002年] 设随机变量X和Y都服从标准正态分布，则( )．A．X+Y服从正态分布B．X2+Y2服从χ2分布C．X2和Y2都服从χ2分布D．X2／Y2服从F分布正确答案：C解析：解一因X～N(0，1)，Y～N(0，1)，故X2～χ2(1)，Y2～χ2(1)．仅(C)入选．解二由于(X，Y)的联合分布是否为二维正态分布未知，又不知道X与Y是否相互独立，因而不能确定X+Y服从正态分布．(A)不对．因X与Y是否独立未知，故X2+Y2是否相互独立也未知，所以也不能确定X2+Y2服从χ2分布，也不能确定X2／Y2服从F分布．(B)、(D)也不对．仅(C)入选．知识模块：概率论与数理统计填空题7．[2015年]设二维随机变量(X，Y)服从正态分布N(1，0；1，1；0)，则P{XY－Y＜0)=___________．正确答案：解析：因(X，Y)～N(1，1；0，1；0)，ρ=0，由命题(3．3．5．1(4))知，X，Y相互独立，则P{XY－Y＜0}=P{(X－1)Y＜0} =P{X－1＜0，Y＞0}+P{X －1＞0，Y＜0} =P{X＜1}P{Y＞0}+P{X＞1}P{Y＜0}．因X～N(1，1)，故P{X＜1)=P{X＞1}=因Y～N(0，1)，故所以注：命题3．3．5．1 (4)若X与Y相互独立，则X与Y一定不相关，但反之不成立．只有当X与Y的联合分布为正态分布时，X与Y相互独立与Y不相关ρXY=0．知识模块：概率论与数理统计8．[2005年] 设二维随机变量(X，Y)的概率分布为若随机事件{X=0}与{X+Y=1}相互独立，则a=__________，b=___________．正确答案：a=0．4，b=0．1解析：解一由知，a+b=0．5．又由事件{X=0)与{X+Y=1}相互独立，有P(X=0，X+Y=1)=P(X=0)P(X+Y=1)，而P(X=0，X+Y=1)=P(X=0，Y=1)=a，P(X=0)=a+0．4，P(X+Y=1)=P(X=0，Y=1)+P(X=1，Y=0)=a+b，故a=(a+0．4)(a+b)=(a+0．4)×0．5．①所以a=0．4，从而b=0．5－a=0．1．解二由解一知a+b=0．5．又由命题3．3．5．2知，秩于是即ab=0．04=0．1×0．4．解二次方程x2－0．5x+0．1×0．4=0，即解(x－0．1)(x－0．4)=0，得x1=0．1，x2=0．4．因而a=0．1或0．4，b=0．4或0．1．为满足独立性，式①应成立．当a=0．1，b=0．4时，式①不成立；当a=0．4，b=0．1时，式①成立．故所求的常数为a=0．4，b=0．1．注：命题3．3．5．2 X与Y相互独立的充分必要条件是联合概率矩阵的秩等于1，这里联合概率矩阵是指由x与y的联合分布律中的概率元素依次所组成的矩阵．知识模块：概率论与数理统计9．[2013年] 设随机变量X服从标准正态分布N(0，1)，则E(Xe2x)=_________．正确答案：2e2解析：解一因X～N(0，1)，故则解二对式①作变量代换x－2=t，则知识模块：概率论与数理统计10．[2011年] 设二维随机变量(X，Y)服从N(μ，μ；σ2，σ2；0)，则E(XY2)=_____________．正确答案：μ(σ2+μ2)解析：N(X，Y)服从二维正态分布，且其相关系数ρ=0，由命题3．3．5．1(4)知X，Y相互独立．由题设知E(X)=μ，E(Y2)=D(y)+[E(y)]2=σ2+μ2，故E(XY2)=E(X)E(Y2)=μ(σ2+μ2)．注：命题3．3．5．1 (4)若X与Y相互独立，则X与Y一定不相关，但反之不成立．只有当X与Y的联合分布为正态分布时，X与Y相互独立与Y不相关ρXY=0．知识模块：概率论与数理统计11．[2002年] 设随机变量X和y的联合概率分布为则X2和Y2的协方差cov(X2，Y2)=___________．正确答案：－0．02解析：解一由cov(X2，Y2)=E(X2Y2)－E(X2)E(Y2)知，需先求出X2，Y2及X2Y2的分布，然后再求其期望值．可用同一表格法一并解决．A则故E(X2)=0．6，E(Y2)=0．5，E(X2Y2)=0．28，因而cov(X2，Y2)=E(X2Y2)－E(X2)E(Y2)=0．28－0．6×0．5=－0．02．解二利用下述公式求之．设X 的分布律为P(X=xi)=pi(i=1，2，…)，则X的函数g(X)的期望若(X，Y)的联合分布律为P(X=xi，Y=yj)=pij(i，j=1，2，…)，N(X，Y)的函数g(X，Y)的期望由式(3．4．2．1)得到于是不用求出X2Y2的分布，直接由定义求得，即E(X2Y2)=02×(－1)2×0．07+02×02×0．18+02×12×0．15+12×(－1)2×0．08+12×02×0．32+12×12×0．20=0．28．又由联合分布律易求得边缘分布律为由式(3．4．1．1)有E(X2)=02×0．4+12×0．6=0．6，E(Y2)=02×0．5+12×0．5=0．5．故cov(X2，Y2)=E(X2Y2)－E(X2)E(Y2)=0．28－0．6×0．5=－0．02．注：公式知识模块：概率论与数理统计12．[2003年] 设随机变量X和Y的相关系数为0．9，若Z=X－0．4，则Y和Z的相关系数为_________．正确答案：0．9解析：解一由Z=X－0．4得到D(Z)=D(X－0．4)=D(X)．解二直接利用公式cov(aX+b，cY+d)=accov(X，Y)(a，b，c，d为常数)，得到解三因Z=X－0．4，故D(Z)=D(X－0．4)=D(X)，且E(Z)=E(X－0．4)=E(X)－0．4，所以cov(Y，Z)=E(YZ)－E(Y)E(Z)=E[Y(X－0．4)]－E(Y)E(X－0．4) =E(XY)－0．4E(Y)－E(Y)[E(X)－0．4] =E(XY)－0．4E(Y)－E(X)E(Y)+0．4E(Y) =E(XY)－E(X)E(Y)=cov(X，Y)．因而知识模块：概率论与数理统计13．[2001年] 设随机变量X和Y的数学期望分别为－2和2，方差分别为1和4，而相关系数为－0．5，则根据切比雪夫不等式P(|X+Y|≥6)≤_________．正确答案：1／12解析：由题设有D(X)=1，D(Y)=4．且ρXY=－0．5，E(X)=2，E(Y)=－2，则注意到E(X+Y)=E(X)+E(Y)=0，由切比雪夫不等式得到P(|X+Y|≥6)=P(|X+Y－0|≥6)=P|X+Y－E(X+Y)|≥6≤D(X+Y)／62，所以P(|X+Y|≥6)≤D(X+Y)／62=3／36=1／12．知识模块：概率论与数理统计解答题解答应写出文字说明、证明过程或演算步骤。