QPSK调制解调完整程序(配有自己的注释)
通信原理的MATLAB实验 QPSK的调制解调报告
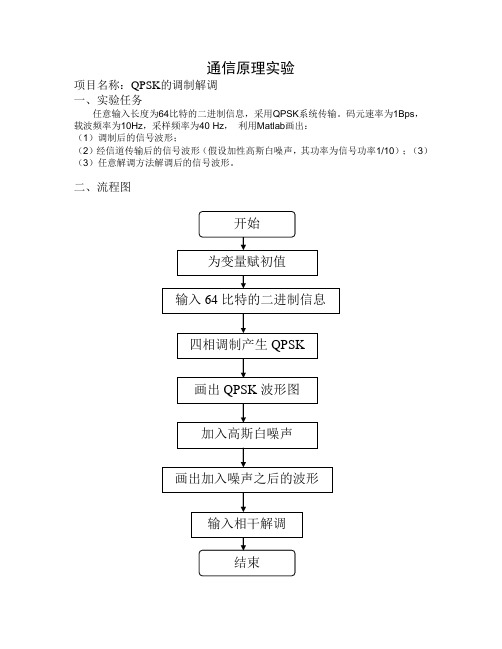
通信原理实验项目名称:QPSK的调制解调一、实验任务任意输入长度为64比特的二进制信息,采用QPSK系统传输。
码元速率为1Bps,载波频率为10Hz,采样频率为40 Hz,利用Matlab画出:(1)调制后的信号波形;(2)经信道传输后的信号波形(假设加性高斯白噪声,其功率为信号功率1/10);(3)(3)任意解调方法解调后的信号波形。
二、流程图三、完整程序Fd=1; %码元速率Fc=10; %载波频率Fs=40; %采样频率N=Fs/Fd;df=10;x=[ 1 1 0 1 1 0];%任意输入64比特的二进制信息M=2; %进制数SNRpBit=10;%加性高斯白噪声,其功率为信号功率的1/10,即信噪比为10 SNR=SNRpBit/log2(M); %转换为码元速率seed=[12345 54321];numPlot=length(x);figure(1)%画出输入二进制序列subplot(211);stem([0:numPlot-1],x(1:numPlot),'bx');title('输入波形’)%调制y=dmod(x,Fc,Fd,Fs,'fsk',M,df);numModPlot=numPlot*Fs;t=[0:numModPlot-1]./Fs;subplot(212);%画出调制后的信号plot(t,y(1:length(t)),'b-');axis([min(t) max(t) -1.5 1.5]);title('调制后的信号')%在已调信号中加入高斯白噪声randn('state',seed(2));y=awgn(y,SNR-10*log10(0.5)-10*log10(N),'measured',[],'dB');%相干解调figure(2)subplot(211);plot(t,y(1:length(t)),'b-');%画出经过信道的实际信号axis([min(t) max(t) -1.5 1.5]);title('加入高斯白噪声后的已调信号')%带输出波形的相干M元频移键控解调subplot(212);stem([0:numPlot-1],x(1:numPlot),'bx');hold on;stem([0:numPlot-1],z1(1:numPlot),'ro');hold off;axis([0 numPlot -0.5 1.5]);title('相干解调后的信号')四、波形。
qpsk软解调算法

qpsk软解调算法
QPSK(Quadrature Phase Shift Keying)软解调算法是一种数字信号解调技术,用于将接收到的QPSK信号还原为原始的数字信号。
以下是QPSK软解调算法的基本步骤:
1.信号分离:首先,将接收到的QPSK信号分离为两个正交分量,即I路(同相分量)和Q路(正交分量)。
2.相位解调:对I路和Q路信号分别进行相位解调。
这通常涉及到与本地振荡器信号的相乘和低通滤波操作。
解调后,每个分量都将产生一个基带信号。
3.抽样判决:对解调后的I路和Q路基带信号进行抽样判决,以确定每个符号的相位状态。
根据相位的不同,可以将解调后的信号映射为4种不同的比特位组合。
4.位同步:在解调过程中,需要确保抽样的时间与发送数据的位同步。
位同步是数字通信中的一个关键问题,需要确保接收端正确地理解发送数据的速率和格式。
5.数据恢复:最后,根据抽样判决的结果,恢复出原始的数字信号。
这一步通常涉及到对数据进行解码,以恢复出原始的比特流。
需要注意的是,QPSK软解调算法的实现可能会因具体的通信系统和硬件平台而有所不同。
在实际应用中,可能还需要考虑其他因素,如信道噪声、多径干扰、载波频率偏移等,这些因素可能会影响解调的性能。
QPSK调制解调完整程序(配有自己的注释)知识分享

Q P S K调制解调完整程序(配有自己的注释)QPSK调制解调完整程序(配有注释)clc;clear all;%假定接收端已经实现载波同步,位同步(盲信号解调重点要解决的问题:载波同步(costas环(未见到相关代码)),位同步(Gardner算法(未见相关代码)),帧同步)% carrier frequency for modulation and demodulationfc=5e6;%QPSK transmitterdata=5000 ; %码数率为5MHZ %原码个数rand_data=randn(1,5000);for i=1:dataif rand_data(i)>=0.5rand_data(i)=1;elserand_data(i)=0;endend%seriel to parallel %同时单极性码转为双极性码for i=1:dataif rem(i,2)==1if rand_data(i)==1I(i)=1;I(i+1)=1;elseI(i)=-1;I(i+1)=-1;endelseif rand_data(i)==1Q(i-1)=1;Q(i)=1;elseQ(i-1)=-1;Q(i)=-1;endendend% zero insertion ,此过程称为成形。
成形的意思就是实现由消息到波形的转换,以便发射,脉冲成形应该是在基带调制之后。
zero=5; %sampling rate 25M HZ ,明白了,zero为过采样率。
它等于采样率fs/码速率。
for i=1:zero*data % 采样点数目=过采样率*原码数目if rem(i,zero)==1Izero(i)=I(fix((i-1)/zero)+1);Qzero(i)=Q(fix((i-1)/zero)+1);elseIzero(i)=0;Qzero(i)=0;endend%pulse shape filter,接着,将进行低通滤波,因为随着传输速率的增大,基带脉冲的频谱将变宽%如果不滤波(如升余弦滤波)进行低通滤波,后面加载频的时候可能会出现困难。
QPSK的调制与解调课程设计

注意事项: a. 信号的相位要保持稳定 b. 接收信号的强度要足够大 c. 解调过程中要避免干扰信号的影响
实验结果分析
实验目的:验证QPSK调制与解调的原理和性能
实验设备:信号源、调制器、解调器、示波器等
实验步骤:设置参数、调制信号、解调信号、观察波形等
实验结果:调制信号的频谱、解调信号的波形、误码率等
03
QPSK信号的生成
信号调制:将信息比特转换为QPSK信号
信号生成:通过I/Q调制器生成QPSK信号
信号频率:QPSK信号的频率为载波频率的4倍
信号相位:QPSK信号的相位有4种可能,对应4种信息比特
QPSK信号的解调
解调原理:利用相位差进行解调
解调方法:采用相位检测器进行解调
解调过程:首先进行相位检测,然后进行信号恢复
QPSK调制与解调在遥感系统中的应用
添加标题
添加标题
添加标题
添加标题
QPSK调制:将遥感数据调制到载波上,提高传输效率
遥感系统:通过卫星、飞机等平台获取地球表面信息
QPSK解调:接收端对载波进行解调,恢复遥感数据
应用优势:抗干扰能力强,传输距离远,数据传输速率高
QPSK调制与解调在其他领域的应用
添加标题
实验过程:包括信号产生、调制、解调、接收等步骤
添加标题
实验不足:在实验过程中遇到了一些困难,如信号干扰、设备故障等
QPSK调制与解调的应用
05
QPSK调制与解调在通信系统中的应用
提高传输速率:QPSK调制可以提高传输速率,满足高速数据传输的需求。
提高抗干扰能力:QPSK调制可以提高系统的抗干扰能力,保证通信质量。
QPSK调制信号的波形
每个相位对应一个比特,0度对应0,180度对应1
四相移相键控(QPSK)调制及解调实验

实验二四相移相键控(QPSK )调制及解调实验一、 实验目的1、了解QPSK 调制解调原理及特性。
2、了解载波在QPSK 相干及非相干时的解调特性。
二、 实验内容1、观察I 、Q 两路基带信号的特征及与输入NRZ 码的关系。
2、观察IQ 调制解调过程中各信号变化。
3、观察解调载波相干时和非相干时各信号的区别。
三、 基本原理(说明:原理部分需简要介绍)1、QPSK 调制原理QPSK 的调制有两种产生方法相乘电路法和选择法。
相乘法:输入信号是二进制不归零的双极性码元,它通过“串并变换”电路变成了两路码元。
变成并行码元后,每个码元的持续时间是输入码元的两倍。
用两路正交载波去调制并行码元。
发射信号定义为:⎪⎩⎪⎨⎧≤≤-+=其他,00],4)12(2cos[/2)(b t T t i ft t E t S ππ其中,i =1,2,3,4;E 是发射信号的每个符号的能量,T 为符号的持续时间,载波频率f 等于nc/T ,nc 为固定整数选择法输入基带信号经过串并变换后用于控制一个相位选择电路,按照当时的输入双比特ab ,决定选择哪个相位的载波输出2、QPSK 解调原理QPSK 接收机由一对共输入地相关器组成。
这两个相关器分别提供本地产生地相干参考信号()t 1φ和()t 2φ。
四、实验步骤(说明:要详细)(1)QPSK 调制程序close all% x1是类似[1 1 -1 -1 -1 -1 1 1]的分布,作用是控制相位的180°反转。
%由于仿真中载波的频率是f=1Hz,所以1s的间隔内有一个完整周期的正弦波。
t=[-1:0.01:7-0.01]; % t共800个数据,-1~7st1=[0:0.01:8-0.01]; %t1也是800个数据点,0 ~8stt=length(t); % tt=800x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt2 = 0:0.01:7-0.01; %t2是700个数据点,是QPSK_rc绘图的下标t3 = -1:0.01:7.1-0.01; %t3有810个数据点,是i_rc的时间变量t4 = 0:0.01:8.1-0.01; %t4有810个数据点,是q_rc的时间变量tt1=length(t1);x2=ones(1,800); %x2是类似于[1 1 -1 -1 1 1 1 1]的分布,作用是控制相位的180°反转for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f); %xrc是一个低通特性的传输函数y1=conv(x1,xrc)/5.5; %y1和x1 实际上没什么区别,仅仅是上升沿、下降沿有点过渡带y2=conv(x2,xrc)/5.5; % y2和x2 实际上没什么区别,仅仅是上升沿、下降沿有点过渡带n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t); % x1就是I dataq=x2.*sin(2*pi*f1*t1); %x2就是Q dataI=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3); % y1就是I data,i_rc可能是贴近实际的波形,i则是理想波形q_rc=y2.*sin(2*pi*f1*t4); %y2就是Q data,q_rc可能是贴近实际的波形,q则是理想波形I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;subplot(3,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(3,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(3,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列');(2)QPSK解调程序clear allclose allbit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3); %bit_I为”奇数序列”,奇数序列是同相分量,以cos为载波bit_Q = bit_in(2:2:1e3); %bit_Q是bit_in的所有偶数下标组成的”偶数序列”,以sin为载波data_I = -2*bit_I+1; % 将bit_I中的1变成-1,0变成1; 注意data_I是500点data_Q = -2*bit_Q+1; %将bit_Q中的1变成-1,0变成1data_I1=repmat(data_I',20,1); %将500行的列向量data_I的共轭转置data_I’复制为20*500的矩阵,20行数据是相同的。
QPSK调制与解调原理

QPSK调制与解调原理QPSK(Quadrature Phase Shift Keying)是一种常用的数字调制技术,它可以将数字信息通过调制信号的相位变化来传输。
QPSK调制与解调原理相互关联且较为复杂,本文将从以下几个方面进行详细介绍。
一、QPSK调制原理QPSK调制原理是将两个独立的调制信号按照正交的方式进行相位调制,得到复杂的调制信号。
其中,正交基是指两个正交信号的相位差为90度。
QPSK调制涉及到两个正交信号,分别记作I通道和Q通道。
将数字信号分成两个部分,分别映射为I通道和Q通道的调制信号。
具体过程如下:1.数字信号进行二进制编码,比如00、01、10、112. 对于每个二进制码组合,分别映射到I通道和Q通道的调制信号,通常采用正交调制方法进行映射。
I通道和Q通道的调制信号可以使用正弦和余弦函数进行表示,假设调制信号频率为f,那么I通道的调制信号可以表示为:I(t) = A*cos(2πf*t + θI),Q通道的调制信号可以表示为:Q(t) = A*sin(2πf*t + θQ)。
3.结合I通道和Q通道的调制信号,可以得到复杂的QPSK调制信号为:S(t)=I(t)+jQ(t),其中j是单位虚数,表示相位90度的旋转。
二、QPSK解调原理QPSK解调的目标是将复杂的调制信号恢复为原始的数字信息。
解调过程主要包含两个环节,分别是载波恢复和解调。
具体过程如下:1. 载波恢复:接收到的调制信号经过放大和频率移位后,通过相干解调方法将信号分为I通道和Q通道两个分支。
在该过程中,需要从已知的参考信号中恢复出原始信号的频率,并根据频率差异对信号进行对齐。
这样,I通道和Q通道的解调信号可以表示为:I'(t) = S(t) *cos(2π*f*t + θ'),Q'(t) = S(t) * sin(2π*f*t + θ')。
2.解调:在解调过程中,需要根据相位信息对I通道和Q通道的解调信号进行处理,得到原始的数字信号。
实验一四相移相键控(QPSK)调制及解调实验

实验一四相移相键控(QPSK)调制及解调实验实验一四相移相键控(QPSK )调制及解调实验一、实验目的1. 了解QPSK 调制解调原理及特性。
2. 了解载波在QPSK 相干及非相干时的解调特性。
二、实验内容1. 观察I 、Q 两路基带信号的特征及与输入NRZ 码的关系。
2. 观察IQ 调制解调过程中各信号变化。
3. 观察解调载波相干时和非相干时各信号的区别。
三、基本原理1. QPSK 调制原理QPSK 利用载波的四种不同相位来表征数字信息。
由于每一种载波相位代表两个比特信息,因此,对于输入的二进制数字序列应该先进行分组,将每两个比特编为一组,然后用四种不同的载波相位来表征。
我们把组成双比特码元的前一信息比特用a 代表,后一信息比特用b 代表。
双比特码元中两个信息比特ab 通常是按格雷码排列的,它与载波相位的关系如表1-1所示,矢量关系如图1-1所示。
表1-1 双比特码元与载波相位关系双比特码元载波相位a B A 方式 B 方式 0 1 1 00 0 1 1225° 315° 45° 135°0° 90° 180° 270°(1,1)(0,1)(0,0)(1,0)45°(1,0)(1,1)(0,1)(0,0)0°参考相位参考相位(a)(b)图1-1 QPSK 信号的矢量图下面以A 方式的QPSK 为例说明QPSK 信号相位的合成方法。
串/并变换器将输入的二进制序列依次分为两个并行序列,然后通过基带成形得到的双极性序列(从D/A 转换器输出,幅度为±2/2)。
设两个双极性序列中的二进制数字分别为a 和b ,每一对ab 称为一个双比特码元。
双极性的a 和b 脉冲通过两个平衡调制器分别对同相载波及正交载波进行二相调制,得到图1-2中虚线矢量,将两路输出叠加,即得到QPSK 调制信号,其相位编码关系如表1-2所示。
QPSK调制解调

QPSK 即4PSK ,正交相移调制。
在看QPSK 之前,先看一下通信系统的调制解调的过程为了方便分析,先假设这里是理想信道,没有噪声,接收端已经载波同步,位同步。
调制后的信号数学模型为:cos()c A w t φ+ 上述的x(t)被调制到了A,ϕ上。
如果调制信息在A 上,就是调幅,如果调制信息在φ上,就是调相。
QPSK 正是通过调整φ的变化,来传输信息。
φ分别取45135225,315︒︒︒︒,,4个相位表示00,01,10,11表示4个信息,调制后的信号表达式为:cos(45),00cos(135),01()cos(225),10cos(315),11c c c c A w t x A w t x s t A w t x A w t x ︒︒︒︒⎧+=⎪+=⎪=⎨+=⎪⎪+=⎩ (cos cos 45sin sin 45),00(cos cos135sin sin135),01()(cos cos 225sin sin 225),10(cos cos315sin sin 315),11c c c c c c c c A w t w t x A w t w t x s t A w t w t x A w t w t x ︒︒︒︒︒︒︒︒⎧-=⎪-=⎪=⎨-=⎪⎪-=⎩sin ),00cos sin ),01()cos sin ),10sin ),11c c c c c c c c w t w t x w t w t x s t w t w t x w t w t x -=-+==--=+= 这样的话,我们调制任何一个信号,都可以转化为调制在同一时刻的两路上的幅度调制后再相加合并为一路输出,而调制模型cos()c A w t φ+中任意的A 和φ,根据正交分解的原理,又可以分解到两个相互正交个坐标轴上,这就是星座映射、IQ 分路的本质原理。
又由于cos()sin()c jw t c c e w t j w t =+,所有我们又经常把需要IQ 分路的调制用c jw t e 这样的复数来表示,也经常说IQ 分别是实部,虚部。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
QPSK调制解调完整程序(配有注释)clc;clear all;%假定接收端已经实现载波同步,位同步(盲信号解调重点要解决的问题:载波同步(costas环(未见到相关代码)),位同步(Gardner算法(未见相关代码)),帧同步)% carrier frequency for modulation and demodulationfc=5e6;%QPSK transmitterdata=5000 ; %码数率为5MHZ %原码个数rand_data=randn(1,5000);for i=1:dataif rand_data(i)>=0.5rand_data(i)=1;elserand_data(i)=0;endend%seriel to parallel %同时单极性码转为双极性码for i=1:dataif rem(i,2)==1if rand_data(i)==1I(i)=1;I(i+1)=1;elseI(i)=-1;I(i+1)=-1;endelseif rand_data(i)==1Q(i-1)=1;Q(i)=1;elseQ(i-1)=-1;Q(i)=-1;endendend% zero insertion ,此过程称为成形。
成形的意思就是实现由消息到波形的转换,以便发射,脉冲成形应该是在基带调制之后。
zero=5; %sampling rate 25M HZ ,明白了,zero为过采样率。
它等于采样率fs/码速率。
for i=1:zero*data % 采样点数目=过采样率*原码数目 if rem(i,zero)==1Izero(i)=I(fix((i-1)/zero)+1);Qzero(i)=Q(fix((i-1)/zero)+1);elseIzero(i)=0;Qzero(i)=0;endend%pulse shape filter,接着,将进行低通滤波,因为随着传输速率的增大,基带脉冲的频谱将变宽%如果不滤波(如升余弦滤波)进行低通滤波,后面加载频的时候可能会出现困难。
%平方根升余弦滤波器% psf=rcosfir(rf,n_t,rate,fs,'sqrt') rate:过采样率,rf:滚降因子,n_t:滤波器阶数,fs:采样率%用在调制或发送之前,用在解调或接受之后,用来降低过采样符号流带宽并不引发ISI(码间串扰)NT=50;N=2*zero*NT; % =500fs=25e6;rf=0.1;psf=rcosfir(rf,NT,zero,fs,'sqrt');% psf大小为500Ipulse=conv(Izero,psf);Qpulse=conv(Qzero,psf);%为什么数字信号传输也要过采样,成形滤波?%答:过采样的数字信号处理起来对低通滤波器的要求相对较低,如果不过采样,滤波的时候滤波器需要很陡峭,指标会很严格%成形滤波的作用是保证采样点不失真。
如果没有它,那信号在经过带限信道后,眼图张不开,ISI非常严重。
成形滤波的位置在基带调制之后。
%因为经成形滤波后,信号的信息已经有所损失,这也是为避免ISI付出的代价。
换句话说,成形滤波的位置在载波调制之前,仅挨着载波调制。
%即:(发送端)插值(采样)-成形-滤波(LPF)-加载频(载波调制)-加噪声至(接收端)乘本振-低通-定时抽取-判决。
%modulationfor i=1:zero*data+N %采样点数目改变(因为卷积的缘故) t(i)=(i-1)/(fs); %这里因为假设载频与码速率大小相等,所以用载频fc乘以过采样率=采样率。
Imod(i)=Ipulse(i)*sqrt(2)*cos(2*pi*fc*t(i));Qmod(i)=Qpulse(i)*(-sqrt(2)*sin(2*pi*fc*t(i)));endsum=Imod+Qmod;%QPSK receiver%demodulationfor i=1:zero*data+NIdem(i)=sum(i)*sqrt(2)*cos(2*pi*fc*t(i));Qdem(i)=sum(i)*(-sqrt(2)*sin(2*pi*fc*t(i)));end%matched filtermtf=rcosfir(rf,NT,zero,fs,'sqrt');Imat=conv(Idem,mtf);Qmat=conv(Qdem,mtf);%data selectionfor i=1:zero*dataIsel(i)=Imat(i+N);Qsel(i)=Qmat(i+N);end%sampler %提取码元for i=1:dataIsam(i)=Isel((i-1)*zero+1);Qsam(i)=Qsel((i-1)*zero+1);end%decision thresholdthreshold=0.2;for i=1:dataif Isam(i)>=thresholdIfinal(i)=1;elseIfinal(i)=-1;endif Qsam(i)>=thresholdQfinal(i)=1;elseQfinal(i)=-1;endend%parallel to serialfor i=1:dataif rem (i,2)==1if Ifinal(i)==1final(i)=1;elsefinal(i)=0;endelseif Qfinal(i)==1final(i)=1;elsefinal(i)=0;endendend% 绘图figure(1)plot(20*log(abs(fft(rand_data))));axis([0 data -40 100]);grid on;title('spectrum of input binary data');figure(2)subplot(221);plot(20*log(abs(fft(I))));axis([0 data -40 140]);grid on;title('spectrum of I-channel data');subplot(222);plot(20*log(abs(fft(Q))));axis([0 data -40 140]);grid on;title('spectrum of Q-channel data');subplot(223);plot(20*log(abs(fft(Izero))));axis([0 zero*data -20 140]);grid on;title('spectrum of I-channel after zero insertion');subplot(224);plot(20*log(abs(fft(Qzero))));axis([0 zero*data -20 140]);grid on;title('spectrum of Q-channel after zero insertion');figure(3);subplot(221);plot(psf);axis([200 300 -0.2 0.6]);title('time domain response of pulse shaping filter');grid on;subplot(222);plot(20*log(abs(fft(psf))));axis([0 N -350 50]);grid on;title('transfer function of pulse shaping filter');subplot(223);plot(20*log(abs(fft(Ipulse))));axis([0 zero*data+N -250 150]);grid on;title('spectrum of I-channel after impulse shaping filter'); subplot(224);plot(20*log(abs(fft(Qpulse))));axis([0 zero*data+N -250 150]);grid on;title('spectrum of Q-channel after pluse shaping filter'); figure(4)subplot(211);plot(20*log(abs(fft(Imod))));axis([0 zero*data+N -250 150]);grid on ;title('spectrum of I-channel after modulation');subplot(212);plot(20*log(abs(fft(Qmod))));axis([0 zero*data+N -250 150]);grid on;title('spectrum of Q-channel after modulation');figure(5)subplot(221);plot(20*log(abs(fft(Idem))));axis([0 zero*data -200 150]);grid on;title('spectrum of I-channel after demodulation');subplot(222);plot(20*log(abs(fft(Qdem))));axis([0 zero*data+N -200 150 ]);grid on;title('spectrum of Q-channel after demodulation');subplot(223);plot(20*log(abs(fft(Imat))));axis([0 zero*data -400 200]);grid on;title('spectrum of I-channel after matched filter'); subplot(224);plot(20*log(abs(fft(Qmat))));axis([0 zero*data -400 200]);grid on;title('spectrum of Q-channel after matched filter');figure(6)subplot(221);plot(20*log(abs(fft(Isam))));axis([0 data -40 150]);grid on;title('spectrum of I-channel after sampler');subplot(222);plot(20*log(abs(fft(Qsam))));axis([0 data -40 150 ]);grid on;title('spectrum of Q-channel after sampler');subplot(223);plot(20*log(abs(fft(Ifinal))));axis([0 data -40 150]);grid on;title('spectrum of I-channel after decision threshold'); subplot(224);plot(20*log(abs(fft(Qfinal))));axis([0 data -40 150]);grid on;title('spectrum of Q-channel after decision threshold'); figure(7)plot(Isel,Qsel);axis([-1.6 1.6 -1.6 1.6]);grid on;title('constellation of matched filter output'); figure(8)plot(Isam,Qsam,'X');axis([-1.2 1.2 -1.2 1.2]);grid on;title('constellation of sampler');figure(9)plot(20*log(abs(fft(final))));axis([0 data 0 100]);grid on;title('aspectrum of final received binary data');。
