苏教版网格中的图形PPT教学课件
三年级下册信息技术课件-第25课组合图形 苏科版新版(共9张PPT)

做运动的小朋友
联系生活
主 体
部件
想一想
做运动的小朋友 球桌
这3幅图中,你想把 哪幅图作为主体?
校园
主 体
自学尝试,小试牛刀
请同学们自学书本第145页起的内容,探究“不同文件间复制 与粘贴”和“粘贴来源”两种添加图形的方法 分别用两种方法把“房子1”添加到“夜空”文件中去
房子1
夜空
•
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021年8月6日星期 五2021/8/62021/8/62021/8/6
•
15、最具挑战性的挑战莫过于提升自 我。。2021年8月2021/8/62021/8/620,不要越轨。2021/8/62021/8/6August 6, 2021
•
17、一个人即使已登上顶峰,也仍要 自强不 息。2021/8/62021/8/62021/8/62021/8/6
谢谢观赏
You made my day!
我们,还在路上……
•
11、越是没有本领的就越加自命不凡 。2021/8/62021/8/62021/8/6Aug-216-Aug-21
•
12、越是无能的人,越喜欢挑剔别人 的错儿 。2021/8/62021/8/62021/8/6Fr iday, August 06, 2021
•
13、知人者智,自知者明。胜人者有 力,自 胜者强 。2021/8/62021/8/62021/8/62021/8/68/6/2021
思考:“不同文件间复制与粘贴”和“粘贴来 源”两种方法有什么不同?
房子2
想一想:用哪种方法添加“房子2”比 较简单?
做一做
做运动的小朋友 球桌
苏教版高中通用技术必修1:设计表现图

1、选用合适的笔来画图(2H 铅笔)
2、在方格纸上按照构思好的 设计方案,画出产品的外观比 例关系。
3、在准备好的透视网格纸上, 画出产品的透视线,先画淡一 些,等画完图形后,再描深轮 廓。
4、画产品的中间调子,注意色彩过渡自然。
5、细致描画产品的亮部及高光部位。
6、描绘产品放置平面上的阴影,突出形体的体积感 和质量感。
A、画两条与水平面 成30°角的射线
B、画一条垂线
C、连接线(内侧 为虚线)
4、直线与曲线的连接
(2)、草图的分类
草图也叫方案草图或设计速写。 根据所处的设计阶段的不同,草图可分 为构思草图和设计草图。
构思草图是以具体图形把想法表现出来。 设计草图是经过整理、选择、修改、和完善的草图。
(3)、草图绘制的步骤
2、草图的绘制
(1)、设计表现的基础
1、徒手画图
第一步,掌握正确的握笔姿势。 第二步,使用铅笔在纸上试着进行徒手自由画线的练习。 第三步,提高对笔的控制能力。 要想徒手使线画的直,可以在画面上作两个点,手控笔, 眼睛注视两点之间。
2、网格法徒手画
要领:与地面垂直的线垂直画,与 地面平行的线按网格的斜线画,同时以 网格上的小格来确定物体的比例关系。
(1)、平面结构形体的正等轴测图的绘制
A、根据形体特征,确定长(X)、宽(Y)、高 (Z)等三轴在图纸上的位置。
B、沿着上述三轴分别量出物体的长、宽、高的 尺寸,画出长方体的轴测图。
C、根据长度方向、高度方向的尺寸,画出左上 角斜切面。
D、根据长度方向、宽度方向的尺寸,画出左前 方斜切面,完成全图。
FORTRAN、LOGO以及VC、VB 等)。
(2)、技术语言的分类
苏教版一年下《认识图形》PPT课件之一共18页

11、不为五斗米折腰。 12、芳菊开林耀,青松冠岩列。怀此 贞秀姿 ,卓为 霜下杰 。
13、归去来兮,田蜀将芜胡不归。 14、酒能祛百虑,菊为制颓龄。 15、春蚕收长丝,秋熟靡王税。
苏教版版一年级数学下册
认识图形
教学目标
1.通过在钉子板上围成长方形、三角形和 正方形等活动,使同学们进一步认识平面 图形。
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
练一练
2.模仿给出的图案画一画。
(1)
练一练Байду номын сангаас
2.模仿给出的图案画一画。
(2)
练一练
2.模仿给出的图案画一画。
(3)
练一练
3.(1)看一看,说说每个图案像什么。
练一练
3.(2)看一看,说说每个图案像什么。
练一练
3.(3)试一试,围出你最喜欢的图案。
谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
2.初步培养同学们的动手操作能力,发展 同学们的空间观念和创新意识。
你能在钉子板上围出
,△,□吗?
你能在钉子板上围出
,△,□吗?
你能在钉子板上围出
,△,□吗?
下面的图形各有几条边?你能围出来吗?
四 边 形
下面的图形各有几条边?你能围出来吗?
形五 边
你还能围出一个六边形吗?
练一练 1.围一围。
苏教版通用技术必修一第六单元第一节《设计表现图》(共49张PPT)

直角坐标轴上单位长度的轴测投影长度与 对应直角坐标轴上单位长度的比值,称为 轴向伸缩系数,X、Y、Z方向的轴向伸缩 系数分别用p、q、r表示
效果图
平面结构体形正等轴测图绘制 是表现物体三维结构特征的图形。 z
30º
30º
y
x
O1 30º
O3
O4
O2
1.按照给出的尺寸画出下面形体的正等轴测 图(保留作图痕迹)。
【答案】
2.下面四个图中,不是正等轴测图的是( C )
3.下列技术语言,属于图表的是( C )
A.纺织机械加工图 B.教学楼建筑施工图 C.书架的草图 D.房间装潢布线图
一、正等测图的两个参数 1.轴间角
由于直角坐标系的三坐标轴对轴测投影面的倾角相等,根据理论分 析三轴测轴的夹角均为120°
2.轴向伸缩系数
理论可以证明正等测三根坐标轴的轴向伸缩系数都是0.82。 如按此系数作图,就意味着在画正等测图时,物体上凡是与坐标轴 平行的线段都应将其实长乘以0.82。 为方便作图通常采用简化的系数,即用1代替0.82。
…
特征: 言简意赅 通俗直观
(1)图样
机械加工图
建筑施工图
(2)图表
(3)模 型
4)符号
7)其他技术语言 口头语言、 计算机演示、 网络语言等等
家里造房子和室内装修,都有哪些图纸?
外观设计效果图
室内设计效果图
建筑施工图
家庭装修布线图
③连接线(内侧 为虚线)
(4)直线与曲线的连接
一年级下册数学课件-2.1 认识图形丨苏教版 (共15张PPT)

2020/6/16
认识图形
( 1 )个
( 2 )个 ( 3 )个 ( 5 )个
12
活动四:找一 找
在生活中,你在哪里见过这些图形?
2020/6/16
认识图形
13
活动五:拼一拼
2020/6/16
认识图形
14
小学数学PPT课件
活动小结:
小朋友们,你们这节课有什么收获呢?
2020/6/16
2020/6/16
认识图形
4
长方形
有四条边,对边相等,
四个直直的角,方方的。
2020/6/16
认识图形
5
小学数学PPT课件
正方形
Hale Waihona Puke 有四条一样长的边,四个直直的角,方方正正的。
2020/6/16
认识图形
6
三角形
有三条边,三个角。
2020/6/16
认识图形
7
圆 没有尖尖的角,圆圆的,不断开。
2020/6/16
1.在操作活动中,让同学们认识长方形、正方形、 三角形、圆,体会“面在体上”。
2.体会长方形、正方形、三角形和圆在生活中的 普遍存在。
3.培养同学们的动手操作、思考和探究能力,并 发展同学们的空间观念。
2020/6/16
认识图形
2
2020/6/16
认识图形
3
下雪啦,下雪啦!
雪地里来了一群 小画家。
认识图形
8
活动一:认一认
长方形 正方形 圆 三角形
2020/6/16
认识图形
9
活动二:摆一摆、围一围
1.用数棒摆出各种图形.
2.在钉子板上围出各种图形.
苏教版网格中的图形PPT课件

C A
B
你能求出 △ ABC的面积吗?
(5)
规定:网格中每个小正方形的边长为1。
2020年10月2日
13
B A
2020年10月2日
(6)
如图(6) 现给一格点线 段AB,你能找出 使△ ABC的面积 为2的C点吗?怎 么找?有几个?
14
C·
B
A
·C
(7)
2020年10月2日
根据以上 操作,你能归纳 出C点的位置有 什么特征吗?
数学活动课
2020年10月2日
网 格 中 的 图 形
1
下列图形分别是1×1、2×2、3×3的方格
(1)
2020年10月2日
(2)
(3)2Βιβλιοθήκη 活动一如图(1)是1×1
的方格,请画出以A
为1个端点的所有对
A· (1)
角线,这样的对角线 有_1__条,其长度为 ____2__。
2020年10月2日
3
A· (2)
条线段AB,使B
B2
B1 点落在格点上,
(4)
且 AB2 2
2020年10月2日
8
A·
·C1 再以AB为边 · C2 画一个等腰三角
形ABC,使点C在
·C3
·B
·C4
(4)
格点上,且另两 边的长都是无理 数。如何画?
2020年10月2日
9
2020年10月2日
10
活动二
25 C
22
A 2B
5
F
2
如图(2)是2×2 的方格,请画出以A 为1个端点的所有对 角线,这样的对角线 有__4__条,其长度和为 __2__5__3__2__.
数学中的格点图形
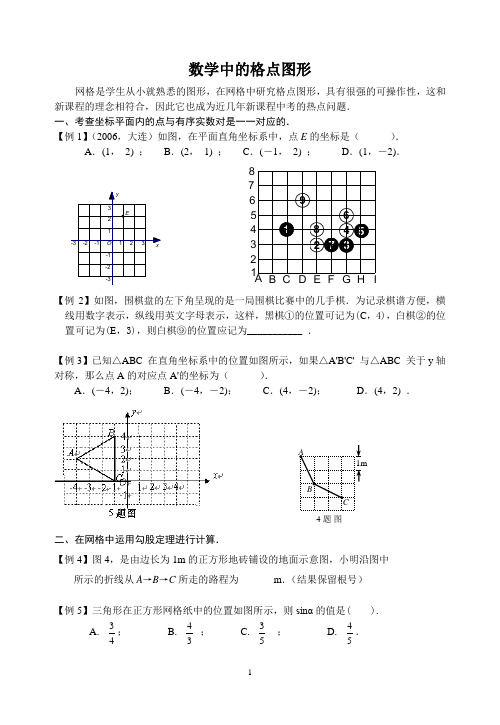
数学中的格点图形网格是学生从小就熟悉的图形,在网格中研究格点图形,具有很强的可操作性,这和新课程的理念相符合,因此它也成为近几年新课程中考的热点问题. 一、考查坐标平面内的点与有序实数对是一一对应的. 【例1】(2006,大连)如图,在平面直角坐标系中,点E 的坐标是( ).A .(1, 2) ;B .(2, 1) ;C .(-1, 2) ;D .(1,-2).图 1Ey x123-1-2-3-3-2-1321O 123574689A C B D E F G H I12345678【例2】如图,围棋盘的左下角呈现的是一局围棋比赛中的几手棋.为记录棋谱方便,横线用数字表示,纵线用英文字母表示,这样,黑棋①的位置可记为(C ,4),白棋②的位置可记为(E ,3),则白棋⑨的位置应记为___________ .【例3】已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y 轴对称,那么点A 的对应点A'的坐标为( ).A .(-4,2);B .(-4,-2);C .(4,-2);D .(4,2) .二、在网格中运用勾股定理进行计算.【例4】图4,是由边长为1m 的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A →B →C 所走的路程为_______m .(结果保留根号)【例5】三角形在正方形网格纸中的位置如图所示,则sinα的值是( ).A . 43; B . 34 ; C . 53 ; D . 54.ABC4题 图1mαABC【例6】如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC 边上的高是().A.322;B.3510;C.355;D.455.【例7】如图,直角坐标系中,△ABC的顶点都在网格点上,其中A点坐标为(2,-1),则△ABC的面积为____平方单位.A BCOxyABCOxyDE F【例8】(2006,广州)如图1,将一块正方形木板用虚线划分成36个全等的小正方形,然后,按其中的实线切成七块形状不完全相同的小木片,制成一副七巧板.用这副七巧板拼成图2的图案,则图2中阴影部分的面积是整个图案面积的( ).1111A. ;B. ;C. ;D. .47822图1 图2【例9】在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-4,-3),D(6,-3),并将各点用线段顺次连接构成一个四边形ABCD.(1)四边形ABCD是什么特殊的四边形?(2)在四边形ABCD内找一点P,使得△APB、△BPC、△CPD、△APD都是等腰三角形,请写出P点的坐标.三、分类讨论思想在格点问题中的运用.【例10】已知在正方形网格中,每个小方格都是边长为1的正方形,A、B 两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形面积为1,则点C的个数为A.3个;B.4个;C.5个;D.6个.【例11】如图所示,A、B是4×5网络中的格点,网格中的每个小正方形的边长为1,请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置.四、网格中图形变换的画图与描述.【例12】在5×5方格纸中将图1中的图形N平移后的位置如图2所示,那么下面平移中正确的是()图1 图2A. 先向下移动1格,再向左移动1格;B. 先向下移动1格,再向左移动2格;C. 先向下移动2格,再向左移动1格;D. 先向下移动2格,再向左移动2格.【例13】如图1,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕O点逆时针方向旋转90°得到△O A′B′.⑴画出△OA′B′;⑵点A′的坐标为________________;⑶求BB′的长.AOB【例14】如图1,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点B2的坐标;(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,画出△AB3C3的图形.图1【例15】如图1,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC与△A′B′C′的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.图1五、网格图形的操作方案设计问题.【例16】如图,在网格中有两个全等的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图(1)、(2)中画出两种不同的拼法.【例17】如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形.如图中的△ABC称为格点△ABC.(1)如果A、D两点的坐标分别是(1,1)和(0,-1),请你在方格纸中建立平面直角坐标系,并直接写出点B、点C的坐标;(2)请根据你所学过的平移、旋转或轴对称等知识,说明图中“格点四边形图案”是如何通过“格点△ABC图案”变换得到的.【例18】请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0).依题意,割补前后图形的面积相等,有25x=x=,解得5的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.请你参考小东同学的做法,解决如下问题: 现有10个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形.要求:在图4中画出分割线,并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.说明:直接画出图形,不要求写分析过程.【例19】操作与探究:(1)图①是一块直角三角形纸片.将该三角形纸片按如图方法折叠,使点A 与点C重合,DE 为折痕.试证明△CBE 等腰三角形;(2)再将图①中的△CBE 沿对称轴EF 折叠(如图②).通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”.你能将图③中的△ABC 折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;(3)请你在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上).请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件时,一定能折成组合矩形?图5图4 图1 图2 图3六、利用格点图形探究规律.【例20】在边长为l 的正方形网格中,按下列方式得到“L ”形图形第1个“L ”形图形的周长是8,第2个“L ”形图形的周长是12, 则第n 个“L ”形图形的周长是①③②ABCBCF 图①图②图③图④。
第三章 网格作图(1)

第三章网格作图网格作图的特点:仅利用无刻度直尺,利用格点来作图,所以在网格中作图时一定要体现出过的格点.基本知识一、网格中作平行图1 图2图1中虚线线段均与线段AB平行,仔细观察,可发现线段AB长宽比为3∶1的矩形对角线,故想要作出与AB线段平行的线,必然也要使得作出的线段是长宽比为3∶1的矩形对角线,所以图1、图2均满足要求,即都与AB平行.二、网格中作垂直图1图1中虚线线段均与线段AB垂直,仔细观察,可发现线段AB长宽比为3∶1的矩形对角线,故想要作出与AB线段垂直的线,必然也要使得作出的线段是长宽比为3∶1的矩形对角线.【与平行的区别在于一个竖方向,一个横方向】三、网格中作垂直平分线在网格中垂直平分线的做法,利用垂直平分线性质逆定理,首先需要找到线段A、B两点距离相等的格点,图1中的C、D、E均满足到A、B距离相等,故连接CE(或者ED或者CD均可).此方法也适用于在网格中作线段中点,如图2图1 图2四、网格中等分线段以作三等分为例,在下列网格中,在线段AB上找一点P,使得BP=2AP.此类作图可利用相似的性质来解决,以下示范3种作法作法一 作法二 作法三五、网格中作相似三角形请分别在图1、2中作出一个△DEF ,使得△DEF 与△ABC 相似(图1和图2中的两个三角形不全等)图1 图2 【解析】在网格图中,三角形的任意一条边均可计算出来,所以常规来说只需计算出每条边,同比放大或缩小即可!本题有个特殊角,即∠ABC =135°,所以先找到135°,该角两边同倍缩小或放大即可!(图1缩小为原来的12,即相似比为1∶2;图2似比为1例题讲解例题1、已知在下列边长为1的网格图中,用3种不同的方法作一个直角三角形,使得该直角三角形面积为8.作法一 作法二 作法三【解析】由题意可知,直角边乘积为16,若均为整数,则有1×16,2×8,4×4;若均为无理;也可以从比例去解决,下面分别以上三中思路各作一个三角形.例题2、如图,是由100个边长为1的小正方形组成的10×10正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.已知△ABC 中,AB ,AC BC =6.(1)请你在所给的网格中画出格点△A 1B 1C 1,使得△A 1B 1C 1与△ABC 相似(画出一个即可,不需证明);(2)试直接写出在所给的网格中与△ABC 相似且面积最大的格点三角形的个数,并画出其中的一个(不需证明).【解析】(1)先画个与△ABC 全等的三角形(如图1),再以∠B 为公共角,将∠B 的边缩小一半即可(如图1)图1 图2(2)因为ABCDNMS S ∆∆=相似比2,故只需使得相似比最大即可,我们找最长边AC格中最长边为对角线,MN=,由此ND DM AB BC =所以可计算出DNDM2中点D 即为关键点,连接DM 、DN 即可.例题3、如图,在每个小正方形的边长为1的网格中,点A 、B 、C 均在格点上.(1)AB 的长等于 ;(2)在△ABC 的内部有一点P ,满足S △P AB ∶S △PBC ∶S △PCA =1∶2∶3,请在如图所示的网格中,用无刻度的直尺,画出点P ,并简要说明点P 的位置是如何找到的(不要求证明).【解析】(1)AB(2)方法一:关注到S △P AB +S △PBC =S △PCA ,可得到S △PCA =12S △ABC .如图1,找到AB 中点D ,过点D 作AC 平行线,交BC 与点E ,所以点P 必然在线段DE 上.在网格中找到一点M ,使得点C 到MB 的距离与点A 到MB 的距离之比为1∶2.如图2,点Q 为AC 三等分点,连接BO ,与线段DE 交点即为点P .方法二:发现AC边上本身就存在点D、E使得AD:EC:DE=1∶2∶3,先作出如下图形,接着利用平行,将△ADB和△BEC面积转化.过点B作AC平行线,与l1交于点H,与l2交于点G,连接EG、DH,易证EG∥BC,DH ∥AB,所以EG与DH交点即为点P.2、请在如图所示的正方形和等边三角形网格内,仅用无刻度的直尺完成下列作图,过点P 向线段AB引平行线.解:如图所示,PQ即为所求.4、如图,方格图中每个小格的边长为1,仅用直尺过点C画线段CD,使CD∥AB,D是格点,过C作AB的垂线CH,垂足为H.连结BC、AD.(1)试猜想:线段BC与线段AD的关系为;(2)请计算:四边形ABCD的面积为;(3)若线段AB的长为m,则线段CH长度为.(用含m的代数式表示)解:(1)∵AD =BC ==BC ∥AD 且BC =AD .故答案为BC ∥AD 且BC =AD ;(2)S ▱ABCD =3×512-⨯1×212-⨯1×412-⨯1×212-⨯1×4=15﹣1﹣2﹣1﹣2=9.故答案为9;(3)∵AB =,S ▱ABCD =9m ,∴AB •CH =9,即CH=m 5=m .故m .图1 图2 图3 图47、图1,图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图1中画出等腰直角△MON ,使点N 在格点上,且∠MON =90°;(2)在图2中以格点为顶点画出一个正方形ABCD ,使正方形ABCD 面积等于(1)中等腰直角△MON 面积的4倍,并将正方形ABCD 分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD 面积没有剩余(画出一种即可).图1 图2 解:(1)如图1所示:∠MON =90°;图1 图2 图3(2)如图2、3所示.10、如图,将线段AB 放在边长为1的小正方形网格,点A 点B 均落在格点上,请用无刻度直尺在线段AB 上画出点P ,使AP =217,并保留作图痕迹.(备注:本题只是找点不是证明,所以只需连接一对角线就行)解:由勾股定理得,AB 224117=+=,所以,AP 2173=时AP ∶BP =2∶1.点P 如图所示.11、如图,在平面直角坐标系中,A (0,4)、B (4,4)、C (6,2). (1)在图中画出经过A 、B 、C 三点的圆弧所在圆的圆心M 的位置; (2)点M 的坐标为 ;(3)判断点D (5,—2)与OM 的位置关系. (3)判断点D (5,﹣2)与⊙M 的位置关系.解:(1)如图1,点M 就是要找的圆心;(2)圆心M 的坐标为(2,0).故答案为(2,0);(3)圆的半径AM 2224=+=25.线段MD 22(52)213=-+=<25,所以点D 在⊙M 内.12、如图,在单位长度为1的正方形网格中,一段圆弧经过格点A 、B 、C . (1)画出该圆弧所在圆的圆心D 的位置(不用写作法,保留作图痕迹),并连接AD 、CD . (2)请在(1)的基础上,以点0为原点、水平方向所在直线为x 轴、竖直方向所在直线为y轴,建立平面直角坐标系,完成下列问题:①OD的半径为(结果保留根号);②若用扇形ADC围成一个圆锥的侧面,则该圆锥的底面圆半径是;③若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.解:(1)根据题意画出相应的图形,如图所示:(2)①在Rt△AOD中,OA=4,OD=2,根据勾股定理得:AD==则⊙D的半径为②AC==CD=AD2+CD2=AC2,∴∠ADC=90°.扇形ADC的弧长==,圆锥的底面的半径=;③直线EC与⊙D的位置关系为相切,理由为:在Rt△CEF中,CF=2,EF=1,根据勾股定理得:CE==在△CDE中,CD=CE=DE=5,∵CE2+CD2=()2+(2=5+20=25,DE2=25,∴CE2+CD2=DE2,∴△CDE为直角三角形,即∠DCE=90°,则CE与圆D相一、构造直角例题1、网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sin A= .【解析】如图,作AD⊥BC于D,CE⊥AB于E,由勾股定理得AB=AC=BC=,AD =ABC 是等腰三角形,由面积相等可得,12BC •AD 12=AB •CE , 即CE 5==,sinA 35CE AC ===,故答案为35.【总结】由于格点三角形各边都可求,所以利用解直角三角形即可求出各个内角的三角函数值.二、角度转换例题2、如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P ,则tan ∠APD 的值是 .思路一:构造直角连接BE ,由四边形EDBC 为正方形可知,CD ⊥BE ,∴tan ∠APD =tan ∠BPF =BFPF,设小正,可得BF =1,CD =2,由△ACP ∽△BDP ,且相似比为3∶1可得PCDP=3, ∴PC CD =34,∴PC =33242⨯=,∴PF =PC —CF =12, ∴tan ∠BPF 1=212=.思路二∶角度转换连接BE ,可知BE ∥CD ,∴∠APD =∠BPF =∠ABE ,连接AE ,AE 和BE 均为正方形对角线,易得AE ⊥BE ,tan ∠ABE =2AEBE=.例题3、在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A 、B 、C 、D 都在格点处,AB 与CD 相交于O ,则tan ∠BOD 的值等于【答案】3 【解析】转化思路一:到格点三角形内,再用例题1的方法(此方法构造情况较多,解法较暴力,在此不一一列举,以下给出三种转化法)转化思路二:思路一的情况下,存在转化出的格点三角形恰好为直角三角形,这类方法最巧妙,但需要学生有较强的观察能力!直角构造思路三:通过连接某些辅助线,构造出直角后直接在直角三角形内求解.2、如图,在4x 5的正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则tan ∠ABC = ;sin ∠ACB = .【解析】找到与A 构成小正方形对角线的格点D 、E ,连接CD ,AE ,EB ,AC 与EB 交于点F .由网格特点和正方形的性质可知,∠BAE =90°,根据勾股定理得,AE =AB =,DB ,DC BE ===,则tan ∠ABC 3DCDB==,又BE ⊥AC ,易得△AEF ∽△BAF ,故13AE EF AF AB AF BF ===,∴19EF BF =,∴BF =910⨯sin ∠ACB=BF BC ===,故答案为3.3、如图,在边长相同的小正方形网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB ,CD 相交于点P ,则APPB的值= ,tan ∠APD 的值= .【解析】∵四边形BCED 是正方形,∴DB ∥AC ,∴△DBP ∽△CAP ,∴AP ACPB DB==3, 连接BE ,∵四边形BCED 是正方形,∴DF =CF 12=CD ,BF 12=BE ,CD =BE ,BE ⊥CD ,∴BF =CF ,根据题意得:AC ∥BD ,∴△ACP ∽△BDP ,∴DP :CP =BD :AC =1:3,∴DP :DF =1:2,∴DP =PF 12=CF 12=BF ,在Rt △PBF 中,tan ∠BPF BF PF ==2,∵∠APD =∠BPF ,∴tan ∠APD =2,故答案为3,2.5、如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O )为60°,A ,B ,C 都在格点上,则tan ∠ABC 的值是 .【解析】如图,连接EA ,EC ,设菱形的边长为a ,由题意得∠AEF =30°,∠BEF =60°,AE =,EB =2a ,∴∠AEC =90°,∵∠ACE =∠ACG =∠BCG =60°, ∴E 、C 、B 共线,在Rt △AEB 中,tan ∠ABC AE BE ===6、如图,网格中的四个格点组成菱形ABCD ,则tan ∠DBC 的值为 .【解析】如图,连接AC 与BD 相交于点O ,∵四边形ABCD 是菱形,∴AC ⊥BD ,BO 12=BD ,CO 12=AC ,由勾股定理得,AC ==,BD ==BO 122==,CO 12=⨯2=tan ∠DBC CO BO ===3.故案为3.7、如图1是由边长为1的小正方形组成的网格,点A 、B 、C 、D 都在网格的格点上,AC 、BD 相交于点O .图1 图2 图3 图4 (一)探索发现(1)如图1,当AB =2时,连接AD ,则∠ADO =90°,BO =2DO ,AD =BO 23=tan ∠AOD = .如图2,当AB =3时,画AH ⊥BD 交BD 的延长线于H ,则AH 32=BO = ,tan ∠AOD = .如图3,当AB =4时,tan ∠AOD = .(2)猜想:当AB =n (n >0)时,tan ∠AOD = .(结果用含n 的代数式表示),请证明你的猜想. (二)解决问题(3)如图,两个正方形的一边CD 、CG 在同一直线上,连接CF 、DE 相交于点O,若tan ∠COE 1713=,求正方形ABCD 和正方形CEFG 的边长之比. 解∶(一)探索发现(1)如图1,当AB =2时,∵BO =2DO ,BO 23=∴OD =又∵∠ADO =90°,AD =tan ∠AOD 3ADOD===3,即tan ∠AOD =3. 如图2,设DCBE 为正方形,连接CE ,交BD 于F .∵四边形BCDE 是正方形, ∴DF =CF =BF 12=BD 12=CE ,BD ⊥CE .根据题意得∶AB ∥DC ,∴△AOB ∽△COD , ∴DO ∶BO =CD ∶AB .当AB =3时,DO ∶BO =1∶3,∴BO 4=.∵S △ABD 12=BD •AH 12=AB •ED ,∴BD •AH =AB •ED ,∴AH 2AB ED BD ⋅===,DO ∶BO =CD ∶AB =1∶3,∴DO ∶DF =1∶2,∴OF ∶DF =1∶2,即OF ∶CF =1∶2.在Rt △OCF 中,tan ∠COF CFOF==2,∵∠AOD =∠COF ,∴tan ∠AOD =2;如图3,当AB =4时,DO ∶BO =CD ∶AB =1∶4,∴DO ∶DF =1∶2.5=2∶5,∴OF ∶DF =3∶5,即OF ∶CF =3∶5.在Rt △OCF 中,tan ∠COF 53CF OF ==,∵∠AOD =∠COF ,∴tan ∠AOD 53=;故答案是32;53;(2)猜想∶当AB =n (n >0)时,tan ∠AOD 11n n +=-(结果用含n 的代数式表示). 证明∶过点A 作AH ⊥BH 于点H ,则AH =BH 2=n .∵AB ∥OD ,∴△AOB ∽△COD , ∴1OB AB nOD CD ==,∴OB 1n =+.∴OH =BH ﹣OB 2=n 1n -+.∴tan ∠AOD 11AHn HDn +===-;故答案是11n n +-; (二)解决问题(3)解:如图4,过点D作DH⊥CF于点H,则tan∠DOHDHHO=.∵∠DOH=∠COE,∴tan∠DOH1713=,又由(一)结论得:117113nn+=-,∴n152=,∴正方形ABCD和正方形CEFG的边长之比为152.图1 图2 图3 图4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/01/22
5
A·
A·
A·
(1条)
(4条)
(9条)
通过以上的实践操作,请同学们猜想:
在4×4的方格中,以A为一个端点的所有对
角线有_1__6__条;
在n×n的方格中,以A为一个端点的所有对
角线有__n__2_条。
2021/01/22
6
2021/01/22
7
B3
B4
从图(4)中
A·
的A点出发画一
条线段AB,使B
B2
B1 点落在格点上,
(4)
且 AB2 2
2021/01/22
8
A·
·C1 再以AB为边 · C2 画一个等腰三角
形ABC,使点C在
·C3
·B
·C4
(4)
格点上,且另两 边的长都是无理 数。如何画?
2021/01/22
9
2021/01/22
10
活动二
25 C
22
A 2B
5
F 2
D1 E
(5)
如图(5)观 察图形关系?
规定:网格中每个小正方形的边长为1。
2021/01/22
11
C A
B
(5)
你能再在图 中画出一个与 △ ABC相似的格 点三角形吗?怎 么画?
规定:网格中每个小正方形的边长为1。
2021/01/22
12
C A
B
你能求出 △ ABC的面积吗?
(5)
规定:网格中每个小正方形的边长为1。
2021/01/22
13
2021/01/22
B A
(6)
如图(6) 现给一格点线 段AB,你能找出 使△ ABC的面积 为2的C点吗?怎 么找?有几个?
14
2021/01/22
C·
B
A
·C
(7)
根据以上 操作,你能归纳 出C点的位置有 什么特征吗?
17
数学活动课
2021/01/22
网 格 中 的 图 形
1
下列图形分别是1×1、2×2、3×3的方格
(1)
2021/01/22
(2)
(3)
2
活动一
如图(1)是1×1
的方格,请画出以A
为1个端点的所有对
A· (1)
角线,这样的对角线 有_1__条,其长度为 ____2__。
2021/01/22
3
A· (2)
如图(2)是2×2 的方格,请画出以A 为1个端点的所有对 角线,这样的对角线 有__4__条,其长度和为 __2__5__3__2__.
2021/01/22
4
·
A
(3)
如图(3)是3×3 的方格,请画出以A 为1个端点的所有对 角线,这样的对角线 有__9__条, 其长度和 为_6 __2 _ _2_1 __ _3 2_1 __ _0 2 _5 _.
15
活动三
2021/01/22
(8)
你能在方格中 画边长为无理数 的格点平行四边 形、格点菱形、 格点梯形吗?
16
THANKS FOR WATCHING
谢谢大家观看
为了方便教学与学习使用,本文档内容可以在下载后随意修改,调整。欢迎下载!
汇报人:XXX
时间:20XX.XX.XX
2021/01/22
