2008年中考题
2008年浙江省金华市中考语文试卷及答案

2008年浙江省金华市中考语文试卷一、语文知识积累及运用(21分,另有附加题4分)1、阅读下面材料,完成后面题目。
(9分)2007年11月30日,驻金华某部军官孟祥斌为救一名轻生的落水女子,毅然从10米高的金华城南桥上跃入冰冷婺江……女青年得救了,孟祥斌不幸牺牲,年仅28岁。
(1)下面是2007年感动中国组委会授予孟祥斌的颁将辞,请根据拼音和语境写出相应的汉字。
(3分)风萧萧江水寒,壮士一去不复fǎn( )。
同样是生命,同样有亲人,他用一次辉huáng( )的陨落换回另外一个生命。
别去问值还是不值,生命的价值从来不是用交换体现。
他在冰冷的河水中睡去,给我们一个温暖的启shì( ).(2) 下面是一位金华歌手写的一首纪念孟祥斌的歌词《这一次》,请选出依次填入空缺处的词语最恰当的一项。
(2分)这一次你纵身一跃,滔滔婺江见证______;这一次你奋力地托举,托起生的希望______人间;这一次你虽不再醒来,却用生命的光芒照亮人间,把生给了别人,用死铸就军魂。
古老的通济为你,金华山水把你……A. 壮烈震撼哽咽惦记B.壮丽震撼哽咽惦记C. 壮丽震撼呜咽铭记D. 壮烈震撼呜咽铭记(3)下面是某校九(1)班黑板报《学英雄,见行动》中的一段文字,画线句子有语病,请加以改正。
(2分)在学习孟祥斌的活动中,我班王丽同学把自己平时节省下来的零花钱捐给了灾区。
事后她觉得自己因为家庭困难捐得少,就把自己心爱的长发剪掉,卖了20元钱,也捐给了灾区。
这种学英雄,见行动,得到了学校领导的表扬。
(4)请用一个成语概括孟祥斌的救人行为。
(2分)2.根据语境把古诗文名句补写完整。
(4分,另有附加题4分)(1)廉政文化进校园,我们懂得了廉洁奉公是我们中华民族的优良传统。
翻开厚重的诗文书卷,展现在我们面前的正是一座座镌刻着“廉洁”与“奉公”的人生丰碑。
陆游的“夜阑卧听风吹雨,______”,沸腾着诗人报效国家的满腔热血;范仲淹的“______,后天下之乐而乐”,寄托着作者以天下为己任的伟大抱负;龚自珍的“落红不是无情物,______”,抒发了诗人无私奉献的真挚情怀;周敦颐的“出淤泥而不染,______”表现了作者清廉自律的高风亮节。
2008年福州市中考数学试题

2008年福州市中考数学试题一. 填空题:(每小题3分,满分36分) 1. -7的绝对值是____________。
2. 分解因式:282x -=______________。
3. 在函数y x =-1中,自变量x 的取值范围是____________。
4. 不等式组x x +≥<⎧⎨⎩1236的解集是______________。
5. 如图,已知:l l 12//,∠=︒1100,则∠=2_____________。
1 l 12 l 26. 对于函数y x =-+21,y 随x 的增大而____________。
7. 一个多边形的每个外角都等于60︒,这个多边形的内角和为____________。
8. 母线长为3cm 底面半径为1cm 的圆柱侧面展开图的面积为___________cm 2。
9. 已知a b ::=31,且a b +=8,则a b -=_________。
10. 已知:在∆ABC 中,∠=︒∠=︒=A B AC 60452,,,则AB 的长为_____________。
11. 观察下列各式:111222233334222+=⨯+=⨯+=⨯…………请你将猜想到的规律用自然数n n ()≥1表示出来__________________。
12. 如图,两个同心圆,过大圆上一点A 作小圆的割线交小圆于B 、C 两点,且AB AC ⋅=4,则图中圆环的面积为_____________。
二. 选择题:(每小题4分,满分32分,每小题都有A 、B 、C 、D 四个选项,其中只有一个选项是正确的,请把正确选项的代号,写在题末的括号内) 13. 下列运算正确的是( ) A. a b c a b c -+=-+() B. a a a 3362+= C. ()x x +=+1122D. 236235a a a ⋅-=-()14. 用科学记数法表示我国的国土面积约为( ) A. 96105.⨯平方千米 B. 96106.⨯平方千米 C. 96107.⨯平方千米 D. 96108.⨯平方千米15. 计算x xx -÷-2122(),所得正确结果是( ) A. xB.-1x C. 1xD.--x x 216. 如果两个圆只有两条公切线,那么这两个圆的位置关系是( ) A. 外离 B. 外切 C. 相交 D. 内切 17. 下列四个命题中错误的是( )A. 两条对角线互相垂直且相等的四边形是正方形B. 菱形的一条对角线平分一组对角C. 顺次连结四边形的各边中点所得的四边形是平行四边形D. 等腰梯形的两条对角线相等18. 随着计算机技术的迅猛发展,电脑价格不断降低。
2008年四川省成都市中考语文真题及答案

2008年四川省成都市中考语文真题及答案全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
A卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷为选择题,第Ⅱ卷为其他类型的题。
A 卷 ( 共 100 分 )第 I 卷( 选择题共 16 分 )注意事项:1. 第I卷共2页,答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在试卷和答题卡上。
考试结束后,监考人员将试卷和答题卡一并收回。
2.第I卷各题均有四个选项,只有一项符合题目要求。
每小题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
请注意机读答题卡的横竖格式。
一、基础知识(10分,每小题2分)1.下面语句中加点字的注音有误的一项是A.人类的智慧与大自然的智慧相比实在是相形见绌.(zhuō),无论是令人厌恶.(wù)的苍蝇蚊子,还是美丽可人的鲜花绿草,都是大自然精巧绝伦的艺术品。
B.我常常把手放在大地上,我会感到她在跳跃.(yuè),和我的心的跳跃是一样的, 它们的热血一直在流,在热情的默契.(qì)里它们彼此呼唤,终有一天它们要汇合在一起。
C.这是某种令人惊骇.(hài)而不知名的杰作,在不可名状的晨曦.(xī)中依稀可见,宛如在欧洲文明的地平线上瞥见的亚洲文明的剪影。
D.峰环水抱的萨尔茨堡,高高低低的房屋鳞次栉.(zhì)比,庄严肃.(sù)穆的修道院坐落在绿树浓阴中。
2.下面语句中书写准确无误的一项是A. 黄土高原啊,只有你,才能承受如此惊心动魄的博击!B. 因为我听到海依然在远方为我喧腾——那雪白的海潮啊,夜夜奔来一次次漫湿了枯干的心灵。
C. 读书的要决,全在于会意。
对于这一点,陶渊明尤其有独到的见解。
D. 不管扔进去什么东西,这个慷概大方的洞全部一视同仁,照收不误。
3.依次填入下列句子横线处的词语,最恰当的一项是①那时候,他已经诗兴不作而研究志趣正浓。
2008年烟台市中考数学试题及答案

(3)若点 P 是抛物线 L1 上的一个动点(P 不与点 A、B
重合),那么点 P 关于原点的对称点 Q 是否在抛物线 L2 上,
请说明理由.
22、(本题满分 8 分) 据研究,当洗衣机中洗衣粉的含量在 0.2%~0.5%之间
时,衣服的洗涤效果较好,因为这时表面活性较大.
现将 4.94 kg 的衣服放入最大容量为 15 kg 的洗衣机
中,欲使洗衣机中洗衣粉的含量达到 0.4%,那么洗衣机中 需要加入多少千克水,多少匙洗衣粉?(1 匙洗衣粉约
①
②
③
④
a. 运动员推出去的铅球(铅球的高度与时间的关系)
b. 静止的小车从光滑的斜面滑下(小车的速度与时间的关
系)
c. 一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧
的长度与所挂重物的质量的关系)
d. 小明从 A 地到 B 地后,停留一段时间,然后按原速度
原路返回(小明离 A 地的距离与时间的关系) 正确的顺序是( )D
A、 abcd B、 adbc C、 acbd D、 acdb 12、如图,在 Rt△ABC 内有边长分别为 a, b, c 的三个正
方形,则 a, b, c 满足的关系式是( )A
17、表 2 是从表 1 中截取的一部分,则 a = _____ .
18 18、如图是某工程队在“村村通”工程中,修筑的公路长
方程可以是______________.
答案不唯一,如 −2 = 1 x−2
15、七(1)班四个绿化小组植树的棵树如下:10,10,x ,
8,已知这组数据的众数和平均数相等,那么这组数据的 中位数是_______棵. 10 16、红丝带是关注艾滋病防治问题的国际性标志.将宽为
昆明市2008年中考数学试题及答案

昆明市2008年中考数学试题及答案(本试卷共三大题25小题,共6页.考试时间120分钟,满分120分)参考公式:①弧长公式180R n l π=,其中l 是弧长,R 是半径,n 是圆心角的度数;②二次函数y =ax 2+bx +c(a ≠0)图像的顶点坐标是(a4b ac 4,a 2b 2--)一、选择题:(每小题3分,满分27.在每小题给出的四个选项中,只有一项是正确的;每小题选出答案后,用2B 铅笔将答题卡上对应题目的答案标号的小框涂黑.)1、32-的绝对值是( ) A .32- B .32 C .23- D .232、下列图形是几家电信公司的标志,其中既是轴对称图形又是中心对称图形的是( )3、2008年“五一”放假期间,昆明市的石林风景区等主要景点共接待游客约96400人,96400 用科学记数法表示为( )A. 49.6410⨯ B. 50.96410⨯ C. 396.410⨯ D. 39.6410⨯4、.已知:如图,∠DAC 是△ABC 的一个外角,∠DAC =850, ∠B =450,则∠C 的度数为( ) A .500 B. 450 C.400. D. 3505、下列运算中,正确的是( )A .2=B .()22224x y x y +=+C .842x x x ÷= D .211224x x x ÷=-+- 6、已知:⊙O 1的半径为3cm ,⊙O 2的半径为5cm ,两圆的圆心距O 1O 2=8cm ,则两圆的位置关系是( )A 外离 B. 外切 C. 相交 D. 内切 7、如图是正方体的平面展开图,每个面上标有一个汉字, 与“油”字相对的面上的字是( )A. 北B. 京C. 奥D.运8、某市道路改造中,需要铺设一条长为1200米的管道,为了尽量减少施工对交通造成的影 响,实际施工时,工作效率比原计划提高了25%,结果提前了8天完成任务。
设原计划每天铺设管道x 米,根据题意,则下列方程正确的是( ) A . 12001200825%x x -= B . 1200120081.25x x-= C .1200120081.25x x-= D .120012008(125%)x x -=- 第七题图油加运奥京北第4题图DCBAA B C D9、如图,在Rt △ABC 中,∠A = 900,A C = 6cm ,AB = 8cm ,把AB 边翻折,使AB 边落在BC 边上,点A 落在点E 处,折痕为BD ,则sin ∠DBE 的值为( ) A .13 B .310CD二.填空题:(每小题3分,满分18分.请考生用黑色碳素笔将答案答在答题卡相应题号后的横线上.)10、当x ≠________时,分式13x -有意义, 11、巳知反比例函数(0)ky k x=≠的图象经过点(-2,5),则k =________. 12、农科院对甲、乙两种甜玉米各10块试验田进行试验后,得到甲、乙两个品种每公顷的平均产量相同,而甲、乙两个品种产量的方差分别为20.01S ≈甲,20.002S ≈乙,则产量较为稳定的品种是________(填“甲”或“乙”)。
2008年中考数学试题及答案解析
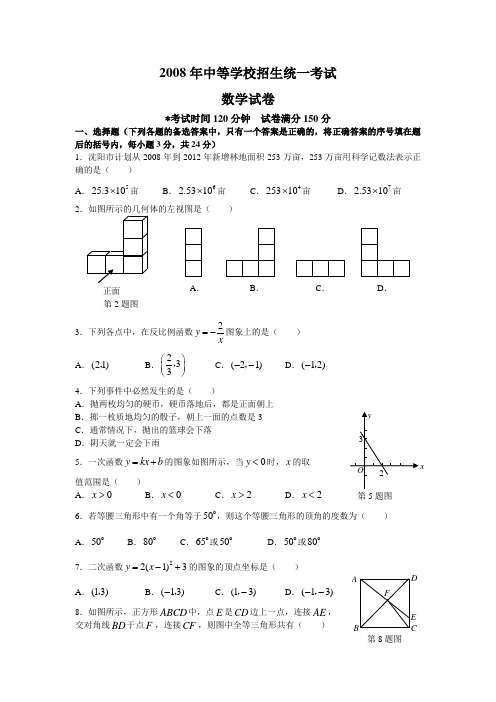
2008年中等学校招生统一考试数学试卷*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( ) A .525.310⨯亩B .62.5310⨯亩C .425310⨯亩D .72.5310⨯亩2)3.下列各点中,在反比例函数2y x=-图象上的是()A .(21),B .233⎛⎫⎪⎝⎭,C .(21)--,D .(12)-,4.下列事件中必然发生的是( )A .抛两枚均匀的硬币,硬币落地后,都是正面朝上B .掷一枚质地均匀的骰子,朝上一面的点数是3C .通常情况下,抛出的篮球会下落D .阴天就一定会下雨5.一次函数y kx b =+的图象如图所示,当0y <时,x 的取 值范围是( ) A .0x > B .0x <C .2x >D .2x <6.若等腰三角形中有一个角等于50,则这个等腰三角形的顶角的度数为( ) A .50B .80C .65或50D .50或807.二次函数22(1)3y x =-+的图象的顶点坐标是( )A .(13),B .(13)-,C .(13)-,D .(13)--, 8.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE , 交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )正面第2题图A .B .C .D .第5题图xADCEFB第8题图A .1对B .2对C .3对D .4对二、填空题(每小题3分,共24分)9.已知A ∠与B ∠互余,若70A ∠=,则B ∠的度数为 . 10.分解因式:328m m -= .11.已知ABC △中,60A ∠=,ABC ∠,ACB ∠的平分线交于点O ,则BOC ∠的度数为 .12.如图所示,菱形ABCD 中,对角线AC BD ,相交于点O ,若再补 充一个条件能使菱形ABCD 成为正方形,则这个条件是 (只填一个条件即可). 13.不等式26x x -<-的解集为 .14.如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且12tan 5BAE ∠=,则河堤的高BE 为 米.15.观察下列图形的构成规律,根据此规律,第8第15题图16.在平面直角坐标系中,点A 的坐标为(11),,点B 的坐标为(111),,点C 到直线AB 的距离为4,且ABC △是直角三角形,则满足条件的点C 有 个.三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.计算:101(1)52-⎛⎫π-+-+- ⎪⎝⎭18.解分式方程:1233xx x=+--.19.先化简,再求值:222()()2y x y x y x y ++---,其中13x =-,3y =.第1个 ……第2个 第3个 第4个ADC BO 第12题图 B C DA 第14题图20.如图所示,在66⨯的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形,如图①中的三角形是格点三角形. (1)请你在图①中画一条直线将格点三角形分割成两部分,将这两部分重新拼成两个不同的格点四边形,并将这两个格点四边形分别画在图②,图③中; (2)直接写出这两个格点四边形的周长.四、(每小题10分,共20分)21.如图所示,AB 是O 的一条弦,OD AB ⊥,垂足为C ,交O 于点D ,点E 在O 上.(1)若52AOD ∠=,求DEB ∠的度数;(2)若3OC =,5OA =,求AB 的长.22.小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局. (1)一次出牌小刚出“象”牌的概率是多少?(2)如果用A B C ,,分别表示小刚的象、虎、鼠三张牌,用1A ,1B ,1C 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.图① 第20题图图②图③第21题图 小刚 小明A 1B 1C 1A B C 第22题图23.在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2)请你将表格补充完整:(3)请从下列不同角度对这次竞赛成绩的结果进行分析:①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩. 六、(本题12分)24.一辆经营长途运输的货车在高速公路的A 处加满油后,以每小时80千米的速度匀速行驶,前往与A 处相距636千米的B 地,下表记录的是货车一次加满油后油箱内余油量y (升)与行驶时间x (1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A 处出发行驶4.2小时到达C 处,求此时油箱内余油多少升?(3)在(2)的前提下,C 处前方18千米的D 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B 地.(货车在D 处加油过程中的时间和路程忽略不计)第23题图 一班竞赛成绩统计图 二班竞赛成绩统计图25.已知:如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AMN △是等腰三角形.(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长ED 交线段BC 于点P .求证:PBD AMN △∽△.八、(本题14分) 26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.2008年沈阳市中等学校招生统一考试C E ND A BM图① C A EM B D N图② 第25题图第26题图数学试题参考答案及评分标准一、选择题(每小题3分,共24分) 1.B 2.A 3.D 4.C 5.C 6.D7.A8.C二、填空题(每小题3分,共24分) 9.2010.2(2)(2)m m m +-11.12012.90BAD ∠=(或AD AB ⊥,AC BD =等)13.4x >14.1215.65 16.8 三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.解:原式1(2)5=+-+- ···························································· 4分125=-+- ··················································································· 5分6= ······································································································ 6分18.解:12(3)x x =-- ·················································································· 2分126x x =--7x = ··········································································································· 5分 检验:将7x =代入原方程,左边14==右边 ························································ 7分所以7x =是原方程的根 ·················································································· 8分 (将7x =代入最简公分母检验同样给分)19.解:原式2222222xy y x xy y x y =++-+-- ················································ 4分 xy =- ········································································································· 6分 当13x =-,3y =时,原式1313⎛⎫=--⨯= ⎪⎝⎭······················································································ 8分 20.解:(1)答案不唯一,如分割线为三角形的三条中位线中任意一条所在的直线等.································· 2分拼接的图形不唯一,例如下面给出的三种情况:图① 图② 图③ 图④图①~图④,图⑤~图⑦,图⑧~图⑨,画出其中一组图中的两个图形. ······················ 6分 (2)对应(1)中所给图①~图④的周长分别为4+8,4+4+ 图⑤~图⑦的周长分别为10,8+8+图⑧~图⑨的周长分别为2+4+ ···································· 10分 四、(每小题10分,共20分) 21.解:(1)OD AB ⊥,AD DB ∴= ··························································· 3分 11522622DEB AOD ∴∠=∠=⨯= ································································· 5分 (2)OD AB ⊥,AC BC ∴=,AOC △为直角三角形, 3OC =,5OA =,由勾股定理可得4AC == ·············································· 8分 28AB AC ∴== ························································································· 10分 22.解:(1)1()3P =一次出牌小刚出象牌“” ··················································· 4分(2)树状图(树形图):·············································································· 8分图⑤ 图⑥图⑦图⑧ 图⑨A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1C开始小刚 小明或列表···························································· 8分 由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种. ········································································ 9分1()3P ∴=一次出牌小刚胜小明. ····································································· 10分 五、(本题12分) 23.解:(1)21······························································································ 2分 (2)一班众数为90,二班中位数为80 ······························································· 6分 (3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好; ···································································································· 8分 ②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好; ················································································································· 10分 ③从B 级以上(包括B 级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好. ······························································································· 12分 六、(本题12分) 24.解:(1)设y 与x 之间的关系为一次函数,其函数表达式为y kx b =+ ················ 1分将(0100),,(180),代入上式得, 10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩20100y x ∴=-+ ·························································································· 4分验证:当2x =时,20210060y =-⨯+=,符合一次函数; 当 2.5x =时,20 2.510050y =-⨯+=,也符合一次函数.∴可用一次函数20100y x =-+表示其变化规律,而不用反比例函数、二次函数表示其变化规律. ··················································· 5分 y ∴与x 之间的关系是一次函数,其函数表达式为20100y x =-+ ··························· 6分 (2)当 4.2x =时,由20100y x =-+可得16y =即货车行驶到C 处时油箱内余油16升. ····························································· 8分 (3)方法不唯一,如:方法一:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 设在D 处至少加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯+=+, ··················································· 11分 解得,69a =(升) ····················································································· 12分方法二:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 汽车行驶18千米的耗油量:1820 4.580⨯=(升) D B ,之间路程为:63680 4.218282-⨯-=(千米)汽车行驶282千米的耗油量:2822070.580⨯=(升) ················································································· 11分 70.510(16 4.5)69+--=(升) ···································································· 12分 方法三:由(1)得,货车行驶中每小时耗油20升, ············································· 9分设在D 处加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯++≤,解得,69a ≥ ····························································································· 11分 ∴在D 处至少加油69升,货车才能到达B 地. ················································· 12分七、(本题12分) 25.证明:(1)①BAC DAE ∠=∠ BAE CAD ∴∠=∠AB AC =,AD AE = ABE ACD ∴△≌△BE CD ∴= ·································································································· 3分 ②由ABE ACD △≌△得ABE ACD ∠=∠,BE CD =M N ,分别是BE CD ,的中点,BM CN ∴= ················································· 4分 又AB AC = ABM ACN ∴△≌△AM AN ∴=,即AMN △为等腰三角形 ···························································· 6分 (2)(1)中的两个结论仍然成立. ···································································· 8分 (3)在图②中正确画出线段PD由(1)同理可证ABM ACN △≌△ CAN BAM ∴∠=∠ BAC MAN ∴∠=∠ 又BAC DAE ∠=∠MAN DAE BAC ∴∠=∠=∠AMN ∴△,ADE △和ABC △都是顶角相等的等腰三角形 ································· 10分 PBD AMN ∴∠=∠,PDB ADE ANM ∠=∠=∠PBD AMN ∴△∽△ ···················································································· 12分 八、(本题14分)26.解:(1)点E 在y 轴上 ·············································································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ································································· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=∴在Rt DOM △中,12DM =,2OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ················································································ 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ·················································································· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:2829y x x =--+ ·················································· 9分(3)存在符合条件的点P ,点Q . ································································· 10分。
2008年山东省青岛市中考数学试题及答案

2008年山东省青岛市中考数学试题(考试时间:120分钟;满分120分)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功! 1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.2.本试题共有24道题,其中1—7题为选择题,请将所选答案的标号,写在第7题后面给出表格的相应位置上:8—14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15—24题请在试题给出的本题位置上做答.一、选择题(本题满分21分,共有7道小题,每小题3分)下列每小题都给出标号为A ,B ,C ,D 的四个结论,其中只有一个是正确的.每小题选对得分;不选,选错或选出的标号超过一个的不得分,请将1—7各小题所选答案的标号填写在第7小题后面表格的相应位置上.1.14-的相反数等于( ) A .14 B .14- C .4D .4-2.下列图形中,轴对称图形的个数是( )A.1 B.2 C.3 D.43.已知1O 和2O 的半径分别为3cm 和2cm ,圆心距124O O =cm ,则两圆的位置关系是( ) A .相切 B .内含 C .外离 D .相交4.某几何体的三种视图如右图所示,则该几何体可能是()A .圆锥体B .球体C .长方体D .圆柱体5.一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色, ,不断重复上述过程.小明共摸了100次,其中20次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有() A .18个 B .15个 C .12个 D .10个 6.如果点11()A x y ,和点22()B x y ,是直线y kx b =-上的两点,且当12x x <时,12y y <,那么函数ky x=的图象大致是( )7.如图,把图①中的ABC △经过一定的变换得到图②中的A B C '''△,如果图①中ABC △上点P 的坐标为()a b ,,那么这个点在图②中的对应点P '的坐标为( ) 主视图 左视图 俯视图x x x x D .A .(23)a b --,B .(32)a b --,C .(32)a b ++,D .(23)a b ++,请将1—7各小题所选答案的标号填写在下表的相应位置上:题号 1 2 3 4 5 6 7 答案二、填空题(本题满分21分,共有7道小题,每小题3分)请将8—14各小题的答案填写在第14小题后面表格的相应位置上. 8.计算:0122-+= .9.化简:293x x -=- .10.如图,在矩形ABCD 中,对角线A CB D ,相交于点O ,若60AOB ∠= ,4AB =cm ,则AC 的长为 cm .11.如图,AB 是O 的直径,弦CD AB ⊥于E ,如果10AB =,8CD =,那么AE 的长为 .12.为了帮助四川地震灾区重建家园,某学校号召师生自愿捐款.第一次捐款总额为20000元,第二次捐款总额为56000元,已知第二次捐款人数是第一次的2倍,而且人均捐款额比第一次多20元.求第一次捐款的人数是多少?若设第一次捐款的人数为x ,则根据题意可列方程为 . 13.某市广播电视局欲招聘播音员一名,对A B ,两名候选人进行了两项素质测试,两人的两项测试成绩如右表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么 (填A 或B )将被录用.14.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF 长为10cm .母线()OE OF 长为10cm .在母线OF 上的点A 处有一块爆米花残渣,且2FA =cm ,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点.则此蚂蚁爬行的最短距离为 cm . 测试项目测试成绩A B面试 90 95 综合知识测试 8580图① 图②请将8—14各小题的答案填写在下表的相应位置上:题号 8 9 10 11 答案题号 12 13 14 答案三、作图题(本题满分6分)用圆规、直尺作图,不写作法,但要保留作图痕迹.15.如图,AB AC ,表示两条相交的公路,现要在BAC ∠的内部建一个物流中心.设计时要求该物流中心到两条公路的距离相等,且到公路交叉处A 点的距离为1000米.(1)若要以1:50000的比例尺画设计图,求物流中心到公路交叉处A 点的图上距离; (2)在图中画出物流中心的位置P .解:(1)四、解答题(本题满分72分,共有9道小题) 16.(本小题满分6分) 用配方法解一元二次方程:2220x x --=.17.(本小题满分6分)某市为调查学生的视力变化情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查A FEO第14题图A CB (2) 1cm的结果,并将所得数据处理后,制成折线统计图和扇形统计图如下:解答下列问题:(1)该市共抽取了多少名九年级学生?(2)若该市共有8万名九年级学生,请你估计该市九年级视力不良(4.9以下)的学生大约有多少人? (3)根据统计图提供的信息,谈谈自己的感想(不超过30字). 18.(本小题满分6分)小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?19.(本小题满分6分)在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB 表示窗户,且2AB =米,BCD 表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD 的最小夹角α为18.6,最大夹角β为64.5.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD 的长是多少米?(结果保留两个有效数字) (参考数据:sin18.60.32=,tan18.60.34=,sin 64.50.90=,tan 64.5 2.1=)时间(年) 0被抽取学生视力在4.9以下 的人数变化情况统计图 A40% B30%C 20%D 10% A :4.9以下B :4.9-5.1C :5.1-5.2D :5.2以上 (每组数据只含最低值不含最高值) 被抽取学生2008年的视 力分布情况统计图20.(本小题满分8分)2008年8月,北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种:A 种船票600元/张,B 种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A ,B 两种船票共15张,要求A 种船票的数量不少于B 种船票数量的一半.若设购买A 种船票x 张,请你解答下列问题:(1)共有几种符合题意的购票方案?写出解答过程; (2)根据计算判断:哪种购票方案更省钱? 21.(本小题满分8分)已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE C G =,连接BG 并延长交DE 于F .(1)求证:BCG DCE △≌△;(2)将DCE △绕点D 顺时针旋转90得到DAE '△,判断四边形E BGD '是什么特殊四边形?并说明理由. 22.(本小题满分10分)某服装公司试销一种成本为每件50元的T 恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y (件)与销售单价x (元)的关系可以近似的看作一次函数(如图). (1)求y 与x 之间的函数关系式;(2)设公司获得的总利润(总利润=总销售额-总成本)为P 元,求P 与x 之间的函数关系式,并写出自变量x 的取值范围;根据题意判断:当x 取何值时,P 的值最大?最大值是多少?23.(本小题满分10分)实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型: 在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机y (件)AB CDEF E 'G摸出的小球至少有10个是同色的,则最少需摸出多少个小球? 为了找到解决问题的办法,我们可把上述问题简单化:(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是:134+=(如图①);(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是:1327+⨯=(如图②)(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是:13310+⨯=(如图③):(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是:13(101)28+⨯-=(如图⑩)模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ; (2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ; (3)若要确保摸出的小球至少有n 个同色(20n <),则最少需摸出小球的个数是 . 模型拓展二:在不透明口袋中装有m 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球: (1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 . (2)若要确保摸出的小球至少有n 个同色(20n <),则最少需摸出小球的个数是 . 问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型; (2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生. 24.(本小题满分12分)已知:如图①,在Rt ACB △中,90C ∠=,4cm AC =,3cm BC =,点P 由B 出发沿BA 方向向点红 黄 红 红或黄或白 图② 黄 白 白 红 黄 白 红或黄或白 图① 红 红 红或黄或白 图③ 红 白 白 白 黄黄 黄红 红 红或黄或白图⑩ 红 白 白 白 黄 黄黄 白 … 红 黄9个 9个9个 ...A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为(s)t (02t <<),解答下列问题: (1)当t 为何值时,PQ BC ∥?(2)设AQP △的面积为y (2cm ),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使线段PQ 恰好把Rt ACB △的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把PQC △沿QC 翻折,得到四边形PQP C ',那么是否存在某一时刻t ,使四边形PQP C '为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.图①2008年山东省青岛市中考数学试题参考答案及评分标准说明:1.如果考生的解法与本解法不同,可参照本评分标准制定相应评分细则.2.当考生的解答在某一步出现错误,影响了后继部分时,如果这一步以后的解答未改变这道题的内容和难度,可视影响程度决定后面部分的给分,但不得超过后面部分应给分数的一半;如果这一步以后的解答有较严重的错误,就不给分.3.为阅卷方便,本解答中的推算步骤写得较为详细,但允许考生在解答过程中,合理省略非关键性的推算步骤.4.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 一、选择题(本题满分21分,共有7道小题,每小题3分)题号 1 2 3 4 5 6 7 答案 A B D D C B C 二、填空题(本题满分21分,共有7道小题,每小题3分)题号 89 10 11 答案 23x +38 2 题号 1213 14答案2020000256000=-xx B412三、作图题(本题满分6分) 15.解:(1)1000米=100000厘米,100000÷50000=2(厘米); ··················· 2′(2) 略. ···························· 6′四、解答题(本题满分72分,共有9道小题) 16.(本小题满分6分)解: 222=-x x , 12122+=+-x x ,3)1(2=-x , ·················· 3′ 31±=-x ,∴311+=x , 312-=x . ······················· 6′17.(本小题满分6分)解:(1)800÷40% = 2000(人); ·················· 2′ (2)80000×40% = 32000(人); ··················· 4′ (3)合理即可. ··························· 6′18.(本小题满分6分)解:····························· 2′∴P (配成紫色)=92,P (配不成紫色)=97.∴小刚得分:92192=⨯,小明得分:97197=⨯,∵9792≠ , ∴ 游戏对双方不公平. ············ 4′ 修改规则的方法不惟一.(如改为:若配成紫色时小刚得7分,否则小明得2分.) ·········· 6′19.(本小题满分6分)解:设CD 为x ,中, 6.18==∠αBDC , 在Rt△BCD∵CDBCBDC =∠tan , ∴x BDC CD BC 34.0tan =∠⋅=. ·········· 2′ 在Rt△ACD 中, 5.64==∠βADC , ∵CDACADC =∠tan , ∴x ADC CD AC 1.2tan =∠⋅=. ·········· 4′ ∵BC AC AB -=,∴x x 34.01.22-=. ··········· 5′1.14x ≈.答:CD 长约为1.14米. ··········· 6′ 20.(本小题满分8分)解:(1)设A 种票x 张,则B 种票)15(x -张,红 白 蓝红 (红,红) (红,白) (红,蓝) 黄 (黄,红) (黄,白) (黄,蓝) 蓝(蓝,红) (蓝,白) (蓝,蓝)根据题意得:152600120(15)5000x x x x -⎧⎪⎨⎪+-⎩≥,≤ ············ 3′ 解得: 5≤x ≤320. ∴满足条件的x 为5或6. ∴共有两种购买方案:方案一:A 种票5张, B 种票10张,方案二:A 种票6张, B 种票9张. ··········· 6′ (2)方案一购票费用: 600×5+120×10=4200(元),方案二购票费用: 600×6+120×9=4680(元), ∵4200<4680,∴ 方案一更省钱. ··········· 8′21.(本小题满分8分)证明:(1) ∵四边形ABCD 是正方形,∴BC=CD ,∠BCD=90°. ∵∠BCD +∠DCE=180°, ∴∠BCD=∠DCE=90°. 又∵CG=CE ,∴△BCG ≌△DCE . ············ 4′ (2)∵△DCE 绕D 顺时针旋转90︒得到△DAE ′,∴CE=AE ′. ∵CE=CG , ∴CG=AE ′.∵四边形ABCD 是正方形, ∴BE ′∥DG ,AB=CD . ∴AB -AE ′ =CD -CG , 即BE ′ =DG .∴四边形DE ′ BG 是平行四边形. ········ 8′22.(本小题满分10分)解:(1)设b kx y x y +=的函数关系式为:与,∵函数图象经过点(60,400)和(70,300),∴⎩⎨⎧+=+=b k b k 7030060400, 解得⎩⎨⎧=-=100010b k . ∴100010+-=x y . ·········· 4′(2))100010)(50(+--=x x P 500001500102-+-=x x P ··········· 6′自变量取值范围:50≤x ≤70. ·········· 7′∵752015002=--=-a b ,10-=a <0. ∴函数500001500102-+-=x x P 图象开口向下,对称轴是直线x=75.∵50≤x ≤70,此时y 随x 的增大而增大,∴当70=x 时,6000=最大值P . ········· 10′23.(本小题满分10分)模型拓展一:(1)1+5=6 ·········· 1′(2)1+5×9=46 ·········· 2′(3)1+5(n -1) ·········· 3′模型拓展二:(1)1+m ·········· 4′(2)1+m (n -1) ········· 5′问题解决:(1)在不透明口袋中放入18种颜色的小球(小球除颜色外完全相同)各40个,现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球? ····································· 8′(2)1+18×(10-1) =163 ······················ 10′24.(本小题满分12分)解:(1)在Rt△ABC 中,522=+=AC BC AB ,由题意知:AP = 5-t ,AQ = 2t ,若PQ ∥BC ,则△APQ ∽△ABC ,∴=AC AQ ABAP , ∴5542t t -=, ∴710=t . ·············· 3′(2)过点P 作PH ⊥AC 于H . B∵△APH ∽△ABC , ∴=BC PH AB AP , ∴=3PH 55t -, ∴t PH 533-=, ∴t t t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=. ·········· 6′ (3)若PQ 把△ABC 周长平分,则AP+AQ=BP+BC+CQ .∴)24(32)5(t t t t -++=+-,解得:1=t .若PQ 把△ABC 面积平分, 则ABC APQ S S ∆∆=21, 即-253t +3t =3.∵ t =1代入上面方程不成立,∴不存在这一时刻t ,使线段PQ 把Rt△ACB 的周长和面积同时平分. ··· 9′(4)过点P 作PM ⊥AC 于M,PN ⊥BC 于N ,若四边形PQP ′ C 是菱形,那么PQ =PC .∵PM ⊥AC 于M ,∴QM=CM .∵PN ⊥BC 于N ,易知△PBN ∽△ABC . ∴AB BP AC PN =, ∴54t PN =, ∴54t PN =, ∴54t CM QM ==, ∴425454=++t t t , 解得:910=t . ∴当910=t 时,四边形PQP ′ C 是菱形. 此时37533=-=t PM , 9854==t CM ,B N在Rt△PMC 中,9505816494922=+=+=CM PM PC , ∴菱形PQP ′ C 边长为9505. 12′。
2008年中考试题汇编(10)

OC B15.如图,画出△OAB绕O点按逆时针方向旋转90°时的△OA′B′.佛山市4.( ).A23. 如图,△ACD、△ABE、△BCF.(1) 当AB≠AC时,证明四边形ADFE为平行四边形;(2) 当AB = AC时,顺次连结A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.汕头市6.已知A B C△的三边长分别为5,13,12,则A B C△的面积为()A.30 B.60 C.78 D.不能确定16.如图3,在A B C△中,10A B A C==,8B C=.用尺规作图作B C边上的中线A D(保留作图痕迹,不要求写作法和证明),并求A D的长.23.(1)如图6,点O是线段A D的中点,分别以A O和D O为边在线段A D同侧作等边三角形O A B和等边三角形O C D,连结A C和B D,相交于点E,连结B C.求AEB∠的大小;(2)如图7,O A B△固定不动,保持O C D△的形状和大小不变,将O C D△绕着点O旋转某一个角(O A B△和O C D△不能重叠),求AEB∠的大小.茂名市2.下列图形中,既是轴对称图形又是中心对称图形的是()第23题图EFDAB CAC图3图6ABCDOE图7ABCDOE10.如图,△ABC 是等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积是△ABC 的面积的 ( )A.91 B.92 C.31 D.9423.如图,在等腰梯形ABCD 中,已知AD ∥BC ,AB =DC ,AD =2,BC =4,延长BC 到E ,使CE =AD .(1)写出图中所有与△DCE全等的三角形,并选择其中一对说明全等的理由;(2)探究当等腰梯形ABCD 的高DF 是多少时,对角线AC 与BD 互相垂直?请回答并说明理由.解:湛江市12. 如图2所示,已知等边三角形ABC的边长为1,按图中所示的规律,用2008个这样的三角形镶嵌而成的四边形的周长是( )A.2008B.2009C.2010 D.201123. 如图7所示,已知等腰梯形ABCD 中,AD ∥BC ,AB =DC ,AC 与BD 相交于点O .请在图中找出一对全等的三角形,并加以证明.肇庆市4.一个正方形的对称轴共有( )A .1条B .2条C .4条D .无数条12.如图3,P 是∠AOB 的角平分线上的一点,PC ⊥OA 于点C ,PD ⊥OB 于点D ,写出图中一对相等的线段(只需写出一对即可) .19.如图4, E 、F 、G 分别是等边△ABC 的边AB 、BC 、AC 的中点.(1) 图中有多少个三角形?(2) 指出图中一对全等三角形,并给出证明.C((第10题图)F EDCBA(第23题图)图2AB┅┅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年河北省初中毕业生升学文化课考试数学试卷本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题. 本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共20分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效. 一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.(08河北)8-的倒数是( ) A .8B .8-C .18D .18-2.(08河北)计算223a a +的结果是( ) A .23aB .24aC .43aD .44a3.(08河北)把某不等式组中两个不等式的解集表示在数轴上,如图1则这个不等式组可能是( ) A .41x x >⎧⎨-⎩,≤B .41x x <⎧⎨-⎩,≥C .41x x >⎧⎨>-⎩,D .41x x ⎧⎨>-⎩≤,4.(08河北)据河北电视台报道,截止到2008年5月21日,河北慈善总会已接受支援汶川地震灾区的捐款15 510 000元.将15 510 000用科学记数法表示为(A .80.155110⨯ B .4155110⨯C .71.55110⨯D .615.5110⨯5.(08河北)图2中的两个三角形是位似图形,它们的位似中心是( A .点P B .点O C .点M D .点N6.(08河北)某县为发展教育事业,加强了对教育经费的投入,2007年投入3 000万元,预计2009年投入5 000万元.设教育经费的年平均增长率为x ,根据题意,下面所列方程正确的是( )A .23000(1)5000x += B .230005000x =C .23000(1)5000x +=%D .23000(1)3000(1)5000x x +++=7.(08河北)如图3,已知O 的半径为5,点O 到弦AB 的距离为3,则 到弦AB 所在直线的距离为2的点有( )A .1个B .2个C .3个D .4个8.(08河北)同时抛掷两枚质地均匀的正方体骰子(骰子每个面上的点数分别为1,2,3,4,41- 图1图2 图35,6).下列事件中是必然事件的是( ) A .两枚骰子朝上一面的点数和为6 B .两枚骰子朝上一面的点数和不小于2 C .两枚骰子朝上一面的点数均为偶数 D .两枚骰子朝上一面的点数均为奇数9.(08河北)如图4,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x ,且010x <≤,阴影部分的面积为y ,则能反映y 与x 之间函数关系的大致图象是( )10.(08河北)有一个四等分转盘,在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌,如图5-1.若将位于上下位置的两个字牌对调,同时将位于左右位置的两个字牌对调,再将转盘顺时针旋转90,则完成一次变换.图5-2,图5-3分别表示第1次变换和第2次变换.按上述规则完成第9次变换后,“众”字位于转盘的位置是( )A .上B .下C .左D .右2008年河北省初中毕业生升学文化课考试数学试卷卷Ⅱ(非选择题,共100分)注意事项:1.答卷Ⅱ前,将密封线左侧的项目填写清楚.2.答卷Ⅱ时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上) 11.(08河北)如图6,直线a b ∥,直线c 与a b , 相交.若170∠=, 则2_____∠=.12.(08河北)当x = 时,分式31x -无意义. 13.(08河北)若m n ,互为相反数,则555m n +-= .14.(08河北)如图7,AB 与O 相切于点B ,AO 的延长线交O 于点图4 x A . x B . x C . D . 图5-1 图5-2 图5-3 …12ba 图6 c连结BC .若36A ∠=,则______C ∠= .15.(08则这些学生成绩的众数为 . 16.(08河北)图8所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是 g 17.(08河北)点(231)P m -,在反比例函数1y x=的图象上,则m = .18.(08河北)图9-1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若6AC =,5BC =,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图9-2所示的“数学风车”,则这个风车的外围周长是.三、解答题(本大题共8个小题;共76分.解答应写出文字说明、证明过程或演算步骤) 19.(08河北)(本小题满分7分)已知2x =-,求21211x x x x -+⎛⎫-÷ ⎪⎝⎭的值.20.(08河北)(本小题满分8分)某种子培育基地用A ,B ,C ,D 四种型号的小麦种子共2 000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C 型号种子的发芽率为95%,根据实验数据绘制了图10-1和图10-2两幅尚不完整的统计图. (1)D 型号种子的粒数是 ; (2)请你将图10-2的统计图补充完整;(3)通过计算说明,应选哪一个型号的种子进行推广; (4)若将所有已发芽的种子放到一起,从中随机取出一粒,求取到B 型号发芽种子的概率.ABC图9-1 图9-2图8A 35%B 20%C 20% D各型号种子数的百分比图10-121.(08河北)(本小题满分8分)如图11,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C . (1)求点D 的坐标; (2)求直线2l 的解析表达式; (3)求ADC △的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.22.(08河北)(本小题满分9分)气象台发布的卫星云图显示,代号为W 的台风在某海岛(设为点O )的南偏东45方向的B点生成,测得OB =.台风中心从点B 以40km/h 的速度向正北方向移动,经5h 后到达海面上的点C 处.因受气旋影响,台风中心从点C 开始以30km/h 的速度向北偏西60方向继续移动.以O 为原点建立如图12所示的直角坐标系.(1)台风中心生成点B 的坐标为 ,台风中心转折点C 的坐标为 ;(结果保留根号)(2)已知距台风中心20km 的范围内均会受到台风的侵袭.如果某城市(设为点A )位于点O 的正北方向且处于台风中心的移动路线上,那么台风从生成到最初..侵袭该城要经过多长时间?图11在一平直河岸l 同侧有A B ,两个村庄,A B ,到l 的距离分别是3km 和2km ,km AB a =(1)a >.现计划在河岸l 上建一抽水站P ,用输水管向两个村庄供水.方案设计某班数学兴趣小组设计了两种铺设管道方案:图13-1是方案一的示意图,设该方案中管道长度为1d ,且1(km)d PB BA =+(其中BP l ⊥于点P );图13-2是方案二的示意图,设该方案中管道长度为2d ,且2(k m )d P A P B =+(其中点A '与点A 关于l 对称,A B '与l 交于点P ).观察计算(1)在方案一中,1d = km (用含a 的式子表示);(2)在方案二中,组长小宇为了计算2d 的长,作了如图13-3所示的辅助线,请你按小宇同学的思路计算,2d = km (用含a 的式子表示). 探索归纳(1)①当4a =时,比较大小:12_______d d (填“>”、“=”或“<”); ②当6a =时,比较大小:12_______d d (填“>”、“=”或“<”); (2)请你参考右边方框中的方法指导, 就a (当1a >时)的所有取值情况进 行分析,要使铺设的管道长度较短, 应选择方案一还是方案二?图13-1 图13-2图13-3如图14-1,ABC △的边BC 在直线l 上,AC BC ⊥,且AC BC =;EFP △的边FP 也在直线l 上,边EF 与边AC 重合,且EF FP =.(1)在图14-1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;(2)将EFP △沿直线l 向左平移到图14-2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;(3)将EFP △沿直线l 向左平移到图14-3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.25.(08河北)(本小题满分12分)研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x (吨)时,所需的全部费用y (万元)与x 满足关系式2159010y x x =++,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p 甲,p 乙(万元)均与x 满足一次函数关系.(注:年利润=年销售额-全部费用) (1)成果表明,在甲地生产并销售x 吨时,11420p x =-+甲,请你用含x 的代数式表示甲地当年的年销售额,并求年利润w 甲(万元)与x 之间的函数关系式; (2)成果表明,在乙地生产并销售x 吨时,110p x n =-+乙(n 为常数),且在乙地当年的最大年利润为35万元.试确定n 的值;(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1),(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得较大的年利润?A (E ) BC (F ) PlllB FC 图14-1图14-2图14-3P26.(08河北)(本小题满分12分)如图15,在Rt ABC △中,90C ∠=,50AB =,30AC =,D E F ,,分别是A C AB BC ,,的中点.点P 从点D 出发沿折线DE EF FC CD ---以每秒7个单位长的速度匀速运动;点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动,过点Q 作射线QK AB ⊥,交折线BC CA -于点G .点P Q ,同时出发,当点P 绕行一周回到点D 时停止运动,点Q 也随之停止.设点P Q ,运动的时间是t 秒(0t >). (1)D F ,两点间的距离是 ;(2)射线QK 能否把四边形CDEF 分成面积相等的两部分?若能,求出t 的值.若不能,说明理由;(3)当点P 运动到折线EF FC -上,且点P 又恰好落在射线QK 上时,求t 的值; (4)连结PG ,当PG AB ∥时,请直接..写出t 的值.图15。
