基于改进正交匹配追踪算法的压缩感知雷达成像方法

合集下载

压缩感知问题统计建模及应用

压缩感知问题统计建模及应用边昂;张建州【摘要】In this paper, a novel statistical model is proposed to describe the Gaussian noisy compressed sensing problem with Gaussian random measurement matrix, and under the statistical framework, some hypothesis tests are used to analyse the performance of the weighted median regression estimate compressive sensing signal reconstruction with an iterative hard threshold under the l0- regularized constraint. The χ2 test based computation sequence is proposed to improve the performance of its coordination descent computation sequence, and F test based data adaptive stopping criterion is presented to take the place of its manual stopping conditions of the maximal number of iterations and the lower bound of the residual energy. Practical performance of the proposal is evaluated via numerical experiments.%对高斯噪声下的高斯随机观测矩阵压缩感知问题建立了新的统计模型，并在该统计模型的基础上，引入相应的统计检验方法对l 0范式约束下的硬阈值加权中值回归重建算法进行分析。

几种压缩感知算法

.1 压缩感知部分压缩感知算法主要可分为三类：贪婪迭代算法、凸凸优化（或最优化逼近方法）和基于贝叶斯框架提出的重构算法。

由于第三类方法注重信号的时间相关性，不适合图像处理问题，故目前的研究成果主要集中在前两类中。

目前已实现6中算法，分别为正交匹配追踪法（OMP）、迭代硬阈值法（IHT）、分段正交匹配追踪法（StOMP）、分段弱正交匹配追踪法（SwOMP）、广义正交匹配追踪（GOMP）、基追踪法（BP）。

1.1 正交匹配追踪法（OMP）在正交匹配追踪OMP中，残差是总与已经选择过的原子正交的。

这意味着一个原子不会被选择两次，结果会在有限的几步收敛。

OMP的算法如下(1)用x表示你的信号，初始化残差e0=x；(2)选择与e0内积绝对值最大的原子，表示为φ1；(3)将选择的原子作为列组成矩阵Φt，定义Φt列空间的正交投影算子为通过从e0减去其在Φt所张成空间上的正交投影得到残差e1；(4)对残差迭代执行(2)、(3)步；其中I为单位阵。

需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵，因此每次都是不同的，所以由它生成的正交投影算子矩阵P每次都是不同的。

(5)直到达到某个指定的停止准则后停止算法。

OMP减去的Pem是em在所有被选择过的原子组成的矩阵Φt所张成空间上的正交投影，而MP减去的Pem是em在本次被选择的原子φm所张成空间上的正交投影。

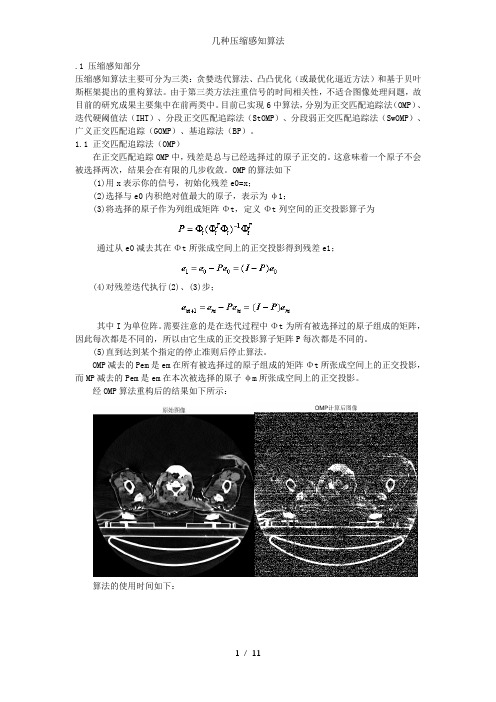
经OMP算法重构后的结果如下所示：算法的使用时间如下：1.2 迭代硬阈值法（IHT）目标函数为这里中的M应该指的是M-sparse，S应该指的是Surrogate。

这里要求：之后我们利用式对目标函数进行变形。

接着便是获得极值点：利用该式进行迭代可以得到极值点，我们需要的是最小值。

此时目标函数的最小值就得到了。

此时便得到我们需要的公式：我们要保证向量y的稀疏度不大于M，即，为了达到这一目标，要保留最大的M项（因为是平方，所以要取绝对值absolute value），剩余的置零（注意这里有个负号，所以要保留最大的M项）。

基于压缩感知信号重建的自适应正交多匹配追踪算法

理，它指出只要信号具有稀疏性或可压缩性，可以通过少量随机采样点来恢复原始信号。在研究和总结传统就匹配算法的基础上，出了一种新的自适应正交多匹配追踪算法（ｄｐｉｅｒｏｏａｍｕｔｍｔｈｎｕｓｉＡＯ提ａａｔｔｇｎｌｌａｃｉｇｐｒｕｔＭｖｏｈｉ．ＭＰ用于稀疏信号的重建。该算法在选择原子匹配迭代时分两个阶段，）引入自适应和多匹配的原则，快了原加子的匹配速度，高了匹配的准确性，提实现了原始信号的精确重建。最后与传统ＯＭＰ算法进行了仿真对比，实
ｍｒｅａｃｎｔｕ，ｅｉ００５，ｈｎ）ｅｔｓｒＩｓｔｔＢｉｎ１０８ＣｉａｉＲｅｗｌｍｅｇｎｏｒｓｉｅｓｎｉｈｏｙｉｅｅｔｙａｓｈａｐｎｅｕｅｐａｈｆｒｔｅｄｖｌｐｅｔｏｅｎｅｙｅｒｉｇｃｍｐｅｓｖｅｓｎｇｔｅｒｎｒｃｎｅｒｓｏｅｄｐａｎｗｔｏｈｅｅｏｍｎｆｓｇｌｐｏｅｓｎｇ，ｗｈｃｅｃｂｅｈｔｉａｅｏｔｕｃｈｅｏｉｉａｉｎｌｆｏａｓｌｍｏｎｔｏａｄｍａｉｎａｒｃｓｉｉｈｄｓｒｓｔａｔｃｎｒｃｎｓｒｔｔｒｇｎｌｓｇａｒｍｍａｌａｕｔｒｎｏｓｍｐｌｎｓｌｎｓｉｉｇａｏｇａｔｉｎａｓｓｒｅｏｏｒｓｉｅ，ｗｈｉｈｄｓｂｙｔｈｒｄｔｏｌＮｙｕｉｔｓｍｐｉｈｅｒｍ．Ｂａｅｎｔｔｄｙａｎｈｅｓｇｌｉｐａｓｒｃｍｐｅｓｂｌｃｉｏｅｓｗｉｈｔｅｔａｉｉｎａｑｓａｌｎｇｔｏｅｓｄｏｈｅｓｕｄｓｕｍｍａｉｅｏｈｅｔａｔｏａｔｈｎｇａｇｉｈｍ，ｔｓｐａｅｐｅｅｔｄｗｄｐｉｅｒｈｇｎａｃｉｇｐｒｕｔｌｏｔｒｚｆｔｒｄｉｎｌｍａｃｉｌｏｒｔｉｈｉｐｒｒｓｎｅａｎｅａａｔｖｏｔｏｏａｍｔｈｎｕｓｉｇｒｈｍｌａｉ

正交匹配追踪算法omp原理

正交匹配追踪算法omp原理
正交匹配追踪算法（Orthogonal Matching Pursuit，简称OMP）是一种用于稀疏重构的迭代算法，主要用于解决压缩感知问题。

其原理如下：
1. 稀疏表示假设：假设信号可以通过少量的原子（基底）的线性组合来表示，即稀疏表示。

2. 初始状态：设置初始残差为输入信号，初始解集为空集。

3. 原子选择：在目前残差中选择一个最适合代表残差的原子（基底）。

4. 矩阵变换：将原子调整为正交的形式，即正交化。

5. 正交投影：计算残差与正交基底的投影，得到投影系数。

6. 更新残差：使用投影系数更新残差。

7. 判断结束：如果残差的能量减少到一定程度，则认为重构已经足够准确，结束算法；否则，返回第3步进行下一个迭代。

8. 输出结果：返回最终的解集，其中每个元素对应一个原子。

OMP算法没有要求输入信号满足特定的分布条件，因此适用
于多种应用场景。

算法通过选择最适合的原子来逐步逼近信号，并且通过迭代追踪算法的方式，能够保证逐步收敛到最优解。

该算法的时间复杂度较低，且能在较短的时间内达到令人满意的重构质量。

基于压缩感知的图像重构算法

基于压缩感知的图像重构算法史久根;吴文婷;刘胜【摘要】There are some problems in the typical gradient projection algorithms in the application of Compressed Sensing(CS), such as the large amount of calculation, the low efficiency of convergence process and excessive dependence on the sparsity of the data matrix. In order to deal with these problems, an efficient recovery algorithm is proposed. This algorithm is based on CS which combines the Quasi-Newton method and the gradient projection method. So it can make full use of the estimating and correcting procedure and the global superlinear convergence of the Quasi-Newton method. By correcting the objective function with the Quasi-Newton method, a more accurate searching direction and fewer iteration can be got. It makes the algorithm perform efficiently with a high convergent reconstruction based on compressed sensing. Experimental results prove that this algorithm shows a good reconstruction and anti-noise performance. Compared with the traditional gradient projection recovery method, the proposed method drops the error rate to make a more stable and convergent reconstruction with fewer iteration.%在图像压缩感知中，梯度投影恢复算法存在收敛速度慢、迭代次数多、对数据稀疏度过分敏感的问题。

Matlab中的压缩感知技术介绍

Matlab中的压缩感知技术介绍近年来，随着信息技术的快速发展，数据量呈指数级增长。

然而，有效地存储和传输这些海量数据成为了一个巨大的挑战。

在大数据时代，如何通过最少的信息来还原出原始数据的准确信息成为了一个重要课题。

在这个背景下，压缩感知技术应运而生。

压缩感知是一种用于从少量观测数据中重建原始信号的技术。

它通过对信号进行线性采样，并利用信号的稀疏性以及随机矩阵的性质，实现了高效的数据压缩和信号恢复。

其中，Matlab作为一种常用的科学计算和数据分析工具，提供了丰富的压缩感知算法和工具包，便于研究人员和工程师进行相关的研究和应用。

在Matlab中，压缩感知技术可以分为两个步骤：信号采样和信号恢复。

首先，信号采样是指对原始信号进行采样，得到部分观测数据。

通常，信号采样可以使用传统的采样方式，如均匀采样或非均匀采样。

然而，压缩感知技术的优势在于它可以通过更少的观测数据来实现相同甚至更好的重建效果。

这是因为压缩感知利用了信号的稀疏性。

稀疏性指的是信号在某个特定域中的大部分系数为零，只有少数系数为非零。

在信号采样过程中，我们可以通过选择适当的观测矩阵（如高斯矩阵、哈达玛矩阵或随机矩阵等）来实现对信号的有效采样。

接下来是信号恢复的过程，它是压缩感知技术的核心。

在信号恢复过程中，我们需要通过观测数据和所选的观测矩阵，利用压缩感知的算法还原出原始信号。

最常用的压缩感知算法是基于贪婪迭代的方法，如正交匹配追踪（OMP）和迭代收缩阈值（IST）算法。

这些算法通过迭代求解最优系数，来实现对原始信号的恢复。

此外，最小二乘（L1）范数优化问题也被广泛应用于信号恢复过程中。

Matlab提供了丰富的工具包和函数，如`l1-magic`和`SparseLab`等，便于研究者选择和使用合适的算法进行信号恢复。

压缩感知技术在许多领域中得到了广泛的应用。

例如，在图像处理领域，压缩感知技术能够实现高效的图像压缩和图像恢复。

在语音信号处理领域，压缩感知技术可以用于语音信号的压缩和噪声抑制。

一种改进的压缩采样匹配追踪算法研究

一种改进的压缩采样匹配追踪算法研究作者：宋丽娟来源：《电脑知识与技术》2014年第02期摘要：该文简单对信号稀疏重建的模型和测量矩阵的设计进行了介绍，主要介绍了几种稀疏重建算法，详细给出压缩采样匹配追踪算法及其改进算法的数学框架和基本思想，从原子选择策略和冗余向量的更新方式对算法进行了比较分析，最后通过模拟实验验证了MP，OMP，CoSaMP和IHTCoSaMP算法的重构效果，同时以MSE为性能指标评价了各种算法的重构质量，实验结果表明改进的压缩抽样匹配追踪算法的运算速度较快，重构质量较高。

关键词：压缩感知；测量矩阵；稀疏重建；匹配追踪中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2014）02-0301-04压缩感知（Compressed sensing）是近年来信号处理领域出现的一种新的理论，它是由D.Donoho [1]、E.Candes [2]以及华裔科学家T.Tao[3]等人提出来的，压缩感知理论是在传统信号处理理论的基础上，获取信号的同时，就对数据进行压缩，传统的信号处理过程中采样数据量大，必须要先采样后压缩，这样做浪费了时间、传感元和存储空间[4，5]。

与传统方式比较，压缩感知对于可稀疏表示的信号，将数据的采集和数据的压缩同时进行，这样使得压缩感知体现了突出的优点以及非常大的应用前景。

压缩感知将采样和压缩同时进行，其中的测量值远小于传统采样的数据量，打破了奈奎斯特定理的瓶颈。

压缩感知主要包含信号的稀疏表示、测量矩阵和信号重建算法三个方面。

该文通过对稀疏重建模型的建立、测量矩阵的构造，比较分析了常用的几种信号重建算法，改进的压缩抽样匹配追踪算法运算速度快，重建质量高。

1 稀疏重建模型的建立2 测量矩阵的设计压缩感知的测量矩阵主要是具有独立同分布的高斯随机矩阵。

2006年Candes等提出的约束等距性理论[3]，指出从测量矩阵中获取的每M个列向量组成的矩阵必须是非奇异的。

分段正交匹配追踪(StOMP)算法改进研究

分段正交匹配追踪(StOMP)算法改进研究汪浩然;夏克文;牛文佳【摘要】信号重构是压缩感知的核心技术之一,而其重构精度和所耗时长直接影响其应用效果.现今分段正交匹配追踪算法(StOMP)因耗时短而得到广泛应用,但也存在着重构精度差、稳定性低的缺点.提出一种基于粒子群优化(PSO)算法且同时具有回溯特性的StOMP改进算法(ba-IWPSO-StOMP),即首先在StOMP算法的一次原子选择上,引入回溯策略,实现原子的二次筛选;在每次迭代计算中,使用具有惯性权重指数递减的PSO(IWPSO)算法对传感矩阵中部分原子进行优化,从而实现更高精度,更少迭代次数的信号重构.对一维信号和二维图像的重构结果表明,在稀疏条件相同的情况下,算法在收敛时间较短的情况下,其重构精度明显优于StOMP等同类算法.%Signal reconstruction is one of the core technologies of compressed sensing, and the reconstruction accuracy and time-consuming directly affects its application effect. Nowadays, Stagewise Orthogonal Matching Pursuit(StOMP) algorithm has been widely used for short running time, but its reconstruction accuracy is unsatisfactory. To make up for the defects of the StOMP algorithm, this paper presents a variant of StOMP, called backtracking-based adaptive and iner-tia weight index decreasing particle swarm optimization-based StOMP(ba-IWPSO-StOMP)algorithm. As an extension of the StOMP algorithm, in each iteration, the proposed ba-IWPSO-StOMP algorithm incorporates a backtracking tech-nique to select atoms by the second screening, then uses the IWPSO algorithm to optimize atoms in the measurement matrix. Through these modifications, the ba-IWPSO-StOMP algorithm achieves superior reconstruction accuracyand less times of iteration compared with other OMP-type algorithms. Moreover, unlike its predecessors, the ba-IWPSO-StOMP algorithm does not require to know the sparsity level in advance. The experiments demonstrate the performance of ba-IWPSO-StOMP algorithm is superior to several other OMP-type algorithms.【期刊名称】《计算机工程与应用》【年(卷),期】2017(053)016【总页数】7页(P55-61)【关键词】压缩感知;分段正交匹配追踪;粒子群优化【作者】汪浩然;夏克文;牛文佳【作者单位】河北工业大学电子与信息工程学院,天津 300401;河北工业大学电子与信息工程学院,天津 300401;河北工业大学电子与信息工程学院,天津 300401【正文语种】中文【中图分类】TP391压缩感知（CS）理论是由Donoho和Candes等在2005年提出的一种从信号稀疏分解和逼近理论发展而来的新的信号处理理论[1-3]。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

基于改进正交匹配追踪算法的压缩感知雷达成像方法
作者：刘记红，黎湘，徐少坤，庄钊文， Liu Ji-hong， Li Xiang， Xu Shao-kun， Zhuang Zhao-wen 作者单位：国防科技大学空间电子信息技术研究所长沙410073
刊名：
电子与信息学报
英文刊名：Journal of Electronics & Information Technology
年，卷(期)：2012,34(6)
1.黄培康;殷红成;许小剑雷达目标特性 2006
2.Donoho D L Compressed sensing[外文期刊] 2006(04)
3.Candes E J;Wakin M B An introduction to compressive sampling[外文期刊] 2008(02)
4.Herman M;Strohmer T High-resolution radar via compressive sensing[外文期刊] 2009(06)
5.Tello M;Lopez-Dekker P;Mallorqui J J A novel strategy for radar imaging based on compressive sensing 2010(12)
6.Ender J H G On compressive sensing applied to radar[外文期刊] 2010(05)
7.Potter L C;Ertin E;Parker J T Sparsity and compressed sensing in radar imaging[外文期刊] 2010(06)
8.Patel V M;Easley G R;Healy D M Compressed synthetic aperture radar 2010(02)
9.焦李成;杨淑嫒;刘芳压缩感知回顾与展望[期刊论文]-电子学报 2011(07)
10.Majumdar A;Krishnan N;Pilled S R B Extensions to orthogonal matching pursuit for compressed sensing 2011
11.Huang S S;Zhu J B Recovery of sparse signals using OMP and its variants:convergence analysis based on RIP 2011(03)
12.Jin J;Gu Y T;Mei S L An improved greedy algorithm for signal recovery from random measurements 2010
13.Fu N;Cao L R;Peng X Y A modified orthogonal matching algorithm using correlation coefficient for compressed sensing 2011
14.Tropp J A;Wright S J Computational methods for sparse solution of linear inverse problems[外文期刊] 2010(06)
15.Liu Y;Wu M Y;Wu S J Fast OMP algorithm for 2D angle estimation in MIMO radar 2010(06)
16.Rivenson Y;Stern A Compressed imaging with a separable sensing operator 2009(06)
17.杜小勇;胡卫东;郁文贤基于稀疏成份分析的逆合成孔径雷达成像技术[期刊论文]-电子学报 2006(03)
本文链接：/Periodical_dzkxxk201206012.aspx。