各材料的恢复系数
常见保温材料传热系数及修正系数

常见保温材料传热系数
及修正系数
Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998
导热系数的修正系数取值问题
建筑保温材料的热工设计计算应当采用计算值,因此在节能设计时,我们需要考虑保温材料在不同情况下的修正系数,保温材料的计算修正系数,可参照现行的国家《民用建筑热工设计规范》(GB50176)或者上海市工程建设规范《住宅建筑围护结构节能应用技术规程》(DG/TJ08)的规定。
在此我们把常用保温材料的修正系数取值归纳如下:
注:1、坡屋面(I型)为瓦材钉挂无细石混凝土整浇层构造类型。
2、其他地区(除上海以外)或围护结构采用特殊施工工艺情况的修正系数取值请参见地方实施细则。
碰撞可能性的判断技巧

碰撞可能性的判断技巧湖北省恩施高中陈恩谱一、问题缘起大部分高中物理资料中,关于二体对心碰撞可能性判断,往往提出的是三个判据:其一,动量守恒判据,其二,能量守恒判据——碰后系统总动能小于等于碰前系统总动能,其三,现实可能性判据——碰前追得上,碰后不对穿。
不过,这种判断方法,一方面要用代入法逐个判断,另一方面是计算量大,而学生往往顾此失彼,甚至记不清有三个判据需要全面考虑。
笔者通过对大量这类习题的研究,得出了一个极其简单的思路,在此与大家分享,并期与同行交流。
二、基本结论所有碰撞的可能,都介于弹性碰撞和完全非弹性碰撞之间。
即:先计算弹性碰撞和完全非弹性碰撞,得出两种情况下物体碰后的速度值,则物体的速度只可能介于这两个值之间。
而:完全非弹性碰撞(碰后共速)好算,弹性碰撞(动能不变)也好算——用动量守恒和能量守恒得出的结论式2211v v v v '+='+(即牛顿速度公式:2112v v v v -='-'),联立动量守恒即可。
三、结论推导1、弹簧模型如右图所示,光滑水平面上,物块B 向右以速度v 0运动,碰上连有弹簧的物块A 。
(1)弹簧压缩阶段,v B 一直大于v A ,对应碰撞过程的压缩阶段,这种情况下,A 、B 不可能分开。
(2)当v A =v B 时,弹簧压缩最短,对应完全非弹性碰撞。
(3)弹簧恢复阶段,v A 大于v B ,这之间任意时刻锁定弹簧,弹性势能无法全部释放出来转化为两物块动能,这对应一般碰撞。
(4)弹簧恢复原长,这对应弹性碰撞。
从上述分析可以看出,A 、B 动量变化(速度变化)最小的是完全非弹性碰撞,A 、B 动量变化(速度变化)最大的是非弹性碰撞,所以先计算弹性碰撞和完全非弹性碰撞,得出两种情况下物体碰后的速度值,则物体的速度只可能介于这两个值之间。
注意,此处我假设A 静止,若A 有初速度,可以以“与A 初速度相等的坐标系”为参考系,从而仍用这个模型分析,将得出相同的结论。
abaqus cdp 混凝土刚度恢复系数 概述及解释说明

abaqus cdp 混凝土刚度恢复系数概述及解释说明1. 引言1.1 概述本篇文章旨在介绍abaqus cdp(Concrete Damaged Plasticity)模型中的混凝土刚度恢复系数,对其进行概述和详细解释说明。
混凝土刚度恢复系数是衡量材料强度退化程度的重要指标,它在结构工程领域广泛应用于预测和评估混凝土结构的性能。
1.2 文章结构本文分为五个部分进行讲述。
首先,在引言部分我们将对整篇文章进行概括性介绍,明确文章的目的和结构。
接下来,正文部分将给出详细的技术信息和理论知识。
第三部分将着重介绍abaqus cdp模型以及其相关知识点,包括cdp模型的定义、刚度恢复系数的定义以及该系数的重要性。
第四部分则会对混凝土刚度恢复系数进行解释说明,主要包括混凝土刚度衰减机理、计算方法及影响因素,以及实际工程应用和实例分析。
在结尾处,我们将给出全文总结和一些思考。
1.3 目的本文的目的有两方面:一方面是介绍abaqus cdp模型中的混凝土刚度恢复系数,明确其在结构工程中的重要性和应用范围;另一方面是对混凝土刚度恢复系数进行详细解释和说明,帮助读者更好地理解该概念及其相关参数。
这里是“1. 引言”部分的内容。
2. 正文在本篇长文中,我们将详细探讨abaqus cdp模型中的混凝土刚度恢复系数(coefficient of degradation and reinforcement proportion,CDP)的概述及其解释说明。
混凝土刚度恢复系数是指在结构分析过程中,考虑混凝土的非线性行为时,在加载和卸载循环之间用于描述混凝土应力-应变关系改变的参数。
它是衡量混凝土素材在荷载作用下承受损伤后能够恢复正常功能的重要指标。
本文将从以下几个方面进行论述。
首先,在第3部分中,我们将简要介绍abaqus cdp模型,并对其背后的理论基础进行阐述。
cdp模型是一种广泛使用的计算机模拟方法,可用于模拟工程结构在各种力学状态下的响应。
力学碰撞中恢复系数取值范围的探讨

力学碰撞中恢复系数取值范围的探讨引言:力学碰撞是物体间相互作用造成的一种现象,而恢复系数则是描述碰撞后物体反弹程度的指标。
恢复系数越大,碰撞后物体反弹的程度越高;恢复系数越小,碰撞后物体反弹的程度越低。
本文将探讨力学碰撞中恢复系数的取值范围对决定碰撞性质的影响,并从实验角度解释可能的原因。
一、恢复系数的定义和计算方法恢复系数(e)是一个无量纲数,用于描述碰撞过程中物体反弹的程度。
根据守恒定律和动量守恒定律,我们可以得到碰撞后物体的速度与碰撞前物体的速度之间的关系:e = (v2' - v1')/ (v1 - v2)其中,v1和v2分别是碰撞前两物体的速度,v1'和v2'分别是碰撞后两物体的速度。
二、理想弹性碰撞理想弹性碰撞是指碰撞过程中没有能量损失,物体之间相互碰撞时没有发生形变。
在理想弹性碰撞中,恢复系数的取值范围应为0到1之间,不包括0和1。
当恢复系数等于0时,碰撞为非弹性碰撞;当恢复系数等于1时,碰撞为完全弹性碰撞。
在完全弹性碰撞中,碰撞后物体能够完全恢复到碰撞前的状态,即物体的动能完全转化为弹性势能。
由于能量守恒定律和动量守恒定律的存在,完全弹性碰撞是理论上的一种极限情况,在实际中很难实现。
三、非弹性碰撞非弹性碰撞是指碰撞过程中发生形变或能量损失的碰撞。
在非弹性碰撞中,恢复系数的取值范围为负数到1之间。
当恢复系数等于0时,碰撞为完全非弹性碰撞,两物体之间发生完全粘连,动能完全转化为内能。
当恢复系数为负数时,碰撞为反弹碰撞,即碰撞过程中物体之间产生的作用力与运动方向相反,这种碰撞常见于车辆碰撞中。
四、实验研究为了验证恢复系数的取值范围对碰撞性质的影响,我们设计了一组实验。
实验步骤:1. 准备两个金属球,分别编号为A和B,质量相等。
2. 在平滑的水平面上,将球A从一定高度自由落下,观察碰撞后球的运动情况。
3. 重复实验多次,记录碰撞前后球的速度和恢复系数。
实验结果:根据实验结果,我们可以得出以下结论:1. 当恢复系数接近于1时,球A与球B之间发生的碰撞趋近于完全弹性碰撞,球A具有较大的反弹速度。
各种材料修正系数
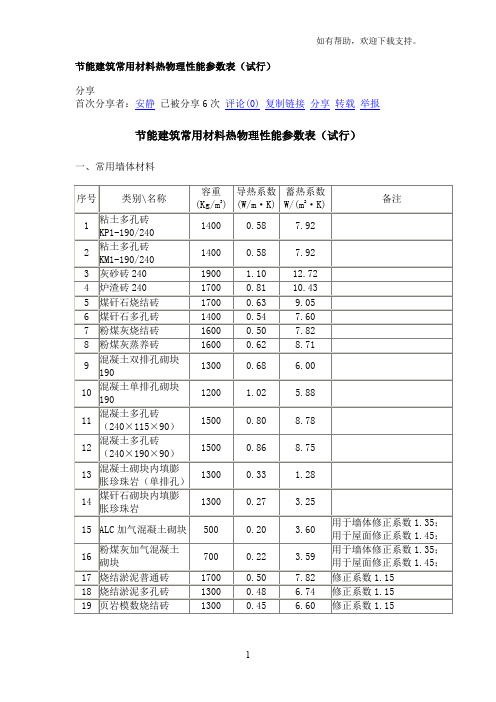
节能建筑常用材料热物理性能参数表(试行)
分享
首次分享者:安静已被分享6次评论(0)复制链接分享转载举报节能建筑常用材料热物理性能参数表(试行)一、常用墙体材料
二、常用保温材料
注:保温装饰板根据所选保温材料不同,选用相应的热工性能参数及修正系数。
三、混凝土
四、粉刷砂浆
五、热绝缘材料
六、木材、建筑板材
七、松散材料
八、其他材料
九、窗的传热系数(略)
注:1.本表中的窗户包括一般窗户、天窗和门上部带玻璃部分。
2.阳台门下部门肚板部位的传热系数,当下部不作保温处理时,应按表中值采用;当作保温处理时,应按计算确定。
3.本表中未包括的新型窗户,其传热系数应按测定值采用。
4.贴Low-E膜的玻璃等效Low-E玻璃。
5.双层窗传热阻=组成该双层窗的两樘单层窗的传热阻之和+0.07。
国内外航空发动机各部件的效率和总压恢复系数

国内外航空发动机各部件的效率和总压恢复系数如今,随着全球经济的发展和人们对旅行需求的增加,航空行业正变得日益繁忙和重要。
而作为现代航空界的核心装备之一,航空发动机的高效与否,直接关系到飞机的可靠性和效能。
尤其是关于国内外航空发动机各部件的效率和总压恢复系数这一主题,它牵涉到航空发动机性能的核心要素,对于我们深入理解航空发动机的工作原理以及未来的改进方向至关重要。
我们先来了解一下航空发动机的构成以及各部件的功能。
航空发动机通常由压气机、燃烧室和涡轮机组成,其中压气机负责将外界空气压缩,提供给燃烧室进行燃烧,再通过涡轮机将燃烧产生的热能转化为动力。
而国内外航空发动机各部件的效率和总压恢复系数是对这个过程进行评价和衡量的重要指标。
效率是指在完成一定工作量的所消耗的能量与所产生的能量之间的比值。
对于航空发动机来说,主要有压气机效率、燃烧效率和涡轮机效率等。
压气机效率主要反映了压气机在将外界空气压缩提高的过程中能量损失的大小,而燃烧效率则衡量了燃烧室将燃料中的化学能转化为热能的能力。
涡轮机效率则是度量了将燃烧产生的热能转化为动力的效果。
提高航空发动机各部件的效率,可以减少功率损失,提高燃烧效率,提高整个发动机的性能和可靠性。
而总压恢复系数是指压气机工作过程中,从进口处到出口处的总压降的恢复程度。
对于航空发动机来说,压缩过程中总压降会导致能量损失,而总压恢复系数可以衡量压气机在压缩过程中能量损失的大小。
提高总压恢复系数,可以减小压气机的能量损失,提高整个发动机的效率和性能。
目前,国内外航空发动机各部件的效率和总压恢复系数的研究正在不断进行。
从简单的工艺改进到新材料的应用,各种方法和技术都被提出和应用于航空发动机的设计和制造过程中。
通过优化流道设计和增加高效燃烧室的应用,可以提高压气机和燃烧室的效率,减小能量损失。
而在涡轮机方面,通过提高叶片材料的温度和强度,可以提高涡轮机的效率。
一些新的燃烧技术和冷却技术的应用也可以有效提高航空发动机的效率和总压恢复系数。
正极反弹系数 -回复

正极反弹系数-回复正极反弹系数(Positive Rebound Coefficient)是指材料受到外力压缩后的恢复能力。
在材料力学中,弹性恢复是指材料在受到应力或外力后能够恢复到原始状态的能力。
正极反弹系数是描述这种能力的指标之一。
本文将从简介、计算方法、影响因素、应用场景等方面逐步回答正极反弹系数这一主题。
第一部分:简介正极反弹系数通常用于描述材料在受到外力后的恢复能力。
根据背景和实际需求,正极反弹系数的计算方法不尽相同。
一般情况下,正极反弹系数越高,说明材料越具有良好的弹性恢复能力,反之则表示其恢复能力较差。
第二部分:计算方法计算正极反弹系数的方法有多种,一种常见的方法是通过比较材料受力前后的形变量来计算。
首先,需要将受力前后的形变量测量出来,然后通过计算公式得出正极反弹系数。
正极反弹系数的计算公式如下:正极反弹系数= (形变量2 - 形变量1) / 形变量1其中,形变量1表示材料受力前的形变量,形变量2表示材料受力后的形变量。
第三部分:影响因素影响正极反弹系数的因素有很多,主要包括材料的硬度、弹性模量、温度等。
硬度是材料抵抗形变的能力,硬度越高,正极反弹系数也会相应增加。
弹性模量是材料抵抗应力的能力,弹性模量越高,正极反弹系数也会相应增加。
温度是影响正极反弹系数的重要因素,温度升高会使材料的弹性减弱,导致正极反弹系数下降。
第四部分:应用场景正极反弹系数在很多领域中有着广泛的应用。
在材料工程中,正极反弹系数可以用来评估材料的弹性恢复能力,帮助工程师选择合适的材料。
在体育器械领域,正极反弹系数可应用于篮球、羽毛球等球类的制作,以提高球的弹性和反弹性能。
在建筑工程中,正极反弹系数可以用于评估建筑物地面材料的耐久性和抗震性能。
在医学领域,正极反弹系数可用于评估人体组织的弹性恢复能力,对于一些疾病的诊断和治疗具有指导作用。
总结:正极反弹系数是用于描述材料弹性恢复能力的指标之一,计算方法主要通过比较材料受力前后的形变量,影响因素包括材料的硬度、弹性模量和温度等。
恢复因素理论力学

v
u
x
e
=
tg
,Leabharlann v1 y(1),(2)
tg
e = 1,
= ,
e = 0,
tg = ,
= , 2
I
e = u − u (e = − v ) 2n 1n
物体接触点碰撞后与碰撞前的速度的
n 法向分量大小之比为一常量
v1n − v2n
vn
7
撞后测到小球回跳的反射角。求:恢复因数e。
解: 小球发生斜碰撞 :入射角,:反射角
x方向动量守恒: v sin = u sin , (1)
y
y方向:(碰撞法线方向)
v2y = u2y = o u1y = u cos , v1y = −v cos
e = − u1y , ev cos = u cos , (2)
声、残余变形),因此小球在
A
碰撞结束后的速度一般情况下
小于碰撞开始时的速度。
h2 h1
牛顿在实验中发现,对于材 料确定的物体,碰撞结束与开始
vA v'A
的速度大小的比值几乎不变,即
e = vA
B
vA
常数e恒为正值(如考虑速度方向,表达式应取绝对值,或加
负号),称为恢复系数(恢复因素)(仅与材料性质有关)。
§3 恢复系数(恢复因素)
一小球铅垂跌落在固定的平面上(这种碰撞称为正碰撞)。 碰撞开始时,其质心速度为v,由于受到固定面的碰撞冲 量作用,质心速度逐渐减小,物体变形逐渐增大,直至速度等 于零为止。此后弹性变形逐渐恢复,物体质心获得反向的速度, 直至两个物体脱离。
1
由于碰撞过程中物体一般
会损失动能(发光、发热、发
板碰撞,撞后测到小球回跳至某高度h2.求:恢复因数e。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各材料的恢复系数计算值
Metals and Ceramics:Predicted COR, e Silicon硅 1.79
Alumina 氧化铝0.45 to 1.63 silicon nitride 氮化硅0.38 to 1.63 silicon carbide 碳化硅0.47 to 1.31 highest amorphous metal 最高的非晶态金属1.27
tungsten carbide 碳化钨0.73 to 1.13 stainless steel 不锈钢0.63 to 0.93 magnesium alloys 镁合金0.5 to 0.89 titanium alloy grade 5 5级钛合金0.84
aluminum alloy 7075-T6 铝合金 7075-T60.75
glass (soda-lime) 玻璃碱石灰0.69
glass (borosilicate) 玻璃硼硅酸盐0.66
nickel alloys 镍合金0.15 to 0.70 zinc alloys 锌合金0.21 to 0.62 cast iron 铸铁0.3 to 0.6 copper alloys 铜合金0.15 to 0.55 titanium grade 2 2级钛0.46
Tungsten 钨0.37
aluminum alloys 3003 6061, 7075-0 铝合金0.35
Zinc 锌0.21
Nickel 镍0.15
Copper 铜0.15
Aluminum 铝0.1
Lead 铅0.08
塑料和橡胶不是理想材料,会高于实际值。
以下仅供参考。
•高分子材料:
•聚丁二烯(高尔夫球壳) 11.8
•丁基橡胶6.24
•EVA 4.85
•弹性聚硅酮类2.80
•聚碳酸酯1.46
•尼龙1.28
•聚乙烯1.24
•聚四氟乙烯1.21
•聚丙烯1.14
•ABS 1.12
•丙烯酸1.06
•PET 0.95
•聚苯乙烯0.87
•PVC 0.86
注意:当速度小于10-6m/s时,恢复系数为1。
大于1的系数说明公式是不正确的,因为用的屈服强度代替动态屈服强度。
引自:
https:///wiki/Coefficient_of_restitution#Range_of_values_for_e_.E2.80.93_ treated_as_a_constant。
