机械制造技术基础-例题-误差统计分析
机械制造技术基础习题分析

名词解释1.刀具耐用度 2.内联系传动链3。
夹紧4。
精基准5.机械加工工艺过程6.变值系统误差7.强迫振动 8。
简单成形运动9.(液压系统的)压力 10.设计基准11.六点定位原理 12.封闭环13.复合成形运动 14.原理误差15。
磨削烧伤 16.完全定位填充题1.金属切削过程中切削力的来源主要有两个,即和.2.夹具的基本组成有元件、装置、元件、和其它元件。
3.根据产品零件的大小和生产纲领,机械制造生产一般可以分为、和三种不同的生产类型。
4.机床精度中对加工精度影响较大的包括机床主轴误差和机床导轨误差。
其中机床主轴回转误差包括、和三种基本形式。
5.下图为车削工件端面的示意图,图上标注的主运动是,主偏角是,刀具前角是 ,加工(过渡)表面是 .6. 数控机床是由以下三个基本部分组成:____________、____________和机床本体。
7. 大规格的换向阀一般采用电液换向阀结构,它是由大规格带阻尼器的液动换向阀和小规格的____________换向阀两部分组合而成。
8. 工艺尺寸链中最终由其它尺寸所间接保证的环,称为____________环。
9. 正态分布曲线中,分布曲线与横坐标所围成的面积包括了全部零件数,故其面积等于____________,其中±3σ范围内的面积为____________。
5。
根据力的三要素,工件夹紧力的确定就是确定夹紧力的大小、____________和作用点。
10. 工件表面粗糙度越小,在交变载荷的作用下,工件的疲劳强度就____________。
11. 在夹紧装置中,基本的夹紧机构类型有:____________、螺旋夹紧机构和偏心夹紧机构.12. 对于在高转速、重载荷条件下工作的轴,其毛坯的制造方法是____________.13。
切削用量三要素是指 ________ 、 ________ 和 __________.14。
基准平面确定后,前刀面由_______和______两个角确定;后刀面由-—和——两个角确定.15. 切削层公称横截面参数有_________、___________。
机械制造基础加工误差的例题
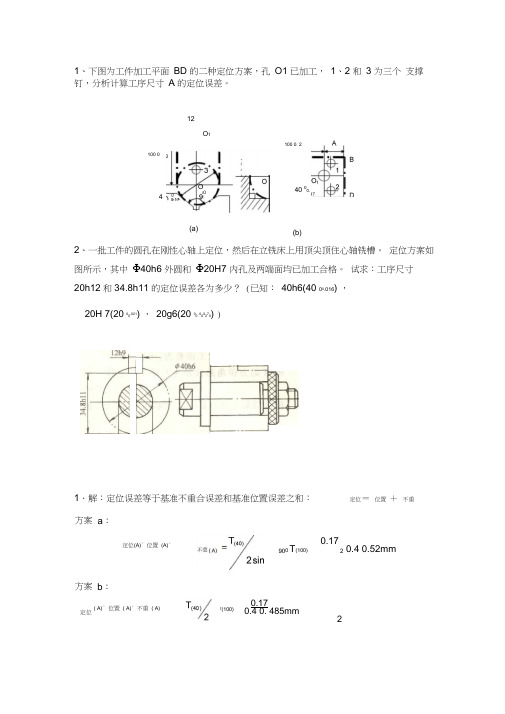
1、下图为工件加工平面 BD 的二种定位方案,孔 O1 已加工, 1、2 和 3 为三个 支撑钉,分析计算工序尺寸 A 的定位误差。
12
2、一批工件的圆孔在刚性心轴上定位,然后在立铣床上用顶尖顶住心轴铣槽。
定位方案如图所示,其中 Φ40h6 外圆和 Φ20H7 内孔及两端面均已加工合格。
试求:工序尺寸 20h12 和34.8h11 的定位误差各为多少? (已知: 40h6(40 00
.016) , 20H 7(20 00.021) , 20g6(20 00..000270) )
1.解:定位误差等于基准不重合误差和基准位置误差之和:
定位= 位置 + 不重
0.17 0.4 0. 485mm
2
(b)
方案 a :
0.17 900 T (100) 2 0.4 0.52mm
方案 b :
定位 0.17 (a) 4 100 0
O 1
O
00 100 0. 2
40 00.
定位(A)= 位置 (A)+
T (100) ( A)= 位置 ( A)+ 不重 ( A)
2.
(1)对于尺寸20h12 设计基准与定位基准均为工件左端面,基准重合;而且采用单一平面定位,
基准位移误差为0,则定位误差为:
d j b 0 0 0
(2)对于尺寸34.8h11
设计基准为外圆下母线,而定位基准为工件轴线,存在基准不重合误差,其值为:
0.016
2 0.008
由于心轴与定位孔是间隙配合,有基准位移误差,其值为最大配合间隙:
j D d min 0.021 0.013 0.007 0.041
总定位误差为:
d j b 0.041 0.008 0.049。
机械制造技术基础---定位误差的分析和计算

定位误差等于工件被加工表面的设计基准, 在加工尺寸方向上的的最 大变动量.
定位误差的分析与计算
(1)
例一:圆柱体零件的直径为d,均用下母线定位,铣平面(如图).在设 计图纸上,其平面的高度有三种不同的尺寸注法.试分别计算其定位误差.
B O A
定位误差的分析与计算
(1-1)
图(a)当平面高度为H 1时,设计基准为上母线B,定位基准为下母线 A,(两基准不重合). 定位误差为: εH1=B1B2= Δd
B O E A F
定位误差的分析与计算 (2)
B O E A F
定位误差的分析与计算 (2)
基准不重合
定位误差的分析与计算 (2)
基准变动 刀位线
定位误差的分析与计算 (2-1)
基准变动 刀位线 基准不重合
定位误差
定位误差的分析与计算 (2-2)
定位误差 刀位线
基准变动
定位误差的分析与计算 (2-3)
B O A
定位误差的分析与计算
(1-2)
图(b)当平面高度为H2时,设计基准为下母线A, 定位基准也为下母线 A(两基准重合). 定位误差为: εH2=0
B O A
定位误差的分析与计算
(1-3)
图(c)当平面高度为H3时,设计基准在中心线O,定位基准为下母线 A(两基准不重合). 定位误差为: = Δd/2
B O A
定位误差的分析与计算 (2)
例一:圆柱体零件的直径为d,均用下母线定位,铣平面(如图).在设 计图纸上,其平面的高度有三种不同的尺寸注法.试分别计算其定位误差.
B O E A F
定位误差的分析与计算 (2)
图(a)当平面高度为H 1时,设计基准为上母线B,定位基准为下母 线A,(两基准不重合). 这时定位误差为:εH1=B1B2=AB2-AB1=(AO2+O2B2)-(AO1+O1B1)
机械制造工艺定位误差经典例题

二、 定位误差的计算 定位误差产生的原因:1、 一批工件,各工件相应表面尺寸和位置,在公差范围内的差异2、定位元件和各元件之间的尺寸和位置公差定位误差允许的大小:小于等于工件有关尺寸或位置公差的1/3 定位误差的组成:基准位移误差:(工件定位基准面的误差,定位元件制造误差,两者的配合间隙) 基准不重合误差:定位基准与工序基准不重合定位误差的计算方法:1、两种极端位置通过几何关系求2、按定位误差的组成(极限位置):c w dw ∆±∆=∆ (同向为正,反向为负)3、用微分方法求[被加工面工序尺寸的标注方向、工序基准、定位基准面、 定位基准、工件在公差范围内变动时定位基准移动方向、 定位基准面变化(工序基准变化方向、定位基准变化方向)、 定位元件的变化]1A )用平面定位(1) 加工面 c w dw ∆+∆=∆2) 加工面=∆dw4、外圆定位:V型块(定位基准——外圆中心线)工件外圆 最小2d T d-→ 最大2d T d+工序尺寸:0H0sin 2222sin222+=+--+=∆ααd T d d T T dwd d工序尺寸:1H2sin 22dd T T dw -=∆α(工件变大→定位基准上移,工序基准下移)工序尺寸:2H2sin 22dd T T dw +=∆α(工件变大→定位基准上移,工序基准上移)校的学生并没有专心听讲、认真思考,而是写其他科目的作业,与周围同学聊天,发短信聊天,等等。
这些现象说明了同学们的思想道德素质建设还需进一步加强。
这件事对我触动很大,让我深切地感到,加强自我修养,应该从我做起,“不以恶小而为之,不以善小而不为”。
作为一名入党积极分子,我感到一定要时刻以一(转载自中国教育文摘,请保留此标记。
)名党员的标准来衡量自己,以一名党员的条件严格要求自己,在周围同学当中时时处处体现出先锋模范作用,只有这样才能有资格加入这个光荣而先进的组织。
我意识到,有时距离成功只有一步之遥,但如果采用消极的态度,可能成功会将自己拒之门外;倘若是积极态度去对待,可能成功就会属于自己。
误差统计分析题库

1.在机床上磨一批mm 0035.018-Φ的光轴,工件尺寸呈正态分布,现测得平均尺寸-x =17.975mm ,均方根差σ=0.01mm ,试:(1)画出工件尺寸误差的分布曲线,并标出公差带; (2)计算该工序的工艺能力系数; (3)估计该工序的废品率;(4)分析产生废品的原因,并提出解决办法。
(12分)解(1)分布曲线及公差带如图:(2)工艺能力系数: C P =T/6σ,C P =0.035/(6×0.01)=0.5833(3)按题意x =17.975mm ,σ=0.01mm ,实际加工尺寸:加工尺寸最大值Amax =x +3σ=17.975+0.03=18.005mm ,最小值Amin =x -3σ=17.975-0.03=17.945mm ,即加工尺寸介于17.945~18.005mm 之间,而T =0.035mm ,肯定有废品。
所以分布在17.965mm 和18mm 之间的工件为合格产品,其余为废品。
因为=σx-x z =01.0975.1718-=2.5,所以F (z )=F (2.5)=0.4938,即平均值右侧废品率为0.5-F (2.5)=0.62%,即18mm 与18.005mm 间为废品;又因为=σx-x z =01.0965.17975.17-=1,所以F (z )=F (1)=0.3413,即平均值左侧废品率为0.5-F (1)=15.87%,即17.945mm 与17.965mm 间为废品,则总废品率为0.62%+15.87%=16.49%。
18mm 与18.005mm 间的废品为可修复废品。
17.945mm 与17.965mm 间的废品为不可修复废品,因其尺寸已小于要求。
(3)产生废品的主要原因是加工精度不够,尺寸分布较散,另外对刀不准,存在系统误差。
2.磨一批工件的外圆,工件尺寸呈正态分布,尺寸公差T =0.02mm ,均方根偏差σ=0.005mm ,公差带对称分布于尺寸分布中心,试: (1)画出销轴外径尺寸误差的分布曲线,并标出公差带; (2)计算该工序的工艺能力系数; (3)估计该工序的废品率。
机械制造定位误差统计

试题名称:机械制造工艺学――误差统计分析一、(15分)有一批轴,它的尺寸为Φ180-00240.mm ,属正态分布,且分布范围与公差带大小相等,设分布中心与公差带中心不重合,相差5微米,求其废品率有多少?二、(10分) 车削一批轴的外圆,其尺寸要求为Φ20±0.06。
若此工序尺寸呈正态分布,公差带中心大于分布中心,其偏值δ=0.03mm ,均方根差σ=0.02mm ,求:(1)这批工件的废品率是多少? (2)指出该工件常值系统误差和随机误差的大小;(3)可采取什么改进措施以消除废品?解:(1)5.102.003.002.097.1994.19==-=-δxx查4332.01=F则0668.04332.05.05.011=-=-='F F废品率为0668.01='F(2)03.02097.19=-=-=∆δx x C12.002.066=⨯==∆δS(3)采用将刀具朝着尺寸变化的方向调整0.015(即直径上增加0.03),使X 与公差带中心重合以消除废品。
三、(10分)某箱体孔,图纸尺寸为Φ50++00090034..,根据过去经验,镗后尺寸呈正态分布,σ=0.003,试分析计算:(1)该工序工艺能力如何?(2)为保证加工要求,应将X 调整到什么尺寸范围? 解:(1)工序精度018.0003.066=⨯=σ 加工要求精度025.0=δ工艺能力系数389.1018.0025.06≈==σδCp 33.1389.167.1>=≥Cp 为一级;说明工艺能力足够,可以允许一定波动。
(2)为保证加工要求018.50009.0009.50min =+=X 025.50009.0034.50max =-=X 又可在50.018~50.025范围内调整。
四、磨一批轴的外圆,若外径公差δ=18μm,此工序的均方根差δ=4μm,且分布中心解:25.2004.0009.0==-σxx查表得:F= 0.4877则F ′=2×(0.5-0.4877)=0.0246若只允许可修废品,则将砂轮朝尺寸变大的方向移动1.5μm 。
机械 加工误差的统计分析

一、概述
在实际生产中,影响加工精度的因素很 多,工件的加工误差是多因素综合作用的结 果,且其中不少因素的作用往往带有随机性。 对于一个受多个随机因素综合作用的工艺系 统,只有用概率统计的方法分析加工误差, 才能得到符合实际的结果。
加工误差的统计分析方法,不仅可以客
观评定工艺过程的加工精度,评定工序能力
1 y e 2
(<x<+, >布曲线的纵坐标,表示工件的分布密度; x——分布曲线的横坐标,表示工件的尺寸或误差; 1 n xi ; x ——算术平均值, x n i 1 σ——均方根偏差(标准差)
1 n 2 ( x x ) ; i n i 1
l)无变值性系统误差(或有但不显著)。
2)各随机误差之间是相互独立的。
3)在随机误差中没有一个是起主导作用
的误差因素。
如图4-31b) 在影响机械加工的诸多误差因素中,如 果刀具尺寸磨损的影响显著,变值性系统误 差占主导地位时,工件的尺寸误差将呈现平 顶分布。平顶分布曲线可以看成是随着时间 而平移的众多正态分布曲线组合的结果。 3.双峰分布 如图4-31c) 若将两台机床所加工的同一种工件混在 一起,由于两台机床的调整尺寸不尽相同, 两台机床的精度状态也有差异,工件的尺寸 误差呈双峰分布。
废品率 0.5-0.49931=0.069% 0.5-0.2881=21.19% 可修复
二. 加工误差的统计分析-工艺过程的分布图分析方法 (一)工艺过程的稳定性
指均值和标准差稳定不变的性能,取决于变值系统误差.
(二)工艺过程分布图分析方法 1、画工件尺寸实际分布图
制作分布图了解质量指标分布、加工能力、是否有废品 1)样本容量的确定
{
4.2 机械加工误差的统计分析

理论上的正态分布曲线是向两边无限延伸的,而在实际生 产中产品的特征值(如尺寸值)却是有限的。
用有限的样本平均值和样本标准偏差作为理 论均值μ和标准偏差σ的估计值。由数理统计 原理得有限测定值的计算公式如下:
1 n
X
n
xi
i 1
1 n
Hale Waihona Puke n i 1(xiX )2
μ
直方图
1)采集数据 样本容量通常取 n = 50~200
➢ 1.画出尺寸分布如图
最大值、最小值、均值、T、6σ
➢ 在磨床上加工销轴,要求外径 d 1200..001463mm ,抽样后 测得 X 11.974mm, 0.005mm ,其尺寸分布符合正态 分布,试分析该工序的加工质量。
➢ 2.求工艺能力系数Cp
Cp
T
6
0.027 0.9 1 6 0.005
50 0.08
4.分布图分析法特点
1)采用大样本,较接近实际地反映工艺过程总体; 2)能将常值系统误差从误差中区分开; 3)在全部样本加工后绘出曲线,不能反映先后顺
序,不能将变值系统误差从误差中区分开; 4)不能及时提供工艺过程精度的信息,事后分析; 5)计算复杂,只适合工艺过程稳定的场合。
分布图分析法的缺点
平均值μ=0,标准差σ=1的正态分 布称为标准正态分布,记为:
x ~ N ( 0, 1 )
0
F(z)
-σ +σ
μz
x(z)
(z=0)
图4-45 正态分布曲线
F(x) 1
e dx x
1 2
x
2
2
y
令:z x
称 z 为标准化变量
