平面四杆机构的类型和应用
平面四杆机构的应用实例

平面四杆机构的应用实例1.引言平面四杆机构是一种常见的机械机构,由四个连杆构成,可以实现复杂的运动转换。
本文将介绍平面四杆机构的基本原理和应用实例。
2.平面四杆机构的原理平面四杆机构由长杆、短杆和两个滑块组成。
其中两个杆通过一个转动副连接,将运动转换为固定副或滑动副。
通过调整杆的长度和滑块位置,可以实现不同的运动传输和控制。
3.平面四杆机构的应用实例3.1提升机构平面四杆机构可以应用于提升机构中,将旋转运动转换为直线提升运动。
例如,用平面四杆机构设计的折叠桌,通过旋转转动将桌面从水平位置折叠到垂直位置,实现收纳和节省空间的效果。
3.2机械手臂平面四杆机构在机械手臂中有广泛的应用。
机械手臂通过调节杆的长度和滑块位置,可以实现多自由度的运动。
例如,用平面四杆机构设计的包装机器人,可以根据不同包装需求,实现抓取、装箱和封口等多种动作。
3.3门闩锁平面四杆机构还可以应用于门闩锁设计中。
通过设置合适的滑块位置和杆的长度,可以确保门闩的顺畅开启和牢固关闭。
例如,用平面四杆机构设计的汽车车门锁,可以实现方便快捷的上锁和解锁操作。
3.4纸币验钞机平面四杆机构也广泛应用于纸币验钞机。
通过合理设计杆的长度和滑块位置,可以实现纸币的输送、旋转和翻转等运动,以进行有效的钞票鉴别。
例如,用平面四杆机构设计的自动柜员机,可以快速准确地辨别真伪纸币并进行存储和取款等操作。
4.结论平面四杆机构作为一种常见的机械机构,具有运动转换和控制的优势,广泛应用于不同领域。
通过合理设计和调整杆的长度和滑块位置,可以实现多样化的运动需求。
无论是折叠桌、机械手臂、门闩锁还是纸币验钞机,平面四杆机构都可以发挥重要的作用,并为人们带来更便捷、高效的生活和工作体验。
平面四杆机构的类型特点及应用概念

平面四杆机构的类型特点及应用概念平行四杆机构的特点是固定杆和活动杆平行且相等长度,其中两个固定连接点和两个活动连接点分别位于固定杆的两端和活动杆的两端。
它的运动可以实现平行移动,适用于汽车悬挂系统、工艺机械等领域。
正交四杆机构的特点是固定杆和活动杆相交且相等长度,其中两个固定连接点和两个活动连接点分别位于固定杆的两端和活动杆的两端。
它的运动可以实现直线运动,适用于推动机械、绞车等领域。
菱形四杆机构的特点是固定杆和活动杆两两相交且相等长度,其中两个固定连接点和两个活动连接点分别位于固定杆的两端和活动杆的两端。
它的运动可以实现平行移动和旋转运动,适用于啮合机构、制造机械等领域。
推动机构的特点是固定杆和活动杆两两平行且相等长度,其中两个固定连接点和两个活动连接点分别位于固定杆的两端和活动杆的两端。
它的运动可以实现直线运动,适用于传动机构、物料输送机械等领域。
平面四杆机构的应用非常广泛。
它可以用于制造机械、工艺机械、汽车悬挂系统、绞车、传动机构、物料输送机械等领域。
在制造机械中,平面四杆机构常用于构建精密机床,如铣床、钻床等。
在工艺机械中,平面四杆机构常用于构建织机、纺机等。
在汽车悬挂系统中,平面四杆机构可以实现汽车悬挂系统的运动,提高汽车悬挂性能。
在绞车中,平面四杆机构可以用于提升和绞丝等工作。
在传动机构中,平面四杆机构可以用于实现直线传动和转动传动。
在物料输送机械中,平面四杆机构可以用于实现物料的输送和分拨。
总之,平面四杆机构具有多种类型和特点,适用于多个领域的应用。
它可以实现复杂的运动轨迹,广泛应用于制造机械、工艺机械、汽车悬挂系统、绞车、传动机构、物料输送机械等领域。
平面四杆机构的基本类型

平面四杆机构是一种常见的机械结构,由四个连杆组成,可以实现转动和传递力量。
根据其连杆排列方式和运动特点,平面四杆机构可以分为以下几种基本类型:
四杆平行机构:四个连杆平行排列的机构,常见的形式是平行四边形。
四杆平行机构具有简单结构和稳定性好的特点,在工程和机械设计中广泛应用。
四杆平行滑块机构:四个连杆中有一个是滑块,可以在平面内作直线运动。
这种机构常见的应用是在平面上实现直线运动,如印刷机的工作台。
四杆旋转机构:四个连杆可以围绕一个固定点旋转,形成一个封闭的轨迹。
这种机构常见的形式是摇杆机构或曲柄摇杆机构,常用于发动机的活塞运动转化为旋转运动。
四杆转动滑块机构:四个连杆中有一个是滑块,可以在平面内作转动运动。
这种机构常见的应用是实现旋转运动和直线运动的转换,如某些机床的进给机构。
这些基本类型的平面四杆机构都具有不同的运动特点和应用场景。
根据具体的工程需求和设计要求,可以选择合适的平面四杆机构类型,并进行优化和改进,以满足特定的运动和力学要求。
平面连杆机构——四连杆机构的类型
曲柄摇杆机构 曲柄摇杆机构的应用
双曲柄机构及其应用
天平中的平行四边形机构
反平行四边形机构及其应用
双摇杆机构 双摇杆机构及其在鹤式起重机中的应用
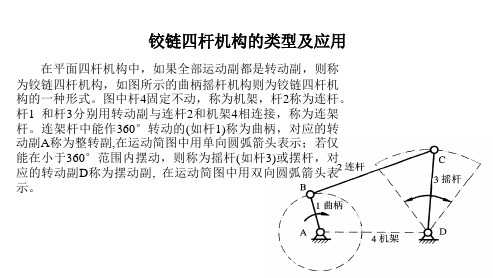
铰链四杆机构的类型及应用
在平面四杆机构中,如果全部运动副都是转动副,则称 为铰链四杆机构,如图所示的曲柄摇杆机构则为铰链四杆机 构的一种形式。图中杆4固定不动,称为机架,杆2称为连杆。 杆1 和杆3分别用转动副与连杆2和机架4相连接,称为连架 杆。连架杆中能作360°转动的(如杆1)称为曲柄,对应的转ห้องสมุดไป่ตู้动副A称为整转副,在运动简图中用单向圆弧箭头表示;若仅 能在小于360°范围内摆动,则称为摇杆(如杆3)或摆杆,对 应的转动副D称为摆动副, 在运动简图中用双向圆弧箭头表 示。
平面四杆机构考研题库

平面四杆机构考研题库平面四杆机构是机械工程中一个重要的研究领域,也是考研中常见的题型之一。
在这篇文章中,我们将探讨平面四杆机构的基本概念、应用以及相关的考研题库。
一、平面四杆机构的基本概念平面四杆机构是由四个连杆组成的机械系统,其中两个连杆为固定连杆,另外两个连杆为运动连杆。
这四个连杆通过铰链连接在一起,形成一个闭合的结构。
平面四杆机构的运动可以通过连杆的长度、角度以及连接方式来调节和控制。
平面四杆机构有许多不同的类型,包括双曲杆机构、平行杆机构、交叉杆机构等。
每种类型的机构都有其特定的运动规律和应用领域。
在考研中,我们需要了解这些基本概念,并能够应用到具体的问题中。
二、平面四杆机构的应用平面四杆机构在工程领域有广泛的应用。
其中一个典型的应用是在机械传动系统中。
通过调节连杆的长度和角度,可以实现不同的运动和力学特性,从而满足不同的工程需求。
另一个常见的应用是在机器人技术中。
平面四杆机构可以用来设计和控制机器人的运动,实现复杂的动作和任务。
例如,通过改变连杆的长度和角度,可以实现机器人的抓取、转动和推动等动作。
平面四杆机构还可以应用于汽车制造、航空航天、医疗设备等领域。
在汽车制造中,平面四杆机构可以用来设计和控制汽车的悬挂系统、转向系统等。
在航空航天中,平面四杆机构可以用来设计和控制飞机的起落架、舵面等。
在医疗设备中,平面四杆机构可以用来设计和控制手术机器人、康复设备等。
三、平面四杆机构考研题库在考研中,平面四杆机构是一个常见的考点。
以下是一些常见的考研题目:1. 请简述平面四杆机构的基本概念和分类。
2. 一台机器人的手臂由两个连杆组成,长度分别为L1和L2。
如果L1=10cm,L2=15cm,连杆之间的夹角为60度,请计算手臂的最大工作范围。
3. 一台汽车的悬挂系统采用平面四杆机构,其中两个连杆的长度分别为L1=30cm,L2=40cm。
请计算当汽车通过一个凸起的路面时,悬挂系统的最大位移。
4. 一台手术机器人的手臂由两个连杆组成,长度分别为L1=20cm,L2=25cm。
§8—2平面四杆机构的类型及应用

图8-3
振动筛机构
在双曲柄机构中,有两种特例: 1)平行四边形机构:其相对两杆平行且相等,如图8-7a 所示。
其运动特性是:
①两曲柄作等速同向转动; ②连杆作平移运动。
图8-7a
应用实例: 图8-8所示的机车车轮的联动机构就利用了特性① ;
图8-8
如图所示的摄影平台升降机构和图8-9 b所示的播种 机料斗机构则是利用了特摇杆长度相等。 图8-12b所示的汽车、拖拉机前轮的转向机构。
图8-12b
二、平面四杆机构的演化型式
(Evolution of Planar Four-bar Linkage)
1、四杆机构演化的目的: 满足运动方面的要求、改善受力状况、满足结构设 计上的要求。 2、四杆机构的演化方法: 1)改变构件的形状和运动尺寸
在图8-14,b所示的曲柄滑块机构中,B点相对于C 点的运动轨迹是αα。
连杆2做成滑块
αα 做成导轨
图8-14 b)
曲柄滑块机构 演化
图8-15 a) 双滑块机构
连杆长→∞,
αα →直线
图8-15 b)
正弦机构s=LABsinψ
2)改变运动副的尺寸
扩大转动副B的半径
使之超过曲柄的长度
图8-16 a) 图8-16 b) 演化 偏心轮机构
摇杆3做成滑块 ββ做成导轨
具有曲线导 轨的曲柄滑 块机构
图8-13 a )
图8-13 b )
图8-13 a )
摇杆长→∞, ββ →直线 摇杆3 →滑块, 转动副D →移动副 偏置(eccentric or e≠0
offset)
对心(in-line) e=0 图8-14 曲柄滑块机构
曲柄滑块机构(slider-crank mechanism)常用在冲床、 内燃机、空压机等机械中。
平面四杆机构的基本类型及应用-精品文档
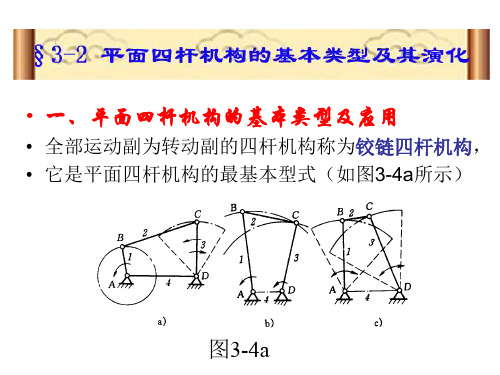
图3-16b
图3-19
图3-20
• 若选用曲柄滑块机构中滑块3作机架(图316c),即演化成移动导杆机构(或称定块 机构)。 • 它应用于手摇卿筒(图3—21)和双作用式 水泵等机械中。
图3—21
图3-16c
(3)变化双移动副机构的机架
• 在图3-15和图3-22a所示的具有两个移动副的四杆机 构中,是选择滑块4作为机架的,称之为正弦机构, 这种机构在印刷机械、纺织机械、机床中均得到广 泛地应用,例如机床变速箱操纵机构、缝纫机中针 杆机构(图3—22d);
铰链四杆机构可分为以下三种类型
1、曲柄摇杆机构
• 铰链四杆机构的两连架杆中一个能作整 周转动,另一个只能作往复摆动的机构。
2、双曲柄机构
铰链四杆机构的两连架杆均能作整周转 动的机构。
• 在双曲柄机构中,若相对两杆平行相 等,称为平行双曲柄机构(图3-9)。 这种机构的特点是其两曲柄能以相同 的角速度同时转动,而连杆作平行移 动。图3-10a所示机车车轮联动机构 和图3-10b所示的摄影平台升降机构 均为其应用实例。
图3-15
图3—22
• 若选取构件1为机架(图3-22b), 则演化成双转块机构,它常应用 作两距离很小的平行轴的联轴器, 图3-22e所示的十字滑块联轴节为 其应用实例;
图3-22b
图3-22e
• 当选取构件3为机架(图3-22c)时, 演化成双滑块机构,常应用它作椭圆 仪(图3—22f)。
图3-22
图 3-11
3、双摇杆机构
双摇杆机构:铰链四杆机构中的两连架杆均不能作 整周转动的机构。
如 图 3 - 12 所 示 鹤 式 起 重 机 的 双 摇 杆 机 构 ABCD,它可使悬挂重物作近似水平直线移动, 避免不必要的升降而消耗能量。在双摇杆机构 中,若两摇杆的长度相等称等腰梯形机构,如 图3—13中的汽车前轮转向机构。
机械原理NO[1].12 8-3 平面四杆机构的基本知识--2
![机械原理NO[1].12 8-3 平面四杆机构的基本知识--2](https://img.taocdn.com/s3/m/f4a7b4b6e87101f69f319596.png)
工程上也常利用死点来工作。
夹具
机械原理
第8章 平面连杆机构及其设计
四、铰链四杆机构的连杆曲线 Coupler-curve of four-bar linkages
在四杆机构运动时,其连杆平面上的每一点均描绘出一条曲线, 称为连杆曲线(coupler curves)
B型
水滴型
面包型
瘦长型
伪椭圆型
三角型
机构尺寸: 各运动副之间的相对位置尺寸(或
角度)以及描绘连杆上某点(该点实现 给定运动轨迹)的位置参数等。
平面连杆机构设计的基本要求:
1。要求从动件满足预定的运动规律要求(函数生成问题); 2。满足预定的连杆位置要求(刚体导引问题); 3。满足预定的轨迹要求(轨迹生成问题)。
机械原理
第8章 平面连杆机构及其设计
最多能解五个精确位置,多于五个位置只能近似求解,少于五个位置可有无穷解。
机械原理
第8章 平面连杆机构及其设计
2。按预定的运动规律设计四杆机构(函数综合)
1)按预定的两连架杆对应位置设计四杆机构:
要求: 3i f (1i ) , i =1、2、…、k
(已知条件)
取杆长的相对变量 a/a=1 , b/a=l, c/a=m , d/a=n 为设计参数,不影响各构件的相对 转角关系,故杆长的设计变量为l、m、 n ,再加上0 、0共5个设计变量。
• (2)改变运动副的尺寸;
• (3)选不同的构件为机架;
• (4)运动副元素的逆换。
机械原理
第8章 平面连杆机构及其设计
• 4.平面四杆机构有曲柄的条件: • (1)各杆长满足杆长条件:最短杆与最长杆的长度之和
应小于或等于其余两杆长度之和; • (2)最短杆为连架杆或机架。 • 5.急回运动及行程速度变化系数: • (1) 急回运动: • 当连机构的主动件为等速回转时,从动件空回行程的平
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四一、已知机架AD =CD =40 mm,设该用作图法求出曲柄
二、设计一曲柄滑最大压力角α=30。
并标明其极位夹角θ
三、试设计一曲柄摇杆机构mm,
l AD =50 mm。
求 l AB 、l (用图解法求解
.平面四杆机构的类型和应用
50 mm,摇杆CD 离机架最近极限机构为曲柄摇杆机构,且行程速比AB 和连杆BC 的长度,并绘出机构
块机构。
已知曲柄长AB =20mm,偏心试用作图法确定连杆长度BC ,滑块,求出其行程速度变化系数K 。
杆机构。
设摇杆两极限位置分别为ϕϕ1150
=
,BC 及行程速比系数K 和最小传动角γmin 。
)
位置β=45
,且
系数K =1.4,试简图。
距e =15mm,其
的最大行程H ,
29040== ;l CD
四、 现 需 设 计 一 铰 摇 杆 的 两 极 限 机 构 的 行 程 速
度 。
五、如图示曲柄滑(1)机构的(
2)最小传(3)滑块3大。
(4)当滑块3(在图中用作
链 四 杆 机 构, 已 知 摇 杆 CD 的 长 度 位 置 与 机 架 AD 所 成 的 角 度ϕ1 比 系 数 K =1, 试 确 定 曲 柄 AB 和 连b
a
块机构的运动简图,试确定当曲柄1行程速度变化系数K 。
动角γmin 的大小。
往复运动时向左的平均速度大还是为主动时,机构是否出现死点,为图法求解)
度 l CD =150 mm ,
ϕ23090==
,,
连 杆 BC 的 长
等速转动时,
向右的平均速度什么?
六、已 知 铰 链 四 杆杆 长 度 分 别 为l AB (1)其连杆BC 的机构;
(2)按上述各杆出现最小传动角的
七、已知铰链四杆曲柄和摇杆的两组其行程速比系数并
杆 机 构 机 架 长 度 l AD =30 mm;其 它=20 mm; l CD =40 mm,问:
长度须满足什么条件才能使该四杆长度并选l BC =35 mm,用适当比例尺位置,并在图上标出γmin 。
机构的机架长500l AD = mm,曲柄长l AB 对应位置如图所示。
试设计此曲柄在图上标出其最小传动角。
它 两 个 连 架 机构为曲柄摇杆画出该机构可能150= mm,及摇杆机构,确定
八、设计一曲柄滑求最小传动角 60=min γ。
(1)用图解法确定连(2)画出滑(3)标出极(4)确定行
九、
设计一偏置曲滑块的行程10021=C C l (1)用作图(2)若滑块转向;
(3)用作图块机构,已知曲柄长度15=AB l mm,偏。
确定连杆的长度BC l ,保留作图线。
块的极限位置;
位夹角θ及行程H ; 程速比系数K 。
柄滑块机构,已知滑块的行程速度变 mm,导路的偏距 20=e mm。
法确定曲柄长度AB l 和连杆长度BC l ; 从点C 1至C 2为工作行程方向,试法确定滑块工作行程和空回行程时的距10=e mm,要化系数K =1.5,
确定曲柄的合理最大压力角。
一、总分12分
(1)按µl =0001. m/m 根据θ=−180
1
(
)K ∠′=C AC 30 ,与以D 为圆心(4分)
(2)以A 为圆心,l l AB EC ==×′20001.(3)以A 为圆心,圆, 与AC 的 延长线交于l BC BC l l =×=×µµl AB =0023. m
l BC =0059. m 二、总分12分
(1)取µl =0001. m/m (2)其最大压力角发生分)
(3)确定尺寸 BC B C =′′=70 mm 参考答案
m/mm 作图;
+
1()K ,可求出θ=30o
,以AC 为一边,为圆心,以DC 长为半径所作的圆弧交于′C 点;,以AC 为半径画弧,交AC ′于 E 点,则 =4620023. m。
(4分)
以l AB l µ==0023000123.. mm 长为半径作线交于B 点,则
B C ′′=×=0001590059.. m (4分)
m/mm 作图。
(4分)
角发生在AB 处于AB '时,作30 角可得C '。
(
作;
径作4
H C C
==
12
415. mm
作极限位置,量得θ=8
K=
+
−
=
+
−
=
180
180
1808
1808
1093
θ
θ
. (4分)
θ
三、总分10分
(1)取比例尺µ
l =1
mm
mm
先将已知条件画出。
(2分)
(2)测得:AC l l
BC AB
126
=−= mm
AC l l
BC AB 264
=+= mm
两式联立求得:l
AB
=19 mm, l BC=45 mm (3分)
(3)测得:θ=∠C AC
12
15=
所以 K=
+
−
=
+
−
=
180
180
18015
18015
118
θ
θ
. (3分)
(4) 测得:γ
min
=42 (2 分〕
四、总分10分
(1)∠=−C DC 219030 mm
又 K=1 A 必在 C 1C 2 的连线上(2)b a CD +==2 b a
−=解得 曲柄 a =连杆 b =225 mm 五、总分10分
(1)θ==10 ,(K 分)
=60
C C l C
D 12== θ=0
连线上。
(5分)
×=2150300 mm CD =150 mm 75 mm
(5分)
θθ+−==1801801901701118 )().。
(2
150
2
min (3)向左大。
(4)会出现,(3
分)
六、总分10
分
1)当l BC 为最长杆时杆机构还应满足下列条件203040+≤+l BC ,故2)当l BC 为最长杆时摇杆机构还应满足下列条件204030+≤+l BC ,故七、(总分10分)
(1)设计如图所示 以 µl =001. m/mm mm
l CD CD l µ⋅==(2)做出机构极限位 (2分)
因为在连杆与曲柄共线时传动角γ=0 。
杆时(即l BC >40 mm),要使机构成为曲柄摇条件:
故4050<≤l BC 。
杆时(即l BC <40 mm),要使 此机构成为曲柄列条件:
故3040≤<l BC 。
(5分)
所示,
/mm 作 图 得l BC BC l µ⋅=01.058=×=32501.05.32=× mm (5分)极限位置,量得
5.18=θ,.1180180K =θ
−θ
+=。
柄摇曲柄580 )
229。
(3分)
min 八、(15分)
(1)连杆长度BC l ;(2)滑块的(3)极位夹(4)行程速比系数K
;如图B 1C 1所示。
(5分) 两极限位置;(4分)
角及行程H 如图所示; (3分)
K=(180+θ)/(180-θ)。
(3分)
60° B 1
极限位置2
θ
极限位置1
九、总分10分
(1〕θ=−+=1801136o
o
()/()K K 取 µl =2 mm/mm
作21C C l 及e ,作θ−=∠=∠ 901221O C C O C C ,得C 1O 和C 2O 的交点O ,以O 为圆心和OC 1为半径作圆周L ,该圆与导路相距为l 的平行线q 相交于A 点,此点即是曲柄回转中心。
从图上量得 1182=AC l mm, 301=AC l mm,从而可求得 442)(12=−=AC AC AB l l l mm,742)(21=+=AC AC BC l l l mm (5分)
(2)根据滑块的工作行程需获得较佳的受力条件和工作较平稳的要求,选定曲柄的回转方向为逆时针。
(2分)
(3)工作行程和空回行程的最大压力角分别为max
α′和max α′′。
(3分)。
