小学六年级奥数- 抓“不变量”解题
六年级奥数分数不变量题

分数应用题
1.某校在一次选举中,需3/4的选票才能当选,计算2/3的选票后,他得到的选票已达到当选票数的5/6,他还要得到剩下选票的几分之几才能当选?
2、某校学生的3/5是男生,男生的1/20想当医生,全校想当医生的学生的3/4是男生。
那么全校女生的几分之几想当医生?
3、甲乙两个仓库共有水泥180吨,如果甲把它的1/3给乙,甲还比乙多10吨,甲乙原来各有多少吨?
4、某校五年级学生参加大扫除的人数是未参加的1/4,后来又有2个同学主动参加,实际参加的人数是未参加人数的1/3,问某班五年级有学生多少人?
5、有科技书和文艺书360本,其中科技书占总数的1/9,现在又买来一些科技书,此时科技书占总数的1/6。
又买来多少本科技书?
6:有10千克蘑菇,它们的含水量是99%,稍经晾晒,含水量下降到98%,晾晒后的蘑菇重多少千克?
7.王叔叔和李叔叔每月工资收入比为3:2,他们两家每月支出为1200元,两家每月结余的钱数比为9;4,王叔叔和李叔叔每月工资各为多少元?
8. 有一堆糖果,其中奶糖占9/20,再放入16块水果糖后,奶糖就只占1/4。
这一堆糖果原来共有多少块?。
六年级奥数--抓不变量解题

一、知识要点一些分数的分子与分母被施行了加减变化,解答时关键要分析哪些量变了,哪些量没有 变。
抓住分子或分母,或分子、分母的差,或分子、分母的和等等不变量进行分析后,再转 化并解答。
二、精讲精练437 将的的分子与分母同时加上某数后得G ,求所加的这个数。
61 9解法一:因为分数的分子与分母加上了一个数,所以分数的分子与分母的差不变,仍是18, 所以,原题转化成了一各简单的分数问题:“一个分数的分子比分母少18,切分子是g分母的G ,由此可求出新分数的分子和分母。
”9g分母:(61-43)+(1— )=819 g分子:81X- =63981-61=20或63-43=20 43 g解法二:所的分母比分子多18,-的分母比分子多2,因为分数的与分母的差不变,所以 61 9-将5的分子、分母同时扩大(18+2=)9倍。
9 -①Q 的分子、分母应扩大:(61-43)・(9-7)=9 (倍) 9 - - -X9 63②约分后所得的G 在约分刖是:Q =不二 =*9 9 9X9 81③ 所加的数是81-61=20答:所加的数是20。
练习1:97 21、 分数有 的分子和分母都减去同一个数,新的分数约分后是三,那么减去的数是多少?181 5六年级奥数——抓“不变量”解题【例题1】43132、分数百的分子、分母同加上一个数后得三,那么同加的这个数是多少?13 5353、w的分子、分母加上同一个数并约分后得亍,那么加上的数是多少?19 758 24、将元这个分数的分子、分母都减去同一个数,新的分数约分后是耳,那么减去的数是79 3多少?【例题2】42将一个分数的分母减去2得耳,如果将它的分母加上1,则得3,求这个分数。
4解法一:因为两次都是改变分数的分母,所以分数的分子没有变化,由“它的分母减去2得5 ”可知,分母比分子的5倍还多2。
由“分母加i得2 ”可知,分母比分子的2倍少1, 从而将原题转化成一个盈亏问题。
小学六年级奥数- 抓“不变量”解题

二、பைடு நூலகம்讲精练
【例题2】
二、精讲精练
练习2:
二、精讲精练
【例题3】
二、精讲精练
练习3:
二、精讲精练
【例题4】
二、精讲精练
练习4:
二、精讲精练
【例题5】
二、精讲精练
练习5:
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
小学六年级奥数- 抓“不变量”解 题
第21讲
专题简析:
一些分数的分子与分母被施行了加减变化,解答时关键要 分析哪些量变了,哪些量没有变。抓住分子或分母,或分 子、分母的差,或分子、分母的和等等不变量进行分析后, 再转化并解答。
二、精讲精练 【例题1】
二、精讲精练 【例题1】
二、精讲精练 练习1:
小学数学6年级培优奥数讲义 第15讲-抓“不变量”解题(教师版)
第15讲抓“不变量”解题教学目标掌握“总量不变”,“相差量不变”和“部分量不变”三种不变量思想,并能用不变量思想解决现实生活中的问题。
知识梳理一个数量的变化,往往会引起其他数量的变化。
如“某班转走3名女生”,女生人数变了,总人数也跟着变了,男生与女生、女生与总人数之间的倍数关系也变了……只有注意到这些变化,才能防止出错。
但在这些数量变化时,与它们相关的另外一些数量却没有改变。
在分析数量关系时,这种不变量常常会起到非常重要的作用。
抓住不变量进行思考,可以顺利解答一些经典的应用题,能达到事半功倍的效果。
根据不变量的不同,可以将“量不变”应用题分为三种类型:“总量不变”应用题、“相差量不变”应用题和“部分量不变”应用题。
典例分析考点一:总量不变题中两个变化的量中,一个量在增加,另一个量减少,但是增加的和减少的同样多,所以两个量的总和保持不变。
解题时,一般把两个量的总和看作单位“1”或者把其中一个量看作是1倍的量。
例1、有一个书架,上层与下层书的数量比是7:8,现从上层拿10本给下层,这时上层与下层的数量比是8:7,求原来上、下层各有多少本?【解析】这道题上下层都发生了变化,但总数量不变,可把总数量看作单位“1”,抓住总数量不变,根据上层与下层的数量比是7:8知上层占总数的7/15,又根据上层与下层的数量比是8:7,知上层占总数的8/15,列式:10÷(8/15-7/15)=150(本),150本为总数量,150÷(7+8)=10(本)7×10=70(本)8×10=80(本)。
例2、小丽有故事书108本,小芳有故事书140本,小芳借了若干本故事书给小丽后,小丽的故事书的本数是小芳的3倍。
问小芳借了多少本故事书给小丽?【解析】小芳借了若干本故事书给小丽前后,小芳和小丽拥有故事书的本数都发生了变化,但两人拥有故事书的总本数不变,这是本题解题的关键。
即(108+140)本就是小芳现有故事书的本数的(3+1)倍,因此小芳现有故事书的本数是(108+140) ÷(3+1)=62本,所以小芳借给小丽故事书的本数是140-62=78(本)。
六年级奥数应用题浓度问题

知识框架、基本概念与关系“溶质之外的物质” 用来溶解溶质的物质100% 溶液=溶质+溶剂——+溶质与溶质的混合体重难点(1)重点:浓度问题中的基本关系,不变量的寻找,浓度三角 (2)难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用浓度问题(1) 溶质 “干货”、“纯货” 被溶解的物质 (2) 溶剂(4) 浓度 、基本方法 混合浓度z% —溶质的量占溶液的量的百分比 甲溶液乙溶液 浓度x%浓度y% z-y : x-z(1) 寻找不变量,按基本关系或比例求解 (2) 浓度三角(如右图所示) 甲溶液质量:乙溶液质量 (3) 列方程或方程组求解(3) 溶液浓度=溶质100%=」质例题精讲一、抓住不变量和浓度基本关系解决问题【例1】某种溶液由40克食盐浓度15%勺溶液和60克食盐浓度10%勺溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少?【巩固】一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【例2】浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖?【巩固】浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8 %的糖水?【例3】买来蘑菇10千克,含水量为99 %,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?【巩固】1000千克葡萄含水率为96.5%,—周后含水率降为96%这些葡萄的质量减少了_______ 千克.【例4】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百分比是 _________ •【巩固】一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%第二次又加入同样多的水,盐水的含盐百分比变为12%第三次再加入同样多的水,盐水的含盐百分比将变为_________ %.二、通过浓度三角解决浓度和实际生活中的配比问题【例5】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70% 的盐水多少克?【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精,需加入水多少克?【例6】瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入10(克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?【巩固】有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【例7】甲瓶中酒精的浓度为70%,乙瓶中酒精的浓度为60%,两瓶酒精混合后的浓度是66% .如果两瓶酒精各用去5升后再混合,则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40% .如果每种酒精都多取20克,混合后纯酒精的含量变为45% .求甲、乙两种酒精原有多少克?【例8】甲种酒精纯酒精含量为72%,乙种酒精纯酒精含量为58%,混合后纯酒精含量为62% .如果每种酒精取的数量比原来都多取15升,混合后纯酒精含量为63.25%.第一次混合时,甲、乙两种酒精均取了多少升?【巩固】甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样?【例9】某班有学生48人,女生占全班的37.5 %,后来又转来女生若干人,这时人数恰好是占全班人数的40%,问转来几名女生?【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支?1【例10】有两包糖,第一包糖由奶糖和水果糖组成,其中-为奶糖;第二包糖由酥1糖和水果糖组成,其中-为酥糖.将两包糖混合后,水果糖占78%,那么5奶糖与酥糖的比例是_________ .【巩固】某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?三、综合运用各种方法解决多溶液、多次配比问题【例11】甲容器中有纯酒精11升,乙容器中有水15升,第一次将甲容器中的一部分纯酒精倒入乙容器,使酒精与水混合。
完整六年级奥数 抓不变量解题

六年级奥数——抓“不变量”解题一、知识要点一些分数的分子与分母被施行了加减变化,解答时关键要分析哪些量变了,哪些量没有变。
抓住分子或分母,或分子、分母的差,或分子、分母的和等等不变量进行分析后,再转化并解答。
二、精讲精练【例题1】437将的分子与分母同时加上某数后得,求所加的这个数。
619解法一:因为分数的分子与分母加上了一个数,所以分数的分子与分母的差不变,仍是18,所以,原题转化成了一各简单的分数问题:“一个分数的分子比分母少18,切分子是7分母的,由此可求出新分数的分子和分母。
”97分母:(61-43)÷(1-)=8197分子:81×=63981-61=20或63-43=20437解法二:的分母比分子多18,的分母比分子多2,因为分数的与分母的差不变,所以6197将的分子、分母同时扩大(18÷2=)9倍。
97①的分子、分母应扩大:(61-43)÷(9-7)=9(倍)9777×963②约分后所得的在约分前是:==98199×9③所加的数是81-61=20答:所加的数是20。
1练习1:9721、分数的分子和分母都减去同一个数,新的分数约分后是,那么减去的数是多少?1815132、分数的分子、分母同加上一个数后得,那么同加的这个数是多少?13535 的分子、分母加上同一个数并约分后得、,那么加上的数是多少?31975824、将这个分数的分子、分母都减去同一个数,新的分数约分后是,那么减去的数是793多少?【例题2】42将一个分数的分母减去2得,如果将它的分母加上1,则得,求这个分数。
534解法一:因为两次都是改变分数的分母,所以分数的分子没有变化,由“它的分母减去2得”5523可知,分母比分子的倍还多2。
由“分母加1得”可知,分母比分子的倍少1,432从而将原题转化成一个盈亏问题。
35分子:(2+1)÷(-)=12243分母:12× -1=172解法二:两个新分数在未约分时,分子相同。
六年级奥数春季班课程

第1讲 抓“不变量”解题一些分数的分子与分母被施行了加减变化,解答时关键要分析哪些量变了,哪些量没有变。
抓住分子或分母,或分子、分母的差,或分子、分母的和等等不变量进行分析后,再转化并解答。
【例1】将4361 的分子与分母同时加上某数后得79,求所加的这个数。
方法指导:解答:【练习1】1、 分数97181 的分子和分母都减去同一个数,新的分数约分后是25,那么减去的数是多少?2、 分数113 的分子、分母同加上一个数后得35,那么同加的这个数是多少?【例2】将一个分数的分母减去2得45 ,如果将它的分母加上1,则得23,求这个分数。
方法指导: 解答:专题解析典型例题【练习2】1、 将一个分数的分母加上2得79 ,分母加上3得34。
原来的分数是多少?2、将一个分数的分母加上2得34 ,分母加上2得45。
原来的分数是多少?【例3】在一个最简分数的分子上加一个数,这个分数就等于57。
如果在它的分子上减去同一个数,这个分数就等于12,求原来的最简分数是多少。
方法指导: 解答:【练习3】1、 一个最简分数,在它的分子上加一个数,这个分数就等于58。
如果在它的分子上减去同一个数,这个分数就等于12,求这个分数。
2、 一个最简分数,在它的分子上加一个数,这个分数就等于67。
如果在它的分子上减去同一个数,这个分数就等于13,求这个分数。
【例4】将一个分数的分母加3得79 ,分母加5得34。
原分数是多少? 方法指导: 解答:【练习4】1、 一个分数,将它的分母加5得56 ,加8得45,原来的分数是多少?(用两种方法)2、 将一个分数的分母减去3,约分后得67 ;若将它的分母减去5,则得78。
原来的分数是多少?(用两种方法做)【例5】有一个分数,如果分子加1,这个分数等于12 ;如果分母加1,这个分数就等于13,这个分数是多少?方法指导: 解答:【练习5】1、 一个分数,如果分子加3,这个分数等于12 ,如果分母加上1,这个分数等于13,这个分数是多少?2、一个分数,如果分子加5,这个分数等于12 ,如果分母减3,这个分数等于13,这个 分数是多少?1、 一个分数,如果分子减1,这个分数等于12 ;如果分母加11,这个分数等于13,这个分数是多少?2、把一个分数的分母减去2,约分后等于34 。
六年级奥数.应用题.浓度问题
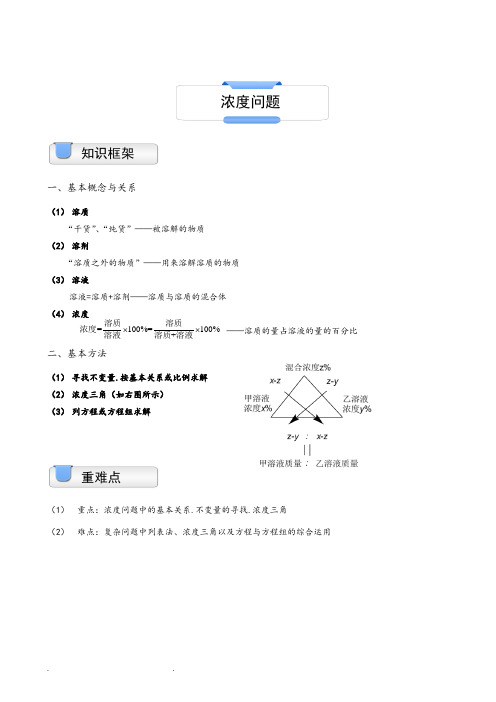
一、基本概念与关系(1) 溶质“干货”、“纯货”——被溶解的物质(2) 溶剂“溶质之外的物质”——用来溶解溶质的物质(3) 溶液溶液=溶质+溶剂——溶质与溶质的混合体(4) 浓度——溶质的量占溶液的量的百分比 二、基本方法(1) 寻找不变量.按基本关系或比例求解(2) 浓度三角(如右图所示)(3) 列方程或方程组求解(1) 重点:浓度问题中的基本关系.不变量的寻找.浓度三角(2) 难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用重难点 知识框架浓度问题=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液例题精讲一、抓住不变量和浓度基本关系解决问题【例1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到.那么这种溶液的食盐浓度为多少?【巩固】一容器内有浓度为25%的糖水.若再加入20千克水.则糖水的浓度变为15%.问这个容器内原来含有糖多少千克?【例2】浓度为20%的糖水40克.要把它变成浓度为40%的糖水.需加多少克糖?【巩固】浓度为10%.重量为80克的糖水中.加入多少克水就能得到浓度为8%的糖水?【例3】买来蘑菇10千克.含水量为99%.晾晒一会儿后.含水量为98%.问蒸发掉多少水份?【巩固】1000千克葡萄含水率为96.5%.一周后含水率降为96%.这些葡萄的质量减少了千克.【例4】将含农药30%的药液.加入一定量的水以后.药液含药24%.如果再加入同样多的水.药液含药的百分比是________.【巩固】一杯盐水.第一次加入一定量的水后.盐水的含盐百分比变为15%;第二次又加入同样多的水.盐水的含盐百分比变为12%.第三次再加入同样多的水.盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例5】有浓度为20%的盐水300克.要配制成40%的盐水.需加入浓度为70%的盐水多少克?【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精.需加入水多少克?【例6】瓶中装有浓度为15%的酒精溶液1000克.现在又分别倒入100克和400克的A、B两种酒精溶液.瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍.那么A种酒精溶液的浓度是百分之几?【巩固】有两种溶液.甲溶液的酒精浓度为15%.盐浓度为10%.乙溶液中的酒精浓度为45%.盐浓度为5%.现在有甲溶液1千克.那么需要多少千克乙溶液.将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【例7】甲瓶中酒精的浓度为70%.乙瓶中酒精的浓度为60%.两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合.则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克.混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克?【例8】甲种酒精纯酒精含量为72%.乙种酒精纯酒精含量为58%.混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升.混合后纯酒精含量为63.25%.第一次混合时.甲、乙两种酒精均取了多少升?【巩固】甲、乙两只装满硫酸溶液的容器.甲容器中装有浓度为8%的硫酸溶液600千克.乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中.才能使这两个容器中的硫酸溶液的浓度一样?【例9】某班有学生48人.女生占全班的37.5%.后来又转来女生若干人.这时人数恰好是占全班人数的40%.问转来几名女生?【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元.黑笔每支定价9元.由于买的数量较多.商店就给予优惠.红笔按定价85%付钱.黑笔按定价80%付钱.如果他付的钱比按定价少付了18%.那么他买了红笔多少支?【例10】有两包糖.第一包糖由奶糖和水果糖组成.其中14为奶糖;第二包糖由酥糖和水果糖组成.其中15为酥糖.将两包糖混合后.水果糖占78%.那么奶糖与酥糖的比例是________.【巩固】某商品76件.出售给33位顾客.每位顾客最多买三件.如果买一件按原定价.买两件降价10%.买三件降价20%.最后结算.平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?三、综合运用各种方法解决多溶液、多次配比问题【例11】甲容器中有纯酒精11升.乙容器中有水15升.第一次将甲容器中的一部分纯酒精倒入乙容器.使酒精与水混合。
