等积变形应用题
等积变形专项练习

等积变形专项练习
1。
在一个底面积是31.4平方厘米的长方体玻璃容器中,有一个底面半径是1厘米的圆锥形铝块完全浸在水中,当从水中取出铝块时,容器的水面下降了0。
2厘米。
这个圆锥形铝块高多少厘米?
2。
用半径10cm高7cm的圆柱形泥巴揉成半径一样大的圆锥形,圆锥的高是多少厘米呢?
3.一个圆柱形的水桶,内部的底面半径是20厘米,高是45厘米,里面盛有30厘米深的水。
将一个底面半径是15厘米的圆锥形铁块完全沉进水里,水不溢出,水面上升了3厘米,圆锥形铁块的高是多少?
4.有一段钢可做一个底面直径8厘米,高9厘米的圆柱形零件.如果把它改制成高是12厘米的圆锥形零件,零件的底面积是多少平方厘米?
5。
一个圆柱形容器的底面半径是4分米,高6分米,里面盛满水,把水倒在棱长是8分米的正方体容器中,水深多少分米?
6.将一个底面直径是20厘米、高是9厘米的金属圆锥,全部浸没在直径是40厘米的圆柱形水槽中且水未溢出。
水槽中的水面会升高多少厘米?
7。
把一个长2米的圆柱截去4分米后,原来的表面积就减少了25.12平方分米,原来圆柱的体积是多少立方分米?
8。
在一个底面是边长为2分米的正方形的长方形水槽中,放入一块青铜(完全浸没在水中),水面上升1分米且水未溢出.(水槽厚度忽略不计)
(1)求这块青铜的体积.
(2)如果把这块青铜铸成一个底面直径是2分米的圆柱,它的高是多少?(得数保留一位小数)
9.(拓展)在一个圆柱形储水桶里,把一段半径是5cm的圆钢全部放入水中,水面就上升9cm;把圆钢竖着拉出水面8cm长后,水面就下降4cm。
求圆钢的体积。
一元一次方程实际应用题之等积变形问题
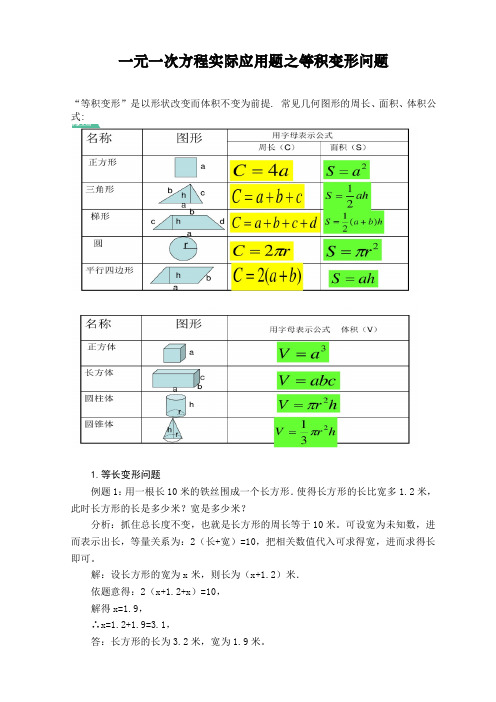
一元一次方程实际应用题之等积变形问题“等积变形”是以形状改变而体积不变为前提. 常见几何图形的周长、面积、体积公式:1.等长变形问题例题1:用一根长10米的铁丝围成一个长方形.使得长方形的长比宽多1.2米,此时长方形的长是多少米?宽是多少米?分析:抓住总长度不变,也就是长方形的周长等于10米。
可设宽为未知数,进而表示出长,等量关系为:2(长+宽)=10,把相关数值代入可求得宽,进而求得长即可。
解:设长方形的宽为x米,则长为(x+1.2)米.依题意得:2(x+1.2+x)=10,解得x=1.9,∴x=1.2+1.9=3.1,答:长方形的长为3.2米,宽为1.9米。
2.等体积变形问题例题2:要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长是多少毫米?分析:抓住锻造前后的体积不变,此题的等量关系为:锻造前的体积=锻造后的体积.据此列方程求解。
要注意的是,题目中已知直径,需要转化为半径。
解:设需截取直径为40mm的圆钢长xmm,60÷2=30(mm)、40÷2=20(mm);依题意得:π×30^2×30=π×20^2×x解得:x=67.5例题3:有一段钢材可作一个底面直径 8 厘米,高 9 厘米的圆柱形零件。
如果把它改制成高是 12 厘米的圆锥形零件,零件的底面积是多少平方厘米?分析:根据“底面直径8厘米,高9厘米的圆柱形零件”,利用圆柱体积公式,可以求出圆柱的体积,又因为把圆柱形的零件改制成圆锥形零件时,此段钢的体积不变,根据体积不变列出方程求解。
解:零件的底面积是x平方厘米。
8÷2=4(厘米)依题意得:3×π×4^2×9=x×12解得:x=36π答:零件的底面积是36π平方厘米。
3.等面积变形问题例题4:如图,某小学将一块梯形空地改成宽为30m的长方形运动场地,要求面积不变.若在改造后的运动场地,小王、小李两人同时从点A出发,小李沿着长方形边顺时针跑,小王则是逆时针跑,并且小王每秒比小李多跑2m,经过10秒钟他们相遇.(1)求长方形的长;(2)求小王、小李两人的速度分析:(1)求得原梯形的面积,利用面积不变和长方形的面积求得长方形的长即可;(2)设小李的速度是xm/s,则小王的速度是(x+2)m/s,利用10秒钟他们相遇所走的路程为长方形的周长列出方程解决问题。
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
一元一次方程应用题(6)(等长变形、等积变形)

一元一次方程应用题(6)(等长变形、等积
变形)
1.假设原长方形的长为x,宽为y,则根据周长公式
2(x+y)=26,可得x+y=13.将长减少1,宽增加2后得到的正方
形的边长为y+2,因此有y+2=x-1.将这两个方程联立解得x=9,y=4,所以原长方形的长为9cm,宽为4cm。
2.圆锥体的体积为1/3πr^2h,圆柱体的体积为πr^2h,两
者相等,因此可得圆柱体的高为8×(30/10)^2=72cm,所以圆
柱体内的水高为8cm。
3.设新的长方形宽为x,则根据折叠后周长不变可得
2x+10=18,解得x=4,因此新的长方形的长为9cm,宽为4cm。
4.正方体的体积为20^3=8000cm^3,盛水量筒的容积为
12×h,其中h为水面升高的高度,因此有12h=8000,解得
h=666.67cm,所以水面升高了666.67/12≈55.56cm。
5.设大长方形面积为S,则重叠部分面积为S/6,小长方
形面积为S/4,阴影部分面积为224cm^2,因此有S/6-S/4=224,解得S=1344,所以重叠部分面积为S/6=224cm^2.
6.(1) 第一个中的水体积为π(4^2)×16=256π,第二个的底
面积为π(8^2)=64π,因此第二个中的水高为256π/64π=4cm。
2) 将1插入2后,1中的水体积为π(4^2)×10=160π,2中的水体积为π(8^2)×10=640π,因此水位上升了640π-
256π=384π,所以水面升高了384π/(π(8^2))≈1.5cm。
等积变形应用题

等积变形应用题等积变形应用题一“等积变形”是以形状改变而体积不变为前提.等积变形类应用题的基本关系式:变形前的体积(容积)=变形后的体积(容积).二练习题1、用直径为4cm的圆钢(截面为圆形的实心长条钢材)铸造3个直径为2cm,高为16cm的圆柱形零件,则需要截取多长的圆钢?2、某铜铁厂要锻造长、宽、高分别为260mm、150 mm、130 mm的长方体毛坯,需要截取地面积为130 mm2的方钢多长?3、某机器加工厂要锻造一个毛胚,上面是一个直径为20毫米,高为40毫米的圆柱,下面也是一个圆柱,直径为60毫米,高为20毫米,问需要直径为40毫米的圆钢多长?4、将一罐满水的直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里,问这时水的高度是多少?5、一个直径为1。
2米高为1.5米的圆柱形水桶,已装满水,向一个底面边长为1米的正方形铁盒倒水,当铁盒装满水时,水桶中的水高度下降了多少米。
6、有一块棱长为4厘米的正方体铜块,要将它熔化后铸成长2厘米、宽4厘米的长方体铜块,铸成后的铜块的高是多少厘米(不计损耗)?7 某工厂锻造直径为60毫米,高20毫米的圆柱形瓶内装水,再将瓶内的水倒入一个底面直径6厘米、高10厘米的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离.8 有一个圆柱形铁块,底面直径为20厘米,高为26厘米,把它锻造成长方体毛胚,若使长方体的长为10π厘米,宽为13厘米,求长方体的高。
9 用一个底面半径为5厘米的圆柱形储油器,油液中浸有钢珠,若从中捞出546π克钢珠,问液面下降了多少厘米?(1立方厘米钢珠7.8克)10 小圆柱的直径是8厘米,高6厘米,大圆柱的直径是10厘米,并且它的体积是小圆柱体体积的2。
5倍,则大圆柱的高是多少厘米?11 一个长、宽、高分别是9厘米、7厘米、3厘米的长方体铁块和一个棱长为5厘米的正方体铁块,熔化成一个圆柱体,其底面直径为20厘米,请求圆柱体的高(π取3。
等积变形应用题练习

பைடு நூலகம்
?
答案:小影所钉长方形的长是16厘米,宽是10厘米。
4、小明的爸爸想用10米铁丝网把墙 当一长边围成一个鸡棚,使长比宽大4 米,问小明的爸爸围成的鸡棚的长和宽 各是多少呢?
墙面
x
铁线
X+4
5、一个长方形的养鸡场的长边靠墙,墙长14 米,其他三边用竹篱笆围成,现有长为35米的 竹篱笆,小王打算用它围成一个鸡场,其中长 比宽多5米;小赵也打算用它围成一个鸡场, 其中长比宽多2米.你认为谁的设计符合实际? 按照他的设计,鸡场的面积是多少?
相等关系:水面增高体积=长方体体积 解:设水面增高 x 厘米. 则
4 x 5 3 3
2
解得: x
45 0 .9 16
因此,水面增高约为0.9厘米.
3、 墙上钉着用一根彩绳围成的梯形形状的 装饰物,小颖将梯形下底的钉子去掉,并将这条 彩绳钉成一个长方形,那么,小颖所钉长方形的 长和宽各为多少厘米?
5.3 练习题
1、 将一个底面直径为10厘米、高为36厘 米的“瘦长”形圆柱锻压成底面直径为20厘 米的“矮胖”形的圆柱,高变成了多少?
想 什么发生了变化? 一 想
什么没有发生变化? 答案:高变成了9厘米。
2、把一块长、宽、高分别为5cm、3cm、3cm的 长方体木块,浸入半径为4cm的圆柱形玻璃杯 中(盛有水),水面大约增高多少?(水不外 溢,结果近似到0.1cm)
墙壁 篱笆
6、 在一个底面直径为3cm,高为22cm的量筒 内装满水,再将筒内的水到入底面直径为7cm,高 为9cm的烧杯内,能否完全装下?若装不下,筒内 水还剩多高?若能装下,求杯内水面的高度。
小学五年级数学思维专题训练—等积变形(含答案解析)
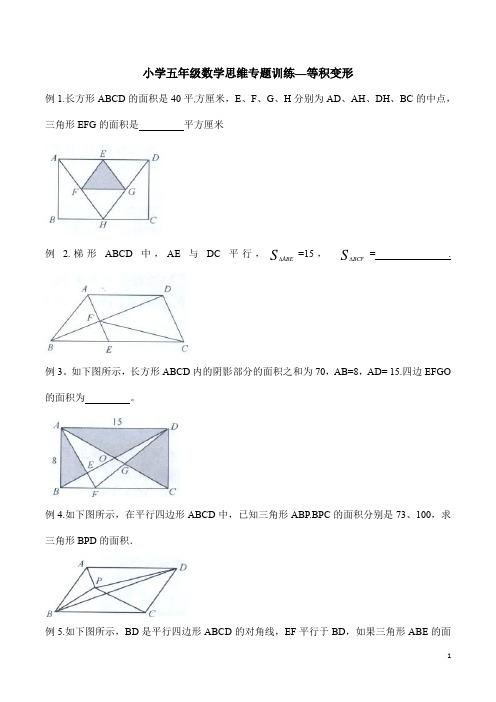
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
一元一次方程_等积变形应用题

一元一次方程解应用题————等积变形问题复习:常用几何图形的计算公式长方形的周长 = 长方形的面积 =三角形的周长 = 三角形的面积 =圆的周长= 圆的面积=长方体的体积 = 圆柱体的体积 =想一想:请指出下列过程中,哪些量发生了变化,哪些量保持不变?1、把一小杯水倒入另一只大杯中;2、用一根15cm长的铁丝围成一个三角形,然后把它围成长方形;3、用一块橡皮泥先做成一个立方体,再把它改变成球。
问题1(1)用一根长8米的铁丝围成一个长方形.使长方形的宽比长少1米,求这个长方形的面积.(2)用一根长8米的铁丝围成一个正方形,求这个正方形的面积.(3)用一根长8米的铁丝围成一个圆,求这个圆的面积.(4)在周长相等的长方形、正方形、圆中,谁的面积最大?谁的面积最小?精讲例题1.将一个底面直径为10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是 20厘米的“矮胖”形圆柱,高变成了多少?等量关系:解设锻压后圆柱的高为x厘米,填写下表锻压前锻压后底面半径高体积练习:1、如图,用直径为200毫米的圆钢,锻造一个长、宽、高分别为300毫米、300毫米和90毫米的长方体毛坯底板,应截取圆钢多少(计算时思考:题目中有哪些已知量和未知量?它们之间有什么关系?如何设未知数?已知:圆钢直径(200mm)、长方体毛胚的长宽高(300mm、300mm、90mm)未知:圆钢的高相等关系:圆钢体积=长方体毛胚的体积设未知数:设应截取圆钢 x 毫米。
2.已知一圆柱形容器底面半径为0.5m,高为1.5m,里面盛有1m深的水,将底面半径为0.3m,高为0.5m的圆柱形铁块沉入水中,问容器水面将升高多少?小结:说说列方程解应用题的一般步骤:1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数.2、用代数式表示有关的量.3、根据等量关系列出方程.4、解方程,求出未知数的值.5、检验求得的值是否正确和符合实际情形,并写出答案.等积变形是以形状改变而体积不变为前提。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等积变形应用题
一“等积变形"是以形状改变而体积不变为前提。
等积变形类应用题的基本关系式:变形前的体积(容积)=变形后的体积(容积)。
二练习题
1、用直径为4cm的圆钢(截面为圆形的实心长条钢材)铸造3个直径为2cm,高为16cm的圆柱形零件,则需要截取多长的圆钢?
2、某铜铁厂要锻造长、宽、高分别为260mm、150 mm、130 mm的长方体毛坯,需要截取地面积为 130 mm2的方钢多长?
3、某机器加工厂要锻造一个毛胚,上面是一个直径为20毫米,高为40毫米的圆柱,下面也是一个圆柱,直径为60毫米,高为20毫米,问需要直径为40毫米的圆钢多长?
4、将一罐满水的直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里,问这时水的高度是多少?
5、一个直径为1.2米高为1.5米的圆柱形水桶,已装满水,向一个底面边长为1米的正方形铁盒倒水,当铁盒装满水时,水桶中的水高度下降了多少米。
6、有一块棱长为4厘米的正方体铜块,要将它熔化后铸成长2厘米、宽4厘米的长方体铜块,铸成后的铜块的高是多少厘米(不计损耗)?
7 某工厂锻造直径为60毫米,高20毫米的圆柱形瓶内装水,再将瓶内的水倒入一个底面直径6厘米、高10厘米的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离。
8 有一个圆柱形铁块,底面直径为20厘米,高为26厘米,把它锻造成长方体毛胚,若使长方体的长为10π厘米,宽为13厘米,求长方体的高。
9 用一个底面半径为5厘米的圆柱形储油器,油液中浸有钢珠,若从中捞出546π克钢珠,问液面下降了多少厘米?(1立方厘米钢珠7.8克)
10 小圆柱的直径是8厘米,高6厘米,大圆柱的直径是10厘米,并且它的体积是小圆柱体体积的2.5倍,则大圆柱的高是多少厘米?
11 一个长、宽、高分别是9厘米、7厘米、3厘米的长方体铁块和一个棱长为5厘米的正方体铁块,熔化成一个圆柱体,其底面直径为20厘米,请求圆柱体的高(π取3.14)
12 一个长方形的周长为36厘米,若长减少4厘米,宽增加2厘米,长方形就变成正方形,求正方形的边长。
13 用一根20厘米的铁丝围成一个长方形(1)使得长方形的长比宽大2.6厘米,此时,长方形的长、宽各是多少厘米?(2)使得长方形的长与宽相等,此时正方形的边长是多少厘米?
14 要锻造一个半径为5厘米,高为8厘米的圆柱形毛胚,应截取半径为4厘米的圆钢多长?
15 .现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?
16 猜想:①在周长不变时,如果围成的图形是长方形,那么当长宽之差越来越小时,长方形
的面积越来越______(填“大”或“小”),②在周长不变时,所围成的各种平面图形中,______的面积最大.。
