一元二次函数函数的根的分布(有图)
高考数学复习课件:二次函数根的分布+(共13张PPT)

求实数m的取值范围,使关于x的一元二次方程
x22(m-1)x 2m 6 0 (1)有两个正根 (2)有一个根为0,一个根为正根
求实数m的取值范围,使关于x的一元二次方程
x22(m-1)x 2m 6 0 (1)有两个正根
(2)有一个根为0,一个根为正根
(3)有两个根,且都大于
1
5 4
(7)一个根在(0,1)内,一个根在(1,4)内
7 , 5 5 4
1.若方程x2 (k 2)x k 0的两根均在(-1,1)内, 求k的取值范围.
2.若一元二次方程mx2 (2m-1)x-m 2 0 的两个实根都小于1,求m的取值范围.
一元二次方程根的分布
根的正负 考虑
判别式 韦达定理
考虑
根的大小
开口方向 判别式 对称轴 特殊点的函数值
1.已知方程 x2-11x m-2 0的两实根都大于 1, 求m的取值范围. 2.已知函数f(x) ex ,关于x的方程
x
f(2 x)-2af(x) a-1 0有四个相异的实根, 则a的取值范围为
3.已知函数 f(x) x2 (1-k)x-k 恰有一个零点 在区间(2,3)内,则实数k的取值范围为
,1
求实数m的取值范围,使关于x的一元二次方程
x22(m-1)x 2m 6 0 (1)有两个正根 (2)有一个根为0,一个根为正根 (3)有两个根,且都大于 1
(4)一个根大于2,一个根小于2 ,1
求实数m的取值范围,使关于x的一元二次方程
x22(m-1)x 2m 6 0
(1)有两个正根
(5)一个根小于2,一个根大于4
(6)有两个根,且都在( m的取值范围,使关于x的一元二次方程
x22(m-1)x 2m 6 0 (1)有两个正根 (2)有一个根为 0,一个根为正根
高二数学根的分布简单逻辑
例3:在边长为a的正方形ABCD中,AB、BC边上各有一 个动点Q、R,且|BQ|=|CR|,试求直线AR与DQ的 交点P的轨迹方程.
解:
交轨法 在直角坐标系内,已知矩形OABC的边长OA=a,OC=b,若D在 AO的延长线上,|DO|=a,设M、N分别是OC、BC边上的动点,使 OM:MC=BN:NC≠0,求直线OM与AN交点P的轨迹方程. 解:
石器时代sf / 石器时代sf
twc19tvu
户照进来的月光时而明亮,时而昏暗。耿正的内心随着月光的明暗变化,也时而清晰,时而迷茫兄妹三人已经默默地在大木床上躺了 好一会儿了,但似乎谁也不想先开口说话。良久,耿英轻轻地说:“哥,咱们的日常消费实在是不能再节俭了,但剩的钱不多了,咱 得赶快想办法赚钱啊!”耿直赶快说:“姐姐,我还可以再少吃一点儿!”耿正摸摸弟弟的头,轻轻地说:“又说傻话了不是!赚不 来钱,光知道扎住嘴巴怎么行啊。哥已经有想法了,只是还有些犹豫不决”看到哥哥一直沉吟着没有下文,耿英轻轻地说:“哥,我 知道,你是在打算利用你那一手好二胡来起步了。我没有说错吧!”耿正吃惊地问:“你怎么知道的?”耿英轻轻地叹一口气,说: “唉,这还不明摆着的事情嘛。连着几天了,你在那几家大酒店的门口望着那些个艺人出神,回来了又拿起咱们的那把二胡不说话我 知道,你一直犹豫不决是因为担心我,你不想让我做卖艺的人其实没有什么的,我也会一些呢,弟弟也能说会唱的最重要的是做这个 不需要本钱,最多也就是再买两个笛子而已咱们不是打听过了嘛,那些个在大酒店里献艺的人赚得银子不少呢咱们可以先做做看的。 等赚到的银子够做其他生意了,咱再改行做其他生意”听妹妹如此说,耿正终于下决心了。第二天一早,耿正兄妹三人洗漱收拾停当 以后,都穿上前年儿刚到汉口镇上时爹爹给他们买的另一套从来没有舍得穿过的新衣服。这套衣服比穿过的那一套略微宽大一些,尤 其耿直的那一套更是大了一号。因此,虽然过去一年半了,他们或多或少地都长高长大了一些,但穿起来一看,衣服都非常合适。耿 直难过地说:“爹怎么知道我会长大这么多啊!”耿英叹一口气,轻轻地说:“咳,爹是看着我们长大的啊!”看到弟弟妹妹提起爹 爹来又要难过了,耿正赶快提醒他们:“今儿个咱们是去应试的,要打起精神来才好,必须注意所有的言行举止啊!”耿英点点头, 轻轻地说:“哥你放心,我知道!”耿直也说:“我也知道!”看看再没有什么需要准备的了,耿正带上那把跟随他们转辗而来的心 爱的二胡,和弟弟妹妹一起,先去“梁计小饭店”吃了最简单的早饭。然后,兄妹三人就直接奔离十字大街不远的“盛元酒店”去了。 兄妹仨前几日在街面上转悠着寻找活儿干的时候,耿正就已经注意到了,这“盛元酒店”在景德镇上虽然算不上数一数二的大酒店, 但其生意却特别好,几乎每日里的午餐和晚餐饭点儿上都是桌桌满座,这就表明,这家酒店的人气儿好!而酒店的人气儿好,也就直 接映射出来,该酒店老板的人品应该不会错的。更重要的是,耿正还留意观察,发现这家酒店的伙计们,对那些来这里献艺的艺人们 都很尊重,客客气气迎进送出的。当然,那些经常来此献艺的几个艺
初中数学一元二次方程的实根分布
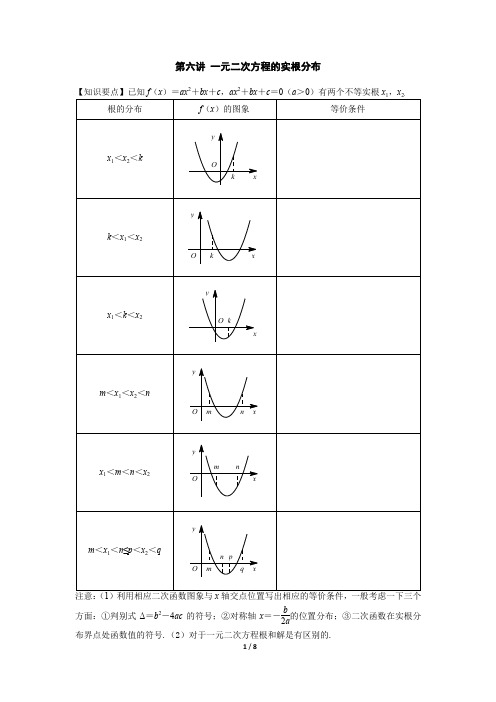
第六讲 一元二次方程的实根分布22.注意:(1)利用相应二次函数图象与x 轴交点位置写出相应的等价条件,一般考虑一下三个方面:①判别式Δ=b 2-4ac 的符号;②对称轴x =-b2a的位置分布;③二次函数在实根分布界点处函数值的符号.(2)对于一元二次方程根和解是有区别的.一、一点同侧两根【例1】若关于x的方程x2-(k+2)x+4=0有两个不等的负根,求实数k的取值范围.【练】若关于x的方程x2+(m+2)x+m+5=0有两个正数根,求实数m的取值范围.【例2】若关于x的方程kx2-2kx+(k-1)=0有两个正实数根,求实数k的取值范围.【练】若关于x的方程2(k+1)x2+4kx+3k-2=0有两个负实根,求实数k的取值范围.【例3】若关于x的方程x2-mx+(3+m)=0有两个大于1的根,求实数m的取值范围.【练】若关于x的方程mx2+(2m-1)x-m+2=0有两个小于1的根,求实数m的取值范围.二、一点异侧两根【例4】若关于x的方程4x2+(m-2)x+m-5=0的一正根和一负根,求实数m的取值范围.【练】若关于x的方程(2m+1)x2-2mx+m-1=0有一正根和一个负根,求实数m的取值范围.【例5】若关于x的方程mx2+(m+2)x+9m=0有两个实数根x1和x2,且x1<1<x2,求m的取值范围.【练】若关于x的二次方程2mx2-2x-3m-2=0的一个根大于1,另一个根小于1,求实数m的取值范围.三、一点一侧有根【例6】若关于x的方程x2-ax+4=0有正实根,则实数a的取值范围是【练】若方程x2+x+a=0至少有一根为非负实数,求实数a的取值范围.【例7】若关于x的方程ax2+2x+1=0至少有一个负实根,求实数a的取值范围.【练】若关于x的一元二次方程mx2+(m-3)x+1=0至少有一个正根,求m的取值范围.四、两点中间两根【例8】若关于x的方程x2-ax+2=0在区间(0,3)内有两个根,求实数a的取值范围.【练】若关于x的方程x2-2ax+a2-1=0的两个不等根在区间(-2,4)上,求实数a 的取值范围.【变】若关于x的二次方程(m-1)x2+(3m+4)x+m+1=0的两个根属于(-1,1),求实数m的取值范围.【例9】当实数a和b满足何条件时,关于x的方程x2+ax+b=0在区间[-2,2]上有两个实根?【练】若关于x的方程x2+(m-1)x+1=0有两个相异的实根,且两根均在区间[0,2]上,求实数m的取值范围.【变】若抛物线y=x2+ax+2与连接两点M(0,1)、N(2,3)的线段有两个相异的交点,求a的取值范围.五、两点中间一根【例10】已知关于x的二次方程(2m+1)x2-2mx+m-1=0有且只有一个实根属于(1,2),且x=1,x=2都不是方程的根,求实数m的取值范围.【练】若关于x的二次方程(3m-1)x2+(2m+3)x-m+4=0有且只有一个实根属于(-1,1),求实数m的取值范围.【变】已知点A、B的坐标分别为(1,0)、(2,0),若二次函数f(x)=x2+(a-3)x+3的图象与线段AB恰有一个交点,求实数a的取值范围.【例11】若关于x的方程ax2+x+a-3=0在(-2,0)上有且只有一个实根,求实数a 的取值范围.【练】若关于x的方程mx2+(2m-3)x+4=0有且只有一个小于1的正根,求实数m的取值范围.六、两点中间有根【例12】若方程x2-2mx+m-1=0在区间(-2,4)上有根,求实数m的取值范围.【练】若关于x的二次方程x2+2mx+2m+1=0在区间(0,2)内至少存在一根,求实数m的范围.【变】已知关于x的方程2ax2+2x-a-3=0在区间[-1,1]上有根,求实数a的取值范围.【例13】集合A={(x,y) | y=x2+mx+2},B={(x,y) | x-y+1,且0≤x≤2},若A∩B≠∅,求实数m的取值范围.【练】已知抛物线y=2x2-mx+m与以点(0,0)和(1,1)为端点的线段(除去两个端点)有公共点,求实数m的取值范围.七、两点隔两根【例14】关于x的方程4x2+(m-2)x+m-5=0的一根小于1,另一根大于2,求实数m的取值范围.【练】若关于x的方程x2+(2m-1)x+m-6=0的一个根不大于-1,另一个根不小于1,求实数m的取值范围.【变1】已知方程(a-1)x2+(2a-6)x-4a+1=0的两根为x1,x2,且-1<x1<1<x2,求实数a的取值范围.【变2】若关于x的方程2x2-(m-2)x-2m2-m=0的两根在区间[0,1]之外,求实数m 的取值范围.八、多点隔两根【例15】若关于x方程x2-mx-m+3=0的一根在区间(0,1)内,另一根在区间(1,2)内,求实数m的取值范围.【练】已知关于x的方程x2+2mx+2m+1.若方程有两个根,其中一个在区间(-1,0),另一根在区间(1,2)内,求m的范围.【变】若mx2-(m-1)x+m2-m+2=0的两根分别在0<x<1和1<x<2的范围内,求实数m的取值范围.【作业】1、已知关于x的方程x2+(m-3)x+m=0,分别在下列条件下,求实数m的取值范围.(1)方程有两个正根;(2)方程两个根均小于1;(3)方程的一个根大于1,另一个根小于1;(4)方程的两个根均在(0,2)内;(5)方程的一个根小于2,另一个根大于4.(6)方程的一个根在(-2,0)内,另一个根在(0,4)内;(7)方程有一个正根,一个负根且正根的绝对值较大;(8)方程的两个根有且仅有一个在(0,2)内;2、若方程x2-4|x|+5=m有四个互不相等的实数根,求实数m的取值范围.3、设|a|=1,b为整数,关于x的方程ax2-2x-b+5=0有两个负实数根,求b的值.4、已知二次函数f(x)=(m+2)x2-(2m+4)x+3m+3与x轴有两个交点,分别在点(1,0)左右两边,求实数m的取值范围.5、求实数m的取值范围,使关于x的方程x2+2(m-1)x+2m+6=0至少有一个正根.6、如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,求实数m的取值范围.7、已知关于x的方程x2+2mx+2m+1=0.若方程两根均在区间(0,1)内,求实数m的取值范围.8、若关于x的方程7x2-(m+13)x+m2-m-2=0在区间(0,1)、(1,2)上各有一个实根,求实数m的取值范围.9、已知关于x的方程x2+(3m-1)x+3m-2=0的两根都属于(-3,3),且其中至少有一个根小于1,求实数m的取值范围.10、求证:关于x的方程3ax2+2bx-(a+b)=0在(0,1)内至少有一个实根.。
二次函数图像解题——根的分布

其交点横坐标便是方程的解,由图知: k 4时, 无解; k = 4或k 3时,有两解; 4 k 3时有四个解; k 3时有三个解.
3
4
y
x
结论: 一元二次方程 ax2 bx c 0(a 0) 在区间上的
实根分布问题.
() 1 一元二次方程有且仅有一个实根属于(m, n)的 充要条件是: f (m) f (n) 0. b 2 4ac 0 a f ( m) 0 a f ( n) 0 m b n 2a
(6) x1,x2有且只有一个根在(k1 , k2)内
k1
k2
f (k1 ) f (k2 ) 0
k1
k2
0 或 b k1 k2 2a
k1
k2
f ( k1 ) 0 或 b k1 k2 k1 2a 2
k1
f ( k2 ) 0 或 k1 k2 b 2 2a k2 k2
(2) 一元二次方程两个实根都属于(m, n)的充要条件是:
(3) 一元二次方程两个实根分别在(m, n)两侧的
a f ( m) 0 充要条件是: a f ( n) 0 (4)一元二次方程两个实根分别在(m, n)同一侧的 充要条件是: 分两类: b 2 4ac 0 () 在(m, n)右侧 a f (n) 0 b n 注:前提 m,n 2a 不是方程(1) b 2 4ac 0 () 在(m, n)左侧 a f (m) 0 b m 2a
不等式组
2 x 变式题:m为何实数值时,关于x的方程 mx (3 m) 0
有两个大于1的根.
一元二次方程的根的分布

情形1 方程根的零分布 :
结论1 一元二次方程ax 2 bx c 0(a 0)有两个正根.
b2 x1 0 x 2 0 x1 x 2 y x1 x 2
c0 O x1
4ac 0 b 0 a c 0 a
2
k的根.
y
a0 0 x2 b k 2a
a0 0 x2 O b 0 k 2a
k x1 O
x
k x1
x
情形2: 方程根的k分布
结论2 一元二次方程ax 2 bx c 0(a〉 有两个小于 0) k的根. b 2 4ac 0 b 2 4ac 0 x1 k ( x1 k ) ( x 2 k ) 0 b k x2 k ( x k )( x k ) 0 2a 1 2
x x
一个正根和一个负根, 求k的范围。
x
结论4 一元二次方程ax bx c 0(a 0)在区间
2
(k1 , k2 )内有且只有一根x1.即k1 x1 k2
f (k1 ) f (k 2 ) 0
y
f (k1 ) 0
a0
x1 O k1
k2
x2
x
f (k 2 ) 0
结论4 一元二次方程ax bx c 0(a〉 的根满足 0)
求函数的零点有两种方法: ①代数法:求方程f(x)=0的实数根; ②几何法:将它与函数y=f(x)的图象联 系起来,并利用函数的性质找出零点。
连续函数在某个区间上存在零点的判别方法:
如果函数y=f(x)在区间[a,b]上的图 象是连续不断一条曲线,并且有 f(a)· f(b)<0,那么,函数y=f(x)在区间 (a,b)内有零点.即存在c∈(a,b),使得 f(c )=0,这个c也就是方程f(x)=0的根.
根的个数判定及一元二次方程根的分布

0 0
(1)已知方程 x2 (m 2)x 2m1 0 有一实根在0和1之间
练 另一实根在之外,求 m 的取值范围。 习 (2)已知关于 x 的方程 x2 (m 2)x 2m 0
的两根为 、 且满足 0 1 ,求 m的取值
范围。
(3)若方程 x2 (k 2)x k 0 的两实根均在区间
练习
已知关于x的一元二次 x2 2m x 2m 1 0
(1)若方程两根均为正,求m的取值范围; (2)若方程两根均为负,求m的取值范围; (3)若方程的一根为正另一根为负,求m范围;
(二)k分布
1.两根均大于k的条件
b2 4ac 0
b 2a
k
af (k ) 0
3.一根大于k一根小于k
比2小,求 m 的取值范围。
(三)区间分布
1. 一个根在区间内另一根在区间外
f (k1) f (k2) 0
2.两根均在区间内
b2 4ac 0
af (k1) 0
Байду номын сангаас
af k1
(k2) 0 b
2a
k2
3.两根分别位于两区间内
f f
(k1 ( p1
) )
f f
(k2 ) ( p2 )
2.两根均小于k的条件呢?
的条件
af (k) 0
练习
(1)已知方程 x2 11x m 2 0 的两实根都大于1,求
m 的取值范围。
(2)若一元二次方程 mx2 (m 1)x 3 0 的两实根都小于2,求 m 的取值范围。
(3)已知方程 x2 2m x 2m2 3 0 有一根大于2,另一根
在[-1,3]内有实根,求a的取值范围;
二、一元二次方程的根的分布
一元二次方程根的分布情况归纳(完整版)

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200axbx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
二次函数根的分布和最值(好)

二次方程根的分布归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =- (2)闭区间二次函数y=f(x)在闭区间[x1, x2]上内有唯一实根的充要条件是什么? 补充:这里x1<x2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(8) 两个根有且仅有一个在(0 . 2)内
y
y
. .. . . .
O
2
x
O
2
x
f (0) f (2) m(3m 2) 0
2020/4/4
9
x2+(m-3)x+m=0
y
y
. .. . ..
O
2
x
O
2
x
f (0) f (2) m(3m 2) 0 0 m 2
或
f
(2)
0且另一根在(0,2)
f
(1)
2m
2
0
f (3) 4m 0
y
.. ..
-2 O 1
m无解
2020/4/4
.
3x
11
一元二次方程ax2+bx+c=0 (a>0)的根的分布
两个根都小于k 两个根都大于k
一根小于K, 一根大于K
y
y
y
O
kx
Ok
k
x
O
x
0
b 2a
k
f (k ) 2020/4/4 0
0
b 2a
3 m 0 m 0
.
m m 9 2020/4/4
y
. Ox 3
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
(3) 两个根都小于1
(m 3)2 4m 0
b 2a
3m 2
1
f (1) 2m 2 0
m m 9 2020/4/4
y
. .. O 1x 4
(5) 一个根大于1,一个根小于1
y
f (1) 2m 2 0
m m 1
. ..
O
1
x
2020/4/4
6
一元二次方程的根的分布
例:已知方程x2+(m-3)x+m=0,求m的范围
(6) 两个根都在(0,2)内
(m 3)2 4m 0
y
0
3
m
2
2
f (0) m 0
.
f (2) 3m 2 0
O
.. 2x
m 32 2020/4/4
m
1
7
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
(7) 一个根小于0,另一根大于2
y
f(0)0
f
(
2
)
0ห้องสมุดไป่ตู้
m0
2020/4/4
. .. O2 x 8
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
k
f (k ) 0
f(k)<0,
12
一元二次方程ax2+bx+c=0 (a>0)的根的分布
两 个 根 都1 2 在 一个根小于k1, (k1,k2 )内 一个根大于k2
x1∈(m,n) x2∈(p,q)
y
O
k1
k2 x
y
k1
O
k2 x
y
O
m
np
q x
0
k
1
b 2a
k2
f
(k 1
)
0
f(k1)f(k2)<0
m
2 3
3 x2
1 3
或 f (0) 0且另一根在(0,2) m 0 x2 3 舍
0 m 2 综上: 2020/4/4
10
3
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
(9)一根在(-2,0)内,另一根在(1,3)内
f (2) m 10 0
f (0) m 0
一元二次方程的根的分布
例:已知方程x2+(m-3)x+m=0,求m的范围
(4) 两个根都大于 1
2
y
(m 3)2 4m 0
b 2a
3 m 2
1 2
f
(1) 2
6m 5 4
0
. .
O1
. x
m 5 m 1
6 2020/4/4
2
5
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
20f20(/4k/4 2 ) 0
f (m) 0
f (n) 0
f
(
p)
0
f (q) 013
2020/4/4
1
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
(1)两个正根
(m 3)2 4m 0
3 m 0
m 0
y
..
O
x
m 0 m 1
2020/4/4
2
一元二次方程的根的分布 例:已知方程x2+(m-3)x+m=0,求m的范围
(2)有两个负根
(m 3)2 4m 0
