第3章内压薄壁容器的应力分析
第3章 回转薄壳应力分析

1.基本概念 ◦ (3)中间面:中间面是与壳体内外表面等距离的中曲面,内外表面间的 法向距离即为壳体壁厚。 ◦ (4) 母线:回转壳体的中间面是由平面曲线绕回转轴旋转一周而成的, 形成中间面的平面曲线称为母线。 (5) 经线:过回转轴作一纵截面与壳体 曲面相交所得的交线。经线与母线的 形状完全相同。 (6) 法线:过经线上任意一点M垂直于 中间面的直线,称为中间面在该点的 法线。法线的延长线必与回转轴相交。
σm
σθ
pa a 2δ b
pa ❖ 椭圆壳体的赤道位置x=a处: σm 2δ
σθ
pa 2δ
2
a2 b2
❖ (1)椭圆封头的中心位置x=0处,经向应力和环向应力相等即:σm=σθ;
❖ (2) 经向应力σm恒为正值,且最大值在x=0处,最小值在x=a处。
❖ (3) 环向应力σθ,在x=0处,σθ>0;在x=a处有三种情况:
15
❖ 典型回转壳体的第一、第二曲率半径举例
D
R
DM M
※※※【注意】组合壳体的交界点的第一、第二曲率半径采用分别讨论 的方法确定!
16
2.基本假设 除假定壳体是完全弹性的,即材料具有连续性、均匀性和各向同性; 薄壁壳体通常还做以下假设使问题简化: ◦(1) 小位移假设 壳体受力以后,各点的位移都远小于壁厚。壳体变形 后可以用变形前的尺寸来代替。 ◦(2) 直法线假设 在变形前垂直于中间面的直线段(法线),在变形后仍 保持直线,并垂直于变形后的中间面。变形前后的法向线段长度不变, 沿厚度各点的法向位移均相同,变形前后壳体壁厚不变。 ◦(3) 不挤压假设 壳体各层纤维变形前后相互不挤压。壳壁法向(半径 方向)的应力与壳壁其他应力分量比较是可以忽略的微小量,其结果 就变为平面问题。
第三章-内压薄壁容器的应力

纬线
平行圆
25
1、基本概念 第一曲率半径R1:过该点的经线在该点的曲率 半径。
第一曲率半径
O
M
M
M
O
N
26
1、基本概念 第一曲率半径R1和第二曲率半径R2
过M点与回转轴作一平面,即 MAO平面,称为经线平面。在经 线平面上,经线AB’上M点的曲 率半径称为第一曲率半径,用R1 表示 ;
后者忽略为零。
9
(2)无力矩理论,即薄膜理论。
假定壳壁如同薄膜一样,只承受拉应力和压应 力,完全不能承受弯矩和弯曲应力。壳壁内的应 力即为薄膜应力。这时壳体的应力状态仅由法向
力N、N确定。
在工程实际中,理想的薄壁壳体是不存在的, 因为即使壳壁很薄,壳体中还会或多或少地存在 一些弯曲应力,所以无力矩理论有其近似性和局 限性。
过N点作一与回转轴垂直的平面 ,该平面与回转轴的交线是一个 圆,称为回转曲面的平行圆,也 称为纬线,此平行圆的圆心一定 在回转轴上;
通过M点的法线垂直于经线AB’
的平面与中见面相割形成的曲线
EMF,这一曲线在M点的曲率半
径称为第二曲率半径,用R2表示
;
27
就普通回转体而言,用与轴线垂直 的平面截取得到的壳体截面与用上 述圆锥面截取得到的壳体截面是不 一样的,前者是壳体的横截面,并 不能截出壳体的真正厚度(圆柱形壳 体除外),而后者称为壳体的锥截面 ,截出的是回转体的真正壁厚;
弯曲应力比薄膜应力小很多,可略去不计。
12
二、 基本概念与基本假设
1. 基本概念 回转壳体:平面内平滑曲线绕平面内固定轴线旋转360° 形成的壳体。没有拐点
内压薄壁容器的应力分析讲解

3.1 薄膜应力理论 3.1.1薄壁容器及其应力特点
2018/10/3 1
筒体段:经线仍保持 直线,与封头联接 处受到约束。 1-薄膜应力 2、3-边缘应力
2018/10/3
2
3.1.2 基本概念与基本假设
1. 基本概念 (1) 旋转壳体 :壳体中面(等分壳体厚度) 是任意直线或平面曲线作母线,绕其同平面 内的轴线旋转一周而成的旋转曲面。
2018/10/3
3
(2) 轴对称 壳体的几何形状、约束条件和所 受外力都是对称于某一轴。 化工用的压力容器通常是轴对称 问题。
2018/10/3 4
2018/10/3 7
(3)旋转壳体的几何概念
母线与经线 法线、平行圆 第一曲率半径:经线曲率半径 第二曲率半径:垂直于经线的平面与中面相割形成的曲 线BE的曲率半径
2018/10/3
5
回转壳中面的几何参数
图2-2 回转壳中面的几何参数
2018/10/3 6
2.基本假设
假定壳体材料有连续性、均匀性和各向同性,即 壳体是完全弹性的。 (1)小位移假设 各点位移都远小于厚度。可用变形前尺寸代替 变形后尺寸。变形分析中高阶微量可忽略。 (2)直线法假设 变形前垂直于中面直线段,变形后仍是直线并 垂直于变形后的中面。变形前后法向线段长度不 变。沿厚度各点法向位移相同,厚度不变。 (3)不挤压假设 各层纤维变形前后互不挤压。
第三章 内压薄壁容器应力云南大学2010版.ppt

代入微体平衡方程式
R
R
==Sp
PP,RR22得==
P2PDD
2
31
PR2 PD
32
圆柱壳壁内应力分布
2 m
33
讨论1:薄壁圆筒上开孔的有利形状
图3-10 薄壁圆筒上开孔
① 环向应力是经向应力 的2倍,所以环向承受应 力更大,环向上就要少削 弱面积,故开设椭圆孔时, 椭圆孔之短轴平行于筒体 轴线,见图
25
2、回转壳体的经向环向应力分析
图3-8 回转壳体的环向应力分析
内压力p在微体abcd上所产生的外力 的合力在法线n上的投影为Pn
Pn pdl1 dl2
在bc与ad截面上经向应力 的m 合力 在法线n上的投影为Nmn
N mn
2 m Sdl2
sin
d1
2
在ab与cd截面上环向应力 的 合力 在法线n 上的投影为 Nn
O1
表示,在图上为线段O1A。
母线
A R1
第一曲率半径
17
母线
回转轴与第二曲率半径
围绕回转轴,可形成一个曲 回转轴 面 , 第 一 曲 率 半 径 O1A 上 到
回转轴O的曲率半径称为第
R1 O
二曲率半径,以R2表示,在
图上为线段OA。
O1
A R2
第一曲率半径
第二曲率半径
18
周向
第一曲率半径与母 线有关;
第三章 内压薄壁容器的应力分析
教学重点:
薄膜理论及其应用
教学难点:
对容器的基本感性认识
1
第一节 回转壳体的应力分析—薄膜应力理论
薄壁容器
第三章-内压薄壁容器设计
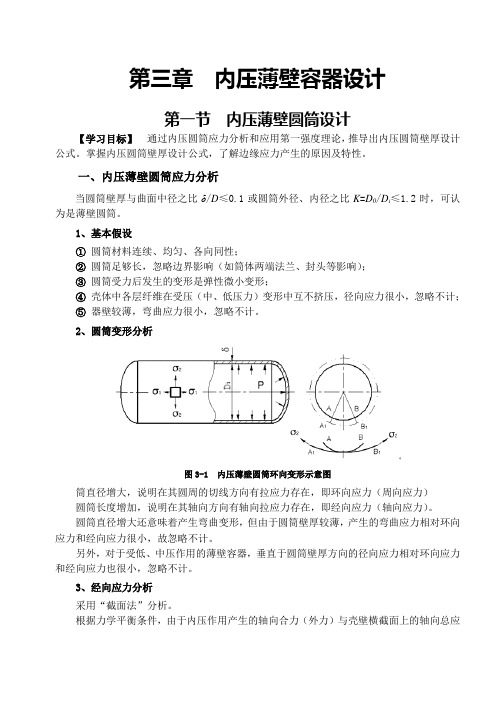
第三章内压薄壁容器设计第一节内压薄壁圆筒设计【学习目标】通过内压圆筒应力分析和应用第一强度理论,推导出内压圆筒壁厚设计公式。
掌握内压圆筒壁厚设计公式,了解边缘应力产生的原因及特性。
一、内压薄壁圆筒应力分析当圆筒壁厚与曲面中径之比δ/D≤0.1或圆筒外径、内径之比K=D0/D i≤1.2时,可认为是薄壁圆筒。
1、基本假设①圆筒材料连续、均匀、各向同性;②圆筒足够长,忽略边界影响(如筒体两端法兰、封头等影响);③圆筒受力后发生的变形是弹性微小变形;④壳体中各层纤维在受压(中、低压力)变形中互不挤压,径向应力很小,忽略不计;⑤器壁较薄,弯曲应力很小,忽略不计。
2、圆筒变形分析图3-1 内压薄壁圆筒环向变形示意图筒直径增大,说明在其圆周的切线方向有拉应力存在,即环向应力(周向应力)圆筒长度增加,说明在其轴向方向有轴向拉应力存在,即经向应力(轴向应力)。
圆筒直径增大还意味着产生弯曲变形,但由于圆筒壁厚较薄,产生的弯曲应力相对环向应力和经向应力很小,故忽略不计。
另外,对于受低、中压作用的薄壁容器,垂直于圆筒壁厚方向的径向应力相对环向应力和经向应力也很小,忽略不计。
3、经向应力分析采用“截面法”分析。
根据力学平衡条件,由于内压作用产生的轴向合力(外力)与壳壁横截面上的轴向总应力(内力)相等,即:124δσππD p D =由此可得经向应力: δσ41pD=图3-2 圆筒体横向截面受力分析4、环向应力分析 采用“截面法”分析。
图3-3 圆筒体纵向截面受力分析根据力学平衡条件,由于内压作用产生的环向合力(外力)与壳壁纵向截面上的环向总应力(内力)相等,即:22δσL LDp = (3-3)由此可得环向应力: δσ22pD= (3-4) 5、结论通过以上分析可以得到结论:122σσ=,即环向应力是经向应力的2倍。
因此,对于圆筒形内压容器,纵向焊接接头要比环向焊接接头危险程度高。
在圆筒体上开设椭圆形人孔或手孔时,应当将短轴设计在纵向,长轴设计在环向,以减少开孔对壳体强度的影响。
化工设备机械基础:第三章 内压薄壁容器的应力分析

上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
代入微体平衡方程式及区域平衡方程式并求解得:
m
PD
4
,
PD
4
推论:对相同的内压,球壳的环向应力要比同直径、 同厚度的圆筒壳的环向应力小一半,这是球壳显著的 优点。
三、受气体内压的椭球壳(椭圆形封头)
上一内容 下一内容 回主目录
(一)壳体理论的基本概念 壳体在外载荷作用下,
要引起壳体的弯曲,这种变 形由壳体内的弯曲和中间面 上的拉或压应力共同承担, 求出这些内力或内力矩的理 论称为一般壳体理论或有力 矩理论,比较复杂;
上一内容 下一内容 回主目录
返回
2020/12/14
第一节 薄膜应力理论
但是,对于壳体很薄,壳体具有连续的几何曲面,所 受外载荷连续,边界支承是自由的,壳体内的弯曲应 力与中间面的拉或压应力相比,可以忽略不计, 认为壳体的外载荷只是由中间面的应力来平衡,这种 处理方法,称为薄膜理论或无力矩理论。 1、有力矩理论 2、无力矩理论(应用无力矩理论,要假定壳体完全弹 性,材料具有连续性、均匀性各各向同性,此外,对 于薄壁壳体,通常采用以下三点假设使问题简化) 1)小位移假设 2)直法线假设 3)不挤压假设
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
一、受气体内压的圆筒形壳体
R1
R2
r
D 2
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
由区域平衡方程式
m
pR2
2
PD
4
代入微体平衡方程式
化工设备机械基础作业答案

《化工设备机械基础》习题解答二、填空题1、钢板卷制的筒体和成型封头的公称直径是指它们的(内)径。
2、无缝钢管做筒体时,其公称直径是指它们的(外)径。
3、查手册找出下列无封钢管的公称直径DN是多少毫米4、压力容器法兰标准中公称压力PN有哪些等级5、管法兰标准中公称压力PN有哪些等级第三章内压薄壁容器的应力分析一、名词解释A组:⒈薄壁容器:容器的壁厚与其最大截面圆的内径之比小于的容器。
⒉回转壳体:壳体的中间面是直线或平面曲线绕其同平面内的固定轴线旋转360°而成的壳体。
⒊经线:若通过回转轴作一纵截面与壳体曲面相交所得的交线。
⒋薄膜理论:薄膜应力是只有拉压正应力没有弯曲正应力的一种两向应力状态,也称为无力矩理论。
⒌第一曲率半径:中间面上任一点M处经线的曲率半径。
⒍小位移假设:壳体受力以后,各点位移都远小于壁厚。
⒎区域平衡方程式:计算回转壳体在任意纬线上径向应力的公式。
⒏边缘应力:内压圆筒壁上的弯曲应力及连接边缘区的变形与应力。
⒐边缘应力的自限性:当边缘处的局部材料发生屈服进入塑性变形阶段时,弹性约束开始缓解,原来不同的薄膜变形便趋于协调,边缘应力就自动限制。
二、判断题(对者画√,错着画╳)A组:1. 下列直立薄壁容器,受均匀气体内压力作用,哪些能用薄膜理论求解壁内应力哪些不能(1) 横截面为正六角形的柱壳。
(×)(2) 横截面为圆的轴对称柱壳。
(√)(3) 横截面为椭圆的柱壳。
(×)(4) 横截面为圆的椭球壳。
(√)(5) 横截面为半圆的柱壳。
(×)(6) 横截面为圆的锥形壳。
(√)2. 在承受内压的圆筒形容器上开椭圆孔,应使椭圆的长轴与筒体轴线平行。
(×)3. 薄壁回转壳体中任一点,只要该点的两个曲率半径R R 21=,则该点的两向应力σσθ=m 。
(√)4. 因为内压薄壁圆筒的两向应力与壁厚成反比,当材质与介质压力一定时,则壁厚大的容器,壁内的应力总是小于壁厚小的容器。
《化工机械基础》第3章 内压薄壁容器的应力
3.1.2 基本概念与基本假设
1. 基本概念
• 回转壳体
——由直线或平 面曲线绕其同 平面内的固定 轴旋转3600而 成的壳体。
4
几个典型回转壳体
5
轴对称——指壳体的几何形状、约束条件和
所受外力都对称于回转轴。
与壳体内外表面等距离的曲面
母线:
6
法线:
经线:
纬线(平形圆):
7
8
2.基本假设:
1
薄膜理论与有矩理论概念:
计算壳壁应力有如下理论: (1)无矩理论,即薄膜理论。 假定壳壁如同薄膜一样,只承 受拉应力和压应力,完全不能承 受弯矩和弯曲应力。壳壁内的应 力即为薄膜应力。
2
(2)有矩理论。壳壁内存在除拉应力或压 应力外,还存在弯曲应力。 在工程实际中,理想的薄壁壳体是不 存在的,因为即使壳壁很薄,壳体中还 会或多或少地存在一些弯曲应力,所以 无矩理论有其近似性和局限性。由于弯 曲应力一般很小,如略去不计,其误差 仍在工程计算的允许范围内,而计算方 法大大简化,所以工程计算中常采用无 矩理论。
D
摺边部分
R 2 r1
2 sin
- r1
32
③ 碟形壳的应力分布
1.b点和c点的R1,R2如何变化? 2.碟形壳与圆筒壳连接点处应力状态如何?
33
3.3 内压容器边缘应力简介
3.3.1 边缘应力概念
压力容器边缘——指“不连续处”,主要是几何不连续及载荷(支 撑)不连续处,以及温度不连续,材料不连续等处。 例如:几何不连续处:
)
pa
※两向应力相等,均为拉应力。
x=a, 即椭球壳的边缘处,
2S pa 2S (2 a b
2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dl1 R1 sin d1 R1 d1
率半径,用R2表示;
若自K2点向回转曲面作一个与回转曲面正交的圆锥面,则该圆
锥面与回转曲面的交线也是一个圆——纬线;
就普通回转体而言,用与轴线垂直的平面截取得到的壳体截面 与用上述圆锥面截取得到的壳体截面是不一样的,前者是壳体
的横截面,并不能截出壳体的真正厚度(圆柱形壳体除外),而
后者称为壳体的锥截面,截出的是回转体的真正壁厚;径向应力作用面来自环向应力作用面
径向应力作用于筒体的横截面上,方向平行于筒体的轴线; 环向应力作用于筒体的纵截面上,方向为切线方向,每一点环 向应力的方向不同。
2. 内压圆筒薄膜应力的计算
2.1
环向应力的计算
外力在y轴方向上投影合力Py
dPy dP sin
Py dP sin Ri l P d sin 2Ri l P Di l P DlP
• 径向应力产生在经线方向,作用在圆锥面与壳体相割所形成的锥截
面上; • 不同纬线上各点的径向应力不同,而同一纬线上的径向应力相等。
4.2
环向应力的计算
•
由于所取单元体很小,可以认为ab、cd上 的环向应力相同,ad、bc上的径向应力也
相等,
ab dl1
ad dl2
Qm 2 m S dl2
内压圆筒径 向应力的计 算公式
m
PD 4S
2.3
圆筒环向应力与径向应力的关系
PD p 2S S 2 D
m
PD P 4S S 4 D
S/D体现着圆筒承压能力的高低,S/D越大,圆筒承压能力 越强。因此,看一个圆筒能耐多大的压力,不能光看它的 壁厚大小; 对于圆筒,其环向应力是径向应力的两倍;
0 0
Dil:承压曲面在假想纵截面的投影面积 ,实际上,
作用在任意曲面上的介质压力,其合力等于压力与该 曲面沿合力方向所得投影面积的乘积,而与曲面形状
无关。
• 与介质内压P相平衡的是作用在单元体筒壁纵向剖面上
的内力的合力Ny :
N y 2S l
显然, Py N y
DlP 2Sl
F Pdl1 dl2
Q 2 S dl1
Pdl1 dl2 Qm sin
d1 d d d Q sin 2 Qm 1 Q 2 2 2 2 2
Pdl1 dl2 m S dl2 d1 S dl1 d 2
PD 2S
内压圆筒环向应 力的计算公式
2.2
径向应力的计算
• 作用在封头内表面上的外力,即介质压力在轴向的合力Pz,
不管封头形状如何,其值均为:
Pz
4
Di P
2
4
Di
内径
D2P
• 作用在圆筒形截面上的应力的合力Nz :
N z DS m
显然, Pz N z
4 D 2 P DS m
中间面:与壳体内外表面等距离的
中曲面;
法线:n,通过经线上任意一点M
垂直于中间面的直线,其延长线必 与回转轴相交。
过M点可作无数平面,每一平面与回转曲面 相交均有交线,每条交线都在M点有不同的曲率 半径,但我们只关心下面三个:
过M点与回转轴作一平面,即MAO平面,
称为经线平面。在经线平面上,经线AB’上
第一曲率半径R1的简单求法:经线的曲率半径;
第二曲率半径R2的简单求法:经线到回转轴的距离。
a b
R2=a? R2=b?
R2=a
3.2
基本假设
小位移假设:壳体受力以后,各点的位移远小于壁厚; 直线法假设:壳体变形前后直线关系保持不变; 不挤压假设:壳体各层纤维变形前后均互不挤压。
4. 任意回转体薄膜应力的计算
第3章 内压薄壁容器的应力分析
第一节、回转壳体的应力分析——薄膜理论
第二节、薄膜理论的应用 第三节、内压圆筒边缘应力的概念
第一节、回转壳体的应力分析 ——薄膜理论
1. 内压薄壁容器及其应力特点
薄壁容器:
S 0.1 Di
Do Di 2S S K 1 2 1.2 Di Di Di
①段:受压前后经线仍近似保 持直线,这部分只承受拉应力,
称为薄膜应力,没有弯曲应力。
②③ 段:由于筒体与封头的变 形不同,其中筒体变形大于封
头的变形,因此在这种连接处
形成了一种相互约束,从而导 致在附近产生附加的弯曲应力,
称为边缘应力。
本章重点介绍薄膜应力,简单 介绍边缘应力。
当圆筒容器承受内压力P作用以后,其直径要稍微增大,故圆筒内 的“环向纤维”要伸长,因此在筒体的纵截面上必定有应力产生, 此应力称为环向应力,以 表示; 由于容器两端是封闭的,在承受内压后,筒体的“纵向纤维”也 要伸长,则筒体横向截面也有应力产生,此应力称为径向应力, m 以 表示。
M点的曲率半径称为第一曲率半径,用R1表 示;
过M点作一与回转轴垂直的平面,该平面与
回转轴的交线是一个圆,称为回转曲面的平 行圆,也称为纬线,此平行圆的圆心一定在 回转轴上; 过M点再作一与经线AB’在M点处切线相垂 直的平面,该平面与回转曲面相交又得一曲 线,这一曲线在M点的曲率半径称为第二曲
4.1 径向应力的计算
Pz
4
D2P
N z m DS sin
4
D 2 P m DS sin
R2
D D 2 R2 sin 2 sin
PR2 m 2S
• 这个公式是计算承受气体内压的回转体在任意纬线上经向应力的一 般公式,称为区域平衡方程式;
若需要在圆筒上开椭圆孔,应按照a还是b开孔呢?
对于圆筒,环向应力是径 向应力的两倍,开椭圆孔时, 应按照b开,以尽量减少纵截 面的削弱程度,从而使环向应 力增加少一些。
a
b
3. 回转体的基本概念与基本假设
3.1 回转体的基本概念
母线:AB 经线:AB’,如果通过回转轴作一
纵截面与壳体曲面相交所得的交线, 与母线的形状相同;
