第二章 内压薄壁圆筒应力分析1
第2章应力分析

29
2.2.4 无力矩理论的应用
D、椭球形壳体
图2-8 椭球壳体的应力
30
2.2.4 无力矩理论的应用
推导思路:
椭圆曲线方程
R1和R2
式(2-5)(2-6)
,
6
2.2 回转薄壳应力分析
2.2.1 薄壳圆筒的应力 2.2.2 回转薄壳的无力矩理论 2.2.3 无力矩理论的基本方程 2.2.4 无力矩理论的应用
7
2.2.1 薄壳圆筒的应力
基本假设:
A
壳体材料连续、均匀、各向同性; 受载后的变形是弹性小变形; 壳壁各层纤维在变形后互不挤压;
应力沿壁t 厚方向均匀分布。
p
r t
∴
D 2t
p
D 2t
p0
H
y g
D 2t p0
0 yH
H y H0
可见
2.2.4 无力矩理论的应用
二、储存液体的回转薄壳
球形壳体
有力矩理论或 弯曲理论 (静不定)
无力矩理论所讨论的问题都是围绕着中面进行的。因壁很薄,沿 壁厚方向的应力与其它应力相比很小,其它应力不随厚度而变,因 此中面上的应力和变形可以代表薄壳的应力和变形。
16
2.2.3 无力矩理论的基本方程
一、壳体微元及其内力分量
微元体:
abdc
经线ab弧长: dl1 R1d
14
2.2.2 回转薄壳的无力矩理论
二、无力矩理论与有力矩理论
平行圆
N
经线
a.
b.
c.
15
浅谈内压薄壁筒形容器应力分析的应用

浅谈内压薄壁筒形容器应力分析的应用《化工设备》课程是技校化机安装专业的技术基础课,而学习内压薄壁筒形容器的应力分析是学好设备课的基础。
应力分析的目的不仅仅是让学生学会内压薄壁筒形容器的应力大小的计算方法及应力分布问题,更重要的是如何运用应力分析的结果去解决实际问题,这也是摆在理论课教师面前的一个难题。
下面,笔者就这个实际问题谈谈自己粗浅的认识和体会。
一应用于内压圆筒纵、环焊缝的焊接质量要求上纵焊缝是钢板卷制完成后形成筒节的连接焊缝,该焊缝受环向应纵焊缝力(环向焊缝是两个筒节之间连接时施焊的焊缝),该焊缝受轴向应力环焊缝(见图 1)。
那么内压圆筒纵、环焊缝的焊接质量要求和应力分析有何关系呢?由内压圆筒的受力分析可知,对一平均径为 D,壁厚为δ的内压筒体,在内部介质压力为 P 时,其器壁受有二向应力状态,一个是沿轴线方向的有使其筒壁纵向纤维拉长的轴向应力σz,一个是与筒体轴线垂直的平面上有使筒体直径增大的环向应力σθ,通过截面分析法得出这二向应力的计算公式分别是σz(轴力)=PD/4δ0、σθ(环力)=PD/2δ0。
又由于纵焊缝受环向应力,环焊缝受轴向应力,且环向应力是轴向应力的两倍,故纵焊缝受到的力大,所以容易开裂,则其焊接时质量要求就高。
但在学习中,许多同学误认为环焊缝受环向应力,纵焊缝受轴向应力,所以环焊缝质量要求高,这是不正确的认识。
教师在讲解时应从应力分析的观点入手,准确分析纵、环焊缝的受力,才可得出正确的结论。
二应用于椭圆形人孔的设置方位上这个问题是我们在实际工作中经常碰到的问题,同时也是教学中的难点问题。
每当讲解该问题时,我都会画出两种方案图,让同学们去讨论,然后选其中一种方案去剖析,最终得到正确结论,两种方案图如图 2、图 3所示。
先假设图2的开设方法成立,然后分析椭圆形人孔侧视图投影面积A1,俯视图投影面积A2,由于在筒壁侧面投影面所受的应力为σθ,俯面投影面所受应力为σz,且侧面器壁受力为A1σθ,俯面器壁受力为A2σz,又由于 A1>A2、σθ>σz,故侧面器壁受力会更大,而俯面器壁受力更小,这会使器壁受力不均匀,增大了因开孔而对器壁产生的强度削弱,不符合等强度理论,因而图 2的开法是错误的,故图 3的开法显然是正确的,使俯面、侧面受力较均匀,从而减少开孔对强度的削弱。
第二章压力容器应力分析

《过程设备设计基础》教案2—压力容器应力分析课程名称:过程设备设计基础专业:过程装备与控制工程任课教师:第2章 压力容器应力分析§2-1 回转薄壳应力分析一、回转薄壳的概念薄壳:(t/R )≤0.1 R----中间面曲率半径 薄壁圆筒:(D 0/D i )max ≤1.1~1.2 二、薄壁圆筒的应力图2-1、图2-2 材料力学的“截面法”三、回转薄壳的无力矩理论1、回转薄壳的几何要素(1)回转曲面、回转壳体、中间面、壳体厚度 * 对于薄壳,可用中间面表示壳体的几何特性。
tpD td pR tpD Dt D p i 22sin 24422====⨯⎰θπθϕϕσσαασπσπ(2)母线、经线、法线、纬线、平行圆(3)第一曲率半径R1、第二曲率半径R2、平行圆半径r(4)周向坐标和经向坐标2、无力矩理论和有力矩理论(1)轴对称问题轴对称几何形状----回转壳体载荷----气压或液压应力和变形----对称于回转轴(2)无力矩理论和有力矩理论a、外力(载荷)----主要指沿壳体表面连续分布的、垂直于壳体表面的压力,如气压、液压等。
P Z= P Z(φ)b、内力薄膜内力----Nφ、Nθ(沿壳体厚度均匀分布)弯曲内力---- Qφ、Mφ、Mθ(沿壳体厚度非均匀分布)c、无力矩理论和有力矩理论有力矩理论(弯曲理论)----考虑上述全部内力无力矩理论(薄膜理论)----略去弯曲内力,只考虑薄膜内力●在壳体很薄,形状和载荷连续的情况下,弯曲应力和薄膜应力相比很小,可以忽略,即可采用无力矩理论。
●无力矩理论是一种近似理论,采用无力矩理论可是壳地应力分析大为简化,薄壁容器的应力分析和计算均以无力矩理论为基础。
在无力矩状态下,应力沿厚度均匀分布,壳体材料强度可以得到合理的利用,是最理想的应力状态。
(3)无力矩理论的基本方程a、无力矩理论的基本假设小位移假设----壳体受载后,壳体中各点的位移远小于壁厚。
考虑变形后的平衡状态时壳用变形前的尺寸代替变形后的尺寸直法线假设----变形前垂直于中面的直线变形后仍为直线,且垂直于变形后的中面。
内压薄壁圆筒容器讲解

pD
≤[σ]tφ
2
实际应用中还必须考虑以下几种情况:
(2)容器内径
内径Di,受力分析中的D是中面直径,D换算成 Di的形式,可得:
D Di
故有: p(Di ) ≤[σ]tφ 2
实际应用中还必须考虑以下几种情况:
(3)计算压力pc
确定筒体厚度的压力为计算压力pc
pc (Di ) t
(二)内压薄壁圆筒容器的强度条件与壁厚计算
按第一强度理论(最大主应力理论),
应使筒体上的最大应力小于或等于圆筒材 料在设计温度下的许用应力[σ]t。对于内压 圆筒,筒体上最大应力为环向应力σt,即:
t
pD
2
≤[σ]t
实际应用中还必须考虑以下几种情况:
(1)焊缝系数
筒体多由钢板卷焊而成,焊缝可能隐含 缺陷,使焊缝及其附近金属的强度低于钢 板本体强度。考虑这种影响引入焊接接头 系数φ:
2
所以内压薄壁圆筒体的计算厚度δ为:
pc Di
2[ ]t
pc
实际应用中还必须考虑以下几种情况:
(4)腐蚀裕量、钢板负偏差与壁厚
考虑到介质或周围大气对筒壁的腐蚀作用,在
确定钢板所需厚度时,还应在计算厚度基础上,加
上腐蚀裕量c2,得设计壁厚
d
C2
pc Di
2[ 差,将设计厚度加上厚度
职业教育应用化工技术专业教学资源库《化工设备认知与制图》课程
内压薄壁圆筒容器
吉林工业职业技术学院
内压薄壁圆筒容器
(一)内压薄壁圆筒容器的应力
设介质压力p,中间直径D,壁厚为δ。
变形分析:在内压力作用下,直径将会变大,长度 也会增长。 受力分析:经向拉力和环向拉力
(一)内压薄壁圆筒容器的应力
内压薄壁圆筒应力分析

mLeabharlann papD2
标准椭圆形封头内的最大薄膜应力与同直径、同厚度的
圆筒形壳体的最大薄膜应力相等。
2021/4/11
14
3.2 薄膜理论的应用
3.2.4 圆锥形壳体中的薄膜应力
圆锥形壳体的使用场合:容器的锥形封头,塔体之间 的变径段,储槽顶盖等。
2021/4/11
15
3.2.4 圆锥形壳体中的薄膜应力
锥形壳体的环向应力是经向应力的两倍。
锥形壳体的应力,随半锥角a的增大而增大,设计 时,a角要合适,不宜太大。
2021/4/11
17
3.2.4 圆锥形壳体中的薄膜应力
四种壳体(圆筒、球、椭球、锥形)的最大薄膜应 力:
max K
pD
2
圆筒形壳体和标准椭球形壳体:K=1 球形壳体:K=0.5 圆锥形壳体:K=1/cosa
值增大时,椭球壳上应力增加,受力情况变差。
2021/4/11
10
3.2.3、受气体内压的椭球壳(椭圆形封头)
2)当 a/b ≤2时,顶点处的应力值最大,赤道处的应力最 小;
顶点处
m
pa ( a)
2 b
赤道处
m
pa
2
pa a2
2 (2 b2 )
2021/4/11
pa (a )
σm
2 b
b 1 a 1.4
4
2 508 48
31.75MPa
Di
(3)下半封头(椭圆,a/b=2)最大应
力出现在顶点:
2021/4/11m
pa ( a)
2 b
2508/ 2 2 63.5MPa 28
19
3.2 薄膜理论的应用
五、受气体内压的碟形壳
内压薄壁容器的应力理论

矩形房间
适用于相对简单的结构,如 矩形房间,美术馆大厅等。
球形温室
适用于各种历史上已经建成 的球形建筑,如巴黎的拉丁 区地下停车场。
应力对薄壁容器的影响
1 测量和检测
2 应对压力波动
对薄壁容器进行应力检测,就可以定期 了解它的强度、稳定性和寿命等数据。
理解应力对薄壁容器的影响,可更好地 利用压实性,降低波动压力,并将其转 换为向设计用的方向施加压力,降低应 力的大小,提高容器的使用寿命。
总结
容器形变
应用应力理论可以避免薄壁容器的变形。
应力计算
运用适当的应力计算方法是保证薄壳结构完整性的核心。
应力影响
掌握应力对薄壁容器的影响,可以更好地利用压实性,降低压力波动,提高其使用寿命。
应力的传递和计算方法
圆筒形
直径方向的应力和周向的 应力不同,对应不同的计 算式,计算方便,适用性 广。
球形
球形内部承受的压力均等, 直接应用高中物理学中的 公式即可,简单有效。
其他形式
最常见的如球筒形容器, 非常复杂的容器需要结合 实践经验进行计算。
应力理论的适用范围
轴对称的薄壳结构
适用于任何几何形状的旋转 体,其表面轮廓相同,沿其 轴线对称。
实际工程中的应用案例
1
内燃机汽缸
是绝大多数机械装置的基础部件,应用广泛,如乘用车、船舶、小型飞机等机器 中都有它的身影。
2
地下储油罐
是油品市场之一,为了保护存储的石油、化工品等流体不泄漏,需要采用薄壳结 构的容器。
3
卫星外壳
是航天器中最复杂、最高科技含量的部分之一,具有优良的结构材料、结构组合 方式,耐热、隔热性能强。
内压薄壁容器的应力理论
薄壁圆筒应力分析

• 引言 • 薄壁圆筒的应力分析基础 • 薄壁圆筒的应力分析方法 • 薄壁圆筒的应力分析实例 • 结论
01
引言
主题简介
薄壁圆筒
薄壁圆筒是指壁厚相对于直径较 小的圆筒形结构,广泛应用于工 程领域。
应力分析
应力分析是研究结构在各种受力 条件下内部应力的分布和大小, 以评估结构的强度、刚度和稳定 性。
05
结论
研究成果总结
薄壁圆筒在承受内压时,其应力分布 呈现出周向对称的特点,且最大应力 出现在圆筒的侧壁处。
在薄壁圆筒的侧壁处,应力呈现出明 显的环向分布特征,且在筒体中部区 域应力值较小。
随着内压的增加,薄壁圆筒的应力逐 渐增大,但当内压达到一定值时,应 力增长速度会逐渐减缓。
薄壁圆筒的应力分布受到材料属性、 圆筒几何尺寸和内压大小等因素的影 响,其中材料属性对最大应力的影响 最为显著。
目的和意义
目的
薄壁圆筒应力分析的目的是确定圆筒 在各种工况下的应力分布和大小,为 结构设计和安全评估提供依据。
意义
薄壁圆筒应力分析的意义在于确保结 构的安全性和可靠性,防止因应力过 大而导致的结构失效或破坏,提高工 程质量和安全性能。
02
薄壁圆筒的应力分析基础
弹性力学基础
弹性力学是研究弹性 物体在外力作用下的 应力、应变和位移关 系的科学。
薄壁圆筒的应力分布可以通过弹性力 学的基本方程求解,并采用适当的边 界条件和初始条件。
03
薄壁圆筒的应力分析方法
解析法
解析法是通过数学公式推导,将实际问题转化为数学问题,从而求解出薄壁圆筒的 应力分布。
解析法具有精度高、理论性强等优点,但求解过程复杂,需要深厚的数学基础。
解析法适用于求解简单的几何形状和边界条件,对于复杂问题可能需要简化模型或 采用其他方法。
内压薄壁圆筒应力分析
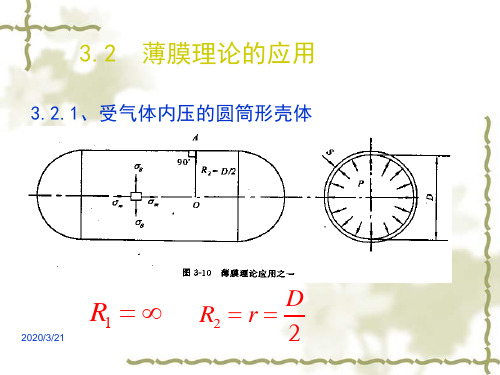
x :椭球壳上任意点距椭球壳中心轴的距离mm。
2020/3/21
O
x2 y2 1 a2 b2
3.2.3、受气体内压的椭球壳(椭圆形封头)
pa
2
σm
b a=b
a pa
pa
2
2
σθ
b a=b
a
pa
2020/3/21 圆球 2
σm
b 1 a 1.4
b
a
σm
b a=2b a
σθ
b 1 a 1.4
2020/3/21
3.2.4 圆锥形壳体中的薄膜应力
最大薄膜应力在锥形壳体大端,在锥顶处, 应力为零。
锥形壳体内最大薄膜应力是同直径同壁厚圆筒形壳 体的薄膜应力的1/cos a 倍。
锥形壳体的环向应力是经向应力的两倍。
锥形壳体的应力,随半锥角a的增大而增大,设计 时,a角要合适,不宜太大。
2020/3/21
②
m
PD
4
P
4 /
D
,
PD
2
P,
2 / D
所以应力与S/D成反比,不能只看壁厚大小 。
2020/3/21
3.2 薄膜理论的应用
3.2.2、受气体内压的球形壳体
2020/3/21
2
,
m
pD
4
2020/3/21
3.2.2、受气体内压的球形壳体
①在直径与内压相同的情况下,球壳内的应力 仅是圆筒形壳体环向应力的一半,即球形壳 体的厚度仅需圆筒容器厚度的一半。
pa
b a=2b a
σθ
pa
3.2.3、受气体内压的椭球壳(椭圆形封头)
pa
σm
b a=2b a pa 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018/10/11
3.1.2 基本概念与基本假设
2、基本假设: 假设壳体是完全弹性的,材料具有连续性、均匀性和 各向同性。 对于薄壁壳体,通常采用以下三点假设使问题简化: (1)小位移假设 受力变形前后结构尺寸不变;
(2)直法线假设
受力变形前后壳体厚度不变; (3)不挤压假设
数学公式:
(1 y ) R1 | y // |
3 /2 2
2、第二曲率半径:通过经线上一点M的法线作垂直于经线的平 面与中间面相割形成的曲线MEF,此曲线在M点处的曲率半径 称为该点的第二曲率半径R2。第二曲率半径的中心落在回转 轴上,其长度等于法线段MK2,即R2=MK2。
2018/10/11
3.1 薄膜应力理论
容器:化工生产所用各种设备外部壳体的总称 如:贮罐、高位槽、换热器、 塔器、反应釜
反应釜
2018/10/11
贮罐
3.1 薄膜应力理论
容器的组成: 筒体(壳体)、封头(端盖)、法兰、支座、接管 及人(手)孔、视镜、安全附件等组成。其中筒体和封头 是容器的主体。
接管 人孔 封头
液面计
2018/10/11
2018/10/11
筒体
支座
3.1.1薄壁容器及其应力特点
1、薄壁容器
S DO < 0.1 即 K = D ≤ 1.2 Di i
其中,S -- 容器的厚度;
Di -- 最大截面圆的内径; DO — 最大截面圆的外径。 应力类型:薄膜应力
2018/10/11
边缘应力
3.1.2 基本概念与基本假设
1、基本概念
3.1.3 回转薄壳的薄膜应力分析
薄膜应力:当壳体壁厚较薄时,不考虑壳体与 其它部件连接处的局部应力,认为经向应力、 环向应力沿壁厚均匀分布,这种应力即薄膜 应力。
2018/10/11
3.1.3 回转薄壳的薄膜应力分析
二、回转壳体的无力矩理论 1、有力矩理论:壳体在外载荷作用下,要引起壳体 的弯曲,这种变形由壳体内的弯曲和中间面上的拉 或压应力共同承担,求出这些内力或内力矩的理论 称为一般壳体理论或有力矩理论,比较复杂;
2018/10/11
3.1.3 回转薄壳的薄膜应力分析
2、 无力矩理论:对于壳体很薄,壳体具有连续
的几何曲面,所受外载荷连续,边界支承是 自由的,壳体内的弯曲应力与中间面的拉或 压应力相比,小到可以忽略不计,认为壳体 的外载荷只是由中间面的应力来平衡,这种 处理方法,称为薄膜理论或无力矩理论。
2018/10/11
2018/10/11
精品课件!
2018/10/11
精品课件!
2018/10/11
3.1.3 回转薄壳的薄膜应力分析
四、薄膜理论的适用条件 薄壁无力矩应力状态的存在,必须满足: 壳体是轴对称的,即几何形状、材料、载荷的对称性与连续 性,同时需要保证壳体应具有自由边缘。1、壳转壳体曲面在 几何上是轴对称,壳体厚度无突变;曲率半径是连续变化的, 材料是各向同性的,且物理性能(主要是E和μ)应当是相同 的; 2、载荷在壳体曲面上的分布是轴对称和连续的; 3、壳体边界的固定形式应该是自由支承的。
2018/10/11
3.1.2 基本概念与基本假设
面: 锥截面: 法线绕旋转轴旋转 一周形成的锥面。该锥面截出的 是壳体的真实壁厚。 横截面: 用垂直于回转轴的平 面截开壳体,则得到的是壳体的 横截面。
2018/10/11
横截面
锥截面 纵截面
3.1.2 基本概念与基本假设
半径:
1、第曲率半径:中间面上任一点M处经线的曲率半径为该点 的“第一曲率半径”R1,R1=MK1。
3.1.3 回转薄壳的薄膜应力分析
三、回转壳体应力分析及基本方程式
1、区域平衡方程式
分析可得:
pR2 m 2S
2、微体平衡方程式
m
2018/10/11
P R1 R2 S
3.1.3 回转薄壳的薄膜应力分析
式中:
S —壳体的壁厚,mm; R1—回转壳体曲面在所求应力点的第一曲率半径,mm; R2—回转壳体曲面在所求应力点的第二曲率半径,mm; σm —经向应力,Mpa; σθ—环向应力,Mpa; P—壳体的内压力,Mpa.
忽略弯曲应力、法向应力的作用,且截面产生的应 力沿壁厚均匀分布 2018/10/11
3.1.3 回转薄壳的薄膜应力分析
一、受力特点
1、在经向方向产生经向应力, 在纬线方向产生环向应力;
2、经向应力作用在圆锥面与 壳体相割所形成的锥截面上, 环向应力作用在经线平面与壳 体相割所形成的纵向截面上; 3、由于轴对称,在同一纬线 上各点的经向应力、环向应力 分别相等。 2018/10/11
2018/10/11
3.1.2 基本概念与基本假设
线:
1、经线:过回转轴的平面与中间面的交线。 2、法线:过中间面上的点且垂直于中间面的直线称为中 间面在该点的法线(法线的延长线必与回转轴相交)。 3、纬线:以法线为母线绕回转轴回转一周所形成的锥截 面与中间面的交线。 4、平行圆:垂直于回转轴的平面与中间面的交线称平行 圆。显然,平行圆即纬线。
回转曲面:以任何直线或平面曲线为母线,绕其同平面 内的轴线(回转轴)旋转一周形成的曲面。容器的主体是 由回转曲面形成的。 母线:绕轴线(回转轴)回转形成回转曲面的平面曲线 或直线。
2018/10/11
3.1.2 基本概念与基本假设
中间面:平分壳体厚度的曲面称为壳体的 中间面,中间面与壳体内外表面等距离, 它代表了壳体的几何特性。 回转壳体:以回转曲面为中间面的壳体 轴对称:我们把几何形状、所受外力、约束 条件都对称于回转轴的问题称为轴对称问题。
