三铰拱的内力计算
合集下载
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第4章 静定拱【圣才出品】
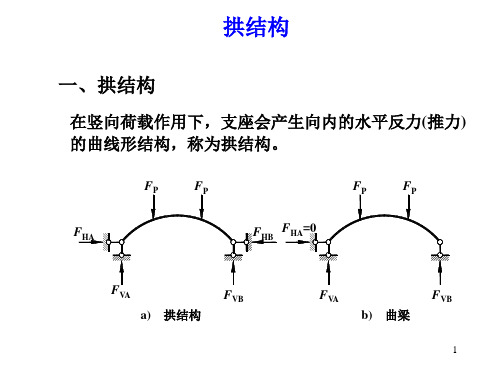
第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】一、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和无拉杆三铰拱的区别与联系二、三铰拱的计算 ★★★★★1．支座反力的计算（见表4-1-3）表4-1-3 支座反力的计算2．内力的计算（见表4-1-4）表4-1-4 三铰拱的内力计算三、三铰拱的合理拱轴线（见表4-1-5） ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1．拱的受力情况和内力计算与梁和刚架有何异同？答：（1）拱与梁的受力情况和内力计算的区别①约束反力方面，拱在竖向荷载作用下会产生水平反力（推力），而梁在竖向荷载作用下不会产生水平反力（推力）；②内力分布方面，由于水平推力的存在，拱的弯矩常比跨度、荷载相同的梁的弯矩小得多，使得拱截面上的应力分布较为均匀；③内力分析方法方面，若只有竖向荷载时，梁只需进行简单的整体分析即可求解，而拱由于水平力的存在，需要整体分析与局部分析相结合。
（2）拱与刚架的受力情况和内力计算的异同①内力分析方法方面，拱与刚架的受力情况和内力计算的特点和所应用方法基本一致，例如三铰刚架也属于拱式结构；②拱的轴线是曲线，刚架杆的轴线是直线，在应用平衡条件计算内力时，拱仍然取投2．在非竖向荷载作用下怎样计算三铰拱的反力和内力？能否使用式（4-1）和（4-2）？答：（1）对于三铰拱承受非竖向荷载的情况，可将非竖向荷载分解为水平荷载和竖向荷载。
（2）仍然可以应用式（4-1）和（4-2），将水平反力加上非竖向荷载水平方向上的分量一起代入公式中进行求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ⎫⎪=⎪⎪=⎬⎪⎪=⎪⎭cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F ϕϕϕϕ⎫=-⎪⎪=-⎬⎪=+⎪⎭3．什么是合理拱轴线？试绘出图4-2-1各荷载作用下三铰拱的合理拱轴线形状。
结构力学 第四章 三铰拱
杆轴线为曲线 在竖向荷载作 用下不产生水 平反力。 平反力。
FP
曲梁
三铰拱
第四章 三铰拱
三、拱常用的形式
静定拱
三铰拱
两铰拱
超静定拱
无铰拱
第四章 三铰拱
四、拱的有关概念
顶铰 拱轴线 平拱 拱趾铰 跨度 拱趾铰 拱轴线 拱（矢）高
斜拱
拉杆拱
第四章 三铰拱 §4-2 三铰拱的支座反力和内力 一、支反力 1、竖向反力 A ∑ M A = 0, VB l − M ABP = 0 H A
第四章 三铰拱
第四章 三铰拱
§4-1 概述 §4-2 三铰拱的支座反力和内力 §4-3 压力线与合理拱轴
第四章 三铰拱
§4-1 概述 实例——拱桥 一、实例 拱桥 拱桥是承受轴向压力为主的拱圈或拱肋作为主要 承受轴向压力为主 拱桥是承受轴向压力为主的拱圈或拱肋作为主要 承重构件的桥梁,拱结构由拱圈(拱肋)及其支座组成。 承重构件的桥梁,拱结构由拱圈(拱肋)及其支座组成。
第四章 三铰拱 [例4-1]三铰拱及其所受荷载如图所示，拱的轴线为抛物线： 1]三铰拱及其所受荷载如图所示，拱的轴线为抛物线： 三铰拱及其所受荷载如图所示 y=4fx(l-x)/l2，求支座反力，并绘制内力图。 求支座反力，并绘制内力图。 解: (1) 反力计算
4 × 4 + 1× 8 ×12 0 VA = VA = 16 = 7kN ( ↑ ) 7kN
M ABP VB = l l 同跨度同荷载简支梁(代 同跨度同荷载简支梁( 的支座反力： 梁）的支座反力：
i i
P
q
C
f
B
l1
l − l1
HB VB
∑ Pa =
VA
三铰拱
M
O
0 FN ( FN d FN ) 0
可得 d FN 0 合理拱轴线方程为
FN q
FN =常数
d 2 qd 0
沿s-s 写出投影方程为
2 FN sin sin d 2
圆弧线
因 d 极小
d 2
返 章
M
0
FH
合理拱轴线方程
例4-2 试求图a所示对称三铰拱在图示荷载作用下的合理拱轴 线。
解：相应简支梁（图b）的弯矩方程为
M
0
1 2
qx ( l x )
0
三铰拱的推力为
FH
0
MC f
4f l
2
ql
2
8f
合理拱轴线方程为
y
M
FH
x (l x )
北京建筑工程学院
三铰拱合理拱轴线形状的确定
三铰拱
14kN m
A
50kN
B
C
75.5kN 58.5kN
175.5 201
M图(kNm)
与三铰拱相应弯矩相比，要大 很多。
北京建筑工程学院
结构力学教研室
三铰拱
计算图（a）斜拱的支反力 时为避免解联立方程，可将反力
分解如图（b）。
由平衡条件可得 （a
F AV F
0 AV
, F BV F
0
FS F AV F1
0 0
轴力以压力为正
北京建筑工程学院
结构力学教研室
三铰拱
三铰拱的内力不但与荷载及三个铰的位置有关，而 且与拱轴线的形状有关。 由于水平推力的存在，拱的弯矩比相应简支梁的弯矩要 小。 三铰拱在竖向荷载作用下轴向受压。
指定三铰拱内力计算及简图
指定三铰拱内力计算及简图姓名：刘风喜班级：土木5班学号：1123310529 一、三铰拱参数及受力三铰拱的轴线方程是：Y=0.1X(20-X),即跨度为20m，矢高为10m受均布荷载q=20KN/m,在X=5,10,15m处受集中荷载F=10KN。
二、计算简图当0<X<5 时，M=215X-0.5qX2-110Y,Fy=215-20X,Fx=110当 5<X<10时，M=215X-0.5qX2-110Y-10(X-5),Fy=215-20X-10,Fx=110当10<X<15时，M=215X-0.5qX2-110Y-10(X-5)-10(X-10),Fy=215-20X-20,Fx=110当15<X<20时，M=215X-0.5qX2-110Y-10(X-5)-10(X-10)-10(X-15),Fy=215-20X-30,F x =110F x=F HF y=F Q0M=M0-F H yF Q=F y cosθ-F x sinθFN=-(Fysinθ+Fxcosθ)F ay=215 F ax=110三、计算表四、内力图五、讨论在相同荷载下，不同拱轴线所对应的内力分布也不同。
特别的，由F y=F Q0说明F y和拱轴线方程（拱的形状，高度）无关，由F x=F H=M c0/f 说明F x只与矢高有关，由M=M0-F H y 说明M只与矢高有关其和形状无关，而F Q , F N 都是θ（tanθ=Y X’）的函数。
所以在相同荷载下，不同拱轴线所对应的内力分布也不同。
04.三铰拱、组合结构
M ( x) M 0 ( x) FHy( x) 0
于是合理拱轴线的方程为：
M 0 ( x) y ( x) FH
例2： 试求图示对称三铰拱在均匀荷载q作 用下的合理轴线。 解：作出相应简支梁如图所示，其弯矩方程为
1 1 2 1 M qlx qx qx (l x) 2 2 2
0 VA
100 9 20 6 3 FHA 12 105kN
0 FVB FVB
C
4m
A
B FHB
x 6m 6m
100 3 20 6 9 12 115kN
FVA
FVB
0 MC 105 6 100 3 FH FHA FHB 82.5kN f 4
2、三铰拱的类型
平拱 斜拱
虚铰拱
二、三铰平拱的计算
1、支座反力的计算
y a2 a1
i
HA
P2 C
f
an
Pn
M B 0
FVA F (l a )F
i
P1
A
B FHB
x l/2 l/2
l
M A 0
FVB l
Fa
FVA P2 P1 FHA C
f
FVB
i i
M C 0
N图
讨论:影响屋架内 力图的主要原因 有两个: ①高跨比f /l D 高跨比越小轴力 NDE=MC0/ f f1=0.5m， 0.75 越大屋架轴力也 F f2=0.7m A 越大。 0.75 0.75 ②f1与f2的关系 当高度f 确定 D 后，内力状态随 D f1与 f2的比例不 f =1.2m f =0 ，2 1 同而变。 D 弦杆轴力变化 幅度不大，但上 4.5 弦杆弯矩变化幅 度很大。
三铰拱及无铰拱
s
S sin
(2) 由∑FR=0，得
0 FQ FQ cos FH sin
l/2 l FP1
FVA
R
FP2 B A
0 FV A
0
A
K C
FP1
K
0 FQ
(3) 由∑FS=0，得
0 FN FQ sin FH cos
M0
F
0 VA
l/2
M
l
0 C
l/2
0 FV B
8
小
FVA=70kN 4m
4m
4m
4m
FVB=50kN
l=16m
得 2) 求φ
x y x 16
2
q=10kN/m A D
0 FV A
FP=40kN B C E
x tan y 1 8
16m
0 FV B
代入各x值，即可查得相应的φ值。 为绘内力图将拱沿跨度分为8个等分，计有9个控制截面， 求出各截面的y、 φ等值，列于表中。
17
2、压力线的用途 (1)求任一拱截面的内力 (2)选择合理拱轴 由上面分析可知，拱的压力线与拱轴曲线形式无关。 因此，有了压力线之后，可以选择合理的拱轴曲线 形式，应使拱轴线与压力线尽量接近（以减少弯 矩），最好重合（此时截面弯矩为零）。对抗拉强 度低的砖石拱和混凝土拱，则要求截面上合力FR 作用点不超出截面核心(对于矩形截面，压力线应 不超过截面对称轴上三等分的中段范围)。
12
(3)计算内力 以截面E为例，计算其内力值。
y 将x =12m代入y 和 y 式中，得yE = 3m， E tan y E = -0.5， F =40kN 查得φ E = -26º34′。因此，有 q=10kN/m
计算图示半圆三铰拱K截面的内力,。已知：q =1kNm,
1-2分析图示体系的几何组成。
1-2 (a)
解本例中共有11根杆件，且没有二元体，也没有附属部分可以去掉。如果将两个三角形看成刚片，选择两个三角形和另一个不与这两个三角形相连的链杆作为刚片（图（a-1））。则连接三个刚片的三铰（二虚、一实）共线，故体系为几何瞬变体系。
1-2 (b)
解体系中有三个三角形和6根链杆，因此，可用三刚片规则分析（图（b-1）），6根链杆构成的三个虚铰不共线，故体系为几何不变体系，且无多余约束。
令内侧受拉为正，则
代入公式，得
*3-2图示柱的A端抗弯刚度为EI，B端为EI/2，刚度沿柱长线性变化。试求B端水平位移。
解以左侧受拉为正，则
代入公式，得
第4章
4-1试确定下列结构的超静定次数。
解去掉7根斜杆，得到图（a-1）所示静定结构。因此，原结构为7次超静定。
解去掉一个单铰和一个链杆，得到图（b-1）所示静定结构。因此，原结构为3次超静定。
由式（a）、（b）和（c）得
FNOG＝FNGH＝FNOH＝0
同理，可判断在TRE三角形中
FNSK＝FNKL＝FNSL＝0
D结点也是“K”结点，且处于对称荷载作用下的对称轴上，故ID、JD杆都是零杆。所有零杆如图（c-1）所示。
第3章
3-1试用直杆公式求图示圆弧型曲梁B点水平位移。EI为常数。
解由图（a）、（b）可知结构在单位力和荷载作用下的内力都是对称的，所以可只对一半进行积分然后乘以2来得到位移。
1-1(e)
解原体系去掉最右边一个二元体后，得到（e-1）所示体系。在该体系中，阴影所示的刚片与支链杆C组成了一个以C为顶点的二元体，也可以去掉，得到（e-2）所示体系。在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。因此，原体系为几何可变体系，缺少一个必要约束。
1-2 (a)
解本例中共有11根杆件，且没有二元体，也没有附属部分可以去掉。如果将两个三角形看成刚片，选择两个三角形和另一个不与这两个三角形相连的链杆作为刚片（图（a-1））。则连接三个刚片的三铰（二虚、一实）共线，故体系为几何瞬变体系。
1-2 (b)
解体系中有三个三角形和6根链杆，因此，可用三刚片规则分析（图（b-1）），6根链杆构成的三个虚铰不共线，故体系为几何不变体系，且无多余约束。
令内侧受拉为正，则
代入公式，得
*3-2图示柱的A端抗弯刚度为EI，B端为EI/2，刚度沿柱长线性变化。试求B端水平位移。
解以左侧受拉为正，则
代入公式，得
第4章
4-1试确定下列结构的超静定次数。
解去掉7根斜杆，得到图（a-1）所示静定结构。因此，原结构为7次超静定。
解去掉一个单铰和一个链杆，得到图（b-1）所示静定结构。因此，原结构为3次超静定。
由式（a）、（b）和（c）得
FNOG＝FNGH＝FNOH＝0
同理，可判断在TRE三角形中
FNSK＝FNKL＝FNSL＝0
D结点也是“K”结点，且处于对称荷载作用下的对称轴上，故ID、JD杆都是零杆。所有零杆如图（c-1）所示。
第3章
3-1试用直杆公式求图示圆弧型曲梁B点水平位移。EI为常数。
解由图（a）、（b）可知结构在单位力和荷载作用下的内力都是对称的，所以可只对一半进行积分然后乘以2来得到位移。
1-1(e)
解原体系去掉最右边一个二元体后，得到（e-1）所示体系。在该体系中，阴影所示的刚片与支链杆C组成了一个以C为顶点的二元体，也可以去掉，得到（e-2）所示体系。在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。因此，原体系为几何可变体系，缺少一个必要约束。
下篇 结构力学部分 第15章 三铰拱
(a) Î޽¹°
(b) Á½½Â¹°
(c) Èý½Â¹°
图15-1
上一页 下一页
返回
第一节 三铰拱的受力特点
拱和梁的主要区别是拱在竖向荷载作用下会产生水 平反力。这种水平反力指向内侧，故又称为推力。由于 推力的存在，拱的弯矩与跨度、荷载相同的梁相比较要 小的多，且主要承受压力，因此更能发挥材料的作用， 并能利用抗拉性能较差而抗压性能较强的材料如砖、石、 混凝土等来建造，这是拱的主要优点。而拱的主要缺点 也正在于支座要承受水平推力，因而要求比梁要具有更 为坚固的基础或支承结构（墙、柱、墩、台等）。可见， 推力的存在与否是区别拱与梁的主要标志。
上一页 下一页
返回
三、内力图的绘制
绘制内力图的一般步骤为： （1）求反力：同简支梁反力的求解。 （2）分段：凡外力不连续点均应作为分段点； 同时，为了绘制内力图将拱轴线沿水平方向等分。 （3）定点：将分段点各截面上的内力值用截面 法求出，并在内力图上用竖标绘出。 （4）连线：根据各段的内力图形状，将其控制 点以直线或曲线相连绘出内力图。
上一页 下一页
返回
一、支座反力的计算
a1 a2 F1 A l/2 l F1 FAx FAy a1 F1 FAx FAy A C FCy l/2 (a) FCx A
f
b1 b2 C f l/2 F2 B F1 A l/2 l F2 B FBx FBy F1 A
0 FAy
a1 a2 C
b1 b2 F2 B l/2
40kN
(b)
FAx FAy
A
B
FBx FBy
5 (c) 7.5 10 7.5 10 9 2.5 _ 2.5 5 46 (e) 9 39 33.5 30.3 30 + 30.3 29 + _
5.2 三铰拱的内力计算
C
0 ，可得
0 FHA 0
FP1Biblioteka A K C0 MCFP2
B
0 FVB
l l FV A FP 1 a1 FH f 0 2 2
0 M C FH f 0
0 MC FH f
0 FVA
l/2
l/2
l
类似平行弦桁架的弦杆内力与 相应梁截面弯矩的内力关系
67
76
78 77.8
B
15
20
15
20
E
M图(kN· m)
FN图(kN)
q=10kN/m C 4.9
FP=40kN C E E yE B FH=60kN
17.9
E y A D x FVA=70kN 4m 4m
4 7.1
A
D 4.9
10
17.9
4
7
B
FH=60kN
f=4m
FQ图(kN)
4m l=16m
FVA=70kN
l=16m q=10kN/m A D FP=40kN B
0 M C 50 8 40 4 FH f 4
C 16m
E
60 kN （推力）
0 FVA
0 FVB
聊城大学建筑工程学院
(2)计算各截面几何参数（y和φ ）
1) 求 y：将l 和f 代入拱轴线方程
4f y 2 x(l x) l
【例5-3】求图示三铰拱式屋架在竖向荷载作用下的支反力和内力。 解： (1) 计算支座反力
q
0 VB
FH 0, FV A F , F V B F
0 VA
y FH FVA
A
三铰拱的内力计算
取半拱： ΣmC=0； XA·4－YA·4=0； XA=1kN
【例4—1】求图示半圆形三铰拱K截面的弯矩。
C K
P=4kN
D
30 30
MK NK K
QK
XA
YA
A
4m
O
B
4m
XB
YB
将拱从K位置截开，取AK。
A XA
YA
ΣmK=0； M K YA 2 X A 2 3 0, MK=－1.464kN.m(外侧受拉)
合理选择拱的轴线可使横截面的弯矩为零。使拱各截面的弯 矩皆为零的轴线称为合理拱轴线，如均布荷载下三铰拱的合理拱 轴线为抛物线。
【例4—1】求图示半圆形三铰拱K截面的弯矩。
C K
P=4kN
D
30 30
C
XC YC
A
XA YA
4m
O
B
4m
XB
YB
A XA
YA
取整体： ΣmB=0； YA·8－P·2=0； YA=1kN
XA
f
YA
l 2
0,
XA
Pl 8f
P
K
C
MK
K αNK
y f y
A
XA YA
x l/2
B
XB
l/4 l/4 YB
A
XA
x
QK
YA
三铰拱支座的水平推力XA=XB的大小与拱的高跨比
跨比
f l
越小
，水平推力XA=XB越大。
f l
有关，高
将拱从K位置截开，取AK。
由 ΣX=0； NKcosα+QKsin α+XA=0 ΣY=0； NKsinα－QKcosα+YA=0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A B
XA YA
O
4m
4m
XB
XA
A YA
YB
பைடு நூலகம்
将拱从K位置截开，取AK。 ΣmK=0； M K YA 2 X A 2 3 0, MK=－1.464kN.m(外侧受拉)
第四章 三铰拱的内力计算
轴线为曲线，在竖向荷载作用下，支座有水平推力的结构 称为拱。
P1
C A B A B
P2
P1
P2
拱 三铰拱为静定结构。
A B
曲梁
f
拱顶到两铰连线的距离 f 称为 拱高。
C
两铰A、B间距 l 称为拱跨；
l/2
l/2
计算图示三铰拱Ｋ截面的内力。 P
K C
C
f
XC
y
A
B
f
A
XA YA
YB
比较可知，三铰拱横截面的弯矩要比同跨度简支梁对应截面 的弯矩小。梁与拱的承载能力主要取决于弯矩，同跨度、同截面 的三铰拱要比简支梁承载能力大。
合理选择拱的轴线可使横截面的弯矩为零。使拱各截面的弯 矩皆为零的轴线称为合理拱轴线，如均布荷载下三铰拱的合理拱 轴线为抛物线。 【例4—1】求图示半圆形三铰拱K截面的弯矩。 P=4kN C
ΣY=0； NKsinα－QKcosα+YA=0
求K截面的轴力NK和剪力QK。
P
K
C
MK
K
α NK QK
f y
A B
y XB XA
A
XA YA
x
x
l/2 l/4 l/4 YB
YA
由ΣmK=0； ＭK+XA·－ YA· y x=0； ＭK=YA·－XA· x y
P
A K B
XA YA
x l
l/4
ＭK=YA· x
l Pl 0, X A 2 8f
P
K
C
MK
K
α QK
NK
f
y
A
B
y
XB
XA
A
XA YA
x YA
x
l/2 l/4 l/4 YB
f 三铰拱支座的水平推力XA=XB的大小与拱的高跨比 有关，高 l f 跨比 越小 ，水平推力XA=XB越大。 l 将拱从K位置截开，取AK。
由
ΣX=0； NKcosα+QKsin α+XA=0
x l/2 l/4
XB
XA
YC YA l/2
l/4 YB
求三铰拱的内力必须先求支座反力。
l 1 取整体，求竖向反力： ΣmB=0； YA l P 0, YA P 4 4
ΣY=0；
3 YA＋YB－P = 0， YB P 4
取半拱，求水平推力： ΣmC=0； X A f YA
K D
C XC YC
30 30
A B
XA YA
O
4m
4m
XB
XA
A YA
YB
取整体： ΣmB=0； YA·－P· 8 2=0； YA=1kN 取半拱： ΣmC=0； XA·－YA· 4 4=0； XA=1kN
【例4—1】求图示半圆形三铰拱K截面的弯矩。
K C
P=4kN
D
MK K
NK QK
30 30
XA YA
O
4m
4m
XB
XA
A YA
YB
பைடு நூலகம்
将拱从K位置截开，取AK。 ΣmK=0； M K YA 2 X A 2 3 0, MK=－1.464kN.m(外侧受拉)
第四章 三铰拱的内力计算
轴线为曲线，在竖向荷载作用下，支座有水平推力的结构 称为拱。
P1
C A B A B
P2
P1
P2
拱 三铰拱为静定结构。
A B
曲梁
f
拱顶到两铰连线的距离 f 称为 拱高。
C
两铰A、B间距 l 称为拱跨；
l/2
l/2
计算图示三铰拱Ｋ截面的内力。 P
K C
C
f
XC
y
A
B
f
A
XA YA
YB
比较可知，三铰拱横截面的弯矩要比同跨度简支梁对应截面 的弯矩小。梁与拱的承载能力主要取决于弯矩，同跨度、同截面 的三铰拱要比简支梁承载能力大。
合理选择拱的轴线可使横截面的弯矩为零。使拱各截面的弯 矩皆为零的轴线称为合理拱轴线，如均布荷载下三铰拱的合理拱 轴线为抛物线。 【例4—1】求图示半圆形三铰拱K截面的弯矩。 P=4kN C
ΣY=0； NKsinα－QKcosα+YA=0
求K截面的轴力NK和剪力QK。
P
K
C
MK
K
α NK QK
f y
A B
y XB XA
A
XA YA
x
x
l/2 l/4 l/4 YB
YA
由ΣmK=0； ＭK+XA·－ YA· y x=0； ＭK=YA·－XA· x y
P
A K B
XA YA
x l
l/4
ＭK=YA· x
l Pl 0, X A 2 8f
P
K
C
MK
K
α QK
NK
f
y
A
B
y
XB
XA
A
XA YA
x YA
x
l/2 l/4 l/4 YB
f 三铰拱支座的水平推力XA=XB的大小与拱的高跨比 有关，高 l f 跨比 越小 ，水平推力XA=XB越大。 l 将拱从K位置截开，取AK。
由
ΣX=0； NKcosα+QKsin α+XA=0
x l/2 l/4
XB
XA
YC YA l/2
l/4 YB
求三铰拱的内力必须先求支座反力。
l 1 取整体，求竖向反力： ΣmB=0； YA l P 0, YA P 4 4
ΣY=0；
3 YA＋YB－P = 0， YB P 4
取半拱，求水平推力： ΣmC=0； X A f YA
K D
C XC YC
30 30
A B
XA YA
O
4m
4m
XB
XA
A YA
YB
取整体： ΣmB=0； YA·－P· 8 2=0； YA=1kN 取半拱： ΣmC=0； XA·－YA· 4 4=0； XA=1kN
【例4—1】求图示半圆形三铰拱K截面的弯矩。
K C
P=4kN
D
MK K
NK QK
30 30