妙解破解的原理
数学解密解开谜题的秘密

数学解密解开谜题的秘密数学作为一门科学,自古以来就是人类解开谜题和难题的利器。
无论是古代的密码破解,还是现代的密码学,数学总是发挥着重要的作用。
在本文中,我们将揭示数学解密的奥秘,并探讨数学是如何帮助我们解开各种谜题的。
1. 数学与密码破解在历史上,密码的使用可以追溯到古埃及和古罗马时期。
在当时,人们使用简单的替换法和移位法来编写密码。
然而,数学家们通过分析出现频率和运用概率论的方法,成功地解密了这些简单的密码。
随着时间的推移,密码变得越来越复杂,普通的解密方法已经不再奏效。
这时,数学的多个分支开始发挥作用。
例如,线性代数用于破解分组密码,而数论和离散数学用于解密基于公钥的密码系统。
通过数学的力量,我们能够解开看似无法攻破的密码,揭示隐藏其中的信息。
2. 数学与信息安全随着科技的进步,互联网的普及,信息的传输和存储变得越来越重要。
信息安全成为了当今社会中不可或缺的一部分。
而数学在信息安全领域起着决定性的作用。
加密算法是保护信息安全的关键。
对称加密和非对称加密是常用的两种加密方式。
对称加密使用同一个密钥进行加密和解密,而非对称加密则使用一对密钥,公钥和私钥。
数学中的数论和代数学理论为这些加密算法提供了坚实的理论基础。
除了加密算法,校验和和散列函数也是信息安全中的重要概念。
校验和用于检测数据传输中的错误,而散列函数用于确保数据的完整性。
这些概念都离不开数学的支持和证明。
3. 数学在数独和数学谜题中的应用数独是一种传统的数字谜题,起源于18世纪瑞士。
虽然数独看似简单,但实际上需要一定的数学知识和推理能力。
通过应用数学的原理,我们可以使用逻辑推理和数学技巧来解决数独难题。
同样地,数学在其他的数学谜题中也发挥着重要作用。
例如,数学家们提出了不少数学问题,如费马大定理、哥德巴赫猜想等等。
通过运用数学的工具和技巧,这些问题不断地被解决或者被证明。
总结:数学解密的秘密就在于它的原理和方法。
数学的逻辑性、严谨性和抽象性使其成为解密谜题的有力工具。
开锁法的原理

开锁法的原理开锁法的原理是指通过一定的技术手段,以非正常的方法打开已经上锁的门、锁具等。
开锁法的原理可以分为物理原理和技术原理两方面。
一、物理原理:1.力学原理:这是最基本的开锁原理之一。
通过利用力的原理,比如破坏锁具的结构或者使用钥匙模拟开锁的力道,使锁芯或锁齿发生位移,从而实现开锁的目的。
2.材料学原理:开锁者通过选择针、螺丝刀、各种钢丝、扁铁等特殊材料,利用其特定的物理性质来突破锁具的防御,例如使用细长的钢丝插入锁芯内部,通过推、拨、撞等方式操纵锁齿,从而成功开锁。
3.磁学原理:磁学原理是利用了磁力对锁芯产生影响的特性。
通过选用特定的磁材料,可以使锁芯或锁齿发生磁场变化,进而打开闭锁。
4.光学原理:开锁法中的一种方法是使用显微镜等光学仪器观察锁齿的形态,进而模拟制作钥匙,实现开锁目的。
二、技术原理:1.密码破解原理:一些高级锁具使用数字密码或电子密码来进行开锁,开锁技术者可以通过破译密码的方法,或者利用工具进行暴力破解,来打开这种锁具。
2.齿轨理论:利用齿轨的原理对某些特定的锁具进行开锁。
一些锁具的锁芯内部存在着特定的轨迹,开锁技术者通过选用合适的工具,可以模拟出这些轨迹,进而开启锁种。
3.探测原理:通过使用特定的工具进行探测,可以获取锁具的内部结构信息,从而发现漏洞,实施开锁。
例如,利用手持探测设备发现电磁信号强度的变化,从而找到与解锁相关的信息。
4.技术性破解原理:开锁技术者通过研究锁具的构造和原理,设计出各种专用工具来实施开锁。
例如,通过模拟钥匙的形状和结构,使用专用工具进行开锁,这就是常见的开挂技术。
需要明确的是,开锁法的原理和技术手段,既可以被用于合法行为如解救被困人员,也可以被用于非法行为如盗窃。
因此,在实际应用中,我们需要根据情况判断,合理使用开锁技术,遵守法律法规,防范利用开锁技术进行犯罪活动。
巧借特殊值法,妙解高考真题

2023年8月上半月㊀学法指导㊀㊀㊀㊀巧借特殊值法,妙解高考真题◉张家港高级中学㊀黄㊀轶㊀㊀摘要:巧妙利用特殊值法,借助特殊值的选取,有时可以更加简捷地求解客观题.本文中结合2022年高考真题,剖析特殊值法的巧妙应用,总结特殊值法的解题技巧与规律.关键词:高考;特殊值;客观题;函数;三角;不等式㊀㊀特殊值法破解数学客观题,有其特殊的优势与美妙的体验,它是数学基础知识㊁基本技能㊁基本思想㊁基本活动经验等 四基 落实并上升到一定高度的特殊 产物 ,是特殊与一般思维的升华.特别在解决一些函数或方程㊁数列㊁三角函数或不等式等的选择题时,利用特殊值法,解题过程简洁明了,很好地提升解题速度与解题效益.下面结合2022年高考数学真题中一些客观题特殊值法的合理选用与巧妙应用加以剖析.1巧判函数图象例1㊀(2022年高考数学全国甲卷理科 5)函数y =(3x -3-x)c o s x 在区间-π2,π2éëêêùûúú的图象大致为(㊀㊀).A.㊀㊀B .C .D.分析:解决此类题的常用思维就是先根据函数的解析式判定函数的奇偶性,再借助特殊值的选取合理排除错误的选项.而此题两次利用函数特殊值的选取,即可将不满足函数值取值情况的图象完美地排除,实现巧妙判定函数图象的目的.解析:选取特殊值x =1,可得f (1)=(31-3-1)c o s 1>0,由此排除选项C ,D ;再选取特殊值x =-1,得f (-1)=(3-1-31) c o s (-1)<0,由此排除选项B .故选择答案:A .点评:巧妙选取特殊值来判断函数或方程所对应的函数图象问题,将特殊值所对应的函数值情况与点的位置特征加以联系与对比,排除不合理的图象选项.对于单选题,在利用特殊值法巧判函数或方程所对应的函数图象问题时,经常要多次利用特殊值的巧妙选取来合理排除,直到剩下最后一个正确答案为止.2判定函数关系式例2㊀(2022年高考数学北京卷 4)已知函数f (x )=11+2x,则对任意实数x ,有(㊀㊀).A.f (-x )+f (x )=0㊀B .f (-x )-f (x )=0C .f (-x )+f (x )=1D.f (-x )-f (x )=13分析:解决此类题的常用思维就是利用题设给出的函数关系式,结合选项中对应函数关系式代入,通过指数运算与变形来转化与验证,进而得以正确判定.而此题选取特殊值加以验证即可正确判定,从而减少数学运算量,这也是一种不错的技巧方法.解析:由函数f (x )=11+2x,选取特殊值x =0,可得f (0)=11+20=12,代入各选项中进行验证,选项B ,C 成立;又选取特殊值x =1,可得f (1)=11+21=13,f (-1)=11+2-1=23,只有选项C 成立.故选择答案:C .点评:在判定一些复杂函数关系式的成立问题时,为避免复杂的逻辑推理与繁杂的数学运算,经常借助一些特殊值的选取,代入函数关系式加以化简与求值,可以很好地优化解题过程,同时对于函数关系式的判定更加直接㊁有效.34Copyright ©博看网. All Rights Reserved.学法指导2023年8月上半月㊀㊀㊀3求解相应函数值例3㊀(2022年高考数学新高考Ⅱ卷 6)角α,β满足s i n (α+β)+c o s (α+β)=22c o s (α+π4)s i n β,则(㊀㊀).A.t a n (α+β)=1B .t a n (α+β)=-1C .t a n (α-β)=1D.t a n (α-β)=-1分析:解决此类题的常用思维就是利用三角恒等变换公式对题设的三角函数方程加以变形与转化,进而结合化简的结果来分析与求解对应的三角函数值问题.而此题结合两次特殊值的选取,即可合理排除不满足条件的选取,简化公式变形与推理过程,优化数学运算.解析:s i n (α+β)+c o s (α+β)=22c o s (α+π4)s i n β.①选取特殊值β=0,代入①式,得s i n α+c o s α=0,即t a n α=-1;再将β=0分别代入四个选项,由此可以排除选项A ,C .选取特殊值α=0,代入①式,可得s i n β-c o s β=0,即t a n β=1;再将α=0分别代入四个选项进行验证,由此可以排除选项B .故选择答案:D .点评:这里很好地通过三角函数关系式中角的变化以及对应选项中的三角函数值不变的特征,利用两次特殊值的选取,结合选项中的三角函数值进行排除.借助特殊值法处理相关数学问题时,有时一次特殊值的选取不能直接达到目的,可以进行第二次特殊值的选取,直至剩下最后一个选项为止.4确定参数取值范围例4㊀(2022年高考数学浙江卷 9)已知a ,b ɪR ,若对任意x ɪR ,a |x -b |+|x -4|-|2x -5|ȡ0,则(㊀㊀).A.a ɤ1,b ȡ3B .a ɤ1,b ɤ3C .a ȡ1,b ȡ3D.a ȡ1,b ɤ3分析:解决此类题的常用思维就是绝对值不等式的函数图象化处理思维㊁参数的分类讨论思维等,过程复杂,讨论繁多.而此题利用特殊值的选取,代入题设的绝对值不等式加以化简,利用含参不等式恒成立的条件确定参数的取值情况,结合各选项中的参数取值范围即可验证与确定.解析:选取特殊值x =4,由a |x -b |+|x -4|-|2x -5|ȡ0,可得a |4-b |-3ȡ0.显然a ʂ0且b ʂ4,观察各选项可知,只有a ȡ1,b ɤ3符合这个结论.故选择答案:D .点评:借助含参绝对值不等式中特殊值的选取,简化不等式,减少变量,借助不等式恒成立等相关知识确定相关参数的取值情况,再结合选项合理验证.在具体借助特殊值法确定参数取值范围的问题时,经常不能直接得到对应参数的取值范围,而是借助选项中参数不同取值范围加以验证与判断,合理排除,巧妙确定.5判断不等式成立例5㊀(2022年高考数学新高考Ⅱ卷 12)(多选题)对任意x ,y ,x 2+y 2-x y =1,则(㊀㊀).A.x +y ɤ1B .x +y ȡ-2C .x 2+y 2ɤ2D.x 2+y 2ȡ1分析:解决此类题的常用思维就是不等式思维㊁配方思维或换元思维等,利用条件中的二元方程,结合基本不等式㊁完全平方公式或三角换元等方法来处理,解题过程较为繁琐.而此题利用特殊值法,根据满足二元方程条件下的特殊值的两次合理选取,即可正确排除对应的选项来达到正确判断的目的,简单快捷.解析:选取特殊值x =y =1,其满足方程x 2+y 2-x y =1,则有x +y =2ɤ1不成立,故选项A 错误;再选取特殊值x =-y =33,其满足方程x 2+y 2-x y =1,则有x 2+y 2=23ȡ1不成立,故选项D 错误;根据多选题 至少有两个选项是正确 的特征,故选择答案:B C .点评:利用特殊值法破解一些数学的综合与创新问题时,有一定的 秒杀 效果,但要注意一般 可遇而不可求 ,不具有可推广性与普及性.如果一定要花大量时间去配凑特殊值,往往得不偿失.这里借助二元方程的结构特征,可以快速选取相应的特殊值来验证,综合多选题的特征,当确定其中两个选项为错误时,则另外两个选项肯定是正确答案.巧借特殊值法,可以在很大程度上简化繁杂的逻辑推理过程与复杂的数学运算过程,但也不能盲目任意选取特殊值,要吻合数学问题中特殊与一般思维之间的联系与转化,才能达到正确使用特殊值法的目的.巧妙借助特殊值法,能很好降低知识复杂层次,弱化基础知识难度,强化数学思想方法,优化数学解题过程,提升数学解题效益,节省宝贵考试时间,真正达到小题小做 小题巧做 小题快做 等良好解题效益.Z44Copyright ©博看网. All Rights Reserved.。
巧借中线定理,妙解高中问题

试题4"'3如图"#在 1569 中#B#H 是69 上的两个 三等分点#5*)64*5)B #!5*)94*5)H#则=A('5BH 的最
小值为
!
分析,结合平面 几 何 图 形 的 直 观$设 出 相 关 的 线
段长 度$结 合 三 角 形 的 中 线 定 理 建 立 相 应 的 关 系 式$
借助题目中的平面向量的数量积的关系式$利用数量
与之相关的平面向量问题$数形结合$直观想象$合理
转化$从而得以解决!
三中线定理在解析几何中的应用
在解析几何中#通 过 题 中 相 应 的 线 段 中 点 条 件#
结合三角形的中线定理来建立对应线段的关系式#综
# #0
#当且仅当:!## 0
!
点评,根据 题 目 条 件 中 的 平 面 几 何 的 图 形 特 征$
以及三角形 的 背 景 与 应 用$综 合 平 面 几 何 的 图 形 特
征)平面向 量 的 性 质 以 及 解 三 角 形 知 识 等 来 综 合 处
理$多知识交汇融合$平面几何直观想象$合理应用解
向量的其他相关知识加以分析与应用!
例!)!*"+年高考数学天津卷文&理科第"#题*
在四边形 569B 中#5B 8 69#56 #!槡'#5B #$#
'5 #'*6#点H 在线段96 的延长线上#且5H#6H#
则*6)B4*5)H #
!
分析,结合平面几何图形的直观想象$以平面四边
形为几何背景$通过相应的边)角的关系与转化$通过平
三角形的相 关 知 识 与 数 形 直 观$进 行 逻 辑 推 理 与 转
同构函数,妙解三角

解法探究2023年12月上半月㊀㊀㊀同构函数,妙解三角◉江苏省扬州市仙城中学㊀程全平㊀㊀摘要:同构意识是高中数学中解决问题时比较常见的一种解题意识与技巧方法.特别在解决一些比较陌生或复杂的三角函数问题时,结合三角关系式的恒等变形与转化,抓住三角关系式的结构特征,合理同构与之相关的函数,进而利用函数的基本性质(奇偶性㊁单调性等)来解决对应的三角函数问题,总结规律.关键词:三角函数;同构;函数;参数;不等式㊀㊀三角函数是高中数学的基本知识内容之一,也是高考考查的主干知识之一.三角函数作为一种特殊的函数,在解决一些相关的三角函数问题时,经常可以借助同构函数,回归函数本质,挖掘函数内涵,利用函数的相关概念㊁基本性质㊁图象等来巧妙转化并加以处理.特别在解决三角函数中的参数取值㊁求函数值㊁大小比较㊁不等式证明等方面都有奇效[1].1参数取值三角函数中的一些参数取值问题,经常借助同构函数思维,结合函数的基本性质来恒等变形与转化,为参数取值的求解提供条件[2].例1㊀(2022年广东省汕头市普通高考第二次模拟考试数学试卷 16)若c o s5θ-s i n5θ<7(s i n3θ-c o s3θ)(θɪ[0,2π)),则θ的取值范围是.分析:根据题设条件,抓住三角关系式的共性特征进行恒等变形与巧妙转化.利用三角函数同名归类,借助不等式的恒等变形,寻找不等式两边的共性,巧妙同构函数,进一步利用导数,合理确定函数的单调性,进而利用函数单调性来转化不等式,即可确定θ的取值范围.解析:由c o s5θ-s i n5θ<7(s i n3θ-c o s3θ),移项整理,可得c o s5θ+7c o s3θ<s i n5θ+7s i n3θ.同构函数f(x)=x5+7x3,xɪ[-1,1],那么不等式c o s5θ+7c o s3θ<s i n5θ+7s i n3θ等价于f(c o sθ)<f(s i nθ).求导可得fᶄ(x)=5x4+21x2ȡ0,则知函数f(x)在区间[-1,1]上是增函数.由f(c o sθ)<f(s i nθ),可得c o sθ<s i nθ.结合θɪ[0,2π),利用正弦函数与余弦函数的图象,可得π4<θ<5π4,所以θ的取值范围是(π4,5π4).故填答案:(π4,5π4).点评:同构函数来处理,相比三角恒等变形与转化来说,更加简单快捷,处理起来也更加巧妙.当然,对于同构函数单调性的判断,也可以采用其他方式,如以上问题中先判断幂函数y=x3和y=x5在相应区间上的单调性,再综合函数的运算形式与对应的单调性性质来确定函数f(x)的单调性.而由三角不等式确定角的取值范围时,也可以利用辅助角公式,结合三角不等式,借助三角函数的图象与性质来转化.2求函数值三角函数的求值问题中,有时比较复杂难以直接下手,可以观察三角关系式的结构特征,合理恒等变形,巧妙同构函数,利用函数的基本性质来变形与应用,实现求函数值的目的.例2㊀(多选题)设s i n(β+π6)+s i nβ=3+12,则s i n(β-π3)=(㊀㊀).A.32㊀㊀B.12㊀㊀C.-12㊀㊀D.-32分析:根据题中三角函数的特殊值,有意识地确定两个特殊角满足三角函数关系式,同构三角函数,确定其周期,结合求导处理以及三角函数关系式的恒等变形(和差化积公式),利用三角函数在一个周期长度内的单调性来确定对应角的取值,从而得以求解对应的三角函数值.解析:由于s i n(β+π6)+s i nβ=3+12=s i nπ3+s i nπ6,s i n(β+π6)+s i nβ=3+12=s i n5π6+s i n2π3,因此可同构函数f(x)=s i n(x+π6)+s i n x,xɪR,易知函数f(x)的周期为2π.求导可得fᶄ(x)=c o s(x+π6)+c o s x=2c o sπ12c o s(x+π12).不妨取一个周期长度x+π12ɪ-π2,3π2éëêêùûúú.当x+π12ɪ-π2,π2éëêêùûúú时,fᶄ(x)ȡ0,函数f(x)872023年12月上半月㊀解法探究㊀㊀㊀㊀单调递增,此时β=π6,可得s i n (β-π3)=-12.当x +π12ɪπ2,3π2éëêêùûúú时,f ᶄ(x )ɤ0,函数f (x )单调递减,此时β=2π3,可得s i n (β-π3)=32.故选择答案:A C .点评:此题以三角等式为问题背景,结合条件来求解相应的三角函数值.常用的解题方法就是利用三角函数的公式变形来处理,过程比较繁杂,运算量比较大.而抓住特殊角满足的三角等式加以切入,巧妙同构三角函数,借助导数法来处理,思维性较强,可以减少数学运算,优化解题过程[3].3大小比较三角函数中也存在一些比较变量大小关系的问题,经常可以借助题设条件,寻找特征,同构函数,进而利用函数的基本性质来合理转化与巧妙应用,实现大小关系的判断.例3㊀已知实数a ,b 满足a s i n a -4b s i n b c o s b =4b 2-a 2+1,则以下各选项中大小关系正确的是(㊀㊀).A.a >2b B .a <2bC .|a |>|2b |D.|a |<|2b |分析:根据题设条件,结合题设中的等式进行同一参数的变形转化,实现等式两边的同型转化,巧妙同构函数;结合函数的奇偶性,以及借助导数法判断函数的单调性,进而利用函数的基本性质来综合分析与处理,实现参数大小关系的判断.解析:由a s i n a -2b s i n2b =4b 2-a 2+1,可得a s i n a +a 2=4b 2+2b s i n 2b +1.又由于a s i n a +a 2=(2b )2+2b s i n2b +1>(2b )2+2b s i n 2b ,因此同构函数f (x )=x s i n x +x 2,x ɪR .因为f (-x )=-x s i n (-x )+(-x )2=x s i n x +x 2=f (x ),所以函数f (x )为偶函数.求导,可得f ᶄ(x )=s i n x +x c o s x +2x .当x ɪ0,π2éëêêùûúú时,f ᶄ(x )ȡ0;当x ɪ(π2,+ɕ)时,f ᶄ(x )=s i n x +x c o s x +2x =s i n x +x +x c o s x +x =(s i n x +x )+x (c o s x +1)>0.所以当x ȡ0时,f ᶄ(x )ȡ0,则知函数f (x )在区间[0,+ɕ)上为增函数.由a s i n a +a 2>(2b )2+2b s i n2b ,可得f (a )>f (2b ).又函数f (x )为偶函数,所以f (|a |)ȡf (|2b |),可得|a |>|2b |.故选择答案:C .点评:在解决此类三角函数问题时,经常要通过三角恒等变换,利用一些相关的关系加以变形,从而寻找问题的同型,实现地位同等策略同构函数的目的,进而借助函数的基本性质来比较大小.4不等式证明三角函数中的不等式证明问题,有时也可以借助代数关系式的结构特征,寻找共性,同构函数,通过函数的基本性质,从函数的思维视角来解决.例4㊀在锐角三角形A B C 中,A ,B ,C 是该三角形的三个内角,试证明:s i n A s i n B s i n C >s i n A +s i n B +s i n C -2.分析:结合题目所要证明的三角不等式,以其中一个内角的正弦值为主元进行恒等变形,通过同构函数,利用锐角三角形各内角的正弦值的取值情况来确定一次函数的单调性,并结合对应的函数值,巧妙转化思维,综合利用函数的单调性来证明对应的三角不等式问题.证明:要证s i n A s i n B s i n C >s i n A +s i n B +s i n C -2,即证(s i n A s i n B -1)s i n C -(s i n A +s i n B )+2>0.同构函数f (x )=(s i n A s i n B -1)x -(s i n A +s i n B )+2,x ɪ(0,1).而f (1)=s i n A s i n B -1-(s i n A +s i n B )+2=(1-s i n A )(1-s i n B )>0(这里0<s i n A <1,0<s i n B <1).结合s i n A s i n B -1<0,可知函数f (x )在区间(0,1)上单调递减.所以函数f (x )在区间(0,1)上恒有f (x )>f (1)>0,则有f (s i n C )>0.因此f (s i n C )=(s i n A s i n B -1)s i n C -(s i n A +s i n B )+2>0.变形转化,可得s i n A s i n B s i n C >s i n A +s i n B +s i n C -2成立,不等式得证.点评:在解决以上三角不等式的证明问题时,如果没有头绪或无从下手,可以合理改变解题方向,通过题目的条件或结论的分析与考查,合理拓展思维,借助主元法等其他方法加以巧妙变形与转化,同构出与问题有关的基本初等函数,利用相应函数的相关知识来寻找与转化解决问题的方法与途径,实现问题的巧妙破解.在破解一些三角函数的相关问题时,关键是抓住题目中三角函数关系式的结构特征,慧眼识别与寻找同型或共性,特别是结合三角恒等变形,巧妙抽象,合理同构函数,利用共性,将一些不熟知的三角函数问题转化为与之相关的其他基本初等函数问题来分析与处理,不断增强创新意识㊁同构意识等,提升创新应用能力,拓展思维,形成数学能力,培养数学核心素养.参考文献:[1]孟美金.寻找同型,同构函数,利用共性[J ].高中数理化,2022(15):48G49.[2]韩文美.巧借导数法妙解三角题[J ].教学考试,2021(2):27G29.[3]张琳琳.函数巧同构导数妙应用[J ].中学数学,2022(19):55G56.Z97。
c8 mac无线路由妙解WPA_WPA2_PIN码密码图文教程
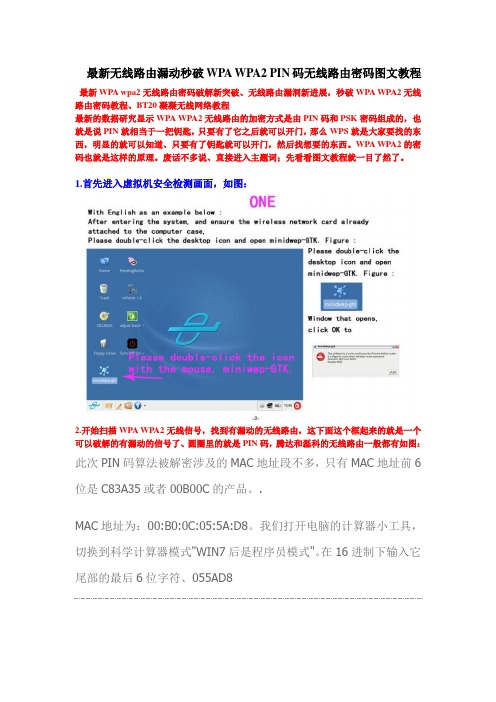
最新无线路由漏动秒破WPA WPA2 PIN码无线路由密码图文教程最新WPA wpa2无线路由密码破解新突破、无线路由漏洞新进展,秒破WPA WPA2无线路由密码教程、BT20凝凝无线网络教程最新的数据研究显示WPA WPA2无线路由的加密方式是由PIN码和PSK密码组成的,也就是说PIN就相当于一把钥匙,只要有了它之后就可以开门,那么WPS就是大家要找的东西,明显的就可以知道、只要有了钥匙就可以开门,然后找想要的东西。
WPA WPA2的密码也就是这样的原理。
废话不多说、直接进入主题词;先看看图文教程就一目了然了。
1.首先进入虚拟机安全检测画面,如图:2.开始扫描WPA WPA2无线信号,找到有漏动的无线路由,这下面这个框起来的就是一个可以破解的有漏动的信号了、圆圈里的就是PIN码,腾达和磊科的无线路由一般都有如图:此次PIN码算法被解密涉及的MAC地址段不多,只有MAC地址前6位是C83A35或者00B00C的产品。
.MAC地址为:00:B0:0C:05:5A:D8。
我们打开电脑的计算器小工具,切换到科学计算器模式"WIN7后是程序员模式"。
在16进制下输入它尾部的最后6位字符、055AD83.当你得到PIN码时,还不能直接使用,因为PIN码一般都是8位数的,所以要换算一下,打开计算器,找到查看,选择科学型,把那个PIN码复制到计算器16进制,然后翻译成都十进制,得到的就是无线路由的PIN码了。
如图所示:4.pin码算出来后,直接复制到选项框内,在框内300的后加上空格-p空格PIN码就可以了,-p 00000000 然后点0K。
如图:5.几分钟后,会自动弹出一个框,那里就是检测的PSK码,也就是上网密码了,如图:最新WPA wpa2无线路由密码破解新突破、无线路由漏洞新进展,秒破WPA WPA2无线路由密码的图文教程就到这里了,BT20凝凝无线网络教程分享大家了,希望可以帮到大家,有什么不明白的地方,可以咨询凝凝无线网络。
魔术破解文档

魔术破解引言魔术是一种古老而神秘的艺术形式,通过巧妙的手法和技巧,使观众感到惊奇和迷惑。
然而,魔术师们并不希望他们的魔术被揭示出来,因为这会削弱其神秘性和吸引力。
然而,一些人对魔术的破解感兴趣,试图揭露魔术背后的秘密。
本文将探讨如何破解魔术以及魔术破解所带来的影响。
魔术破解的方法观察和分析破解魔术的第一步是仔细观察和分析。
观察魔术师的表演,注意他们的动作、眼神和手指的动作。
魔术师经常使用分散注意力的技巧,让观众注意其他地方,从而达到隐藏他们的魔术手法的目的。
研究和实践理解和破解魔术离不开对魔术原理的研究和实践。
了解不同类型的魔术,学习和尝试各种魔术技巧。
这需要时间和耐心,但通过不断地实践和研究,逐渐了解魔术师使用的技巧和手法。
合作与分享魔术破解可以是一个团队合作的过程。
魔术爱好者可以互相交流和分享他们的发现。
通过与其他人合作,可以以更快的速度破解魔术,并且有更多的机会发现一些隐藏的技巧和手法。
魔术破解的影响魔术的魅力丧失一旦魔术被破解,观众将不再感到惊奇和神秘。
魔术师的表演失去了魔力,变得平淡无奇。
人们会变得对魔术失去兴趣,可能会转向其他形式的娱乐。
魔术师的努力付之一炬魔术师花费了大量的时间和精力来学习和表演魔术。
魔术破解可能会削弱魔术师的动力和激情,因为他们的表演不再那么神秘和令人难以置信。
这可能导致一些才华横溢的魔术师放弃魔术,转而选择其他职业。
刺激创新和改进尽管魔术破解可能会对魔术师产生负面影响,但它也可以激励魔术师创新和改进。
一旦某个魔术被揭示出来,魔术师就需要想出新的魔术来保持观众的兴趣。
这种竞争和创新的压力可以促使魔术界不断发展和进步。
结论魔术破解是一个有趣和挑战性的过程,它可以让人们更深入地了解并欣赏魔术。
然而,我们也要意识到,揭示魔术背后的秘密可能会削弱其魅力,并对魔术师产生不良影响。
魔术师们需要继续创新和改进,以保持观众的兴趣。
对于观众来说,我们可以欣赏魔术的神秘性和技巧,并享受它所带来的惊喜和娱乐。
密码破解原理

密码破解原理
密码破解的原理是通过尝试不同的可能性来找到正确的密码。
密码通常是使用算法将输入的明文转换为密文,以提高安全性。
密码破解者可以利用以下几种方法来破解密码。
1. 字典攻击:这种方法是使用事先准备好的字典或常用密码列表来尝试破解密码。
密码破解程序会逐个尝试字典中的每个单词或短语,并与目标密码进行比较,直到找到匹配的密码为止。
2. 暴力破解:这种方法是通过尝试所有可能性的组合来破解密码。
密码破解程序会从最短的密码开始尝试,逐渐增加密码长度和复杂度,直到找到匹配的密码。
3. 推测密码:密码破解者可能会使用目标个人的信息,如姓名、生日、家庭地址等来猜测密码。
他们可能会尝试使用这些信息的不同组合来破解密码。
4. 社会工程学:此方法是通过与目标个人进行交互,获取与密码相关的信息。
密码破解者可能会使用欺骗、欺骗或其他技术手段来获取目标个人的密码。
为了增加密码的安全性,用户应该选择使用强密码,即由大写字母、小写字母、数字和特殊字符组成的复杂密码。
此外,定期更改密码并避免在多个网站或应用程序中使用相同的密码也是重要的安全实践。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
妙解破解的原理
不可不说一下学习破解的三个阶段:
初级,修改程序,用ultraedit等工具修改exe文件,称暴力破解,简称爆破.
中级,追出软件的注册码.
高级,写出注册机.
先说这爆破.所谓爆破,就是指通过修改可执行文件的源文件,来达到相应的目的.你不明白?呵呵,举个例子好了,比如说某共享软件,它比较用户输入的注册码,如果用户输入的,跟它通过用户名(或其它)算出来的注册码相等的话(也就是说用户输入的注册码正确了),那么它就会跳到注册成功的地方去,否则就跳到出错的地方去.
明白过来了吧,我们只要找到这个跳转指令,把它修改为我们需要的“造型”,这样,我们是不是就可以为所欲为了?(某软件双手放在胸口,你要干嘛?)
常见的修改方法有两种,我给你举例说明:
no.1
在某软件中,这样来进行注册:
00451239CALL00405E02(关键CALL,用来判断用户输入的注册码是否正确)
0045123DJZ004572E6(!!!<——此为关键跳转,如果用户输入的注册码正确,就跳向成功处,即004572E6处)
0045XXXXYYYYYYYYYY
XXXXXXXXYYYYYYYYYY
XXXXXXXXYYYYYYYYYY
XXXXXXXX执行到此处,就提示用户注册失败
……提示用户注册码不正确等相关信息
……
004572E6……<——(注册成功处!!!)
……提示用户注册成功等相关信息
呵呵,看明白了吗?没有的话,我来给你讲一下.在软件执行到00451239处的时候,CALL置0045E02处来进行注册码判断.接着回来后就来一个跳转语句,即如果用户输入的注册码正确就跳到004572E6处,跳到此处,就算是注册成功了.如果用户输入的注册码不正确的话,那么就不会在0045123D处进行跳转,而一直执行下去.在下面等它的,是注册失败部分.
想明白了吗?嘿嘿……没错,我们只要把那个关键跳转JZ给改为JNZ(如果用户输入的注册码错误,就注册成功,输入正确则注册失败).当然你也可以将JNZ修改为Jmp,这样的话,你输入的注册码无论正确与否.都可以注册成功.
no.2
我们再来讲一下另外的一种情况:
00451239CALL00405E02(关键CALL,用来判断用户输入的注册码是否正确)
0045123DJNZ004572E6(!!!<——此为关键跳转,如果用户输入的注册码不正确,就跳向失败处,即004572E6处)
0045XXXXYYYYYYYYYY
XXXXXXXXYYYYYYYYYY
XXXXXXXXYYYYYYYYYY
XXXXXXXX执行到此处,就提示用户注册成功
……提示用户注册成功等相关信息
……
004572E6……<——(注册失败处!!!)
……提示用户注册码不正确等相关信息
这次我相信,并且深信不疑.你一定明白了.我还是不明白……倒……
你一定看出跟第一种情况不同的地方了吧.没错!它与第一种不同的,就是第一种情况是如果
注册码正确,就跳到注册成功处,如果没有跳走,就会执行到失败处.而这一种情况则是如果注册码不正确,就跳到注册失败处,否则将执行到注册成功处.
这种情况的修改,除了把JNZ改为JZ外,还可以将其改为Nop,Nop这个指令没有任何意义,将该条指令修改为Nop后,便可随意输入注册码来进行注册了.
原理以经给你讲了,下面我们再来讲一下具体的修改办法吧.(我假设你以经明白了我所说的工具的使用方法)
先说一下虚拟地址和偏移量转换的问题,在SoftICE和W32Dasm下显示的地址值是所谓的内存地址(memoryoffset),或称之为虚拟地址(VirualAddress,V A).
而十六进制工具里,如:Hiew、HexWorkshop等显示的地址就是文件地址,称之为偏移量(Fileoffset)或物理地址(RAWoffset).
当我们要通过那些十六进制工具来对可执行文件中的相应指令进行修改的话,先要找到
它的Fileoffset.我们没有必要去使用那些专门的转换工具,在W32Dasm中就有这个功能,比如说你W32Dasm中来到0045123D处,在W32Dasm界面下方的状态栏中就会出现该条指令的虚拟地址和偏移地址,即@:0045123D@offset0005063Dh后面的这个0005063Dh就是相应的偏移地址.我们得到该地址后,便可用UltraEdit等十六进制工具来对可执行文件进行修改了.比如使用UltraEdit,你先用UltraEdit打开该可执行文件,然后按Ctrl G,接着输入你得到的偏移地址,就可以来到其相应的机器码处.
再给你讲一下机器码,所谓的机器码.就是你看到的那些个十六进制数据了.还记的它们
与汇编指令是一一对应的吗?
以下这几个是爆破时要用到的,其它的如果感兴趣,可自行查看相关资料:
JZ=74;JNZ=75;JMP=EB;Nop=90
爆破的时候,只要对以上机器码进行相应的修改就行了,比如第一种情况的时候,可以将74修
改为EB,即将JZ修改为JMP.而第二种情况,责需将75修改为90,即将JNZ修改为Nop.
本章只讲原理,具体一点的.如怎样找到关键跳转等,我们在下一章中再讲.(一个砖头飞
了上来!嘿嘿,这次被俺接到了)
上边讲了爆破的原理,你需要明白的是.爆破只是你学习Crack的开始,是很简单的手段.刚入
门的时候可以玩玩儿,但希望你不要就此不前!
嘿嘿,再说了.人家的软件中不是都说了嘛,不准对其进行逆向修改.你动了人家的身子,怎么能不买帐呢?)
偶就不喜欢爆破,做不出注册机也要找出注册码.否则我就不会去注册这个软件,既然想不掏钱,就要靠你自己的本事.(等以后我有钱了,会考虑去注册那些优秀的共享软件的).,从某种意义上来说,我是一个正人君子.
其实要找到注册码并不是一件多么难的事,我是指你所针对的软件不太那个的时候不过你无需惧怕.
刚才我们说爆破的时候不提到过关键CALL吗?一般情况下,这个关键CALL就是对两个注册码(一个是软件自身通过你的注册名或机器什么的计算出来的正确的注册码,令一个就是你输入的错误的注册码)进行比较.我前边提到过,CALL之前一般会把所用到的数据先放到一个地方,CALL过去的时候再从这些地方把先前放入的数据取出来,进行相应的处理.这个关键CALL也是这样,在CALL之前,一般会把那两个注册码放到堆栈或某个寄存器中.嘿嘿,我们只要在调试器中,单步执行到该CALL,在未进去之前通过CALL之前的指令判断其将正确的和不正确的注册码放到哪里了.然后再用相应指令进行查看就成了,我说过不难的.
下面列出两个最常见的情况(可参考相关教程):
no.1
moveax[]这里可以是地址,也可以是其它寄存器
movedx[]同上,该条指令也可以是popedx
call00??????关键call
testeaxeax
jz(jnz)或jne(je)关键跳转
看明白了吧,在关键CALL之前,软件会把两个注册码分别放入eax和edx中,你只要在CALL
处下deax或dedx就能看到正确的注册码了.
moveax[]这里可以是地址,也可以是其它寄存器
movedx[]同上,该条指令也可以是popedx
call00??????关键call
jne(je)关键跳转
以上两种情况最为常见,而那些个不太常见的情况,我们这里就不再提了.到下下一章的时候,我会给你讲相关方法的……
关于查找软件注册码的部分,就到这里.具体内容,下下一章咱们再说.(不是说了吗?我以经可以接到你的砖头了,干嘛还要丢呢?)
,再来说的所谓的高级阶段,如果你相信自己.并且热爱Crack,那么你一定会熬到这
个阶段的,只是时间因人而异.
其实分析软件的算法,是有好多技巧在里面的.呵呵,最起码我刚开始的时候就摸不着头脑,那么多CALL,每个看起来,都很重要,都追一遍?结果连好多API都被追了进去.等你自己真正用心分析了一个软件的算法,并写出了注册机后.你就会明白其中的道理了.。
