第二章激光工作物质及基本原理.
第2章-激光基本原理

考虑光子只可能存在两种不同的偏振状态,在体积V内, ν 到ν +Δν频率间隔内, 因能量、动量及偏振状态的不同,并根据(2-3)式和(2-14), 所有可能的光子状态数为
与(2-10)式的结果相一致。
这表明从波动的观点得到光的模式数,与从光子的观点得到光子的量子状 态数是相同的。
2.1.2 光子的相干性和光子简光度
故在体积V内,在 ν 到ν +Δν 频率间隔内,光的模式数为
光子的动量与坐标之间存在海森堡测不准关系
光子坐标x测量值越准确,则动量px的测量值就越不准确 只能在相空间划出面积元Δpx Δx=h,ΔpyΔy=h,Δpz Δz=h 来确定光子的一种状态
在六维相空间(x,y,z,Px,Py,Pz)内,光子的一种状态 所对应的相空间体积元为
2.1 相干性的光子描述
2.1.1 光子的基本性质
光子的基本性质: 1. 光子的能量与光波频率对应,即 式中h为普朗克常数。 2. 光子具有运动质量m,可表示为 光子的静止质量为零。 3. 光子的动量 与单色平面光波的波矢 对应:
式中 ; 单位矢量。
为光子运动方向(平面波的传播方向)上的
上述相空间体积元称为相格。 相格是相空间中用任何实验所能分辨的最小尺度。
光子以动量Px,Py,Pz组成的动量空间内,它的一种运动状态占 据动量空间的体积元 由(2-13)得 上式中的V= ΔxΔyΔz是光子运动的体积。
讨论在 ν 到ν +Δν 频率间隔内,因光子的动量不同,所可能存在的状态数。 相当于求出光子在动量空间中一个半径为 ,厚度为 的球壳 内,可能有的光子状态数为 ,如图2.3所示。
光的相干性可以定义为: 不同空间点、不同时刻的光波场的某种特性(如相位)的相关性。
激光的原理特性和应用

第二章激光与半导体光源激光的原理、特性和应用发光二极管与半导体激光器§2-1 激光的工作原理一、光的发射与光的吸收当原子从高能级向低能级跃迁时,将两能级之差部分以光子形式发射出去,称光的发射;当原子从低能级向高能级跃迁时,将吸收两能级之差部分的光子能量,称光的吸收。
光的发射和吸收过程满足相同的规律:两能级之差决定发射和吸收光子的频率光发射的三种跃迁过程1自发辐射:处在高能级的原子以一定的几率自发的向低能级跃迁,同时发出一个光子的过程,a)图;2 受激辐射过程:在满足两能级之差的外来光子的激励下,处在高能级的原子以一定的几率自发向低能级跃迁,同时发出另一个与外来光子频率相同的光子,b)图;两种辐射过程特点的比较:自发辐射过程是随机的,发出一串串光波的相位、传播方向、偏振态都彼此无关,辐射的光波为非相干光;受激辐射的光波,其频率、相位、偏振状态、传播方向均与外来的光波相同,辐射的光波是相干光。
3 受激吸收过程:在满足两能级之差的外来光子的激励下,处在低能级的原子向高能级跃迁,c)图受激辐射与受激吸收过程同时存在:实际物质原子数很多,处在各个能级上的原子都有,在满足两能级能量之差的外来光子激励时,两能级间的受激辐射和受激吸收过程同时存在。
当吸收过程占优势时,光强减弱;当受激辐射占优势时,光强增强。
二、粒子数反转与光放大当一束频率为的光通过具有能级E1和E2(假定E2>E1)的介质时,将同时发生受激辐射和受激吸收过程,在dt时间内,单位体积内受激吸收的光子数为dN12,受激辐射的光子数为dN21 ,设两能级上的原子数为N1、N2(正常情况下N2> N1),有dN21/ dN12 =B N2/ N1,比例系数B与能级有关。
1、N2/ N1<1时,高能级E2上原子数少于低能级E1上原子数(称正常分布),有dN21 < dN12,表明光经介质传播的过程中受激辐射的光子数少于受激吸收的光子数,宏观效果表现为光被吸收。
激光原理第二章答案

第二章 开放式光腔与高斯光束1. 证明121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=,写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,入射光线首先经界面1折射,然后在介质2中自由传播横向距离d ,最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
3.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下列图所示:其往返矩阵为:由于是共焦腔,则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解:共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。
则1221,1Lg g R ==-,再根据稳定性条件 1201g g <<可得22011LR R L <-<>⇒。
第2章陈鹤鸣激光原理

1
Ani
如果同时存在非辐射跃迁,则寿命也缩短。
2.2.2 受激吸收
E2
h
E1
吸收前
吸收后
h E2 E1
受激吸收跃迁几率:
W12
( dn12 dt
)st
1 n1
W12 B12
与原子本身性质和辐射场能量密度有关
B12 :受激吸收跃迁爱因斯坦系数
只与原子本身性质有关
2.2.3 受激辐射
对激光工作物质的要求:尽可能在其工作粒子的特定能级 间实现较大程度的粒子数反转;使这种反转在整个激光发射 作用过程中尽可能有效地保持下去。
2.4.3 泵浦源
作用:对激光工作物质进行激励,将激活粒子 从基态抽
运到高能级,以实现粒子数反转。
泵浦方式:
气体激光器气体放电激励示意图
1. 光泵浦; 2. 气体放电激励 3. 化学激励 4. 电子注入
I 0 —— z 0 处的初始光强
②大信号增益系数:
g0 g(I)
I(z) 1
Is
I s ——饱和光强(决定于增益介质的性质)
I(z) Is
g(I) g0
进一步讨论可知,增益系数还与光的频率有关。
(2) 损耗系数
dI(z) 1
dz I(z)
损耗因素:衍射、散射、透射、吸 收等
激发态
非辐射跃迁
泵浦
E2
亚稳态 (激光上能级)
产生激光
E1
基态 (激光下能级)
红宝石中铬离子能级图
Energy
E3
Laser Radiation
E2 Fast transition
Abs. E1
N
激光原理与技术完整ppt课件

够存在于腔内的驻波(以某一波矢k为标志)称为电磁被的模式或光波模。一种模式是电
磁波运动的一种类型,不同模式以不同的k区分。同时,考虑到电磁波的两种独立的偏振,
同一波矢k对应着两个具有不同偏振方向的模。
精选ppt
9
下面求解空腔v内的模式数目。设空腔为V=ΔxΔyΔz的立方体,则沿三个
坐标轴方向传播的波分别应满足的驻波条件为
第八章 激光器特性的控制和改善
8.1 模式选择 8.2 频率稳定 8.3 Q调制 8.4 注入锁定 8.5 锁模
精选ppt
5
第九章 激光器件
9.1 固体激光器 9.2 气体激光器 9.3 半导体激光器 9.4 染料激光器
精选ppt
6
第一章 激光的基本原理
本章概激光器基本原理。讨论的重点是光的相干性和光波模式的联系、光的受激辐
(1.1.4)
式中E0为光波电场的振幅矢量,ν为单色平面波的频率,r为空间位置坐标矢量,k为波
矢。而麦克斯韦方程的通解可表为一系列单色平面波的线性叠加。
在自由空间,具有任意波矢k的单色平面波都可以存在。但在一个有边界条件限制的
空间V(例如谐振腔)内,只能存在一系列独立的具有特定波矢k的平面单色驻波。这种能
第六章 激光器的放大特性
6.1 激光放大器的分类 6.2 均匀激励连续激光放大器的增益特性 6.3 纵向光均匀激励连续激光放大器
的增益特性 6.4 脉冲激光放大器的增益特性 6.5 放大的自发辐射(ASE) 6.6 光放大的噪声
精选ppt
4
第七章 激光振荡的半经典理论
7.1 激光振荡的自洽方程组 7.2 原子系统的电偶级距 7.3 密度距阵
二、光波模式和光子状态相格 从上面的叙述已经可以看出,按照量子电动力学概念,光波的模式和光子的状态是等
激光原理与技术--第二章 激光器的工作原理

0.3GHz
q
2L
q
2 5 101 m 6.328107 m
1.5803106
q 1.5 10 9 Hz 5 310 8 Hz
34
第三十四页,共60页。
激光的产生
激光振荡示意图
35
第三十五页,共60页。
❖ 三能级系统
粒子数反转激励条件
激光的产生有三个能级
E 下能级,基态能级: 1
上能级,亚稳态能级:
a) 三能级
E3
A30
S32
W03
E2
A21 B12 B21
E1
E0
b) 四能级
量子效率0
亚稳态发射的荧光光子数 工作物质从光泵吸收的光子数
1
2
三能级1
=
S32 S32 +A31
2
A21 A21 S21
四能级1
=
S32
S32 +A30
+A31
优质红宝石: 0.7
钕玻璃: 0.4
50
纵模的频率间隔:
q
q1
q
C
2L
18
第十八页,共60页。
腔的纵模在频率尺度上是等距离排列的
激光器谐振腔内可能存在的纵模示意图
19
第十九页,共60页。
ቤተ መጻሕፍቲ ባይዱ
q 0.5109 Hz
❖ L=10厘米和L=30厘米的He-Ne气体激光器
L=10厘米的He-Ne气体激光器
q 1.5109 Hz
L=30厘米的He-Ne气体激光器
21 第二十一页,共60页。
激光谐振腔内低阶纵模分布示意图
22 第二十二页,共60页。
激光纵模分布示意图
激光原理第二章 激光器的工作原理
可以证明,在对称共焦腔内,任意傍轴光线可往返多次
而不横向逸出,而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理 论的基础上,因此,对称共焦腔是最重要和最具有代表性的 一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞,g1=g2=1, g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔,由一个凹面镜和一个凸面镜组成,对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔,R1=R2=L,因而,g1=0,g2=0,对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔,由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1,g2=1/2
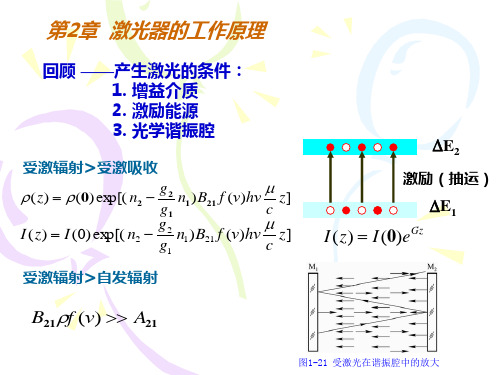
1. 工作物质 2. 激励能源
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实 现粒子数反转? 粒子数反转和什么因素有关?
速率方程方法: 量子理论的一种简化形式
——速率方程理论:把光频电磁场看成量子化的光子,把 物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦 点且:
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特 性
优点: 形式特别简单, 且可给出激光的强度特性,并粗略描 述烧孔、兰姆凹陷、多模竞争等效应
激光原理技术及应用第一章 第二章

激光原理
1
2021/5/19
课时及考试
上课时间:18周,复习 1周 成绩计算:考勤(10分),作业(30分),考试(60分) 参考书:《激光原理技术及应用》 李相银等,哈工大出
自然加宽:
Q值越高,线宽越窄,单色性越好
54
2021/5/19
单模激光的线宽极限
稳定的激光增益等于损耗, Q值无穷大; 自发辐射的影响 纵模频率:
频率漂移:折射率和温度 He-Ne激光器, 百分之一, 106Hz,
55
2021/5/19
第二章 激光工作物质及基本原理
2.1 黑体辐射与普朗克公式 绝对黑体:完全吸收投射于它的任何频率的电磁辐
41
2021/5/19
影响纵模数的因素:荧光线宽,谐振频率间隔
线宽越大,纵模数越多;
谐振腔的频率间隔越小(L越大), 纵模数越多 CO2, 10.6um 光谱线宽度:108Hz,腔长1m,频率间
隔:Δν=c/2ηL=1.5×108Hz,单纵模 氩离子激光器0.5145um, 光谱线宽度6.0×108Hz,
光量子:ε0=hν
57
2021/5/19
普朗克公式
模式:振子的振动状态。 温度T的热平衡条件下,黑体辐射分配到每个模式上的平
48
2021/5/19
激光工作物质内部损耗
不均匀:折射、发射 能级:吸收光子 气体激光器均匀性好于固体
49
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T=6000K
T=5000K
T=4000K
T=3000K
0.02.0x10 Nhomakorabea3
4.0x10
3
nm
6.0x10
3
8.0x10
3
黑体热辐射能谱 实验曲线
5
维恩(Wien)位移定律在短波 ( , T ) 部分与实验结果吻合与实验结 实验曲线 果吻合得很好,但长波却不行。 Wien理论 瑞利—金斯(Rayleigh-Jeans) 定律在长波部分与实验结果比 较吻合。但在紫外区竟算得单 色辐出度为无穷大—所谓的 “紫外灾难”。 Rayleigh 利用经典理论无法解释黑体辐 -Jeans 射现象。正如1900年开耳文指 出的晴朗的物理学理论大厦上 T=1646K 空,飞来“两朵乌云”之一, 它动摇了经典物理的基础。
12
受激吸收跃迁几率W12 定义:单位时间从低能级向高能级跃迁的原子数与 低能级原子数n1的比值,即
dn12 1 W12 dt st n1
W12另一表示公式:
(2.7)
W12 B12
(2.8)
B12为受激吸收爱因斯坦系数, 为辐射光场的能量密度
13
三.受激辐射
6
普朗克能量子假说
1900年,德国物理学家普朗克 ( , T ) (Plank)提出量子假说1918 实验曲线 年获Nobel奖) :
8h 1 c 3 e h / kT 1
3
普朗克 理论值
式中:k为玻尔兹曼常数, h称为普朗克常数。
T=1646K
空腔辐射体的单色辐出度与 波长的能谱曲线
可以证明,A21为原子在E2能级上平均寿命(自发辐射寿命)τs的倒数, 即
A21
1
s
(2.6)
11
二.受激吸收
能级 E2 h E1
外来光子通过处于低能级 的原子系统
能级 E2 原子吸收 光子跃迁 E1
原子吸收光子hυ从低能级跃 迁到高能级
受激吸收不仅与原子本身特性有关,同时还受来自辐射光场的影响。
g1和g2为原子处于能级E1和E2的几率
16
§2.3 谱线加宽及谱线宽度
线型函数
均匀加宽
非均匀加宽
综合加宽
17
线型函数
自发辐射功率是频率的函数 自发辐射的中心频率为υ0,在υ~ υ+ d υ范 围内的自发辐射功率为P(υ) d υ ,于是自发 辐射总功率P为
P()
P P d
~ , g 0 0
~ , g 0 0 2
1 0 2
~ , g ~ , 0 0 g 0 0 2 2
0
19
一.均匀加宽
1.自然加宽
根据经典电子理论,原子可以视为电偶级子当正负电子中心做频率 为0的相对谐振运动时候,电偶级子就会发射频率为0的电子波,由 于电偶级子发射电磁波的同时,本身的能量随时间t指数衰减,因此电 磁波在空间的电矢量为:
激光原理
第二章 激光工作物质及基本原理
1
§2.1 黑体辐射与普朗克公式
黑体辐射
普朗克能量子假说
2
热辐射现象
热辐射现象是是物体由于自身温度高于环境温度(分子、 原子受到热激发)而产生的向外辐射电磁波的现象。
物体在任何温度下都会辐射能量。并且其辐射能量的大小 及辐射能量按波长的分布都与温度有关。 物体既会辐射能量,也会吸收能量。物体在某个频率范围 内发射电磁波能力越大,则它吸收该频率范围内电磁波能 力也越大。 辐射和吸收的能量恰相等时称为热平衡。此时温度恒定不 变。
能级 E2 h E1
激发态原子自发的从高能级 跃迁到低能级释放光子
E1
处于高能级的激发态原子
自发辐射具有偶然性,是一种只与原子本身特性有关的随机过程。
10
自发辐射跃迁几率A21 定义:单位时间内高能态上的原子(设为n2个 )中 发生自发辐射的原子数(dn21/dt)sp与n2的比值,也称 为自发辐射爱因斯坦系数。 dn21 1 A21 (2.3) dt sp n2
7
Plank量子假说对黑体辐射的解释
绝对黑体空腔内的光以驻波的形式存在,并且空腔中的驻波是一系列的 谐振子,只能取一些分立的能量,即 0, ,2 ,3 ,4 ...
0 0 0 0
S 其中, 0 h ,Plank常数h=6.626×10-34J· 空腔内每一个驻波,即每一个谐振子的平均能量为 E 单位体积内频率在υ到υ+d υ之间的驻波数为
3
黑体与黑体辐射
绝对黑体是指在任何温度下, 全部吸收任何波长的辐射的 物体。绝对黑体是一种理想 的模型,开有小孔的不透光 空腔可视成黑体。
绝对黑体既是完全的吸收体, 也是理想的发射体。
小孔的不透光空腔
4
※ 每一条曲线都有一 个极大值。
※ 随着温度的升高, 黑体的单色辐出度迅速 增大,并且曲线的极大 值逐渐向短波方向移动。
能级 E2 h E1
外来光子经过处于高能级 的激发态原子系统
能级 E2
h h
E1
高能级原子受激发跃迁到低能级 辐射出光子hυ,产生光放大
14
受激辐射跃迁几率W12 定义:单位时间从高能级向低能级发生受激辐射跃 迁的原子数与高能级原子数的比值,即
dn21 1 W21 dt st n2
(2.19)
0 0
线型函数的定义:
P ~ g , 0 P (2.21)
图2.3 自发辐射的频率分布
~ , d g 0
P d 1
P
(2.20)
18
线宽
~, g 0
谱线半宽Δυ即谱线加宽 的线宽为: 半极大值对应的频率差值 (参见右图)
W21另一表示公式:
(2.9)
W21 B21
(2.8)
B21为受激辐射爱因斯坦系数, 为辐射光场的能量密度
15
四.爱因斯坦关系式
根据粒子数守恒与plank黑体辐射能量密度公式 导出爱因斯坦关系式
B12 g1 B21 g 2 A21 8h 3 n h 3 B21 c (2.15) (2.16)
h e h / kT 1
8 3 n d 3 d c
因此黑体辐射的单色辐照度即单位体积单位频段内辐射的能量为:
8h 3 1 c 3 e h / kT 1
(2.2)
8
§2.2 光和物质的三种相互作用及爱因斯
坦关系式
自发辐射
受激吸收
受激辐射
9
一.自发辐射
能级 E2
