教学项目:判断三角形类型程序的测试
教学项目:判断三角形类型程序的测试

教学项目:判断三角形类型程序的测试需求:(程序的规格说明要求)有一个程序,用来判断一个三角形的类型。
输入三个整数a、b和c分别作为三角形的三条边的边长,通过程序来判断由这三条边构成的三角形类型是等边三角形、等腰三角形、一般三角形还是非三角形(不能构成一个三角形)。
用决策表法对该程序进行测试。
分析:等价类划分法和边界值分析方法的局限性等价类划分法和边界值分析方法比较适合输入变量或输入条件相互独立的情况,但是当输入变量或输入条件相互依赖、相互制约的时候,采用等价类划分法和边界值分析方法是难以描述的,测试效果也很难保障。
在一些数据处理问题当中,某些操作的实施依赖于多个逻辑条件的组合,即:针对不同逻辑条件的组合值,分别执行不同的操作。
决策表很适合于处理这类问题。
分析:什么是决策表?1、决策表也称判定表,是分析和表达多逻辑条件下执行不同操作的情况的工具。
2、决策表能够将复杂的问题按照各种可能的情况全部列举出来,简明并避免遗漏,设计出完整的测试用例集合。
在所有的黑盒测试方法中,基于决策表(也称判定表)的测试是最为严格、最具有逻辑性的测试方法。
知识点:采用决策表法设计测试用例的步骤:(1)列出所有的条件桩和动作桩。
(2)确定规则的个数。
有n个条件(每个条件取真、假值的情况)的决策表有2n个规则。
(3)填入条件项。
(4)填入动作项,得到初始决策表。
(5)简化决策表,合并相似规则(相同动作)。
如果两条或多条规则的动作项相同,条件项只有一项不同,则可以将该项合并,合并后的条件项用符号“-”表示,说明执行的动作与该条件的取值无关,称为无关条件。
(6)根据决策表设计测试用例。
一条规则一个测试用例,排除掉不可能的规则。
解答:(1)列出所有的条件桩和动作桩。
条件桩—列出问题的所有条件。
(通常认为列出的条件的先后次序无关紧要)动作桩—列出问题规定的可能采取的操作。
(这些操作的排列顺序没有约束)运用决策表设计测试用例时,可将条件理解为输入,将动作理解为输出。
软件测试三角形类型判断程序实验报告

南通大学
软件测试
——三角形类型判断
学院:计算机科学与技术学院
班级:软外1 1 1
学号: 1113122022
姓名:王治
一、实验题目
测试三角形类型判断程序
二、实验开发工具:
Eclipse、JUnit、Ant
三、编码实现三角形类型判断程序:
class Triangle{
private double a, b, c;
public Triangle ( double a, double b, double c ){ this.a = a;
this.b = b;
this.c = c;
}
/*
返回值为1表示是等边三角形
返回值为2表示是等腰三角形
返回值为3表示是其他种类三角形
返回值为-1表示不能构成三角形
*/
public int type (){
//to be added
}
四、设计测试用例
建立一个被JUnit测试的类
建立对应的JUnit Test类
不能构成三角形的测试用例
构成等边三角形的测试用
构成等腰三角形的测试用例
构成其他种类三角形的测试用例
三角形有一条边是非正数
四、编写ant脚本驱动测试用例。
经典黑盒测试(判断三角形的形状)
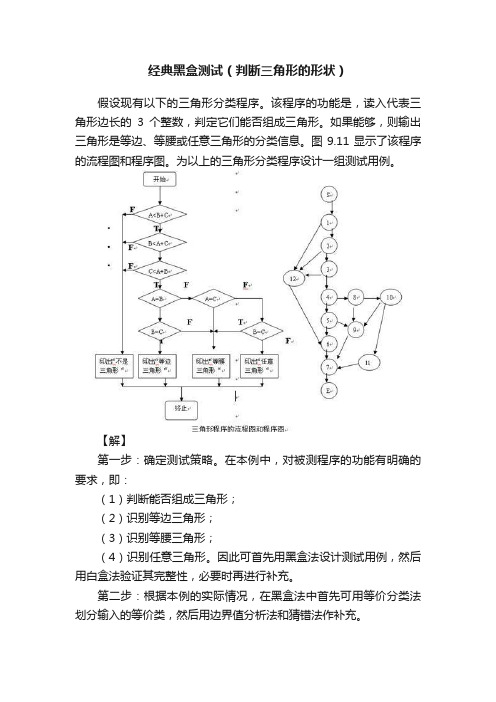
经典黑盒测试(判断三角形的形状)假设现有以下的三角形分类程序。
该程序的功能是,读入代表三角形边长的3个整数,判定它们能否组成三角形。
如果能够,则输出三角形是等边、等腰或任意三角形的分类信息。
图9.11显示了该程序的流程图和程序图。
为以上的三角形分类程序设计一组测试用例。
【解】第一步:确定测试策略。
在本例中,对被测程序的功能有明确的要求,即:(1)判断能否组成三角形;(2)识别等边三角形;(3)识别等腰三角形;(4)识别任意三角形。
因此可首先用黑盒法设计测试用例,然后用白盒法验证其完整性,必要时再进行补充。
第二步:根据本例的实际情况,在黑盒法中首先可用等价分类法划分输入的等价类,然后用边界值分析法和猜错法作补充。
等价分类法:有效等价类输入3个正整数:(1)3数相等(2)3数中有2个数相等,比如AB相等(3)3数中有2个数相等,比如BC相等(4)3数中有2个数相等,比如AC相等(5)3数均不相等(6)2数之和不大于第3数,比如最大数是A(7)2数之和不大于第3数,比如最大数是B(8)2数之和不大于第3数,比如最大数是C无效等价类:(9)含有零数据(10)含有负整数(11)少于3个整数(12)含有非整数(13)含有非数字符边界值法:(14)2数之和等于第3数猜错法:(15)输入3个零(16)输入3个负数第三步:提出一组初步的测试用例,如下表所示:第四步:用白盒法验证第三步产生的测试用例的充分性。
结果表明,上表中的前8个测试用例,已能满足对被测程序图的完全覆盖,不需要再补充其他的测试用例。
软件测试-判断三角形形状路径白盒测试

三角形白盒测试要求要求:,其他1 ) 自备 C 语言程序(可从 C 语言程序设计的教科书上摘录若干典型程序C++ 、C# 、Java 程序均可);#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){int a,b,c;printf(" 输入三角形的三个边 :");scanf("%d %d %d",&a,&b,&c);if(a<=0||b<=0||c<=0)printf(" 不符合条件,请重新输入 a,b,c\n");else if(a+b<=c||abs(a-b)>=c)printf("不是三角形\n");else if(a==b&&a==c&&b==c)printf("这个图为等边三角形\n");else if(a==b||a==c||b==c)printf("这个图为等腰三角形\n");elseprintf("这个图为一般三角形\n");2)根据该程序绘制对应的程序流程图;/ 幟沖迈〃軾已等堆卄琳::矗歴# 输山养赠〃诚日等山/ / 输出水呈/3)分别根据程序流程图给出符合语句覆盖、判定覆盖、条件覆盖、路径覆盖以及判定/条件覆盖和条件组合覆盖的的测试用例以及预期的运行结果;语句覆盖判断覆盖条件覆盖判定1 : 1-1(a<=0) 1-2(b<=0) 1-3(c<=0)判定2: 2-1(a+b<=c) 2-2(|a-b|>=c) 判定3: 3-1(a==b)判定4: 4-1(a==c)判定5: 5-1(a==c)判定 6: 6-1(b==c)判定/条件覆盖、条件组合覆盖、路径覆盖4)根据程序流程图画出流图,并确定线性独立路径的基本集合,然后给出符合各集合的测试用例;路径1: 1-2-3路径2: 1-2-4-5-7-9-12-13路径3: 1-2-4-5-7-9-10-13路径4: 1-2-4-5-7-10-13 路径5: 1-2-4-5-8-10-13。
判断三角形类型的程序

判断三角形类型的程序三角形是几何学中的一个基本概念,它是由三条线段组成的闭合图形。
根据三角形的边长和角度,我们可以将它们分为不同的类型。
在本文中,将介绍如何编写一个程序来判断三角形的类型。
我们需要了解三角形的基本概念。
三角形的边可以分为三个部分:两条边和一个底边。
而三个角则是由这三条边所形成的。
根据三角形的边长和角度,我们可以将三角形分为以下几种类型:等边三角形、等腰三角形、直角三角形、钝角三角形和锐角三角形。
在编写程序之前,我们需要确定程序的输入和输出。
输入应该是三角形的三条边长,而输出则应该是三角形的类型。
根据输入的三条边长,我们可以使用一些条件判断语句来确定三角形的类型。
下面是一个简单的示例程序:```pythondef triangle_type(a, b, c):if a == b == c:return "等边三角形"elif a == b or a == c or b == c:return "等腰三角形"elif a**2 + b**2 == c**2 or a**2 + c**2 == b**2 or b**2 + c**2 == a**2:return "直角三角形"elif a**2 + b**2 < c**2 or a**2 + c**2 < b**2 or b**2 + c**2 < a**2:return "钝角三角形"else:return "锐角三角形"a = float(input("请输入三角形的第一条边长:"))b = float(input("请输入三角形的第二条边长:"))c = float(input("请输入三角形的第三条边长:"))print("这是一个", triangle_type(a, b, c))```在上述的程序中,我们首先定义了一个函数`triangle_type`,它接受三个参数a、b、c,分别代表三角形的三条边长。
软件测试作业三角形判定

实验报告
课程名称:软件测试
实验项目:判断三角形
专业班级:软件0505班
姓名:
学号:
指导教师:**
沈阳工业大学实验报告
(适用计算机程序设计类)
专业班级:软件学院学号:姓名:实验名称:
附件A 沈阳工业大学实验报告
(适用计算机程序设计类)
专业班级:软件0505 学号:姓名:实验步骤或程序:
1.设计窗口
2.设计结构
ModelMain是程序的主入口,主要实现窗口的建立,从键盘接收三个变量,调用Triangle 类的构造方法和判断方法,并打印出结果。
Judge是一个判断接口定义了3个方法
Triangle是三角形类,实现了Judge接口
3.设计接口
4.实现内部功能
5.输出结果。
三角形程序白盒测试

执行路径:1-2-3-7-12
请输入能构成三角形的整数。
Case35
a=’g’,b=’6’,c=’h’
请输入能构成三角形的整数。
执行路径:1-2-3-7-12
请输入能构成三角形的整数。
Case36
a=’h’,b=’发’,c=’52’
请输入能构成三角形的整数。
执行路径:1-2-3-7-12
a=’5.3’,b=’3.0’,c=’2.3’
请输入能构成三角形的整数。
满足:F4,T5,F6
请输入能构成三角形的整数。
Case14
a=’6’,b=’2.3’,c=’3
请输入能构成三角形的整数。
满足:T4,F5,T6
请输入能构成三角形的整数。
Case15
a=’2’,b=’3’,c=’5’
请输入能构成三角形的整数。
执行路径:1-2-3-7-12
请输入能构成三角形的整数。
Case21
a=’1’,b=’2’,c=’3’
请输入能构成三角形的整数。
执行路径:1-2-3-4-5-7-12
请输入能构成三角形的整数。
Case22
a=’15’,b=’2’,c=’5’
请输入能构成三角形的整数。
执行路径:1-2-3-4-5-7-12
Case1
a=’三’,b=’角’,c=’形’
请输入能构成三角形的整数。
执行路径:1-2-3-7-12
请输入能构成三角形的整数。
Case2
a=’5’,b=’2’,c=’2’
请输入能构成三角形的整数。
执行路径:1-2-3-4-5-6-9-10-12
请输入能构成三角形的整数。
Case3
判定三角形的程序及黑盒白盒测试

判定三角形的程序及黑盒白盒测试LtD黑盒白盒测试实验报告学院:计算机科学与工程专业:软件工程姓名:张子晗软件测试方案测试目的1.练习并掌握软件测试管理的一般过程与步骤2.掌握测试管理的人工过程和能通过相关管理软件实现以下操作:1)创立和管理多个测试组和用户2)配置测试环境,编写详细测试方案,安排测试进度3)实施测试,执行测试4)对测试进行评估测试题目关于三角形问题的测试测试方法1.对于主题进行黑盒测试,测试内容包括等价类划分测试,边界值分析测试,决策表方法使用。
2.对于主题进行白盒测试,测试内容包括语句覆盖测试,分支覆盖测试,条件覆盖测试,分支/条件覆盖测试,条件组合覆盖测试以及根本路径测试。
测试资料1.黑盒测试:黑盒测试也称功能测试,它是通过测试来检测每个功能是否都能正常使用。
在测试中,把程序看作一个不能翻开的黑盒子,在完全不考虑程序内部结构和内部特性的情况下,在程序接口进行测试,它只检查程序功能是否按照需求规格说明书的规定正常使用,程序是否能适当地接收输入数据而产生正确的输出信息。
黑盒测试着眼于程序外部结构,不考虑内部逻辑结构,主要针对软件界面和软件功能进行测试。
黑盒测试是以用户的角度,从输入数据与输出数据的对应关系出发进行测试的。
很明显,如果外部特性本身设计有问题或规格说明的规定有误,用黑盒测试方法是发现不了的。
2.白盒测试:白盒测试又称结构测试、透明盒测试、逻辑驱动测试或基于代码的测试。
白盒测试是一种测试用例设计方法,盒子指的是被测试的软件,白盒指的是盒子是可视的,你清楚盒子内部的东西以及里面是如何运作的。
"白盒"法全面了解程序内部逻辑结构、对所有逻辑路径进行测试。
"白盒"法是穷举路径测试。
在使用这一方案时,测试者必须检查程序的内部结构,从检查程序的逻辑着手,得出测试数据。
贯穿程序的独立路径数是天文数字。
采用什么方法对软件进行测试呢?常用的软件测试方法有两大类:静态测试方法和动态测试方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学项目:判断三角形类型程序的测试
需求:(程序的规格说明要求)
有一个程序,用来判断一个三角形的类型。
输入三个整数a、b和c分别作为三角形的三条边的边长,通过程序来判断由这三条边构成的三角形类型是等边三角形、等腰三角形、一般三角形还是非三角形(不能构成一个三角形)。
用决策表法对该程序进行测试。
分析:等价类划分法和边界值分析方法的局限性
等价类划分法和边界值分析方法比较适合输入变量或输入条件相互独立的情况,但是当输入变量或输入条件相互依赖、相互制约的时候,采用等价类划分法和边界值分析方法是难以描述的,测试效果也很难保障。
在一些数据处理问题当中,某些操作的实施依赖于多个逻辑条件的组合,即:针对不同逻辑条件的组合值,分别执行不同的操作。
决策表很适合于处理这类问题。
分析:什么是决策表?
1、决策表也称判定表,是分析和表达多逻辑条件下执行不同操作的情况的工具。
2、决策表能够将复杂的问题按照各种可能的情况全部列举出来,简明并避免遗漏,设计出完整的测试用例集合。
在所有的黑盒测试方法中,基于决策表(也称判定表)的测试是最为严格、最具有逻辑性的测试方法。
知识点:采用决策表法设计测试用例的步骤:
(1)列出所有的条件桩和动作桩。
(2)确定规则的个数。
有n个条件(每个条件取真、假值的情况)的决策表有2n个规则。
(3)填入条件项。
(4)填入动作项,得到初始决策表。
(5)简化决策表,合并相似规则(相同动作)。
如果两条或多条规则的动作项相同,条件项只有一项不同,则可以将该项合并,合并后的条件项用符号“-”表示,说明执行的动作与该条件的取值无关,称为无关条件。
(6)根据决策表设计测试用例。
一条规则一个测试用例,排除掉不可能的规则。
解答:
(1)列出所有的条件桩和动作桩。
条件桩—列出问题的所有条件。
(通常认为列出的条件的先后次序无关紧要)
动作桩—列出问题规定的可能采取的操作。
(这些操作的排列顺序没有约束)
运用决策表设计测试用例时,可将条件理解为输入,将动作理解为输出。
分析:这一步是关键,如何得到三角问题的“条件桩”和“行动桩” ?
我们可以通过分析三角问题的处理过程得到:
当判断出a=b=c时,程序输出“等边三角形”。
当判断出a=b或b=c或a=c时,程序输出“等腰三角形”。
当a!=b且b!= c且c!=a时,程序输出“一般三角形”
可以看出程序的输出由a,b,c之间是否相等的关系决定,即a=b?, a=c?, b=c?,这样我们可以把a=b?, a=c?, b=c?当作条件桩,把程序的输出当作动作桩。
列出所有的条件桩与动作桩,如下表:
条件桩动作桩
C1:A1:非三角形
C2:A2:一般三角形
C3:A3:等腰三角形
C4:A4:等边三角形
A5:不可能
(2)确定规则的个数。
条件项—针对条件桩给出的条件列出所有可能的取值
动作项—指出在条件项的各组取值情况下应采取的动作
将任何一个条件组合的特定取值及相应要执行的动作称为一条规则。
在决策表中贯穿条件项和动作项的一列就是一条规则。
分析:有n个条件的决策表有2n个规则(每个条件取真、假值的情况)。
规则的个数为:24=?
(3)填入条件项。
(4)填入动作项,得到初始决策表。
决策表通常由以下4部分组成:
条件桩—列出问题的所有条件
条件项—针对条件桩给出的条件列出所有可能的取值
动作桩—列出问题规定的可能采取的操作
动作项—指出在条件项的各组取值情况下应采取的动作
将任何一个条件组合的特定取值及相应要执行的动作称为一条规则。
在决策表中贯穿条件项和动作项的一列就是一条规则。
选项规则12345678910111213141516
条件桩C1:a,b,c构成三角形N N N N N N N N Y Y Y Y Y Y Y Y C2:a=b?Y Y Y Y N N N N Y Y Y Y N N N N C3:a=c?Y Y N N Y Y N N Y Y N N Y Y N N C4:b=c?Y N Y N Y N Y N Y N Y N Y N Y N
动作桩A1:非三角形y y y y y y y y
A2:一般三角形Y A3:等腰三角形y Y Y
A4:等边三角形y
A5:不可能y y Y
(5)简化决策表,合并相似规则。
如果两条或多条规则的动作项相同,条件项只有一项不同,则可以将该项合并,合并后
的条件项用符号“-”表示,说明执行的动作与该条件的取值无关,称为无关条件。
选项规则123456789
条件桩C1:a,b,c构成三角形N Y Y Y Y Y Y Y Y C2:a=b?~Y Y Y Y N N N N C3:a=c?~Y Y N N Y Y N N C4:b=c?~Y N Y N Y N Y N
动作桩A1:非三角形Y
A2:一般三角形Y A3:等腰三角形y Y Y
A4:等边三角形y
A5:不可能y y Y
三角形问题合并后的决策表
(6)根据决策表设计测试用例。
一条规则一个测试用例,排除掉不可能的规则。
对每一条规则设计一个测试用例:
测试用例编号a b c预期输出
1231非三角形
2222等边三角形3???不可能4???不可能
5556等腰三角形6???不可能
7343等腰三角形8344等腰三角形9345一般三角形
去掉不存在的情况:
测试用例编号a b c预期输出
T1231非三角形
T2222等边三角形
T5556等腰三角形
T7343等腰三角形
T8344等腰三角形
T9345一般三角形
小结:
1、在所有的黑盒测试方法中,基于决策表(也称判定表)的测试是最为严格、最具有逻辑性的测试方法。
2、决策表也称判定表是分析和表达多逻辑条件下执行不同操作的情况的工具。
3、决策表优点:能够将复杂的问题按照各种可能的情况全部列举出来,简明并避免遗漏,
设计出完整的测试用例集合。
缺点:不能表达重复执行的操作,例如循环结构。
4、决策表通常由以下4部分组成:
(1)条件桩—列出问题的所有条件。
(2)条件项—针对条件桩给出的条件列出所有可能的取值。
(3)动作桩—列出问题规定的可能采取的操作。
(4)动作项—指出在条件项的各组取值情况下应采取的动作。
将任何一个条件组合的特定取值及相应要执行的动作称为一条规则。
在决策表中贯穿条件项和动作项的一列就是一条规则。
5、采用决策表法设计测试用例的步骤:
(1)列出所有的条件桩和动作桩。
(2)确定规则的个数。
有n个条件的决策表有2n个规则(每个条件取真、假值的情况)。
(3)填入条件项。
(4)填入动作项,得到初始决策表。
(5)简化决策表,合并相似规则。
如果两条或多条规则的动作项相同,条件项只有一项不同,则可以将该项合并,合并后的条件项用符号“-”表示,说明执行的动作与该条件的取值无关,称为无关条件。
(6)根据决策表设计测试用例。
一条规则一个测试用例,排除掉不可能的规则。
6、决策表适用于下列情况:
(1) 规格说明以决策表形式给出,或很容易转换成决策表。
(2) 条件的排列顺序不会也不应影响执行哪些操作。
(3) 规则的排列顺序不会也不应影响执行哪些操作。
(4) 每当某一规则的条件已经满足,并确定要执行的操作后,不必检验别的规则。
(5) 如果某一规则得到满足,要执行多个操作,这些操作的执行顺序无关紧要。
