CPA 财务成本管理 第41讲 期权价值评估方法(一)二叉树模型
期权定价二叉树模型精讲共41页文档

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
期权定价ቤተ መጻሕፍቲ ባይዱ叉树模型精讲
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
二叉树模型介绍

5)偏离均衡价格时的套利: 如果期权的价值超过了$0.633,构造该 组合的成本就有可能低于$4.367,并将 获得超过无风险利率的额外收益; 如果期权的价值低于$0.633,那么卖空 该证券组合将获得低于无风险利率的资 金。
2、一般结论
1)条件: 考虑一个无红利支付的股票,股 票价格为S。 基于该股票的某个衍生证券的当 前价格为f。 假设当前时间为零时刻,衍生证 券给出了在T时刻的盈亏状况 。
看跌期权的价值是$4.1923。 利用每个单步二步二叉树向回倒推算, 也可以得到这个结果。
四、美式期权
1、方法: 从树图的最后末端向开始的起点倒推计 算。 在每个节点检验提前执行是否最佳。 在最后节点的期权价值与欧式期权在最 后节点的期权价值相同。
在较早的一些节点,期杈的价值是取如 下两者之中较大者: 1).由公式f=e-rT[pfu+(1-p)fd] 求出的值。 2).提前执行所得的收益。
该组合的现值 ( S u f u )e S f
rT
该组合的成本
则有: S f (Su f u )e
rT
rT
得到: f e [ pfu (1 p) f d ]
d 其中 : p ud e
rT
3、股票预期收益的无关性
衍生证券定价公式没有用到股票上升和 下降的概率。 人们感觉:假设如果股票价格上升的概 率增加,基于该股票的看涨期权价值也 增加,看跌期权的价值则减少。
3、风险中性估值(risk-neutralvaluation): 把金融资产放在风险中性的世界去估值 即为期权和其它衍生证券估值时,世界 是风险中性的。 在风险中性世界中得到的价格,在现实 世界中也是正确的。
期权二叉树定价模型

期权二叉树定价模型期权二叉树定价模型是一种常用的金融衍生品定价模型,用于计算期权合约的公平价格。
该模型基于二叉树的数据结构,将时间分为离散的步长,在每个步长上模拟期权的价格变化。
在期权二叉树定价模型中,二叉树的每个节点表示期权的一个可能价格,树的每一层表示时间的一个步长。
从根节点开始,根据期权的流动性和到期前可执行的次数,构建二叉树模型。
在每个节点上,计算期权的价值,以确定其合理价格。
在构建二叉树模型时,需要考虑期权的标的价格、波动率、到期时间和无风险利率等因素。
这些因素将被用来计算每个节点上的期权价格。
在每个步长上,通过向上或向下移动树的节点,模拟标的价格的波动,从而更新节点上的期权价格。
在二叉树的叶子节点上,期权的价值是已知的,可以直接计算。
在其他节点上,通过对未来价格的概率分布进行加权,计算期权的合理价格。
树的最后一层即为到期时间,即期权到期时的状态。
根据到期状态计算出期权的现值,并通过向根节点回溯,确定期权的公平价格。
期权二叉树定价模型的优点在于能够在离散时间步长上快速确定期权的价格,并且可以灵活地应用于不同类型的期权合约。
此外,该模型对于包含多个期权合约的复杂结构,如欧洲期权、美式期权和亚洲期权等,也具有较高的适用性。
然而,期权二叉树定价模型也存在一些局限性。
首先,该模型假设标的价格的波动服从几何布朗运动,这在实际市场中并不成立,因此模型的有效性有一定的限制。
其次,通过选择适当的步长数和树的深度来平衡精确度和计算效率是一个挑战。
总的来说,期权二叉树定价模型是一个常用且有效的金融工具,可以用于估计期权合约的公平价格。
该模型基于二叉树的数据结构,通过离散时间步长模拟期权的价格变化,并通过回溯计算确定期权的公平价格。
虽然该模型存在一定的局限性,但在实际应用中仍被广泛应用。
期权二叉树定价模型是一种基于离散时间步长和二叉树结构的金融衍生品定价模型。
它是Black-Scholes模型的一种改进方法,通过模拟期权价格的变化来计算期权的公平价格。
期权定价的二叉树模型
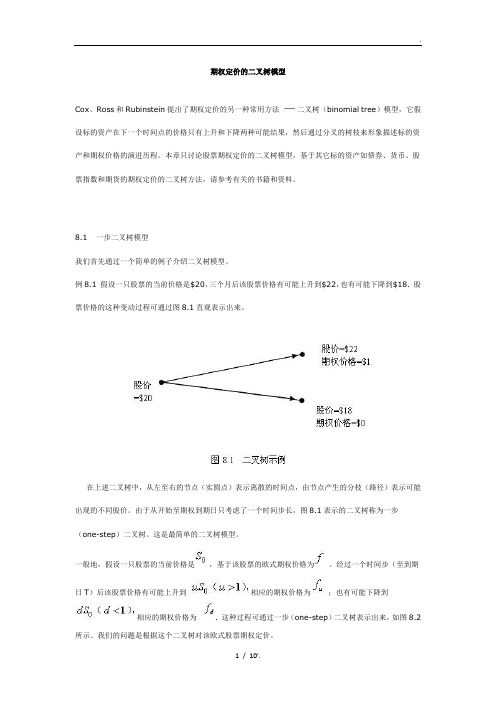
期权定价的二叉树模型Cox、Ross和Rubinstein提出了期权定价的另一种常用方法二叉树(binomial tree)模型,它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果,然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。
本章只讨论股票期权定价的二叉树模型,基于其它标的资产如债券、货币、股票指数和期货的期权定价的二叉树方法,请参考有关的书籍和资料。
8.1 一步二叉树模型我们首先通过一个简单的例子介绍二叉树模型。
例8.1 假设一只股票的当前价格是$20,三个月后该股票价格有可能上升到$22,也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。
在上述二叉树中,从左至右的节点(实圆点)表示离散的时间点,由节点产生的分枝(路径)表示可能出现的不同股价。
由于从开始至期权到期日只考虑了一个时间步长,图8.1表示的二叉树称为一步(one-step)二叉树。
这是最简单的二叉树模型。
一般地,假设一只股票的当前价格是,基于该股票的欧式期权价格为。
经过一个时间步(至到期日T)后该股票价格有可能上升到相应的期权价格为;也有可能下降到相应的期权价格为. 这种过程可通过一步(one-step)二叉树表示出来,如图8.2所示。
我们的问题是根据这个二叉树对该欧式股票期权定价。
为了对该欧式股票期权定价,我们采用无套利(no arbitrage)假设,即市场上无套利机会存在。
构造一个该股票和期权的组合(portfolio),组合中有股的多头股票和1股空头期权。
如果该股票价格上升到,则该组合在期权到期日的价值为;如果该股票价格下降到,则该组合在期权到期日的价值为。
根据无套利假设,该组合在股票上升和下降两种状态下的价值应该相等,即有由此可得(8.1)上式意味着是两个节点之间的期权价格增量与股价增量之比率。
在这种情况下,该组合是无风险的。
以表示无风险利率,则该组合的现值(the present value)为,又注意到该组合的当前价值是,故有即将(8.1)代入上式,可得基于一步二叉树模型的期权定价公式为(8.2)(8.3)需要指出的是,由于我们是在无套利(no arbitrage)假设下讨论欧式股票期权的定价,因此无风险利率应该满足: .现在回到前面的例子中,假设相应的期权是一个敲定价为$21,到期日为三个月的欧式看涨权,无风险的年利率为12%,求该期权的当前价值。
期权定价的二叉树模型

03
二叉树模型在期权定价中 的应用
二叉树模型在欧式期权定价中的应用
欧式期权定义
二叉树模型原理
欧式期权是一种只能在到期日行权的期权。
二叉树模型是一种离散时间模型,通过构造 一个二叉树来模拟股票价格的演变过程。
模型参数
定价过程
包括无风险利率、股票波动率、期权行权价 等。
从到期日逆推至起始时间,考虑各种可能的 价格路径,计算期权的预期收益,并使用无 风险利率折现至起始时间。
与其他理论的结合
二叉树模型与其它金融理论的结合也是理论研究的一个重要方向,如将二叉 树模型与随机过程理论、博弈论等相结合,以提供更深入、更全面的分析框 架。
二叉树模型的应用研究进展
扩展到其他金融衍生品
二叉树模型在期权定价方面的应用已经非常成熟,研究者们正在将其应用于其他金融衍生品的定价,如期货、 掉期等。
案例一:某公司股票期权定价
背景介绍
某上市公司股票期权激励计划需要为期权定价,以确定向员工发 放的期权数量和行权价格。
模型应用
根据二叉树模型,预测股票价格的上涨和下跌幅度,并计算期权 的内在价值和时间价值。
结论分析
根据计算结果,确定期权的行权价格和数量,实现了员工激励与公 司发展的双赢。
案例二:某交易所债券期权定价
调整利率和波动率
根据市场数据和实际情况,调整利率和波动率的参数,可以提 高模型的拟合度。
模型的选择与比较
1 2
基于误差
比较不同模型的预测误差,选择误差最小的模 型。
基于风险
比较不同模型的风险指标,选择风险最小的模 型。
3
基于解释性
选择更具有解释性的模型,以便更好地理解市 场行为和风险。
05
期权定价的二叉树模型介绍

计算期权的价值
计算期权的现值
根据预期收益和折现率,我们可以计算出期权的现值。 看涨期权的现值是每个节点的股票价格与执行价格的差 值与风险中性概率的乘积之和;看跌期权的现值是每个 节点的执行价格与股票价格的差值与风险中性概率的乘 积之和。
校准二叉树模型参数
为了使模型的预测结果与实际期权价格一致,我们需要 校准模型参数。通常,我们使用历史数据来估计参数, 例如股票价格的波动率和无风险利率。
建立二叉树
以时间步长为单位,从最后一个时间步长开始,依 次向前建立二叉树,每个节点代表一个时间步长。
确定初始股票价格
确定股票的当前价格
通常以市场价格为基础确定初始股票价格 。
考虑股息
如果股票在期权有效期内发放股息,需要 在每个时间步长上调整股票价格。
确定无风险利率与时间步长
要点一
确定无风险利率
无风险利率是投资者在相同风险水平下可以获得的最低 回报率。
05
二叉树模型的结果分析
模拟结果展示
假设一个股票价格变动模型,通过二叉树模型模拟股 票价格的涨跌情况,并计算期权的价值。
根据不同的利率和波动率等参数设置,模拟不同的股 票价格路径,从而得到期权价格的模拟结果。
结果分析与比较
将模拟结果与实际期权价格进行比较,分析二叉树模型 定价的准确性。
对比不同参数设置下的模拟结果,分析利率和波动率等 因素对期权价格的影响。
期权定价的二叉树模型介绍
2023-11-06
目 录
• 引言 • 二叉树模型基本原理 • 构建二叉树模型 • 计算期权价值 • 二叉树模型的结果分析 • 二叉树模型在金融实践中的应用 • 结论与展望
01
引言
研究背景与意义
注会考试《财务成本管理》知识点:期权估价(3)

注会考试《财务成本管理》知识点:期权估价(3)为了方便备战2013注册会计师考试的学员,中华会计网校论坛学员精心为大家分享了注册会计师考试各科目里的重要知识点,希望对广大考生有帮助。
一、叉数期权定价模型(一)单项二叉数定价模型1,二叉数模型的假设:(1)市场投资没有交易成本(2)投资者都是价格的接受者(3)允许完全使用卖空所得款项(4)允许以无风险利率借入或贷出款项(5)未来股票的价格将是两种可能值中的一个2,C0=[(1+r-d)/(u-d)]*[Cu/(1+r)]+[(u-1-r)/(u-d)]*[Cd/(1+r)](二)两期二叉数定价模型:由单期模型向两期模型的扩展,不过是单期模型的两次应用。
先利用单期定价模型,根据Cuu和Cud计算节点Cu的价值,利用Cud和Cdd计算Cd的价值;然后,再次利用单期定价模型,根据Cu和Cd计算C0的价值。
从后向前推进。
Cu=[(1+r-d)/(u-d)]*[Cuu/(1+r)]+[(u-1-r)/(u-d)]*[Cud/(1+r)]Cd=[(1+r-d)/(u-d)]*[Cud/(1+r)]+[(u-1-r)/(u-d)]*[Cdd/(1+r)](三)多期二叉数定价模型u=1+上升百分比=eσ根号td=1-下降百分比=1/u(1)确定每期股价变动乘数:u、d(2)建立股票价格二叉数(3)根据股票价格二叉数和执行价格,构建期权价值的二叉数:构建顺序由后向前,逐级推进。
二叉数方法是一种近似的方法,期数越多,计算结果与布莱克-斯科尔斯定价模型的计算结果的差额越小。
二、莱克——斯科尔斯模型的假设:(1)在期权寿命期内,买方期权标的股票不发放股利,也不做其他分配;(2)股票或期权的买卖没有交易成本;(3)短期的无风险利率是已知的,并且在期权寿命期内保持不变;(4)任何证券购买者都能以短期的无风险利率借得任何数量的资金;(5)允许卖空,卖空者将立即得到所卖空股票当天价格的资金;(6)看涨期权只能在到期日执行;(7)所有证券交易都是连续发生的,股票价格随机游走。
期权定价的二叉树模型学习笔记(I)

期权定价的二叉树模型学习笔记(I)编者按:二叉树模型是金融衍生产品期权定价的离散模型.人们可以借助二叉树模型分别对欧式看涨看跌期权、美式看涨看跌期权进行期权金定价.抛开金融意义不谈,单从数学角度出发,这部分运用的数学知识仅是微积分的基本知识点.额外需要注意的是,在二叉树章节中反向归纳法(倒向归纳法)是特别重要的一种方法,其在涉及到有关期权问题的证明中显得尤为重要.之所以运用反向归纳法,是因为期权定价中我们已知未来某一时刻的期权状态,由此出发逐步倒向递推在时刻的价格.本系列是笔者学习二叉树模型所做的课堂笔记一部分,仅供参考!Hedging Concept(套期保值概念)Firstly,we should learn the definition of One-Period & Two-State.Definition1.1(One-Period): Assets are traded at & only, hence the term one period.Definition1.2(Two-State): At the risky asset has two possible values(states):& ,with their probabilities satisfying Question:If risky asset and risk free asset ,known ,when two possibilities,.(for strike price ,expired time .) If known at ,how to find out whenDefinition1.3(Hedging Definition):For a given option ,trade shares of the underlying asset in the opposite direction so that the portfoliois risk-free.We can solve Meanwhile,we can getDefine a new Probability MeasureNotice that期权价的期望表示和风险中性测度Notice that denotes that the expectation of the random variable under the probability measure .Let be a certain risky asset, and is a risk-free asset, then iscalled the discounted price(also known as the relative price) of the risky asset at time .Theorem2.1:Under the probability measure ,an option's discounted price is its expectation on the expiration date.i.e Remark:In order to examine the meaning of the probability measure ,consider is an underlying risky asset.It is easy to calculateRisk-Neutral World(风险中性世界)Definition3.1(Risk-Neutral World):Under the probability measure ,the expected return of a risky asset at is the same as the return of a risk-free bond.A financial market possessing this property is called a Risk-Neutral World.Definition3.2(Risk-neutral measure):The probability measure defined byis called by risk-neutral measure.Definiton3.3(The risk-neutral price):The option price given under the risk-neutral measure is called the risk-neural price. Replication(复制),等价性定理In a market consisted of a risky asset and a risk-free asset ,if there exists a portfoliosuch that the value of the portfolio is equal to the value of the option at ,then is called a replicating portfolio of the option ,then option priceTheorem4.1:In a market consisted of•a risky asset ;•a risk-free asset .Then is true if and only if the market is arbitrage-free.In fact, if the market is arbitrage-free, then there exists a risk-neutral measure defined bysuch that二叉树的构造This means that if at the initial time the price of the underlying asset is , then at , will have possible values Denote未完待续......。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第41讲:期权价值评估方法(一)二叉树模型
所谓二叉树,就是假设股价的未来走向有两种可能,其实教材的例8-10就是最简单的二叉树模型——单期二叉树,单期是指期权的有效期内只做一次股价变动的假设。
然而,真实情况是股价每天都在变化,单期二叉树的假设过于简单,计算结果当然也不够精确。
因此,我们可以把时间细分,多做几次股价变动的假设,形成两期二叉树和多期二叉树,期数越多,计算结果越精确。
1、两期二叉树
教材例8-11:沿用例8-10的数据,S0=50,X=52.08,现在把6个月分成两期,每期3个月,每期股价的变动有两种可能:上升22.56%或下降18.4%,无风险报酬率为每3个月1%。
每期的计算和例8-10完全一样,之前也论证过复制原理和风险中性原理等效,偷懒起见,我们就用简单点的风险中性原理。
第1步:建立股价二叉树
注意:下角标表示股价的升价,比如S uu表示第1期升,第2期升;S du表示第1期升,第2期降;S dd表示第1期降,第2期降,以此类推。
第2步:建立期权二叉树
注意,股价二叉树是从前往后推(从第0期算到最后1期),期权二叉树是从后往前推(从最后1期算回第0期)。
第1期的计算
风险中性原理隆重登场。
1%=22.56%×上行概率-18.4%×(1-上行概率)
第0期(现在)的计算
C 0 = (C u ×0.47363+C d ×0.52637)/(1+1%)
= (10.8×0.47363+0×0.52637)/(1+1%)=5.06
大家不难发现,建立两期期权二叉树,就是对风险中性原理的两次应用。
计算结果5.06比上一讲的6.62更精确些。
2、多期二叉树
讲到这儿,还有最后一个参数可能大家有些疑惑,那就是上行乘数u 和下行乘数d ,这是拍脑袋拍出来的吗?当然不是啦。
大家想想,这两个参数反映的是股价波动的幅度,在统计学中用标准差(σ)表示(第四章讲投资组合的时候说过,温故而知新哦),因此,u 和d 必然跟σ有关系。
u =e σ√t
d =1u
来看教材的例8-12:沿用例8-10的数据,S 0=50,X=52.08,把6个月分为6期,每期1个月,股价波动率(标准差)为0.4068,年无风险报酬率为4%。
第1步:建立股价二叉树
u =e σ√t =e 0.4068√1/12
=1.1246,d =11.1246
=0.8892
计算说明:横向乘上行乘数,斜向乘下行乘数。
×1.1246
×0.8892
下角标u、d表示上行和下行的次数,比如,S u6表示连续6次上行,S d6表示连续6次下行,S d2u表示下行2次,上行1次,以此类推。
第2步:建立期权二叉树
再次强调,期权要从最后1期算回第0期。
第5期的计算
4%/12=(1.1246-1)×上行概率-(1-0.8892)×(1-上行概率)
第0期(现在)的计算
C0 = (8.52×0.47363+2.3×0.52637)/(1+4%/12) = 5.30
跟两期二叉树相比,虽然计算复杂了,但结果又精确了一些。
当然,考试不会这么变态考6期,从往年情况来看,最多考两期。
如果大家对多期二叉树的计算感兴趣,建议使用excel,show给大家看啊。
这一讲的内容就这些,大家注意掌握二叉树的计算原则,尤其是股价从前往后算,期权从后往前算,作业还是最后布置。
