2014初中数学基础知识讲义—一元一次不等式
一元一次不等式

一元一次不等式在数学中,不等式是一种数学表达式,用于描述两个数或两个表达式之间的大小关系。
一元一次不等式是一种常见的不等式形式,其中仅包含一个未知数,并且未知数的最高次项为一次。
一元一次不等式的一般形式为:ax + b > 0(或≥ 0、< 0、≤ 0),其中a和b为已知实数。
这样的不等式可以理解为一条直线上的所有点组成的集合,分为两个部分:使不等式成立的部分和使不等式不成立的部分。
在图形上,不等式表示两个部分之间的分界线。
首先,我们来看如何解一元一次不等式。
为了解不等式,我们可以通过一系列的代数操作来求解未知数的取值范围。
例如,对于不等式2x + 3 > 0,我们可以先将常数项移到右侧,得到2x > -3。
然后,再将系数2除到未知数x上,得到x > -3/2。
最后,我们得到解集{x | x > -3/2},表示所有大于-3/2的实数为不等式的解。
除了求解不等式,我们还可以对一元一次不等式进行一些常见的运算,如加减乘除、取倒数等。
这些运算与求解方程的方法相似,但需要注意不等号方向的变化。
举个例子,对于不等式3x - 2 > 4,我们可以进行如下的操作来解题:1. 将常数项移到右侧,得到3x > 6。
2. 除以系数3,得到x > 2。
我们将得到解集{x | x > 2},表示所有大于2的实数为不等式的解。
在解一元一次不等式时,我们也需要注意些特殊情况。
当不等式中存在分数、绝对值、平方等特殊函数时,我们需要根据具体情况采取相应的处理方法。
例如,对于不等式|x + 1| > 3,我们需要将绝对值拆解成两个不等式:x + 1 > 3 或 x + 1 < -3。
然后,我们分别解这两个不等式,得到解集{x |x > 2}和{x | x < -4}。
最后,我们得到整个不等式的解集是{x | x < -4 或x > 2},表示所有小于-4或大于2的实数为不等式的解。
初一数学讲义:一元一次不等式(组)

初一数学讲义一元一次不等式(组)一.教学衔接1.检查上周练习,并复习回顾考点。
2.引入新课。
二.教学新课【考点归纳】考点一、不等式的概念1、不等式:用不等号表示不等关系的式子,叫做不等式。
2、不等式的解集:对于一个含有未知数的不等式,任何一个适合这个不等式的未知数的值,都叫做这个不等式的解。
3、对于一个含有未知数的不等式,它的所有解的集合叫做这个不等式的解的集合,简称这个不等式的解集。
4、求不等式的解集的过程,叫做解不等式。
5、用数轴表示不等式的方法考点二、不等式基本性质1、不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
2、不等式两边都乘以(或除以)同一个正数,不等号的方向不变。
3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变。
考点三、一元一次不等式1、一元一次不等式的概念:一般地,不等式中只含有一个未知数,未知数的次数是1,且不等式的两边都是整式,这样的不等式叫做一元一次不等式。
2、解一元一次不等式的一般步骤:(1)去分母(2)去括号(3)移项(4)合并同类项(5)将x项的系数化为1考点四、一元一次不等式组1、一元一次不等式组的概念:几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
2、几个一元一次不等式的解集的公共部分,叫做它们所组成的一元一次不等式组的解集。
3、求不等式组的解集的过程,叫做解不等式组。
4、当任何数x都不能使不等式同时成立,我们就说这个不等式组无解或其解为空集。
5、一元一次不等式组的解法(1)分别求出不等式组中各个不等式的解集(2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
熟记要点:1.不等式的性质(重点是性质三)2.利用不等式的性质解不等式,并把解集在数轴上表示出来。
步骤:去分母,去括号,移项,合并同类项,系数化为一;其中去分母与系数化为一要特别小心,因为要在不等式两端同时乘或除以某一个数,要考虑不等号的方向是否发生改变的问题。
初中数学知识点精讲精析 一元一次不等式

第四节一元一次不等式要点精讲一、一元一次不等式概念不等式的左右两边都是整式,只含有一个未知数,并且未知数的次数是1,像这样的等式,叫做一元一次不等式.二、一元一次不等式与一元一次方程的相同点和不同点:1.相同点:二者都只含有一个未知数,未知数的最高次数都是1,左右两边都是整式.2.不同点:一元一次不等式表示不等关系,用不等号连接.一元一次方程表示相等关系,用等号连接.三、一元一次不等式的解法:1.一元一次不等式的解法类似于一元一次方程的解法;2.不等式的两边除以同一个负数时,不等号的方向必须改变;3.在数轴上表示不等式的解集时,应注意解集含有等号时,用实心圆点,解集不含等号时,用空心圆圈.相关链接等式概念一般的,用符号“=”连接的式子叫做等式.注意:等式的左右两边是代数式.典型解析1.解不等式21312x x-≤+,并把它的解集在数轴上表示出来.【答案】去分母,得2(21)3(1)x x-≤+,去括号,得4233x x-≤+,∴原不等式的解集为5x≤.在数轴上表示为:【解析】利用不等式的基本性质,先去分母、去括号,再移项、合并同类项即可求得原不等式的解集.不等式的解集在数轴上表示的方法:>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.中考案例1.(2012•广州)不等式x﹣1≤10的解集是_______.【答案】x≤11【解析】首先移项,然后合并同类项即可求解.解:移项,得:x≤10+1,则不等式的解集是:x≤11.故答案是:x≤11.针对训练1.不等式组23013202xx-<⎧⎨+>⎩()()的整数解是________.2.不等式60x->的解集是________.3.不等式7—2x>1的正整数解是________.4.苹果的进价是每千克3.8元,销售中估计有5%的苹果正常损耗.为避免亏本,商家把售价应该至少定为每千克________元.5.解不等式组:()x302x133x>+⎧⎪⎨-+≥⎪⎩,并判断是否满足该不等式组.6.解不等式组:22(1)43x xxx-<-⎧⎪⎨≤-⎪⎩7.苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:①每亩水面的年租金为500元,水面需按整数亩出租;②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;(1)若租用水面n亩,则年租金共需__________元;(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);(3)李大爷现在奖金25000元,他准备再向银行贷不超过25000元的款,用于蟹虾混合养殖.已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35000元?8.我国东南沿海某地区的风力资源丰富,一年内日平均风速不小于3米/秒的时间共约160天,其中日平均风速不小于6米/秒的时间约占60天.为了充分利用“风能”这种“绿色能源”,该地拟建一个小型风力发电场,决定选用A、B两种型号的风力发电机.根据产品说明,这两种风力发电机在各种风速下的日发电量(即一天的发电量)如下表:根据上面的数据回答:(1)若这个发电场购x 台A 型风力发电机,则预计这些A 型风力发电机一年的发电总量至少为___________千瓦·时;(2)已知A 型风力发电机每台0.3万元,B 型风力发电机每台0.2万元.该发电场拟购置风力发电机共10台,希望购机的费用不超过2.6万元,而建成的风力发电场每年的发电总量不少于102000千瓦·时,请你提供符合条件的购机方案.参考答案1.【答案】0,1【解析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).最后在取值范围内找到整数解:由(1)得32x <,由(2)得23x >-.所以不等式组230320x x -<⎧⎨+>⎩解集为2332x -<<,则整数解是0,1.2.【答案】X>6【解析】由不等式的基本性质,将不等式两边同时加6,不等号的方向不变.得到不等式的解集为:6x >.3.【答案】1,2【解析】利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的正整数即可: 解不等式7-2x >1的解集为x <3.由于小于3的正整数有1,2,因此不等式7—2x >1的正整数解是为1,2.4.【答案】4【解析】设商家把售价应该定为每千克x 元,因为销售中估计有5%的苹果正常损耗,故每千克苹果损耗后的价格为x (1-5%),根据题意列出不等式:x (1-5%)≥3.8,解得,x≥4.所以为避免亏本,商家把售价应该至少定为每千克4元.5.【答案】解:()()()x 3012x 133x 2>⎧+⎪⎨-+≥⎪⎩由(1)得:x >-3,由(2)得:x≤1.∴原不等式组的解集是:-3<x≤1.∵10,∴103>-,∴-3<≤1.∴【解析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).最后利用无理数的估算即可解决问题.6.【答案】x ≤3【解析】由22(1)x x -<-,得x >0;由43x x ≤-,得x ≤3.∴原不等式组的解集为0<x ≤3.解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).7.【答案】(1)500n .(2)每亩收益=4×1400+20×160=8800,每亩成本=4×(75+525)+20×(15+85)+500=4900,每亩利润=8800-4900=3900.(3)设应该租n 亩水面,并向银行贷款x 元,可使年利润超过35000元,则年内总成本为 4900n =25000+x ,即x =4900 n -25000①根据题意,有 25000 (1400416020)(25000 1.08)35000 x n x ⎧⎨⨯+⨯-+⎩≤②≥③将①代入②,得4900 n-25000≤25000, 即 n≤500004900≈10.2.将①代入③,得3508n ≥33000,即 n≥330003508≈9.4.∴ n =10(亩). x =4900 ×10 -25000=24000(元).∴李大爷应该租10亩水面,并向银行贷款24000元,可使年利润超过35000元.【解析】(1)年租金=每亩水面的年租金×亩数.(2)年利润=收益-成本=(蟹苗收益+虾苗收益)-(蟹苗成本+虾苗成本)-水面年租金-饲养总费用(3)设应该租n 亩水面,并向银行贷款x 元,可使年利润超过35000元.依题意,有①年内总成本为: 4900n =25000+x ;②向银行贷款不超过25000元:x ≤25000;③年利润超过35000元:(1400416020)(25000 1.08)35000n x ⨯+⨯-+≥.解之即得所求.8.【答案】:(1)12600x .(2)设购A 型风力发电机x 台,则购B 型风力发电机10-x 台,根据题意,得()()0.3x 0.210x 2.612600x 780010x 102000⎧+-≤⎪⎨+-≥⎪⎩,解得5≤x ≤6.∴符合条件的购机方案有二个:方案1:购A 型风力发电机5台,购B 型风力发电机5台;方案2:购A 型风力发电机6台,购B 型风力发电机4台.【解析】(1)根据题意,有一台A 型风力发电机一年的发电总量至少为60×150+(160-60)×36=12600千瓦·时,所以x 台A 型风力发电机一年的发电总量至少为12600x 千瓦·时.(2)不等式的应用解题关键是找出不等量关系,列出不等式求解.本题不等量关系为:①购A 型风力发电机的费用+购B 型风力发电机的费用“不超过”2.6万元0.3x+1.2(10-x )≤2.6;②A 型风力发电机每年的发电量+B 型风力发电机每年的发电量“不少于”102000千瓦·时12600x +()780010x - 102000≥其中一台B 型风力发电机一年的发电总量至少为60×90+(160-60)×24=7800千瓦·时.。
初中数学知识归纳一元一次不等式组

初中数学知识归纳一元一次不等式组初中数学知识归纳 - 一元一次不等式组一元一次不等式组是初中数学中的一个重要概念,它涉及到不等式的解与图像的表示。
本文将对一元一次不等式组进行归纳,以帮助读者加深对该知识点的理解。
一、一元一次不等式组的基本概念及表示方法一元一次不等式组是由若干个一元一次不等式组成的方程组。
一元一次不等式组一般以下列形式表示:⎧⎨⎩a₁x + b₁y + c₁z ... = d₁a₂x + b₂y + c₂z ... = d₂a₃x + b₃y + c₃z ... = d₃...aₙx + bₙy + cₙz ... = dₙ其中,a₁、b₁、c₁等为常数系数,x、y、z等为变量,d₁、d₂、d₃等为等式右边的常数。
每一个不等式都可以表示为平面上的一条直线,而一元一次不等式组则可以表示为多条直线构成的图形。
二、一元一次不等式组的解集对于一元一次不等式组,可以有以下几种情况:情况一:无解当一元一次不等式组中的不等式互相矛盾时,即不等式组的解空间为空时,我们可以判断该不等式组无解。
情况二:唯一解当一元一次不等式组中的不等式互相兼容且形成一个可行区域时,我们可以通过求解相应的方程组,找到该不等式组的唯一解。
情况三:无数解当一元一次不等式组中的不等式互相兼容且形成一条线时,我们可以判断该不等式组有无数个解。
根据以上情况,我们可以通过解方程组、画图等方法来求解一元一次不等式组,并得到相应的解集。
三、一元一次不等式组的解集表示方法一元一次不等式组的解集可以用多种表示方法,主要有数学符号表示、图像表示和区间表示:1. 数学符号表示当一元一次不等式组存在唯一解时,我们可以用具体的数值来表示解集,例如{x=2, y=3}。
若不等式组有无数解,我们可以用参数的形式表示解集,例如{x=t, y=t+1}。
2. 图像表示我们可以将一元一次不等式组中的不等式转化为直线的形式,然后根据不等式的符号关系来确定线段的可行区域。
一元一次不等式概念

一元一次不等式的基本性质
1 加减法性质
对不等式的两边同时加减一个数,不等式的 关系不改变。
2 乘除法性质
对不等式的两边同时乘除一个正数,不等式 的关系不改变;对不等式的两边同时乘除一 个负数,不等式的关系改变。
3 倒置性质
如果改变不等式两边的位置,不等式的关系 将相反。
4 传递性质
如果 a > b 且 b > c,则 a > c。
一元一次不等式的绝对值不等式
定义
绝对值不等式是一种特殊的一 元一次不等式,其中包含一个 未知数的绝对值表达式。
Байду номын сангаас解法
通过分情况讨论和绝对值的性 质,我们可以求解绝对值不等 式并得到其解集。
示例
例如,|2x + 3| < 7 是一个绝对 值不等式。
一元一次不等式在生活中的应用
1 经济学
不等式可以用来描述资源分配、生产优化和供求平衡等经济学问题。
一元一次不等式的图形表示
数轴
数轴可以帮助我们直观地表示一 元一次不等式中未知数的取值区 间。
阴影区域
阴影区域表示满足一元一次不等 式的所有解的范围。
开圈与实心圈
不等式中使用的开圈和实心圈表 示边界是否包含在解集里。
一元一次不等式的解集概念
一元一次不等式的解集是满足不等式的所有实数的集合。解集可能是一个区 间、一个点或者空集。
一元一次不等式的等效变形
1
消去常数项
通过加减法,将常数项移到不等式的右边,变成0。
2
移项
通过加减法,将未知数的系数移到不等式的右边,变成0。
3
合并同类项
将不等式中同类项的系数相加合并。
一元一次不等式的加减法
一元一次不等式讲义
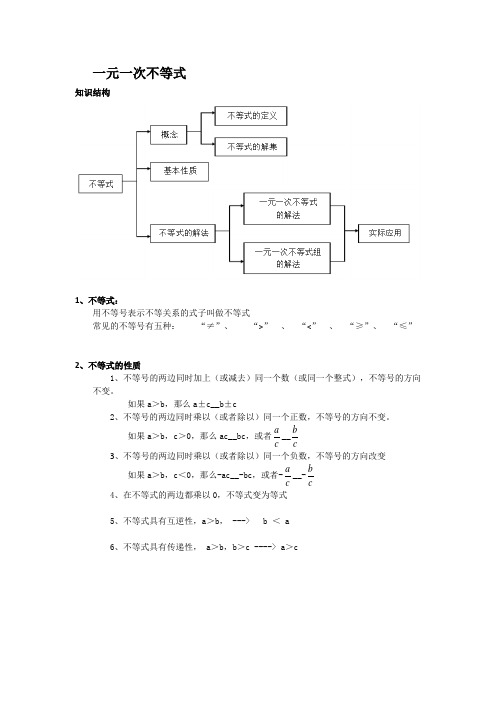
一元一次不等式知识结构1、不等式:用不等号表示不等关系的式子叫做不等式常见的不等号有五种: “≠”、 “>” 、 “<” 、 “≥”、 “≤”2、不等式的性质1、不等号的两边同时加上(或减去)同一个数(或同一个整式),不等号的方向不变。
如果a >b ,那么a ±c__b ±c2、不等号的两边同时乘以(或者除以)同一个正数,不等号的方向不变。
如果a >b ,c >0,那么ac__bc ,或者c a __c b 3、不等号的两边同时乘以(或者除以)同一个负数,不等号的方向改变如果a >b ,c <0,那么-ac__-bc ,或者-c a __-cb 4、在不等式的两边都乘以0,不等式变为等式5、不等式具有互逆性,a >b , ---> b < a6、不等式具有传递性, a >b ,b >c ----> a >c小练习1、用不等式表示数量的关系①a是正数②a是非负数③a不比0大④a与b的差是负数⑤a的相反数不大于1⑥a的相反数与a的一半的差不是正数2、如果a>b,则2a>a+b,是根据:不等式的两边同时加上一个数,不等号方向不变。
(1)如果a>b,则3a>3b,是根据:(2)如果a>b,则-a<-b,是根据:(3)如果a>1,则a<a²,是根据:(4)如果a<-1,则a²>a,是根据:3、设a,b,c都是实数,用a去乘以不等式的两边,不等号方向不变;用b去除不等式的两边,不等号方向改变;用c去乘不等式的两边,不等号变为等号,则a,b,c的大小关系是:()4、如果a>b,则下列各式不成立的是()A、a+4>b+4B、2+3a>2+3bC、a-6>b-6D、4-3a>4-3b5、如果a>b,则下列各式成立的是()A、b-a <0B、ac <bcC、a/b >1D、-b <-a一元一次不等式:1、一元一次不等式的定义:只含有一个未知数,并且未知数的最高次数是1,系数不等于0的不等式,叫做一元一次不等式2、一元一次不等式的标准形式:经过去分母、去括号、移项、合并同类项等变形后,能化为ax <b 或ax >b 的形式(其中a ≠0)3、不等式的解的定义:能使不等式成立的未知数的值叫做不等式的解 4、不等式的解集:·一个含有未知数的不等式的解的全体叫做这个不等式的解集。
一元一次不等式及其应用讲义

一元一次不等式及其应用【知识讲解】1、一元一次不等式的概念类似于一元一次方程,含有一个未知数,未知数的次数为1的不等式叫做一元一次不等式。
2、不等式的解集满足不等式的所有解的集合叫做不等式的解集,通常用数轴表示出来。
3、不等式的性质①若b a >,则c b c a ±>±;②若0,>>c b a ,则bc ac > 或cb c a >;③若,0,<>c b a 则bc ac <或cb ca <。
④若b a >,则a b <。
⑤若c b b a >>,,则c a >;⑥若a b b a ≥≥,,则b a =;⑦若02≤a ,则0=a 。
4、一元一次不等式的解法一元一次不等式的解法与一元一次方程的解法类似,但要特别注意不等式性质③,不等号要变号。
5、一元一次不等式的应用列一元一次不等式解实际应用问题,可类比列一元一次方程解应用问题的方法和技巧,不同的是,列不等式解应用题,寻求的是不等式关系,做题时特变注意题中关于不等的关系词。
【例题讲解】例1、解不等式215323x x +≤+-,并把它的解集在数轴上表示出来。
例2、若实数1>a ,则实数312,32,+=+==a P a N a M ,的大小关系为( )。
A 、M N P >>B 、P N M >>C 、M P N >>D 、N P M >>例3、已知关于x 的方程16325+-=-m x m x 的解满足23≤<-x ,求m 的整数值。
例4、已知x x x 34)32(2)1(5+++>+,化简|21||12|x x +--。
例5、某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器供选择,其中每台机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元。
初中数学知识归纳一元一次不等式的概念和性质

初中数学知识归纳一元一次不等式的概念和性质初中数学知识归纳:一元一次不等式的概念和性质一元一次不等式是初中数学中重要的内容之一,它在数学解题中具有广泛的应用。
了解一元一次不等式的概念和性质,对于我们掌握解一元一次不等式的方法和应用具有重要意义。
本文将对一元一次不等式的概念和性质进行归纳和总结。
一、概念一元一次不等式是指只有一个未知数的一次方程,且方程中含有一个不等号。
它是一种以未知数为变量的不等式类型。
一元一次不等式的一般形式为:ax+b>0,其中a、b为已知的实数常数,而x是未知的实数。
在解一元一次不等式时,我们需要找到使不等式成立的解集。
二、性质1. 加减性质:若a>b,则a+c>b+c,a-c>b-c。
这是因为对于不等式两边同时加或减同一个数,不等式的大小关系不变。
2. 倍数性质:若a>b>0,则ac>bc,a/c>b/c。
这是因为对于正实数a、b,以及正实数c,当a>b时,a和b的比值大于1,而c是正实数,所以ac和bc的大小关系与a和b相同。
3. 倒数性质:若a>b>0,则1/a<1/b。
这是因为a、b是正实数,而且a>b,所以1/a和1/b的大小关系与a和b相反。
4. 乘除性质:若a>b>0,c>d>0,则a/c>b/d,ad>bc。
这是因为对于正实数a、b、c、d,以及a>b>0和c>d>0,可以得到a/c>b/d(乘法性质)和ac>bd(乘法性质),同时根据乘法性质,如果ac>bd且c>0,那么ad>bc。
5. 反号性质:若a>b,则-a<-b。
这是因为对于不等式两边同时乘以-1,不等式的大小关系翻转。
6. 绝对值性质:若|a|>|b|,则a^2>b^2。
这是因为当a和b的绝对值大小关系相同时,a^2和b^2的大小关系与a和b相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用不等号连接起来的式子叫做不等式. 常见的不等号有五种: “≠”、 “>” 、 “<” 、 “≥”、 “≤”.
a 的3倍与2的差不小于5,用不等式表示为 代数式
1
13
m --值为正数,m 的范围是 2.不等式的解与解集
不等式的解:使不等式成立的未知数的值,叫做不等式的解.
不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。
解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
3.不等式的基本性质(重点)
(1)若a <b ,则a +c c b +; (2)若a >b ,c >0则ac bc (或c a c
b ); (3)若a >b ,
c <0则ac bc (或
c a c
b
). 说明:常见不等式所表示的基本语言与含义还有:
①若a -b >0,则a 大于b ;②若a -b <0,则a 小于b ;③若a -b ≥0,则a 不小于b ;④若a -b ≤0,则a 不大于b ;⑤若ab >0或
0a b >,则a 、b 同号;⑥若ab <0或0a
b
<,则a 、b 异号。
任意两个实数a 、b 的大小关系:①a -b>O ⇔a>b ;②a -b=O ⇔a=b ;③a-b<O ⇔a<b .
不等号具有方向性,其左右两边不能随意交换:但a <b 可转换为b >a ,c ≥d 可转换为d ≤c 。
1、(2013四川南充市) 不等式x+2>6的解集为_______________ 2、(2013广州市)已知a >b,c 为任意实数,则下列不等式中总是成立的是( )
<b+c B. a -c >b -c C. ac <bc D. ac >bc 1、(2013广东汕头)不等式3x ﹣9>0的解集是
2、(2013广东肇庆)解不等式:04)3(2>-+x ,并把解集在数轴上表示出来.
知识梳理:
初中数学基础知识讲义—一元一次不等式(组)
4.一元一次不等式(重点)
只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.
注:其标准形式:ax+b<0或ax+b≤0,ax+b>0或ax+b≥0(a≠0).
5.解一元一次不等式的一般步骤(重难点)
(1)去分母;(2)去括号;(3)移项; (4)合并同类项;(5)化系数为1.
说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方.
(2013呼和浩特)解不等式:5(x–2)+8<6(x–1)+7
1、(2013郴州)解不等式4(x﹣1)+3≥3x,并把解集在数轴上表示出来
2、(2013巴中)解不等式:,并把解集表示在数轴上
6.一元一次不等式组:几个合在一起就组成一个一元一次不等式组.一般地,几个不等式的解集的,叫做由它们组成的不等式组的解集.
7.由两个一元一次不等式组成的不等式组的解集有四种情况:(已知a b
<)
(2013山西)不等式组的解集是
8.易错知识辨析:
(1)不等式的解集用数轴来表示时,注意“空心圆圈”和“实心点”的不同含义.
(2)解字母系数的不等式时要讨论字母系数的正、负情况. 如不等式ax b
>(或ax b
<)(0
a≠)的形式的解集:当0
a>时,
b
x
a
>(或
b
x
a
<)当0
a<时,
b
x
a
<(或
b
x
a
>)当0
a<时,
b
x
a
<(或
b
x
a
>已知关于x的不等式2<x
a)
1(-的解集为x<
a
-
1
2
,则a的取值范围是_____
1、(2013贵州六盘水)已知不等式10
x-≥,此不等式的解集在数轴上表示为()
2、(2013四川攀枝花)下列说法中,错误
..的是()
A. 不等式2
<
x的正整数解中有一个 B. 2
-是不等式0
1
2<
-
x的一个解
C. 不等式9
3>
-x的解集是3
-
>
x D. 不等式10
<
x的解有无数个
3、(2013乐山)若a>b,则下列不等式变形错误
..的是() A.a+1 > b+1 B.
a
2
>
b
2
C. 3a-4 > 3b-4
D.4-3a > 4-3b
4、(2013湖南益阳)如图,数轴上表示的是下列哪个不等式组的解集()
A.
5
3
x
x
≥-
⎧
⎨
>-
⎩
B.
5
3
x
x
>-
⎧
⎨
≥-
⎩
C.
5
3
x
x
<
⎧
⎨
<-
⎩
D.
5
3
x
x
<
⎧
⎨
>-
⎩
5、(2013贵州遵义)如图,数轴上表示某不等式组的解集,则这个不等式
组可能是()
A.B.C.D.
6、(2013年吉林省)不等式2x-1>x的解集为_________
7、(2013湖南湘潭)不等式组
⎩
⎨
⎧
<
>
-
3
1
1
x
x
的解集为
8、(2013巴中)解不等式:,并把解集表示在数轴上
8、(2013三明)(1)解不等式组并把解集在数轴上表示出来;
9、(2013南平)解不等式组:10、(2013浙江省绍兴)解不等式组:
254(2)
2
1
3
x x
x x
+<+
⎧
⎪
⎨
-<
⎪⎩
中考零距离训练
【提高训练】 1、(2013铜仁)不等式2m-1≤6的正整数解是 2、(2013白银)不等式2x+9≥3(x+2)的正整数解是 . 3、(2013河南)不等式组⎩⎨
⎧>+≤1
22
x x 的最小整数解为( ) A . 1- B . 0 C . 1 D . 2
4、(2013雅安)不等式组213
112
x -<⎧⎪
⎨-≤⎪⎩的整数解有( ) 个 A . 1 B . 2 C . 3 D . 4
5、(2013孝感)使不等式x ﹣1≥2与3x ﹣7<8同时成立的x 的整数值是( )A.3,4 B.4,5 C.3,4,5 D. 不存在
6、(2013包头)不等式(x ﹣m )>3﹣m 的解集为x >1,则m 的值为
7、(2013湖北随州)若不等式0
0x b x a -<⎧⎨+>⎩
的解集为2<x<3,则a,b 的值分别为( )
A .-2,3
B .2,-3
C .3,-2
D .-3,2
8、(2013山东省荷泽市)若不等式组{
3x
x m
>>的解集是x>3,则m 的取值范围是______ 9、(2013•荆门)若关于x 的一元一次不等式组 有解,则m 的取值范围为( )
A.m>
B.m ≤
23 C.m<2
3
D.m ≤
10(2013湖北襄阳)若不等式组1+240x a
x >⎧⎨-⎩
≤有解,则a 的取值范围是( ) A .a ≤3
B .a <3 C
.a <2
D .a ≤2
11、(2013鄂州)若不等式组的解集为3≤x ≤4,则不等式ax+b <0的解集为
.
12、(2013益阳)已知一次函数y=x ﹣2,当函数值y >0时,自变量x 的取值范围在数轴上表示正确的是( )
A .
B .
C .
D . 13、(2013日照)如果点P (2x +6,x -4)在平面直角坐标系的第四象限内,那么x 的取值范围在数轴上可表示为( )
14、(2013玉林)不等式组⎪⎪⎩⎪⎪⎨⎧≤-≥-212
1112
1
x x 的整数解. 15、(2013菏泽)
,并指出它的所有非负整数解。
