2020年重庆市中考数学第18题专题突破
2020年中考数学一轮复习讲义(上海专版) 专题18 概率初步(解析版)

专题18 概率初步一、确定事件和随机事件1、确定事件必然发生的事件:在一定的条件下重复进行试验时,在每次试验中必然会发生的事件。
不可能发生的事件:有的事件在每次试验中都不会发生,这样的事件叫做不可能的事件。
2、随机事件:在一定条件下,可能发生也可能不放声的事件,称为随机事件。
二、随机事件发生的可能性一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。
对随机事件发生的可能性的大小,我们利用反复试验所获取一定的经验数据可以预测它们发生机会的大小。
要评判一些游戏规则对参与游戏者是否公平,就是看它们发生的可能性是否一样。
所谓判断事件可能性是否相同,就是要看各事件发生的可能性的大小是否一样,用数据来说明问题。
三、概率的意义与表示方法1、概率的意义一般地,在大量重复试验中,如果事件A 发生的频率mn 会稳定在某个常数p 附近,那么这个常数p 就叫做事件A 的概率。
2、事件和概率的表示方法一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P四、确定事件和随机事件的概率之间的关系1、确定事件概率(1)当A是必然发生的事件时,P(A)=1(2)当A是不可能发生的事件时,P(A)=02、确定事件和随机事件的概率之间的关系事件发生的可能性越来越小0 1概率的值不可能发生必然发生事件发生的可能性越来越大五、列表法求概率1、列表法用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
2、列表法的应用场合当一次试验要设计两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
六、树状图法求概率1、树状图法就是通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法。
2、运用树状图法求概率的条件当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
【例1】(2019•上海)一枚材质均匀的骰子,六个面的点数分别是1,2,3,4,5,6,投这个骰子,掷的点数大于4的概率是.【分析】先求出点数大于4的数,再根据概率公式求解即可.【解答】解:Q在这6种情况中,掷的点数大于4的有2种结果,∴掷的点数大于4的概率为21 63 =,故答案为:13.【例2】(2018•上海)从27,π,3这三个数中选一个数,选出的这个数是无理数的概率为.【分析】由题意可得共有3种等可能的结果,其中无理数有π、3共2种情况,则可利用概率公式求解.【解答】解:Q在27,π,3这三个数中,无理数有π,3这2个,∴选出的这个数是无理数的概率为23,故答案为:23.1.(2019•虹口区二模)下列事件中,必然事件是()A.在体育中考中,小明考了满分B.经过有交通信号灯的路口,遇到红灯C.抛掷两枚正方体骰子,点数和大于1D.四边形的外角和为180度.【分析】根据事件发生的可能性大小判断相应事件的类型即可.【解答】解:A、在体育中考中,小明考了满分是随机事件;B、经过有交通信号灯的路口,遇到红灯是随机事件;C、抛掷两枚正方体骰子,点数和大于1是必然事件;D、四边形的外角和为180度是不可能事件,故选:C.2.(2019•青浦区二模)将分别写有“创建”、“智慧”、“校园”的三张大小、质地相同的卡片随机排列,那么恰好排列成“创建智慧校园”的概率是.【分析】根据题意画出三张卡片排列的所有等可能结果,再由树状图确定恰好排列成“创建智慧校园”的结果数,依据概率公式可得答案.【解答】解:根据题意,画树状图如下:由树状图可知,共有6种等可能排列的方式,其中恰好排列成“创建智慧校园”的只有1种,∴恰好排列成“创建智慧校园”的概率是16,故答案为16.3.(2019•浦东新区二模)从1、2、3这三个数中任选两个组成两位数,在组成的所有两位数中任意抽取一个数,这个数恰好是偶数的概率是.【分析】列举出所有情况,看末位是2的情况占所有情况的多少即可.【解答】解:共有6种情况,是偶数的有2种情况,所以组成的两位数是偶数的概率为13,故答案为:13.4.(2019•静安区二模)从0,1,2,3这四个数字中任取3个数,取得的3个数中不含2的概率是.【分析】利用列举法展示所有4种等可能的结果数,再确定取得的3个数中不含2的结果数,然后根据概率公式求解.【解答】解:从0,1,2,3这四个数字中任取3个数有0、1、2;0、1、3;0、2、3;1、2、3四种等可能的结果数,所以取得的3个数中不含2的概率14 =.故答案为14.5.(2019•虹口区二模)一个不透明的袋中装有4个白球和若干个红球,这些球除颜色外其他都相同,摇匀后随机摸出一个球,如果摸到白球的概率为0.4,那么红球有个.【分析】设红球有x个,根据摸到白球的概率为0.4列出方程,求出x的值即可.【解答】解:设红球有x个,根据题意得:40.44x=+, 解得:6x =,答:红球有6个;故答案为:6.6.(2019•嘉定区二模)不透明的袋中装有8个小球,这些小球除了有红白两种颜色外其它都一样,其中2个小球为红色,6个小球为白色,随机地从袋中摸取一个小球是红球的概率为 .【分析】用红色小球的个数除以球的总个数即可得.【解答】解:Q 袋子中共有8个小球,其中红色小球有2个,∴随机地从袋中摸取一个小球是红球的概率为2184=, 故答案为:14. 7.(2019•松江区二模)在不透明的盒子中装有4个黑色棋子和若干个白色棋子,每个棋子除颜色外其它完全相同,从中随机摸出一个棋子,摸到黑色棋子的概率是13,那么白色棋子的个数是 . 【分析】设白色棋子的个数为x ,利用概率公式得到4143x =+,然后利用比例性质求出x 即可. 【解答】解:设白色棋子的个数为x , 根据题意得4143x =+, 解得8x =,即白色棋子的个数为8.故答案为8.8.(2019•徐汇区二模)在不透明的盒子中装有5个黑色棋子和15个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑色棋子的概率是 .【分析】直接利用概率公式求解. 【解答】解:任意摸出一个棋子,摸到黑色棋子的概率515154==+. 故答案为14.9.(2019•金山区二模)从方程20x =1-,2240x x -+=中,任选一个方程,选出的这个方程无实数解的概率为 .1-,再计算2240x x -+=的△0<,因此也无实数解,再利用概率可得答案.【解答】解:Q 11x -=-,2240x x -+=无实数解,∴无实数解的概率为23, 故答案为:23. 10.(2019•普陀区二模)如图,一个大正方形被平均分成9个小正方形,其中有2个小正方形已经被涂上阴影,在剩余的7个白色小正方形中任选一个涂上阴影,使图中涂上阴影的三个小正方形组成轴对称图形,这个事件的概率是 .【分析】直接利用轴对称图形的性质进而结合概率公式得出答案.【解答】解:如图所示:在剩余的7个白色小正方形中任选一个涂上阴影,使图中涂上阴影的三个小正方形组成轴对称图形,符合题意的有:1,2,3,4,5共5个,故这个事件的概率是:57. 故答案为:57.11.(2019•闵行区二模)从一副52张没有大小王的扑克牌中任意抽取一张牌,那么抽到A 的概率是 .【分析】直接利用概率求法进而得出答案.【解答】解:从一副52张没有大小王的扑克牌中任意抽取一张牌,那么抽到A 的概率是:415213=. 故答案为:113. 12.(2019•黄浦区二模)掷一枚质地均匀的正方体骰子,骰子的六个面分别标有1到6的点数,向上的一面出现的点数是2的倍数的概率是 .【分析】共有6种等可能的结果数,其中点数是2的倍数有2、4和6,从而利用概率公式可求出向上的一面出现的点数是2的倍数的概率.【解答】解:掷一次骰子,向上的一面出现的点数是2的倍数的有2、4,6,故骰子向上的一面出现的点数是2的倍数的概率是:31 62 =.故答案为:12.13.(2019•长宁区二模)掷一枚材质均匀的骰子,掷得的点数为素数的概率是.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:掷一枚质地均匀的骰子,掷得的点数可能是1、2、3、4、5、6中的任意一个数,共有六种可能,其中2、3、5是素数,所以概率为31 62 =,故答案为:12.14.(2019•杨浦区三模)在“石头、剪刀、布”的游戏中,两人打出相同标识手势的概率是.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人打出相同标识手势的情况,再利用概率公式求解即可求得答案.【解答】解:画树状图得:Q共有9种等可能的结果,两人打出相同标识手势的有3种情况,∴两人打出相同标识手势的概率是:31 93 =.故答案为:13.15.(2019•崇明区二模)从1、2、3、4、5、6、7、8这八个数中,任意抽取一个数,那么抽得的数是素数的概率是.【分析】根据素数定义,让素数的个数除以数的总数即为所求的概率.【解答】解:1Q,2,3,4,5,6,7,8这8个数有4个素数,2∴,3,5,7;故取到素数的概率是12.故答案为:12.。
2020重庆中考数学18题专题及答案二

2020重庆中考数学18题专题及答案二中考数学18题专题及答案二1. 一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用,已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车每次运货物的吨数之比为1:3;若甲、丙两车合运相同次数运完这批货物时,甲车共运了120吨,若乙、丙两车合运相同次数运完这批货物时,乙车共运了180吨.则这批货物共 240 吨.解:设货物总吨数为x吨.甲每次运a吨,乙每次运3a吨,丙每次运b吨.,=,解得x=240.故答案为:240.2.某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用了4380 朵.解:设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆.由题意,有,由①得,3x+2y+2z=580③,由②得,x+z=150④,把④代入③,得x+2y=280,∴2y=280-x⑤,由④得z=150-x⑥.∴4x+2y+3z=4x+(280-x)+3(150-x)=730,∴黄花一共用了:24x+12y+18z=6(4x+2y+3z)=6×730=4380.故黄花一共用了4380朵.3.一个水池装一个进水管和三个同样的出水管,先打开进水管,等水池存一些水后再打开出水管(进水管不关闭).若同时打开2个出水管,那么8分钟后水池空;如果同时打开3个出水管,则5分钟后水池空.那么出水管比进水管晚开 40 分钟.考点:三元一次方程组的应用.解:设出水管比进水管晚开x分钟,进水管的速度为y,出水管的速度为z,则有:,两式相除得:,解得:x=40,即出水管比进水管晚开40分钟.故答案为:40.4. 某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是11∶10 。
2020重庆中考数学18题专题及答案

中考数学18题专题及答案 1. 含有同种果蔬但浓度不同的A 、B 两种饮料,A 种饮料重40千克,B 种饮料重60千克现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同,那么从每种饮料中倒出的相同的重量是__ 24____千克设A 种饮料的浓度为a ,B 种饮料的浓度为b ,各自倒出和倒入的果蔬质量相同可设为x 千克,由于混合后的浓度相同,由题意可得:()()40604060x a xb x b xa-+-+=去分母()()604060406040x a xb x b xa -+=-+,去括号得:2400606024004040a xa xb b bx xa -+=-+移项得:6060404024002400xa xb bx xa b a -++-=-合并得:()()1002400b a x b a -=-所以:24x =2. 从两块分别重10千克和15千克且含铜的百分比不同的合金上各切下重量相等的一块,再把切下的每一块与另一块切后剩余的部分合在一起,熔炼后两者含铜的百分比恰好相等,则切下的一块重量是 6 千克。
设切下的一块重量是x 千克,设10千克和15千克的合金的含铜的百分比为a ,b ,=,整理得(b-a )x=6(b-a ),x=63.设有含铜百分率不同的两块合金,甲重40公斤,乙重60公斤.从这两块合金上切下重量相等的一块,并把所切下的每块与另一种剩余的合金加在一起,熔炼后两者的含铜百分率相等,则切下的合金重(24公斤 )设含铜量甲为a 乙为b ,切下重量为x .根据设有含铜百分率不同的两块合金,甲重40公斤,乙重60公斤,熔炼后两者的含铜百分率相等,列方程求解.解:设含铜量甲为a,乙为b,切下重量为x.由题意,有=,解得x=24.切下的合金重24公斤.1、四川省安岳县,是我国的柠檬生产基地。
超市里有一种柠檬水,由水和柠檬汁混合配制。
2020重庆中考数学18题专题及答案word.doc

中考数学18题专题及答案1.含有同种果蔬但浓度不同的A、B两种饮料,A种饮料重40千克,B种饮料重60千克现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同,那么从每种饮料中倒出的相同的重量是__ 24____千克设A种饮料的浓度为a,B种饮料的浓度为b,各自倒出和倒入的果蔬质量相同可设为x千克,由于混合后的浓度相同,由题意可得:()() 40604060x a xb x b xa-+-+=去分母()()604060406040x a xb x b xa-+=-+,去括号得:2400606024004040a xa xb b bx xa-+=-+移项得:6060404024002400xa xb bx xa b a-++-=-合并得:()()1002400b a x b a-=-所以:24x=2. 从两块分别重10千克和15千克且含铜的百分比不同的合金上各切下重量相等的一块,再把切下的每一块与另一块切后剩余的部分合在一起,熔炼后两者含铜的百分比恰好相等,则切下的一块重量是 6 千克。
设切下的一块重量是x千克,设10千克和15千克的合金的含铜的百分比为a,b,= ,整理得(b-a)x=6(b-a),x=63.设有含铜百分率不同的两块合金,甲重40公斤,乙重60公斤.从这两块合金上切下重量相等的一块,并把所切下的每块与另一种剩余的合金加在一起,熔炼后两者的含铜百分率相等,则切下的合金重(24公斤)设含铜量甲为a乙为b,切下重量为x.根据设有含铜百分率不同的两块合金,甲重40公斤,乙重60公斤,熔炼后两者的含铜百分率相等,列方程求解.解:设含铜量甲为a,乙为b,切下重量为x.由题意,有=,解得x=24.切下的合金重24公斤.1、四川省安岳县,是我国的柠檬生产基地。
超市里有一种柠檬水,由水和柠檬汁混合配制。
购买1吨柠檬汁的钱可以购买20吨的水。
2020重庆中考复习数学第18题专题训练八(含答案)

2020重庆中考复习数学第18题专题训练(含答案)例1、如图,在平面直角坐标系中,已知A(0,6),B(2,0),C(6,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连接CF交DE于点P,则CP的最大值.练习:在平面直角坐标系中,已知A(0,4)、B(1,0)、C(4,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连CF交DE于P,则CP的最大值为.例2、如图,在△ABC中,AB≠AC,∠BAC≠90°,AC=4,BC=3,∠BCA=45°,点D在线段BC 一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.正方形ADEF的边DE与线段CF相交于点P,则线段CP长的最大值为.练习:如图,在△ABC中,AB≠AC,∠BAC≠90°,AC=2,BC=3,∠BCA=45°,点D在线段BC一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.正方形ADEF的边DE与线段CF相交于点P,则线段CP长的最大值为.例3、如图,在平面直角坐标系中,点A的坐标为(﹣4,0),点B是y轴上一个动点,以AB为边在AB 的下方作等边△ABC,则线段OC的最小值为.练习:1、如图,在平面直角坐标系中,A(﹣3,0),点B是y轴正半轴上一动点,点C、D在x正半轴上.以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,则OP的最小值为.2、在平面直角坐标系中,已知点A(4,0),点B为y轴正半轴上一个动点,连接AB,以AB为一边向下作等边△ABC,连结OC,则OC的最小值为.参考答案解析例1、(2019秋•赣榆区期末)如图,在平面直角坐标系中,已知A(0,6),B(2,0),C(6,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连接CF交DE于点P,则CP的最大值.解:如图,作FQ⊥y轴于点Q,∴∠FQA=∠AOD=90°,∴∠F AQ+∠AFQ=90°,∵四边形ADEF是正方形,∴F A=AD,∠F AD=90°,∴∠F AQ+∠DAO=90°,∴∠AFQ=∠DAO,在△AFQ和△DAO中,,∴△AFQ≌△DAO(AAS),∴FQ=OA=OC=6,又FQ∥OC,且∠FQO=90°,∴四边形OCFQ是矩形,∴∠PCD=∠AOD=90°,∵∠ADE=90°,∴∠ADO+∠CDP=90°,且∠OAD+∠ADO=90°,∴∠OAD=∠CDP,且∠PCD=∠AOD=90°,∴△AOD∽△DCP,∴,设OD=x,则CD=6﹣x(2≤x≤6),∴,∴PC=﹣(x﹣3)2+,∴CP的最大值为,练习:(2016春•武汉校级月考)在平面直角坐标系中,已知A(0,4)、B(1,0)、C(4,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连CF交DE于P,则CP的最大值为1.解:如图,作FQ⊥y轴于点Q,∴∠FQA=∠AOD=90°,∴∠F AQ+∠AFQ=90°,∵四边形ADEF是正方形,∴F A=AD,∠F AD=90°,∴∠F AQ+∠DAO=90°,∴∠AFQ=∠DAO,在△AFQ和△DAO中,,∴△AFQ≌△DAO(AAS),∴FQ=OA=OC=4,又FQ∥OC,且∠FQO=90°,∴四边形OCFQ是矩形,∴∠PCD=∠AOD=90°,∵∠ADE=90°,∴△AOD∽△DCP,∴=,设OD=x,则CD=4﹣x(1≤x≤4),则=,即PC=﹣x2+x=﹣(x﹣2)2+1,∴当x=2时,PC最大=1,例2、(2017•越秀区校级二模)如图,在△ABC中,AB≠AC,∠BAC≠90°,AC=4,BC=3,∠BCA =45°,点D在线段BC一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.正方形ADEF 的边DE与线段CF相交于点P,则线段CP长的最大值为.解:如图,过点A作AG⊥AC交CB的延长线于点G,过点A作AQ⊥BC交CB的延长线于点Q,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,在△GAD与△CAF中,,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.∵DE与CF交于点P时,此时点D位于线段CQ上,∵∠BCA=45°,AC=4,∴由勾股定理得AQ=CQ=4.设CD=x,∴DQ=4﹣x,∵∠ADB+∠ADE+∠PDC=180°且∠ADE=90°,∴∠ADQ+∠PDC=90°,又∵在Rt△PCD中,∠PDC+∠DPC=90°,∴∠ADQ=∠DPC,∵∠AQD=∠DCP=90°,∴△AQD∽△DCP,∴,∴.∴CP=﹣x2+x=﹣(x﹣2)2+1.∴当x=2时,CP有最大值1.练习:如图,在△ABC中,AB≠AC,∠BAC≠90°,AC=2,BC=3,∠BCA=45°,点D在线段BC一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.正方形ADEF的边DE与线段CF相交于点P,则线段CP长的最大值为.解:过点A作AG⊥AC交BC于点G,∴AC=AG,可证△GAD≌△CAF,∴∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°,即CF⊥BD.过点A作AQ⊥BC交CB的延长线于点Q,∵DE与CF交于点P时,此时点D位于线段CQ上,∵∠BCA=45°,AC=2,∴由勾股定理可求得AQ=CQ=2.设CD=x,∴DQ=2﹣x,∵∠ADB+∠ADE+∠PDC=180°且∠ADE=90°,∴∠ADQ+∠PDC=90°,又∵在直角△PCD中,∠PDC+∠DPC=90°,∴∠ADQ=∠DPC,∵∠AQD=∠DCP=90°,∴△AQD∽△DCP,∴=,∴=.∴CP=﹣x2+x=﹣(x﹣1)2+.∴当x=1时,CP有最大值.例3、如图,在平面直角坐标系中,点A的坐标为(﹣4,0),点B是y轴上一个动点,以AB为边在AB 的下方作等边△ABC,则线段OC的最小值为.解:如图,以OA为对称轴作等边△ADE,连接EC,并延长EC交x轴于点F.在△AEC与△ADB中,,∴△AEC≌△ADB(SAS),∴∠AEC=∠ADB=120°,∴∠OEF=60°,∴OF=OA=4,∴点P在直线EF上运动,当OC⊥EF时,OC最小,∴OC=OF=2,则OC的最小值为2.练习:如图,在平面直角坐标系中,A(﹣3,0),点B是y轴正半轴上一动点,点C、D在x正半轴上.以AB 为边在AB的下方作等边△ABP,点B在y轴上运动时,则OP的最小值为.解:以OA为对称轴作等边△ADE,连接EP,并延长EP交x轴于点F.可得△AEP≌△ADB,∴∠AEP=∠ADB=120°,∴∠OEF=60°,∴OF=OA=3,∴点P在直线EF上运动,当OP⊥EF时,OP最小,∴OP=OF=,则OP的最小值为.2、在平面直角坐标系中,已知点A(4,0),点B为y轴正半轴上一个动点,连接AB,以AB为一边向下作等边△ABC,连结OC,则OC的最小值为2.解:如图,以OA为对称轴作等边△ADE,连接EC,并延长EC交x轴于点F.在△AEC与△ADB中,,∴△AEC≌△ADB(SAS),∴∠AEC=∠ADB=120°,∴∠OEF=60°,∴OF=OA=4,∴点C在直线EF上运动,当OC⊥EF时,OC最小,∴OC=OF=2,则OC的最小值为2.。
2020重庆中考复习数学第18题专题训练七(含答案解析)

2020重庆中考复习数学第18题专题训练七(含答案解析)例1、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最小值为练习:在△ABC中,∠ACB=90°,∠B=60°,AB=4,点D是直线BC上一动点,连接AD,在直线AD的右侧作等边△ADE,连接CE,当线段CE的长度最小时,线段CD的长度为例2、如图,已知△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点D为直线AB上一动点,将线段CD绕点C逆时针旋转60°得到线段CE,连接ED、BE,当BE最小时,线段AD的值为例3、(2018秋•鄞州区期末)如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC 上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是.练习:如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC 外作等边△BDE.若F为DE中点,则CF的最小值为.例4、(2019•安徽模拟)如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2,Q为AC上的动点,P为Rt△ABC内一动点,且满足∠APB=120°,若D为BC的中点,则PQ+DQ的最小值是参考答案解析例1、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最小值为解:∵∠ACB=90°,∴∠ACD=90°,在AC的右侧作等边△ACF,连接EF,如图所示:则AC=AF=CF=AC=5,∠CAF=∠AFC═60°,∵△ADE是等边三角形,∴AD=AE,∠DAE=60°=∠CAF,∴∠CAD=∠F AE,在△DAC和△EAF中,,∴△DAC≌△EAF(SAS),∴∠ACD=∠AFE=90°,∴∠CFE=90°﹣60°=30°,当CE⊥EF时,CE有最小值,∴CE的最小值=CF=;练习:在△ABC中,∠ACB=90°,∠B=60°,AB=4,点D是直线BC上一动点,连接AD,在直线AD的右侧作等边△ADE,连接CE,当线段CE的长度最小时,线段CD的长度为解:如图,以AC为边作等边△ACF,连接DF,∵∠ACB=90°,∠B=60°,AB=4,∴AC=2,∵△ACF是等边三角形,∴CF=AC=AF=2,∠BCF=60°,∵△ADE是等边三角形,∴AD=AE,∠F AC=∠DAE=60°,∴∠F AD=∠CAE,∴△ACE≌△AFD(SAS)∴CE=DF,∴DF⊥BC时,DF的长最小,即CE的长最小,∵∠FCD'=90°﹣60°=30°,D'F⊥CB,∴CD'=CF=3,例2、如图,已知△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点D为直线AB上一动点,将线段CD绕点C逆时针旋转60°得到线段CE,连接ED、BE,当BE最小时,线段AD的值为解:如图,以BC为边作等边△BCF,连接DF,∵∠ACB=90°,∠BAC=30°,AB=4,∴∠ABC=60°,BC=2,∵将线段CD绕点C逆时针旋转60°得到线段CE,∴CD=CE,∠DCE=60°,∵△BCF是等边三角形,∴CF=BC=BF=2,∠BCF=60°=∠DCE,∴∠BCE=∠DCF,且BC=CF,DC=CE,∴△BCE≌△FCD(SAS)∴BE=DF,∴DF⊥AB时,DF的长最小,即BE的长最小,∵∠FBD'=180°﹣60°﹣60°=60°,D'F⊥AB,∴BD'=BF=1,∴AD'=AB+BD'=5,例3、如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是2.解:以BC为边作等边三角形BCG,连接FG,AG,作GH⊥AC交AC的延长线于H,∵△BDE和△BCG是等边三角形,∴DC=EG,∴∠FDC=∠FEG=120°,∵DF=EF,∴△DFC≌△EFG(SAS),∴FC=FG,∴在点D的运动过程中,AF+FC=AF+FG,而AF+FG≥AG,∴当F点移动到AG上时,即A,F,G三点共线时,AF+FC的最小值=AG,∵BC=CG=AB=2,AC=2,在Rt△CGH中,∠GCH=30°,CG=2,∴GH=1,CH=,∴AG===2,∴AF+CF的最小值是2.练习:如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC 外作等边△BDE.若F为DE中点,则CF的最小值为.解:如图,过点D作DG⊥BC于G,过点F作FH⊥BC于H,设等边△BDE的边长为x,∵∠ABC=30°,∴BG=x,DG=x,∵∠ABC=30°,△BDE是等边三角形,∴∠CBE=90°,∵F为DE中点,∴FH是梯形BEDG的中位线,∴FH=(x+x)=x,∵∠ACB=90°,∠ABC=30°,AC=4,∴AB=2×4=8,BC=4,又∵BH=BG=x,∴CH=4﹣x,在Rt△CFH中,CF2=CH2+FH2=(4﹣x)2+(x)2=x2﹣6x+48=(x﹣4)2+36,∵D为线段AB上一个动点,∴0<x<8,∴当x=4时,CF2有最小值36,∴CF的最小值为=6.例4、如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2,Q为AC上的动点,P为Rt△ABC 内一动点,且满足∠APB=120°,若D为BC的中点,则PQ+DQ的最小值是解:如图以AB为边,向左边作等边△ABE,作△ABE的外接圆⊙O,连接OB,则点P在⊙O上.在Rt△ABC中,∵∠ACB=90°,∠ABC=60°,BC=2,∴AB=4,则易知OB=4,OB⊥BC,作点D关于AC的对称点D′,连接OD′,OP,PD′,PD′交AC于Q,则PQ+QD=PQ+QD′=PD′,∵PD′≥OD′﹣OP,OP=OB=4,OD′==,∴PD′≥﹣4,∴PQ+DQ的最小值为﹣4,。
两年中考模拟2020年中考数学:等腰三角形与直角三角形(学生版)
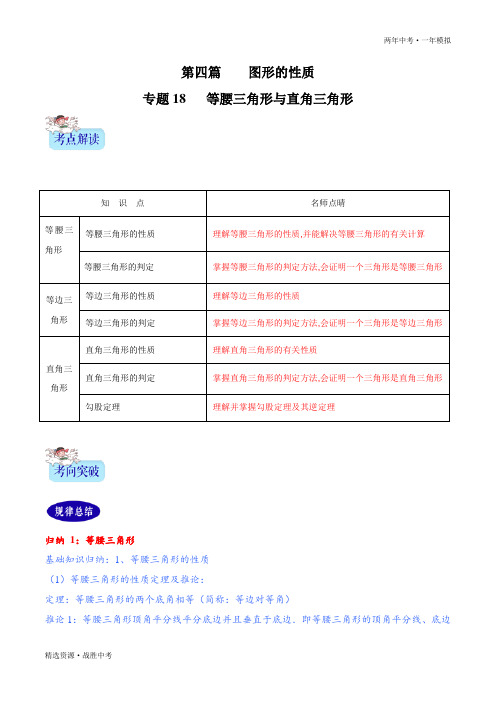
第四篇图形的性质专题18等腰三角形与直角三角形知识点名师点晴等腰三角形等腰三角形的性质理解等腰三角形的性质,并能解决等腰三角形的有关计算等腰三角形的判定掌握等腰三角形的判定方法,会证明一个三角形是等腰三角形等边三角形等边三角形的性质理解等边三角形的性质等边三角形的判定掌握等边三角形的判定方法,会证明一个三角形是等边三角形直角三角形直角三角形的性质理解直角三角形的有关性质直角三角形的判定掌握直角三角形的判定方法,会证明一个三角形是直角三角形勾股定理理解并掌握勾股定理及其逆定理归纳1:等腰三角形基础知识归纳:1、等腰三角形的性质(1)等腰三角形的性质定理及推论:定理:等腰三角形的两个底角相等(简称:等边对等角)推论1:等腰三角形顶角平分线平分底边并且垂直于底边.即等腰三角形的顶角平分线、底边上的中线、底边上的高重合.推论2:等边三角形的各个角都相等,并且每个角都等于60°.2、等腰三角形的判定等腰三角形的判定定理及推论:定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.基本方法归纳:①等腰直角三角形的两个底角相等且等于45°②等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角). ③等腰三角形的三边关系:设腰长为a ,底边长为b ,则2b <a ④等腰三角形的三角关系:设顶角为顶角为∠A ,底角为∠B 、∠C ,则∠A =180°—2∠B ,∠B =∠C =2180A ∠-︒ 注意问题归纳:等腰三角形的性质与判定经常用来计算三角形的角的有关问题,并证明角相等的问题.【例1】(2019内蒙古包头市,第10题,3分)已知等腰三角形的三边长分别为a 、b 、4,且a 、b 是关于x 的一元二次方程x 2﹣12x +m +2=0的两根,则m 的值是( )A .34B .30C .30或34D .30或36归纳 2:等边三角形基础知识归纳:1.定义三条边都相等的三角形是等边三角形.2.性质:等边三角形的各角都相等,并且每一个角都等于60°3.判定三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.基本方法归纳:线段垂直平分线上的一点到这条线段的两端距离相等;到一条线段两端点距离相等的点,在这条线段的垂直平分线上.注意问题归纳:三个角都相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形.【例2】(2019四川省宜宾市,第7题,3分)如图,∠EOF的顶点O是边长为2的等边△ABC的重心,∠EOF 的两边与△ABC的边交于E,F,∠EOF=120°,则∠EOF与△ABC的边所围成阴影部分的面积是()A.32B.235C.33D.34归纳3:直角三角形基础知识归纳:有一个角是直角的三角形叫作直角三角形直角三角形的性质:(1)直角三角形两锐角互余.(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;(3)在直角三角形中,斜边上的中线等于斜边的一半.基本方法归纳:(1)两个内角互余的三角形是直角三角形.(2)三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形.注意问题归纳:注意区分直角三角形的性质与直角三角形的判定,在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,它的逆命题不能直接使用.【例3】(2019山东省东营市,第14题,3分)已知等腰三角形的底角是30°,腰长为23,则它的周长是.归纳4:勾股定理基础知识归纳:直角三角形的两条直角边a、b的平方和等于斜边c的平方,即:a2+b2=c2;基本方法归纳:如果三角形的三条边a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形.注意问题归纳:勾股定理的逆定理也是判定直角三角形一种常用的方法,通常与直角三角形的性质结合起来考查.【例4】(2019北京,第12题,2分)如图所示的网格是正方形网格,则∠P AB+∠PBA= °(点A,B,P是网格线交点).【2019年题组】一、选择题1.(2019四川省内江市,第9题,3分)一个等腰三角形的底边长是6,腰长是一元二次方程x2﹣8x+15=0的一根,则此三角形的周长是()A.16B.12C.14D.12或162.(2019宁夏,第5题,3分)如图,在△ABC中AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为()A.40°B.45°C.55°D.70°3.(2019山西省,第5题,3分)如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC与点E,若∠1=145°,则∠2的度数是()A.30°B.35°C.40°D.45°4.(2019衢州,第7题,3分)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是()A.60°B.65°C.75°D.80°5.(2019湖北省荆州市,第5题,3分)如图,矩形ABCD的顶点A,B,C分别落在∠MON的边OM,ON上,若OA=OC,要求只用无刻度的直尺作∠MON的平分线.小明的作法如下:连接AC,BD交于点E,作射线OE,则射线OE 平分∠MON.有以下几条几何性质:①矩形的四个角都是直角,②矩形的对角线互相平分,③等腰三角形的“三线合一”.小明的作法依据是()A.①②B.①③C.②③D.①②③6.(2019湖南省常德市,第7题,3分)如图,在等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为42,则四边形DBCE的面积是()A.20B.22C.24D.267.(2019湖南省长沙市,第12题,3分)如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD55BD的最小值是()A.25B.45C.53D.108.(2019辽宁省丹东市,第7题,3分)等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是()A.8B.9C.8或9D.129.(2019台湾,第4题,3分)图1的直角柱由2个正三角形底面和3个矩形侧面组成,其中正三角形面积为a,矩形面积为b.若将4个图1的直角柱紧密堆叠成图2的直角柱,则图2中直角柱的表面积为何?()A.4a+2b B.4a+4b C.8a+6b D.8a+12b10.(2019甘肃省天水市,第8题,4分)如图,等边△OAB的边长为2,则点B的坐标为()A.(1,1)B.(3C.3,1)D.33)11.(2019内蒙古赤峰市,第14题,3分)如图,小聪用一张面积为1的正方形纸片,按如下方式操作:①将正方形纸片四角向内折叠,使四个顶点重合,展开后沿折痕剪开,把四个等腰直角三角形扔掉;②在余下纸片上依次重复以上操作,当完成第2019次操作时,余下纸片的面积为()A .22019B .201812C .201912 D .20201212.(2019台湾,第9题,3分)公园内有一矩形步道,其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成.如图表示此步道的地砖排列方式,其中正方形地砖为连续排列且总共有40个.求步道上总共使用多少个三角形地砖?( )A .84B .86C .160D .16213.(2019四川省内江市,第10题,3分)如图,在△ABC 中,AB =2,BC =3.6,∠B =60°,将△ABC 绕点A 顺时针旋转得到△ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为( )A .1.6B .1.8C .2D .2.614.(2019四川省成都市,第5题,3分)将等腰直角三角形纸片和矩形纸片按如图方式叠放在起,若∠1=30°,则∠2的度数为( )A .10°B .15°C .20°D .30°15.(2019四川省眉山市,第11题,3分)如图,在矩形ABCD 中,AB =6,BC =8,过对角线交点O 作EF ⊥AC 交AD 于点E ,交BC 于点F ,则DE 的长是( )A.1B.74C.2D.12516.(2019四川省绵阳市,第10题,3分)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则(sinθ﹣cosθ)2=()A.15B.55C.355D.9517.(2019滨州,第10题,3分)满足下列条件时,△ABC不是直角三角形的为()A.AB41=,BC=4,AC=5B.AB:B C:A C=3:4:5C.∠A:∠B:∠C=3:4:5D.|cosA12-|+(tanB33-)2=018.(2019聊城,第11题,3分)如图,在等腰直角三角形ABC中,∠BAC=90°,一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B,将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,下列结论中错误的是()A.AE+AF=AC B.∠BEO+∠OFC=180°C.OE+OF2=BC D.S四边形AEOF12=S△ABC19.(2019江苏省苏州市,第10题,3分)如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,DE交AC于点E.若DE=1,则△ABC的面积为()A.42B.4C.25D.820.(2019浙江省宁波市,第9题,4分)已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为()A.60°B.65°C.70°D.75°21.(2019浙江省宁波市,第12题,4分)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出()A.直角三角形的面积B.最大正方形的面积C.较小两个正方形重叠部分的面积D.最大正方形与直角三角形的面积和22.(2019浙江省湖州市,第9题,3分)在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是()A.22B.5C.352D.1023.(2019海南,第12题,3分)如图,在Rt△ABC中,∠C=90°,AB=5,BC=4.点P是边AC上一动点,过点P 作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为()A.813B.1513C.2513D.321324.(2019湖北省咸宁市,第2题,3分)勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是()A.B.C.D.25.(2019湖北省黄石市,第8题,3分)如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和∠BDC的角平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD+∠CED=()A.125°B.145°C.175°D.190°26.(2019辽宁省朝阳市,第7题,3分)把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是()A.83°B.57°C.54°D.33°27.(2019辽宁省锦州市,第7题,2分)在矩形ABCD中,AB=3,BC=4,M是对角线BD上的动点,过点M作ME ⊥BC于点E,连接AM,当△ADM是等腰三角形时,ME的长为()A.32B.65C.32或35D.32或65二、填空题28.(2019四川省宜宾市,第16题,3分)如图,△ABC和△CDE都是等边三角形,且点A、C、E在同一直线上,AD 与BE、BC分别交于点F、M,BE与CD交于点N.下列结论正确的是(写出所有正确结论的序号).①AM=BN;②△ABF≌△DNF;③∠FMC+∠FNC=180°;④111 MN AC CE=+29.(2019自贡,第18题,4分)如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则cos(α+β)= .30.(2019江苏省连云港市,第15题,3分)如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(4,1,3),按此方法,则点C的坐标可表示为.31.(2019江苏省镇江市,第8题,2分)如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1= °.32.(2019浙江省温州市,第16题,5分)图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为分米;当OB从水平状态旋转到OB'(在CO延长线上)时,点E绕点F随之旋转至OB'上的点E'处,则B'E'﹣BE为分米.33.(2019湖北省荆门市,第15题,3分)如图,在平面直角坐标系中,函数ykx(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为.34.(2019湖北省黄冈市,第16题,3分)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是.35.(2019辽宁省锦州市,第16题,3分)如图,边长为4的等边△ABC,AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边△OBA1,边OA1与AB交于点O1,以O1B为边作等边△O1BA2,边O1A2与A1B交于点O2,以O2B为边作等边△O2BA3,边O2A3与A2B交于点O3,…,依此规律继续作等边△O n﹣1BA n,记△OO1A的面积为S1,△O1O2A1的面积为S2,△O2O3A2的面积为S3,…,△O n﹣1O n A n﹣1的面积为S n,则S n=.(n≥2,且n为整数)36.(2019广安,第13题,3分)等腰三角形的两边长分别为6cm,13cm,其周长为cm.37.(2019四川省成都市,第12题,4分)如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为.38.(2019广西桂林市,第17题,3分)如图,在平面直角坐标系中,反比例ykx=(k>0)的图象和△ABC都在第一象限内,AB=AC52=,BC∥x轴,且BC=4,点A的坐标为(3,5).若将△ABC向下平移m个单位长度,A,C两点同时落在反比例函数图象上,则m的值为.39.(2019新疆,第14题,5分)如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为.40.(2019江苏省徐州市,第18题,3分)函数y=x+1的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有个.41.(2019湖南省常德市,第14题,3分)如图,已知△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD',且点D'、D、B三点在同一条直线上,则∠ABD的度数是.42.(2019甘肃省白银市,第17题,4分)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .43.(2019贵州省毕节市,第17题,5分)如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为度.44.(2019内蒙古通辽市,第15题,3分)腰长为5,高为4的等腰三角形的底边长为.45.(2019四川省巴中市,第15题,4分)如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC=.46.(2019四川省广元市,第13题,3分)如图,△ABC中,∠ABC=90°,BA=BC=2,将△ABC绕点C逆时针旋转60°得到△DEC,连接BD,则BD2的值是.47.(2019四川省泸州市,第16题,3分)如图,在等腰Rt△ABC中,∠C=90°,AC=15,点E在边CB上,CE=2EB,点D在边AB上,CD⊥AE,垂足为F,则AD的长为.48.(2019山东省威海市,第13题,3分)把一块含有45°角的直角三角板与两条长边平行的直尺如图放置(直角顶点在直尺的一条长边上).若∠1=23°,则∠2=°.49.(2019山东省威海市,第17题,3分)如图,在四边形ABCD中,AB∥CD,连接AC,BD.若∠ACB=90°,AC=BC,AB=BD,则∠ADC=°.50.(2019枣庄,第17题,4分)把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD= .51.(2019山东省淄博市,第17题,4分)如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.如图1,当CD12=AC时,tanα134=;如图2,当CD13=AC时,tanα2512=;如图3,当CD14=AC时,tanα3724=;……依此类推,当CD11n=+AC(n为正整数)时,tanαn= .52.(2019山西省,第15题,3分)如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为cm.53.(2019广西,第18题,3分)如图,AB与CD相交于点O,AB=CD,∠AOC=60°,∠ACD+∠ABD=210°,则线段AB,AC,BD之间的等量关系式为.54.(2019江苏省宿迁市,第17题,3分)如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C 在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是.55.(2019湖北省鄂州市,第15题,3分)如图,已知线段AB=4,O是AB的中点,直线l经过点O,∠1=60°,P点是直线l上一点,当△APB为直角三角形时,则BP= .56.(2019湖南省株洲市,第13题,3分)如图所示.在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E、F分别为MB、BC的中点,若EF=1,则AB= .57.(2019湖南省株洲市,第18题,3分)如图所示,在平面直角坐标系xOy中,在直线x=1处放置反光镜Ⅰ,在y轴处放置一个有缺口的挡板Ⅱ,缺口为线段AB,其中点A(0,1),点B在点A上方,且AB=1,在直线x=﹣1处放置一个挡板Ⅲ,从点O发出的光线经反光镜Ⅰ反射后,通过缺口AB照射在挡板Ⅲ上,则落在挡板Ⅲ上的光线的长度为.58.(2019湖南省邵阳市,第17题,3分)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是.59.(2019西藏,第15题,3分)若实数m 、n 满足|m ﹣3|4n +-=0,且m 、n 恰好是直角三角形的两条边,则该直角三角形的斜边长为 .60.(2019贵州省毕节市,第19题,5分)三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C 在FD 的延长线上,点B 在ED 上,AB ∥CF ,∠F =∠ACB =90°,∠E =45°,∠A =60°,AC =10,则CD 的长度是 .61.(2019贵州省铜仁市,第16题,4分)如图,在△ABC 中,D 是AC 的中点,且BD ⊥AC ,ED ∥BC ,ED 交AB 于点E ,BC =7cm ,AC =6cm ,则△AED 的周长等于 cm .62.(2019辽宁省丹东市,第13题,3分)如图,在△ABC 中,∠C =90°,DE 是AB 的垂直平分线,AD 恰好平分∠BAC .若DE =1,则BC 的长是 .63.(2019辽宁省大连市,第13题,3分)如图,△ABC 是等边三角形,延长BC 到点D ,使CD =AC ,连接AD .若AB =2,则AD 的长为 .64.(2019辽宁省抚顺市,第17题,3分)如图,在Rt △ABC 中,∠ACB =90°,CA =CB =2,D 是△ABC 所在平面内一点,以A ,B ,C ,D 为顶点的四边形是平行四边形,则BD 的长为 .65.(2019黑龙江省鸡西市,第9题,3分)一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,则CD的长为.66.(2019黑龙江省齐齐哈尔市,第16题,3分)等腰△ABC中,BD⊥AC,垂足为点D,且BD12=AC,则等腰△ABC底角的度数为.三、解答题67.(2019内蒙古呼和浩特市,第18题,6分)如图,在△ABC中,内角A、B、C所对的边分别为a、b、c.(1)若a=6,b=8,c=12,请直接写出∠A与∠B的和与∠C的大小关系;(2)求证:△ABC的内角和等于180°;(3)若()12a b caa b c c++=-+,求证:△ABC是直角三角形.68.(2019四川省巴中市,第18题,8分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.(1)求证:EC=BD;(2)若设△AEC三边分别为a、b、c,利用此图证明勾股定理.69.(2019四川省达州市,第20题,7分)如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=3.(1)尺规作图:不写作法,保留作图痕迹.①作∠ACB的平分线,交斜边AB于点D;②过点D作BC的垂线,垂足为点E.(2)在(1)作出的图形中,求DE的长.70.(2019山东省菏泽市,第23题,10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:B P⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=62,AD=3,求△PDE的面积.【2018年题组】一、选择题1.(2018浙江省湖州市,第5题,3分)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是()A.20°B.35°C.40°D.70°2.(2018兰州,第5题,4分)如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是()A.50°B.60°C.65°D.70°3.(2018贵州省安顺市,第6题,3分)一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是()A.12B.9C.13D.12或94.(2018辽宁省丹东市,第5题,3分)如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB与点E,已知△BCE的周长为10,且BC=4,则AB的长为()A.3B.4C.5D.65.(2018辽宁省营口市,第6题,3分)如图,在△ABC中,AB=AC,∠BAC=100°,在同一平面内,将△ABC绕点A 顺时针旋转到△AB1C1的位置,连接BB1,若BB1∥AC1,则∠CAC1的度数是()A.10°B.20°C.30°D.40°6.(2018台湾省,第11题,3分)如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?()A.115B.120C.125D.1307.(2018山东省德州市,第12题,4分)如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③四边形ODBE的面积始终等于433;④△BDE周长的最小值为6.上述结论中正确的个数是()A.1B.2C.3D.48.(2018四川省达州市,第8题,3分)如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为()A.32B.2C.52D.39.(2018广西梧州市,第7题,3分)如图,在△ABC中,AB=AC,∠C=70°,△AB'C'与△ABC关于直线EF对称,∠CAF=10°,连接BB',则∠ABB'的度数是()A.30°B.35°C.40°D.45°10.(2018江苏省宿迁市,第6题,3分)若实数m、n满足等式|m﹣4n =0,且m、n恰好是等腰△ABC 的两条边的边长,则△ABC的周长是()A.12B.10C.8D.611.(2018广西玉林市,第9题,3分)如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC 为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是()A.平行B.相交C.垂直D.平行、相交或垂直12.(2018浙江省台州市,第10题,4分)如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B'DE,若B'D,B'E分别交AC于点F,G,连接OF,OG,则下列判断错误的是()A.△ADF≌△CGEB.△B'FG的周长是一个定值C.四边形FOEC的面积是一个定值D.四边形OGB'F的面积是一个定值13.(2018兰州,第7题,4分)如图,边长为4的等边△ABC中,D、E分别为AB,AC的中点,则△ADE的面积是()A3333B C24 . .D.314.(2018福建省A,第5题,4分)如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于()A.15°B.30°C.45°D.60°15.(2018辽宁省鞍山市,第7题,3分)如图,在等边三角形ABC中,AE=CD,CE与BD相交于点G,EF⊥BD于点F,若EF=2,则EG的长为()A.334B.433C.332D.416.(2018内蒙古包头市,第8题,3分)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为()A.17.5°B.12.5°C.12°D.10°17.(2018吉林省长春市,第8题,3分)如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=kx(x>0)的图象上,若AB=2,则k的值为()A.4B.22C.2D.218.(2018四川省内江市,第12题,3分)如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为()A.(﹣4,﹣5)B.(﹣5,﹣4)C.(﹣3,﹣4)D.(﹣4,﹣3)19.(2018四川省凉山州,第3题,4分)如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以O为圆心,OB 长为半径作弧,交数轴于点C,则OC长为()A.3B.2C.3D.520.(2018四川省南充市,第8题,3分)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD 的中点,若BC=2,则EF的长度为()A.12B.1C.32D321.(2018四川省攀枝花市,第4题,3分)如图,等腰直角三角形的顶点A、C分别在直线a、b上,若a∥b,∠1=30°,则∠2的度数为()A .30°B .15°C .10°D .20°22.(2018四川省泸州市,第8题,3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a ,较短直角边长为b .若ab =8,大正方形的面积为25,则小正方形的边长为( )A .9B .6C .4D .323.(2018四川省绵阳市,第11题,3分)如图,△ACB 和△ECD 都是等腰直角三角形,CA =CB ,CE =CD ,△ACB 的顶点A 在△ECD 的斜边DE 上,若AE 2=,AD 6=,则两个三角形重叠部分的面积为( )A .2B .32-C .31-D .33-24.(2018山东省东营市,第10题,3分)如图,点E 在△DBC 的边DB 上,点A 在△DBC 内部,∠DAE =∠BAC =90°,AD =AE ,AB =AC .给出下列结论:①BD =CE ;②∠ABD +∠ECB =45°;③BD ⊥CE ;④BE 2=2(AD 2+AB 2)﹣CD 2.其中正确的是( )A .①②③④B .②④C .①②③D .①③④25.(2018山东省枣庄市,第10题,3分)如图是由8个全等的小矩形组成的大正方形,线段AB 的端点都在小矩形的顶点上,如果点P 是某个小矩形的顶点,连接P A 、PB ,那么使△ABP 为等腰直角三角形的点P 的个数是()A.2个B.3个C.4个D.5个26.(2018山东省枣庄市,第12题,3分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为()A.32B.43C.53D.8527.(2018山东省淄博市,第11题,4分)如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为()A.4B.6C.43D.828.(2018山东省淄博市,第12题,4分)如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为()A.25394+B.25392+C.18253+D.3182+29.(2018山东省滨州市,第1题,3分)在直角三角形中,若勾为3,股为4,则弦为()A.5B.6C.7D.830.(2018山东省莱芜市,第8题,3分)在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在第三象限,且在反比例函数y=kx的图象上,则k=()A.3B.4C.6D.1231.(2018山东省菏泽市,第3题,3分)如图,直线a∥b,等腰直角三角板的两个顶点分别落在直线a、b上,若∠1=30°,则∠2的度数是()A.45°B.30°C.15°D.10°32.(2018山东省青岛市,第6题,3分)如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕EF交BC于点F.已知EF=32,则BC的长是()A.322B.32C.3D.3333.(2018山西省,第8题,3分)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C,此时点A'恰好在AB边上,则点B'与点B之间的距离为()A.12B.6C.62D.6334.(2018广西贺州市,第10题,3分)如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为()A.32B.33C.6D.6235.(2018江苏省南通市,第5题,3分)下列长度的三条线段能组成直角三角形的是()A.3,4,5B.2,3,4C.4,6,7D.5,11,1236.(2018江苏省扬州市,第7题,3分)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是()A.BC=EC B.EC=BE C.BC=BE D.AE=EC37.(2018江苏省扬州市,第8题,3分)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是()A.①②③B.①C.①②D.②③38.(2018浙江省温州市,第10题,4分)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为()A.20B.24C.994D.53239.(2018海南省,第12题,3分)如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为()A.6B.8C.10D.1240.(2018湖北省孝感市,第10题,3分)如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE ⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(3﹣1)EF.其中正确结论的个数为()A.5B.4C.3D.241.(2018湖北省荆州市,第4题,3分)如图,两条直线l1∥l2,Rt△ACB中,∠C=90°,AC=BC,顶点A、B分别在l1和l2上,∠1=20°,则∠2的度数是()A.45°B.55°C.65°D.75°42.(2018湖北省荆门市,第11题,3分)如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为()。
2020重庆中考复习数学第18题《七类最值问题的求解策略》

2020重庆中考复习第18题《七类最值问题的求解策略》类型一:旋转三角形利用三点共线求最值例1、如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段.EF绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为练习1、如图,在平行四边形ABCD中,∠A=45°,AB=4,AD=2,M是AD边的中点,N是AB边上一动点,将线段MN绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值.2、(2019秋•海曙区校级月考)如图,菱形ABCD的边长是6,∠A=60°,E是AD的中点,F是AB边上一个动点,EG=EF且∠GEF=60°,则GB+GC的最小值是 .A类型二:旋转三角形利用四点共线求最值例2、如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .练习如图,矩形ABCD中,AB=2,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是.类型三:旋转三角形利用垂线段最短求最值例2、如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .练习1、(2019秋•东台市期中)如图,正方形ABCD中边长为6,E为BC上一点,且BE=1.5,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .2、如图,长方形 ABCD 中,AB=3,BC=4,E 为 BC 上一点,且 BE=2,F 为 AB 边上的一个动点,连接 EF,将 EF 绕着点 E 顺时针旋转 45˚到 EG 的位置,连接 FG 和 CG,则 CG 的最小值为.3、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为 .类型四:利用二次函数求最值例3、如图,在ABC ∆中,090ACB ∠=,5,2AC BC ==,点D 是AC 边上一点,连接BD ,将线段BD 绕点D 逆时针旋转090得线段ED ,连接AE ,则AE 的最小值为 .A例4、(2010秋•东城区期末)如图,在△ABC 中,∠ACB 为锐角,点D 为射线BC 上一动点,连接AD ,将线段AD 绕点A 逆时针旋转90°得到AE ,连接EC .若点D 在线段BC 上运动,DF ⊥AD 交线段CE 于点F ,且∠ACB =45°,,则线段CF 长的最大值为.例5、如图,在△ABC 中,∠BAC =120°,AB =AC =6,D 为边AB 上一动点(不与B 点重合),连接CD ,将线段CD 绕着点D 逆时针旋转90°得到DE ,连接BE ,则S △BDE 的最大值为 .练习1、如图,矩形ABCD中,AB=2,BC=4,点E是矩形ABCD的边AD上的一动点,以CE为边,在CE的右侧构造正方形CEFG,连结AF,则AF的最小值为 .2、(2019秋•黄陂区期中)如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=2,则△BDE面积的最大值为 .类型五:构造等边三角形求最值例6、如图,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4,若BD⊥CD,垂足为点D,则对角线AC的长的最大值为.练习如图,在四边形ABCD 中,AB =6,BC =4,若AC =AD ,且∠ACD =60°,则对角线BD 的长的最大值为 .类型六:利用对称求最值例7、(2019•成都)如图,在边长为1的菱形ABCD 中,∠ABC =60°,将△ABD 沿射线BD 的方向平移得到△A 'B 'D ',分别连接A 'C ,A 'D ,B 'C ,则A 'C +B 'C 的最小值为 .练习:如图,在矩形ABCD 中,AB =,1BC =,将ABD ∆沿射线DB 平移到A B D '''∆,连接B C D C ''、,则+B C D C ''的最小值为 .类型七:利用基本不等式求最值参考答案类型一:旋转三角形利用三点共线求最值例1、如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为.解:如图,取AB的中点N.连接EN,EC,GN,(即将△EAF绕点E逆时针旋转60°得△ENG)作EH ⊥CD交CD的延长线于H.∵四边形ABCD是菱形,∴AD=BD,∵AE=ED,AN=NB,∴AE=AN,∵∠A=60°,∴△AEN是等边三角形,∴∠AEN=∠FEG=60°,∴∠AEF=∠NEG,∵EA=EN,EF=EG,∴△AEF≌△NEG(SAS),∴∠ENG=∠A=60°,∵∠ANE=60°,∴∠GNB=180°﹣60°﹣60°=60°,∴点G的运动轨迹是射线NG,易知B,E关于射线NG对称,∴GB=GE,∴GB+GC=GE+GC≥EC,在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,∴DH=DE=1,EH=,在Rt△ECH中,EC==2,∴GB+GC≥2,∴GB+GC的最小值为2.练习1、如图,在平行四边形ABCD中,∠A=45°,AB=4,AD=2,M是AD边的中点,N是AB边上一动点,将线段MN绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值.解:如图,作ME⊥AD交AB于E,连接EN′、AC、作CF⊥AB于F.∵∠MAE=45°,∴△MAE是等腰直角三角形,∴MA=ME,∵∠AME=∠NMN′=90°,∴∠AMN=∠EMN′,∵MN=MN′,∴△AMN≌△EMN′,∴∠MAN=∠MEN′=45°,∴∠AEN′=90°,∴EN′⊥AB,∵AM=DM=,AB=4,∴AE=2,EB=2,∴AE=EB,∴N′B=N′A,∴N′B+N′C=N′A+N′C,∴当A、N′、C共线时,N′B+N′C的值最小,最小值=AC,在Rt△BCF中,∵BC=AD=2,∠CBF=∠DAB=45°,∴CF=BF=2,在Rt△ACF中,AC ==22、(2019秋•海曙区校级月考)如图,菱形ABCD的边长是6,∠A=60°,E是AD的中点,F是AB边上一个动点,EG=EF且∠GEF=60°,则GB+GC的最小值是 .AA解:取AB的中点H,连接HG、HE、HG、BE、CE,则△AEF≌△HEG∴∠GHE=∠A=60°,∴HG∥AD,可知△BHG≌△EHG,∴BG=GE,∴CE的长就是GB +GC的最小值;在Rt△EBC中,EB=3,BC=6,∴EC=3,∴GB+GC的最小值3.类型二:旋转三角形利用四点共线求最值例2、如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .解析:如图,将△ABP绕着点B逆时针旋转60°,得到△DBE,连接EP,CD,∴△ABP≌△DBE∴∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,∴△BPE是等边三角形∴EP=BP∴AP+BP+PC=PC+EP+DE,∴当点D,点E,点P,点C共线时,PA+PB+PC有最小值CD∵∠ABC=30°=∠ABP∠+PBC,∴∠DBE∠+PBC=30°,∴∠DBC=90°,∴CD==.练习如图,矩形ABCD中,AB=2,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是.解:由旋转的性质可知:△PFC是等边三角形,∴PC=PF,∵PB=EF,∴PA+PB+PC=PA+PF+EF,∴当A、P、F、E共线时,PA+PB+PC的值最小,∵四边形ABCD是矩形,∴∠ABC=90°,∴tan∠ACB==,∴∠ACB=30°,AC=2AB=4,∵∠BCE=60°,∴∠ACE=90°,∴AE==2.类型三:旋转三角形利用垂线段最短求最值例2、如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .解析:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动将△EFB绕点E旋转60°,使EF与EG重合,得到△EFB≌△EHG,从而可知△EBH为等边三角形,点G在垂直于HE的直线HN上,作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM为矩形,则CM=MP+CP=HE+EC=1+=,CG的最小值为.练习1、(2019秋•东台市期中)如图,正方形ABCD中边长为6,E为BC上一点,且BE=1.5,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .解:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动将△EFB绕点E旋转60°,使EF与EG重合,得到△EFB≌△EHG,从而可知△EBH为等边三角形,点G在垂直于HE的直线HN上,作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM为矩形,则CM=MP+CP=HE+EC ==,故答案为:.2、如图,长方形 ABCD 中,AB=3,BC=4,E 为 BC 上一点,且 BE=2,F 为 AB 边上的一个动点,连接 EF,将 EF 绕着点 E 顺时针旋转 45˚到 EG 的位置,连接 FG 和 CG,则 CG 的最小值为.F解析:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动,将△EFB绕点E旋转45°,使EF与EG重合,得到△EFB≌△EHG,从而可知△EBH为等腰直角三角形,点G在垂直于HE的直线HG上,作CM⊥HG,则CM即为CG的最小值,作EN⊥CM,可知四边形HENM为矩形,则CM=MN+CN=HE EC=123、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB 上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为 .解析:将线段AE绕点E逆时针旋转120°得到EH,连接HG,过点H作HM⊥AD,∵四边形ABCD是平行四边形,∴∠A∠+B=180°,∴∠A=120°,∵将线段AE绕点E逆时针旋转120°得到EH,将线段EF绕点E逆时针旋转120°得到EG,∴EF=EG=4,AE=EH,∠AEH=∠FEG=120°,∴∠DEH =60°,∠AEF =∠HEG ,且EF =EG ,AE =EH ,∴△AEF ≌△HEG (SAS ) ∴∠A =∠EHG =120°=∠AEH ,∴AD ∥HG ,∴点G 的轨迹是过点H 且平行于AD 的直线, ∴当DG ⊥HG 时,线段GD 长度有最小值,∵∠HEM =60°,EH =4,HM ⊥AD , ∴EM =2,MH =EM =2,∴线段GD 长度的最小值为2,类型四:利用二次函数求最值例3、如图,在ABC ∆中,090ACB ∠=,5,2AC BC ==,点D 是AC 边上一点,连接BD ,将线段BD 绕点D 逆时针旋转090得线段ED ,连接AE ,则AE 的最小值为 .AA解:过E 作EF ⊥AC 于点F . 则∠EFD =90°,∵090ACB ∠=,∴∠EFD=∠C ,∵ED=DB ,∠FED =∠CDB ,∴△EFH ≌△EDC , ∴DF =CB =2,EF CD =,设AD x =,则2AF x =+,5EF CD x==-, ∴AE ===32x =时,AE 有最小值2. 例4、(2010秋•东城区期末)如图,在△ABC 中,∠ACB 为锐角,点D 为射线BC 上一动点,连接AD ,将线段AD 绕点A 逆时针旋转90°得到AE ,连接EC .若点D 在线段BC 上运动,DF ⊥AD 交线段CE 于点F ,且∠ACB =45°,,则线段CF 长的最大值为.解:过A 作AM ⊥BC 于M ,EN ⊥AM 于N ,如图,∵线段AD 绕点A 逆时针旋转90°得到AE ,∴∠DAE =90°,AD =AE ,∴∠NAE =∠ADM , 易证得Rt △AMD ≌Rt △ENA ,∴NE =AM ,∵∠ACB =45°,∴△AMC 为等腰直角三角形,∴AM =MC ,∴MC =NE ,∵AM⊥BC,EN⊥AM,∴NE∥MC,∴四边形MCEN为平行四边形,∵∠AMC=90°,∴四边形MCEN为矩形,∴∠DCF=90°,∴Rt△AMD∽Rt△DCF,∴=,设DC=x,∵∠ACB=45°,,∴AM=CM=3,MD=3﹣x,∴=,∴CF=﹣x2+x,∴当x=1.5时有最大值,最大值为0.75.例5、如图,在△ABC中,∠BAC=120°,AB=AC=6,D为边AB上一动点(不与B点重合),连接CD,将线段CD绕着点D逆时针旋转90°得到DE,连接BE,则S△BDE的最大值为 .解:作CM⊥AB于M,EN⊥AB于N,∴∠EDN+∠DEN=90°,∵∠EDC=90°,∴∠EDN+∠CDM=90°,∴∠DEN=∠CDM,在△EDN和△DCM中∴△EDN≌△DCM(AAS),∴EN=DM,∵∠BAC=120°,∴∠MAC=60°,∴∠ACM=30°,∴AM=AC=6=3,∴BM=AB+AM=6+3=9,设BD=x,则EN=DM=9﹣x,∴S△BDE==(9﹣x)=﹣(x﹣4.5)2+,∴当BD=4,5时,S△BDE有最大值为.练习1、如图,矩形ABCD中,AB=2,BC=4,点E是矩形ABCD的边AD上的一动点,以CE为边,在CE的右侧构造正方形CEFG,连结AF,则AF的最小值为 .解:过F作FH⊥ED,∵正方形CEFG,∴EF=EC,∠FEC=∠FED+∠DEC=90°,∵FH⊥ED,∴∠FED+∠EFH=90°,∴∠DEC=∠EFH,且EF=EC,∠FHE=∠EDC=90°,∴△EFH≌△EDC(AAS),∴EH=DC=2,FH=ED,∴AF===∴当AE=1时,AF的最小值为3 .2、(2019秋•黄陂区期中)如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=2,则△BDE面积的最大值为 .解:作CM⊥AB于M,EN⊥AB于N,∴∠EDN+∠DEN=90°,∵∠EDC=90°,∴∠EDN+∠CDM=90°,∴∠DEN=∠CDM,在△EDN和△DCM中,∴△EDN≌△DCM(AAS),∴EN=DM,∵∠BAC=120°,∴∠MAC=60°,∴∠ACM=30°,∴AM=AC=2=1,∴BM=AB+AM=2+1=3,设BD=x,则EN=DM=3﹣x,∴S△BDE==(3﹣x)=﹣(x﹣1.5)2+,∴当BD=1.5时,S△BDE有最大值为,类型五:构造等边三角形求最值例6、如图,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4,若BD⊥CD,垂足为点D,则对角线AC的长的最大值为.CA解析:如图,以BC为边作等边三角形BCE,过点E作EF⊥BC于点F,连接DE,∵AB=BD,∠ABC=∠DBE,BC=BE,∴△ABC≌△DBE,∴DE=AC,∵在等边三角形BCE中,EF ⊥BC,∴BF =BC=2,∴EF=BF=×2=2,以BC为直径作⊙F,则点D在⊙F上,连接DF ,∴DF =BC=×4=2,∴AC =DE ≤DF+EF=2+2,即AC的最大值为2+2.练习如图,在四边形ABCD中,AB=6,BC=4,若AC=AD,且∠ACD=60°,则对角线BD的长的最大值为 .解析:将AB绕点A顺时针旋转60°得到线段AK,连接BK、DK.则AK=AB=BK=6,∠KAB=60°,∴∠DAC=∠KAB,∴∠DAK=∠CAB,在△DAK和△CAB中,,∴△DAK≌△CAB(SAS)∴DK=BC=4,∵DK+KB≥BD,DK=4,KB=AB=6∴当D、K、B共线时,BD的值最大,最大值为DK+KB=10.类型六:利用对称求最值例7、(2019•成都)如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为 .解法一:∵在边长为1的菱形ABCD 中,∠ABC =60°,∴AB =CD =1,∠ABD =30°, ∵将△ABD 沿射线BD 的方向平移得到△A 'B 'D ',∴A ′B ′=AB =1,A ′B ′∥AB ,∵四边形ABCD 是菱形,∴AB =CD ,AB ∥CD ,∴∠BAD =120°,∴A ′B ′=CD ,A ′B ′∥CD , ∴四边形A ′B ′CD 是平行四边形,∴A ′D =B ′C ,∴A 'C +B 'C 的最小值=A ′C +A ′D 的最小值,∵点A ′在过点A 且平行于BD 的定直线上, ∴作点D 关于定直线的对称点E ,连接CE 交定直线于A ′,则CE 的长度即为A 'C +B 'C 的最小值,∵∠A ′AD =∠ADB =30°,AD =1,∴∠ADE =60°,DH =EH =AD =,∴DE =1,∴DE =CD ,∵∠CDE =∠EDB ′+∠CDB =90°+30°=120°,∴∠E =∠DCE =30°,∴CE =2×CD =.解法二:练习:如图,在矩形ABCD 中,AB =,1BC =,将ABD ∆沿射线DB 平移到A B D '''∆,连接B C D C ''、,则+B C D C ''的最小值为 .解法一: 解法一:解法三: 解法四:类型七:利用基本不等式求最值解:原式=1111+12a a++⨯=11+12a a a ++=2222+32a a a a +++=2232+32a a a a a ++-+=21+32aa a -+=112+3a a -+12a a +≥ ,1+35a a ∴+≥,1513a a ∴≤++,1513a a ∴-≥-++, 1142+3a a∴-≥-+.当2a a =,即a =时有最小值4-,此时2b =.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
——————————————————————————————2020年重庆市中考数学第18题专题突破1.含有同种果蔬但浓度不同的A 、B 两种饮料,A 种饮料重40千克,B 种饮料重60千克现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同,那么从每种饮料中倒出的相同的重量是_____________千克【分析】典型的浓度配比问题:溶液的浓度=溶质的质量/全部溶液质量.在本题中两种果蔬的浓度不知道,但是因为倒出的和倒入果蔬质量相同,所以原A 种饮料混合的总质量仍然是后40千克,原B 种饮料混合的总质量仍然是后60千克.可设A 种饮料的浓度为a ,B 种饮料的浓度为b ,各自倒出和倒入的果蔬质量相同可设为x 千克,由于混合后的浓度相同,由题意可得:()()40604060x a xb x b xa -+-+= 去分母()()604060406040x a xb x b xa -+=-+,去括号得:2400606024004040a xa xb b bx xa -+=-+移项得:6060404024002400xa xb bx xa b a -++-=-合并得:()()1002400b a x b a -=-所以:24x =2. 从两块分别重10千克和15千克且含铜的百分比不同的合金上各切下重量相等的一块,再把切下的每一块与另一块切后剩余的部分合在一起,熔炼后两者含铜的百分比恰好相等,则切下的一块重量是 。
解:设切下的一块重量是x 千克,设10千克和15千克的合金的含铜的百分比为a ,b ,= ,整理得(b-a )x=6(b-a ),x=63.设有含铜百分率不同的两块合金,甲重40公斤,乙重60公斤.从这两块合金上切下重量相等的一块,并把所切下的每块与另一种剩余的合金加在一起,熔炼后两者的含铜百分率相等,则切下的合金重( )A .12公斤B .15公斤C .18公斤D .24公斤考点:一元一次方程的应用.分析:设含铜量甲为a 乙为b ,切下重量为x .根据设有含铜百分率不同的两块合金,甲重40公斤,乙重60公斤,熔炼后两者的含铜百分率相等,列方程求解.解:设含铜量甲为a,乙为b,切下重量为x.由题意,有=,解得x=24.切下的合金重24公斤.故选D.4.一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用,已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车每次运货物的吨数之比为1:3;若甲、丙两车合运相同次数运完这批货物时,甲车共运了120吨,若乙、丙两车合运相同次数运完这批货物时,乙车共运了180吨.则这批货物共吨.解:设货物总吨数为x吨.甲每次运a吨,乙每次运3a吨,丙每次运b吨.,=,解得x=240.故答案为:240.5.某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用了朵.解:设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆.由题意,有,由①得,3x+2y+2z=580③,由②得,x+z=150④,把④代入③,得x+2y=280,∴2y=280-x⑤,由④得z=150-x⑥.∴4x+2y+3z=4x+(280-x)+3(150-x)=730,∴黄花一共用了:24x+12y+18z=6(4x+2y+3z)=6×730=4380.故黄花一共用了4380朵.6.一个水池装一个进水管和三个同样的出水管,先打开进水管,等水池存一些水后再打开出水管(进水管不关闭).若同时打开2个出水管,那么8分钟后水池空;如果同时打开3个出水管,则5分钟后水池空.那么出水管比进水管晚开分钟.考点:三元一次方程组的应用.解:设出水管比进水管晚开x分钟,进水管的速度为y,出水管的速度为z,则有:,两式相除得:,解得:x=40,即出水管比进水管晚开40分钟.故答案为:40.7.(1)一种商品原来的销售利润率是47%.现在由于进价提高了5%,而售价没变,所以该商品的销售利润率变成了.(2)某商品现在的进价便宜20%,而售价未变,则其利润比原来增加了30个百分点,那么原来的利润率为。
7.某商人经营甲、乙两种商品,每件甲种商品的利润率为40%,每件乙种商品的利润率为60%,当售出的乙种商品的件数比甲种商品的件数多50%时,这个商人得到的总利润率是50%;当售出的乙种商品的件数比甲种商品的件数少50%时,这个商人得到的总利润率是。
考点:二元一次方程的应用.专题:应用题;方程思想.:解:设甲进价为a元,则售出价为1.4a元;乙的进价为b元,则售出价为1.6b元;若售出甲x件,则售出乙1.5x件.=0.5,解得a=1.5b,∴售出的乙种商品的件数比甲种商品的件数少50%时,甲种商品的件数为y时,乙种商品的件数为0.5y.这个商人的总利润率为===45%.故答案为:45%.8. 某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是。
解:设一月份的售出价为x,销售量为y,则有买入价为x×(1-20%)=80%x一月毛利润总额为x×20%×y= 二月的售出价为x(1-10%)=90%x每台毛利为90%x-80%x=10%二月的销售台数为y×(1+120%)=220%y所以二月毛利润总额为10%x×220%y=22%xy二月份的毛利润总额与一月份的毛利润总额之比是22%:=11:109.某公司生产一种饮料是由A,B两种原料液按一定比例配制而成,其中A原料液的成本价为15元/千克,B原料液的成本价为10元/千克,按现行价格销售每千克获得70%的利润率.由于市场竞争,物价上涨,A原料液上涨20%,B原料液上涨10%,配制后的总成本增加了12%,公司为了拓展市场,打算再投入现总成本的25%做广告宣传,如果要保证每千克利润不变,则此时这种饮料的利润率是分析:根据题意计算出涨价后,原A价格为18元,B上涨10%,变为11元,得出总成本上涨12%,即可得出涨价前每100千克成本以及涨价后每100千克成本,进而得出x的值即可得出答案.解答:解:原料液A的成本价为15元/千克,原料液B的成本价为10元/千克,涨价后,原A价格上涨20%,变为18元;B上涨10%,变为11元,总成本上涨12%,设每100千克成品中,二原料比例A占x千克,B占(100-x)千克,则涨价前每100千克成本为15x+10(100-x),涨价后每100千克成本为18x+11(100-x),18x+11(100-x)=[15x+10(100-x)]•(1+12%),解得:x= 100/7千克,100-x= 600/7千克,即二者的比例是:A:B=1:6,则涨价前每千克的成本为 15/7+ 60/7= 75/7元,销售价为 127.57元,利润为7.5元,原料涨价后,每千克成本变为12元,成本的25%=3元,保证利润为7.5元,则利润率为:7.5÷(12+3)=50%.10.“节能减排,低碳经济”是我国未来发展的方向,某汽车生产商生产有大、中、小三种排量的轿车,正常情况下的小排量的轿车占生产总量的30%,为了积极响应国家的号召,满足大众的消费需求准备将小排量轿车的生产量提高,受其产量结构调整的影响,大中排量汽车生产量只有正常情况下的90%,但生产总量比原来提高了7.5%,则小排量轿车生产量应比正常情况增加 %。
分析:要求小排量轿车生产量应比正常情况增加的百分数,就要先设出未知数x,再通过阅读,理解题意.本题的等量关系是调整后的三种排量的轿车生产总量不变.为了方便做题,我们可以设调整前的总量为a.解:设小排量轿车生产量应比正常情况增加的百分数为x,汽车原总量为a.则可得方程:30%a(1+x)+70%a×90%=(1+7.5%)a,解得x≈48.3%.故填48.3.11.某公司销售A、B、C三种产品,在去年的销售中,高新产品C的销售金额占总销售金额的40%.由于受国际金融危机的影响,今年A、B两种产品的销售金额都将比去年减少20%,因而高新产品C是今年销售的重点.若要使今年的总销售金额与去年持平,那么今年高新产品C的销售金额应比去年增加 %.一元一次方程的应用.专题:增长率问题.(1-20%)解:设今年高新产品C的销售金额应比去年增加x,根据题意得:0.4(1+x)+(1-40%)=1,解得x=30%,故填30.12.烧杯甲中盛有浓度为a% 的盐水m升,烧杯乙中盛有浓度为 b%的盐水m升(a>b),现将甲中盐水的1/4倒入乙中,混合均匀后再由乙倒回甲,估甲中的盐水恢复为m升,则互掺后甲、乙两烧杯中含有纯盐量的差与互掺前甲、乙两烧杯中含有纯盐量的差之比为______.根据烧杯甲中盛有浓度为a%的盐水m升,烧杯乙中盛有浓度为b%的盐水m升(a>b),得出两烧杯的纯盐量的差,再表示出甲中盐水的倒入乙中,混合均匀后再由乙倒回甲后,两烧杯的纯盐量,进而得出答案.解答:解:∵烧杯甲中盛有浓度为a%的盐水m升,烧杯乙中盛有浓度为b%的盐水m升(a >b),∴两烧杯的纯盐量的差为:ma%-mb%=m(a%-b%),∵将甲中盐水的倒入乙中,混合均匀后再由乙倒回甲,∴盐水倒入乙中后,烧杯乙浓度为:=,再根据混合均匀后再由乙倒回甲,∴倒回甲后,甲的含盐量为:ma%+×m=ma%+b%,乙的含盐量为:m,∴互掺后甲、乙两烧杯中含有纯盐量的差为:m(a%-b%),∴互掺后甲、乙两烧杯中含有纯盐量的差与互掺前甲、乙两烧杯中含有纯盐量的差之比为:,故答案为:.13.市场上一种茶饮料由茶原液与纯净水按一定比例配制而成,其中购买一吨茶原液的钱可以买20吨纯净水。
由于今年以来茶产地云南地区连续大旱,茶原液收购价上涨50%,纯净水价也上涨了8%,导致配制的这种茶饮料成本上涨20%,问这种茶饮料中茶原液与纯净水的配制比例为。
分析:设这种茶饮料中茶原液与纯净水的配制比例为a:b,购买一吨纯净水的价格是x,那么购买茶原液的价格就是20x,根据茶原液收购价上涨50%,纯净水价也上涨了8%,导致配制的这种茶饮料成本上涨20%,可列出方程求得比例.解:设这种茶饮料中茶原液与纯净水的配制比例为a:b,购买一吨纯净水的价格是x,=,=.故答案为:2:15.14.重庆长安汽车公司经销豪华级、中高级、中级、紧凑级四种档次的轿车,在去年的销售中,紧凑级轿车的销售金额占总销售金额的60%,由于受到国际金融危机的影响,今年豪华、中高、中级轿车的销售金额都将比去年减少30%,因而紧凑级轿车是今年销售的重点,若要使今年的总销售额与去年持平,那么今年紧凑级轿车的销售金额应比去年增加 %分析:设去年四种档次的轿车销售额共a元,其中紧凑级轿车销售额是60%a元,则豪华、中高、中级轿车销售额共(1-60%)a元;设今年紧凑级轿车的销售金额应比去年增加的百分数为x,则今年紧凑级轿车销售额是60%(1+x)a元,豪华、中高、中级轿车销售额共(1-60%)(1-30%)a元,根据今年的总销售额与去年持平,列方程求解.解答:解:设今年紧凑级轿车的销售金额应比去年增加的百分数为x,依题意得:60%(1+x)a+(1-60%)(1-30%)a=a,解得:x=0.2=20%.答:今年紧凑级轿车的销售金额应比去年增加20%.15.某果蔬饮料由果汁、疏菜汁和纯净水按一定质量比配制而成,纯净水、果汁、蔬菜汁的价格比为1:2:2,因市场原因,果汁、蔬菜汁的价格涨了15%,而纯净水的价格降了20%,但并没有影响该饮料的成本(只考虑购买费用),那么该种饮料中果汁与蔬菜汁的质量和与纯净水的质量之比为分析:设纯净水、果汁、蔬菜汁的价格为a,2a,2a,设纯净水、果汁、疏菜汁按一定质量比为x:y;z,根据因市场原因,果汁、蔬菜汁的价格涨了15%,而纯净水的价格降了20%,但并没有影响该饮料的成本(只考虑购买费用),可列出方程求解.解;设纯净水、果汁、蔬菜汁的价格为a,2a,2a,设纯净水、果汁、疏菜汁按一定质量比为x:y:z, ax+2ay+2az=ax(1-80%)+2ay(1+15%)+2az(1+15%),0.2x=0.3(y+z),(y+z):x=2:3.故答案为:2:3.16.(2010巴蜀)超市出售某种蔗糖每袋可获利20%,由于近来西南地区蔗糖产地连续干旱,导致这种蔗糖进价增长了25%,超市将这种蔗糖的售价提高,以保证每袋获利金额不变,则提价后的利润率为16%.分析:由题意,y-x(1+25%)=x•20%,可到y值,有利润率=( 售价-进价)/进价从而得到答案.解:设原来每袋蔗糖的进价是x,进价增长后为y,则由题意得:利润率=(1+25%)x+20%x-x(1+25%)/x(1+25%)=16%.17.(巴蜀2020—2021下期二次模)商场购进一种商品若干件,每件按进价加价30元作为标价,可售出全部商品的65%,然后将标价下降10%,这样每件仍可以获利18元,又售出全部商品的25%,为了确保这批商品总的利润不低于25%,则剩余商品的售价最低应为元/件.75。
