《管理运筹学》习题集-34页文档资料
管理运筹学复习题及部分参考答案

一、名词解释 1.模型 2.线性规划 3.树 4.网络 5.风险型决策二、简答题 1.简述运筹学的工作步骤。
2.运筹学中模型有哪些基本形式 3.简述线性规划问题隐含的假设。
4.线性规划模型的特征。
5.如何用最优单纯形表判断线性规划解的唯一性或求出它的另一些最优解 6.简述对偶理论的基本内容。
7.简述对偶问题的基本性质。
8.什么是影子价格?同相应的市场价格之间有何区别,以及研究影子价格的意义。
9.简述运输问题的求解方法。
10.树图的性质。
11.简述最小支撑树的求法。
12.绘制网络图应遵循什么规则。
三、书《收据模型与决策》2.13 14. 有如下的直线方程:2x 1 +x 2 =4 a. 当x 2 =0 时确定x 1 的值。
当x 1 =0 时确定x 2 的值。
b. 以x 1 为横轴x 2 为纵轴建立一个两维图。
使用a 的结果画出这条直线。
c. 确定直线的斜率。
d. 找出斜截式直线方程。
然后使用这个形式确定直线的斜率和直线在纵轴上的截距。
答案: 14. a. 如果x 2 =0,则x 1 =2。
如果x 1 =0,则x 2 =4。
c. 斜率= -2 d. x 2 =-2 x 1 +4 2.40 你的老板要求你使用管理科学知识确定两种活动(和)的水平,使得满足在约束的前提下总成本最小。
模型的代数形式如下所示。
Maximize 成本=15 x 1 +20 x 2 约束条件约束1:x 1 + 2x 2 10 约束2:2x 1 3x 2 6 约束3:x 1 +x 2 6和x 1 0,x 2 0 a. 用图解法求解这个模型。
b. 为这个问题建立一个电子表格模型。
c. 使用Excel Solver 求解这个模型。
答案: a. 最优解:(x 1 , x 2 )=(2, 4),C=110 b c.活动获利 1 2总计水平A B C 1 2 2 3 1 1 10 10 8 6 6 6 单位成本方案15 20 2 4 $110.00 3.2 考虑具有如下所示参数表的资源分配问题: 资源每一活动的单位资源使用量可获得的资源数量 1 2 1 2 3 2 3 2 1 3 4 10 20 20 单位贡献$20 $30 单位贡献=单位活动的利润b. 将该问题在电子表格上建模。
《管理运筹学》第四版课后习题
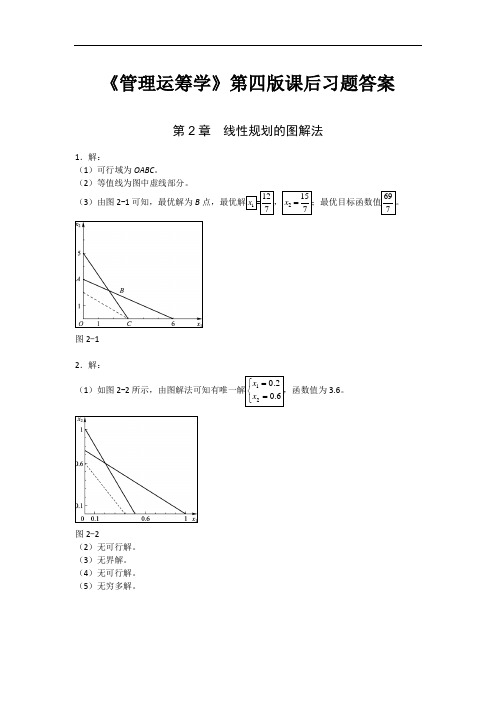
《管理运筹学》第四版课后习题答案第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解1x=127,2157x=;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6xx=⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解3.解:(1)标准形式(2)标准形式(3)标准形式4.解: 标准形式松弛变量(0,0) 最优解为 ,x 2=3/2。
5.解:标准形式剩余变量(0, 0, 13) 最优解为 x 1=1,x2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
(2(3 (4(5)最优解为 x 1=8,x 2(61,所以最优解不变。
7.解:设x ,y 分别为甲、乙两种柜的日产量,目标函数z=200x +240y , 线性约束条件:即作出可行域.解⎩⎨⎧=+=+162202y x y x 得)8,4(Q 272082404200=⨯+⨯=最大z答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.8.解:设需截第一种钢板x 张,第二种钢板y 张,所用钢板面积zm2. +2y , 线性约束条件: ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≥+≥+≥+0027315212y x y x y x y x 作出可行域,并做一组一组平行直线x +2y=t .解⎩⎨⎧=+=+12273y x y x 得)2/15,2/9(E.但E 不是可行域内的整点,在可行域的整点中,点)8,4(使z 取得最小值。
答:应截第一种钢板4张,第二种钢板8张,能得所需三种规格的钢板,且使所用钢板的面积最小.9.解:设用甲种规格原料x 张,乙种规格原料y 张,所用原料的总面积是zm 2,目标函数z=3x +2y ⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+003222y x y x y x 作出可行域.作一组平等直线3x +2y=t . 解⎩⎨⎧=+=+3222y x y x 得)3/1,3/4(CC 不是整点,C 不是最优解.在可行域内的整点中,点B(1,1)使z 取得最小值. z 最小=3×1+2×1=5,答:用甲种规格的原料1张,乙种原料的原料1张,可使所用原料的总面积最小为5m 2.10.解:设租用大卡车x 辆,农用车y 辆,最低运费为z 元.目标函数为z=960x +360y .线性约束条件是⎪⎩⎪⎨⎧≥+≤≤≤≤1005.28200100y x y x 作出可行域,并作直线960x +360y=0. 即8x +3y=0,向上平移由⎩⎨⎧=+=1005.2810y x x 得最佳点为()10,8作直线960x +360y=0. 即8x +3y=0,向上平移至过点B(10,8)时,z=960x +360y 取到最小值.z 最小=960×10+360×8=12480答:大卡车租10辆,农用车租8辆时运费最低,最低运费为12480元.11.解:设圆桌和衣柜的生产件数分别为x 、y ,所获利润为z ,则z=6x +10y .⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+005628.008.07209.018.0y x y x y x 即⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+001400728002y x y x y x 作出可行域.平移6x +10y=0 ,如图⎩⎨⎧=+=+1400728002y x y x 得⎩⎨⎧==100350y x 即C(350,100).当直线6x +10y=0即3x +5y=0平移到经过点C(350,100)时,z=6x +10y 最大12.解:模型12max 500400z x x =+ 1211121223003540224401.2 1.5300,0x x x x x x x x ++≤≤≤≤≥(1)1150x =,270x =,即目标函数最优值是103 000。
管理运筹学习题集

增设销售店个数
营业区A
营业区B
营业区C
1
100
120
150
2
160
150
165
3
190
170
175
4
200
180
190
4.某工厂与用户签订了4个月的交货合同如表5—2所示,该厂仓库的存货能力为4万件,每万件的生产费用为20000元,在进行生产的月份,工厂要支出固定费用6000元,仓库的保管费每万件每月1500元,假定开始时及4月底交货后无存货,试问应在每月各生产多少件产品,才能满足交货任务,同时使总费用最小?
第一目标:充分利用正常的生产能力,避免开工不足;
第二目标:优先满足老客户的需求,A,B,C3种型号的电脑各为50台、50台、80台,同时根据3种电脑的纯利润分配不同的加权系数;
第三目标:限制装配线加班时间,最好不超过200小时;
第四目标:满足各种型号电脑的销售目标,A,B,C3种型号分别为100台、120台、100台,再根据3种电脑的纯利润分配不同的加权系数;
3
4
6
2
3
3600
打磨
4
3
5
6
4
3950
上漆
2
3
3
4Байду номын сангаас
3
2800
利润(百元)
2.7
3
4.5
2.5
3
11.某厂生产甲、乙、丙三种产品,分别经过A,B,C三种设备加工。已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表1—17所示。
表1—3产品生产工艺消耗系数
甲
乙
丙
《管理运筹学》复习题及参考答案

《管理运筹学》复习题及参考答案一、选择题1. 管理运筹学的研究对象是()A. 生产过程B. 管理活动C. 经济活动D. 运筹问题参考答案:D2. 以下哪个不属于管理运筹学的基本方法?()A. 线性规划B. 整数规划C. 非线性规划D. 人力资源规划参考答案:D3. 在线性规划中,约束条件是()A. 等式B. 不等式C. 方程组D. 矩阵参考答案:B4. 以下哪种方法不属于线性规划的对偶问题求解方法?()A. 单纯形法B. 对偶单纯形法C. 拉格朗日乘数法D. 牛顿法参考答案:D5. 在目标规划中,以下哪个不是目标约束的类型?()A. 等式约束B. 不等式约束C. 目标函数约束D. 线性约束参考答案:C二、填空题1. 管理运筹学的核心思想是______。
参考答案:最优化2. 在线性规划中,最优解存在的条件是______。
参考答案:可行性、有界性3. 整数规划的求解方法主要有______和______。
参考答案:分支定界法、动态规划法4. 在目标规划中,目标函数的求解方法有______、______和______。
参考答案:单纯形法、拉格朗日乘数法、动态规划法5. 非线性规划问题可以分为______、______和______。
参考答案:无约束非线性规划、约束非线性规划、非线性规划的对偶问题三、判断题1. 管理运筹学的研究对象是管理活动。
()参考答案:正确2. 在线性规划中,最优解一定存在。
()参考答案:错误3. 整数规划的求解方法比线性规划复杂。
()参考答案:正确4. 目标规划的求解方法与线性规划相同。
()参考答案:错误5. 非线性规划问题一定比线性规划问题复杂。
()参考答案:错误四、计算题1. 某工厂生产甲、乙两种产品,甲产品每件利润为10元,乙产品每件利润为8元。
生产甲产品每件需消耗2小时机器工作时间,3小时人工工作时间;生产乙产品每件需消耗1小时机器工作时间,2小时人工工作时间。
工厂每周最多可利用机器工作时间100小时,人工工作时间150小时。
《管理运筹学》试题及答案

中国矿业大学2010~2011学年第二学期《 管理运筹学 》模拟试卷一考试时间:120 分钟 考试方式:闭 卷1212121212max 334262180,0z x x x x x x x x x x =+⎧⎪+≤⎪⎪-+≤⎨⎪+≤⎪≥≥⎪⎩2. 用表上作业法求下表中给出的运输问题的最优解。
答案: 1.解:加入人工变量,化问题为标准型式如下:1234512312412512345max 3300042.6218,,,,0z x x x x x x x x x x x s t x x x x x x x x =++++++=⎧⎪-++=⎪⎨++=⎪⎪≥⎩(3分)下面用单纯形表进行计算得终表为:所以原最优解为 *(3,0,1,5,0)T X =2、解:因为销量:3+5+6+4+3=21;产量:9+4+8=21;为产销平衡的运输问题。
(1分)由最小元素法求初始解:(5分)用位势法检验得:(7分)所有非基变量的检验数都大于零,所以上述即为最优解且该问题有唯一最优解。
此时的总运费:min 45594103112011034150z =⨯+⨯+⨯+⨯+⨯+⨯+⨯=。
3、解:系数矩阵为:1279798966671712149151466104107109⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(3分)从系数矩阵的每行元素减去该行的最小元素,得:50202 23000 010572 98004 06365⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦经变换之后最后得到矩阵:70202 43000 08350 118004 04143⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦相应的解矩阵:01000 00010 00001 00100 10000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(13分)由解矩阵得最有指派方案:甲—B,乙—D,丙—E,丁—C,戊—A 或者甲—B,乙—C,丙—E,丁—D,戊—A (2分)所需总时间为:Minz=32 (2分)中国矿业大学2010~2011学年第二学期《管理运筹学》模拟试卷二考试时间:120 分钟考试方式:闭卷1.求解下面运输问题。
《管理运筹学》习题集

物流管理教研室
1.什么是线性规划?线性规划三要素是什么?
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
5.用表格单纯形法求解如下线性规划。
1
1
1
100
B(小时)
10
4
5
600
C(小时)
2
2
6
300
单位产品利润(元)
10
6
4
(1)建立线性规划模型,求该厂获利最大的生产计划。
(2)产品丙每件的利润增加到多大时才值得安排生产?如产品丙每件的利润增加到6,求最优生产计划。
(3)产品甲的利润在多大范围内变化时,原最优计划保持不变?
(4)设备A的能力如为100+10q,确定保持原最优基不变的q的变化范围。
表5—11单位:万元
增设销售店个数
营业区A
营业区B
营业区C
1
100
120
150
2
160
150
165
3
190
170
175
4
200
180
190
4.某工厂与用户签订了4个月的交货合同如表5—12所示,该厂仓库的存货能力为4万件,每万件的生产费用为20000元,在进行生产的月份,工厂要支出固定费用6000元,仓库的保管费每万件每月1500元,假定开始时及4月底交货后无存货,试问应在每月各生产多少件产品,才能满足交货任务,同时使总费用最小?
7
9
5
3
2
0
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
.解:标准化.列出单纯形表412b02[8]2 /80868 /641241/41/81/8]/8(1/4/(1/813/265/4/43/4(13/2/(1/4 0-1/23/21/222806-221-12-502故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
《管理运筹学》习题集

1
1
100
B(小时)
10
4
5
600
C(小时)
2
2
6
300
单位产品利润(元)
10
6
4
(1)建立线性规划模型,求该厂获利最大的生产计划。
(2)产品丙每件的利润增加到多大时才值得安排生产?如产品丙每件的利润增加到6,求最优生产计划。
(3)产品甲的利润在多大范围内变化时,原最优计划保持不变?
(4)设备A的能力如为100+10q,确定保持原最优基不变的q的变化范围。
第五目标:装配线加班时间尽可能少。
请列出相应的目标规划模型,并用LINGO软件求解。
2.已知3个工厂生产的产品供应给4个客户,各工厂生产量、用户需求量及从各工厂到用户的单位产品的运输费用如表4—1所示。由于总生产量小于总需求量,上级部门经研究后,制定了调配方案的8个目标,并规定了重要性的次序。
表4—1工厂产量—用户需求量及运费单价单位:元/单位
用户
工厂
用户1
用户2
用户3
用户4
生产量
工厂1
5
2
6
7
工厂2
3
5
4
6
工厂3
4
5
2
3
需求量(单位)
200
100
450
250
第一目标:用户4为重要部门,需求量必须全部满足;
第二目标:供应用户1的产品中,工厂3的产品不少于100个单位;
第三目标:每个用户的满足率不低于80%;
第四目标:应尽量满足各用户的需求;
热处理(2种方案)
检验
方案
生产费用
方案
生产费用
方案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料 斤)
(公 60
50
200
4 200
设备 C(小时)
10
3 000
设备 D(小时)
20
4 500
据市场分析,甲、乙产品销售价格分别为 13 700 元和 11 640 元,试确定
获利最大的产品生产计划。
(1)设产品甲的计划生产量为 x1,产品乙的计划生产量为 x2,试建立其线 性规划的数学模型;若将材料约束加上松弛变量 x3,设备 C 约束加上松弛变量 x4,设备 D 约束加上松弛变量 x5,试化成标准型。
Max Z=4x1+x2+2x3
s.t. (1)求出该问题产值最大的最优解和最优值。
(2)求出该问题的对偶问题的最优解和最优值。
(3)给出两种资源的影子价格,并说明其经济含义;第一种资源限量由 2
变为 4,最优解是否改变?
(4)代加工产品丁,每单位产品需消耗第一种资源 2 单位,消耗第二种资
源 3 单位,应该如何定价?
样的投资方案,才能使该公司在这个计划期获得最大利润?
10.某家具制造厂生产五种不同规格的家具。每种家具都要经过机械成
型、打磨、上漆几道主要工序。每种家具的每道工序所用时间、每道工序的
可用时间、每种家具的利润由表 1—16 给出。问工厂应如何安排生产,使总利
润最大?
表 1—16 家具生产工艺耗时与利润表
划模型,求将可供电量用完的最低总费用分配方案。
表 2 单位电力输电费单位:元
城市电站
A
B
C
Ⅰ
15
18
22
第2页
Ⅱ
21
25
16
9.某公司在 3 年的计划期内,有 4 个建设项目可以投资:项目Ⅰ 从第一年
到第三年年初都可以投资。预计每年年初投资,年末可收回本利 120%,每年又
可以重新将所获本利纳入投资计划;项目Ⅱ 需要在第一年初投资,经过两年
Right hand Side Ranges
第6页
Resource
Current Rhs
Allowable Increase
Allowable Decrease
材料
4 200
300
450
设备 C
3 000
360
900
设备 D
4 500
Infinity
300
试问非紧缺资源最多可以减少到多少,而紧缺资源最多可以增加到多少?
所需时间 (小时)
生产工序
1
2
3
4
5
每道工序可用 时间(小时)
成型
3
4
6
2
3
3 600
打磨
4
3
5
6
4
3 950
上漆
2
3
3
4
3
2 800
利润(百 2.7 3 4.5 2.5 3
元)
第3页
11.某厂生产甲、乙、丙三种产品,分别经过 A,B,C 三种设备加工。已知
生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如
6.某企业生产甲、乙两种产品,产品生产的工艺路线如图 2—1 所示,试统计单
位产品的设备工时消耗,填入表 2—7。又已知材料、设备 C 和设备 D 等资源
的单位成本和拥有量如表 2—7 所示。
图 2—1 工艺路线
表 2—7 资源消耗与资源成本表
资源
产品 资源消耗
资源成本
甲
乙 元/单位资源
资源拥有量
第5页
(2)利用 LINDO 软件求得:最优目标函数值为 18 400,变量的最优取值分
别为 x1=20,x2=60,x3=0,x4=0,x5=300,则产品的最优生产计划方案是什么?并解 释 x3=0,x4=0,x5=300 的经济意义。
(3)利用 LINDO 软件对价值系数进行敏感性分析,结果如下:
Obj Coefficient Ranges
表 1—17 所示。
表 1—17 产品生产工艺消耗系数
甲
乙
丙
设备能力
A(小时)
1
1
1
100
B(小时)
10
4
5
600Βιβλιοθήκη C(小时)22
6
300
单位产品利润
10
6
4
(元)
(1)建立线性规划模型,求该厂获利最大的生产计划。
(2)产品丙每件的利润增加到多大时才值得安排生产?如产品丙每件的利
润增加到 6,求最优生产计划。
自治区重点产业紧缺人才专业建设
物流管理专业——课程建设 管理运筹学 习题集 物流管理教研室
2014 年 3 月
第1页
第一章 线性规划 1.什么是线性规划?线性规划三要素是什么? 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其 相互关系。 5.用表格单纯形法求解如下线性规划。
7.用大 M 法求解如下线性规划。
8. A,B,C 三个城市每年需分别供应电力 320,250 和 350 单位,由Ⅰ,Ⅱ
两个电站提供,它们的最大可供电量分别为 400 单位和 450 单位,单位费用如
表 1—15 所示。由于需要量大于可供量,决定城市 A 的供应量可减少 0~30 单
位,城市 B 的供应量不变,城市 C 的供应量不能少于 270 单位。试建立线性规
(5)写出本题中线性规划的对偶模型;如果对甲乙产品生产计划的线性规
可收回本利 150%,又可以重新将所获本利纳入投资计划,但用于该项目的最
大投资额不得超过 20 万元;项目Ⅲ 需要在第二年年初投资,经过两年可收
回本利 160%,但用于该项目的最大投资额不得超过 15 万元;项目Ⅳ 需要在
第三年年初投资,年末可收回本利 140%,但用于该项目的最大投资额不得超
过 10 万元。在这个计划期内,该公司第一年可供投资的资金有 30 万元。问怎
Variable
Current Coef
Allowable Increase
Allowable Decrease
x1
200
88
x2
240
26.67
20 73.33
试问如果生产计划执行过程中,甲产品售价上升到 13 800 元,或者乙产品
售价降低 60 元,所制定的生产计划是否需要进行调整?
(4)利用 LINDO 软件对资源向量进行敏感性分析,结果如下:
(3)产品甲的利润在多大范围内变化时,原最优计划保持不变?
(4)设备 A 的能力如为 100+10q,确定保持原最优基不变的 q 的变化范围。
(5)如合同规定该厂至少生产 10 件产品丙,试确定最优计划的变化。
第4页
第 2 章 对偶规划 1.对偶问题和对偶变量(即影子价值)的经济意义是什么? 2.什么是资源的影子价格?它与相应的市场价格有什么区别? 3.如何根据原问题和对偶问题之间的对应关系,找出两个问题变量之间、 解及检验数之间的关系? 4.已知线性规划问题
