方块数字加加看
四阶行列式运算

四阶行列式运算嘿,你们知道吗?我觉得四阶行列式运算可有意思啦!有一天,我在数学书上看到了四阶行列式运算,一开始我完全不知道这是啥玩意儿。
我就想啊,这到底是个啥神秘的东西呢?后来老师给我们讲了,我才慢慢明白一点。
老师说,四阶行列式就像一个大拼图。
比如说,我们有四个大方块,每个方块里又有四个小方块。
这四个大方块就像是四阶行列式的四行,每个大方块里的四个小方块就像是四列。
我们要做的呢,就是把这些小方块里的数字加加减减,算出一个结果来。
老师给我们举了个例子。
有四个数字方块,第一个方块里有 1、2、3、4,第二个方块里有 5、6、7、8,第三个方块里有 9、10、11、12,第四个方块里有 13、14、15、16。
老师说,我们要按照一定的方法来算这个四阶行列式。
我看着这些数字,脑袋都大了。
但是老师很有耐心地一步一步教我们。
老师说,先从第一行开始,选一个数字,然后再从第二行、第三行、第四行分别选一个数字,但是要保证这四个数字不在同一列上。
比如说,我们可以选第一行的第一个数字 1,第二行的第二个数字 6,第三行的第三个数字 11,第四行的第四个数字 16。
然后把这四个数字乘起来,得到1×6×11×16 = 1056。
接着,再选另外一组数字,比如第一行的第二个数字 2,第二行的第三个数字 7,第三行的第四个数字 12,第四行的第一个数字 13。
把这四个数字也乘起来,得到2×7×12×13 = 2184。
就这样,我们要选好多组数字,把它们乘起来。
然后呢,有些组的结果是正的,有些组的结果是负的。
最后把这些结果加起来,就是四阶行列式的结果啦。
我跟着老师的步骤,一步一步地算,虽然有点慢,但是我觉得很有成就感。
我发现,四阶行列式运算就像玩游戏一样,只要我们认真去做,就能找到其中的乐趣。
后来,我又做了一些其他的四阶行列式运算的题目。
有时候会算错,但是我不灰心,我会仔细检查,找出错误的地方,然后改正过来。
人教版一年级数学思维训练第十三讲数方块

第十三章 数方块知识导航一些小方块堆放在一起,数它们的个数时,或一层一层地数,或一排一排地数;先数能看见的,再数看不见的,要一个不漏地数出来。
图解思维训练题例1 下图的方块组中有几个小方块?为什么呢?图解思路如上图所示,能看到的小方块有A、B、C三个,看不到的是在小方块A下方有一个,因此一共有4个。
规范解答一共有4个小方块。
例2 如图所示,左边的A、B两个方块组拼起来后,变成了右边的方块组C,方块组A、B、C各有几个小方块?方块组C中有几个小方块是看得见的?有几个是看不见的?图解思路A、B两个方块组所有的小方块都能看得见,方块组A有6个小方块,方块组B有2个小方块,方块组C是由方块组A和方块组B组成的,因此方块组C有8个小方块。
其中,有7个小方块是看得见的,有1个是看不见的。
规范解答方块组A有6个小方块,方块组B有2个小方块,方块组C有8个小方块;方块组C中有7个小方块是看得见的,有1个是看不见的。
例3 如图所示,左边的方块组可以拆分成右边的两个方块组,这三个方块组各有小方块多少个?左边的方块组中有几个小方块是看不见的,把它拆分后,就看得见了,请标出这些小方块。
图解思路如图所示,在拆分之后可以看到的之前看不到的小方块是A和B,并可清楚地看到右边两方块组中小方块的数量,进而推导出左边方块组中小方块的数量。
规范解答如图所示,标出的小方块A和B即为拆分前看不到的小方块,各方块组中小方块的数量从左向右依次为7个,5个,2个。
例4 数一数,图中一共有多少个小方块?图解思路如图所示,我们能够清楚地看到A、B、C、D、E、F六个小方块,而在小方块A和小方块B的下方还各有一块,因此,一共有8个小方块。
规范解答一共有8个小方块。
例5 如图所示,左边的两组方块拼起来会是右边的哪一组?请用直线连起来。
图解思路按照箭头所指的方向,在脑中把小方块拼起来即可。
规范解答如图所示。
例6 数一数,图中有几个小方块?图解思路如图所示,从上往下数第一层有3个小方块,第二层有7个小方块,第三层有10个小方块,因此一共有3+7+10=20(个)小方块。
数字魔方破解

数字魔方破解数字魔方是一种备受欢迎的智力玩具,以其独特的设计和挑战性的解谜游戏而闻名。
它由三个面组成,每个面都有三列(从左到右)和三行(从上到下)的方格。
现在,我将向您介绍一种破解数字魔方的方法,帮助您更好地理解和解决这个谜题。
为了更好地解释这种破解方法,让我们把每个面的九个小方块编号为1到9,按照从左到右、从上到下的顺序。
我们的目标是将数字魔方的所有面上的数字排列成正确的顺序,这意味着每个面都必须是从1到9的连续数列。
步骤一:解决第一层的中心方块数字魔方的第一层中心方块是不会移动的,所以我们可以先把它们放在正确的位置上。
确保每个中心方块与其相邻的边方块颜色相匹配。
步骤二:解决第一层的边方块接下来,我们将关注第一层的边方块。
我们需要将它们放置在相邻的中心方块旁边,并确保颜色匹配。
要做到这一点,我们可以通过以下的方法来移动边方块:- 把边方块移动到相应目标位置的前面或后面。
- 通过顺时针或逆时针旋转相应的面来移动边方块。
- 当边方块移动到正确的位置时,将其与中心方块配对,使得颜色匹配。
重复这一步骤,直到第一层的边方块全部放置正确为止。
步骤三:解决第一层的角方块在这一步,我们需要将第一层的角方块放到它们的正确位置。
我们可以通过如下的方法来移动角方块:- 把角方块移动到相应目标位置的前面或后面。
- 通过顺时针或逆时针旋转相应的面来移动角方块。
当角方块被移动到正确的位置时,对准其相应的中心方块,使得颜色匹配。
重复这一步骤,直到第一层的角方块全部放置正确为止。
步骤四:解决第二层的边方块正确解决第二层的边方块是下一步的目标。
为了完成这一步,我们可以使用以下步骤:- 将第二层的边方块移动到相应目标位置的前面或后面。
- 通过顺时针或逆时针旋转相应的面来移动边方块。
- 当边方块被移动到正确的位置时,将其与相应的中心方块配对,使颜色匹配。
重复这一步骤,直到第二层的边方块全部放置正确为止。
步骤五:解决最后一层的边方块现在,我们的目标是解决最后一层的边方块。
用“方格+数字”法表示物体

用“方格+数字”法表示物体邮编:315324 浙江省慈溪市周巷镇中心小学邵建亿人教版小学数学五上年级第三单元《观察物体》,只有3个例题,3课时。
单元教学目标是:1.使学生经历观察的过程,让学生认识到从不同的位置观察物体,所看到的形状是不同的。
2.通过观察实物,能正确辨认从正面、侧面、上面观察到的两个物体或一组立体图形的位置关系和形状。
3.通过拼搭活动,培养学生的空间想像和推理能力。
配套的练习主要有两类:一类是观察物体(主要指方块),画出从正面、左面、上面所看到的图形。
另一类是根据从一个方向或几个方向看到的图形,想象、猜测、拼摆出原来的物体。
在以往五上年级观察物体的教学中,最为困惑的是有的学生不教也会,有的学生怎么也教不会。
特别是如上所述的第二类练习情况,学生想出来了,如何跟同学表达交流?学生摆出来了,如何展示给其他同学看?这一直是我困惑的问题。
五上《学习方法指导丛书》p33有这么一题:用4个立方体,按要求摆一摆。
(1)如果从正面看,是,可以怎样摆?(2)再从左面看,是,应该怎样摆?(3)从上面看,还是,又该怎么摆?根据从正面看到的图形进行拼摆,会有多种摆法。
再根据从左面和上面看到的图形对所拼搭的立体图形进行调整。
这就要求学生要根据已有的图形的表象,不断在头脑中对这些表象进行组合和调整,最后再通过拼摆进行验证,从而使学生的空间想像力和思维能力得到充分的锻炼。
通常方法丛书用来布置回家作业,于是有学生问我:“可以怎样摆要不要写?怎样写?”确实,学生摆出来的东西,如何反馈呢?我说:“自己动脑筋,能让人家看懂你是怎么摆的就行了。
”有的学生开始模仿三维立体画图,有的画出来的图形密密麻麻,作业本上已经画不下了,有的画出的图形表达不了摆的成果,有的则无从下手。
反馈第(1)题的时候,我问:“你可以摆出几种?上来摆给同学看。
”有不少学生说是6种,于是我抽几个上来摆。
问题出来了,就是演示的方块积木虽然比学生的大很多,但是呈现给全班同学看,由于学生坐的位置远近不同,观察角度不同,所以很难统一观察的效果。
数字连连看连接相同的数字培养观察力和记忆力

数字连连看连接相同的数字培养观察力和记忆力数字连连看:连接相同的数字培养观察力和记忆力数字连连看是一种益智类游戏,通过找出相同的数字并将它们连接起来,以提高观察力和记忆力。
这款游戏以其简单有趣的玩法和可玩性而受到广大玩家的喜爱。
本文将介绍数字连连看的规则和玩法,并探讨如何通过这款游戏培养观察力和记忆力。
一、游戏规则和玩法数字连连看是一款基于数字的消除类游戏。
游戏规则通常如下:1. 游戏界面:游戏界面由一个方形网格组成,网格上会有不同的数字方块。
2. 数字方块:每个数字方块上都有一个特定的数字,数字的种类和数量根据游戏设定而定。
常见的数字包括0到9。
3. 连接方式:玩家需要通过在相邻方块之间连接路径,将相同的数字方块连接起来。
4. 连接路径:连接路径通常有一定的限制条件,比如路径不能超过两次转弯或路径长度不能超过一定的限制。
5. 消除规则:当玩家成功连接两个相同数字的方块时,这两个方块将同时消失,如此类推。
6. 游戏目标:玩家的目标是通过消除所有数字方块来完成游戏。
二、培养观察力数字连连看作为一款观察力训练游戏,可以帮助玩家培养观察力的以下几个方面:1. 注意力集中:在数字连连看中,玩家需要注意每个数字方块的位置和数值。
只有通过集中注意力,才能准确找到相同的数字进行连接。
2. 形状辨识:数字方块的形状各不相同,玩家需要准确辨识各个方块的形状,以便快速找到相同的数字进行连接。
3. 图案记忆:通过玩数字连连看,玩家可以逐渐记住不同数字方块的图案,增强对数字方块的记忆力。
三、培养记忆力数字连连看作为一种记忆力训练游戏,可以帮助玩家培养记忆力的以下几个方面:1. 数字记忆:当玩家点击一个数字方块时,需要记住该方块的数值,并在之后的游戏中找到相同的数字方块。
通过不断重复这个过程,可以提高数字的记忆能力。
2. 位置记忆:数字连连看要求玩家找到相同数字方块的位置,这需要玩家同时记住不同方块的位置信息,通过找出相同的数字连接起来。
一年级数学数方块个数练习大合集
例题详解
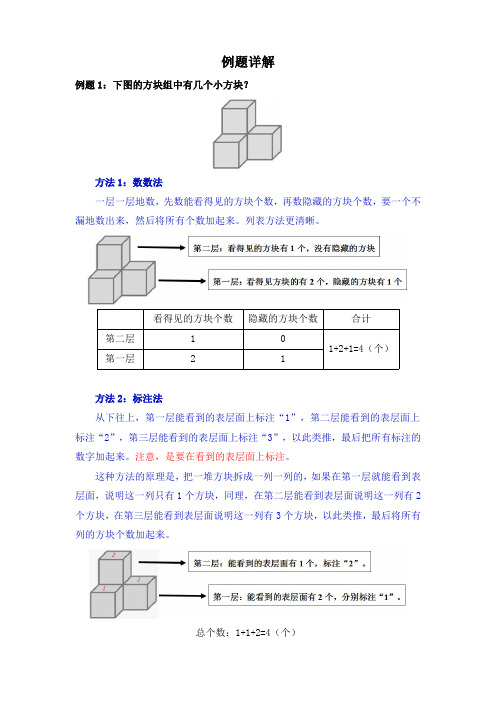
例题1:下图的方块组中有几个小方块?
方法1:数数法
一层一层地数,先数能看得见的方块个数,再数隐藏的方块个数,要一个不漏地数出来,然后将所有个数加起来。
列表方法更清晰。
看得见的方块个数隐藏的方块个数合计第二层10
1+2+1=4(个)第一层21
方法2:标注法
从下往上,第一层能看到的表层面上标注“1”,第二层能看到的表层面上标注“2”,第三层能看到的表层面上标注“3”,以此类推,最后把所有标注的数字加起来。
注意,是要在看到的表层面上标注。
这种方法的原理是,把一堆方块拆成一列一列的,如果在第一层就能看到表层面,说明这一列只有1个方块,同理,在第二层能看到表层面说明这一列有2个方块,在第三层能看到表层面说明这一列有3个方块,以此类推,最后将所有列的方块个数加起来。
总个数:1+1+2=4(个)
例题2:
右图的方块组中有几个小方块?
例题3:
右图的方块组中有几个小方块?
巩固练习
下图的方块组中各有几个小方块?
()个()个
()个()个
()个()个
()个()个。
一年级数方块数到头痛,下面用规律完美解决,看懂了教孩子特简单

一年级数方块数到头痛,下面用规律完美解决,看懂了教孩子
特简单
今天来教下孩子,数方块的技巧
数方块好多学生是看到哪里数哪里很容易搞乱了。
今天说下顺序叠加法,我总结了一个方法我感觉是最不容易出错的方法,下面我来讲。
从上面往下面数。
比如上图,
第一题
我们要从上往下加,上面第一排是1个,
下面第二排我们看到独立的2个方块且上面没有方块,那么第二排就是2+1(上面的方块对应的下面)=3就是第二排的数。
一共是1+(2+1)=4
第二题,
上面一排独立的1个方块,
第二排我们看到1(独立的且上面没有方块的)+1(上面对应的下面是,也是上面一排的得数)=2,
第三排我们看到2个独立上面没有方块的,2+2(第二排的得数)=4
一共1+2+4=7
第三题,1(第一排独立的)。
2(独立上面且没有方块)+1(第一排的得数)=3.
3(独立上面且没有方块)+3(第二排的得数)=6
一共是1+3+6=10
第四题直接用规律做:(1)+(3+1是前面括号得数)+(1+4是前面括号得数)+(4+5是前面括号得数)=19个
下面的题目我直接写规律解题
一,1+(3+1)=4 二,1+(2+1)=4 三,1+(3+1)=4 四,1+1+(3+1)=6
五,1+(3+1)=5。
二年级奥数数方块

归纳法
定义:通过观察特例,总结出一般性规律和性质的方法 适用范围:适用于具有递归、重复、规律性的问题 解题步骤:先观察数方块的特点,找出规律,然后总结出解题方法 注意事项:归纳法需要有一定的数学基础和逻辑推理能力
知识的联系。
培养思维能力: 通过数方块的问 题,培养逻辑思 维能力、空间想 象能力和创造力。
感谢您的耐心观看
汇报人:Biblioteka 数方块与加减法的关 系:通过计算方块的 总数,可以锻炼学生 的加减法运算能力。
数方块与空间思维能力 的关系:数方块需要学 生具备一定的空间思维 能力,有助于提高学生 的空间认知能力。
数方块与数学应用题目 的联系:数方块可以作 为数学应用题目的素材 ,帮助学生理解数学在 实际生活中的应用。
数方块在生活中的应用
数方块的练习与提高
数方块练习题目的选择
基础题目:适合初 学者,帮助熟悉数 方块的基本技巧
难度适中题目:适 合有一定基础的学 生,提高数方块的 能力
难度较大题目:适 合高水平学生,挑 战数方块的极限
变式题目:通过改变 方块的排列方式或增 加干扰项,提高数方 块的应变能力
数方块练习的方法与技巧
掌握基本概念:理解方块、行列、层等的概念,为后续练习打下基础。 逐步提高难度:从简单的数方块开始,逐渐增加难度,提高自己的观察和计数能力。 掌握规律:观察方块的排列规律,通过归纳总结,快速准确地数出方块的数量。 多做习题:通过大量的练习,巩固所学知识,提高数方块的准确性和速度。
观察法:通过观察方块的排列规律,找出解题方法。 分类法:将方块按照不同的类型进行分类,然后分别计算每种类型的数量。 排除法:通过排除一些不可能的情况,缩小解题范围。 归纳法:通过归纳总结,找出方块排列的规律,从而解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
神秘方块
Albrecht Dürer And his magic square E-mail文化传播网
神秘方块On the wall to the right hangs the magic square Dürer created.
163213 510118 96712 415141
It looks like this.
And what is the magic?
It is the number 34!
This number is the sum of the various fields within the magic square.
太神奇了!
用横、竖、斜各种方式将数字加起来都是34
横着加起来
163213
510118
96712
415141 The sum of all rows is 34!
竖着加起来
163213
510118
96712
415141 The sum of all columns is 34!
各角加起来
163213
510118
96712
415141 The sum of all corners is 34!
类似位置加起来
163213
510118
96712
415141
Move the fields one step clockwise and it is still 34!
163213 510118
96712 415141
Move the fields another step and it is still 34!
163213
510118
96712
415141
The sum of the fields in the center is 34!
这些位置加起来163213 510118 96712 415141
5 + 9 + 8 + 12 = 34
163213 510118 96712 415141 3 + 2 + 15 + 14 = 34
163213 510118 96712 415141163213 510118 96712 415141
The same is true for the diagonals. . .
163213 510118 96712 415141163213 510118 96712 415141
And so on: 34!
此神秘方块他创于1514年
163213
510118
96712
415141
1514年
Dürer created this square in 1514. “D“ for Dürer is the 4th letter of the alphabet and “A“ for Albrecht is the 1st!
Genius!
. . . He was very proud for creating this magic square –
and he should be!
这人确实是天才
二○一三年七月二十四日星期三
更多精彩请点击这里访问。
