自动控制原理简明教程5 (1)
自动控制原理简明教程 第五章 频率响应法

这时,求扰动输入下的误差传递函数 en(s) ,
先求 E(s) 0 C(s) 1GG((s)s) N(s)
而
e(n s)
NE((ss))
1
G(s) G(s)
则 ess(2 t) An e(n j)sin(t en( j))
幅频特性
相频特性
二.频率特性的物理意义及求解方法
R
ur
C uc
RC网络微分方程为:
优点:
(1).可以根据系统的开环频率特性判断闭环系 统的稳定性,而不必求解特征方程。
(2).很容易研究系统的结构,参数变化对系统性 能的影响,并可指出改善系统性能的途径,便于
对系统进行校正。
(3).提供了一种通过实验建立元件或系统数 学模型的方法。
(4).可以方便地设计出使系统噪声小到规定 程度的系统。
一.比例环节
传递函数为G(s)=k
频率特性为 G( jw) ke j 0
幅频特性为 A(w)=k
相频特性为 (w) 0
极坐标图和伯德图为:
L(w)(dB)
20lgk
(w)(度) 0.1 1 10 100
w
0
w
-30
Bode图
j
w=0
w
0k
w
极坐标图
二.积分环节和微分环节
积分环节: G(s) C(s) R(s) 1/ s
w? ?
450 W=1/T
1 W=0 w
对数幅频特性:L(w) 20lg 1 T 2w2 1
20lg T 2w2 1
当wT≥1时,L(w)≈-20lgwT
当wT≥1时,L(w)可用一条斜率为-20dB/dec的渐近 直线来表示。
当wT≤1时,L(w)≈0,是一条与0分贝线重合的直线。 两直线交于横坐标w=1/T的地方。
自动控制原理5课件简化版
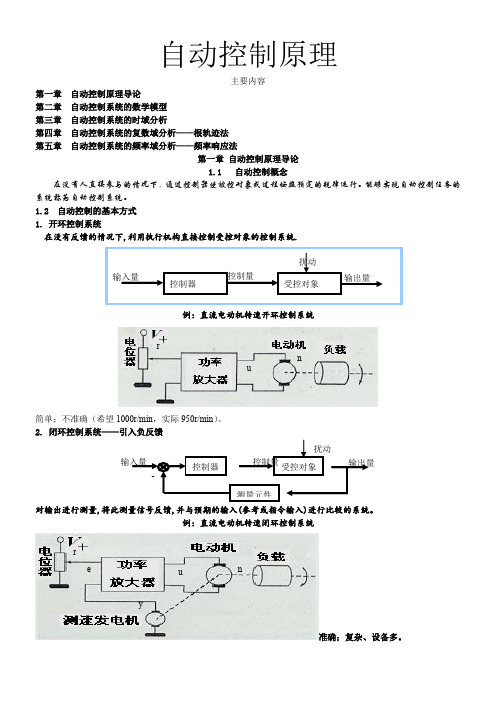
自动控制原理主要内容第一章 自动控制原理导论第二章 自动控制系统的数学模型 第三章 自动控制系统的时域分析第四章 自动控制系统的复数域分析——根轨迹法 第五章 自动控制系统的频率域分析——频率响应法第一章 自动控制原理导论 1.1 自动控制概念在没有人直接参与的情况下,通过控制器使被控对象或过程按照预定的规律运行。
能够实现自动控制任务的系统称为自动控制系统。
1.2 自动控制的基本方式 1. 开环控制系统在没有反馈的情况下,利用执行机构直接控制受控对象的控制系统.例:直流电动机转速开环控制系统简单;不准确(希望1000r/min ,实际950r/min )。
2. 闭环控制系统——引入负反馈对输出进行测量,将此测量信号反馈,并与预期的输入(参考或指令输入)进行比较的系统。
例:直流电动机转速闭环控制系统准确;复杂、设备多。
renuy控制器受控对象输入量输出量控制量扰动测量元件 -控制器受控对象输入量输出量控制量扰动unr1.3 对控制系统性能的基本要求-----稳定:有一定的稳定裕量。
稳定性是压倒一切的。
对线性系统,有成熟的稳定性分析方法。
对非线性复杂系统,很难,需要高深的数学——是自动控制重要研究内容。
符合要求的动态响应特性。
满足要求的稳态响应(静态精度)。
1.4 自动控制系统的组成 受控系统第二章 自动控制系统的数学模型 2.1 控制系统的输入/输出模型(I/O 模型) 设线性定常系统用系统的输入、输出信号或其变换式所表示的数学模型。
当I/O 为:r(t) c(t) 时域:微分方程 R(s) C(s) 复数域:传递函数 R(j ) C(j ) 频域:频域特性描写线性定常系统的微分方程)()()()(01111t c a t c dt d a t c dt d a t c dt d a n n n n n n ++++--- )()()()( 01111t r b t r dt db t r dt d b t r dt d b m m m m m m ++++=---),,1,0(),,,1,0(m j b n i a j i ==例:试求RLC 串联电路的微分方程。
自动控制原理简明教程第二版5 第五章 频率响应分析法

15
5.2.2. 典型环节的频率特性曲线绘制方法
(1)比例环节 ) (2)惯性环节 ) (3)振荡环节 ) (4)积分环节 ) (5)其他典型环节与最基本环节的关系 )
16
(1) 比例环节的幅相频率特性曲线
传递函数: 传递函数: G ( s ) = K ( K > 0) 由传递函数得频率特性表达式: 由传递函数得频率特性表达式:
2 2
ω 2ζ ωn ϕ (ω ) = −arctg ω 1 − ( )2 ωn
对数频率特性
2 2 ω 2 ω L(ω ) |= 20 lg A(ω ) = -10 lg 1 − ( ) + 2ζ ωn ωn ω
8
2.对数频率特性曲线(对数坐标图或伯德图) .对数频率特性曲线(对数坐标图或伯德图) 对数频率特性曲线包括对数幅频特性和对数相频特性两条曲线 由频率特性 G( jω) =
1 jϕ(ω) = A(ω)e 1+ jωT
对数幅频特性 L(ω) = 20lg G( jω) = 20lg A(ω) = −20lg
U2 (s) 1 = U1(s) Ts +1
G(s) =
输入正弦信号 u1 ( t ) = A sin ω t
1 1 Aω U1(s) = ⋅ 2 输出响应 U2 (s) = Ts +1 Ts +1 s +ω2
3
5.1.2 频率特性的定义
输出响应 U2 (s) = 输出响应
u2 t) = (
1 1 Aω U1(s) = ⋅ 2 Ts +1 Ts +1 s +ω2
13
5.2.1. 典型环节
《自动控制原理》胡寿松自动控制原理简明教程第5章详解

bm1s bm an1s an
➢ 惯性环节:1/(Ts+1),式中T>0
➢ 一阶微分环节:(Ts+1),式中T>0
➢ 积分环节:1/s
➢ 微分环节:s
➢ 振荡环节:1/[(s/ωn)2+2ξs/ωn+1];式中ωn>0,0 < ξ <1 ➢ 二阶微分环节:(s/ωn)2+2 ξ s/ωn+1;式中ωn>0,0 < ξ <1
线性分度,单位是分贝(dB);对数相频曲线的纵坐标按 φ(ω) 线性分度,单位是度(°)。由此构成的坐标系称为 半对数坐标系。
ω和lgω的关系表
① ω轴为对数分度, 即采 用相等的距离代表相等的 频率倍增,在伯德图中横 坐标按μ=lgω均匀分度。 ② ω=0在对数分度的坐标系中的负无穷远处,ω =0不可能 在横坐标上表示出来,横坐标上表示的最低频率由所感兴 趣的频率范围确定。 ③ 从表中可以看出,ω的数值每变化10倍, 在对数坐标 上lgω相应变化一个单位。 频率变化10倍的一段对数刻度 称为“十倍频程”, 用“dec”表示。
arctg
2
曲线起自幅角
为-v90°的
无穷远处。
1. 极坐标图的起点
2T T 2
2
tan
1
2T T 2 2
1
0 L 0dB
-40
0 90
0
180
L 20 lgT 2 40 lgT
180
n
1 T
90
1 10 TT
40dB dec
(a) (b)
➢ 延迟环节
Gs eTs
G j e jT G j 1 G j T
精确曲线
自动控制原理简明教程第二版课后答案第五章习题答案
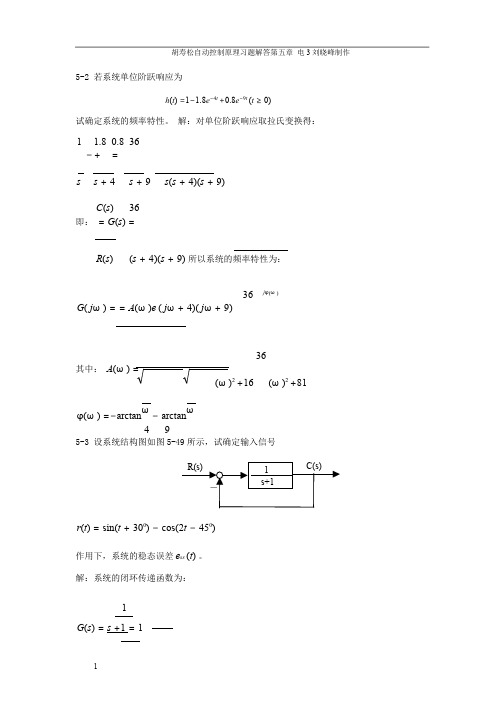
5-13 试用奈氏判据分宾判断题 5-5,5-6 系统的闭环稳定性。 解:5-5 (1)τ > T 时系统闭环稳定。 (2)T >τ 5-6 (1)ν =1 时系统闭环稳定。 (2)ν = 2,3,4 时系统闭环不稳定。 5-14 已知下列系统开环传递函数(参数 K,T,Ti > 0;i = 1,2,,6 ) : 时系统闭环不稳定。
8
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
L(ω ) (dB)
60 40 20
-20 -40 -20
0
0.1 1 2 10
-40 20 -60
100ω
ω 0 − 90
−180
5-11 绘制下列函数的对数幅频渐进特性曲线:
2
(1)G(s) =
(2s +1)(8s +1) 200 (2)G(s) = s 2(s +1)(10s +1)
1
所以:G(s) = 100(0.001s/ω
1
+1)
(s
/ω 1 +1)(s /100 +1)
11
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
(b)G(s) = s 102 (s(s/ω /ω
21
++11) )
(c)
G(s) = (s
2
2ξ ω nKs+2ω + s
n 2
ω
n
2
)(s /10 +1)
0.5 −87.2
1 −92.1
3 −164
5 − 216
7 − 234.5
10 − 246
自动控制原理简明教程第二版课后答案第五章习题答案

5-9 已知系统开环传递函数
10 G(s)H(s) = s(s +1)(s 2 /4 +1)
试绘制系统概略开环幅相曲线。 解:
5-10 已知系统开环传递函数
7
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
G(s)H(s) =
2
s
1( s
s + 921) + 3s + s 1
要求选择频率点,列表计算 A(ω ) ,L(ω )和 ϕ(ω ) ,并据此在对数坐标纸上绘制系统开环 对数频率特性曲线。
5-5 已知系统开环传递函数
G(s)H(s) = s K2 ((
τ
Ts
s+ 1 ) + 1 ) ;
K,τ ,T > 0
试分析并绘制 τ > T 和 T >τ 解:相频特性为
情况下的概略开环幅相曲线。
ϕ(ω ) =−1800 + τ ω − arctanTω
(1) τ > T 时,ϕ(ω ) >−1800 概略开环幅相曲线如下
(1) τ < T 时,ϕ(ω ) <−1800 概略开环幅相曲线如下
5-6 已知系统开环传递函数
1 G(s)H(s) = ν s (s +1)(s + 2)
4
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
试分别绘制 ν =1,2,3,4 时系统的概略开环幅相曲线。 解: (1)ν = 1 时系统的概略开环幅相曲线如下:
8
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
L(ω ) (dB)
60 40 20
-20 -40 -20
0
自动控制原理_05

8
6
稳态误差: ess (t) Rm A()sin(t ) ()
1.58sin(2t 48.4 )
11
4.频率特性的表示法
将G(jω)写成复数形式:G( j) P() jQ()
Im
Q( )
G( j) P() Re[G( j)] ---实频特性
频率特性: 线性定常系统的频率特性是零初 始条件下稳态输出正弦信号与输入正弦信号 的复数比(频域)。
2.介绍几个名词:
幅值比:同频率下输出信号与输入信号的幅值 之比。B/A
相位差:同频率下输出信号的相位与输入信号
的相位之差。φ
7
幅频特性:幅值比与频率之间的关系。
相频特性:相位差与频率之间的关系。 幅频特性和相频特性统称为频率特性 幅相特性: 将幅频和相频画到一起。 矢量端点的轨迹。
s2
1 3s
4
微分方程为:y(t )
x(t)
d2 dt 2
1 3 d
dt
4
d 2 y(t) dt 2
3 dy(t) dt
4 y(t)
x(t)
频率特性为:G(
j )
y( j ) x( j )
(
j )2
1 3(
j )
4
15
二、 频率特性的几何表示法
频率特性的极坐标图(幅相图)/奈魁斯特图 频率特性的对数坐标图/伯德图 频率特性的对数幅相图/尼柯尔斯图
第五章 线性系统的频域分析法
本章主要内容:
5.1 频率特性 5.2 典型环节和开环频率特性曲线的绘制 5.3 频率域稳定判据 5.4 稳定裕度 5.5 闭环系统的频域性能指标
自动控制原理简明教程

电位计+连杆—人脑:记住水位的期望值;
浮子—人眼:观察水池的实际水位;
电位计+连杆—人脑: 反映误差(=水位的期望值-实际 值);
电动机—人手:调节进水阀门开度,执行控制作用。
是一个反复观察测量、比较、调整执行的过程,力图 将水池水位的期望值与实际值间的差值减为0,即误差为 0。
控制过程:测量(测量反馈机构)—浮子 比较(比较机构)—电位计+连杆 执行(执行机构)—电动机
• 现代控制理论
• 60~70年代形成 适用于MIMO (多输入-多输出)系统 • 基于: 冷战时期空间技术,计算机技术 • 目标:最优控制 • 基本方法:状态空间表达式
研究对象 数学工具 常用分析方法
局限性
经典控 单输入-单输 微分方程, 时域分析法, 对复杂多变量系统、
制理论 出线性定常 传递函数 频域分析法, 时变和非线性系统
系统
根轨迹分析法
无能为力
现代控 制理论
多输入-多输 出变系数, 非线性等系
统
线性代数、 矩阵理论
状态空间法
比较繁琐(但由于 计算机技术的的迅 速发展,这一局限
性已克服)
Show
二、反馈控制系统的基本组成部分
r ( t ) 给定 元件
输入量
比较
+元件e(t) 串联 + - 偏差 校正元件 -
信号
放大 元件
给定元件——其作用是给出与期望的输出相对应的系统 输入量,是一类产生系统控制指令的装置。
测量反馈元件——如传感器和测量仪表,感受或测量被 控变量的值并把它变换为与输入量同一物理量后,再反 馈到输入端以作比较。
作为研究自动控制系统的分析与综合的方法来说, 对单输入单输出系统常采用的是时域法、频域法、根 轨迹法以及目前广泛应用的计算机辅助设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特点
⑴ 控制系统及其元部件的频率特性可运用分析法和实验 方法获得,并可用多种形式的曲线表示,故系统分析和控制 器设计可应用图解法进行,在工程上获得了广泛应用。 ⑵ 频率特性物理意义明确。对于一阶和二阶系统,频域 性能指标和时域性能指标有确定的对应关系;对于高阶系统, 可建立近似的对应关系。 ⑶ 控制系统的频域设计可兼顾动态响应和噪声抑制两方 面的要求。 ⑷ 频域分析法不仅适用于线性定常系统,还可推广应用 于某些非线性控制系统。
比例环节:K 惯性环节:1/(Ts+1),式中T>0 一阶微分环节:(Ts+1),式中T>0 积分环节:1/s 微分环节:s
b0 s m b1 s m 1 bm 1 s bm G( S ) H ( s ) a 0 s n a 1 s n 1 a n 1 s a n
0
P
Re
频率特性、传递函数、微分方程的关系
s j
传递函数
d s dt
频率特性
G( j ) G( s)
s j
系统
d j dt
微分方程
频率特性是传递函数的特例,是定义在复平面虚轴上的传 递函数,因此频率特性与系统的微分方程、传递函数一样反映 了系统的固有特性。 s j 10 10 例: G ( s ) G ( j ) j ( j 3) s( s 3)
P3
100
十倍频程
十倍频程 十倍频程
半对数坐标纸
对数坐标图的特点
(1) 由于横坐标采用对数刻度,将低频段相对展宽了(低频段 频率特性的形状对于控制系统性能的研究具有较重要的意 义),而将高频段相对压缩了。因此采用对数坐标既可以 拓宽视野,又便于研究低频段的特性。 (2) 当系统由多个环节串联而成时,系统的频率特性为各环 节频率特性的乘积,由于对数可将乘除运算变成加减运算。
T
1 T L T 20 lg 2 3dB
20
20dB dec
T 45
0 45
90
一阶微分环节 G(s)=Ts+1 G(s)=Ts+1
L( ) 20lg 1 2T 2
j
ω
0
1
ω=0
ω<<1/T, L(ω)≈20lg1=0 ω>>1/T, L(ω)≈20lgωT =20(lgω-lg1/T)
0 -90 -180
微分环节
G ( s ) s, G ( j ) j
2
L(ω)=20lgω φ(ω)=90o
j
L
20 0 0.1
20 dB dec
1 10
0
0 90 0
惯性环节 G(s)=1/(Ts+1)
G( j ) 1 1 e jarctgT 1 jT 1 2T 2 1 G( j ) 0 2 2 1 T
振荡环节:1/[(s/ωn)2+2ξ s/ωn+1];式中ωn>0,0 < ξ <1 二阶微分环节:(s/ωn)2+2 ξ s/ωn+1;式中ωn>0,0 < ξ <1
K (1 2 s ) 1 1 K (1 2 s ) s(1 0.1s ) s 1 0.1s
例 : G ( s)
t
用R(jω)和C(jω)分别表示输入信号A sinωt和输出信号 cs(t)=A sin(ωt+φ), 则输出稳态分量与输入正弦信号的复数比 称为该系统的频率特性函数, 简称频率特性, 记作
C ( j ) G( j ) A( )e j ( ) R( j )
G ( j ) G ( j ) P ( ) jQ( )
第五章 线性系统的频域分析法
§5.1 §5.2 §5.3 §5.4 §5.5 频率特性 典型环节和开环系统频率特性 频率域稳定判据 稳定裕度 开环频率特性与时域指标的关系
§5.6
闭环系统的频域性能指标
自动控制原理课程的任务与体系结构
频域分析是在正弦输入信号作用下,考察系统稳态输 出与输入量之间的振幅比和相位差的变化规律,其基本思想是 把控制系统中的各个变量看成一些由不同频率正弦信号组合而 成的信号,系统响应为对不同频率信号的响应的总和。
t AT eT 2 2 1 T
s2 2
A 1 T
2 2
sin( T - arctan T)
暂态分量
稳态分量
uos (t )
A 1 T
2 2
sin(t -arctanT)
A A()sin t ()
A(ω) 称幅频特性,φ(ω)称相频特性。 二者统称为频率特性。 系统对正弦输入信号的稳态响应称频率响应。
ui t sin t U i s
建模 ui R i uo C0 C1s C2 1T A U o ( s) 2 2 2 i Cuo s 1 T s s 1 T s 2 t AT A ui CR uo uo T uo (t ) e sin T cos cos T sin 2 2 1 T 1 2T2 Ui [CR s 1] Uo
线性分度,单位是分贝(dB);对数相频曲线的纵坐标按 φ (ω) 线性分度,单位是度(°)。由此构成的坐标系称为
半对数坐标系。
ω和lgω的关系表
① ω轴为对数分度, 即采 用相等的距离代表相等的 频率倍增,在伯德图中横 坐标按μ=lgω均匀分度。 ② ω=0在对数分度的坐标系中的负无穷远处,ω =0不可能 在横坐标上表示出来,横坐标上表示的最低频率由所感兴 趣的频率范围确定。 ③ 从表中可以看出,ω的数值每变化10倍, 在对数坐标 上lgω相应变化一个单位。 频率变化10倍的一段对数刻度
j
=∞
0 = 100 =5
=0 1 =1
=3 =2
2. 对数频率特性曲线(Bode图) 又称为伯德曲线(伯德图),由对数幅频曲线和对数相
频曲线组成,是工程中广泛应用的一组曲线。
对数幅频曲线的横坐标采用对数分度(μ=lgω),单位为 弧度/秒(rad/s),纵坐标按
L() 20lg G( j) 20lg A()
j 0
L(ω)=-20lgω φ(ω)=-90o
L
20
0
1
两重积分 G ( j )
1 ( j ) 2
0 0.1 -20
10 20 dB dec
40 dB dec
L 20lg 1 G j 180
2
40lg
L
20 0
!高频放大 !抑制噪声能力下降
20dB dec
1 T
( ) arctgT
T 1 TL T 20lg 2 3dB10 T
100 T
T 45
90 45 0
振荡环节
1 G s 2 2 T s 2 Ts 1 1 G j 2 2 T j 2 T j 1 1 G j 2 2 2 2 1 T 2 T
频率特性,则很容易写出实验对象的频率特性表达式或传递
函数。
转折频率
精确曲线 渐近线
3. 对数幅相曲线(Nichols)
对数幅相图的横坐标表示对数相频特性的相角,纵坐标表
示对数幅频特性的幅值的分贝数,又称尼柯尔斯曲线。
§ 5.2 典型环节和开环频率特性
§5.2.1 典型环节
典型环节
例:RC电路的幅相频率特性。
ui R C uo
Uo ( j ) 1 1 G( j ) Ui ( j ) 1 RCj 1 Tj
G(jω)=R(ω)+jI(ω)
代数式
A( )
1
=|G(jω)|∠G(jω)
=A(ω)ejφ(ω)
极坐标式
指数式
2T 2 1
∠G(jω)=-arctanTω
j
( ) -arctg T 0 G j 10
0 1
! 低通 滤波特性
1 T 10 T 100 T
G j 0
2
L
0
L( ) 20lg 1 2T 2
ω<<1/T, L(ω)≈-20lg1=0 ω>>1/T, L(ω)≈-20lgωT =-20(lgω-lg1/T)
§5.2.2 典型环节的频率特性
比例环节
频率特性 G(jω)=K
j
L
0
K>1 K=1
0
k
K<1
·
0
比例环节的 对数频率特性曲线
比例环节K的幅相曲线
对数幅频特性和对数相频特性分别是: L(ω)=20lg| G(jω)|=20lgK 和φ(ω)=0
积分环节
1 1 1 G( s ) , G( j ) s j 2
§ 5.1 频率特性
§5.1.1 频率特性的基本概念
例:RC 电路如图所示,ui(t)=Asinwt, 求uo(t)=?
ui t
i ui t
R
C
uo t
0
uo t
解:
U o ( s) 1 T CR 1 1T G( s) U i ( s) CRs 1 Ts 1 s 1 T
幅频特性 A( ) | G ( j ) | P 2 ( ) Q 2 ( )
