题型四_几何图形的折叠与动点问题

合集下载

高中数学立体几何动点和折叠问题-含答案

高中数学立体几何动点和折叠问题-含答案1.在正方体ABCD-A1B1C1D1中，BC的中点为M，点P在正方体的表面DCC1D1上移动，且满足∠APD=∠MPC。

求三棱锥P-BCD的体积的最大值。

2.△ABC是边长为23的等边三角形，E、F分别为AB、AC的中点，沿EF把四面体OAEF折起，使点A翻折到点P的位置，连接PB、PC。

当四棱锥P-BCFE的外接球的表面积最小时，求四棱锥P-BCFE的体积。

3.△ABC是边长为23的等边三角形，E、F分别在线段AB、AC上滑动，且EF//BC，沿EF把△AEF折起，使点A翻折到点P的位置，连接PB、PC。

求四棱锥P-BCFE的体积的最大值。

4.已知三棱锥P-ABC满足PA⊥底面ABC，在△ABC中，AB=6，AC=8，且AB⊥AC，D是线段AC上一点，且AD=3DC，球O为三棱锥P-ABC的外接球，过点D作球O的截面。

若所得截面圆的面积的最小值与最大值之和为44π，则求球O的表面积。

5.已知A、B、C、D四点均在半径为R(R为常数）的球O的球面上运动，且AB=AC，AB⊥AC，AD⊥BC。

若四面体ABCD的体积的最大值为V，求V的值。

6.已知A、B、C是球O的球面上的三点，AB=2，AC=23，∠ABC=60°，且三棱锥O-ABC的体积为V。

求V的值。

7.已知三棱柱ABC-A1B1C1内接于一个半径为3的球，四边形A1ACC1与B1BCC1为两个全等的矩形，M是A1B1的中点，且C1M=√3.求三棱锥C1-ABC的体积。

8.在四棱柱ABCD-A1B1C1D1中，底面四边形ABCD是菱形，∠ADC=120°，连接AC，BD交于点O，A1O⊥平面ABCD，AO=BD=4，点C'与点C关于平面BC1D对称。

求三棱锥C'-ABD的体积。

1.删除该题，因为这明显是一道数学计算题，没有文章可言。

2.球O的表面积为4π，则球O的体积为(4/3)π。

2020中考数学几何图形的折叠与动点问题(含答案)

2020中考数学几何图形的折叠与动点问题（含答案）1.如图，在矩形ABCD中，AB＝4，AD＝9，点E在BC上，CE＝4，点F是AD 上的一个动点，若把△BEF沿EF折叠，点B落在点B′处，当点B′恰好落在矩形ABCD的一边上，则AF的长为________．第1题图3或11 32.如图，矩形纸片ABCD中，AB＝4，AD＝6，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是________．第2题图6－25≤BP≤43.如图，在矩形ABCD中，AB＝2，AD＝6，E，F分别是线段AD、BC上的点，连接EF，使四边形ABFE为正方形，若点G是AD上的动点，连接FG，将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上，对应点为P，则线段AP的长为__________．第3题图4或4－224.如图，在四边形ABCD中，AD∥BC(AD＜BC)，AB与CD不平行，AB＝CD＝5，BC＝12，点E是BC上的动点，将∠B沿着AE折叠，使点B落在直线AD上的点B′处，DB′＝1，直线BB′与直线DC交于点H，则DH＝________．第4题图5 11或5135.如图，已知AD∥BC，AB⊥BC，AB＝8，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC 于点M，N.当点B′分线段MN为3∶5的两部分时，EN的长为________．第5题图355 11或539 136.如图，在矩形纸片ABCD中，AB＝6，BC＝8，点P是对角线BD上一动点，将纸片折叠，使点C与点P重合，折痕为EF，折痕EF的两端分别在BC、DC边上(含端点)，当△PDF为直角三角形时，FC的长为________．第6题图24 7或8 37.如图，正方形的边长为4，E是BC的中点，点P是射线AD上一动点，过P作PF⊥AE于F.若以P、F、E为顶点的三角形与△ABE相似，则P A＝________．第7题图2或58.如图，矩形ABCD中，AB＝1，AD＝2，E是AD中点，点P在射线BD上运动，若△BEP为等腰三角形，则线段BP的长度等于____________．第8题图2或53或6559.如图，在▱ABCD中，∠B＝30°，AB＝AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD、BC于点E、F；点M是边AB的一个三等分点．则△AOE 与△BMF的面积比为__________．第9题图3∶4或3∶810.如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝2，E为斜边AB的中点，点P是射线BC上的一个动点，连接AP、PE，将△AEP沿着边PE折叠，折叠后得到△EP A′，若△EP A′与△ABC的另一个交点为F，当EF＝14AB时，则BP的长为________．第10题图2或2311.已知△ABC ，以AB 为直径的⊙O 交AC 于点D ，交BC 于点E ，连接ED ，若ED ＝EC .(1)求证：AB ＝AC ；(2)①若AB ＝4，BC ＝23，则CD ＝________； ②当∠A ＝________时，四边形ODEB 是菱形．第1题图1．(1)证明：∵ED ＝EC ，∴∠EDC ＝∠C ， ∵∠EDC ＋∠ADE ＝180°，∠B ＋∠ADE ＝180°， ∴∠EDC ＝∠B ，∴∠B ＝∠C ， ∴AB ＝AC ； (2)解：①32；如解图，连接BD ，第1题解图∵AB 为∵O 的直径，∵BD ∵AC ，设CD ＝a ，由(1)知AC ＝AB ＝4，则AD ＝4－a ，在Rt∵ABD 中，由勾股定理可得BD 2＝AB 2－AD 2＝42－(4－a )2，在Rt∵CBD 中，由勾股定理可得BD 2＝BC 2－CD 2＝(23)2－a 2， ∵42－(4－a )2＝(23)2－a 2，解得a ＝32，即CD ＝32. ∵60°.如解图，连接OD 、OE ，∵四边形ODEB 是菱形，∵OB ＝BE ，又∵OB ＝OE ，∵∵OBE 是等边三角形，∵∵OBE ＝60°， ∵OD ∵BE ，∵∵BOD ＝120°，∵∵A ＝12∵BOD ＝60°.12 .如图，在▱ABCD 中，AD ＝4，AB ＝5，延长AD 到点E ，连接EC ，过点B 作BF ∥CE 交AD 于点F ，交CD 的延长线于点G .(1)求证：四边形BCEF 是平行四边形；(2)①当DF ＝______时，四边形BCEF 是正方形； ②当GFGD ＝________时，四边形BCEF 是菱形．第2题图13. (1)证明：∵四边形ABCD 是平行四边形，∴EF ∥BC . ∵BF ∥CE ，∴四边形BCEF 是平行四边形；(2)解：①1;∵四边形BCEF 是正方形，∵BF ＝BC ＝AD ＝4，∵FBC ＝∵AFB ＝90°， ∵AF ＝AB 2－BF 2＝52－42＝3. ∵AD ＝4，∵DF ＝AD －AF ＝4－3＝1. ∵45. ∵四边形BCEF 是菱形， ∵BF ＝BC ＝AD ＝4.∵四边形ABCD 是平行四边形，∵CD ∵AB ， ∵GD AB ＝GF BF ，即GF GD ＝BF AB ＝45.14.如图，AB 是半圆O 的直径，射线AM ⊥AB ，点P 在AM 上，连接OP 交半圆O 于点D ，PC 切半圆O 于点C ，连接BC .(1)求证：BC ∥OP ；(2)若半圆O 的半径等于2，填空：①当AP ＝________时，四边形OAPC 是正方形；②当AP ＝________时，四边形BODC 是菱形．第3题图解：(1)证明：连接OC ，AC ，如解图所示， ∵AB 是直径，AM ⊥AB ， ∴BC ⊥AC ，AP 是半⊙O 的切线，又∵PC是半⊙O的切线，∴P A＝PC，又∵OA＝OC，∴OP⊥AC，∴BC∥OP；(2)① 2；② 2 3.∵若四边形OAPC是正方形，则OA＝AP，∵OA＝2，∵AP＝2；∵若四边形BODC是菱形，则CB＝BO＝OD＝DC，∵AB＝2OB，∵ACB＝90°，∵AB＝2BC，∵∵BAC＝30°，∵ABC＝60°，∵BC∵OP，∵∵AOP＝∵ABC＝60°，又∵∵OAP＝90°，OA＝2，∵∵OP A＝30°，∵OP＝4，∵AP＝22222-OAOP＝2 3.=4-第3题解图15.如图，在△ABC中，∠ACB＝90°，线段BC的垂直平分线DE交BC于点D，交AB于点E，点F在DE的延长线上，AF＝CE且F不与E重合．(1)求证：△EF A≌△ACE；(2)填空：①当∠B＝_________°时，四边形ACEF是菱形；②当∠B＝_________°时，线段AF与AB垂直．第4题图(1)证明：如解图，第4题解图∵ED是BC的垂直平分线，∴EB＝EC，ED⊥BC，∴∠3＝∠4，∵∠ACB＝90°，∴FE∥AC，∴∠1＝∠5，∵∠2与∠4互余，∠1与∠3互余，∴∠1＝∠2＝∠5，∴AE＝CE.又∵AF＝CE，∴AE＝AF，∴∠5＝∠F，在△EF A和△ACE中，AF＝AE＝EC，∠1＝∠2＝∠5＝∠F，∴△EF A≌△ACE.(2)解：① 30；②45.∵∵四边形ACEF是菱形，∵AC＝CE，∵CE是Rt∵ABC斜边AB的中线，∵CE＝AE＝BE，∵AE＝AC＝CE，∵∵ACE是等边三角形,∵∵1＝60°，则∵B＝30°,∵当∵B＝30°时，四边形ACEF是菱形；∵由(1)知∵EF A∵∵ACE，∵∵AEC＝∵EAF，∵AF∥CE，∵AF∵AB，∵CE∵AB，∵CE＝EB，∵∵3＝∵4＝45°，∵当∵B＝45°时，线段AF与AB垂直．16.如图，AB是⊙O的直径，E是⊙O外一点，过点E作⊙O的两条切线ED，EB，切点分别为点D，B.连接AD并延长交BE延长线于点C，连接OE.(1)试判断OE与AC的关系，并说明理由；(2)填空：①当∠BAC＝_________°时，四边形ODEB为正方形；②当∠BAC＝30°时，ADDE的值为________．第5题图5.解：(1)OE∥AC，OE＝12AC.理由：连接OD，如解图，第5题解图∵DE，BE是⊙O的切线，∴OD⊥DE，AB⊥BC，∴∠ODE＝∠ABC＝90°，∵OD＝OB，OE＝OE，∴Rt△ODE≌Rt△OBE(HL)，∴∠1＝∠2.∵∠BOD＝∠A＋∠3，OA＝OD，∴∠A＝∠3，∴∠2＝∠A，∴OE∥AC；∵OA＝OB，∴EC＝EB，∴OE是△ABC的中位线，∴OE＝12AC.(2)①45；②3.∵要使四边形ODEB是正方形，由ED＝EB，∵ODE＝∵ABC＝90°,只需∵DOB ＝90°，∵∵A＝45°；∵过O作OH∵AD于H,∵∵A＝30°，OA＝OD,∵∵3＝∵A＝30°，∵OD，∵∵ODE＝90°，∵1＝∵3＝30°，∵OD，∵ADDE＝3.17.如图，将⊙O的内接矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连接BC1，∠ACB＝30°，AB＝1，CC1＝x.(1)若点O与点C1重合，求证：A1D1为⊙O的切线；(2)①当x＝________时，四边形ABC1D1是菱形；②当x＝________时，△BDD1为等边三角形．第6题图(1)证明：∵四边形ABCD为矩形，∴∠D＝90°，∵把△ACD沿CA方向平移得到△A1C1D1，∴∠A1D1O＝∠D＝90°，∴A1D1⊥OD1，∴A1D1为⊙O的切线；(2)解：①1；②2.∵如解图∵，连接AD1，当x＝1时，四边形ABC1D1是菱形；第6题解图∵理由：由平移得：AB＝D1C1，且AB∵D1C1，∵四边形ABC1D1是平行四边形，∵∵ACB＝30°，∵∵CAB＝60°，∵AB＝1，∵AC＝2，∵x＝1，∵AC1＝1，∵AB＝AC1，∵∵AC1B是等边三角形，∵AB＝BC1，∵四边形ABC1D1是菱形；∵如解图∵所示，当x＝2时，∵BDD1为等边三角形，第6题解图∵则可得BD＝DD1＝BD1＝2，即当x＝2时，∵BDD1为等边三角形．。

中考数学专题复习——四边形中的折叠、剪切、旋转与动点最值问题

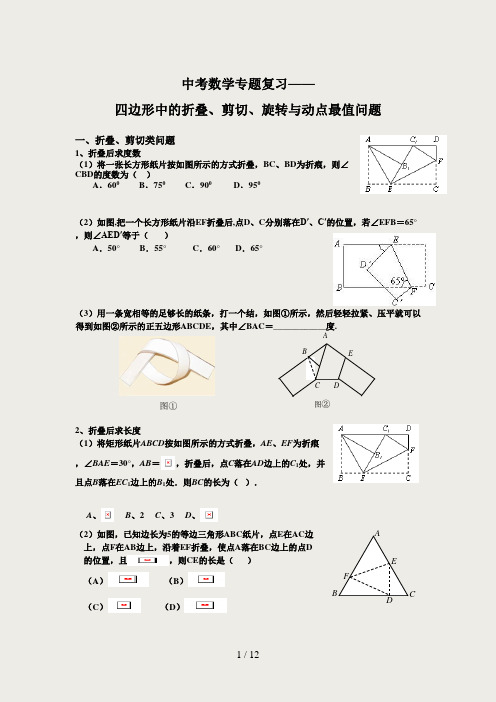
C DEB A图② 中考数学专题复习——四边形中的折叠、剪切、旋转与动点最值问题一、折叠、剪切类问题1、折叠后求度数（1）将一张长方形纸片按如图所示的方式折叠，BC 、BD 为折痕，则∠CBD 的度数为（）A ．600B ．750C ．900D ．950（2）如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D′、C′的位置，若∠EFB ＝65°，则∠AED′等于（）A ．50°B ．55°C ．60°D ．65°（3）用一条宽相等的足够长的纸条，打一个结，如图①所示，然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE ，其中∠BAC ＝____________度.2、折叠后求长度（1）将矩形纸片ABCD 按如图所示的方式折叠，AE 、EF 为折痕，∠BAE ＝30°，AB ＝，折叠后，点C 落在AD 边上的C 1处，并且点B 落在EC 1边上的B 1处．则BC 的长为（）． A 、B 、2C 、3D 、（2）如图，已知边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折叠，使点A 落在BC 边上的点D 的位置，且，则CE 的长是（）（A ）（B ）（C ）（D ）图①ABCDEF（3）如图，将边长为8㎝的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ，则线段CN 的长是（） A ．3cm B ．4cm C ．5cm D ．6cm（4）如图，将矩形纸ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH ，若EH ＝3厘米，EF ＝4厘米，则边AD 的长是___________厘米.（5）如图，是一张矩形纸片ABCD ，AD =10cm ，若将纸片沿DE 折叠，使DC 落在DA 上，点C 的对应点为点F ，若BE =6cm ，则CD =（6）如图（1），把一个长为、宽为的长方形（）沿虚线剪开，拼接成图（2），成为在一角去掉一个小正方形后的一个大正方形，则去掉的小正方形的边长为（） A ． B ． C ．D ．3、折叠后求面积（1）如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AE 与BC 交于点F ，则△CEF 的面积为（）N M FEDCBAmnnn （2（1A ．4B ．6C ．8D ．10（2）如图，正方形硬纸片ABCD 的边长是4，点E 、F 分别是AB 、BC 的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是（） A ．2 B ．4 C ．8 D ．10（3）如图a ，ABCD 是一矩形纸片，AB ＝6cm ，AD ＝8cm ，E 是AD 上一点，且AE ＝6cm 。

2019年河南中考数学之选择、填空重难点题型：专题四几何图形的折叠与动点问题

折叠后点位置的不确定
8．(2018· 达州)如图，Rt△ABC 中，∠C＝90° ，AC＝2，BC＝5，点 D 是 BC 边上一点，且 CD＝1，点 P 是线段 DB 上一动点，连接 AP，以 AP 为斜边在 AP 的下方作等腰直角三角形 AOP.在点 P 从点 D 运动至点 B 的过程中，点 O 的运动路径长为 2 2 ．
4．如图，在直角坐标系中，点 A(4，0)，B(0，2)，过点 A 的直线 l⊥AB，点 P 是直线 l 上一动点，过点 P 作 PC⊥x 轴，垂足为点 C，把△ACP 沿 AP 翻折，使点 C 落在点 D 处，且以点 A，D，P 为顶点的三角形与△ABP 相似，则所有满足条件的点 P 的坐标是 (5，2)或(8，8)或(0，－8)或(3，－2) ．
12．(2018· 安阳一模改编)在矩形 ABCD 中，AB＝4，BC＝9，点 E 是 AD 边上一动点，将△ABE 折叠，点 A 的对应点为 A′，若点 A′到矩形较长两对边的距离之比为 1∶3， 4 4 则线段 AE 的长为 5 15或7 7或 4 3 ． 13．如图，在矩形 ABCD 中，AB＝3，AD＝6，点 E 为 AD 边上一点，将△ABE 沿 BE 折叠，点 A 落在点 A′处，取 BE 的中点 F，连接 A′F，当 A′F 平行于矩形的某条边时，AE 的长为
折叠后特殊三角形的判定
1．(2018· 宜宾)如图，在矩形 ABCD 中，AB＝3，CB＝2，点 E 为线段 AB 上的动点，将△CBE 沿 CE 折叠，使点 B 落在矩形内点 F 处，下列结论正确的是 ①②③ 所有正确结论的序号) ．(写出
①当 E 为线段 AB 中点时，AF∥CE； 9 ②当 E 为线段 AB 中点时，AF＝； 5 13－2 13 ③当 A，F，C 三点共线时，AE＝； 3 ④当 A，F，C 三点共线时，△CEF≌△AEF.

九年级数学专题复习图形的折叠和动点问题

中考冲刺：动手操作与运动变换型问题【中考展望】1．对于实践操作型问题，在解题过程中学生能够感受到数学学习的情趣与价值，经历“数学化”和“再创造”的过程，不断提高自己的创新意识与综合能力，这是《全日制义务教育数学课程标准(实验稿)》的基本要求之一，因此，近年来实践操作性试题受到命题者的重视，多次出现.2．估计在今年的中考题中，实践操作类题目依旧是出题热点，仍符合常规题型，与三角形的全等和四边形的性质综合考查．需具备一定的分析问题能力和归纳推理能力．图形的设计与操作问题，主要分为如下一些类型：1．已知设计好的图案，求设计方案(如：在什么基本图案的基础上，进行何种图形变换等)．2．利用基本图案设计符合要求的图案(如：设计轴对称图形，中心对称图形，面积或形状符合特定要求的图形等)．3．图形分割与重组(如：通过对原图形进行分割、重组，使形状满足特定要求)．4．动手操作(通过折叠、裁剪等手段制作特定图案)．解决这样的问题，除了需要运用各种基本的图形变换(平移、轴对称、旋转、位似)外，还需要综合运用代数、几何知识对图形进行分析、计算、证明，以获得重要的数据，辅助图案设计．另外，由于折叠操作相当于构造轴对称变换，因此折叠问题中，要充分利用轴对称变换的特性，以获得更多的图形信息．必要时，实际动手配合上理论分析比单纯的理论分析更为快捷有效．从历年中考来看，动态问题经常作为压轴题目出现，得分率也是最低的.动态问题一般分两类，一类是代数综合题，在坐标系中有动点，动直线，一般是利用多种函数交叉求解.另一类就是几何综合题，在梯形，矩形，三角形中设立动点、线以及整体平移翻转，对考生的综合分析能力进行考查.所以说，动态问题是中考数学当中的重中之重，只有完全掌握，才有机会拼高分.【方法点拨】实践操作问题：解答实践操作题的关键是要学会自觉地运用数学知识去观察、分析、抽象、概括所给的实际问题，揭示其数学本质，并转化为我们所熟悉的数学问题．解答实践操作题的基本步骤为：从实例或实物出发，通过具体操作实验，发现其中可能存在的规律，提出问题，检验猜想．在解答过程中一般需要经历操作、观察、思考、想象、推理、探索、发现、总结、归纳等实践活动过程，利用自己已有的生活经验和数学知识去感知发生的现象，从而发现所得到的结论，进而解决问题．动态几何问题：1、动态几何常见类型（1）点动问题（一个动点）（2）线动问题（二个动点）（3）面动问题（三个动点）2、运动形式平移、旋转、翻折、滚动3、数学思想函数思想、方程思想、分类思想、转化思想、数形结合思想4、解题思路（1）化动为静，动中求静（2）建立联系，计算说明（3）特殊探路，一般推证【典型例题】类型一、图形的剪拼问题例1．直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形．方法如下(如图所示)：请你用上面图示的方法，解答下列问题：(1)对下图中的三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形面积相等的矩形；(2)对下图中的四边形，设计一种方案，将它分成若干块，再拼成一个与原四边形面积相等的矩形．举一反三：【变式】把一张正方形纸片如图①、图②对折两次后，再按如图③挖去一个三角形小孔，则展开后图形是（）A． B． C． D．类型二、实践操作例2．如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．（1）求证：∠APB=∠BPH；（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；（3）设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．例3．刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①中，∠B＝90°，∠C＝60°，∠A＝30°，BC＝6 cm；图②中，∠D＝90°，∠E＝45°，DE＝4 cm．图③是刘卫同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上(移动开始时点D与点A重合)．(1)在△DEF沿AC方向移动的过程中，刘卫同学发现：F、C两点间的距离逐渐________．(填“不变”、“变大”或“变小”)(2)刘卫同学经过进一步地研究，编制了如下问题：问题①：当△DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行?问题②：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形?问题③：在△DEF的移动过程中，是否存在某个位置，使得∠FCD＝15°？如果存在，求出AD的长度；如果不存在，请说明理由．请你分别完成上述三个问题的解答过程．举一反三：【变式】如图，直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图，其中DC∥OB，OB=6,CD=BC=4，BC⊥OB于B,以O为坐标原点，OB所在直线为x轴建立平面直角坐标系，开发区综合服务管理委员会（其占地面积不计）设在点P（4,2）处.为了方便驻区单位准备过点P修一条笔直的道路（路宽不计），并且是这条路所在的直线将直角梯形OBCD分成面积相等的两部分，你认为直线是否存在？若存在求出直线的解析式,若不存在，请说明理由.类型三、平移旋转型操作题例4．两个全等的直角三角形ABC和DEF重叠在一起，其中∠A＝60°，AC＝1．固定△ABC不动，将△DEF进行如下操作：(1)如图所示，△DEF沿线段AB向右平移(即D点在线段AB内移动)，连结DC、CF、FB，四边形CDBF 的形状在不断地变化，但它的面积不变化，请求出其面积．(2)如图所示，当D点移动到．AB的中点时，请你猜想四边形CDBF的形状，并说明理由．(3)如图所示，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB 边上，此时，点恰好与B点重合，连结AE，请你求出sinα的值．类型四、动态数学问题例5．如图，在平面直角坐标系中，点C的坐标为（0，4），动点A以每秒1个单位长的速度，从点O 出发沿x轴的正方向运动，M是线段AC的中点．将线段AM以点A为中心，沿顺时针方向旋转90°，得到线段AB，过点B作x轴的垂线，垂足为E，过点C作y轴的垂线，交直线BE于点D，运动时间为t秒．（1）当点B与点D重合时，求t的值；（2）当t为何值时，S△BCD=？举一反三：【变式】如图，平行四边形ABCD中，AB=10，AD=6，∠A=60°，点P从点A出发沿折线AB-BC以每秒1个单位长的速度向点C运动，当P与C重合时停止运动，过点P作AB的垂线PQ交AD或DC于Q．设P 运动时间为t秒，直线PQ扫过平行四边形ABCD的面积为S．求S关于t的函数解析式．【巩固练习】一、选择题1. 将一张正方形纸片按如图所示对折两次，并在如图位置上剪去一个圆形小洞后展开铺平得到的图形是（）A ．B ．C ．D ．2. 一张正方形的纸片，如图1进行两次对折，折成一个正方形，从右下角的顶点，沿斜虚线剪去一个角剪下的实际是四个小三角形，再把余下的部分展开，展开后的这个图形的内角和是多少度？（）A ．1080°B ．360°C ．180°D ．900°3. 如图，把矩形ABCD 对折，折痕为MN （图甲），再把B 点叠在折痕MN 上的B ′处.得到Rt △AB ′E （图乙），再延长EB ′交AD 于F ，所得到的△EAF 是（）A. 等腰三角形B. 等边三角形C. 等腰直角三角形D. 直角三角形4. 如图，已知边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折叠，使点A 落在BC 边上的点D 的位置，且ED ⊥BC ，则CE 的长是（）A 、10315-B 、1053-C 、535-D 、20103-二、填空题5.如图(1)是一个等腰梯形，由6个这样的等腰梯形恰好可以拼出如图(2)所示的一个菱形．对于图(1)中的等腰梯形，请写出它的内角的度数或腰与底边长度之间关系的一个正确结论：．6．如图,△ABC中,∠BAC=600,∠ABC=450,AB=22,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F ,连接EF,则线段EF长度的最小值为___________7．如图①，在四边形ABCD中，AD∥BC，∠C=90°，CD=6cm．动点Q从点B出发，以1cm/S的速度沿BC运动到点C停止，同时，动点P也从B点出发，沿折线B→A→D运动到点D停止，且PQ⊥BC．设运动时间为t（s），点P运动的路程为y（cm），在直角坐标系中画出y关于t的函数图象为折线段OE 和EF（如图②）．已知点M（4，5）在线段OE上，则图①中AB的长是cm．三、解答题8．阅读下列材料：小明遇到一个问题：5个同样大小的正方形纸片排列形式如图(1)所示，将它们分割后拼接成一个新的正方形．他的做法是：按图(2)所示的方法分割后，将三角形纸片①绕AB的中点D旋转至三角形纸片②处，依此方法继续操作，即可拼接成一个新的正方形DEFG．请你参考小明的做法解决下列问题：(1)现有5个形状、大小相同的矩形纸片，排列形式如图(3)所示．请将其分割后拼接成一个平行四边形．要求：在图(3)中画出并指明拼接成的平行四边形(画出一个符合条件的平行四边形即可)；(2)如图(4)，在面积为2的平行四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，分别连结AF、BG、CH、DE得到一个新的平行四边形MNPQ．请在图(4)中探究平行四边形MNPQ面积的大小(画图并直接写出结果)．9. 如图(a)，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸……．已知标准纸的短边长为a．(1)如图(b)，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：第一步将矩形的短边AB与长边AD对齐折叠，点B落在AD上的点B′处，铺平后得折痕AE；第二步将长边AD与折痕AE对齐折叠，点D正好与点E重合，铺平后得折痕AF；则AD:AB的值是________，AD，AB的长分别是________，________；(2)“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等?若相等，直接写出这个比值；若不相等，请分别计算它们的比值；(3)如图(c)，由8个大小相等的小正方形构成“L”型图案，它的4个顶点E，F，G，H分别在“16开”纸的边AB，BC，CD，DA上，求DG的长；(4)已知梯形MNPQ中，MN∥PQ，∠M＝90°，MN＝MQ＝2PQ，且四个顶点M，N，P，Q都在“4开”纸的边上，请直接写出两个符合条件且大小不同的直角梯形的面积．10. 操作与探究(1)图(a)是一块直角三角形纸片．将该三角形纸片按图中方法折叠，点A与点C重合，DE为折痕．试证明△CBE是等腰三角形；(2)再将图(b)中的△CBE沿对称轴EF折叠(如图(b))．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图(c)中的△ABC折叠成一个组合矩形吗？如果能折成，请在图(c)中画出折痕；(3)请你在图(d)的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；(4)有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四边上)．请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足什么条件时，一定能折成组合矩形?11.在图1至图5中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE＝2b，且边AD和AE 在同一直线上．操作示例：当2b＜a时，如图1，在BA上选取点G，使BG＝b，连接FG和CG，裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．思考发现：小明在操作后发现：该剪拼方法是先将△FAG绕点F逆时针旋转90°到△FEH的位置，易知EH与AD在同一直线上，连接CH．由剪拼方法可得DH＝BG，故△CHD≌△CGB，从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置．这样，对于剪拼得到的四边形FGCH(如图所示)，过点F作FM⊥AE于点M(图略)，利用SAS公理可判断△HFM≌△CHD，易得FH＝HC＝GC＝FG，∠FHC＝90°．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．实践探究：(1)正方形FGCH的面积是________；(用含a、b的式子表示)(2)类比图1的剪拼方法，请你就图2至图4的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展：小明通过探究后发现：当b≤a时，此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．当b＞a时，如图所示的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．12. 已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．。

专题4几何图形的折叠与动点问题

8．(2017·平顶山二模)如图，在矩形纸片 ABCD 中，AB＝5， AD＝2，点 P 在线段 AB 上运动，设 AP＝x，现将纸片折叠，使点 D 与点 P 重合，得折痕 EF(点 E，F 为折痕与矩形边的交点)，再将纸片还原，则四边形 EPFD 为菱形时， x 的取值范围是_2_≤_x_≤_5______.
＝
3 5
x.
由
折
叠
的
性
质
可
知
，
∠HED ＝
∠FED.
又
∵∠EHD ＝
∠EFD＝90°，ED＝ED，∴△EHD≌△EFD(AAS)，
∴EH＝EF，即 2－x＝35x，解得 x＝54.综上所述，BE 的长度为 12或54.
15 【答案】 2或4
类型2 折叠后点位置的不确定
(2017·许昌二模)如图，矩形 ABCD 中，AB＝8，BC ＝15，点 E 是 AD 边上一点，连接 BE，把△ABE 沿 BE 折叠，使点 A 落在 A′处．点 F 是 CD 边上一点，连接 EF，把△DEF 沿 EF 折叠，使点 D 落在直线 EA′上的点 D′处．当点 D′ 落在 BC 边上时，AE 的长为________．
6．已知正方形 ABCD 的面积为 12，若平面内存在一点 E，使得△ABE 为等边三角形，且在对角线 AC 上有一点 P，使 PD＋PE 的和最小，则这个最小值为_2___3_或__3__2_＋___6__.
7．(2017·营口)在矩形纸片 ABCD 中，AD＝8，AB＝6，E 是边 BC 上的点，将纸片沿 AE 折叠，使点 B 落在点 F 处，连接 FC，当△EFC 为直角三角形时，BE 的长为__3_或__6____.
第11题图

题型四几何图形的折叠与动点问题

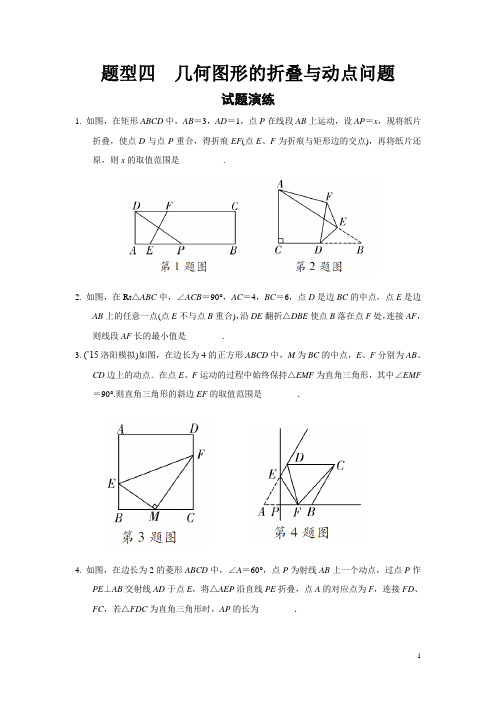
题型四几何图形的折叠与动点问题试题演练1. 如图，在矩形ABCD中，AB＝3，AD＝1，点P在线段AB上运动，设AP＝x，现将纸片折叠，使点D与点P重合，得折痕EF(点E、F为折痕与矩形边的交点)，再将纸片还原，则x的取值范围是__________.2. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，点D是边BC的中点，点E是边AB上的任意一点(点E不与点B重合)，沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF长的最小值是________．3. (’15洛阳模拟)如图，在边长为4的正方形ABCD中，M为BC的中点，E、F分别为AB、CD边上的动点．在点E、F运动的过程中始终保持△EMF为直角三角形，其中∠EMF ＝90°.则直角三角形的斜边EF的取值范围是________．4. 如图，在边长为2的菱形ABCD中，∠A＝60°，点P为射线AB上一个动点，过点P作PE⊥AB交射线AD于点E，将△AEP沿直线PE折叠，点A的对应点为F，连接FD、FC，若△FDC为直角三角形时，AP的长为________．5. 如图，正方形ABCD的边长为2，∠DAC的平分线AE交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ＋PQ的最小值为________．6. 如图，在矩形ABCD中，AD＝3，AB＝4，点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D′落在矩形的对角线上时，DE的长为________．7. 如图，矩形纸片ABCD中，AB＝8，将纸片折叠，使顶点B落在边AD上，对应点为点E，若BG＝10，则折痕FG的长为________．8. 如图，在Rt△ABC中，∠ABC＝90°，AC＝10，BC＝8，AD是∠BAC的平分线，点E是斜边AC上的一点，且AE＝AB，沿△DEC的一个内角平分线折叠，使点C落在DE所在直线上，则折痕的长度为________．9. (’15商丘模拟)如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点E是AB边上一动点，过点E作DE⊥AB交AC边于点D，将∠A沿直线DE翻折，点A落在线段AB 上的点F处，当△BCF为等腰三角形时，AE的长为________．10. (’15郑州模拟)如图，在矩形ABCD中，AD＝6，CD＝4，AD的中点为E，点F是AB边上一点(不与A、B重合)，连接EF，把∠A沿EF折叠，使点A落在点G处，连接CG.则线段CG的取值范围是________．11. (’15江西)如图，在△ABC中，AB＝BC＝4，AO＝BO，P是射线CO上的一个动点，∠AOC＝60°，则当△P AB为直角三角形时，AP的长为________．12. 如图，在矩形ABCD中，AB＝12，BC＝8，点E是边BC上一动点，把△DCE沿DE折叠得△DFE，射线DF交直线CB于点P，当△AFD为等腰三角形时，DP的长为_____【答案】1. 1≤x≤3【解析】通过观察图形，可得当点E与点A重合时AP最小，则AP＝EP＝AD ＝1；当点P与点B重合时，AP最大，则AP＝3，∴1＜AP≤3，则x的取值范是1≤x≤3.2. 2【解析】由题意得：DF＝DB，∴点F在以D为圆心，BD为半径的圆上，作⊙D，连接AD交⊙D于点F，此时AF值最小；∵点D是边BC的中点，∴CD＝BD＝3；而AC＝4.由勾股定理得：AD2＝AC2＋CD2∴AD＝5，而FD＝3，∴F A＝5－3＝2，即线段AF长的最小值是2.3. 4≤EF≤5【解析】∵点M为BC的中点，正方形ABCD的边长为4，∴BM＝CM＝2，∵∠EMF＝90°，∴∠BME＋∠CMF＝90°，∵∠CFM＋∠CMF＝90°，∴∠BME＝∠CFM，又∵∠B＝∠C＝90°，∴△BME∽△CFM，∴BMCF＝BECM，∴BE·CF＝BM·CM＝2×2＝4，∵CF最大时为4，此时BE＝1，BE最大时为4，此时CF＝1，∴0≤|CF－BE|≤3，过点E 作EG⊥CD于点G，则EG＝BC＝4，在Rt△EFG中，EF2＝EG2＋FG2＝16＋(CF－BE)2，∴16≤EF2≤16＋9，∴4≤EF≤5.4. 12或32 【解析】根据题意可得△FDC 为直角三角形时分三种情况考虑：(1)如解图①，当∠FDC ＝90°时，DF ⊥AB ，在△AFD 中，∠A ＝60°，AD ＝2，∴AF ＝1，AP ＝12；(2)如解图②，当∠DCF ＝90°时，CF ⊥AB ，在△CFB 中，∠CBF ＝60°，BC ＝2，∴BF ＝1，AF ＝3，AP ＝32；(3)当∠DFC ＝90°，不存在．综上可知AP 的值为12或32.5. 2 【解析】如解图，作D 关于AE 的对称点D ′，则D ′落在对角线AC 上，过点D ′作 D ′P ′⊥AD 于点P ′，∴D ′P ′即为DQ ＋PQ 的最小值，∵DD ′⊥AE ，∴∠AFD ＝∠AFD ′，∵AF ＝AF ，∠DAF ＝∠D ′AF ，∴△DAF ≌△D ′AF ，∴AD ＝AD ′＝2，∵四边形ABCD 是正方形，∴∠DAD ′＝45°，∴AP ′＝P ′D ′，∴在Rt △AP ′D ′中，P ′D ′2＋AP ′2＝AD ′2， AD ′2＝4，∴P ′D ′＝2，即DQ ＋PQ 的最小值为 2.6. 32或94【解析】分两种情况进行讨论，设DE ＝x .ⅰ)D ′落在AC 上，如解图1，在Rt △ED ′C 中，EC ＝4－x ，D ′C ＝AC －AD ′＝5－3＝2，ED ′＝x ，根据ED ′2＋D ′C 2＝EC 2可得x 2＋22＝(4－x )2，解得x ＝32；ⅱ)D ′落在BD 上，如解图2，设DD ′交AE 于F 根据轴对称性质可知AE 垂直平分DD ′.在Rt △DF A 中，sin ∠ADF ＝AF AD ，∵sin ∠ADF ＝sin ∠ADB ＝AB BD ＝45，∴AF AD ＝45，又∵AD ＝3，∴AF ＝125，∴DF ＝95，又∵∠DEF ＝∠ADF ，∴sin ∠DEF ＝sin ∠ADF ＝45，∴DF DE ＝45，即95DE ＝45，∴DE ＝95×54＝94.综上DE 的长为32或94.7. 55或45 【解析】分两种情况讨论：(1)如解图①，过点G 作GH ⊥AD 于点H ，则四边形ABGH 为矩形，∴GH ＝AB ＝8，由图形折叠可知△BFG ≌ △EFG ，∴EG ＝BG ＝10，∠B ＝∠FEG ＝90°，∴EH ＝6，AE ＝4，∠AEF ＋∠HEG ＝90°，∵∠AEF ＋∠AFE ＝90°，∴∠HEG ＝∠AFE ，又∵∠A ＝∠EHG ＝90°，∴△EAF ∽△GHE ，∴EF EG ＝AE GH，∴EF ＝5，∴FG ＝102＋52＝55；(2)如解图②，由图形的折叠可知四边形ABGF ≌四边形HEGF ，∴BG ＝EG ，AB ＝EH ，∠BGF ＝∠EGF ，∵EF ∥BG ，∴∠BGF ＝∠EFG ，∴∠EFG ＝∠EGF ，∴EF ＝EG ，∴BG ＝EF ，∴四边形BGEF 为平行四边形，∵EF ＝EG ，∴平行四边形BGEF 为菱形，连接BE ，∴BE 、FG 互相垂直平分．在Rt △EFH 中，EF ＝BG ＝10，EH ＝AB ＝8，由勾股定理可得FH ＝AF ＝6，∴AE ＝AF ＋EF ＝16，∴BE ＝AE 2＋AB 2＝85，∴BO ＝45，∴OG ＝BG 2－BO 2＝25，∵四边形BGEF 为菱形，∴FG ＝2OG ＝4 5.8. 1227或352【解析】在Rt △ABC 中，∠ABC ＝90°，AC ＝10，BC ＝8，∴AB ＝102－82＝6，则AE ＝6，EC ＝AC －AE ＝10－6＝4；∵AB ＝AE ，∠BAD ＝∠EAD ，AD ＝AD ，∴△ABD ≌△AED ，∴BD ＝DE ，∠B ＝∠AED ＝90°，设BD ＝x ，则DE ＝x ，CD ＝8－x ，∴x 2＋42＝(8－x )2，解得：x ＝3，∴CD ＝5，DE ＝3.(1)如解图①，若沿∠DEC 的角平分线EG 折叠，使点C 落在ED 延长线上F 点处，过G 分别作GM ⊥EC ，GN ⊥EF ，垂足分别为M 、N .∴GN＝GM ，∵S △DEC ＝12×3×4＝6，S △DEG ＝12×3·GN ＝32GN ，S △CEG ＝12×4·GM ＝2GM ，∴2GM ＋32GN ＝6，即2GN ＋32GN ＝6，解得：GN ＝127，故EG ＝1227；(2)如解图②，若沿∠EDC 的角平分线DG 折叠，使点C 落在DE 延长线上F 点处．∴CG ＝FG ，DC ＝DF ＝5，∵DE＝3，∴EF ＝2，设CG ＝y ，则FG ＝y ，EG ＝4－y ，∴(4－y )2＋22＝y 2，解得：y ＝52，∴EG＝4－52＝32，∵DE ＝3，∴DG ＝（32）2＋32＝94＋9＝352. 9. 1或54或710【解析】本题考查三角形的折叠，等腰三角形的性质求线段的长．在Rt △ABC 中，AC ＝4，BC ＝3，由勾股定理得AB ＝AC 2＋BC 2＝5.由折叠性质得AE ＝EF ，在△BCF 中，当BF ＝BC 时，有BF ＝AB －AF ＝AB －2AE ＝3，则AE ＝1; 当BF ＝CF 时，过BC 中点作AC 的平行线，交AB 于点F ，此时F 点满足题意，且AF ＝BF ＝52，则AE ＝54；当CF ＝CB 时，如解图，过C 作CN ⊥AB 于点N .由等面积法得CN ＝AC ·BC AB ＝125.由△BCN ∽△BAC ，得BN BC ＝BC AB ，则BN ＝95.由等腰三角形三线合一性质得FN ＝BN ＝95，则AE ＝12AF ＝12(AB －BF )＝12×(5－185)＝710. 10. 2537＜CG ＜213 【解析】如解图所示，在Rt △ADC 中，AD ＝6，CD ＝4，∴AC ＝AD 2＋CD 2＝213，把∠A 沿EB 折叠，此时CG 最小，使点A 落在点G 处，连接AG ，DG ，∴∠EAG ＝∠EGA ，AE ＝EG ，∵AE ＝DE ，∴EG ＝ED ，∴∠ADG ＝∠EGD ，∴∠AGD ＝∠AGE ＋∠EGD ＝∠DAG ＋∠ADG ＝90°，∵AE ＝3，AB ＝4，∴BE ＝AE 2＋AB 2＝5，∵12AG ·BE ＝AE ·AB ，∴AG ＝245，在Rt △ADG 中，DG ＝AD 2－AG 2＝62－（245）2＝185，过G 点作MN ⊥AD ，∴∠AMG ＝∠AGD ＝90°，∵∠MAG ＝∠GAD ，∴△AMG ∽△AGD ，∴AM AG＝MG DG ＝AG AD ，即：AM 245＝MG 185＝2456，∴AM ＝9625，MG ＝7225，∵BN ＝AM ＝9625，MN ＝CD ＝4，∴CN ＝6－9625＝5425，GN ＝4－7225＝2825，在Rt △CNG 中，CG ＝CN 2＋GN 2＝2537.在Rt △ABC 中，AC ＝AB 2＋BC 2＝213，∴线段CG 的取值范围是2537＜CG ＜213.11. 2或23或27 【解析】由于点P 在射线CO 上运动，∴当△P AB 为直角三角形时，有三种情况：(1)当∠APB ＝90°时，①如解图①，当点P 在线段CO 上时，∵AB ＝BC ＝4，AO ＝BO ，∴AO ＝2，∴PO ＝AO ＝2，∵∠AOC ＝60°，∴△APO 是等边三角形，∴AP ＝AO ＝2；②如解图②所示，当点P 在CO 的延长线上时，∵AB ＝BC ＝4，AO ＝BO ，∠AOC ＝60°，∴OP ＝OA ＝OB ＝2，∵∠POB ＝∠AOC ＝60°，∴△POB 是等边三角形，即PB ＝OB ＝2，∴AP ＝AB 2－PB 2＝42－22＝23；(2)当∠ABP ＝90°时，如解图③所示，∵AB ＝BC ＝4，AO ＝BO ，∴AO ＝BO ＝2，又∵∠BOP ＝∠AOC ＝60°，∠ABP ＝90°，∴BP ＝23，在Rt △APB 中，AP ＝AB 2＋PB 2＝42＋（23）2＝27；∴AP 的长度为2或23或27.12. 92或4877【解析】∵四边形ABCD 是矩形，∴AD ＝BC ＝8，AB ＝DC ＝12，AD ∥BC ，∠C ＝90°.∵把△DCE 沿DE 折叠得△DFE ，∴DC ＝DF ＝12.∵AD ≠DF ，∴△AFD 为等腰三角形只有两种情况： (1)当AF ＝FD ＝12时，如解图①，过点F 作FM ⊥AD于点M ，∴AM ＝MD ＝4，在Rt △MDF 中，由勾股定理，得MF ＝122－42＝82，∵AD ∥BC ，∴∠MDF ＝∠DPC .∵∠DMF ＝∠C ＝90°，∴△MDF ∽△CPD ，∴MF CD ＝FD PD ，即：8212＝12PD，解得PD ＝92； (2)当AD ＝AF ＝8时，如解图②，DF 的延长线交CB 的延长线于点P ，过点A 作AN ⊥DF 于点N, ∴FN ＝ND ＝6，在Rt △AND 中，由勾股定理，得AN ＝82－62＝27，∵AD ∥BC ，∴∠ADN ＝∠DPC ，∵∠AND ＝∠C ＝90°， ∴△AND ∽△DCP ，∴AN CD ＝AD PD ，即：2712＝8PD ，解得PD ＝4877.综上所述，DP 的长为92或4877。

矩形折叠问题及动点问题精讲

A
O
F
D
C
E
B
F
C
ห้องสมุดไป่ตู้
新知探究
一、矩形折叠问题
例1、如图，在矩形纸片ABCD中，AB=6cm，BC=8cm，将矩形纸片折叠，使点C与点A重合. (3)四边形AFCE是什么四边形？说明理由．答：四边形AFCE是菱形． A 理由：∵四边形ABCD是矩形， ∴AD∥BC，OD＝OB，OA＝OC， ∴∠EDO＝∠CBO ∵∠BOF＝∠DOE B ∴△BOF≌△DOE ∴OE＝OF ∵OA＝OC ∴四边形AFCE是平行四边形，由对折可得EF⊥AC ∴四边形AFCE是菱形．
设DF=x，由折叠的性质得 10 EF=FC=6－x，DE=AD－AE=2，在Rt△DEF中，由勾股定理得DE2+DF2=EF2，即22＋x2=(6－x)2，
6-x
8 解得DF=x= 3 .
自主练习
一、矩形折叠问题
3、如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，则AM的长是（） x 9-x A．1.5 B．2 C．2.25 D．2.5 6 9 析解：如图，连结MB，MB′，由折叠的性质可知MB＝MB′， 3 设AM=x，在Rt△ABM中，BM2=AB2+AM2，在Rt△MDB′中，B′M2=MD2+DB′2， ∴AB2+AM2=MD2+DB′2，即92＋x2=(9－x)2＋(9－3)2，解得x=2，即AM=2．
∴DQ=CP 即 16－t＝21－2t 2t 解得 t=5 21-2t ∴当 t=5秒时，四边形PQDC是平行四边形
自主练习
二、特殊四边形动点问题

中考复习讲义：图形折叠中的动点问题及几何动态问题解题新策略

中考热点Ⅰ：图形折叠中的动点问题一、问题导读折叠类综合问题，题型多样、变化灵活、知识点多，蕴含丰富数学思想方法。

折叠类综合问题不仅能是考查学生空间想象能力与动手操作能力的实践操作题，而基于折叠操作的动点问题，常常是近年来各省市中考数学选填空题压轴题，甚至解答题中出现不少，操作+动点加重学生的思维容量，学生在解答时往往顾此失彼，患得患失，给学生造成很大麻烦，复习应加强这方面学习思考及巩固练习，解决折叠问题时，首先要对图形折叠有一准确定位，把握折叠的实质，抓住图形之间最本质的位置关系，从点、线、面三个方面入手，发现其中变化的和不变的量。

应注意的事一般要根据点的运动和图形的变化过程，对其不同情况进行分类求解二、典例精析类型一:折叠成特殊三角形的动点问题例1(2018·河南中考题)如图，∠MAN＝90°，点C在边AM上，AC＝4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E.当△A′EF为直角三角形时，AB的长为________．【分析】当△A′EF为直角三角形时，存在两种情况：①∠A′EF＝90°，②∠A′FE＝90°进行讨论．【解答】当△A′EF为直角三角形时，存在两种情况：①当∠A′EF＝90°时，如解图①，∵△A′BC与△ABC关于BC所在直线对称，∴A′C＝AC＝4，∠ACB＝∠A′CB.∵点D，E分别为AC，BC的中点，∴D、E是△ABC的中位线，∴DE∥AB，∴∠CDE＝∠MAN＝90°，∴∠CDE＝∠A′EF，∴AC∥A′E，∴∠ACB＝∠A′EC，∴∠A′CB＝∠A′EC，∴A′C＝A′E＝4.在Rt△A′CB中，∵E是斜边BC的中点，∴BC＝2A′E＝8，由勾股定理，得AB ＝BC －AC ，∴AB＝4√3；②当∠A′FE＝90°时，如解图②，∵∠ADF＝∠A＝∠DFB＝90°.∴∠ABF＝90°，∵△A′BC与△ABC关于BC所在直线对称，∴∠ABC＝∠CBA′＝45°，∴△ABC是等腰直角三角形，∴AB＝AC＝4；综上所述，AB的长为4√3或4.方法归纳：解决这类综合问题，我们要学会由于动点进一步发现图形中的数量关系的是否具有多样性；其次要把握折叠的变化规律，充分挖掘图形的几何性质，将其中的基本的数量关系用方程的形式表达出来，运用所学知识合理、有序、全面的解决问题类型二：点的位置不确定例2.如图，已知AD∥BC，AB⊥BC，AB＝3，点E为射线BC上一个动点，连接AE，将△ABE 沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于点M，N.当点B′为线段MN的三等分点时，BE的长为________．【分析】根据勾股定理，可得EB′，根据相似三角形的性质，可得EN的长，根据勾股定理，可得答案．【解答】由翻折的性质，得AB＝AB′，BE＝B′E.方法归纳：这类不但考察学生对基本几何图形性质的掌握情况，而且可以培养学生的空间思维能力和运动变化观念，提高学生的实践操作水平。

初三复习数学几何中折叠问题 4大类分类含答案

初中数学中的折叠问题折叠问题（对称问题）是近几年来中考出现频率较高的一类题型，学生往往由于对折叠的实质理解不够透彻，导致对这类中档问题失分严重。

本文试图通过对在初中数学中经常涉及到的几种折叠的典型问题的剖析，从中抽象出基本图形的基本规律，找到解决这类问题的常规方法。

其实对于折叠问题，我们要明白：1、折叠问题（翻折变换）实质上就是轴对称变换．2、折叠是一种对称变换，它属于轴对称．对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3、对于折叠较为复杂的问题可以实际操作图形的折叠，在画图时，画出折叠前后的图形，这样便于找到图形之间的数量关系和位置关系．4、在矩形（纸片）折叠问题中，重合部分一般会是一个以折痕为底边的等腰三角形5、利用折叠所得到的直角和相等的边或角，设要求的线段长为x，然后根据轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求解．一、矩形中的折叠1．将一张长方形纸片按如图的方式折叠，其中BC，BD为折痕，折叠后BG和BH在同一条直线上，∠CBD= 度．BC、BD是折痕，所以有∠ABC = ∠GBC，∠EBD = ∠HBD则∠CBD = 90°折叠前后的对应角相等2．如图所示，一张矩形纸片沿BC折叠，顶点A落在点A′处，再过点A′折叠使折痕DE∥BC，若AB=4，AC=3，则△ADE的面积是．沿BC折叠，顶点落在点A’处，根据对称的性质得到BC垂直平分AA’，即AF = 12AA’，又DE∥BC，得到△ABC ∽△ADE，再根据相似三角形的面积比等于相似比的平方即可求出三角形ADE的面积= 24对称轴垂直平分对应点的连线3．如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线BD 重合，得折痕DG ，求AG 的长．由勾股定理可得BD = 5，由对称的性质得△ADG ≌ △A ’DG ，由A ’D = AD = 3，AG ’ = AG ，则A ’B = 5 – 3 = 2，在Rt △A ’BG 中根据勾股定理，列方程可以求出AG 的值根据对称的性质得到相等的对应边和对应角，再在直角三角形中根据勾股定理列方程求解即可4．把矩形纸片ABCD 沿BE 折叠，使得BA 边与BC 重合，然后再沿着BF 折叠，使得折痕BE 也与BC 边重合，展开后如图所示，则∠DFB 等于（）根据对称的性质得到∠ABE=∠CBE ，∠EBF=∠CBF ，据此即可求出∠FBC 的度数，又知道∠C=90°，根据三角形外角的定义即可求出∠DFB = 112.5°注意折叠前后角的对应关系5．如图，沿矩形ABCD 的对角线BD 折叠，点C 落在点E 的位置，已知BC=8cm ，AB=6cm ，求折叠后重合部分的面积． ∵点C 与点E 关于直线BD 对称，∴∠1 = ∠2 ∵AD ∥BC ，∴∠1 = ∠3∴∠2 = ∠3 ∴FB = FD设FD = x ，则FB = x ，FA = 8 – x在Rt △BAF 中，BA 2 + AF 2 = BF 2∴62 + (8 - x)2 = x 2 解得x = 254所以，阴影部分的面积S △FBD = 12 FD ×AB = 12 ×254 ×6 = 754cm2重合部分是以折痕为底边的等腰三角形6．将一张矩形纸条ABCD 按如图所示折叠，若折叠角∠FEC=64°，则∠1= 度；△EFG 的形状三角形．∵四边形CDFE 与四边形C ’D ’FE 关于直线EF 对称∴∠2 = ∠3 = 64°∴∠4 = 180° - 2 × 64° = 52° ∵AD ∥BC321F E D C B A54132G D‘FC‘DAGA'CA B D∴∠1 = ∠4 = 52°∠2 = ∠5又∵∠2 = ∠3∴∠3 = ∠5∴GE = GF∴△EFG是等腰三角形对折前后图形的位置变化，但形状、大小不变，注意一般情况下要画出对折前后的图形，便于寻找对折前后图形之间的关系，注意以折痕为底边的等腰△GEF7．如图，将矩形纸片ABCD按如下的顺序进行折叠：对折，展平，得折痕EF（如图①）；延CG折叠，使点B落在EF上的点B′处，（如图②）；展平，得折痕GC（如图③）；沿GH折叠，使点C落在DH上的点C′处，（如图④）；沿GC′折叠（如图⑤）；展平，得折痕GC′，GH（如图⑥）．（1）求图②中∠BCB′的大小；（2）图⑥中的△GCC′是正三角形吗？请说明理由．（1）由对称的性质可知：B’C=BC，然后在Rt△B′FC中，求得cos∠B’CF= 12，利用特殊角的三角函数值的知识即可求得∠BCB’= 60°；（2）首先根据题意得：GC平分∠BCB’，即可求得∠GCC’= 60°，然后由对称的性质知：GH是线段CC’的对称轴，可得GC’= GC，即可得△GCC’是正三角形．理清在每一个折叠过程中的变与不变8．如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为四边形BCFE与四边形B′C′FE关于直线EF对称，则①②③④这四个三角形的周长之和等于正方形ABCD的周长折叠前后对应边相等9．如图，将边长为4的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，求四边形BCFE的面积设AE = x，则BE = GE = 4 - x，在Rt△AEG中，根据勾股定理有：AE2 + AG2 = GE2即：x2 + 4 = (4 - x)2解得x = 1.5，BE = EG = 4 – 1.5 = 2.5∵∠1 + ∠2 = 90°，∠2 + ∠3 = 90°∴∠1 = ∠3又∵∠A = ∠D = 90°∴△AEG ∽△DGP∴AEDG=EGGP，则1.52=2.5GP，解得GP =103PH = GH – GP = 4 - 103=23∵∠3 = ∠4，tan∠3 = tan∠1 = 3 4∴tan∠4 = 34，FHPH=34，FH =34×PH =34×23=12∴CF = FH = 1 2∴S梯形BCFE = 12(12+52)×4 = 6注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等10．如图，将一个边长为1的正方形纸片ABCD折叠，使点B落在边AD上不与A、D 重合．MN为折痕，折叠后B’C’与DN交于P．(1)连接BB’，那么BB’与MN的长度相等吗？为什么？(2)设BM=y，AB’=x，求y与x的函数关系式；(3)猜想当B点落在什么位置上时，折叠起来的梯形MNC’B’面积最小？并验证你的猜想．(1)BB’ = MN过点N作NH∥BC交AB于点H），证△ABB’≌△HNM(2)MB’ = MB = y，AM = 1 – y，AB’ = x在Rt△ABB’中BB’ = AB2 + AB'2= 1 + x2因为点B与点B’关于MN对称，所以BQ = B’Q，则BQ = 12 1 + x2由△BMQ∽△BB’A得BM×BA = BQ×BB’PC'NB CA DMB'QPHC'NB CA DMB'∴y = 12 1 + x2× 1 + x2=12(1 + x2)(3) 梯形MNC′B′的面积与梯形MNCB的面积相等由(1)可知，HM = AB’ = x，BH = BM – HM = y – x，则CN = y - x∴梯形MNCB的面积为：12(y – x + y) ×1 = 12(2y - x)= 12(2×12(1 + x2) – x)= 12(x -12)2 +38当x = 12时，即B点落在AD的中点时，梯形MNC’B’的面积有最小值，且最小值是38二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）∵∠α= ∠1，∠2 = ∠1∴∠α= ∠2∴2∠α+∠ABE=180°，即2∠α+30°=180°，解得∠α=75°．题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB是以折痕AB为底的等腰三角形12．如图，将一宽为2cm的纸条，沿BC，使∠CAB=45°，则后重合部分的面积为作CD⊥AB，∵CE∥AB，∴∠1=∠2，根据翻折不变性，∠1=∠BCA，故∠2=∠BCA．∴AB=AC．又∵∠CAB=45°，∴在Rt△ADC中，AC = 2 2 ，AB = 2 2S△ＡＢＣ＝12AB×CD = 2 2a2130°BEFACD在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm 的长方形纸条成如图所示的形状，那么折痕PQ 的长是如图，作QH ⊥PA ，垂足为H ，则QH=2cm ，由平行线的性质，得∠DPA=∠PAQ=60° 由折叠的性质，得∠DPA =∠PAQ ， ∴∠APQ=60°，又∵∠PAQ=∠APQ=60°， ∴△APQ 为等边三角形，在Rt △PQH 中，sin ∠HPQ = HQPQ∴32 = 2PQ ，则PQ = 433注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQ14．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（）图c 图b图aCDGFEC GDFEFBCAEBB∵AD ∥BC ，∴∠DEF=∠EFB=20°，在图b 中，GE = GF ，∠GFC=180°-2∠EFG=140°，在图c 中∠CFE=∠GFC-∠EFG=120°，本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b ∠GFC=140°，图c 中的∠CFE=∠GFC-∠EFG15．将一张长为70 cm 的长方形纸片ABCD ，沿对称轴EF 折叠成如图的形状，若折叠后，AB 与CD 间的距离为60cm ，则原纸片的宽AB 是（）设AB=xcm ．右图中，AF = CE = 35，EF = x根据轴对称图形的性质，得AE=CF=35-x （cm ）．则有2（35-x ）+x=60， x=10．16．一根30cm 、宽3cm 的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P 的长度相等，则最初折叠时，求MA 的长将折叠这条展开如图，根据折叠的性质可知，两个梯形的上底等于纸条宽，即3cm ，下底等于纸条宽的2倍，即6cm ，两个三角形都为等腰直角三角形，斜边为纸条宽的2倍，即6cm ，故超出点P 的长度为（30-15）÷2=7.5， AM=7.5+6=13.5GEFD AE FD B C A B C 60cm三、三角形中的折叠17．如图，把Rt △ABC （∠C=90°），使A ，B 两点重合，得到折痕ED ，再沿BE 折叠，C 点恰好与D 点重合，则CE ：AE=18．在△ABC 中，已知AB=2a ，∠A=30°，CD 是AB 边的中线，若将△ABC 沿CD 对折起来，折叠后两个小△ACD 与△BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的14 ．（1）当中线CD 等于a 时，重叠部分的面积等于；（2）有如下结论（不在“CD 等于a ”的限制条件下）：①AC 边的长可以等于a ；②折叠前的△ABC 的面积可以等于32a 2；③折叠后，以A 、B 为端点的线段AB 与中线CD 平行且相等．其中，结论正确（把你认为正确结论的代号都填上，若认为都不正确填“无”）． (1)∵CD = 12 AB∴∠ACB = 90°∵AB = 2a ，BC = a ，∴AC = 3a ∴S △ABC = 12 ×AC ×BC = 32a 2∴重叠部分的面积为：14×32a 2 = 38a 2(2)若AC = a ，如右图∵AD = a ，∴∠2 = 180°- 30°2 = 75°∠BDC = 180°- 75°= 105° ∴∠B'DC = 105°∴∠3 = 105°- 75°= 30° ∴∠1 = ∠3 ∴AC ∥B'D∴四边形AB'DC 是平行四边形∴重叠部分△CDE 的面积等于△ＡＢＣ的面积的14若折叠前△ABC 的面积等于32a 2 过点C 作CH ⊥AB 于点H ，则 12 ×AB ×CH = 32a 2 B'CDAB231EB'CDBACH =32a 又tan ∠1 =CH AH∴AH = 32a∴BH = 12a则tan ∠B =CHBH，得∠B = 60° ∴△CBD 是等边三角形 ∴∠2 = ∠4∴∠3 = ∠4，AD ∥CB 2又CB 2 = BC = BD = a ，∴CB 2 = AD ∴四边形ADCB 2是平行四边形则重叠部分△CDE 的面积是△ABC 面积的14(3)如右图，由对称的性质得，∠3 = ∠4，DA = DB 3 ∴∠1 = ∠2又∵∠3 + ∠4 = ∠1 +∠2 ∴∠4 = ∠1 ∴AB 3∥CD注意“角平分线+等腰三角形”的基本构图，折叠前后图形之间的对比，找出相等的对应角和对应边19．在△ABC 中，已知∠A=80°，∠C=30°，现把△CDE 沿DE 进行不同的折叠得△C ′DE ，对折叠后产生的夹角进行探究：（1）如图（1）把△CDE 沿DE 折叠在四边形ADEB 内，则求∠1+∠2的和；（2）如图（2）把△CDE 沿DE 折叠覆盖∠A ，则求∠1+∠2的和；（3）如图（3）把△CDE 沿DE 斜向上折叠，探求∠1、∠2、∠C 的关系．（1）根据折叠前后的图象全等可知，∠1=180°-2∠CDE ，∠2=180°-2∠CED ，再根据三角形内角和定理比可求出答案；（2）连接DG ，将∠ADG+∠AGD 作为一个整体，根据三角形内角和定理来求；3241EHB 2DABC3412B 3DA BC在第一次折叠中可得到∠EAD = ∠FAD在第二次折叠中可得到EF是AD的垂直平分线，则AD⊥EF∴∠AEF = ∠AFE∴△AEF是等腰三角形(1)由折叠可知∠AEB = ∠FEB，∠DEG = ∠BEG而∠BEG = 45°+ ∠α因为∠AEB + ∠BEG + ∠DEG = 180°所以 45°+ 2（45°+∠α）= 180°∠α = 22.5°由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

2020年中考数学动态问题-折叠中有关计算题型(含答案)

专题04 动点折叠类问题中有关计算题型一、基础知识点综述动点型问题是指题设中的图形中存在一个或多个动点，它们在线段、射线、直线、抛物线、双曲线、弧线等上运动的一类非常具有开放性的题目. 而从其中延伸出的折叠问题，更能体现其解题核心——动中求静，灵活运用相关数学知识进行解答，有时需要借助或构造一些数学模型来解答.实行新课标以来，各省（市）的中考数学试卷都会有此类题目，这些题目往往出现在选择、填空题的压轴部分，题型繁多，题意新颖，具有创新力. 其主要考查的是学生的分析问题及解决问题的能力.要求学生具备：运动观点；方程思想；数形结合思想；分类讨论思想；转化思想等等.通过研究历年中考真题并结合2019年各省（市）的中考真题，特总结出此专题. 期望能给各位老师及同学以学习教学一些启发，一些指引，培养出学生的解题素养.下面我们从几个例题中展开论述，逐层拨开它的神秘面纱.二、精品例题解析题型一：图形折叠中的计算例1.（2019·青岛）如图，在正方形纸片ABCD 中，E 是CD 的中点，将正方形纸片折叠，点B 落在线段AE 上的点G 处，折痕为AF ．若AD＝4 cm，则CF 的长为cm ．例2. 如图，矩形ABCD中，AB=36BC=12，E为AD的中点，F为AB上一点，将△AEF沿EF折叠后，点A恰好落在CF上的点G处，则折痕EF的长是例3.（2019·连云港）如图，在矩形ABCD中，AD＝22AB．将矩形ABCD对折，得到折痕MN；沿着CM折叠，点D的对应点为E，ME与BC的交点为F；再沿着MP折叠，使得AM与EM重合，折痕为MP，此时点B的对应点为G．下列结论：①△CMP是直角三角形；②点C、E、G不在同一条直线上；③PC＝62MP；④BP＝22AB；⑤点F是△CMP外接圆的圆心，其中正确的个数为（）A．2个B．3个C．4个D．5个例4.（2019·潍坊）如图，在矩形ABCD中，AD=2，将∠A向内折叠，点A落在BC上，记为A’，折痕为DE. 若将∠B沿EA’向内折叠，点B恰好落在DE上，记为B’，则AB=例5.（2019·天津）如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE,折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上. 若DE=5，则GE的长为例6.（2019·南充）如图，正方形MNCB 在宽为2的矩形纸片一端，对折正方形MNCB 得到折痕AE ，再翻折纸片，使AB 与AD 重合.以下结论错误的是（） A.52102+=AH B.215-=BC CD C.EH CD BC ⋅=2 D.515sin +=∠AHD例7.（2019·金华）如图，将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线减去一个角，展开铺平后得到图⑤，其中FM ，GN 是折痕，若正方形EFGH 与五边形MCNGF 面积相等，则FMGF 的值是（）A. 522B. 21-C. 12D. 22例8.（2019·重庆）如图，在△ABC 中，D 是AC 边上的中点，连结BD ，把△BDC 沿BD 翻折，得到△BDC'，DC ’与AB 交于点A ’，连结AC'，若AD =AC ’=2，BD =3，则点D 到BC 的距离为（）A ．233B ．7213C ．7D ．13例9.（2019·重庆）如图，在△ABC 中，∠ABC=45°，AB=3，AD ⊥BC 于点D ，BE ⊥AC 于点E ，AE=1. 连接DE ，将△ADE 沿直线AE 翻折至△ABC 所在的平面内，得△AEF ，连接DF ，过点D 作DG ⊥DE 交BE 于点G. 则四边形DFEG 的周长为（） A. 8 B. 42 C. 224+ D. 322+题型二：图形折叠中证明、计算题例10.（2019·滨州）如图，矩形ABCD 中，点E 在边CD 上，将△BCE 沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作FG ∥CD 交BE 于点G ，连接CG.（1）求证：四边形CEFG 是菱形；（2）若AB=6，AD=10，求四边形CEFG 的面积.二、精品例题解析题型一：图形折叠中的计算例1.（2019·青岛）如图，在正方形纸片 ABCD 中， E 是 CD 的中点，将正方形纸片折叠，点 B 落在线段AE 上的点 G 处，折痕为 AF ．若 AD ＝4 cm ，则 CF 的长为 cm ．【答案】625-【分析】要求CF 的长，观察图形，发现CF 在Rt △CEF 中，想到用勾股定理求解，然而EF 的长度是未知的，求解难度较大；再观察图形，发现CF=BC －BF ，只要求出BF 长度即可，而BF=GF ，进而想到利用面积法来求解，设CF=x ，BF=GF=4－x ，列方程求解x 即可.【解析】解：∵四边形ABCD 是正方形，∴AD=CD=BC=4，∠C=∠D=90°，设CF=x ，由折叠知：BF=GF=4－x ，∵E 是CD 中点，∴DE=2，在Rt △ADE 中，由勾股定理得：AE=5ADE ABF AEF CEF ABCD S S S S S =+++△△△△正方形即：()()111116424425422222x x x =⨯⨯+⨯⨯-+⨯-+⨯⨯ 解得：x=65-，故答案为：65-. 例2. 如图，矩形ABCD 中，AB=36BC=12，E 为AD 的中点，F 为AB 上一点，将△AEF 沿EF折叠后，点A 恰好落在CF 上的点G 处，则折痕EF 的长是【分析】EF 在Rt △AEF 中，求出AF 的长即可利用勾股定理求解折痕EF 的长度；连接CE ，可证△CEG ≌△CED ，得EF ⊥CE ，设AF=x ，利用CF 2=BF 2+BC 2，CF 2=EF 2+CE 2，列出方程求解AF 的长. 【答案】215.【解析】解：∵E 是AD 的中点，∴AE=ED ，由折叠知：AE=EG ，∴EG=DE,连接CE ，在Rt △CDE 和Rt △CDG 中，CE=CE ，EG=AE=DE∴Rt △CDE ≌Rt △CDG∴∠GEC=∠DEC ，∴∠FEC=90°，设AF=x ，则BF=36x ，BC=AD=12，在Rt △EFC 和Rt △BFC 中，由勾股定理得：222222AE AF DE CD BF BC +++=+即：(()22222266363612x x +++=-+，解得：x=26， ∴()22626215+=故：答案为215.例3.（2019·连云港）如图，在矩形ABCD中，AD＝22AB．将矩形ABCD对折，得到折痕MN；沿着CM折叠，点D的对应点为E，ME与BC的交点为F；再沿着MP折叠，使得AM与EM重合，折痕为MP，此时点B的对应点为G．下列结论：①△CMP是直角三角形；②点C、E、G不在同一条直线上；③PC＝6MP；④BP＝2AB；⑤点F是△CMP外接圆的圆心，其中正确的个数为（）A．2个B．3个C．4个D．5个【答案】B.【解析】解：由折叠性质知：∠DMC＝∠EMC，∠AMP＝∠EMP，∵∠AMD＝180°，∴∠PME+∠CME＝12×180°＝90°，∴△CMP是直角三角形；故①正确；由折叠知：∠D＝∠MEC＝90°，∠MEG＝∠A＝90°，∴∠GEC＝180°，即点C、E、G在同一条直线上，故②错误；∵AD＝2，设AB＝x，则AD＝2，由折叠知：DM＝12AD2x，由勾股定理得：CM3x，∵∠PMC ＝90°，MN ⊥PC ，∴△CMN ∽△CPM ，∴CM 2＝CN •CP ，∴CP 22x =，∴PN ＝CP ﹣CN ＝2x ，由勾股定理得：PM x ，∴PC PM=即PC MP ，故③错误；PB x ，AB PB=∴PB ＝2AB ，故④正确，由折叠知：CD ＝CE ，EG ＝AB ，AB ＝CD ，∴CE ＝EG ，∵∠CEM ＝∠G ＝90°，∴FE ∥PG ，∴CF ＝PF ，∵∠PMC ＝90°，∴CF ＝PF ＝MF ，∴点F 是△CMP 外接圆的圆心，故⑤正确；故答案为：B ．例4.（2019·潍坊）如图，在矩形ABCD 中，AD=2，将∠A 向内折叠，点A 落在BC 上，记为A ’，折痕为DE. 若将∠B 沿EA ’向内折叠，点B 恰好落在DE 上，记为B ’，则AB=【答案】232 33+.【解析】解：由折叠知：∠AED=∠DEA’=∠BEA’，而∠AED+∠DEA’+∠BEA’=180°，∴∠AED=∠DEA’=∠BEA’=60°，∴∠EDA=∠EDA’=∠CDA’=30°,∵AD=2，∴A’E=AE=323 33AD=，∴BE=32'33A E=,即AB=AE+BE=2323+.例5.（2019·天津）如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE,折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上. 若DE=5，则GE的长为【答案】49 13.【解析】解：∵四边形ABCD 是正方形，∴∠D=∠DAB=90°，AD=AB ，由折叠性质知：AE ⊥BF ，∴∠DAE+∠BAE=∠ABF+∠BAE=90°，即∠DAE=∠ABF ，∴△ADE ≌△BAF ，∴AF=DE=5，由勾股定理得：AE=BF=13，∴AG=2×51213⨯=12013， ∴GE=AE －AG=4913. 故答案为：4913. 例6.（2019·南充）如图，正方形MNCB 在宽为2的矩形纸片一端，对折正方形MNCB 得到折痕AE ，再翻折纸片，使AB 与AD 重合.以下结论错误的是（） A.52102+=AH B.215-=BC CD C.EH CD BC ⋅=2 D.515sin +=∠AHD【答案】D.【解析】解：由折叠知：四边形BADH 为菱形，∴EH=BE+BH在Rt △ABE 中，由勾股定理得：225BE AE +=∴5，5，在Rt △AEH 中，由勾股定理，得：AH 2=()2222512=1025EH AE +=+++，故A 正确；CD=AD －AC=5－1，BC=2，∴51CD BC -=，故B 正确； BC 2=4，CD ×EH=（5－1）×（5+1）=4，故C 正确；∵∠AHD=∠AHE ，∴515sin sin +≠=∠=∠AH AE AHE AHD 故D 错误，即答案为D.例7.（2019·金华）如图，将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线减去一个角，展开铺平后得到图⑤，其中FM ，GN 是折痕，若正方形EFGH 与五边形MCNGF 面积相等，则FMGF 的值是（）A. 52-B. 21C. 12D. 22【答案】A.【解析】解：设正方形ABCD 的边长为a ，连接HF ，GE 交于点O ，则GE ⊥HF ，∠GFH=45°，∴2, 由题意知：正方形EFGH 、与其它四个五边形的面积均相等，∴正方形EFGE 面积为：25a ，即GF=55a ， ∴FO=2251022GF a a =⨯= FM=OM －FO=102a a - ∴105221025a a FM GF a --==，故答案为A.例8.（2019·重庆）如图，在△ABC 中，D 是AC 边上的中点，连结BD ，把△BDC 沿BD 翻折，得到△BDC'，DC ’与AB 交于点A ’，连结AC'，若AD =AC ’=2，BD =3，则点D 到BC 的距离为（）A ．233 B ．7213 C ．7 D ．13【答案】B.【解析】解：如图，连接CC ’，交BD 于M ，过D 作DH ⊥BC ’于H ，∵AD=AC ’=2，AD=CD=2，由翻折知：CD=DC ’=2，∠DBC=∠BDC ’，∴△ADC ’为等边三角形，DH 即为所求，∴∠ACC ’=∠DC ’C=30°，∴DM=1，C ’M= 3 ∵BD=3， ∴BM=BD －DM=2，在Rt △BMC ’中，由勾股定理得：BC ’= 22'7C M BM +=,∵'11''22BC D S BD MC BC DF =⋅=⋅△ ∴DH=3217，故答案为：B.例9.（2019·重庆）如图，在△ABC 中，∠ABC=45°，AB=3，AD ⊥BC 于点D ，BE ⊥AC 于点E ，AE=1. 连接DE ，将△ADE 沿直线AE 翻折至△ABC 所在的平面内，得△AEF ，连接DF ，过点D 作DG ⊥DE 交BE 于点G. 则四边形DFEG 的周长为（） A. 8 B. 42 C. 224+ D. 322+【答案】B.【解析】解：∵∠ABC ＝45°，AD ⊥BC 于点D ，∴∠BAD ＝90°﹣∠ABC ＝45°，∴△ABD 是等腰直角三角形，∴AD ＝BD ，∴∠GBD+∠C ＝90°，∵∠EAD+∠C ＝90°，∴∠GBD ＝∠EAD ，∵∠ADB ＝∠EDG ＝90°，∴∠ADB ﹣∠ADG ＝∠EDG ﹣∠ADG ，即∠BDG ＝∠ADE ，∴△BDG ≌△ADE ，∴BG ＝AE ＝1，DG ＝DE ，∵∠EDG ＝90°，∴△EDG 为等腰直角三角形，∴∠AED ＝∠AEB+∠DEG ＝90°+45°＝135°，∵△AED 沿直线AE 翻折得△AEF ，∴△AED ≌△AEF ，∴∠AED ＝∠AEF ＝135°，ED ＝EF ，∴∠DEF ＝360°﹣∠AED ﹣∠AEF ＝90°，∴△DEF 为等腰直角三角形，∴EF ＝DE ＝DG ，在Rt △AEB 中，由勾股定理得：BE ＝，∴GE ＝BE ﹣BG ＝﹣1，在Rt △DGE 中，DG ＝DE=2GE ＝2﹣2，∴EF ＝DE ＝2﹣2，在Rt △DEF 中，DF ＝DE ＝﹣1，∴四边形DFEG 的周长为：GD+EF+GE+DF ＝2（2）+2（1）＝+2，题型二：图形折叠中证明、计算题例10.（2019·滨州）如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG.（1）求证：四边形CEFG是菱形；（2）若AB=6，AD=10，求四边形CEFG的面积.【分析】（1）由翻折性质并借助全等三角形的性质和菱形的判定方法证明结论成立；（2）由勾股定理，可以求得AF的长，并求得EF和DF的值，从而可以得到四边形CEFG的面积．【答案】见解析.【解析】（1）证明：由题意可得：△BCE≌△BFE，∴∠BEC＝∠BEF，FE＝CE，∵FG∥CE，∴∠FGE＝∠CEB，∴∠FGE＝∠FEG，∴FG＝FE，专题04 动点折叠类问题中有关计算题型∴FG＝EC，∴四边形CEFG是平行四边形，又∵CE＝FE，∴四边形CEFG是菱形；（2）∵矩形ABCD中，AB＝6，AD＝10，BC＝BF，∴∠BAF＝90°，AD＝BC＝BF＝10，∴AF＝8，∴DF＝2，设EF＝x，则CE＝x，DE＝6﹣x，在Rt△FDE中，由勾股定理得：22+（6﹣x）2＝x2，解得，x＝10 3，即CE＝10 3，∴四边形CEFG的面积是：CE•DF＝103×2＝203．。

中考数学专题题型讲练过关题型04 几何图形的折叠与动点问题

1.如图,等边三角形ABC的边长为2,D,E分别是边AB,AC上的点,沿DE所在的直线折叠∠A,使点A的对应点P始终落在边BC上,若△BDP是直角三角形,则AD的长为.(第1题)(第2题)2.[2018周口地区模拟]如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5,D是BC上一动点(点D不与点B,C重合),连接AD,将△ACD沿AD折叠,点C落在点E处,DE交AB于点F,当△DEB是直角三角形时,DF的长为.3.[2018新乡一模]如图,菱形ABCD的边长是4,∠DAB=60°,点M,N分别在边AD,AB上,且MN⊥AC,垂足为点P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP 的长为.4.[2018郑州外国语三模]如图,已知在等腰三角形ABC中,AB=AC=,BC=4,点D从点A出发,以每秒个单位长度的速度向点B运动,同时点E从点B出发,以每秒4个单位长度的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F.设运动时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为.5.[2017郑州适应性]如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为点C,把△ACP沿AP翻折180°,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为.6.[2017郑州八中三模]如图,在Rt△ABC中,AB=3,BC=4,点P是射线BC上一个动点,连接AP,将△ABP沿AP折叠,当点B的对应点B'落在BC的垂直平分线上时,则BP的长为.7.[2017许昌二模]如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A'处.点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA'上的点D'处.当点D'落在BC边上时,AE的长为.8.[2018信阳二模]在矩形纸片ABCD中,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线分别交边CD,AB于点E,F,则EF的长为.9.[2018平顶山二模]如图,已知矩形ABCD,AB=2,AD=6,点E,F分别是线段AD,BC上的点,且四边形ABFE是正方形,若点G是线段AD上的动点,连接FG,将矩形沿FG折叠,使得点C的对应点P落在正方形ABFE的对角线所在的直线上,则线段AP的长为.10.[2018许昌一模]如图,矩形纸片ABCD中,AB=3,AD=5,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形的边交于E,F两点,要使折痕始终与边AB,AD有交点,BP 的取值范围是.11.[2017平顶山二模]如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x.现将纸片折叠,使点D与点P重合,得折痕EF(点E,F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是.12.如图,已知矩形ABCD中,AB=4,BC=2,点M,E在边AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的值最小时,ME的长度为.13.[2019原创]如图,矩形ABCD中,AB=4,AD=9,点E,F分别是BC,AD上的动点,∠FEC为钝角,沿直线EF翻折矩形,点C,D的对应点分别为C',D',若C',D',B在同一条直线上,且=,则AF的长为.14.[2018四川泸州]如图,等腰三角形ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为.15.[2018河南省实验三模]如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB 的中点,P是射线BC上的一个动点,连接AP,PE,将△AEP沿着边PE折叠,折叠后得到△EPA',若折叠后△EPA'与△BEP的重叠部分的面积恰好为△ABP面积的,则此时BP的长为.参考答案1.4-6或3-∵△ABC是等边三角形,∴∠B=60°.由折叠可知,AD=DP,设AD=DP=x,则BD=2-x.当∠DPB=90°时,DP=BDsin B,即x=(2-x),解得x=4-6;当∠BDP=90°时,DP=BDtan B,即x=(2-x),解得x=3-.故AD的长为4-6或3-.2.或在Rt△ABC中,BC===4.由折叠可知AE=AC=3,DC=DE.分三种情况讨论.①当∠DEB=90°时,如图(1)所示,点E与点F重合,EB=2.设DC=ED=x,则BD=4-x.在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4-x)2,解得x=,∴DE=.②当∠EDB=90°时,如图(2)所示,由折叠可知∠AED=∠C=90°,又∠EDB=90°,∴四边形ACDE为矩形,又∵AC=AE,∴矩形ACED为正方形,∴CD=AC=3,∴DB=BC-DC=4-3=1.∵DF∥AC,∴△BDF∽△BCA,∴=,即=,解得DF=.③当∠EBD=90°时,AC∥BE,此时点A到BE的距离为BC的长,而AE=AC<BC,故此种情况不存在.综上可知,DF的长为或.图(1)图(2)3.或2-2由题意可知,当A'D=CD时,点A'与点A或点C重合,不符合题意,故需分以下两种情况讨论.①如图(1),当A'D=A'C时,∠A'DC=∠A'CD=30°,∴∠AA'D=60°,又∵∠CAD=30°,∴∠ADA'=90°,∴AA'===.由折叠可得AP=AA'=.②如图(2),当CA'=CD=4时,连接BD交AC于点O,则在Rt△COD中,CO=CD×cos30°=4×=2,∴AC=4,∴AA'=AC-A'C=4-4.由折叠可得AP=AA'=2-2.综上可知,AP的长为或2-2.图(1)图(2)4.,或根据题意可得AD=t,BE=4t,则BD=-t,CE=4-4t.易证△BDE∽△CEF,∴=,∴BD·CF=CE·BE.分以下三种情况讨论.①如图(1),当点F在线段AC上,且AF=AD=t时,CF=BD=-t,∴(-t)2=4t(4-4t),解得t=(不合题意的解已舍去).②如图(2),当点F在CA的延长线上,且AF=AD=t时,CF=+t,∴(-t)(+t)=4t(4-4t),解得t=(不合题意的解已舍去).③如图(3),当点F在CA的延长线上,且DF=AD=t时,过点B作BM⊥AC,垂足为点M,设AM=x,由勾股定理可得AB2-AM2=BC2-CM2,即()2-x2=42-(+x)2,解得x=.取AF的中点H,连接DH,则∠HDA=∠MBA,∴sin∠HDA=sin∠MBA,即=,∴=,解得AH=t,∴AF=t,∴(-t)(+t)=4t(4-4t),解得t=(不合题意的解已舍去).综上所述,t的值为,或.图(1)图(2)图(3)5.(,1),(4,4),(,-1)或(0,-4)∵点A(2,0),点B(0,1),∴OA=2,OB=1,AB==.由题意可得,△ACP≌△ADP,要使△ADP与△ABP相似,则△ACP与△ABP相似.由PA⊥AB,PC⊥x轴,易得△ACP∽△BOA,则==.(1)如图(1),当点P在x轴的上方时,设AC=m,则PC=2m,PA=m.①当△ACP∽△PAB时,有=,即=,解得m=,∴PC=1,OC=2+=,∴点P的坐标为(,1);②当△ACP∽△BAP时,有=,即=,解得m=2,∴PC=4,OC=2+2=4,∴点P的坐标为(4,4).(2)如图(2),当点P在x轴的下方时,设AC=m,则PC=2m,则PA=m.①当△ACP∽△PAB时,有=,即=,解得m=,∴PC=1,OC=2-=,∴点P的坐标为(,-1);②当△ACP∽△BAP,∴=,即=,解得m=2,∴PC=4,OC=2-2=0,∴点P的坐标为(0,-4).综上所述,点P的坐标为(,1),(4,4),(,-1)或(0,-4).图(1)图(2)6.或如图,作BC的垂直平分线分别交AC,BC于点D,E.(1)当点P在线段BC上时,如图(1),过点A作AF⊥ED交ED的延长线于点F,易得AF=BE=BC=2,AB'=AB=3.设BP=B'P=x,B'E=m,则PE=2-x.易证△AB'F∽△B'PE,∴=,即=,∴m=x.在Rt△PB'E中,B'P2=PE2+B'E2,则x2=(2-x)2+(x)2,解得x1=,x2=(不合题意,舍去),此时BP的长为.(2)当点P在BC的延长线上时,如图(2),过点B'作B'M⊥BA交BA 的延长线于点M,过点P作PN⊥MB'交MB的延长线于点N,则四边形MBEB'是矩形,MB'=BE=2,AB=AB'=3,∴AM=.设BP=B'P=y,则NB'=y-2.易证△MAB'∽△NB'P,∴=,即=,则NP=.在Rt△NPB'中,由勾股定理,得NP2+B'N2=B'P2,即+(y-2)2=y2,解得y=(不合题意,舍去)或y=.图(1)图(2)7.或设AE=x,则DE=15-x,根据折叠的特征,得A'E=AE=x,D'E=DE=15-x,∠AEB=∠A'EB,A'B=AB=8,∴D'A'=15-2x.∵AD∥BC,∴∠AEB=∠CBE,∴∠D'EB=∠CBE,∴D'B=D'E=15-x.在Rt△BA'D'中,由勾股定理,得A'B2+A'D'2=D'B2,即(15-x)2=82+(15-2x)2,解得x=.8.6或2分以下两种情况讨论.①如图(1),当点P在CD上时,∵PD=3,CD=AB=9,∴CP=6,∴CP=BC,∴点C与点E重合,∴四边形PFBE是正方形,∴EF=6.②如图(2),当点P在AD上时,连接BP,过点E作EQ⊥AB于点Q,∵PD=3,AD=6,∴AP=3,∴PB===3.易得△ABP∽△QEF,∴=,即=,解得EF=2.综上,EF的长为6或2.图(1)图(2)9.4或4-2由折叠知PF=CF.∵四边形ABCD是矩形,∴CD=AB=2,BC=AD=6.∵四边形ABFE是正方形,∴AE=EF=FB=AB=2,∴FC=BC-FB=6-2=4,AF=2,∴FP=4.分以下三种情况讨论.①如图(1),当点P落在BE的延长线上时,由正方形的性质可知,直线BE垂直平分线段AF,∴AP=FP=4.②如图(2),当点P落在EB的延长线上时,同理可得AP=FP=4.③如图(3),当点P落在FA的延长线上时,AP=FP-AF=4-2.综上,线段AP的长为4或4-2.图(1)图(2)图(3)10.1≤BP≤3①如图(1),当点F,D重合时,BP的值最小.根据折叠的性质知,PF=AF=5.在Rt△PFC中,PF=5,FC=3,则PC=4,∴BP=1.②如图(2),当点E,B重合时,BP的值最大.由折叠的性质可得BP=AB=3.故BP的取值范围是1≤BP≤3.图(1)图(2)11.2≤x≤5由题意知,DE=EP,DF=PF,要使四边形EPFD为菱形,只需DE=DF即可.如图(1),若点E在AD上,点F在BC上,此时DE≤2,而DF>5,∴DE≠DF,四边形EPFD不是菱形;如图(2),若点E在AD上,点F在CD上,∠EDF=90°,若DE=DF,则∠DEF=∠DFE=45°,此时四边形EPFD为正方形,则点E与点A重合,即图(3)为图(2)的特殊情形,此时AP=2;如图(4),若点E 在AB上,点F在CD上.∵AB∥CD,∴∠DFE=∠PEF.由折叠的性质可知,∠DEF=∠PEF,∴∠DEF=∠DFE,∴DE=DF,此时四边形EPFD总是菱形.综上所述,当2≤x≤5时,四边形EPFD是菱形.图(1)图(2)图(3)图(4)12.如图,作点M关于直线CD的对称点M',连接M'B交CD于点P,此时PB+PM的值最小.∵四边形ABCD为矩形,∴DP∥AB,∴△M'DP∽△M'AB,∴=,即=,∴DP=.由折叠的性质可知AE=EP,设EM=a,则DE=1-a,EP=AE=1+a.在Rt△DEP中,DE2+DP2=EP2,即(1-a)2+()2=(1+a)2,解得a=.故当PB+PM的值最小时,ME的长度为.13.连接BF,∵=,∴=.∵D'C'=DC=4,∴BD'=2.设AF=x,则FD'=9-x.∵BF为Rt△ABF和Rt△BD'F的公共边,∴AB2+AF2=BD'2+D'F2,∴42+x2=22+(9-x)2,解得x=.14.18连接AD,∵EG垂直平分线段AC,∴DA=DC,∴DF+DC=DF+AD,∴当A,D,F三点共线时,DF+DC的值最小,最小值就是线段AF的长.过点A作AH⊥BC于点H,∵BC·AH=120,BC=20,∴AH=12.∵AB=AC,AH⊥BC,∴BH=CH=10.∵BF=3FC,∴CF=FH=5,∴AF===13,∴DF+DC的最小值为13,∴△CDF周长的最小值为13+5=18.15.2或2∵∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,∴AB=4,AE=AB=2,BC=2.分以下两种情况讨论.①若PA'与AB交于点F,连接A'B,如图(1).由折叠的性质可知S△A'EP=S△AEP,A'E=AE=2.∵点E是AB的中点,∴S△BEP=S△AEP=S△ABP.由题可知S△EFP=S△ABP,∴S△EFP=S△BEP=S△AEP=S△A'EP,∴EF=BE=BF,PF=A'P=A'F,∴四边形A'EPB是平行四边形,∴BP=A'E=2.②若EA'与BC交于点G,连接A'B,如图(2).同理可得GP=BP=BG,EG=EA'=×2=1,∴四边形A'BEP是平行四边形,∴A'P=BE=AE,且A'P∥BE,∴四边形A'PAE是平行四边形,∴AP=A'E=2,∴AP=AC,即点P与点C重合,∴BP=BC=2.综上所述,BP的长为2或2.图(1)图(2)。

(完整版)几何图形折叠问题

HistudyjiftS7^i viPTUk帮助预子個建持续迸步的孚刃力几何图形折叠问题【疑难点拨】1. 折叠（翻折）问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用•解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.2. 折叠（翻折）意味着轴对称，会生成相等的线段和角，这样便于将条件集中•如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解.3. 矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度•矩形中的两次或多次折叠通常出现“一线三直角”的模型（如图），从而构造相似三角形，利用相似三角形求边或者角的度数.4. 凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量.1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆 .2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等. 【基础篇】一、选择题：1. . （2018?四川凉州？ 3分）如图将矩形 ABCD&对角线BD 折叠，使C 落在C'处，BC'交AD 于点E ,则下到结论不一定成立的是（）AD=BCB .Z EBD=/ EDB C.A ABE^A CBD D sin / ABE*A.IHistudyjlftS7^l viPTUk帮助预子個建持续iS步的孚刃力2. （2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB已知OA=6取OA的中点C,过点C作CD L OA交理于点D,点F是上一点.若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD, DF, FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（___________ .A. 36 n -108 B . 108-32 n C. 2 n D.nABC AB=AC / BAC=90，点E为AB中点.沿过点E的直线折5. （2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上,点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4胚且/ AFG=60 , GE=2BG则折痕EF的长为（）A. 1B.说C. 2D.加如图，矩形纸片ABCD中, AB=4, BC=6将厶ABC沿AC折叠，使点B落在点E处，CE交AD 叠，使点B与点A重合，折痕现交于点F.已知E一，则BC的长是（3. （2017浙江衢州）于点F,则DF的长等于（）4. （2018 •山东青岛• 3分）如图，三角形纸片B. 3.2C. 3HiSMldy」畅字刃VIPT住叱帮朗预子陶建持续进步的孚刃门二、填空题:6. （2018 •辽宁省盘锦市）如图，已知Rt△ ABC中，/ B=90°, / A=60°, AC=2三+4,点M N分别在线段AC.ABD恰好落在线段BC上，当△ DCM为直角三角形时，折痕MN勺长为.ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C2=75°, EF= + 1,则BC的长-3分）如图，将矩形ABCD沿 EF折叠，使点B落在AD边上的点G处，点C落在点H处,BG 则/ AGB=三、解答与计算题：9. （2018 •广东• 7分）如图，矩形ABCD中, AB> AD,把矩形沿对角线AC所在直线折叠，使点B落在点E处,上，将厶ANM沿直线Mr折叠，使点A的对应点8. （2018 •湖南省常德7. （2018 •山东威海• 8分）如图，将矩形已知/ DGH=30，连接(1)求证：△ ADE^A CEDAE交CD于点F,连接DEHistudyjlftS7^]l viPTUk|帮助预子陶建持续进步的孚刃力|10—（ 2018?山东枣庄？ 10分）如图，将矩形— D 交AF 于点G,连接DG（1）求证：四边形EFDG 是菱形；（2）探究线段EG GF AF 之间的数量关系，并说明理由；（3）若 AG=6 EG=2E ，求 BE 的长.【能力篇】一、选择题： 11.（ 2018 •辽宁省阜新市）如图，将等腰直角三角形ABC （/ B=90°）沿EF 折叠，使点A 落在BC 边的中点A处，BC=8,那么线段AE 的长度为（）12.（ 2018 •四川省攀枝花・3分）如图，在矩形 ABCD 中, E 是AB 边的中点，沿 EC 对折矩形ABCD 使B 点落在点P 处，折痕为EC 连结AP 并延长AP 交CD 于 F 点，连结CP 并延长CP 交AD 于Q 点.给出以下结论： ① 四边形AECF 为平行四边形； ② / PBA=Z APQ③ 厶FPC 为等腰三角形； ④ 厶 APB^A EPC 其中正确结论的个数为（）A . 1 B. 2 C. 3D. 4C. 6D. 7D GECEB .A .亠13. （2018 •湖北省武汉• 3分）如图，在O O 中，点C 在优弧-I.上，将弧「■沿BC 折叠后刚好经过 AB 的中点 D.若O O 的半径为匚AB=4,则BC 的长是（、填空ABCD 中，点E 是CD 的中点，将△ BCE 沿BE 折叠后得到△ BEF14. （2018 •辽宁省葫芦岛市）如图，在矩形15. （ 2018 •四川宜宾• 3分）如图，在矩形 ABCD 中, AB=3 CB=2,点E 为线段AB 上的动点，将△ CBE 沿 CE ①当E 为线段AB 中点时，AF// CE; ②当E 为线段AB 中点时，AF=9 ;5④当 A F 、C 三点共线时，△ CEF ^A AEF.DG 1且点F 在矩形ABCD 勺内部，将 BF 延长交AD 于点G.若 =' ，则折叠，使点B 落在矩形内点F 处，下列结论正确的是（写出所有正确结论的序③当A F 、C 三点共线时,AE='HiSMiaa快乐字刃I VIPT 性叱帮朗滋子陶建持续进步的孚刃门GvPEDU !BCEDCA'B三、解答与计算题:16. (2018 •湖北省宜昌• 11分)在矩形 ABCD 中, AB=12 P 是边AB 上一点，把△ PBC 沿直线PC 折叠，顶点B 的对应点是点 G,过点B 作BEL CG 垂足为E 且在AD 上, BE 交PC 于点F . (1)如图1,若点E 是AD 的中点，求证：△ AEB^A DEC (2)如图2,①求证：BP=BF③当BP=9时，求 BE?EF 的值.②当 AD=25 且 AE v DE 时，求 cos / PCB 的值; 17. (2018 •广东• 7分)如图，矩形ABCC 中，AB> AD,把矩形沿对角线 AC 所在直线折叠，使点B 落在点E 处, AE 交CD 于点F ,连接DE (1)求证：△ ADE^A CED (2)求证：△ DEF 是等腰三角形.HiSMc!®快S 字刃丄VIP 亍性比帮朗预子陶建持续进步的孚刃门■ BC *HiStUCU快乐字刃VIPT性比帮助预子问建持续迸步的字刃力18. （2018?江苏盐城？10分）如图，在以线段二5■为直径的上取一点，连接、就•将_二弓匚沿.止翻折后得到□.（1 ）试说明点在上；（2）在线段.：「的延长线上取一点，使上厂—」一丄.求证：三壬为①门的切线；（3）在（2）的条件下，分别延长线段、匚吕相交于点，若m厂=J，二匸=-,求线段的长•【探究篇】19. （2018年江苏省泰州市？12分）对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD 边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）（2）将该矩形纸片展开.①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P,再将该矩形纸片展开.求证：/ HPC=90 ;②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P 在折痕上，请简要说明折叠方法•（不需说明理由）（1）根据以上操作和发现，求的值;设四边形BEFC 的面积为S ,求S 与x 之间的函数表达式，并求出 S 的最小值.(2) 随着点M 在边AD 上位置的变化，△ PDM 的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值;(3) 沿直线EF 折叠，使点B 的对应点M 始终落在边AD 上（点M 不与点A D 重合），点C 落在点N 处，MN W CD 交3 .....HistudyjlftS7^l VIPTlik帮助预子陶建持续iS步的孚刃力几何图形折叠问题【疑难点拨】1. 折叠（翻折）问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用•解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.2. 折叠（翻折）意味着轴对称，会生成相等的线段和角，这样便于将条件集中•如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解.3. 矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度•矩形中的两次或多次折叠通常出现“一线三直角”的模型（如图），从而构造相似三角形，利用相似三角形求边或者角的度数.4. 凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量.1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等.【基础篇】一、选择题：1. . （2018?四川凉州？3分）如图将矩形ABCD&对角线BD折叠，使C落在C'处，BC'交AD于点E,则下到结论不一定成立的是（）A. AD=BCB.Z EBD=/ EDBC.A ABE^A CBD D sin / ABE*ED【分析】主要根据折叠前后角和边相等找到相等的边之间的关系，即可选出正确答案.【解答】解：A、BC=BC, AD=BC二AD=BC，所以正确.B、 / CBD2 EDB / CBD=/ EBD EBD2 EDB正确.AED、T sin / ABE』,BE•••Z EBD=/ EDB••• BE=DEHistudyjlftS7^l VIPTlik帮助预子陶建持续iS步的孚刃力• sin / ABE^.ED故选：C.HistudyjlftS7^ll viPTUk|帮助预子詞11持续进步的字刃力|【点评】本题主要用排除法，证明 A , B , D 都正确，所以不正确的就是—C,排除法也是数学中一种常用的解题方法. 2.（2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB 已知OA=6取OA 的中点C,过点C 作CDL OA 交丽于点D,点F 是廳上一点.若将扇形BOD 沿 OD 翻折，点B 恰好与点F 重合，用剪刀沿着线段 BD, DF , FA 依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（ __________ . A . 36 n -108 B . 108-32 n C . 2 n D.n【考点】MO 扇形面积的计算；P9:剪纸问题.1【分析】先求出/ ODC M BOD=30，作DEL OB 可得DE= OD=3先根据S 弓形BD =S 扇形BOD - & BOD 求得弓形的面积,2再利用折叠的性质求得所有阴影部分面积.【解答】解：如图，••• CD L OA•••/ DCO M AOB=90 ,•••/ ODC M BOD=30 ,则剪下的纸片面积之和为 12X （ 3 n- 9） =36 n- 108, 故答案为： 36 n- 108 .故选 A 3.（2017浙江衢州）如图，矩形纸片 ABCD 中, AB=4, BC=6将厶ABC 沿 AC 折叠，使点B 落在点E 处，CE 交AD于点F ,则DF 的长等于（）…S 弓形B[=S 扇形X 6X 3=3n- 9,•/ OA =OD =OB =6OC |OA作DE L OB 于点E ,则 DE= OD=3c Mg 心BOD _d BOD=His【udy 』?i 乐字刃］vi 卩卞性比帮朗预子陶建持续迸步的孚刃门【考点】PB 翻折变换（折叠问题）；LB :矩形的性质.【分析】根据折叠的性质得到 AE=AB / E=Z B=90°,易证Rt △ AEF ^ Rt △ CDF ,即可得到结论设FA=x ,则FC=x , FD=6- x ,在Rt △ CDF 中利用勾股定理得到关于 x 的方程x 2=42+（ 6-x ）【解答】解：•••矩形 ABCD 沿对角线AC 对折，使△ ABC 落在厶ACE 的位置, ••• AE=AB / E=Z B=90°,又•••四边形ABCD 为矩形， • AB=CD • AE=DC 而/ AFE=Z DFC•••在△ AEF 与厶CDF 中，ZAFE-ZCFD•••△ AEF ^A CDF ( AAS ,• EF=DF ；•••四边形ABCD 为矩形， • AD=BC=6 CD=AB=4 •/ Rt △ AEF ^ Rt △ CDF • FC=FA设 FA=x ,贝U FC=x , FD=6- x , 13 在 Rt △ CDF 中，CF=C D+DF ,即 x 2=42+ (6 - x ) 2,解得 x= , 则 FD=6- x=. 故选：B.HiStUdyjl?iS7^l VIPTUk帮朗预子陶建持续进步的孚刃门D.5, 7EF=DF ；易得FC=FA,解方程求出x .B- AC4. （2018 •山东青岛• 3分）如图，三角形纸片ABC AB=AC / BAC=90，点E为AB中点.沿过点E的直线折叠，使点B与点A重合，折痕现交于点F.已知EF=，贝U BC的长是（）2A. .B. 3、2C. 3D. 3 3【分析】由折叠的性质可知/ B=Z EAF=45，所以可求出/ AFB=90，再直角三角形的性质可知EF丄AB,所以AB=AC!的长可求，再利用勾股定理即可求出BC的长.【解答】解：•••沿过点E的直线折叠，使点B与点A重合，•••/ B=Z EAF=45 ,•••/ AFB=90° ,•••点E为AB中点，1 3•EF= —AB, EF= ,2 2•AB=AC=3•••/ BAC=90 ,•BC=3.2 ,故选：B.【点评】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用，求出/ AFB=9C°是解题的关键.5. （2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上,点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4胚且/ AFG=60 , GE=2BG则折痕EF的长为（）HiStUdyjl?iS7^l VIPTUk帮朗预子陶建持续is步的孚刃门【考点】PB:翻折变换（折叠问题）；LB:矩形的性质.【分析】由折叠的性质可知，DF=GF HE=CE GH=DC/ DFE=/ GFE结合/ AFG=60即可得出/ GFE=60，进而可得出△ GEF为等边三角形，在Rt△ GHE中,通过解含30度角的直角三角形及勾股定理即可得出GE=2EC DC= EC,再由GE=2BG吉合矩形面积为4 ，即可求出EC的长度，根据EF=GE=2EC卩可求出结论.【解答】解：由折叠的性质可知，DF=GF HE=CE GH=DC Z DFE=Z GFE•••/ GFE+Z DFE=180 -Z AFG=120 ,•••/ GFE=60 .•/ AF// GE Z AFG=60 ,•Z FGE=/ AFG=60 ,•△ GEF为等边三角形，•EF=GE•••/ FGE=60，/ FGE+Z HGE=90 ,•Z HGE=30 .在Rt△ GHE中, Z HGE=30 ,•GE=2HE=C,•GH= =*$HE= CE•/ GE=2BG•BC=BG+GE+EC=4EC•••矩形ABCD勺面积为 4 ,•4EC?^EC=4 ,•EC=1, EF=GE=2故选C.二、填空题：6. （2018 •辽宁省盘锦市）如图，已知Rt△ ABC中，Z B=90°, Z A=60°, AC=2 :;+4,点M N分别在线段AC.AB上，将△ ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△ DCM为直角三角形时，折痕MN勺长为 .帮朗滋子陶建持续迸步的孚刃门①如图，当/ CDM=90时，△ CDM是直角三角形,•••在Rt△ ABC中，/ B=90°, / A=60° AC=^+4, /-Z C=30°, AB^ AC五+-,由折叠可得:Z MDN Z A=60°1_ 1_Z BDN=30，•/ BN空DN爰AN •/丄術+卸BN= AB= ：,■2硬+4•• AN=2BN="Z DNB=60 , /Z ANM Z DNM=60，/•/ AMN=60 , •師+4•• AN=MN=";【解答】解：分两种情况：②如图，当/ CMD=90时，△ CDM是直角三角形,帮助预子问il持续迸步的孚刃力I □ ~I] ■由题可得：/ CDM=60 , / A=Z MDN=60 , /-Z BDN=60 , / BND=30 BD空DN= AN, BN庐BD\1AB巫+2 ,1_/• AN=2, BN^3,过N 作NH L AM于H,贝UZ ANH=30 , /• AH空AN=1, HN昉,由折叠可得：Z AMN Z DMN=45 ,/•△ MNH是等腰直角三角形，/• HM=HN= :,/ MN= ■.故答案为：'或；7. （2018 •山东威海• 8分）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C与AD边上的点K重合，FH为折痕.已知Z 仁67.5 ° ,Z 2=75°, EF= + 1,求BC的长.【分析】由题意知Z 3=180 ° - 2 Z 1=45°、Z 4=180°- 2Z 2=30 °、BE=KE KF=FC 作KM L BC,设KM=x 知EM=x MF= x,根据EF的长求得x=1，再进一步求解可得.【解答】解：由题意，得：Z 3=180 °- 2 Z 1=45°,Z 4=180°- 2Z 2=30 °, BE=KE KF=FC设KM=x 贝U EM=x MF^J x,x+ V3x^3+1,解得：x=1,••• EK=J办KF=2,.BC=BE+EF+FC=EK+EF+KF=3++J：,• BC的长为【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等.8. （2018 •湖南省常德・3分）如图，将矩形ABC［沿EF折叠，使点B落在AD边上的点G处，点C落在点H处, 已知Z DGH=30，连接BG 则Z AGB= 75如图，过点K作KM L BC于点M帮朗预子陶建持续进步的孚刃门/ EBC-Z EBG即：/ GBC M BGH由平行线的性质可知/ AGB=Z GBC从而易证/ AGB2 BGH据此可得答案.【解答】解：由折叠的性质可知：GE=BE / EGH M ABC=90 ,•••/ EBG=Z EGB•••/ EGH-Z EGB玄EBC-Z EBG 即：/ GBC=/ BGH又••• AD// BC•Z AGB=Z GBC•Z AGB=Z BGHvZ DGH=30 ,•Z AGH=150 ,•Z AGB二Z AGH=75 ,2故答案为：75°.【点评】本题主要考查翻折变换，解题的关键是熟练掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等.三、解答与计算题：9. (2018 •广东• 7分)如图，矩形ABCD中, AB> AD,把矩形沿对角线AC所在直线折叠，使点B落在点E处,AE交CD于点F,连接DE(1)求证：△ ADE^A CED(2)求证：△ DEF是等腰三角形.【分析】(1)根据矩形的性质可得出AD=BC AB=CD结合折叠的性质可得出AD=CE AE=CD进而即可证出△ ADE◎ △ CED( SSS ;(2)根据全等三角形的性质可得出Z DEF=Z EDF利用等边对等角可得出EF=DF由此即可证出△ DEF是等腰三角形.HiSMlda快乐字刃I VI PT住叱帮朗预子陶建持续进步的孚刃门【解答】证明：(1)：四边形ABCD是矩形，••• AD=BC AB=CD由折叠的性质可得：BC=CE AB=AE•AD=CE AE=CDC AD=CE在厶人。

(完整版)四边形题型归纳

四边形题型归纳题型一：翻折问题（特殊四边形的折叠问题）1沿特殊四边形的对角线折叠【例1】如图，矩形纸片ABCD，AB=2， / ADB=30，沿对角线BD折叠（使△ ABD和2、沿特殊四边形的对称轴折叠【例2】如图，已知矩形ABCD的边AB=2 , AB^ BC ,矩形ABCD的面积为S,沿矩形的对称轴折叠一次得到一个新的矩形，则这个新矩形对角线长为3•使特殊四边形的对角顶点重合折叠【例3】如图，梯形纸片ABCD , / B=60 , AD // BC, AB=AD=2 , BC=6，将纸片折叠,使点B与点D重合，折痕为AE，贝U CE= ___________ .4•使特殊四边形一顶点落在其一边上而折叠【例4】如图，折叠矩形的一边CD，使点C落在AB上的点F处，已知AB=10cm , BC=8cm ,贝U EC 的长为______ •D] ] CE、百fA F B△ EBD落在同一平面内），则A、E两点间的距离为_______________D F C D CA B2B E C5•使特殊四边形两顶点落在其一边上而折叠【例5】如图，在梯形ABCD中，DC // AB，将梯形对折，使点D、C分别落在AB上的D、C处，折痕为EF，若CD=3cm , EF=4cm，则AD +BC = ________ cm.6•使特殊四边形一顶点落在其对称轴上而折叠（1）EF上的G点处，则/ DKG= _____7.使特殊四边形一顶点落在其对称轴上而折叠（2）点折至MN上，落在点P的位置，折痕为BQ，连结PQ.（1）求MP的长度；⑵求证：以PQ为边长的正方形的面积等于I .8.两次不同方式的折叠【例8】如图，将一矩形形纸片按如图方式折叠，BC、BD为折痕，折叠后AB与EB在同一条直线上，则/ CBD的度数为（）A.大于90 °B.等于90 °C.小于90 °D.不能确定【例6】如图，已知EF为正方形ABCD的对称轴，将/ A沿DK折叠，使它的顶点A落在【例7】如图，有一块面积为1的正方形ABCD , M、N分别为AD、BC边的中点，将CDIAC E<\JA BD【变式1】在矩形ABCD中AB=4, BC=3按下列要求折叠，试求出所要求结果（1）如图，把矩形ABCD沿着对角线BD折叠得△ EBD BE交CD于点F,求出BFD；（2）如图，折叠矩形ABCD使AD与对角线BD重合，求折痕DE的长；（3）如图，折叠矩形ABCD使点D与点B重合，求折痕EF的长；（4）如图，E是AD上一点，把矩形ABCD沿着BE折叠，若点A恰好落在CD上的点F处, 求AE的长。

中考数学中的折叠问题

中考数学中的折叠问题在中考数学中，折叠问题是一种常出现的问题，它主要考察学生的空间想象能力和对几何图形的理解。

这种问题通常以一个二维图形经过折叠变为三维图形的方式出现，需要学生运用逻辑推理和空间想象能力来解答。

折叠问题主要分为两类：一类是折叠前后的形状变化问题，另一类是折叠后立体图形的三视图问题。

前者主要考察的是学生对于空间图形的变换和对称的理解，而后者则更注重学生的空间想象能力和对立体图形的认知。

解决折叠问题，首先需要理解折痕的含义。

折痕是二维图形折叠成三维图形时的痕迹，也是三维图形展开为二维图形时的路径。

在解决折叠问题时，需要找出图形中的对称点、线段和角度，并理解它们在折叠后的变化。

对于三视图问题，则需要通过观察和分析立体图形的各个面，尝试从不同的角度去看待问题。

例如，一个长方形纸片折叠后可以得到一个正方形纸片，这个过程可以通过平移和旋转来实现。

在这个问题中，学生需要理解长方形和正方形的关系，以及折叠过程中哪些元素发生了变化，哪些元素保持不变。

又比如，一个三角形纸片折叠后可以得到一个立体图形，这个过程中需要对三角形的一些基本性质进行深入的理解。

解决折叠问题时，首先需要明确问题的类型，然后针对不同类型的问题采取不同的解题策略。

对于形状变化问题，可以通过画图的方式帮助理解；对于三视图问题，可以通过将立体图形转化为平面图形的方式来寻找答案。

同时，建议学生在平时的学习中多进行一些类似题目的练习，以增强自己的空间想象能力和逻辑推理能力。

中考数学中的折叠问题是一种考察学生空间想象能力和逻辑推理能力的问题。

解决这类问题需要学生对几何图形的性质有深入的理解，并能够灵活运用这些性质去解决问题。

也需要学生有一定的空间感知能力和逻辑推理能力。

因此，建议学生在平时的学习中多进行练习，提高自己的解题能力。

折叠最值模型是指将一个平面图形沿着一条直线折叠，使得折叠后的图形在直线的一侧，并且使得折叠后的图形在直线两侧的部分对称。

空间几何中的折叠问题例题和知识点总结

空间几何中的折叠问题例题和知识点总结在空间几何的学习中，折叠问题是一个重要且具有一定难度的考点。

通过折叠，可以将平面图形转化为空间图形，从而增加了问题的复杂性和抽象性。

下面，我们将通过一些例题来深入探讨空间几何中的折叠问题，并对相关知识点进行总结。

一、折叠问题的基本概念折叠问题通常是指将一个平面图形沿着某条直线或折线进行折叠，使其成为一个空间几何体。

在这个过程中，图形的某些元素（如线段的长度、角度的大小等）保持不变，而有些元素则会发生变化。

例如，将一个矩形沿着其中一条边折叠，可以得到一个三棱柱；将一个直角三角形沿着斜边折叠，可以得到一个三棱锥。

二、折叠问题的关键知识点1、不变量在折叠过程中，有些量是不变的。

例如，折叠前后对应线段的长度不变，对应角度的大小不变。

2、垂直关系折叠前后，原来垂直的线段和平面在折叠后仍然垂直。

3、距离和角度的变化折叠后，某些线段之间的距离和角度会发生变化，需要根据折叠的方式和几何关系进行重新计算。

三、例题分析例 1：已知矩形 ABCD 中，AB ＝ 3，BC ＝ 4。

现将矩形沿着对角线 AC 折叠，求折叠后点 B 到平面 ACD 的距离。

解：首先，通过勾股定理求出 AC 的长度：AC ＝√（AB²＋ BC²) ＝ 5设点 B 折叠后对应的点为 B'，由于折叠前后三角形 ABC 的面积不变。

三角形 ABC 的面积＝ 1/2 × AB × BC ＝ 1/2 × AC × h （h 为点 B 到平面 ACD 的距离）所以 h ＝（AB × BC) ／ AC ＝（3 × 4) ／ 5 ＝ 12 ／ 5例 2：如图，在直角三角形 ABC 中，∠ACB ＝ 90°，AC ＝ 2，BC ＝ 1，将三角形 ABC 沿斜边 AB 折叠，得到三棱锥 C ABD。

求证：平面 CAD ⊥平面 BAD。