知识讲解+圆周运动和向心加速度
为什么物体在圆周运动中会有向心加速度

为什么物体在圆周运动中会有向心加速度物体在圆周运动中会有向心加速度的原因有三个:方向改变、速度改变和加速度的大小。
首先,物体在圆周运动中会有向心加速度,是因为其运动方向不断改变。
根据牛顿第一定律,物体会继续保持匀速直线运动状态,除非有外力作用。
在圆周运动中,物体沿着圆周轨迹做匀速运动,但是其速度方向却不断改变,因此需要有一个向心力来改变其运动方向。
这个向心力的作用方向指向圆心,所以物体在圆周运动中会有向心加速度。
其次,物体在圆周运动中会有向心加速度,是因为其速度大小改变。
根据牛顿第二定律,物体的加速度与作用力成正比,与物体质量成反比。
在圆周运动中,向心力就是物体所受的作用力,其大小与物体的质量以及圆周运动的半径和速度有关。
当物体的速度增加时,向心力也会增加,从而导致向心加速度的增加。
因此,物体在圆周运动中会有向心加速度。
最后,物体在圆周运动中会有向心加速度,是因为加速度的大小需要满足对应的运动条件。
根据圆周运动的速度和半径关系,我们可以推导出向心加速度的表达式:向心加速度等于速度的平方除以圆周半径。
这表明,物体在圆周运动中的向心加速度与其速度的平方成正比,与圆周半径成反比。
通过这个公式,我们可以定量地描述物体在圆周运动中的向心加速度,从而更好地理解其运动特性。
综上所述,物体在圆周运动中会有向心加速度的原因是其运动方向改变、速度大小改变和加速度满足运动条件。
了解这些原因有助于我们更深入地理解物体在圆周运动中的特性,并为相关问题的解决提供参考。
通过研究圆周运动的向心加速度,我们可以更好地理解和应用物理学知识,推动科学技术的发展。
05.05圆周运动—向心力和向心加速度(来源分析)
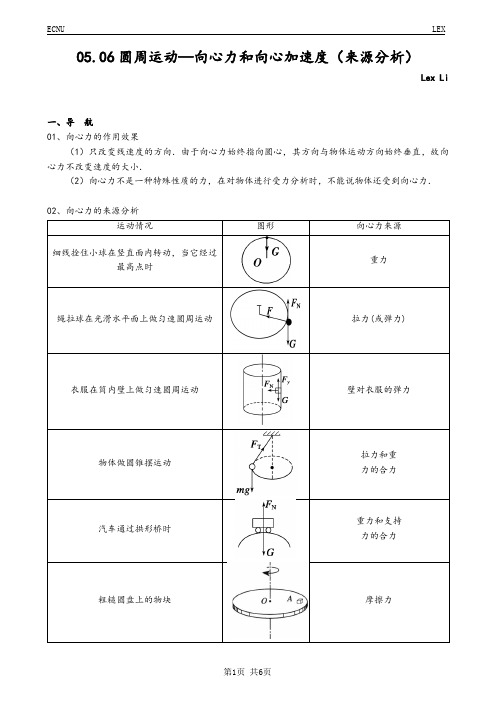
05.06圆周运动—向心力和向心加速度(来源分析)Lex Li一、导航01、向心力的作用效果(1)只改变线速度的方向.由于向心力始终指向圆心,其方向与物体运动方向始终垂直,故向心力不改变速度的大小.(2)向心力不是一种特殊性质的力,在对物体进行受力分析时,不能说物体还受到向心力.02、向心力的来源分析二、再接再厉01、如图所示,细线的一端有一小球,另一端有光滑的固定轴O,现给小球一个初速度V0,使球和细线一起绕O轴在竖直面内转动,不计空气阻力,则:(1)求小球在A点处的向心力及细线的拉力;(2)若物体在B点处的速度变为V,求此时的向心力及细线的拉力;(3)求小球过最高点D的最小速度。
02、如图所示,细线的一端有一小球质量m=1 kg,另一端有光滑的固定轴O,现给小球一个初速度V0,使球和细线一起绕O轴在在光滑水平面上做匀速圆周运动,不计空气阻力,则:(1)若细线长L=1 m,V0=5 m/s,求细线的拉力;(2)若细线所能承受的最大力为100 N,求小球的最大速度。
03、如图所示,质量m=2 kg的物块在一半径R=0.1 m的圆柱形桶壁(桶壁粗糙)上,圆桶绕中心轴转动角速度ω=20 rad/s,则:(1)求物块所受的摩擦力;(2)求物块受到的向心力;(3)若物块与桶壁间的滑动摩擦因素μ=0.5,求物块不下滑的最小角速度。
04、如图所示,“飞椅”的游乐项目,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘.转盘可绕穿过其中心的竖直轴转动,当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求:(1)飞椅的转动半径R及向心力F;(2)钢绳的弹力T;(3)转盘转动的角速度ω与夹角θ的关系.05、如图所示,公路在通过小型水库泄洪闸的下游时常常要修建凹型桥(图甲),也叫“过水路面”.现有一“过水路面”的圆弧半径为50 m,一辆质量为800 kg的小汽车驶过“过水路面”.当小汽车通过“过水路面”的最低点时速度为5 m/s.g取10 m/s2,则:(1)问此时汽车的压力为?对路面的压力为多大?(2)若修建凸型桥(图甲)圆弧半径仍为50 m,一辆质量为800 kg的小汽车驶过最高点时速度为10m/s,此时汽车的向心力为多大,对路面的压力为又为多大?06、如图所示,质量为m的小物体A在水平转台上随转台以频率f作匀速圆周运动,物体到转轴的距离为d,物体与转台间的动摩擦因数为μ,求:(1)物体所需要的向心力;(2)物体所受到的转台对它的支持力和摩擦力.(3)为使物体保持距离d随转台一起转动,转台转动的角速度应满足什么条件?07、长L=0.5 m的细绳拴着小水桶绕固定轴在竖直平面内转动,桶中有质量m=0.5 kg的水(g取10 m/s2),求:(1)在最高点时,水不流出的最小速率是多少?(2)在最高点时,若速率v=3 m/s,水对桶底的压力为多大?08、长度为0.5 m的轻杆OA绕O点在竖直平面内做圆周运动,A端连着一个质量m=2 kg的小球.求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向(提示:杆对球可提供支持力,也可提供拉力):(1)杆做匀速圆周运动的转速为2.0 r/s;(2)杆做匀速圆周运动的转速为0.5 r/s.09、原长为L的轻弹簧一端固定一小铁块,另一端连接在竖直轴OO′上,小铁块放在水平圆盘上,若圆盘静止,把弹簧拉长后将小铁块放在圆盘上,使小铁块能保持静止的弹簧的最大长度为5L/4,现将弹簧长度拉长到6L/5后,把小铁块放在圆盘上,在这种情况下,圆盘绕中心轴OO′以一定角速度匀速转动,如图教2-2-2所示.已知小铁块的质量为m,为使小铁块不在圆盘上滑动,圆盘转动的角速度ω最大不得超过多少?05.06圆周运动—向心力和向心加速度(来源分析)Lex Li04、解:依题意得:(2)设转盘角速度为ω,夹角为θ 座椅到中心的距离:R =r +L sin θ对座椅受力分析有:F =mg tan θ=mRω2 联立两式得ω=g tan θr +L sin θ.05、解:依题意得:汽车在“过水路面”的最低点时受力如图所示,由牛顿第二定律得:N -mg =mv 2r.解得:N =mg +m v 2r =(800×10+800×2550)N =8 400 N ,根据牛顿第三定律,汽车对路面的压力N ′=F N =8 400 N.06、解:依题意得:(1)物体随转台做圆周运动其向心加速度a =ω2r =(2πf )2d ,由牛顿第二定律得 F 向=m (2πf )2d =2m π2f 2d(2)物体在竖直方向上处于平衡状态,所以物体受到平台的支持力为G ,物体在水平面内只可能受到摩擦力,所以摩擦力提供物体做圆周运动的向心力,F f =F 向=2m π2f 2d .(3)物体受到的滑动摩擦力近似等于最大静摩擦力,当物体所受到的摩擦力不足以改变物体的速度的方向时,物体将相对平台发生滑动,所以μmg ≥m ω2d ,即ω≤μg /d . 07、解:依题意得:(1)若水恰不流出,则有:mg =m v 20L所求最小速率:v 0= gL = 10×0.5 m/s = 5 m/s =2.24 m/s.(2)设桶对水的压力为N ,则有:mg +N =m v 2LN =m v 2L -mg =0.5×90.5N -0.5×10 N=4 N由牛顿第三定律得知,水对桶底的压力:N ′=N =4 N.08、解:依题意得:(1)小球在最高点的受力如图所示: 杆的转速为2.0 r/s 时,ω=2πn =4π rad/s 由牛顿第二定律得:F +mg =mLω2故小球所受杆的作用力:F =mLω2-mg =2×(0.5×42×π2-10)N ≈138 N 即杆对小球提供了138 N 的拉力由牛顿第三定律知小球对杆的拉力大小为138 N,方向竖直向上.(2)杆的转速为0.5 r/s时,ω′=2π·n=π rad/s同理可得小球所受杆的作用力:F=mLω′2-mg=2×(0.5×π2-10)N≈-10 N.力F为负值表示它的方向与受力分析中所假设的方向相反,故小球对杆的压力大小为10 N,方向竖直向下.【审题指导】解答该题应把握以下两点:(1)最高点时,杆对球的弹力和球的重力的合力充当向心力.(2)杆对球可能提供支持力,也可能提供拉力.09、解:依题意得:以小铁块为研究对象,圆盘静止时:设铁块受到的最大静摩擦力为f max,由平衡条件得f max=kL/4.圆盘转动的角速度ω最大时,铁块受到的摩擦力f max与弹簧的拉力kx的合力提供向心力,由牛顿第二定律得kx+f max=m(6L/5)ω2max.又因为x=L/5.解以上三式得角速度的最大值ωmax=3k/(8m).。
为什么物体在圆周运动中会有向心加速度和离心加速度

为什么物体在圆周运动中会有向心加速度和离心加速度在物体进行圆周运动时,会经历向心加速度和离心加速度的作用。
这两种加速度是圆周运动中的重要概念,它们与物体的运动轨迹密切相关。
本文将通过解释原理、实例分析以及应用场景等方面,深入探讨物体在圆周运动中产生向心加速度和离心加速度的原因。
一、向心加速度:使物体向圆心靠拢的力量在圆周运动中,物体做匀速运动并不会感到有向心加速度的作用。
然而,当物体的速度发生变化,即速度大小或方向发生改变时,向心加速度就会出现。
向心加速度是使物体向圆心靠拢的力量。
根据牛顿第二定律,物体所受的合力与其产生的加速度成正比。
在圆周运动中,向心加速度的大小与物体的速度和运动半径有关。
公式为:a = v² / r其中,a表示向心加速度,v表示物体的速度,r表示运动半径。
可见,当速度增大或半径减小时,向心加速度将增加。
例如,当我们驾驶车辆进行弯道行驶时,车辆会产生向心加速度。
车速越快或转弯半径越小,向心加速度越大。
这是因为车辆在弯道上受到向圆心的力量,使其保持在弯道上。
二、离心加速度:使物体远离圆心的力量与向心加速度相对应,离心加速度是使物体远离圆心的力量。
当物体在圆周运动中半径发生改变时,离心加速度就会产生。
离心加速度的大小与向心加速度相等,但方向相反。
它是物体想要离开圆心的力量。
同样根据牛顿第二定律,离心加速度的公式为:a = v² / r当物体的速度增大或运动半径增大时,离心加速度也会增加。
例如,我们在过山车上体验高速旋转时,会感到向外的离心力。
这是因为定速旋转的过山车会让乘客体验到离心加速度,使他们感觉被推离中心点。
三、向心加速度和离心加速度的应用1. 引力与向心力的平衡:在地球的自转运动中,物体固定在地球表面,受到地球引力和向心力的平衡作用。
这个平衡使得物体保持在地球表面,不会被向外的离心力推离。
2. 公路弯道设计:在设计公路弯道时,工程师需要考虑到车辆在弯道时产生的向心加速度和离心加速度,以确保车辆行驶的安全性。
高中物理圆周运动和向心加速度专题讲解

圆周运动和向心加速度【要点梳理】要点一、圆周运动的线速度 要点诠释:1、线速度的定义:圆周运动中,物体通过的弧长与所用时间的比值,称为圆周运动的线速度。
公式:tlv ∆∆=(比值越大,说明线速度越大) 方向:沿着圆周上各点的切线方向 单位:m/s 2、 说明1)线速度是指物体做圆周运动时的瞬时速度。
2)线速度的方向就是圆周上某点的切线方向线速度的大小是tl∆∆的比值。
所以v 是矢量。
3)匀速圆周运动是一个线速度大小不变的圆周运动。
4)线速度的定义式tlv ∆∆=,无论是对于变速圆周运动还是匀速圆周运动都成立,在变速圆周运动中,只要t ∆取得足够小,公式计算的结果就是瞬时线速度注:匀速圆周运动中的“匀速”二字的含义:仅指速率不变,但速度的方向(曲线上某点的切线方向)时刻在变化。
【典型例题】类型一、描述匀速圆周运动的各个物理量例1、一个直径为1.4m 的圆盘以中心为轴匀速转动,转速为2转/秒,求圆盘边缘一点的线速度、角速度、周期和向心加速度。
例2、 (2015 海南会考模拟)如图所示,钟表的秒针、分针、时针转动周期、角速度都不同,下列说法中正确的是( )A .秒针的周期最大,角速度最大B .秒针的周期最小,角速度最大C .时针的周期最大,角速度最大D .时针的周期最小,角速度最大 【解析】时针的周期是12h ,分针的周期是1h ,秒针的周期是1min ,秒针的周期最小,根据2Tπω=可知秒针的角速度最大,故A 错误B 正确;时针的周期是12h ,分针的周期是1h ,秒针的周期是1min ,时针的周期最大,根据2Tπω=可知时针的角速度最小,故CD 错误。
【变式】电风扇叶片边缘一点的线速度为56.7m/s ,若它转动半径为18cm ,求电扇转动的角速度和周期。
【解析】根据线速度与角速度的关系r v ω=得)s (02.022)rad/s (315=====v rT T rv rv ππω所以又因为要点二、描写圆周运动的角速度 要点诠释:1、角速度的定义:圆周运动物体与圆心的连线扫过的角度θ∆与所用时间t ∆的比值叫做角速度。
高三物理圆周运动、向心加速度、向心力知识精讲

高三物理圆周运动、向心加速度、向心力【本讲主要内容】圆周运动、向心加速度、向心力描述圆周运动的量间的关系,实际圆周运动问题中的向心力分析。
【知识掌握】 【知识点精析】1、匀速圆周运动的特点如果质点沿圆周运动,在相等的时间里通过的弧长相等,这种运动叫匀速圆周运动。
匀速圆周运动的轨迹为曲线,v 方向时刻在变,快慢程度不改变,是变速运动,做匀速圆周运动的物体状态是非平衡态,所受合外力不为零,是变加速运动(a 方向时刻在变)。
2、描述圆周运动的物理量(1)线速度:线速度大小又叫速率,用v 表示,tSv =,S 为弧长,t 为通过这段弧长的时间,速率越大则沿弧运动得越快。
线速度的方向为圆的切线方向。
线速度就是圆周运动的瞬时速度。
(2)角速度:连接质点和圆心的半径转过的角度ϕ,与所用时间的比叫角速度tϕω=。
ϕ的单位是弧度,时间t 单位是秒,ω的单位就是弧度/秒,用字母表示为s rad /,角速度的大小描述了做圆周运动绕圆心转动快慢程度。
角速度大则绕圆心转得快。
对一个不变形的物体转动中任何点转过的角度都相同,所以角速度都相同。
(3)周期:使圆周运动的物体运动一周的时间叫周期,用字母T 表示,单位为秒。
周期描述圆周运动重复的快慢,也反映了转动快慢。
周期越小,转动越快。
(4)频率:1秒内完成圆周运动的次数叫频率。
它是周期的倒数,单位是1/秒。
用符号f 表示,单位又叫赫兹(Hz ),f 越大,转动就越快。
(5)转速:工程技术中常用。
定义为每秒转过的圈数,数值与频率相同,单位也是1/秒。
(6)f T v 、、、ω的关系: T = 1/f = 2π/ω = 2π•r /v ω = 2π/T = 2π•f = v /r v = ω•r = 2π•r /T = 2π•f •r Tf n 1== 例1、地球自转的问题讨论1:比较在北京和在赤道两处物体随地球做自转的角速度。
地球表面上的物体随地球做匀速圆周运动的角速度都相同。
圆周运动中的牛顿第二定律和向心加速度的关系

圆周运动中的牛顿第二定律和向心加速度的关系牛顿第二定律是经典力学中的基本定律之一,它描述了物体在受到力的作用下发生加速度的现象。
而在圆周运动中,物体在维持其运动轨道时需要受到向心力的作用,这与牛顿第二定律密切相关。
本文将探讨圆周运动中牛顿第二定律与向心加速度之间的关系。
在介绍牛顿第二定律和向心加速度的关系之前,我们先来了解一下牛顿第二定律的具体内容。
牛顿第二定律可以用数学公式表示为:F = m * a其中,F代表物体所受的合力,m代表物体的质量,a代表物体的加速度。
该公式表明,物体的加速度与作用于其上的力成正比,与物体的质量成反比。
在圆周运动中,物体维持其运动轨道需要受到向心力的作用。
向心力是指指向圆心的力,其大小与物体质量、速度和运动轨道半径有关。
根据牛顿第二定律,我们可以推导得出向心加速度的表示公式。
假设物体在半径为r的圆周运动中,其线速度为v,向心加速度为a。
根据牛顿第二定律,我们可以得到如下等式:F = m * a其中,F表示向心力。
由于向心力与物体质量无关,我们可以将等式改写为:F = m * a = m * (v^2 / r)根据圆周运动特性,向心力可以等于物体的质量乘以向心加速度:F = m * a = m * (v^2 / r) = m * a_c其中,a_c表示向心加速度。
通过比较上述等式,我们可以得到向心加速度的表示公式:a_c = v^2 / r这个公式表明,在圆周运动中,物体的向心加速度与其线速度的平方成正比,与运动半径成反比。
向心加速度越大,物体受到的向心力就越大,因此才能维持其在曲线轨道上的运动。
需要注意的是,向心加速度的方向永远指向圆心,而不是物体运动的方向。
这是因为向心加速度是为了使物体维持曲线轨道运动而产生的加速度,而非线速度方向上的加速度。
综上所述,牛顿第二定律和向心加速度在圆周运动中有着密切的关系。
牛顿第二定律描述了物体在圆周运动中受到的合力与其向心加速度的关系,而向心加速度的大小又与物体的线速度平方和运动半径有关。
考点2匀速圆周运动 线速度、角速度和周期 向心加速度和向心力(知识梳理)

考点2 匀速圆周运动、线速度、角速度和周期、向心加速度和向心力第一部分 考纲扫描1.了解线速度、角速度、周期、频率、转速等概念。
理解向心力及向心加速度。
2.能结合生活中的圆周运动实例熟练地应用向心力和向心加速度处理问题。
3.能正确处理竖直平面内的圆周运动。
4.了解离心现象。
第二部分 知识梳理一、描述圆周运动的物理量1.线速度①定义:质点做圆周运动通过的弧长l 与通过这段弧长所用的时间t 的比值叫做圆周运动的线速度。
②线速度的公式为:2l r v t Tπ==。
③方向为沿圆周的切线方向。
作匀速圆周运动的物体速度方向时刻在变化,因此匀速圆周运动是一种变速运动。
2.角速度①定义:用连接物体和圆心的半径转过的角度θ跟转过这个角度所用的时间t 的比值叫做角速度。
②公式为:2t Tθπω==,单位是:弧度/秒(rad/s)。
3.周期①定义:做匀速圆周运动的物体运动一周所用的时间,称为周期。
周期越大,运动越慢。
②公式:2r T vπ= 频率——质点在1秒内转动的圈数。
频率越大,物体运动越快。
转数——质点每秒钟(或每分钟)所转过的圈数。
常用的单位有:转/分(r/min)。
4.描述匀速圆周运动的各个物理量的关系①角速度ω与周期的关系是:ω=2π/T②角速度和线速度的关系是:v=ωr③周期与频率的关系是: 1T f=; ④向心加速度与以上各运动学物理量之间的关系:a=2v r=2r ω=224r T π 5.描述圆周运动的力学物理量是向心力(F 向):它的作用是改变速度的方向。
描述圆周运动的运动学物理量和力学物理量之间的关系是:F 向= m 2v r= m 2r ω =m 224r T π=ma 。
[规律总结]在分析传送带或边缘接触问题时,要抓住的关系是:同转轴的各点角速度相同,而同一皮带(不打滑时)或相吻合的两轮边缘的线速度相同。
当分析既不同轴又不同皮带的问题时,往往需要找一个联系轴与皮带的中介点作为桥梁。
人教版高一物理必修第二册第六章《圆周运动》向心加速度

这[例个题力2]可能长沿为什L的么细方线向,?一端拴一质量为m的小球,一端固定于O点.
[这例个题力1]可自能行沿车什的么小方齿向轮?A、大齿轮B、后轮C是相互关联的三个转动部分,如图所示。
小质球点在 做水匀平速面圆内周做运匀动速,圆从周A运运动动到(这B,种线运速动度通从常v被A变称成为v“B圆,锥速摆度运的动变”化),量如Δ图v,甲如所何示表. 示?
Δv vA vB
B
O
A
当自Δt 行取车值正不常断骑变行小时,AΔ、v 的B、方C向三与轮v边A的缘方上向的关点系的如向何心变加化速?度的大小如何比较?
当Δt 取值不断变小,Δv 的方向与v 的方向关系如何变化? 受质到点指 做向匀太速阳圆的周引运力动作,用从A运动到B,线速度从vA变成vB,速度的变化量Δv,如何表示?
Δv 当你Δ能t足画够出小Δt,时v间A内,速vB度的变夹化角量θ 就Δv足吗够?小。
v [所例求题加2]速度长a为是Lt的A时细刻线的,瞬一时端加拴速一度质吗量?为得m的小球,一端固定于O点.
A 质此点时做θ 所匀对速的圆弦周长运和动弧,长从近A运似动相到等B。,线速度从vA变成vB,速度的变化量Δv,如何表示?
看,向心加速度与半径成正比;
匀速圆周运动的实质是什么?
当Δt足够小,Δv=v∙θ
受到指向太阳的引力作用
当Δt足够小,vA,vB的夹角θ 就足够小。
从公式
看,向心加速度与半径成反比;
从公式
看,向心加速度与半径成正比;
地球受到什么力的作用?
质点做匀速圆周运动,从A运动到B,线速度从vA变成vB,速度的变化量Δv,如何表示?
变速曲线运动 运动状态改变 这个力可能沿什么方向?
质点做匀速圆周运动,从A运动到B,线速度从vA变成vB,速度的变化量Δv,如何表示?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆周运动和向心加速度【要点梳理】要点一、圆周运动的线速度 1、线速度的定义:圆周运动中,物体通过的弧长与所用时间的比值,称为圆周运动的线速度。
公式:tlv ∆∆=(比值越大,说明线速度越大) 方向:沿着圆周上各点的切线方向 单位:m/s 2、 说明1)线速度是指物体做圆周运动时的瞬时速度。
2)线速度的方向就是圆周上某点的切线方向线速度的大小是tl∆∆的比值。
所以v 是矢量。
3)匀速圆周运动是一个线速度大小不变的圆周运动。
4)线速度的定义式tlv ∆∆=,无论是对于变速圆周运动还是匀速圆周运动都成立,在变速圆周运动中,只要t ∆取得足够小,公式计算的结果就是瞬时线速度注:匀速圆周运动中的“匀速”二字的含义:仅指速率不变,但速度的方向(曲线上某点的切线方向)时刻在变化。
要点二、描写圆周运动的角速度 1、角速度的定义:圆周运动物体与圆心的连线扫过的角度θ∆与所用时间t ∆的比值叫做角速度。
公式:t∆∆=θω 单位:rad s /(弧度每秒)2、说明:1)这里的θ∆必须是弧度制的角。
2)对于匀速圆周运动来说,这个比值是恒定的,即匀速圆周运动是角速度保持不变的圆周运动。
3)角速度的定义式t∆∆=θω,无论是对于变速圆周运动还是匀速圆周运动都成立,在变速圆周运动中,只要t ∆取得足够小,公式计算的结果就是瞬时角速度。
4)关于ω的方向:中学阶段不研究。
5)同一个转动的物体上,各点的角速度相等例如:木棒以它上面的一点为轴匀速转动时,它上面的各点与圆心的连线在相等时间内扫过的角度相等。
即:3、关于弧度制的介绍(1)角有两种度量单位:角度制和弧度制(2)角度制:将一个圆的周长分为360份,其中的一份对应的圆心角为一度。
因此一个周角是3600,平角和直角分别是1800和900。
(3)弧度制:定义半径长的弧所对应的圆心角为一弧度,符号为rad 。
一段长为l ∆的圆弧对应的圆心角是rl∆=∆θ rad, θ∆=∆r l (4)特殊角的弧度值:在此定义下,一个周角对应的弧度数是:()rad rrππθ22==;平角和直角分别是2ππ和 (rad )。
(5)同一个角的角度α和用弧度制度量的θ之间的关系是:παθ180=rad , 0180⨯=πθα 要点三、匀速圆周运动的周期与转速1、周期的定义:做匀速圆周运动的物体运动一周所用的时间叫做周期,单位:s 。
它描写了圆周运动的重复性。
2、周期T 的意义:不难看到,周期是圆周运动的线速度大小和方向完全恢复初始状态所用的最小时间;周期长说明圆周运动的物体转动得慢,周期短说明转动得快。
观察与思考:同学们看一看你所戴的手表或者墙上钟表上的时、分、秒针,它们的周期分别是多少?想一想角速度和周期的关系如何?(秒针的周期最小,其针尖的线v 最大,ω也最大。
) 3、匀速圆周运动的转速转速n :指转动物体单位时间内转过的圈数。
单位: r/s (转每秒),常用的单位还有r /min (转每分)关系式:nT 1=s(n 单位为r/s)或T n =60s(n 单位为r/min)注意:转速与角速度单位的区别:角速度转速():/():/ωrad sn r s ⎧⎨⎩要点四、描述圆周运动快慢的几个物理量的相互关系因为这几个都是描述圆周运动快慢,所以它们之间必然有内在联系 1、线速度、角速度和周期的关系匀速圆周运动的线速度和周期的关系2rv T π=匀速圆周运动的角速度和周期的关系Tπω2=匀速圆周运动的角速度和周期有确定的对应关系:角速度与周期成反比。
2、线速度、角速度与转速的关系:匀速圆周运动的线速度与转速的关系:2v rn π=(n 的单位是r/s ) 匀速圆周运动的角速度与转速的关系:n πω2=(n 的单位是r/s ) 3、线速度和角速度的关系: (1)线速度和角速度关系的推导:特例推导:设物体沿半径为r 的圆周做匀速圆周运动,在一个T时间内转过2πr 的弧长及2π角度,则:T Tr v πωπ22==ωr v =⇒ 一般意义上的推导:由线速度的定义:t l v ∆∆=而θ∆=∆r l ,所以r tv ∆∆=θ又因为t∆∆=θω,所以ωr v =(2) 线速度和角速度的关系:ωr v = ω=v r可知:ω一定时v r ∝,r v 一定时∝ω。
同理: v 一定时ω∝1r,r 一定时ω∝v 。
(3)对于线速度与角速度关系的理解:是一种瞬时对应关系,即某一时刻的线速度与这一时刻的角速度的关系,适应于匀速圆周运动和变速圆周运动。
要点五、圆周运动的向心加速度1、向心加速度产生的原因:向心加速度由物体所受到的向心力产生,根据牛顿第二定律知道,其大小由向心力的大小和物体的质量决定。
2、向心加速度大小的计算方法: (1)由牛顿第二定律计算:F a m=向向 ;(2)由运动学公式计算:22v a r v rωω===向 如果是匀速圆周运动则有:22222244v a r r r f v r Tπωπω=====向 3、向心加速度a 的方向:沿着半径指向圆心,时刻在发生变化,是一个变量。
4、向心加速度的意义:在一个半径一定的圆周运动中,向心加速度描述的是线速度方向改变的快慢。
5、关于向心加速度的说明(1)从运动学上看:速度方向时刻在发生变化,总是有0≠∆v 必然有向心加速度;(2)从动力学上看:沿着半径方向上指向圆心的的合外力必然产生指向圆心的向心加速度。
加速度是个矢量,既有大小又有方向,匀速圆周运动中加速度大小不变,而方向却不断变化。
因此,匀速圆周运动不是匀变速运动。
【典型例题】类型一、描述匀速圆周运动的各个物理量例1、一个直径为1.4m 的圆盘以中心为轴匀速转动,转速为2转/秒,求圆盘边缘一点的线速度、角速度、周期和向心加速度。
【解析】由题意可知,。
s n m r /r 2,7.0==再根据公式,1,n 2,2nT rn v ===πωπ,可得:。
例2 、机械手表(如图所示)的分针与秒针从第一次重合至第二次重合,中间经历的时间为( )A .5960min B .1min C .6059min D .6160min 【解析】先求出分针与秒针的角速度: 2rad /s 3600πω=分,2rad /s 60πω=秒. 设两次重合的时间间隔为△t ,则有t ϕω=分分△,t ϕω=秒秒△,2ϕωπ-=分秒,即22360060s s min 225959603600t ππππϕω====--分秒△,故C 正确. 【答案】C 举一反三【变式】电风扇叶片边缘一点的线速度为56.7m/s ,若它转动半径为18cm ,求电扇转动的角速度和周期。
【解析】根据线速度与角速度的关系r v ω=得)s (02.022)rad/s (315=====v rT T rv rv ππω所以又因为类型二、向心加速度的计算例3、在长20cm 的细绳的一端系一个小球,绳的另一端固定在水平桌面上,使小球以5m/s 的速度在桌面上做匀速圆周运动,求小球运动的向心加速度和转动的角速度。
【解析】由题意可知s m v m r /5,20.0==根据向心加速度的计算公式222512502025=====v a m /s r .v,rad /srωω向由可得角速度:例4、如图所示,定滑轮的半径,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度=2m/s 做匀加速运动。
在重物由静止下落距离为1m 的瞬间,滑轮边缘上的点的角速度多大?向心加速度多大?【思路点拨】这是一个关于变速圆周运动向心加速度计算的问题。
物体的速度时刻等于轮缘上一点的线速度,求出物体下落1m 时的瞬时速度,然后利用角速度、向心加速度和线速度的关系可以求解。
【解析】 (1)重物下落1m 时,瞬时速度为s m s m as v /2/1222=⨯⨯==显然,滑轮边缘上每一点的线速度也都是2m/s ,故滑轮转动的角速度,即滑轮边缘上每一点的转动角速度为:s rad s rad r v /100/02.02===ω (2)向心加速度为:2222/200/02.0100s m s m r a =⨯==ω【总结升华】此题讨论的是变速运动问题,重物落下的过程中滑轮转动的角速度,轮上各点的线速度都在不断增加,但在任何时刻角速度与线速度的关系,向心加速度与角速度、线速度的关系r r22ω==v a 仍然成立。
类型三、皮带传动问题 例5、如图,主动轮匀速转动,通过皮带不打滑地带动从动轮转动,已知分别为上的中点,轮边缘上一点,轮边缘上一点,为皮带上一点。
试比较:(1)A 、B 、C 点线速度的大小?(2)A 、B 、E 、F 各点角速度的大小? (3)E 、F 点线速度的大小? 【解析】(1)因为皮带传动过程与轮子不打滑,所以A 、B 、C 三个点可以看成是皮带上的三个点,相同时间必定通过相同的路程,因此,A 、B 、C 点的线速度相等,这也是两个轮子的联系。
即(2)比较各点角速度: 比较B A ωω、应通过入手分析r vr r v v BA B A =⎩⎨⎧==ω且因为2B B B A A A r v r v ωω212===所以 因为A 、F 是同一物体上的点,角速度必然相等即F A ωω=,同理E B ωω= 所以(3)由F E v v =所以【总结升华】(1)同一转动物体上的各点,角速度必然相等;(2)皮带传动时,与皮带接触的点线速度相等。
例6、如图所示为录音机在工作时的示意图,轮子1是主动轮,轮子2为从动轮,轮1和轮2就是磁带盒内的两个转盘,空带一边半径为r 1=0.5cm ,满带一边半径为r 2=3cm ,已知主动轮转速不变,恒为n 1=36 r/min ,试求:(1)从动轮2的转速变化范围; (2)磁带运动的速度变化范围.【解析】本题应抓住主动轮(r 1)的角速度恒定不变这一特征,再根据同一时刻两轮磁带走动的线速度相等,从磁带转动时半径的变化来求解.(1)因为v r ω=,且两轮边缘上各点的线速度相等,所以2121226060n n r r ππ=,即1212r n n r =. 当r 2=3cm 时,从动轮2的转速最小,2min 0.536r /min 6r /min 3n =⨯=.当磁带走完,即r 2=0.5cm ,r 1=3cm 时,从动轮2的转速最大,为2max 336r/min 216r/min 0.5n =⨯=,故从动轮2的转速变化范围是6 r/min ~216 r/min .(2)由112v r n π=得知:10.5r =cm 时,22360.5102m /s 0.019m /s 60v π-=⨯⨯⨯=, 13r =cm 时,22363102m /s 0.113m /s 60v π-'=⨯⨯⨯=.故磁带的速度变化范围是0.019 m/s ~0.113 m/s .【总结升华】解答本题的关键是掌握磁带传动装置中主动轮、从动轮上各点线速度、角速度之间的关系,并且注意从动轮转速的变化及磁带速度的变化是由于转动半径的变化引起的. 举一反三【变式】图中所示为一皮带传动装置,右轮的半径为r ,a 是它边缘上的一点,左侧是一轮轴,大轮的半径为4r ,小轮的半径为2r .b 点在小轮上,到小轮中心的距离为r .c 点和d 点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑.则a 、b 、c 、d 的线速度之比 ;角速度之比 ;向心加速度之比 。
