D_重庆市2014年中考数学试卷含答案解析

合集下载

重庆市2014年初中学业水平A测试数学含答案

重庆市2014年初中毕业暨高中招生考试·数学(A卷) 本卷难度：适中难度系数：0.60易错题：7、24、25较难题：22、23(全卷共五个大题，满分150分，考试时间120分钟)参考公式：抛物线y＝ax2＋bx＋c(a≠0)的顶点坐标为(－b2a，4ac－b24a)，对称轴为x＝－b2a.一、选择题(本大题12个小题，每小题4分，共48分)在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将正确答案的代号填在对应的括号内．1. 实数－17的相反数是()A. 17B. 117 C. －17 D. －1172. 计算2x6÷x4的结果是()A. x2B. 2x2C. 2x4D. 2x103. 在a中，a的取值范围是()A. a≥0B. a≤0C. a＞0D. a＜04. 五边形的内角和是()A. 180°B. 360°C. 540°D. 600°5. 2014年1月1日零点，北京、上海、重庆、宁夏的气温分别是－4 ℃、5 ℃、6 ℃、－8 ℃，当时这四个城市中，气温最低的是( )A. 北京B. 上海C. 重庆D. 宁夏6. 关于x的方程2x－1＝1的解是()A. x＝4B. x＝3C. x＝2D. x＝17. 2014年8月26日，第二届青奥会将在南京举行，甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备．在某天“110米跨栏”训练中，每人各跑5次，据统计，他们的平均成绩都是13.2秒，甲、乙、丙、丁的成绩的方差分别是0.11、0.03、0.05、0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是()A. 甲B. 乙C. 丙D. 丁8. 如图，直线AB∥CD，直线EF分别交直线AB、CD于点E、F，过点F作FG⊥FE，交直线AB于点G.若∠1＝42°，则∠2的大小是()A. 56°B. 48°C. 46°D. 40°第8题图第9题图9. 如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC＋∠AOC＝90°，则∠AOC的大小是()A. 30°B. 45°C. 60°D. 70°10. 2014年5月10日上午，小华同学接到通知，她的作文通过了《我的中国梦》征文选拔，需尽快上交该作文的电子文稿．接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一会儿，小华继续录入并加快了录入速度，直至录入完成．设从录入文稿开始所经过的时间为x，录入字数为y，下面能反映y与x的函数关系的大致图象是()11. 如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第(1)个图形中面积为1的正方形有2个，第(2)个图形中面积为1的正方形有5个，第(3)个图形中面积为1的正方形有9个，….按此规律，则第(6)个图形中面积为1的正方形的个数为()第11题图A. 20B. 27C. 35D. 4012. 如图，反比例函数y＝－6x在第二象限的图象上有两点A、B，它们的横坐标分别为－1、－3，直线AB与x轴交于点C，则△AOC的面积为(C)第12题图A. 8B. 10C. 12D. 24二、填空题(本大题6个小题，每小题4分，共24分)在每小题中，请将答案直接填在对应的横线上．13. 方程组⎩⎪⎨⎪⎧x ＝3x ＋y ＝5的解是．14. 据有关部门统计，截止到2014年5月1日，重庆市私家小轿车已达到563000辆，将563000这个数用科学记数法表示为．15. 如图，菱形ABCD 中，∠A ＝60°，BD ＝7，则菱形ABCD 的周长为．第15题图第16题图第18题图16. 如图，△OAB 中，OA ＝OB ＝4，∠A ＝30°，AB 与⊙O 相切于点C ，则图中阴影部分的面积为．(结果保留π)17. 从－1，1，2这三个数字中，随机抽取一个数，记为a .那么，使关于x 的一次函数y ＝2x ＋a 的图象与x 轴、y 轴围成的三角形面积为14，且使关于x 的不等式组⎩⎪⎨⎪⎧x ＋2≤a 1－x ≤2a有解．．的概率为． 18. 如图，正方形ABCD 的边长为6，点O 是对角线AC 、BD 的交点，点E 在CD 上，且DE ＝2CE ，连接BE .过点C 作CF ⊥BE ，垂足是F ，连接OF ，则OF 的长为 .三、解答题(本大题2个小题，每小题7分，共14分)解答时每小题必须写出必要的演算过程或推理步骤．19. 计算：4＋(－3)2－20140×|－4|＋(16)－1.20. 如图，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sin C 的值．第20题图四、解答题(本大题4个小题，每小题10分，共40分)解答时每小题必须写出必要的演算过程或推理步骤．21. 先化简，再求值：1x ÷(x 2＋1x 2－x －2x －1)＋1x ＋1，其中x 的值为方程2x ＝5x －1的解．第22题图22. 为鼓励创业，市政府制定了小型企业的优惠政策，许多小型企业应运而生．某镇统计了该镇今年1～5月新注册小型企业的数量，并将结果绘制成如下两种不完整的统计图：(1)某镇今年1～5月新注册小型企业一共有家，请将折线统计图补充完整；(2)该镇今年3月新注册的小型企业中，只有2家是餐饮企业．现从3月新注册的小型企业中随机抽取2家企业了解其经营状况，请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率．23. 为丰富居民业余生活，某居民区组建筹委会，该筹委会动员居民自愿集资建立一个书刊阅览室．经预算，一共需要筹资30000元，其中一部分用于购买书桌、书架等设施，另一部分用于购买书刊．(1)筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？(2)经初步统计，有200户居民自愿参与集资，那么平均每户需集资150元．镇政府了解情况后，赠送了一批阅览室设施和书籍．这样，只需参与户共集资20000元．经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了a %(其中a ＞0)，则每户平均集资的资金在150元的基础上减少了109a %，求a 的值．24. 如图，△ABC 中，∠BAC ＝90°，AB ＝AC ，AD ⊥BC ，垂足是D ，AE 平分∠BAD ，交BC 于点E .在△ABC 外有一点F ，第24题图使F A ⊥AE ，FC ⊥BC . (1)求证：BE ＝CF ；(2)在AB 上取一点M ，使BM ＝2DE ，连接MC ，交AD 于点N ，连接ME . 求证：①ME ⊥BC ；②DE ＝DN .五、解答题(本大题共2个小题，每小题12分，共24分)解答时每小题必须写出必要的演算过程或推理步骤．25. 如图，抛物线y＝－x2－2x＋3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．(1)求点A、B、C的坐标；(2)点M为线段．．AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；(3)在(2)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G(点G在点F的上方)．若FG＝22DQ，求点F的坐标．第25题图26. 已知：如图①，在矩形ABCD中，AB＝5，AD＝203，AE⊥BD，垂足是E.点F是点E关于AB的对称点，连接AF、BF.(1)求AE和BE的长；(2)若将△ABF沿着射线BD方向平移，设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度)，当点F分别平移到线段AB、AD上时，直接写出相应的m的值；(3)如图②，将△ABF绕点B顺时针旋转一个角α(0°＜α＜180°)，记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q.是否存在这样的P、Q两点，使△DPQ 为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．第26题图重庆市2014年初中毕业暨高中招生考试(A卷)1. A【解析】只有符号不同的两个数互为相反数，17与－17符号不同，故－17的相反数为17.2. B【解析】同底数幂相除，底数不变，指数相减．由此可得，2x6÷x4＝2x6－4＝2x2.3. A【解析】本题考查二次根式有意义的条件．在二次根式中，被开方数必须是非负数，即要大于等于0，故a的取值范围为a≥0.易错警示：在二次根式中，要注意被开方数可以等于0，不要丢解．4. C【解析】本题考查多边形的内角和计算．n边形的内角和公式为：(n－2)×180°，由此可得五边形的内角和为：(5－2)×180°＝3×180°＝540°.备考指导：多边形的有关性质：(1)n边形的内角和为：(n－2)·180°；(2)任意多边形的外角和为：360°；(3)正n边形的每个内角为：（n－2）·180°n，每个外角为：360°n.5. D【解析】本题考查实数的大小比较．－4、5、6、－8这四个数中，按大小顺序排列为：6＞5＞－4＞－8，因此最小的数是－8，它对应的城市为宁夏，所以宁夏的气温最低．方法归纳：实数的大小比较中，正数都大于0，0大于一切负数．两个负数比较大小，绝对值大的反而小；在比较实数的大小时，也可利用数轴法，先把这些数在数轴上表示，然后利用数轴上右边的数总比左边的数大即可．试题点评：以各地气温为背景，考查实数比较大小，这种命题方式新颖，不仅考查了数学知识，更体现出数学在实际生活中的应用价值．6. B【解析】本题考查分式方程的解法．分式方程两边同时乘以最简公分母(x－1)，得：x－1＝2，移项，合并同类项，得：x＝3.检验：把x＝3代入x－1中，值不等于零，所以x＝3是原分式方程的解．方法指导：①把分式方程“转化”为整式方程的条件是去掉分式方程中的分母．如何去掉分母是解分式方程的关键步骤；②用最简公分母乘以分式方程中的每一项，从而约去分母．但要注意去分母时，注意切勿漏乘常数项；③解分式方程可能产生“增根”的情况，则验根是解分式方程的必要步骤．一题多解：本题也可以通过利用选项代入方程验证求出方程的解．7. D【解析】本题考查方差的意义．由于这四位运动员的平均成绩相同，且四位运动员成绩的方差大小为：s2甲＝0.11＞s2丙＝0.05＞s2乙＝0.03＞s2丁＝0.02，因此可知丁的方差最小，根据方差越小，成绩越稳定，故丁的成绩最稳定．方法指导：方差反映一组数据在其平均数左右波动的大小，方差越大，数据波动就越大，越不稳定；方差越小，数据波动就越小，越稳定．第8题解图8. B【解析】本题考查了平行线性质及垂线性质的运用．∵AB∥CD，∴∠1＝∠EFD＝42°，又∵FG⊥FE，∴∠EFG＝90°，又∠CFD＝180°，∴∠2＝180°－∠EFG－∠EFD＝180°－90°－42°＝48°.思维方式：利用平行线性质求角度：先观察要求角与已知角的位置关系，再选择合理的角度进行等量代换，因此需要熟练掌握平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．另外在解题中要注意平角、直角及三角形内角和、三角形内外角关系等知识的运用．第9题解图9. C【解析】本题考查了圆周角的定理．在同圆或等圆中，根据同弧所对的圆周角等于圆心角的一半，可得：∠AOC＝2∠ABC，∴∠ABC＋∠AOC＝3∠ABC ＝90°，解得∠ABC＝30°，∴∠AOC＝60°.方法指导：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于所对圆心角的一半．在具体解答问题时，找准同弧所对的圆周角及圆心角，然后利用此定理解题即可．10. C【解析】根据本题题意，应分为三段函数来呈现：①小华在电脑上打字录入文稿一段时间，此时录入字数随着时间的增加而增加，应为过原点的一条呈上升趋势的直线；②因事暂停，录入的字数不增加，但时间依旧增加，应为平行于x轴的一条直线；③小华继续录入并加快了录入速度，随着时间的增大，字数增加地更剧烈，为一条上升趋势更明显的直线，因此C选项正确．一题多解：排除法：根据题意可知，小华同学录入作文，共分三个阶段，分别是开始、暂停、加快录入速度，所以可排除选项B；因为y轴表示的是录入字数，所以第一、三段图象应该是一直向上的线段，排除选项A；中间休息时，字数不变，所以第二段应该是平行于x轴的一条线段，故选择C.方法归纳：判断实际问题函数图象的方法：①找起点：结合题干中所给自变量及因变量的取值范围，对应到图象中找相对应点；②找特殊点：即交点或转折点，说明图象在此点处将发生变化；③判断图象趋势：判断出函数的增减性；④看是否与坐标轴相交，即此时有一个变量为0.11. B【解析】观察图形可看出，第n个图形有n行，且上一行总比下一行的个数多1，将每一行个数相加即可求解．第(1)个图形中正方形的个数为：2；第(2)个图形中正方形的个数为：2＋3＝5；第(3)个图形中正方形的个数为：2＋3＋4＝9；第(4)个图形中正方形的个数为：2＋3＋4＋5＝14；第(5)个图形中正方形的个数为：2＋3＋4＋5＋6＝20; 由此可得，第(6)个图形中正方形的个数为：2＋3＋4＋5＋6＋7＝27.方法指导：解图形规律探索题的方法：第一步：写序号：记每组图形的序数为“1，2，3，…，n”；第二步：数图形个数：在图形数量变化时，要记出每组图形的表示个数；第三步：寻找图形数量与序数n的关系：图示法：针对寻找第n个图形表示的数量时，先将后一个图形的表示个数与前一个图形的个数进行比对，通常作差(商)来观察是否有恒定量的变化，然后按照定量变化推导出具体某个图形的个数；若当图形变化规律不明显时，如本题第1个数字为2，第2个数字为5，第3个数字为9，第4个数字为14时，可进行图示法：可以看出每组数字之间的差值依次为从3开始的连续整数；然后再根据其每组数字本身特征逆推其规律，从而寻找出第n 个图形的表示个数．第12题解图12. 【教你审题】本题要求△AOC 的面积，只要知道点A 与点C 的坐标即可，而点C 在直线AB 上，故要求点C 坐标需求直线AB 的解析式，因此结合反比例函数解析式及A 、B 点坐标可将问题解决．C 【解析】本题考查反比例函数性质、待定系数法求直线解析式及三角形面积的计算．∵点A 、B 都在反比例函数y ＝－6x 图象上，且点A 、B 的横坐标分别是－1、－3，代入到函数解析式中，可得A 、B 两点的纵坐标为6、2，∴A(－1，6)，B(－3，2)，设直线AB 的解析式为：y ＝kx ＋b ，代入A 、B 两点，得：⎩⎪⎨⎪⎧2＝－3k ＋b 6＝－k ＋b ，解得：⎩⎪⎨⎪⎧k ＝2b ＝8，则直线AB 的解析式为：y ＝2x ＋8，令y ＝0，解得：x ＝－4，则点C 的坐标为(－4，0)，∴OC ＝4，S △AOC ＝12OC·|y A |＝12×4×6＝12.解题突破：解决此题的关键是求出点C 的坐标，又因为点C 在直线AB 上，因此只需求出直线AB 的解析式，即可求出C 点的坐标．思维方式：就本题而言，点A 、B 在反比例函数y ＝－6x 上，即A 、B 点坐标分别可由反比例函数解析式求得．其次利用待定系数法求出其解析式．然后令直线AB 的解析式y 值为0，即可求得C 点坐标．13. ⎩⎪⎨⎪⎧x ＝3y ＝2 【解析】把x ＝3代入x ＋y ＝5中，即3＋y ＝5，解得：y ＝2，因此方程组的解为：⎩⎪⎨⎪⎧x ＝3y ＝2. 方法归纳：解二元一次方程组的方法主要有两种：①代入消元法，代入消元法的步骤中起到消元目的的是“代入”，要把方程组中较简单的一个方程变形，把其中一个未知数用另外一个未知数来表示，代入另外一个方程，就可达到消元的目的；②加减消元法，在加减消元法中起到消元目的的是“加减”，要先把两个方程中的某个未知数的系数化为相同或互为相反的数，再实施加减，最后实现消元．14. 5.63×105 【解析】本题考查大数的科学记数法．将一个较大数表示成a×10n 的形式，其中1≤a ＜10，本题中a ＝5.63，n 的值等于原数的整数位数减去1，本题中n ＝6－1＝5，因此563000＝5.63×105.15. 28 【解析】本题考查菱形性质的计算．∵菱形的四条边都相等，∴AB ＝AD ，又∵∠A ＝60°，则△ABD 是等边三角形，∴AB ＝BD ＝7，则菱形ABCD 的周长为4×7＝28.思维方式：在菱形中若存在一个顶角为60°，则连接另外两点的对角线所分割的两个三角形为等边三角形，故在计算时，可借助等边三角形的性质进行求解．第15题解图16. 43－4π3【解析】本题考查阴影部分面积的计算，涉及扇形及三角形面积的计算．通过图形可知，S 阴影＝S △AOB －S 扇形；∵AB 与⊙O 相切，切点为点C ，根据切线的性质可知，OC ⊥AB ，又∵OA ＝OB ＝4，∠A ＝30°，∴OC ＝2，利用勾股定理，可得：AC ＝23，BC ＝AC ＝23，则AB ＝43，∴S △AOB ＝12×43×2＝43，∵在Rt △AOC 中，∠A ＝30°，∴∠AOC ＝60°，则∠AOB ＝120°，则S 扇形＝n πr 2360＝120π×4360＝4π3.则S阴影＝43－4π3.第16题解图一题多解：由题可知△AOB 关于OC 对称，∴可先计算△AOC 的相关量，再乘以2即可．方法指导：阴影部分面积的求法：①公式法：针对规则的扇形，可直接利用公式S ＝n πr 2360＝12rl 进行计算；②割补法：针对不规则的图形，可将不规则图形经过平移或分割转化为几个规则图形，进行面积的和或差计算；③等积变换法：针对不规则的图形，将不规则的图形拼凑成等积的规则图形求解．17. 13 【解析】本题考查一次函数、不等式组及概率相关计算的综合运用．对于函数y ＝2x ＋a ，令y＝0，解得x ＝－a 2，令x ＝0，则y ＝a ，又∵此直线与x 轴、y 轴围成的三角形的面积为14，则有|－a 2|·|a|·12＝14，即a 24＝14，解得：a ＝±1；又∵不等式组中x ＋2≤a 得，x≤a －2，解1－x≤2a ，得x≥1－2a ，则此不等式组的解集为：1－2a≤x≤a －2，当a ＝1时，－1≤x≤－1，此时不等式组的解为x ＝－1；当a ＝－1时，3≤x≤－3，此时不等式组无解；综上所述不等式组有解时，需a ＝1，则从－1、1、2这三个数中，随机抽取一个数是1的概率为13，即满足要求的概率为13.难点突破：解答本题的关键是确定a 的值，首先通过一次函数与x 轴、y 轴围成的三角形的面积求出a 的值，再解出不等式组，并代入两值，看哪个值能保证此不等式组有解，即可确定a 的值．18. 【思路点拨】过点O 作OG ⊥OF ，交BF 于点G ，这样构造出两个全等三角形△OBG 、△OCF ，得出BG ＝FC ，再利用勾股定理与相似三角形的性质求出线段EF 、BG 、CF 的长度，最后根据勾股定理求出OF 的长．655【解析】过点O 作OG ⊥OF ，交BF 于点G ，∵AC 与BD 是正方形ABCD 的对角线，∴∠BOC＝90°，则∠BOG ＝∠FOC ，又∵OB ＝OC ，∠BGO ＝90°＋∠OFG ，∠OFC ＝90°＋∠OFG ，∴∠BGO ＝∠OFC ，则△OBG ≌△OCF ，∴OG ＝OF ，BG ＝CF ，∵CD ＝6，DE ＝2CE ，解得CE ＝2，在Rt △BEC 中，由勾股定理得，BE ＝210，∵∠ECB ＝∠CFE ＝90°，∠OBG ＝∠FCO ，∠OBC ＝∠DCO ＝45°，∴∠EBC ＝∠FCE ，∴△CEF ∽△BEC ，则CE 2＝EF·BE ，则EF ＝105，∴BF ＝9105，在Rt △FEC 中，利用勾股定理可得，CF ＝CE 2－EF 2＝22－（105）2＝3105，故GF ＝BF －BG ＝9105－3105＝6105，在等腰Rt △OGF 中，OF ＝GF·sin 45°＝6105×22＝655.第18题解图速解技巧：本题可利用射影定理，求出EF 、CF 达到快速解题．难点突破：本题的难点在于①合理添加辅助线作OG ⊥OF ，使△OBG 与△OFC 全等；②在Rt △BEC 中和Rt △FEC 中，利用相似性及勾股定理分别求出线段BE 、CF 、EF 的长度，进而求出BF ＝BE －EF ，GF ＝BF －BG ，最后利用三角函数的定义求出OF 的长度．19.解：原式＝2＋9－1×4＋6(5分) ＝13.(7分)20.解：∵AD ⊥BC ，∴tan ∠BAD ＝BDAD ，(1分)∵tan ∠BAD ＝34，AD ＝12，∴34＝BD12，(2分)∴BD ＝9.(3分)∴CD ＝BC －BD ＝14－9＝5.(4分)∴在Rt △ADC 中，AC ＝AD 2＋CD 2＝122＋52＝13，(6分) ∴sin C ＝AD AC ＝1213.(7分)21.解：原式＝1x ÷[x 2＋1x （x －1）－2x －1]＋1x ＋1(1分)＝1x ÷x 2＋1－2x x （x －1）＋1x ＋1(2分) ＝1x ·x （x －1）（x －1）2＋1x ＋1(4分) ＝1x －1＋1x ＋1(6分) ＝x ＋1（x ＋1）（x －1）＋x －1（x ＋1）（x －1）＝2xx 2－1.(7分) 解方程2x ＝5x －1，得：x ＝13.(9分)当x ＝13时，原式＝2×13（13）2－1＝－34.(10分)22.(1)解：16；(2分) 补图如下：第22题解图①(5分)(2)解：用A 1，A 2表示餐饮企业，B 1，B 2表示非餐饮企业，画树状图如下：第22题解图②(8分) 或列表(8分)由树状图或列表可知，共有12种等可能情况，其中所抽取的企业恰好都是餐饮企业的有2种． ∴所抽取的企业恰好都是餐饮企业的概率为P ＝212＝16.(10分)23.(1)解：设用于购买书桌、书架等设施的资金为x 元，由题意得： 30000－x ≥3x ，(3分) 解得x ≤7500.(5分)答：最多花7500元购买书桌、书架等设施．(2)解：由题意，得：200(1＋a %)·150(1－109a %)＝20000，(8分)设x ＝a %，则3(1＋x )(1－109x )＝2，整理得，10x 2＋x －3＝0，解得x1＝－0.6(舍)，x2＝0.5，(9分)∴a%＝0.5，∴a＝50.(10分)24.(1)证明：如解图，∵∠BAC＝90°，AF⊥AE，∴∠1＋∠EAC＝90°，∠2＋∠EAC＝90°，∴∠1＝∠2，(1分)又∵AB＝AC，∴∠B＝∠ACB＝45°.∵FC⊥BC，∴∠FCA＝90°－∠ACB＝90°－45°＝45°，∴∠B＝∠FCA，(2分)∴△ABE≌△ACF(ASA)，(3分)∴BE＝CF.(4分)(2)证明：①过E作EG⊥AB于点G.∵∠B＝45°，∴△GBE是等腰直角三角形，∴BG＝EG，∠3＝45°，(5分) ∵AD⊥BC，AE平分∠BAD，∴EG＝ED，∴BG＝ED，∵BM＝2ED，∴BM＝2BG，即G是BM的中点，(6分)∴EG是BM的垂直平分线，∴EB＝EM，∴∠4＝∠3＝45°，∴∠MEB＝∠4＋∠3＝45°＋45°＝90°，即ME⊥BC.(7分)②∵AD⊥BC，∴ME∥AD，∴∠5＝∠6，∵∠1＝∠5，∴∠1＝∠6，∴AM＝EM，∵MC＝MC，∴Rt△AMC≌Rt△EMC(HL)，(8分)∴∠7＝∠8，∵∠BAC＝90°，AB＝AC，∴∠ACB＝45°，∠BAD＝∠CAD＝45°，∴∠5＝∠7＝22.5°，AD＝CD，∵∠ADE＝∠CDN＝90°，∴△ADE≌△CDN(ASA)，(9分)∴DE＝DN.(10分)25.(1)解：y＝－x2－2x＋3，令x＝0，得y＝3，则C(0，3)，(1分)令y＝0，得－x2－2x＋3＝0，解得x1＝－3，x2＝1，∴A(－3，0)，B(1，0)．(3分)(2)解：由x＝－－22×（－1）＝－1得抛物线的对称轴为直线x＝－1.(4分) 设点M(x，0)，P(x，－x2－2x＋3)，其中－3＜x＜－1.∵P 、Q 关于直线x ＝－1对称，设Q 的横坐标为a ，则a －(－1)＝－1－x ，∴a ＝－2－x ，∴Q (－2－x ，－x 2－2x ＋3)(5分)∴MP ＝－x 2－2x ＋3，PQ ＝－2－x －x ＝－2－2x ，∴周长d ＝2(－2－2x －x 2－2x ＋3)＝－2x 2－8x ＋2＝－2(x ＋2)2＋10，∴当x ＝－2时，d 取最大值．(6分)此时，M (－2，0)，∴AM ＝－2－(－3)＝1，设直线AC 的解析式为y ＝kx ＋b (k ≠0)，则⎩⎪⎨⎪⎧3＝b 0＝－3k ＋b ，解得⎩⎪⎨⎪⎧b ＝3k ＝1. ∴直线AC 的解析式为y ＝x ＋3.将x ＝－2代入y ＝x ＋3得y ＝1，∴E (－2，1)，∴EM ＝1，(7分)∴S △AEM ＝12AM ·ME ＝12×1×1＝12.(8分)第25题解图(3)解：由(2)知，当矩形PMNQ 的周长最大时，x ＝－2，此时点Q (0，3)，与点C 重合，∴OQ ＝3. 将x ＝－1代入y ＝－x 2－2x ＋3，得y ＝4，∴D (－1，4)．如解图，过D 作DK ⊥y 轴于K ，则DK ＝1，OK ＝4，∴QK ＝OK －OQ ＝4－3＝1，∴△DKQ 是等腰直角三角形，DQ ＝ 2.(9分)∴FG ＝22DQ ＝22×2＝4，(10分)设F (m ，－m 2－2m ＋3)，G (m ，m ＋3)，则FG ＝(m ＋3)－(－m 2－2m ＋3)＝m 2＋3m ，∵FG ＝4，∴m 2＋3m ＝4，解得m 1＝－4，m 2＝1，当m ＝－4时，－m 2－2m ＋3＝－(－4)2－2×(－4)＋3＝－5，当m ＝1时，－m 2－2m ＋3＝－12－2×1＋3＝0，∴F (－4，－5)或(1，0)．(12分)26.(1)解：∵AB ＝5，AD ＝203， ∴由勾股定理得BD ＝AB 2＋AD 2＝52＋（203）2＝253，(1分) ∵12AB ·AD ＝S △ABD ＝12BD ·AE ， ∴12×5×203＝12×253AE ，解得AE ＝4，(3分)∴BE ＝AB 2－AE 2＝52－42＝3.(4分)(2)解：m ＝3；(6分)m ＝163.(8分)第26题解图①【解题提示】当F 在AB 上时，BB 0＝m ，∵△BGB 0∽△BAD ，如解图①，∴B 0G AD ＝BB 0BD ， ∴B 0G 203＝m 253， ∴B 0G ＝45m ，∵点E 、F 关于AB 对称，∴AF ＝AE ＝4，BF ＝BE ＝3.∴A 0F ＝AF ＝4，B 0F ＝BF ＝3，第26题解图②∵S △A 0FB 0＝12A 0B 0·FH ＝12A 0F ·FB 0 ∴12×5·FH ＝12×3×4，解得FH ＝125， ∴45m ＝125，即m ＝3.当F 在AD 上时，如解图②，BB 0＝m ，则DB 0＝253－m ，∵∠DB 0K ＝∠FB 0K ，又∵B 0K ⊥DF ，B 0K ＝B 0K ，∴△DB 0K ≌△FB 0K ，∴DB 0＝FB 0＝3，即253－m ＝3，∴m ＝163. (3)解：存在．理由如下：①当DP ＝DQ 时，若点Q 在线段BD 的延长线上时，如解图③，有∠Q ＝∠1，则∠2＝∠1＋∠Q ＝2∠Q ，第26题解图③∵∠3＝∠4＋∠Q ，∠3＝∠2，∴∠4＋∠Q ＝2∠Q ，∴∠4＝∠Q ，∴A ′Q ＝A ′B ＝5，∴F ′Q ＝4＋5＝9，在Rt △BF ′Q 中，92＋32＝(253＋DQ )2， ∴253＋DQ ＝±310， ∴DQ ＝310－253或DQ ＝－310－253(舍)；(9分)第26题解图④若点Q 在线段BD 上时，如解图④，有∠1＝∠2＝∠4，∵∠1＝∠3，∴∠3＝∠4，∵∠3＝∠5＋∠A ′，∠A ′＝∠CBD ，∴∠3＝∠5＋∠CBD ＝∠A ′BQ ，∴∠4＝∠A ′BQ ，∴A ′Q ＝A ′B ＝5，∴F ′Q ＝5－4＝1，∴BQ ＝32＋12＝10，∴DQ ＝BD －BQ ＝253－10.(10分) ②当PD ＝PQ 时，如解图⑤，∠PDQ ＝∠PQD ，第26题解图⑤∵∠BQA ′＝∠PQD ，∠F ′A ′B ＝∠ADB ，∴△A ′BQ 为等腰三角形，∴A ′B ＝BQ ，∴DQ ＝BD －BQ ＝253－5＝103.(11分)第26题解图⑥③当QP ＝QD 时，如解图⑥，∠P ＝∠PDB ＝∠BA ′F ′，则DP ∥BA ′，A ′在BC 上，∴BQ ＝52×54＝258， ∴DQ ＝BD －BQ ＝253－258＝12524.(12分)。

2024年重庆市中考真题数学试卷(A卷)含答案解析

2024年重庆市中考真题（A卷）数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列四个数中，最小的数是（）A．2-B．0C．3D．1 2 -2．下列四种化学仪器的示意图中，是轴对称图形的是（）A．B．C．D．【答案】C【分析】此题考查了轴对称图形的概念，根据概念逐一判断即可，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线(成轴）对称，熟练掌握知识点是解题的关键．【详解】A、不是轴对称图形，故本选项不符合题意；B、不是轴对称图形，故本选项不符合题意；C、是轴对称图形，故本选项符合题意；D、不是轴对称图形，故本选项不符合题意；故选：C．3．已知点()3,2-在反比例函数()0ky k x=≠的图象上，则k 的值为（）A ．3-B ．3C ． 6-D ．64．如图，AB CD ∥，165∠=︒，则2∠的度数是（）A ．105︒B ．115︒C ．125︒D ．135︒【答案】B【分析】本题主要考查了平行线的性质，根据平行线的性质得3165∠=∠=︒，由邻补角性质得23180∠+∠=︒，然后求解即可，熟练掌握两直线平行，同位角相等是解题的关键．【详解】解：如图，∵AB CD ∥，∴3165∠=∠=︒，∵23180∠+∠=︒，∴2115∠=︒，故选：B ．5．若两个相似三角形的相似比是1:3，则这两个相似三角形的面积比是（）A ．1:3B ．1:4C ．1:6D ．1:9【答案】D【分析】此题考查了相似三角形的性质，根据“相似三角形的面积比等于相似比的平方”解答即可．【详解】解：两个相似三角形的相似比是1:3，则这两个相似三角形的面积比是1:9，故选：D ．6．烷烃是一类由碳、氢元素组成的有机化合物质，下图是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子．第1种如图①有4个氢原子，第2种如图②有6个氢原子，第3种如图③有8个氢原子，……按照这一规律，第10种化合物的分子结构模型中氢原子的个数是（）A ．20B ．22C ．24D ．26【答案】B【分析】本题考查数字的变化类，根据图形，可归纳出规律表达式的特点，再解答即可．【详解】解：由图可得，第1种如图①有4个氢原子，即2214+⨯=第2种如图②有6个氢原子，即2226+⨯=第3种如图③有8个氢原子，即2238+⨯=⋯，∴第10种化合物的分子结构模型中氢原子的个数是：221022+⨯=；故选：B ．7．已知m =m 的范围是（）A ．23m <<B ．34m <<C ．45m <<D ．56m <<8．如图，在矩形ABCD 中，分别以点A 和C 为圆心，AD 长为半径画弧，两弧有且仅有一个公共点．若4=AD ，则图中阴影部分的面积为（）A ．328π-B ．4π-C ．324π-D ．8π-根据题意可得2AC AD =∵矩形ABCD ，∴AD BC =在Rt ABC △中，AB =9．如图，在正方形ABCD 的边CD 上有一点E ，连接AE ，把AE 绕点E 逆时针旋转90︒，得到FE ，连接CF 并延长与AB 的延长线交于点G ．则FGC E的值为（）AB C D 由旋转得,90EA EF AEF =∠=︒，∵四边形ABCD 是正方形，∴90D Ð=°，DC AB ∥，DA =∴D H ∠=∠，10．已知整式1110:n n n n M a x a x a x a --++++ ，其中10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ．下列说法：①满足条件的整式M 中有5个单项式；②不存在任何一个n ，使得满足条件的整式M 有且只有3个；③满足条件的整式M 共有16个．其中正确的个数是（）A ．0B ．1C ．2D ．3【答案】D【分析】本题考查的是整式的规律探究，分类讨论思想的应用，由条件可得04n ≤≤，再分类讨论得到答案即可．【详解】解：∵10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ，∴04n ≤≤，当4n =时，则2104345a a a a a +++++=，∴41a =，23100a a a a ====，满足条件的整式有4x ，当3n =时，则210335a a a a ++++=，∴()()3210,,,2,0,0,0a a a a =，()1,1,0,0，()1,0,1,0，()1,0,0,1，满足条件的整式有：32x ，32x x +，3x x +，31x +，当2n =时，则21025a a a +++=，∴()()210,,3,0,0a a a =，()2,1,0，()2,0,1，()1,2,0，()1,0,2，()1,1,1，满足条件的整式有：23x ，22x x +，221x +，22x x +，22x +，21x x ++；当1n =时，则1015a a ++=，∴()()10,4,0a a =，()3,1，()1,3，()2,2，满足条件的整式有：4x ，31x +，3x +，22x +；当0n =时，005a +=，满足条件的整式有：5；∴满足条件的单项式有：4x ，32x ，23x ，4x ，5，故①符合题意；不存在任何一个n ，使得满足条件的整式M 有且只有3个；故②符合题意；满足条件的整式M 共有1464116++++=个．故③符合题意；故选D二、填空题11．计算：011(3)(2π--+＝．12．若一个多边形的每一个外角都等于40°，则这个多边形的边数是．【答案】9【详解】解：360÷40=9，即这个多边形的边数是9．故答案为：9．13．重庆是一座魔幻都市，有着丰富的旅游资源．甲、乙两人相约来到重庆旅游，两人分别从A 、B 、C 三个景点中随机选择一个景点游览，甲、乙两人同时选择景点B 的概率为．由图可知，共有9种等可能的情况，其中甲、乙两人同时选择景点∴甲、乙两人同时选择景点B 的的概率为19，故答案为：19．14．随着经济复苏，某公司近两年的总收入逐年递增．该公司2021年缴税40万元，2023年缴税48.4万元，该公司这两年缴税的年平均增长率是．【答案】10%【分析】本题主要考查一元二次方程的应用．设平均增长率为x ，然后根据题意可列方程进行求解．【详解】解：设平均增长率为x ，由题意得：()240148.4x +=，解得：10.110%x ==，2 2.1x =-（不符合题意，舍去）；故答案为：10%．15．如图，在ABC 中，延长AC 至点D ，使CD CA =，过点D 作DE CB ∥，且DE DC =，连接AE 交BC 于点F ．若CAB CFA ∠=∠，1CF =，则BF = ．【答案】3【分析】先根据平行线分线段成比例证AF EF =，进而得22DE CD AC CF ====，4AD =，再证明CAB DEA ≌，得4BC AD ==，从而即可得解．16．若关于x 的不等式组()411321x x x x a -⎧<+⎪⎨⎪+≥-+⎩至少有2个整数解，且关于y 的分式方程13211a y y-=---的解为非负整数，则所有满足条件的整数a 的值之和为．17．如图，以AB 为直径的O 与AC 相切于点A ，以AC 为边作平行四边形ACDE ，点D 、E 均在O 上，DE 与AB 交于点F ，连接CE ，与O 交于点G ，连接DG ．若10,8AB DE ==，则AF = ．DG = ．∵以AB 为直径的O 与AC ∴AB AC ⊥，∴90CAB ∠=︒，∵四边形ACDE 为平行四边形，∴∥D E A C ，8AC DE ==，18．我们规定：若一个正整数A 能写成2m n -，其中m 与n 都是两位数，且m 与n 的十位数字相同，个位数字之和为8，则称A 为“方减数”，并把A 分解成2m n -的过程，称为“方减分解”．例如：因为26022523=-，25与23的十位数字相同，个位数字5与3的和为8，所以602是“方减数”，602分解成26022523=-的过程就是“方减分解”．按照这个规定，最小的“方减数”是．把一个“方减数”A 进行“方减分解”，即2A m n =-，将m 放在n 的左边组成一个新的四位数B ，若B 除以19余数为1，且22m n k +=（k 为整数），则满足条件的正整数A 为．三、解答题19．计算：(1)()()22x x y x y -++；(2)22111a a a a -⎛⎫+÷ ⎪+．20．为了解学生的安全知识掌握情况，某校举办了安全知识竞赛．现从七、八年级的学生中各随机抽取20名学生的竞赛成绩（百分制）进行收集、整理、描述、分析．所有学生的成绩均高于60分（成绩得分用x 表示，共分成四组：A ．6070x <≤；B ．7080x <≤；C ．8090x <≤；D ．90100x <≤），下面给出了部分信息：七年级20名学生的竞赛成绩为：66，67，68，68，75，83，84，86，86，86，86，87，87，89，95，95，96，98，98，100.八年级20名学生的竞赛成绩在C 组的数据是：81，82，84，87，88，89．七、八年级所抽学生的竞赛成绩统计表年级七年级八年级平均数8585中位数86b 众数a 79根据以上信息，解答下列问题：(1)上述图表中=a ______，b =______，m =______；(2)根据以上数据分析，你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好？请说明理由（写出一条理由即可）；(3)该校七年级有400名学生，八年级有500名学生参加了此次安全知识竞赛，估计该校七、八年级参加此次安全知识竞赛成绩优秀()90x >的学生人数是多少？【答案】(1)86，87.5，40；(2)八年级学生竞赛成绩较好，理由见解析；(3)该校七、八年级参加此次安全知识竞赛成绩优秀的学生人数是320人．【分析】（1）根据表格及题意可直接进行求解；（2）根据平均分、中位数及众数分析即可得出结果；（3）由题意可得出参加此次竞赛活动成绩优秀的百分比，然后可进行求解；本题主要考查扇形统计图及中位数、众数、平均数，熟练掌握扇形统计图及中位数、众数、平均数是解题的关键．【详解】（1）根据七年级学生竞赛成绩可知：86出现次数最多，则众数为86，八年级竞赛成绩中A 组：2010%2⨯=（人），B 组：2020%4⨯=（人），21．在学习了矩形与菱形的相关知识后，小明同学进行了更深入的研究，他发现，过矩形的一条对角线的中点作这条对角线的垂线，与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形，可利用证明三角形全等得到此结论．根据他的想法与思路，完成以下作图与填空：(1)如图，在矩形ABCD中，点O是对角线AC的中点．用尺规过点O作AC的垂线，分别交AB，CD于点E，F，连接AF，CE．（不写作法，保留作图痕迹）(2)已知：矩形ABCD，点E，F分别在AB，CD上，EF经过对角线AC的中点O，且⊥．求证：四边形AECF是菱形．EF AC证明：∵四边形ABCD是矩形，．∴AB CD∠=∠．∴①，OCF OAE∵点O是AC的中点，∴②．∴CFO AEO≅△△（AAS）．∴③．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．进一步思考，如果四边形ABCD 是平行四边形呢？请你模仿题中表述，写出你猜想的结论：④．【答案】(1)见解析(2)①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形【分析】本题主要考查了矩形的性质，平行四边形的性质与判定，菱形的判定，垂线的尺规作图：（1）根据垂线的尺规作图方法作图即可；（2）根据矩形或平行四边形的对边平行得到OFC OEA ∠=∠，OCF OAE ∠=∠，进而证明()AAS CFO AEO ≌，得到OF OE =，即可证明四边形AECF 是平行四边形．再由EF AC ⊥，即可证明四边形AECF 是菱形．【详解】（1）解：如图所示，即为所求；（2）证明：∵四边形ABCD 是矩形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．猜想：过平行四边形的一条对角线的中点作这条对角线的垂线，与平行四边形两边相交的两点和这条对角线的两个端点构成的四边形是菱形；证明：∵四边形ABCD 是平行四边形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．故答案为：①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形．22．为促进新质生产力的发展，某企业决定投入一笔资金对现有甲、乙两类共30条生产线的设备进行更新换代．(1)为鼓励企业进行生产线的设备更新，某市出台了相应的补贴政策．根据相关政策，更新1条甲类生产线的设备可获得3万元的补贴，更新1条乙类生产线的设备可获得2万元的补贴．这样更新完这30条生产线的设备，该企业可获得70万元的补贴．该企业甲、乙两类生产线各有多少条？(2)经测算，购买更新1条甲类生产线的设备比购买更新1条乙类生产线的设备需多投入5万元，用200万元购买更新甲类生产线的设备数量和用180万元购买更新乙类生产线的设备数量相同，那么该企业在获得70万元的补贴后，还需投入多少资金更新生产线的设备？【答案】(1)该企业甲类生产线有10条，则乙类生产线各有20条；(2)需要更新设备费用为1330万元23．如图，在ABC 中，6AB =，8BC =，点P 为AB 上一点，过点P 作PQ BC ∥交AC 于点Q ．设AP 的长度为x ，点P ，Q 的距离为1y ，ABC 的周长与APQ △的周长之比为2y ．(1)请直接写出1y ，2y 分别关于x 的函数表达式，并注明自变量x 的取值范围；(2)在给定的平面直角坐标系中画出函数1y ，2y 的图象；请分别写出函数1y ，2y 的一条性质；(3)结合函数图象，直接写出12y y >时x 的取值范围．（近似值保留一位小数，误差不超过0.2）（3）解：由函数图象可知，当12y y >时x 的取值范围2.26x <≤．24．如图，甲、乙两艘货轮同时从A 港出发，分别向B ，D 两港运送物资，最后到达A 港正东方向的C 港装运新的物资．甲货轮沿A 港的东南方向航行40海里后到达B 港，再沿北偏东60︒方向航行一定距离到达C 港．乙货轮沿A 港的北偏东60︒方向航行一定距离到达D 港，再沿南偏东30︒方向航行一定距离到达C 港． 1.41≈ 1.73≈，2.45≈）(1)求A ，C 两港之间的距离（结果保留小数点后一位）；(2)若甲、乙两艘货轮的速度相同（停靠B 、D 两港的时间相同），哪艘货轮先到达C 港？请通过计算说明．∴90AEB CEB ∠=∠=︒，由题意可知：45GAB ∠=︒，∴45BAE ∠=︒，∴cos 40cos AE AB BAE =∠=⨯∴tan 202tan CE BE EBC =∠=25．如图，在平面直角坐标系中，抛物线()240y ax bx a =++≠经过点()1,6-，与y 轴交于点C ，与x 轴交于A B ，两点（A 在B 的左侧），连接tan 4AC BC CBA ∠=，，．(1)求抛物线的表达式；(2)点P 是射线CA 上方抛物线上的一动点，过点P 作PE x ⊥轴，垂足为E ，交AC 于点D ．点M 是线段DE 上一动点，MN y ⊥轴，垂足为N ，点F 为线段BC 的中点，连接AM NF ，．当线段PD 长度取得最大值时，求AM MN NF ++的最小值；(3)将该抛物线沿射线CA 方向平移，使得新抛物线经过（2）中线段PD 长度取得最大值时的点D ，且与直线AC 相交于另一点K ．点Q 为新抛物线上的一个动点，当QDK ACB ∠∠=时，直接写出所有符合条件的点Q 的坐标．∴()4,0A -，设直线AC 的解析式为y =代入()4,0A -，得04m =-解得1m =，∴直线AC 的解析式为y =()当0y =时，046x =--，解得32x =-，∴3,02G ⎛⎫- ⎪⎝⎭∵()4,0A -，()0,4C ，∴OA OC =，∴45OAC OCA ∠=∠=︒，∵DR x ∥轴，26．在ABC 中，AB AC =，点D 是BC 边上一点（点D 不与端点重合）．点D 关于直线AB 的对称点为点E ，连接,AD DE ．在直线AD 上取一点F ，使EFD BAC ∠∠=，直线EF 与直线AC 交于点G ．(1)如图1，若60,,BAC BD CD BAD α∠=︒<∠=，求AGE ∠的度数（用含α的代数式表示）；(2)如图1，若60,BAC BD CD ∠=︒<，用等式表示线段CG 与DE 之间的数量关系，并证明；(3)如图2，若90BAC ∠=︒，点D 从点B 移动到点C 的过程中，连接AE ，当AEG △为等腰三角形时，请直接写出此时CG AG 的值．∵EFD BAC ∠∠=，BAC ∠∴60EFD ∠=︒∵1EFD BAD ∠=∠+∠=∠∴160α∠=︒-，∵,AB AC EFD BAC =∠=∠∴=45ABC ∠︒，由轴对称知EAB ∠=∠试题31设BAD BAE β∠=∠=，∴90DAC GAF ∠=∠=︒∴GAE EAF GAF ∠=∠-∠∵GE GA =，。

2014重庆中考数学试卷A

2014中考数学试卷精编word版2014年重庆市中考数学试卷（满分150分，考试时间120分钟）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.（2014重庆市A卷，1，4分）实数－17的相反数是（）A．17 B．11 C．－17 D．? 1717642. （2014重庆市A卷，2，4分）计算2x?x的结果是（）A．x B．2x C．2x D．2x3（2014重庆市A卷，3，4分）a的取值范围是（）A．a?0 B．a?0 C．a?0 D．a?04. （2014重庆市A卷，4，4分）五边形的内角和是（）A．180° B．360° C．540° D．600°5. （2014重庆市A卷，5，4分）2014年1月1日零点，北京、上海、重庆、宁夏的气温分别是－4℃、5℃、6℃、－8℃，当时这四个城市中，气温最低的是（）A．北京 B．上海 C．重庆 D．宁夏 224102?1的解是（） x?1A．x?4 B．x?3 C．x?2 D．x?1 6（2014重庆市A卷，6，4分）关于x的方程7. （2014重庆市A卷，7，4分）2014年8月26日，第二届表奥会将在南京举行，甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备．在某天“110米跨栏”训练中，每人各跑5次，据统计，他们的平均成绩都是13.2秒，甲、乙、丙、丁的成绩的方差分别是0.11、0.03、0.05、0.02．则当天这四位运动员“110米跨栏”的训练成绩最稳定的是（）A．甲 B．乙 C．丙 D．丁8.（2014重庆市A卷，8，4分）如图，直线AB∥CD，直线EF分别交直线AB、CD于点EF，过点F作FG⊥FE，交直线AB于点G．若∠1=42°，则∠2的大小是（）A．56° B．48° C．46° D．40°AC8题图BD精品资源 JSCM中考团队合作共赢。

2014年中考数学二轮精品复习试卷(四边形)含答案解析

2014年中考数学二轮精品复习试卷：四边形1、如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD 于点O，连结AO，下列结论不正确的是【】A．△AOB≌△BOC B．△BOC≌△EOD C．△AOD≌△EOD D．△AOD≌△BOC2、（2013年四川资阳3分）如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是【】A．48 B．60 C．76 D．803、正六边形的边心距与边长之比为A．B．C．1：2 D．4、如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是A．矩形B．菱形C．正方形D．梯形5、如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB 中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为A．78°B．75°C．60°D．45°6、如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD至点E，使ME=MC，以DE为边作正方形DEFG，点G在边CD上，则DG 的长为A．B．C．D．7、如图，梯形ABCD中，AD∥BC，AB=，BC=4，连结BD，∠BAD的平分线交BD于点E，且AE∥CD，则AD的长为【】A．B．C．D．128、如图，菱形ABCD中，，AB=4，则以AC为边长的正方形ACEF的周长为【】A．14 B．15 C．16 D．179、如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，若AB=2，则C′D的长为【】A．1 B．2 C．3 D．410、下列命题中是假命题的是【】A．平行四边形的对边相等B．菱形的四条边相等C．矩形的对边平行且相等D．等腰梯形的对边相等11、如图，在平行四边形ABCD中，AB=4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG=1，则AE的边长为A．B．C．4 D．812、如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边做平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边做平行四边形AO1C2B；…；依此类推，则平行四边形AO4C5B的面积为A．cm2B．cm2 C．cm2D．cm213、下列命题中的真命题是A．三个角相等的四边形是矩形B．对角线互相垂直且相等的四边形是正方形C．顺次连接矩形四边中点得到的四边形是菱形D．正五边形既是轴对称图形又是中心对称图形14、如图，在菱形ABCD中，∠BAD=2∠B，E，F分别为BC，CD的中点，连接AE、AC、AF，则图中与△ABE全等的三角形（△ABE除外）有A．1个B．2个C．3个D．4个15、在梯形ABCD中，AD∥BC，对角线AC和BD交于点O，下列条件中，能判断梯形ABCD是等腰梯形的是【】A．∠BDC =∠BCD B．∠ABC =∠DAB C．∠ADB =∠DAC D．∠AOB =∠BOC16、如图，矩形纸片ABCD中，AB=6cm，BC=8cm，现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为【】A．6cm B．4cm C．2cm D．1cm17、如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC 交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有【】个．A．2 B．3 C．4 D．518、顺次连接等腰梯形四边中点所得的四边形一定是【】A．矩形B．正方形C．菱形D．直角梯形19、如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则GT=A．B．C．2 D．120、如图，在平行四边形ABCD中，AB＞CD，按以下步骤作图：以A为圆心，小于AD 的长为半径画弧，分别交AB、CD于E、F；再分别以E、F为圆心，大于EF的长半径画弧，两弧交于点G；作射线AG交CD于点H。

2024年重庆市中考数学试题B卷(含答案)

重庆市2024年初中学业水平暨高中招生考试数学试题（B卷）（全卷共三个大题，满分150分，考试时间120分钟）注意事项：1．试题的答案书写在答题卡上，不得在试题卷上直接作答；2．作答前认真阅读答题卡上的注意事项；3．作图（包括作辅助线）请一律用黑色2B铅笔完成；4．考试结束，由监考人员将试题卷和答题卡一并收回．参考公式：抛物线()20y ax bx c a=++≠的顶点坐标为24,24b ac ba a⎛⎫-- ⎪⎝⎭，对称轴为2bxa=-．一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．1.下列各数中最小的数是（）A.1-B.0C.1D.2【答案】A【解析】【分析】根据正数大于0，0大于负数，即可作出判断．【详解】1-是负数，其他三个数均是非负数，故1-是最小的数；故选：A．【点睛】本题考查了有理数大小的比较：负数小于一切非负数，明确此性质是关键．2.下列标点符号中，是轴对称图形的是（）A.B.C.D.【答案】A【解析】【分析】本题考查轴对称图形的识别．解题的关键是理解轴对称的概念（如果一个平面图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴），寻找对称轴，图形两部分沿对称轴折叠后可重合．据此对各选项逐一进行判断即可．【详解】解：A．该标点符号是轴对称图形，故此选项符合题意；B．该标点符号不是轴对称图形，故此选项不符合题意；C．该标点符号不是轴对称图形，故此选项不符合题意；D ．该标点符号不是轴对称图形，故此选项不符合题意．故选：A ．3.反比例函数10y x =-的图象一定经过的点是（）A.()1,10 B.()2,5- C.()2,5 D.()2,8【答案】B【解析】【分析】本题考查了求反比例函数值．熟练掌握求反比例函数值是解题的关键．分别将各选项的点坐标的横坐标代入，求纵坐标，然后判断作答即可．【详解】解：解：当1x =时，10101y =-=-，图象不经过()1,10，故A 不符合要求；当2x =-时，1052y =-=-，图象一定经过()2,5-，故B 符合要求；当2x =时，1052y =-=-，图象不经过()2,5，故C 不符合要求；当2x =时，1052y =-=-，图象不经过()2,8，故D 不符合要求；故选：B ．4.如图，AB CD ∥，若1125∠=︒，则2∠的度数为（）A .35︒ B.45︒ C.55︒ D.125︒【答案】C【解析】【分析】本题考查了平行线的性质，邻补角的定义，根据邻补角的定义求出3∠，然后根据平行线的性质求解即可．【详解】解：如图，∵1125∠=︒，∴3180155∠=︒-∠=︒，∵AB CD ∥，∴2355∠=∠=︒，故选：C ．5.若两个相似三角形的相似比为1:4，则这两个三角形面积的比是（）A.1:2B.1:4C.1:8D.1:16【答案】D【解析】【分析】本题主要考查了相似三角形的性质，根据相似三角形的面积之比等于相似比的平方进行求解即可．【详解】解：∵两个相似三角形的相似比为1:4，∴这两个三角形面积的比是221:41:16=，故选：D ．6.估计的值应在（）A.8和9之间B.9和10之间C.10和11之间D.11和12之间【答案】C【解析】【分析】本题考查的是二次根式的乘法运算，无理数的估算，先计算二次根式的乘法运算，再估算即可．6=，而45<=，∴10611<<，故答案为：C7.用菱形按如图所示的规律拼图案，其中第①个图案中有2个菱形，第②个图案中有5个菱形，第③个图案中有8个菱形，第④个图案中有11个菱形，…，按此规律，则第⑧个图案中，菱形的个数是（）A.20B.21C.23D.26【答案】C【解析】【分析】本题考查了图形类的规律探索，解题的关键是找出规律．利用规律求解．通过观察图形找到相应的规律，进行求解即可．【详解】解：第①个图案中有()131112+⨯-+=个菱形，第②个图案中有()132115+⨯-+=个菱形，第③个图案中有()133118+⨯-+=个菱形，第④个图案中有()1341111+⨯-+=个菱形，∴第n 个图案中有()131131n n +-+=-个菱形，∴第⑧个图案中菱形的个数为38123⨯-=，故选：C ．8.如图，AB 是O 的弦，OC AB ⊥交O 于点C ，点D 是O 上一点，连接BD ，CD ．若28D ∠=︒，则OAB ∠的度数为（）A.28︒B.34︒C.56︒D.62︒【答案】B【解析】【分析】本题考查了圆周角定理，等腰三角形的性质等知识，利用圆周角定理求出COB ∠，根据等腰三角形的三线合一性质求出AOB ∠，等边对等角然后结合三角形内角和定理求解即可．【详解】解：∵28D ∠=︒，∴256BOC D ∠=∠=︒，∵OC AB ⊥，OA OB =，∴2112AOB BOC ∠=∠=︒，OAB OBA ∠=∠，∴()1180342OAB AOB ∠=︒-∠=︒，故选：B ．9.如图，在边长为4的正方形ABCD 中，点E 是BC 上一点，点F 是CD 延长线上一点，连接AE ，AF ，AM 平分EAF ∠．交CD 于点M ．若1BE DF ==，则DM 的长度为（）A.2B.C.D.125【答案】D【解析】【分析】本题主要考查了正方形的性质，全等三角形的性质与判定，勾股定理，先由正方形的性质得到904ABE ADC ADF C AB AD CD BC ====︒====∠∠∠∠，，再证明()SAS ABE ADF △≌△得到AE AF =，进一步证明()SAS AEM AFM △≌△得到EM FM =，设DM x =，则14EM FM DF DM x CM CD DM x ==+=+=-=-，，在Rt CEM △中，由勾股定理得()()222134x x +=+-，解方程即可得到答案．【详解】解：∵四边形ABCD 是正方形，∴904ABE ADC ADF C AB AD CD BC ====︒====∠∠∠∠，，又∵1BE DF ==，∴()SAS ABE ADF △≌△，∴AE AF =，∵AM 平分EAF ∠，∴EAM FAM ∠=∠，又∵AM AM =，∴()SAS AEM AFM △≌△，∴EM FM =，设DM x =，则14EM FM DF DM x CM CD DM x ==+=+=-=-，，在Rt CEM △中，由勾股定理得222EM CE CM =+，∴()()222134x x +=+-，解得125x =，∴125DM =，故选：D ．10.已知整式1110:n n n n M a x a x a x a --++++ ，其中10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ．下列说法：①满足条件的整式M 中有5个单项式；②不存在任何一个n ，使得满足条件的整式M 有且只有3个；③满足条件的整式M 共有16个．其中正确的个数是（）A.0B.1C.2D.3【答案】D【解析】【分析】本题考查的是整式的规律探究，分类讨论思想的应用，由条件可得04n ≤≤，再分类讨论得到答案即可．【详解】解：∵10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ，∴04n ≤≤，当4n =时，则2104345a a a a a +++++=，∴41a =，23100a a a a ====，满足条件的整式有4x ，当3n =时，则210335a a a a ++++=，∴()()3210,,,2,0,0,0a a a a =，()1,1,0,0，()1,0,1,0，()1,0,0,1，满足条件的整式有：32x ，32x x +，3x x +，31x +，当2n =时，则21025a a a +++=，∴()()210,,3,0,0a a a =，()2,1,0，()2,0,1，()1,2,0，()1,0,2，()1,1,1，满足条件的整式有：23x ，22x x +，221x +，22x x +，22x +，21x x ++；当1n =时，则1015a a ++=，∴()()10,4,0a a =，()3,1，()1,3，()2,2，满足条件的整式有：4x ，31x +，3x +，22x +；当0n =时，005a +=，满足条件的整式有：5；∴满足条件的单项式有：4x ，32x ，23x ，4x ，5，故①符合题意；不存在任何一个n ，使得满足条件的整式M 有且只有3个；故②符合题意；满足条件的整式M 共有1464116++++=个．故③符合题意；故选D二、填空题：（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上．11.计算：023-+=______．【答案】3【解析】【分析】原式第一项利用绝对值的代数意义化简，第二项利用零指数幂法则计算即可得到结果．【详解】解：原式=2+1=3，故答案为：3．【点睛】此题考查了有理数的运算，熟练掌握运算法则是解本题的关键．12.甲、乙两人分别从A 、B 、C 三个景区中随机选取一个景区前往游览，则他们恰好选择同一景区的概率为________．【答案】13【解析】【分析】本题考查了列表法与树状图法：画树状图展示所有9种等可能的结果数，找出甲、乙恰好游玩同一景点的结果数，然后根据概率公式求解．【详解】解：画树状图如下：由图可知，共有9种等可能的情况，他们选择同一个景点有3种，故他们选择同一个景点的概率是：3193=，故答案为：13．13.若正多边形的一个外角是45°，则该正多边形的边数是_________.【答案】8【解析】【分析】根据多边形外角和是360度，正多边形的各个内角相等，各个外角也相等，直接用36045︒÷︒可求得边数．【详解】解：多边形外角和是360度，正多边形的一个外角是45︒，360458∴︒÷︒=即该正多边形的边数是8，故答案为：8．【点睛】本题主要考查了多边形外角和以及多边形的边数，解题的关键是掌握正多边形的各个内角相等，各个外角也相等．14.重庆在低空经济领域实现了新的突破．今年第一季度低空飞行航线安全运行了200架次，预计第三季度低空飞行航线安全运行将达到401架次．设第二、第三两个季度安全运行架次的平均增长率为x ，根据题意，可列方程为________．【答案】()22001401x +=【解析】【分析】本题主要考查了一元二次方程的实际应用，设第二、第三两个季度安全运行架次的平均增长率为x ，则第二季度低空飞行航线安全运行了()2001x +架次，第三季度低空飞行航线安全运行了()22001x +架次，据此列出方程即可．【详解】解：设第二、第三两个季度安全运行架次的平均增长率为x ，由题意得，()22001401x +=，故答案为：()22001401x +=．15.如图，在ABC 中，AB AC =，36A ∠=︒，BD 平分ABC ∠交AC 于点D ．若2BC =，则AD 的长度为________．【答案】2【解析】【分析】本题主要考查了等腰三角形的性质与判定，三角形内角和定理，三角形外角的性质，先根据等边对等角和三角形内角和定理求出72C ABC ∠=∠=︒，再由角平分线的定义得到36ABD CBD ∠=∠=︒，进而可证明A ABD BDC C ==∠∠，∠∠，即可推出2AD BC ==．【详解】解：∵在ABC 中，AB AC =，36A ∠=︒，∴180722A C ABC ︒︒-∠∠=∠==，∵BD 平分ABC ∠，∴1362ABD CBD ABC ∠=∠=∠=︒，∴72A ABD BDC A ABD C ==+=︒=∠∠，∠∠∠∠，∴AD BD BD BC ==，，∴2AD BC ==,故答案为：2．16.若关于x 的一元一次不等式组2133423x x x a +⎧≤⎪⎨⎪-<+⎩的解集为4x ≤，且关于y 的分式方程8122a y y y --=++的解均为负整数，则所有满足条件的整数a 的值之和是________．【答案】12【解析】【分析】本题主要考查了根据分式方程解的情况求参数，根据不等式组的解集求参数，先解不等式组中的两个不等式，再根据不等式组的解集求出2a >；解分式方程得到102a y -=，再由关于y 的分式方程8122a y y y --=++的解均为负整数，推出10a <且6a ≠且a 是偶数，则210a <<且6a ≠且a 是偶数，据此确定符合题意的a 的值，最后求和即可．【详解】解：2133423x x x a +⎧≤⎪⎨⎪-<+⎩①②解不等式①得：4x ≤，解不等式②得：2x a <+，∵不等式组的解集为4x ≤，∴24a +>，∴2a >；解分式方程8122a y y y --=++得102a y -=，∵关于y 的分式方程8122a y y y --=++的解均为负整数，∴1002a -<且102a -是整数且102202a y -+=+≠，∴10a <且6a ≠且a 是偶数，∴210a <<且6a ≠且a 是偶数，∴满足题意的a 的值可以为4或8，∴所有满足条件的整数a 的值之和是4812+=．故答案为：12．17.如图，AB 是O 的直径，BC 是O 的切线，点B 为切点．连接AC 交O 于点D ，点E 是O 上一点，连接BE ，DE ，过点A 作AF BE ∥交BD 的延长线于点F ．若5BC =，3CD =，F ADE ∠=∠，则AB 的长度是________；DF 的长度是________．【答案】①.203##263②.83##223【解析】【分析】由直径所对的圆周角是直角得到90ADB BDC ∠=∠=︒，根据勾股定理求出4BD =，则3cos 5CD C BC ==，由切线的性质得到90ABC ∠=︒，则可证明C ABD ∠=∠，解直角三角形即可求出20cos 3BD AB ABD ==∠；连接AE ，由平行线的性质得到BAF ABE ∠=∠，再由F ADE ∠=∠，ADE ABE ∠=∠，推出F BAF ∠=∠，得到203BF AB ==，则208433DF BF BD =-=-=．【详解】解：∵AB 是O 的直径，∴90ADB BDC ∠=∠=︒，在Rt BDC中，由勾股定理得4BD ==，∴3cos 5CD C BC ==，∵BC 是O 的切线，∴90ABC ∠=︒，∴90C CBD CBD ABD +=+=︒∠∠∠∠，∴C ABD ∠=∠，在Rt △ABD 中，4203cos 35BD AB ABD ===∠；如图所示，连接AE，∵AF BE ∥，∴BAF ABE ∠=∠，∵F ADE ∠=∠，ADE ABE ∠=∠，∴F BAF ∠=∠，∴203BF AB ==，∴208433DF BF BD =-=-=；故答案为：203；83．【点睛】本题主要考查了切线的性质，同弧所对的圆周角相等，直径所对的圆周角是直角，勾股定理，解直角三角形，等腰三角形的判定等等，证明F BAF ∠=∠是解题的关键．18.一个各数位均不为0的四位自然数M abcd =，若满足9a d b c +=+=，则称这个四位数为“友谊数”．例如：四位数1278，∵18279+=+=，∴1278是“友谊数”．若abcd 是一个“友谊数”，且1b a c b -=-=，则这个数为________；若M abcd =是一个“友谊数”，设()9M F M =，且()13F M ab cd++是整数，则满足条件的M 的最大值是________．【答案】①.3456②.6273【解析】【分析】本题主要考查了新定义，根据新定义得到9a d b c +=+=，再由1b a c b -=-=可求出a 、b 、c 、d 的值，进而可得答案；先求出9999099M a b =++，进而得到()36981313F M ab cda b a ++++=++，根据()13F M ab cd++是整数，得到369813a b a ++++是整数，即3613a b ++是整数，则36a b ++是13的倍数，求出8a ≤，再按照a 从大到小的范围讨论求解即可．【详解】解：∵abcd 是一个“友谊数”，∴9a d b c +=+=，又∵1b a c b -=-=，∴45b c ==，，∴36a d ==，，∴这个数为3456；∵M abcd =是一个“友谊数”，∴100010010M a b c d=+++()10001001099a b b a=++-+-9999099a b =++，∴()11110119M F M a b ==++，∴()13F M ab cd++1111011101013a b a b c d++++++=()111101*********a b a b b a +++++-+-=12011013a b ++=1173104613a a b ++++=369813a b a ++=++，∵()13F M ab cd++是整数，∴369813a b a ++++是整数，即3613a b ++是整数，∴36a b ++是13的倍数，∵a b c d 、、、都是不为0的正整数，且9a d b c +=+=，∴8a ≤，∴当8a =时，313638a b ≤++≤，此时不满足36a b ++是13的倍数，不符合题意；当7a =时，283635a b ≤++≤，此时不满足36a b ++是13的倍数，不符合题意；当6a =时，253632a b ≤++≤，此时可以满足36a b ++是13的倍数，即此时2b =，则此时37d c ==，，∵要使M 最大，则一定要满足a 最大，∴满足题意的M 的最大值即为6273；故答案为：3456；6273．三、解答题：（本大题8个小题，第19题8分，其余每题各10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．19.计算：（1）()()()312a a a a -+-+；（2）22241244x x x x -⎛⎫+÷ ⎪--+⎝⎭．【答案】（1）42a -（2）2x x +【解析】【分析】本题主要考查了整式的混合计算，分式的混合计算∶（1）先根据单项式乘以多项式的计算法则和多项式乘以多项式的计算法则去括号，然后合并同类项即可得到答案；（2）先把小括号内的式子通分，再把除法变成乘法后约分化简即可得到答案．【小问1详解】解：()()()312a a a a -+-+22322a a a a a =-+-+-42a =-；【小问2详解】解：22241244x x x x -⎛⎫+÷ ⎪--+⎝⎭()()()2222222x x x x x +--+=÷--()()()22222x x x x x -=⋅-+-2x x =+．20.数学文化有利于激发学生数学兴趣．某校为了解学生数学文化知识掌握的情况，从该校七、八年级学生中各随机抽取10名学生参加了数学文化知识竞赛，并对数据（百分制）进行整理、描述和分析（成绩均不低于70分，用x 表示，共分三组：A ．90100x ≤≤，B ．8090x ≤<，C ．7080x ≤<），下面给出了部分信息：七年级10名学生的竞赛成绩是：76，78，80，82，87，87，87，93，93，97．八年级10名学生的竞赛成绩在B 组中的数据是：80，83，88，88．七、八年级抽取的学生竞赛成绩统计表年级平均数中位数众数七年级8687b 八年级86a 90根据以上信息，解答下列问题：（1）填空：=a ________，b =________，m =________；（2）根据以上数据，你认为该校七、八年级中哪个年级学生数学文化知识较好？请说明理由（写出一条理由即可）；（3）该校七年级学生有500人，八年级学生有400人．估计该校七、八年级学生中数学文化知识为“优秀”()90x ≥的总共有多少人？【答案】（1）88；87；40（2）八年级学生数学文化知识较好，理由见解析（3）310人【解析】【分析】本题主要考查了中位数，众数，用样本估计总体，扇形统计图等等：（1）根据中位数和众数的定义可求出a 、b 的值，先求出把年级A 组的人数，进而可求出m 的值；（2）根据八年级学生成绩的中位数和众数都比七年级学生成绩的高即可得到结论；（3）用七年级的人数乘以七年级样本中优秀的人数占比求出七年级优秀人数，用八年级的人数乘以八年级样本中优秀的人数占比求出八年级优秀人数，再二者求和即可得到答案．【小问1详解】解：八年级C 组的人数为1020%2⨯=人，而八年级B 组有4人，则把八年级10名学生的成绩按照从低到高排列，处在第5名和第6名的成绩分别为88分，88分，∴八年级学生成绩的中位数8888882a +==；∵七年级10名学生成绩中，得分为87分的人数最多，∴七年级的众数87b =；由题意得，1041020%%100%40%10m --⨯=⨯=，∴40m =；故答案为：88；87；40；【小问2详解】解：八年级学生数学文化知识较好，理由如下：∵两个年级10名学生的平均成绩相同，但是八年级学生成绩的中位数和众数都比七年级学生成绩的高，∴八年级学生数学文化知识较好；【小问3详解】解：350040040%31010⨯+⨯=人，∴估计该校七、八年级学生中数学文化知识为“优秀”的总共有310人．21.在学习了矩形与菱形的相关知识后，小明同学进行了更深入的研究，他发现，过矩形的一条对角线的中点作这条对角线的垂线，与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形，可利用证明三角形全等得到此结论．根据他的想法与思路，完成以下作图与填空：（1）如图，在矩形ABCD 中，点O 是对角线AC 的中点．用尺规过点O 作AC 的垂线，分别交AB ，CD 于点E ，F ，连接AF ，CE ．（不写作法，保留作图痕迹）（2）已知：矩形ABCD ，点E ，F 分别在AB ，CD 上，EF 经过对角线AC 的中点O ，且EFAC ⊥．求证：四边形AECF 是菱形．证明：∵四边形ABCD 是矩形，∴AB CD ．∴①，OCF OAE ∠=∠．∵点O 是AC 的中点，∴②．∴CFO AEO ≅△△（AAS ）．∴③．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．进一步思考，如果四边形ABCD 是平行四边形呢？请你模仿题中表述，写出你猜想的结论：④．【答案】（1）见解析（2）①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形【解析】【分析】本题主要考查了矩形的性质，平行四边形的性质与判定，菱形的判定，垂线的尺规作图：（1）根据垂线的尺规作图方法作图即可；（2）根据矩形或平行四边形的对边平行得到OFC OEA ∠=∠，OCF OAE ∠=∠，进而证明()AAS CFO AEO ≌，得到OF OE =，即可证明四边形AECF 是平行四边形．再由EF AC ⊥，即可证明四边形AECF 是菱形．【小问1详解】解：如图所示，即为所求；【小问2详解】证明：∵四边形ABCD 是矩形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．猜想：过平行四边形的一条对角线的中点作这条对角线的垂线，与平行四边形两边相交的两点和这条对角线的两个端点构成的四边形是菱形；证明：∵四边形ABCD 是平行四边形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．故答案为：①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形．22.某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务，选派甲、乙两人分别用A 、B 两种外墙漆各完成总粉刷任务的一半．据测算需要A 、B 两种外墙漆各300千克，购买外墙漆总费用为15000元，已知A 种外墙漆每千克的价格比B 种外墙漆每千克的价格多2元．（1）求A 、B 两种外墙漆每千克的价格各是多少元？（2）已知乙每小时粉刷外墙面积是甲每小时粉刷外墙面积的45，乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时．问甲每小时粉刷外墙的面积是多少平方米？【答案】（1）A 种外墙漆每千克的价格为26元，则B 种外墙漆每千克的价格为24元．（2）甲每小时粉刷外墙的面积是25平方米．【解析】【分析】本题考查的是分式方程的应用，一元一次方程的应用，理解题意建立方程是解本题的关键；（1）设A 种外墙漆每千克的价格为x 元，则B 种外墙漆每千克的价格为()2x -元，再根据总费用为15000元列方程求解即可；（2）设甲每小时粉刷外墙面积为y 平方米，则乙每小时粉刷外墙面积是45y 平方米；利用乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时．从而建立分式方程求解即可．【小问1详解】解：设A 种外墙漆每千克的价格为x 元，则B 种外墙漆每千克的价格为()2x -元，∴()300300215000x x +-=，解得：26x =，∴224x -=，答：A 种外墙漆每千克的价格为26元，B 种外墙漆每千克的价格为24元．【小问2详解】设甲每小时粉刷外墙面积为y 平方米，则乙每小时粉刷外墙面积是45y 平方米；∴500500545y y -=，解得：25y =，经检验：25y =是原方程的根且符合题意，答：甲每小时粉刷外墙的面积是25平方米．23.如图，在ABC 中，6AB =，8BC =，点P 为AB 上一点，过点P 作PQ BC ∥交AC 于点Q ．设AP 的长度为x ，点P ，Q 的距离为1y ，ABC 的周长与APQ △的周长之比为2y．（1）请直接写出1y ，2y 分别关于x 的函数表达式，并注明自变量x 的取值范围；（2）在给定的平面直角坐标系中画出函数1y ，2y 的图象；请分别写出函数1y ，2y 的一条性质；（3）结合函数图象，直接写出12y y >时x 的取值范围．（近似值保留一位小数，误差不超过0.2）【答案】（1）()()124606063y x x y x x=<≤=<≤，（2）函数图象见解析，1y 随x 增大而增大，2y 随x 增大而减小（3）2.26x <≤【解析】【分析】本题主要考查了一次函数与反比例函数综合，相似三角形的性质与判定：（1）证明APQ ABC ∽，根据相似三角形的性质得到APQABC C PQ AP C BC AB==△△，据此可得答案；（2）根据（1）所求利用描点法画出对应的函数图象并根据函数图象写出对应的函数图象的性质即可；（3）找到一次函数图象在反比例函数图象上方时自变量的取值范围即可．【小问1详解】解：∵PQ BC ∥，∴APQ ABC ∽，∴APQABC C PQ AP C BC AB==△△，∴12686y x AB y AP x ===，∴()()124606063y x x y x x =<≤=<≤，；【小问2详解】解：如图所示，即为所求；由函数图象可知，1y 随x 增大而增大，2y 随x 增大而减小；【小问3详解】解：由函数图象可知，当12y y >时x 的取值范围2.26x <≤．24.如图，A ，B ，C ，D 分别是某公园四个景点，B 在A 的正东方向，D 在A 的正北方向，且在C 的北偏西60︒方向，C 在A 的北偏东30︒方向，且在B 的北偏西15︒方向，2AB =千米．1.41≈，1.73≈2.45≈）（1）求BC 的长度（结果精确到0.1千米）；（2）甲、乙两人从景点D 出发去景点B ，甲选择的路线为：D C B --，乙选择的路线为：D A B --．请计算说明谁选择的路线较近？【答案】（1）2.5千米（2）甲选择的路线较近【解析】【分析】本题主要考查了解直角三角形的实际应用：（1）过点B 作BE AC ⊥于E ，先求出45ACB ∠=︒，再解Rt ABE △得到BE =千米，进一步解Rt BCE即可得到 2.5sin BE BC BCE ==≈∠千米；（2）过点C 作CF AD ⊥于D ，先解Rt ABE △得到1AE =千米，则(1AC AE CE =+=+千米，再Rt AFC △得到12CF +=千米，32AF +=千米，最后解Rt DCF 得到36DF +=千米，333CD +=千米，即可得到33 4.033CD BC ++=+千米， 5.15AD AB +≈千米，据此可得答案．【小问1详解】解：如图所示，过点B 作BE AC ⊥于E ，由题意得，903060901575CAB ABC =︒-︒=︒=︒-︒=︒∠，∠，∴18045ACB CAB ABC ∠=︒-∠-∠=︒，在Rt ABE △中，902AEB AB =︒=∠，千米，∴cos 2cos60BE AB BAE =⋅=⋅︒=∠千米，在Rt BCE 中， 2.5sin sin 45BE BC BCE ===︒∠千米，∴BC 的长度约为2.5千米；【小问2详解】解：如图所示，过点C 作CF AD ⊥于D ，在Rt ABE △中，cos 2cos601AE AB BAE =⋅=⋅︒=∠千米，∴(13AC AE CE =+=+千米，在Rt AFC △中，(13sin 13sin 302CF AC CAF +=⋅∠=+⋅︒=千米，(33cos 13cos302AF AC CAF =⋅∠=⋅︒=千米，在Rt DCF 中，3090DCF DFC =︒=︒∠，∠，∴1333tan tan 3026DF CF DCF +=⋅=⋅︒=∠千米，13332cos cos303CF CD DCF ++===︒∠千米，∴336 4.033CD BC ++=+≈千米，33332 5.1562AD AB DF AF AB +++=++=++≈千米，∵4.03 5.15<，∴甲选择的路线较近．25.如图，在平面直角坐标系中，抛物线23y ax bx =+-与x 轴交于()1,0A -，B 两点，交y 轴于点C ，抛物线的对称轴是直线52x =．（1）求抛物线的表达式；（2）点P 是直线BC 下方对称轴右侧抛物线上一动点，过点P 作PD x ∥轴交抛物线于点D ，作PE BC ⊥于点E ，求52PD PE +的最大值及此时点P 的坐标；（3）将抛物线沿射线BC 552PD PE +取得最大值的条件下，点F 为点P 平移后的对应点，连接AF 交y 轴于点M ，点N 为平移后的抛物线上一点，若45NMF ABC ∠-∠=︒，请直接写出所有符合条件的点N 的坐标．【答案】（1）215322y x x =--（2）52PD PE +最大值为152；()5,3P -；（3）573,4732N ⎛- ⎝⎭或131113,2⎛⎫- ⎪ ⎪⎝⎭【解析】【分析】（1）直接利用待定系数法求解抛物线的解析式即可；（2）如图，延长PE 交x 轴于G ，过P 作PH y ∥轴于H ，求解223635BC =+=，可得625sin 535OB BCO BC ∠===，证明255PE PH =，设215,322P x x x ⎛⎫-- ⎪⎝⎭，2132PH x x =-+，25PD x =-，再建立二次函数求解即可；（3）由抛物线沿射线BC 方向平移5个单位，即把抛物线向左平移2个单位，再向下平移1个单位，可得新的抛物线为：211722y x x =--，()3,4F -，如图，当N 在y 轴的左侧时，过N 作NK y ⊥轴于K ，证明()0,1M -，可得45AMO OAM FMK ∠=∠=︒=∠，证明NMK ABC ∠=∠，如图，当N 在y 轴的右侧时，过M 作y 轴的垂线，过N '作N T '⊥过M 的垂线于T ，同理可得：N MT ABC '∠=∠，再进一步结合三角函数建立方程求解即可．【小问1详解】解：∵抛物线23y ax bx =+-与x 轴交于()1,0A -，B 两点，交y 轴于点C ，抛物线的对称轴是直线52x =，∴30522a b b a --=⎧⎪⎨-=⎪⎩，解得1252a b ⎧=⎪⎪⎨⎪=-⎪⎩，∴215322y x x =--；【小问2详解】解：如图，延长PE 交x 轴于G ，过P 作PH y ∥轴于H，∵当2153022y x x =--=时，解得：11x =-，26x =，∴()6,0B ，当0x =时，=3y -，∴()0,3C -，∴BC ==，∴25sin 5OB BCO BC ∠===，∵PD x 轴，∴PHE BCO ∠=∠，∴25sin 5PE PHE PH ∠==，∴255PE PH =，∵()6,0B ，()0,3C -，设BC 为3y mx =-，∴630m -=，解得：12m =，∴直线BC 为：132y x =-，设215,322P x x x ⎛⎫-- ⎪⎝⎭，∴1,32H x x ⎛⎫- ⎪⎝⎭，∴2132PH x x =-+，∵抛物线215322y x x =--的对称轴为直线52x =，∴25PD x =-，∴2552512532252PD PE x x x ⎛⎫+=-+-+ ⎪⎝⎭21552x x =-+-，当55122x =-=⎛⎫⨯- ⎪⎝⎭时，52PD PE +取得最大值，最大值为152；此时()5,3P -；【小问3详解】解：∵抛物线沿射线BC方向平移个单位，即把抛物线向左平移2个单位，再向下平移1个单位，∴新的抛物线为：211722y x x =--，()3,4F -，如图，当N 在y 轴的左侧时，过N 作NK y ⊥轴于K ，∵()1,0A -，同理可得：直线AF 为=1y x --，当0x =时，1y =-，∴()0,1M -，∴45AMO OAM FMK ∠=∠=︒=∠，∵45NMF ABC ∠-∠=︒，∴4545NMK ABC ∠+︒-∠=︒，∴NMK ABC ∠=∠，∴1tan tan 2NMK ABC ∠=∠=，设211,722N n n n ⎛⎫-- ⎪⎝⎭，∴211121722NKn MK n n -==--++，解得：5732n =或5732+（舍去）∴573,42N ⎛- ⎝；如图，当N 在y 轴的右侧时，过M 作y 轴的垂线，过N '作N T '⊥过M 的垂线于T，同理可得：N MT ABC '∠=∠，设211,722N x x x ⎛-'⎫- ⎪⎝⎭，则(),1T x -，同理可得：211711222x x x --+=，∴1x =+或1，∴13112N ⎛⎫+ ⎝'⎪⎪⎭．【点睛】本题属于二次函数的综合题，难度很大，考查了待定系数法，二次函数的性质，锐角三角函数的应用，关键是做出合适的辅助线进行转化，清晰的分类讨论是解本题的关键．26.在Rt ABC △中，90ACB ∠=︒，AC BC =，过点B 作BD AC ∥．（1）如图1，若点D 在点B 的左侧，连接CD ，过点A 作AE CD ⊥交BC 于点E ．若点E 是BC 的中点，求证：2AC BD =；（2）如图2，若点D 在点B 的右侧，连接AD ，点F 是AD 的中点，连接BF 并延长交AC 于点G ，连接CF ．过点F 作FM BG ⊥交AB 于点M ，CN 平分ACB ∠交BG 于点N ，求证：2AM CN BD =+；（3）若点D 在点B 的右侧，连接AD ，点F 是AD 的中点，且AF AC =．点P 是直线AC 上一动点，连接FP ，将FP 绕点F 逆时针旋转60︒得到FQ ，连接BQ ，点R 是直线AD 上一动点，连接BR ，QR ．在点P 的运动过程中，当BQ 取得最小值时，在平面内将BQR 沿直线QR 翻折得到TQR △，连接FT ．在点R 的运动过程中，直接写出FT CP 的最大值．【答案】（1）证明见解析（2）证明见解析（3）2++【解析】【分析】（1）证明()ASA ACE CBD ≌得到BD CE =，再由点E 是BC 的中点，得到22BC CE BD ==，即可证明2AC BD =；（2）如图所示，过点G 作GH AB ⊥于H ，连接HF ，先证明()AAS AGF DBF ≌，得到AG BD =，BF GF =，再证明AHG 是等腰直角三角形，得到2222AH AG ==；由直角三角形斜边上的中线的性质可得12FH FC BF BG ===，则FBH FHB FBC FCB ==∠∠，∠∠，进而可证明290HFC ABC ==︒∠∠，则HFM CFN =∠∠；设CBG x ∠=，则4590ABG x CGB x =︒-=︒-∠，∠，可得135HMF BFM FBM x =+=︒-∠∠∠由角平分线的定义可得1452GCN ACB ==︒∠∠，则可证明HMF CNF =∠∠，进而证明()AAS HFM CFN ≌，得到HM CN =，即可证明22AM BD CN =+；（3）如图所示，过点D 作DH AC ⊥交AC 延长线与H ，连接FH ，则四边形BCHD 是矩形，可得BC DH AC ==，证明FDH △是等边三角形，得到60DFH FDH ==︒∠∠，进而得到30BDA DAH ==︒∠∠，30FHA FAH ==︒∠∠；由旋转的性质可得60FQ FP PFQ DFH ==︒=，∠∠，证明()SAS DFQ HFP ≌，得到30FDQ FHP ==︒∠∠，则点Q 在直线DQ 上运动，设直线DQ 交FH 于K ，则113022DK FH FK FH FDK FDH ===︒⊥，，∠，可得60BDQ ∠=︒，由垂线段最短可知，当BQ DQ ⊥时，BQ 有最小值，则30DBQ ∠=︒，设6AC DH a ==，则AH ==6BD CH a ==-，则3DQ a =-，9BQ a =-；再求出3FK a =，则DK =，3QK DK DQ a =-=，由勾股定理得FQ =；由全等三角形的性质可得3PH DQ a ==-，则3CP a =-；由折叠的性质可得9TQ BQ a ==-，由FT FQ TQ ≤+，得到当点Q 在线段FT 上时，FT CP 此时有最大值，最大值为FQ TQ CP+，据此代值计算即可．【小问1详解】证明：∵90ACB ∠=︒，BD AC ∥，∴18090CBD ACB ∠∠︒︒=-=，∵AE CD ⊥，∴90ACD CAE ∠+∠=︒，∵90ACD BCD ∠+∠=︒，∴CAE BCD ∠=∠，又∵90AC CB CBD ACE ===︒，∠∠，∴()ASA ACE CBD ≌，∴BD CE =，∵点E 是BC 的中点，∴22BC CE BD ==，∴2AC BD =；【小问2详解】证明：如图所示，过点G 作GH AB ⊥于H ，连接HF ，∵BD AC ∥，∴FBD FGA D FAG ==∠∠，∠∠，∵点F 是AD 的中点，∴AF DF =，∴()AAS AGF DBF ≌，∴AG BD =，BF GF =，∵90AC BC ACB =∠=︒，，∴45CAB ACB ∠=∠=︒，∵GH AH ⊥，∴AHG 是等腰直角三角形，∴2222AH AG BD ==；∵90BHG BCG BF GF ==︒=∠∠，，∴12FH FC BF BG ===，∴FBH FHB FBC FCB ==∠∠，∠∠，∴22GFH FBH FHB FBH GFC FBC FCB FBC =+==+=∠∠∠∠，∠∠∠∠，∴22290HFC GFH GFC FBH FBC ABC =+=+==︒∠∠∠∠∠∠，∵FM BG ⊥，∴90BFM ∠=︒，∴HFM CFN =∠∠；设CBG x ∠=，则4590ABG x CGB x =︒-=︒-∠，∠，∴135HMF BFM FBM x =+=︒-∠∠∠，∵CN 平分ACB ∠，∴1452GCN ACB ==︒∠，∴135CNF CGN GCN x =+=︒-∠∠∠，∴HMF CNF =∠∠，∴()AAS HFM CFN ≌，∴HM CN =，∵AM AH HM =+，∴22AM BD CN =+；【小问3详解】解：如图所示，过点D 作DH AC ⊥交AC 延长线与H ，连接FH ，∵90BD AC ACB =︒∥，∠，∴90BCH CBD ==︒∠∠，∵DH AC ⊥，∴四边形BCHD 是矩形，∴BC DH AC ==，∵点F 是AD 的中点，且AF AC =，∴2222AD AF DH FH DF ====，∴FDH △是等边三角形，∴60DFH FDH ==︒∠∠，∴30BDA DAH ==︒∠∠，∴30FHA FAH ==︒∠∠，由旋转的性质可得60FQ FP PFQ DFH ==︒=，∠∠，∴DFQ HFP =∠∠，。

2014年中考数学二轮精品复习试卷(三角形)含答案解析

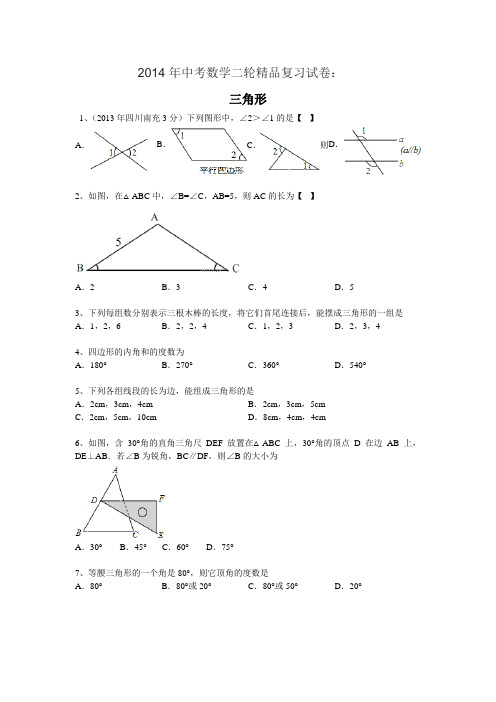
2014年中考数学二轮精品复习试卷：三角形1、（2013年四川南充3分）下列图形中，∠2＞∠1的是【】A．B．C．则D．2、如图，在△ABC中，∠B=∠C，AB=5，则AC的长为【】A．2 B．3 C．4 D．53、下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，44、四边形的内角和的度数为A．180°B．270°C．360°D．540°5、下列各组线段的长为边，能组成三角形的是A．2cm，3cm，4cm B．2cm，3cm，5cmC．2cm，5cm，10cm D．8cm，4cm，4cm6、如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D在边AB上，DE⊥AB．若∠B为锐角，BC∥DF，则∠B的大小为A．30° B．45° C．60°D．75°7、等腰三角形的一个角是80°，则它顶角的度数是A．80°B．80°或20°C．80°或50°D．20°8、在△ABC中，∠BAC=90°，AB=3，AC=4．AD平分∠BAC交BC于D，则BD的长为A．B．C．D．9、（2013年四川资阳3分）一个正多边形的每个外角都等于36°，那么它是【】A．正六边形B．正八边形C．正十边形D．正十二边形10、（2013年四川南充3分）如图，△ABC中，AB=AC,∠B=70°，则∠A的度数是【】A．70°B．55°C．50°D．40°11、（2013年广东梅州3分）若一个多边形的内角和小于其外角和，则这个多边形的边数是【】A．3 B．4 C．5 D．612、已知△ABC的各边长度分别为3cm，4cm，5cm，则连结各边中点的三角形的周长为A．2cm B．7cm C．5cm D．6cm13、如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C 的度数为A．50°B．60°C．70°D．80°14、如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ的长为A．B．C．3 D．415、如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为A．20 B．18 C．14 D．1316、如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E 以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t ＜6），连接DE，当△BDE是直角三角形时，t的值为A．2 B．2.5或3.5 C．3.5或4.5 D．2或3.5或4.517、如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD 于点O，连结AO，下列结论不正确的是【】A．△AOB≌△BOC B．△BOC≌△EOD C．△AOD≌△EOD D．△AOD≌△BOC18、如图，已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a 且AM+MN+NB的长度和最短，则此时AM+NB=A．6 B．8 C．10 D．1219、（2013年四川资阳3分）如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是【】A．48 B．60 C．76 D．8020、（2013年四川攀枝花3分）如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC 绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=【】A．30°B．35°C．40°D．50°二、填空题()21、一个六边形的内角和是 .22、如图，某山坡的坡面AB=200米，坡角∠BAC=30°，则该山坡的高BC的长为米。

重庆市2014年初中学业水平B测试数学含答案

重庆市2014年初中毕业暨高中招生考试·数学(B卷) 本卷难度：适中难度系数：0.60易错题：7、14较难题：18、26(全卷共5个大题，满分150分，考试时间120分钟)参考公式：抛物线y＝ax2＋bx＋c(a≠0)的顶点坐标为(－b2a，4ac－b24a)，对称轴为x＝－b2a.一、选择题(本大题12个小题，每小题4分，共48分)在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将正确答案的代号填在对应的括号内．1. 某地连续四天每天的平均气温分别是：1 ℃，－1 ℃，0 ℃，2 ℃，则平均气温中最低的是()A. －1 ℃B. 0 ℃C. 1 ℃D. 2 ℃2. 计算5x2－2x2的结果是()A. 3B. 3xC. 3x2D. 3x43. 如图，△ABC∽△DEF，相似比为1∶2，若BC＝1，则EF的长是()A. 1B. 2C. 3D. 4第3题图第4题图第8题图4. 如图，直线AB ∥CD ，直线EF 分别交AB 、CD 于点E 、F .若∠AEF ＝50°，则∠EFC 的大小是( ) A. 40° B. 50° C. 120° D. 130°5. 某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参加比赛．为此，初三(1)班组织了五轮班级选拔赛．在这五轮选拔赛中，甲、乙两位同学的平均分都是96分，甲的成绩的方差是0.2，乙的成绩的方差是0.8.根据以上数据，下列说法正确的是( )A. 甲的成绩比乙的成绩稳定B. 乙的成绩比甲的成绩稳定C. 甲、乙两人的成绩一样稳定D. 无法确定甲、乙的成绩谁更稳定 6. 若点(3，1)在一次函数y ＝kx －2(k ≠0)的图象上，则k 的值是( ) A. 5 B. 4 C. 3 D. 17. 分式方程4x ＋1＝3x 的解是( )A. x ＝1B. x ＝－1C. x ＝3D. x ＝－38. 如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，∠ACB ＝30°，则∠AOB 的大小为( ) A. 30° B. 60° C. 90° D. 120°9. 夏天到了，某小区准备开放游泳池，物业管理处安排一名清洁工对一个无水的游泳池进行清洗．该工人先只打开一个进水管，蓄了少量水后关闭进水管并立即进行清洗，一段时间后，再同时打开两个出水管将池内的水放完．随后将两个出水管关闭，并同时打开两个进水管将水蓄满．已知每个进水管的进水速度与每个出水管的出水速度相同．从工人最先打开一个进水管开始，所用的时间为x ，游泳池内的蓄水量为y ，则下列各图中能够反映y 与x 的函数关系的大致图象是( )10. 下列图形都是按照一定规律组成，第一个图形中共有2个三角形，第二个图形中共有8个三角形，第三个图形中共有14个三角形，…，依此规律，第五个图形中三角形的个数是( )第10题图A. 22B. 24C. 26D. 2811. 如图，菱形ABCD的对角线AC、BD相交于点O，AC＝8，BD＝6，以AB为直径作一个半圆，则图中阴影部分的面积为()A. 25π－6B. 252π－6 C.256π－6 D.258π－6第11题图第12题图12. 如图，正方形ABCD 的顶点B 、C 在x 轴的正半轴上，反比例函数y ＝kx (k ≠0)在第一象限的图象经过顶点A (m ，2)和CD 边上的点E (n ，23)．过点E 的直线l 交x 轴于点F ，交y 轴于点G (0，－2)．则点F 的坐标是( )A. (54，0)B. (74，0)C. (94，0)D. (114，0)二、填空题(本大题6个小题，每小题4分，共24分)在每小题中，请将答案直接填在对应的横线上． 13. 实数－12的相反数是．14. 函数y ＝1x －2中，自变量x 的取值范围是．15. 在2014年重庆市初中毕业生体能测试中，某校初三有7名同学的体能测试成绩(单位：分)如下：50，48，47，50，48，49，48.这组数据的众数是．16. 如图，C 为⊙O 外一点，CA 与⊙O 相切，切点为A ，AB 为⊙O 的直径，连接CB .若⊙O 的半径为2，∠ABC ＝60°，则BC ＝．第16题图第18题图17. 在一个不透明的盒子里装着4个分别标有数字1，2，3，4的小球，它们除数字不同外其余完全相同，搅匀后从盒子里随机取出1个小球，将该小球上的数字作为a 的值，则使关于x 的不等式组⎩⎪⎨⎪⎧x >2a －1x ≤a ＋2只．有．一个整数解的概率为 . 18. 如图，在边长为62的正方形ABCD 中，E 是AB 边上一点，G 是AD 延长线上一点，BE ＝DG ，连接EG ，CF ⊥EG 交EG 于点H ，交AD 于点F ，连接CE ，BH .若BH ＝8，则FG三、解答题(本大题2个小题，每小题7分，共14分)解答时每小题必须给出必要的演算过程或推理步骤．19. 计算：(－3)2＋|－2|－20140－9＋(12)－1.20. 如图，在△ABC 中，CD ⊥AB ，垂足为D .若AB ＝12，CD ＝6，tan A ＝32，求sin B ＋cos B 的值．第20题图四、解答题(本大题4个小题，每小题10分，共40分)解答时每小题必须给出必要的演算过程或推理步骤．21. 先化简，再求值：(x －1－3x ＋1)÷x 2＋4x ＋4x ＋1，其中x 是方程x －12－x －25＝0的解．22. 重庆市某餐饮文化公司准备承办“重庆火锅美食文化节”．为了解市民对火锅的喜爱程度，该公司设计了一个调查问卷，将喜爱程度分为A (非常喜欢)、B (喜欢)、C (不太喜欢)、D (很不喜欢)四种类型，并派业务员进行市场调查．其中一个业务员小丽在解放碑步行街对市民进行了随机调查，并根据调查结果制成了如下两幅不完整的统计图．请结合统计图所给信息解答下列问题：(1)在扇形统计图中C 所占的百分比是22%；小丽本次抽样调查的人数共有50人；请将折线统计图补充完整；(2)为了解少数市民很不喜欢吃火锅的原因，小丽决定在上述调查结果中从“很不喜欢”吃火锅的市民里随机选出两位进行电话回访，请你用列表法或画树状图的方法，求所选出的两位市民恰好都是男性的概率．第22题图23. 某生态农业园种植的青椒除了运往市区销售外，还可以让市民亲自去生态农业园购买．已知今年5月份该青椒在市区、园区的销售价格分别为6元/千克、4元/千克，今年5月份一共销售了3000千克，总销售额为16000元．(1)今年5月份该青椒在市区、园区各销售了多少千克？(2)6月份是青椒产出旺季，为了促销，生态农业园决定6月份将该青椒在市区、园区的销售价格均在今年5月份的基础上降低a%.预计这种青椒在市区、园区的销售量将在今年5月份的基础上分别增长30%、20%.要使得6月份该青椒的总销售额不低于18360元，则a的最大值是多少？24. 如图，在△ABC中，∠ACB＝90°，第24题图AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G，F为AB边上一点，连接CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.五、解答题(本大题2个小题，每小题12分，共24分)解答时每小题必须给出必要的演算过程或推理步骤．25. 如图，已知抛物线y＝－x2＋2x＋3与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，连接BC.(1)求A、B、C三点的坐标；第25题图(2)若点P为线段BC上的一点(不与B、C重合)，PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求△BPN的周长；(3)在(2)的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在点Q，使得△CNQ为直角三角形，求点Q的坐标．26. 如图①，在▱ABCD中，AH⊥DC，垂足为H，AB＝47，AD＝7，AH＝21.现有两个动点E、F 同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动．在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，当点E运动到点C时，E、F两点同时停止运动，设运动时间为t秒．(1)求线段AC的长；(2)在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出相应的自变量t的取值范围；(3)当等边△EFG的顶点E到达点C时，如图②，将△EFG绕着点C旋转一个角度α(0°<α<360°)．在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′，设直线F′G′与射线．．AC分别．．DC、射线相交于M、N两点．试问：是否存在点M、N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出线段CM的长度；若不存在，请说明理由．第26题图重庆市2014年初中毕业暨高中招生考试(B卷)1.A【解析】∵－1＜0＜1＜2，∴这四天的平均气温中最低的是－1 ℃.方法归纳：两个正数比较大小，绝对值大的数比较大；两个负数比较大小，绝对值大的数反而小．正数大于0，负数小于0，正数大于一切负数．要求最大数，在正数中找，要求最小数，在负数中寻找．2.C【解析】由合并同类项法则可知，5x2－2x2＝(5－2)x2＝3x2.方法归纳：合并同类项：只把系数相加减，相同字母及字母的指数不变，熟练掌握合并同类项法则是解题的关键．3.B【解析】∵△ABC∽△DEF，相似比为1∶2，∴BC∶EF＝1∶2.又∵BC＝1，∴EF＝2.第3题解图方法归纳：相似三角形的性质：①相似三角形的对应角相等；②相似三角形的对应线段(边、高、中线、角平分线)的比等于相似比；③相似三角形的周长比等于相似比，面积比等于相似比的平方．4.D【解析】∵AB∥CD，∠AEF＝50°，∴∠EFC＝180°－∠AEF＝180°－50°＝130°(两直线平行，同旁内角互补)．第4题解图一题多解：∵AB∥CD，∠AEF＝50°，∴∠EFD＝∠AEF＝50°(两直线平行，内错角相等)，∴∠EFC ＝180°－50°＝130°(平角的定义)．思维方式：解答与平行线有关的角度计算问题，一般是利用平行线的性质，建立已知角与要求的角之间的数量关系，所以需要熟练掌握平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．5.A【解析】在平均数相同的情况下，方差越小，其波动性就越小，就越稳定．甲、乙两名同学的平均数相同，甲同学的方差为0.2，乙同学的方差为0.8，∵0.2＜0.8，∴甲同学的成绩比乙同学稳定．方法归纳：方差反映一组数据在其平均数左右波动的大小，方差越大，数据波动就越大，越不稳定；方差越小，数据波动就越小，越稳定．6.D【解析】∵点(3，1)在一次函数y＝kx－2(k≠0)的函数图象上，将点(3，1)代入一次函数关系式得，1＝3k－2，解得k＝1.速解技巧：如果一个点在某函数图象上，那么这个点的坐标满足函数关系式，故可列函数关系式令左右两边相等，即可以把点的坐标代入函数关系式求未知量．7.C【解析】去分母：方程两边同时乘以x(x＋1)，得4x＝3(x＋1)，去括号，得4x＝3x＋3，移项，得4x－3x＝3，合并同类项，得x＝3，经检验x＝3是原方程的解．方法指导：①把分式方程“转化”为整式方程的条件是去掉分式方程中的分母．如何去掉分式方程中的分母是解分式方程的“关键”步骤；②用分式方程中各项的最简公分母乘方程的两边，从而约去分母．但要注意用最简公分母乘方程的两边各项时，切勿漏项；③解分式方程可能产生“增根”的情况，则验根是解分式方程的必要步骤．8.B【解析】∵四边形ABCD是矩形，AC与BD相交于点O，∴OB＝OC，∵∠ACB＝30°，∴AB＝12AC＝OA，∠DBC＝30°，∠ABO＝∠ABC－∠DBC＝90°－30°＝60°，∴△ABO为等边三角形，∴∠AOB＝60°.第8题解图方法指导：矩形是特殊的平行四边形，它具有平行四边形的所有性质，同时还有自己特有的性质：矩形的对角线相等，矩形的四个角都是直角．9.C【解析】池内蓄水量为y，所用时间为x.本题共分为四个时间段：①打开一个进水管，蓄入少量水后关闭，y随着x的增加而增加；②关闭进水管后，进行清洗一段时间，时间x增加，y保持不变；③同时打开两个出水管，将水放完，y随着x的增加而增小；④打开两个进水管，将水蓄满，y随着x的增加而增加，且速度大于第一个时间段的速度．综上所述，第一段和第四段为增函数，第三段为减函数，第二段为常量函数．观察图象可知选C.归纳总结：本题首先应该明确函数图象的横轴和纵轴表示的量，再根据实际情况来判断函数图象，需注意速度大说明在相等的时间内，水量增加或减少的要多，表现在函数图象上就是速度大的函数图象的走势相对要陡．10.C【解析】第一个图形中有2个三角形：6×1－4＝2；第二个图形中有8个三角形：6×2－4＝8；第三个图形中有14个三角形：6×3－4＝14；…第n个图形中有三角形的个数为：6n－4.由以上规律可得，第五个图形中有三角形的个数为：6×5－4＝26.方法归纳：对于图形规律题，可以从以下方法入手．①将所给图形的数量表示出来，并标记序号1，2，3，…；②比较每一序号对应的数字之间的关系，通过作差或商的形式观察是否含有定量；③将标记的序号记为n，按照整理好的数据得出第n个式子即通式；④将所要求的序号代入通式即可求出此时图形的数量．11.D【解析】解答本题的关键是知道S阴影＝S半圆ABO－S△AOB，而△AOB是直角三角形，∵四边形ABCD 是菱形，∴AC ⊥BD ，∵AC ＝8，BD ＝6.∴OA ＝4，OB ＝3.在Rt △AOB 中，由勾股定理得AB ＝5，由图可得，阴影部分的面积＝半圆ABO 的面积－△AOB 的面积．∵半圆ABO 的面积＝12×π×(12AB)2＝12×(52)2π＝258π，S △AOB ＝12×AO×OB ＝12×4×3＝6，∴阴影部分的面积＝258π－6.第11题解图方法归纳：求阴影部分的面积，常用的计算方法有：(1)直接用公式求解；(2)将所求面积分割后，利用规则图形的面积相互加减求解；或利用旋转将部分阴影图形移位后，组成规则图形求解；(3)将阴影中某些图形等积变形后移位，重组成规则图形求解；(4)将阴影图形看成是一些基本图形覆盖而成的重叠部分，用整体和差法求解．12. 【教你审题】要求F 点的坐标，需先求得直线l 的解析式，又E 、G 在直线l 上，则要求出E 点坐标，而点A 、E 的坐标与正方形，反比例函数都有关，故可由此得到m 、n 关系，并将A 、E 坐标化入反比例函数中，联立方程进而求得E 点坐标．C 【解析】∵四边形ABCD 是正方形，点A 的坐标为(m ，2)，∴正方形ABCD 的边长为2，即BC ＝2.∵点E 的坐标为(n ，23)，点E 在边CD 上，∴点E 的坐标为(m ＋2，23)．把A(m ，2)和E(m ＋2，23)代入y ＝k x ，得⎩⎨⎧2＝k m23＝k m ＋2，解得⎩⎪⎨⎪⎧k ＝2m ＝1，∴点E 的坐标为(3，23)．∵点G 的坐标为(0，－2)，设直线GE 为：y ＝ax ＋b.列方程得，⎩⎪⎨⎪⎧－2＝b 23＝3a ＋b ，解得⎩⎪⎨⎪⎧a ＝89b ＝－2，∴直线GE 的解析式为：y ＝89x －2.∵点F 在直线GE 上，且点F 在x 轴上，可设点F 的坐标为(c ，0)，代入GE 的解析式，令y ＝0，求得c ＝94，∴点F 的坐标为(94，0)．第12题解图难点突破：利用正方形的性质找出点A和点E之间的坐标存在的数量关系是本题的难点，再利用两点确定一条直线，用待定系数法求出直线GE的函数关系式，该一次函数与x轴的交点就是点F，从而求出点F的坐标．13. 12【解析】∵只有符号不同的两个数互为相反数，∴－12的相反数是12.方法指导：相反数的性质包括：①a的相反数为－a；②若a、b互为相反数，则a＋b＝0；③在数轴上，表示互为相反数(0除外)的两个点位于原点两侧，且关于原点对称．14.x≠2【解析】在分式中，∵分母不能为0，∴x－2≠0，解得x≠2.备考指导：对于函数自变量取值范围，常考的类型如下：15. 48【解析】众数是一组数据中出现次数最多的那个数据，一组数据中众数可能有一个，也可能有多个．这组数据：50、48、47、50、48、49、48中，出现次数最多的是48，共出现了三次，因此48是众数．16. 8【解析】∵AC是⊙O的切线，AB是⊙O的直径，∴AB⊥AC.∵∠CBA＝60°，∴∠C＝30°.∵OA ＝OB＝2，∴AB＝4，在Rt△ABC中，30°角所对的边是斜边的一半，∴BC＝8.第16题解图试题点评：本题考查两个知识点：1.在直角三角形中，30度角所对的直角边等于斜边的一半；2.切线垂直于经过切点的半径．17. 14【解析】本题关键找到满足不等式组只有一个整数解时的a 值，共有几种情况，因为抽到的a值共有四种情况：①当a ＝1时，不等式组⎩⎪⎨⎪⎧x>2a －1x≤a ＋2的解集为1＜x≤3，有两个整数解；②当a ＝2时，不等式组⎩⎪⎨⎪⎧x>2a －1x≤a ＋2的解集为3＜x≤4，有一个整数解；③当a ＝3时，不等式组⎩⎪⎨⎪⎧x ＞2a －1x≤a ＋2的解集为空集，无解；④当a ＝4时，不等式组⎩⎪⎨⎪⎧x ＞2a －1x≤a ＋2的解集为空集，无解．∴共有一种情况符合要求，因此只有一个整数解的概率为14.方法归纳：掌握此类问题，需熟练掌握求概率公式：P(A)＝mn ，其中n 为所有事件的总数，m 为事件A发生的总次数．18. 【教你审题】连接CG ，HD ，可证出△CBE ≌△CDG ，由全等三角形的性质可得出CE ＝CG ，即△CEG 为等腰直角三角形，由正方形对角线的性质可得出三点B 、H 、D 在一条直线上．由三角形相似和勾股定理可求出FG 的长度．52 【解析】连接CG 、HD.∵四边形ABCD 是正方形，∴∠ABC ＝∠CDG ＝90°，在△CBE 和△CDG中，⎩⎪⎨⎪⎧BC ＝CD ∠EBC ＝∠GDC BE ＝DG ，∴△CBE ≌△CDG ，∴CE ＝CG ，∠BCE ＝∠DCG ，∵∠BCD ＝90°，∴∠BCE ＋∠ECD＝∠DCG ＋∠ECD ＝90°，∴△ECG 为等腰直角三角形，∴∠HEC ＝45°，由∠EHC ＝∠EBC ＝90°，∴点B 、C 、H 、E 四点共圆，∴∠HBC ＝∠HEC ＝45°，∴点B 、H 、D 三点共线，∵正方形的边长为62，在Rt △DBC 中，由勾股定理，得BD ＝BC 2＋CD 2＝（62）2＋（62）2＝12，∴DF BC ＝FH HC ＝DH BH ＝12－88，∴DF ＝32，在Rt △CDF 中，由勾股定理，得CF ＝FD 2＋CD 2＝（32）2＋（62）2＝310，∴CH ＝210，在Rt △CEH 中，BE ＝EC 2－BC 2＝（45）2－（62）2＝22，∴DG ＝BE ＝22，即FG ＝FD ＋DG ＝32＋22＝5 2.第18题解图思维方式：问题求解过程中需要对基本图形或模式图形(如△CGE 为等腰直角三角形，点B 、C 、H 、E 四点共圆，点B 、H 、D 三点共线等)灵活构造、识别、利用．这样突破问题就能顺畅得多．难点突破：本题的解题关键是利用正方形的性质和三角形全等证明三点B 、H 、D 共线，再利用相似三角形对应边成比例列出方程，求出所要求的线段的长．本题难度比较大，综合知识面广，辅助线也较多，是一道压轴题．19.解：原式＝9＋2－1－3＋2(4分) ＝9.(7分)20.解：在Rt △ACD 中， ∵tan A ＝CD AD ＝32，∴AD ＝CD 32＝6×23＝4，(2分)∴BD ＝AB －AD ＝12－4＝8，(3分)在Rt △BCD 中，BC ＝CD 2＋BD 2＝62＋82＝10，(5分) ∴sin B ＋cos B ＝CD BC ＋BD BC ＝610＋810＝1.4.(7分)21.解：解方程x －12－x －25＝0，系数化为整数得，5(x －1)－2(x －2)＝0，去括号得， 5x －5－2x ＋4＝0，合并同类项得，3x ＝1，系数化为1得， x ＝13，(2分)原式＝(x 2－1x ＋1－3x ＋1)·x ＋1（x ＋2）2＝x 2－4x ＋1·x ＋1（x ＋2）2 ＝x －2x ＋2，(9分) 当x ＝13时，原式＝13－213＋2＝－57.(10分)22.(1)解：22%，50.(3分) 补充折线统计图如解图①：第22题解图①(5分)(2)解：根据题意，“很不喜欢”吃火锅的人数为3人，其中男性2人，分别记为男1，男2，女性1人．画树状图如解图②：第22题解图②∵共有6种等可能的结果，两次结果都是男性的有2种情况， ∴P (两次都是男性)＝26＝13.(10分)23.(1)解：设今年5月份该青椒在市区销售x 千克，园区销售y 千克．根据题意，得：⎩⎪⎨⎪⎧x ＋y ＝30006x ＋4y ＝16000，(2分)解得：⎩⎪⎨⎪⎧x ＝2000y ＝1000.(4分)答：今年5月份该青椒在市区销售2000千克，园区销售1000千克．(5分)(2)解：根据题意，列不等式得：6(1－a %)〔2000×(1＋30%)〕＋4(1－a %)〔1000×(1＋20%)〕≥18360，(7分)15600(1－ a %)＋4800(1－ a %)≥18360， 20400(1－ a %)≥18360，解得a ≤10，(9分) ∴a 的最大值是10.(10分)24.(1)证明：∵∠ACB ＝90°，AC ＝BC ， ∴∠CAB ＝45°， ∵CG 平分∠ACB ，∴∠BCG ＝12∠ACB ＝45°，∴∠CAB ＝∠BCG ，(2分)在△ACF 和△CBG 中，⎩⎪⎨⎪⎧∠ACF ＝∠CBG AC ＝BC ∠CAB ＝∠BCG ，∴△ACF ≌△CBG ，(4分) ∴AF ＝CG .(5分)第24题解图(2)证明：如解图，延长CG 交AB 于点H . ∵AC ＝BC, CG 平分∠ACB ， ∴CH ⊥AB ，且点H 是AB 中点， ∴∠D ＝∠CGE ，又∵AD ⊥AB ， ∴CH ∥AD ， ∴点G 是BD 中点， ∴DG ＝GB ， ∵△ACF ≌△CBG ，∴CF ＝BG ，∴CF ＝DG ，(7分)在△AED 和△CEG 中，⎩⎪⎨⎪⎧AE ＝CE ∠DEA ＝∠GEC ∠D ＝∠CGE ，∴△AED ≌△CEG ，(8分) ∴DE ＝GE ，∴DG ＝2DE ，又∵CF ＝ DG ，∴CF ＝2DE .(10分)25.(1)解：当y ＝0时，－x 2＋2x ＋3＝0，解得：x 1＝－1，x 2＝3，∴A (－1，0)，B (3，0)，(2分)当x ＝0时，y ＝3，∴C (0，3)，(3分)∴点A 、B 、C 的坐标分别是A (－1，0)，B (3，0)，C (0，3)．(4分)(2)解：设△BCM 的面积为S ，点M 的坐标为(a ，－a 2＋2a ＋3)，则OC ＝3，OB ＝3，ON ＝a ，MN ＝－a 2＋2a ＋3，BN ＝3－a .根据题意，S ＝S 四边形OCMN ＋S △MNB －S △COB ＝12(OC ＋MN )·ON ＋12MN ·NB －12OC ·OB ＝12〔3＋(－a 2＋2a ＋3)〕a ＋12(－a 2＋2a ＋3)(3－a )－ 12×3×3＝－32a 2＋92a ＝－32(a －32)2＋278， ∴当a ＝32时，S 有最大值，(6分) 此时，ON ＝a ＝32，BN ＝3－a ＝32， ∵OC ＝OB ＝3，∠COB ＝90°，∴∠PBN ＝45°，∴PN ＝BN ＝32，根据勾股定理，得PB ＝PN 2＋BN 2＝322， ∴△BPN 的周长＝32＋32＋322＝3＋322.(8分) (3)解：根据题意，抛物线的对称轴是直线x ＝1.Ⅰ. 如解图①，以CN 为直径作圆，分别交抛物线的对称轴于点Q 1、Q 2，连接CQ 1、NQ 2，作O 1F ⊥y 轴交y 轴于点F ，则∠CQ 1N ＝∠CQ 2N ＝90°.①∵∠FQ 1C ＋∠CQ 1D ＝∠DQ 1N ＋∠CQ 1D ，∴∠FQ 1C ＝∠DQ 1N ，又∵∠Q 1FC ＝∠Q 1DN ＝90°，∴△FQ 1C ∽△DQ 1N ，∴CF DN ＝Q 1F Q 1D ，即CF 12＝13＋CF，解得：CF ＝－3＋112或CF ＝－3－112(舍去)，∴DQ 1＝OC ＋CF ＝3＋－3＋112＝3＋112， ∴Q 1(1，3＋112)；(9分) ②与①同理可证△DNQ 2∽△DQ 1N ，∴Q 2D DN ＝DN Q 1D ，即Q 2D 12＝123＋112，解得：Q 2D ＝11－34， ∴Q 2(1，－11－34)．(10分) Ⅱ. 如解图②，过点N 作CN 的垂线，交对称轴于点Q 3.∵∠Q 3ND ＋∠ODC ＝∠OCN ＋∠ODC ＝90°，∴∠Q 3ND ＝∠OCN ，又∵∠COD ＝∠NDQ 3＝90°，∴△Q 3ND ∽△NCO ，∴Q 3D ON ＝DN OC ，即Q 3D 32＝123，解得：Q 3D ＝14， ∴Q 3(1，－14)；(11分) Ⅲ. 如解图③，过点C 作CN 的垂线，交对称轴于点Q 4.作CE ⊥DQ 4于E .∵∠Q 4CE ＋∠ECN ＝∠OCN ＋∠ECN ＝90°，∴∠Q 4CE ＝∠OCN ，又∵∠CON ＝∠CEQ 4＝90°，∴△Q 4CE ∽△NCO ，∴Q 4E ON ＝CE OC ，即Q 4E 32＝13，解得：Q 4E ＝12， ∴DQ 4＝3＋12＝72，∴Q 4(1，72)．综上所述，点Q 的坐标为：Q 1(1，3＋112)，Q 2(1，－11－34)，Q 3(1，－14)，Q 4(1, 72)(12分)第25题解图26.(1)解：如解图①，在▱ABCD 中，DC ＝AB ＝47，在Rt △ADH 中，DH ＝AD 2－AH 2＝72－（21）2＝27，∴HC ＝DC －DH ＝47－27＝27，在Rt △ACH 中，AC ＝CH 2＋AH 2＝（27）2＋（21）2＝7.(4分) (2)解：S ＝⎩⎪⎨⎪⎧3t 2（0≤t ≤73）－1353t 2＋8435t －9835（73＜t ≤4）233t 2－2833t ＋9833（4＜t ≤7）.(8分)【解法提示】▱ABCD 中，AB ∥CD .∴∠ACD ＝∠BAC ，∵Rt △ACH 中，tan ∠ACD ＝AH HC ＝2127＝32，第26题解图①∴tan ∠BAC ＝32，在运动过程中，AE ＝t ，AF ＝3t ，∴EF ＝2t ，作GK ⊥AC 于点K ，则EK ＝t ，GK ＝3t ，∴tan ∠GAK ＝GK AK ＝3t 2t ＝32＝tan ∠BAC ， ∴∠GAK ＝∠BAC ，即点G 在直线AB 上．①如解图①，当0≤t ≤73时，△EFG 与△ABC 的重叠部分就是△EFG ， ∴S ＝12EF ·GK ＝12·2t ·3t ＝3t 2； ②如解图②，当73＜t ≤4时，设BC 、GF 相交于点L ，过点B 作BT ∥AF ，交FG 延长线于点T . ∴△BTG ∽△AFG ，∴BT AF ＝BG AG，在Rt △AGK 中，AG ＝AK 2＋GK 2＝（2t ）2＋（3t ）2＝7t ， ∴BG ＝AB －AG ＝7(4－t )，∴BT 3t ＝7（4－t ）7t， ∴BT ＝12－3t ，过点B 作BI ⊥AF 于点I ，过点L 作MN ∥BI ，分别交AF 、BT 于点M 、N .则MN ＝BI ，且MN ⊥AF , MN ⊥BT ，第26题解图②∵KG ∥BI ，∴△AGK ∽△ABI ，∴BI GK ＝AB AG ，即BI 3t ＝477t，解得BI ＝43，∴MN ＝BI ＝43，∵BT ∥AF ， ∴△BTL ∽△CFL ，∴LM LN ＝CF BT ，∴LM 43－LM ＝3t －712－3t，解得：LM ＝123t －2835， ∴S ＝S △GEF －S △LCF ＝12EF ·GK －12CF ·ML ＝3t 2－12(3t －7)·123t －2835＝－1353t 2＋8435t －9835； ③如解图③，当4＜t ≤7时，过点B 作BT ∥AF ，交EG 于点T .过点L 作MN ⊥AF ，分别交AF 、BT 于点M 、N . 由②可知，MN ＝43，∵BT ∥AF ，∴△GBT ∽△GAE ，∴BT AE ＝BG AG，第26题解图③由①知，AG ＝7t ，∴BG ＝AG －AB ＝7t －47，∴BT t ＝7t －477t，解得：BT ＝t －4，∵BT ∥AF ，∴△BTL ∽△CEL ，∴ML NL ＝CE BT ， ∴ML 43－ML ＝7－t t －4，解得：ML ＝283－43t 3， ∴S ＝12EC ·LM ＝12(7－t )· 283－43t 3＝233t 2－2833t ＋9833.第26题解图④(3)解：存在．(9分)理由：如解图④，当F′G′∥AD时，∠M＝∠D，由(1)可知，AD＝AC，∴∠D＝∠ACD＝∠MCN，∴∠MCN＝∠M，∴△CMN是以∠MCN为底角的等腰三角形．根据题意，CF′＝F′G′＝CG′＝14.过点C作CZ⊥F′M，延长ZC交AD的延长线于点Q，则QZ⊥AD. Rt△CF′Z中，CZ＝CF′·sin∠F′＝14·sin60°＝73，(10分)∵S△ADC＝12AD·CQ＝12DC·AH，∴7CQ＝47×21，解得：CQ＝4 3.(11分) ∵F′G′∥AD，∴△CNM∽△CAD，∴CMCD＝CZCQ，即CM47＝7343，解得：CM＝77.(12分)。

重庆市2014年中考数学试题B卷(word版)

4题图FEDC BA3题图FECBA8题图ODCBAyy y y xxxxDCBA义务教育基础课程初中教学资料重庆市2014年初中毕业暨高中招生考试数学试题（B 卷）（满分：150分时间：120分钟）参考公式:抛物线y ＝ax 2＋bx ＋c(a ≠0)的顶点坐标为)44,2(2a b ac a b --,对称轴公式为ab x 2-=.一、选择题：（本大题共12个小题，每小题4分，共48分）1、某地连续四天每天的平均气温分别是：1℃，－1℃，0℃，2℃，则平均气温中最低的是（） A 、－1℃ B 、0℃ C 、1℃ D 、2℃2、计算2252x x -的结果是（） A 、3 B 、3x C 、23x D 、43x3、如图，△ABC ∽△DEF ，相似比为1：2，若BC ＝1，则EF 的长是（） A 、1 B 、2 C 、3 D 、44、如图，直线AB ∥CD ，直线EF 分别交AB 、CD 于点E 、F ，若∠AEF ＝50°，则∠EFC 的大小是（）A 、40°B 、50°C 、120°D 、130°5、某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参加比赛。

为此，初三（1）班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是96分，甲的成绩的方差是0.2，乙的成绩的方差是0.8，根据以上数据，下列说法正确的是（）A 、甲的成绩比乙的成绩稳定B 、乙的成绩比甲的成绩稳定C 、甲、乙两人的成绩一样稳定D 、无法确定甲、乙的成绩谁更稳定 6、若点（3，1）在一次函数2(0)y kx k =-≠的图象上，则k 的值是（） A 、5 B 、4 C 、3 D 、1 7、分式方程431x x=+的解是（） A 、1x = B 、1x =- C 、3x = D 、3x =-8、如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，∠ACB ＝30°，则∠AOB 的大小为（） A 、30° B 、60° C 、90° D 、120°9、夏天到了，某小区准备开放游泳池，物业管理处安排一名清洁工对一个无水的游泳池进行清洗。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

重庆市 2014 年初中毕业暨高中招生考试数学试题（B 卷）
（满分：150 分时间：120 分钟）
参考答案与试题解析
一、选择题（本大题共 12 小题，每小题 4 分，共 48 分）
1．（4 分）（2014•重庆）某地连续四天每天的平均气温分别是：1℃、﹣1℃、0℃、2℃，
则平均气温中最低的是（）
A．﹣1℃
B．0℃
C．1℃
D．2℃
专题：应用题．
分析：根据正数大于一切负数解答．
解答：解：∵1℃、﹣1℃、0℃、2℃中气温最低的是﹣1℃，
∴平均气温中最低的是﹣1℃．故选 A．点评：本题考查了有理数的大小比较，是基础题，熟记正数大于一切负数是解题的关键．
2．（4 分）（2014•重庆）计算 5x2﹣2x2 的结果是（）
3．（4 分）（2014•重庆）如图，△ABC∽△DEF，相似比为 1：2．若 BC=1，则 EF 的长是（）
A．1
B．2
C．3
D．4
考点：相似三角形的性质．菁优网版权所有
分析：根据相似三角形对应边的比等于相似比即可求解．
ቤተ መጻሕፍቲ ባይዱ
解答：解：∵△ABC∽△DEF，相似比为 1：2， ∴ =，
∴EF=2BC=2．
解答：解：∵矩形 ABCD 的对角线 AC，BD 相交于点 O，
∴OB=OC，
∴∠OBC=∠ACB=30°，
∴∠AOB=∠OBC+∠ACB=30°+30°=60°．故选 B．点评：本题考查了矩形的性质，等边对等角的性质以及三角形的一个外角等于与它不相邻
的两个内角的和的性质，熟记各性质是解题的关键．
9．（4 分）（2014•重庆）夏天到了，某小区准备开放游泳池，物业管理处安排一名清洁工
对一个无水的游泳池进行清洗，该工人先只打开一个进水管，蓄了少量水后关闭进水管并
立即进行清洗，一段时间后，再同时打开两个出水管将池内的水放完，随后将两个出水管
关闭，并同时打开两个进水管将水蓄满．已知每个进水管的进水速度与每个出水管的出水
考点：方差．菁优网版权所有
分析：根据方差的意义可作出判断，比较出甲乙的方差大小即可．
解答：解：∵甲的成绩的方差是 0.2，乙的成绩的方差是 0.8，0.2＜0.8，
∴甲的成绩比乙的成绩稳定，
故选：A．点评：本题考查方差了的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明
这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
∴3k﹣2=1，解得 k=1．故选 D．点评：本题考查了一次函数图象上点的坐标特征，准确计算是解题的关键．
7．（4 分）（2014•重庆）分式方程
= 的解是（）
A．x=1
B． x=﹣1
C．x=3
D． x=﹣3
考点：解分式方程．菁优网版权所有
专题：计算题．
分析：分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可得到分式方程的解．
加比赛，为此，初三（1）班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学
的平均分都是 96 分，甲的成绩的方差是 0.2，乙的成绩的方差是 0.8．根据以上数据，下列
说法正确的是（）
A．甲的成绩比乙的成绩稳定
B．乙的成绩比甲的成绩稳定
C．甲、乙两人的成绩一样稳定
D．无法确定甲、乙的成绩谁更稳定
故选 B．点评：本题考查了相似三角形的性质：相似三角形对应边的比等于相似比．
4．（4 分）（2014•重庆）如图，直线 AB∥CD，直线 EF 分别交 AB，CD 于点 E，F．若 ∠AEF=50°，则∠EFC 的大小是（）
A．40°
B．50°
C．120°
考点：平行线的性质．菁优网版权所有
A．3
B．3x
C．3x2
D．3x4
考点：合并同类项．菁优网版权所有
分析：根据合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，进行运算即可．
解答：解：原式=5x2﹣2x2
=3x2．故选：C．点评：此题考查了合并同类项的知识，属于基础题，解答本题的关键是掌握合并同类项的法则．
速度相同，从工人最先打开一个进水管开始，所用时间为 x，游泳池内的蓄水量为 y，则下
列各图中能够反映 y 与 x 的函数关系的大致图象是（）
A
B
C
D
．
．
．
．
考点：函数的图象．菁优网版权所有
分析：根据题目中叙述的过程，开始打开一个进水管，游泳池内的蓄水量逐渐增多；一段时间后，再同时打开两个出水管将池内的水放完，游泳池内的蓄水量逐渐减少直到水量为 0，并且时间比开始用的少；随后将两个出水管关闭，并同时打开两个进水管将水蓄满，游泳池内的蓄水量增多．
分析：根据两直线平行，同旁内角互补列式计算即可得解．解答：
解：∵AB∥CD， ∴∠EFC=180°﹣∠AEF=180°﹣50°=130°．
D．130°
故选 D．点评：本题考查了平行线的性质，熟记性质是解题的关键．
5．（4 分）（2014•重庆）某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参
O，∠ACB=30°，则∠AOB 的大小为（）
A． 30°
B． 60°
C． 90°
D． 120°
考点：矩形的性质．菁优网版权所有
分析：根据矩形的对角线互相平分且相等可得 OB=OC，再根据等边对等角可得 ∠OBC=∠ACB，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
6．（4 分）（2014•重庆）若点（3，1）在一次函数 y=kx﹣2（k≠0）的图象上，则 k 的值是
（） A．5
B．4
C．3
D．1
考点：一次函数图象上点的坐标特征．菁优网版权所有
分析：把点的坐标代入函数解析式计算即可得解．
解答：解：∵点（3，1）在一次函数 y=kx﹣2（k≠0）的图象上，
解答：解：去分母得：4x=3x+3，解得：x=3，经检验 x=3 是分式方程的解．故选 C
点评：此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
8．（4 分）（2014•重庆）如图，在矩形 ABCD 中，对角线 AC，BD 相交于点