线性回归分析报告地基本步骤
回归分析的基本步骤

回归分析的基本步骤回归分析是一种用来探究变量之间关系的统计方法。
通过回归分析,可以确定自变量对因变量的影响程度,并用回归方程来预测因变量的值。
本文将介绍回归分析的基本步骤,包括数据收集与准备、回归模型的选择、模型拟合以及模型评估等。
数据收集与准备在进行回归分析之前,首先需要收集与问题相关的数据。
这些数据可以通过实验、观测或问卷调查等方式获得。
在数据收集过程中需要注意保证数据的准确性和完整性,以及避免数据的缺失。
收集到数据后,还需要进行数据的预处理。
这包括数据的清洗和转换。
数据清洗主要是去除异常值和错误数据。
数据转换可以包括对变量进行标准化、对非线性关系进行变量转换等操作,以使数据符合回归分析的假设。
回归模型的选择在回归分析中,需要选择适当的回归模型来描述自变量和因变量之间的关系。
常见的回归模型包括线性回归模型、多项式回归模型、指数回归模型等等。
在选择回归模型时,需要考虑以下几点:1.因变量和自变量之间的关系类型:线性还是非线性关系;2.自变量之间是否存在多重共线性:即自变量之间是否存在相关性;3.应用领域的特点:不同领域对变量之间关系的要求不同。
模型拟合选择好回归模型后,需要对模型进行拟合。
拟合模型的目标是通过最小化残差平方和来找到最优的回归系数。
常用的拟合方法有最小二乘法和最大似然法。
最小二乘法是通过最小化实际观测值与回归模型预测值之间的差异来确定回归系数。
最大似然法是基于观测数据的概率分布来估计模型参数。
两种方法都可以得到相似的结果,选择哪种方法取决于实际问题和数据的性质。
模型评估在模型拟合完成后,需要对模型进行评估。
评估模型的好坏可以通过各种统计指标来衡量,如决定系数(R-squared)、均方差(MSE)等。
决定系数是指模型能够解释因变量变异性的比例,其取值范围为0到1。
值越接近1,说明模型对数据的拟合程度越好。
均方差是指观测值与模型预测值之间的平均偏差。
均方差越小,说明模型的预测精度越高。
论述一元线性回归的基本步骤

论述一元线性回归的基本步骤
一元线性回归是一种统计学方法,用来描述两个变量之间的线性关系,并建立相应的回归模型。
基本的步骤包括:
(1)确定数据源和变量:从数据源中收集相关的数据,并确定要进行研究的变量:x代表自变量,y代表因变量。
(2)进行各种统计分析:绘制散点图或残差图,用于可视化数据并判断是否存在线性关系;同时,计算出x与y之间的相关系数,试图发现x与y 之间的关联,以确定是否存在线性回归关系。
(3)拟合线性模型:使用常见的最小二乘法方法根据已有数据估计线性模型,即拟合误差平方和最小化的拟合直线,从而得到线性回归模型。
(4)检验线性模型:检验线性模型的有效性是至关重要的一步,可以检验残差图的正态分布假设、小概率假设和模型假设,可以构建R2、F值、AIC和BIC等指标,以进一步确定模型的有效性。
(5)预测新数据:如果经过上述模型检验发现线性模型是有效的,则可以用该模型预测新数据的结果。
总的来说,一元线性回归的基本步骤主要是确定数据源和变量,进行各种统计分析,拟合线性模型,检验模型的有效性,最后利用模型预测新的数据。
线性回归分析

线性回归分析线性回归是一种用来建立和预测变量间线性关系的统计分析方法。
它可以帮助我们了解变量之间的相互影响和趋势,并将这些关系用一条直线来表示。
线性回归分析常被应用于经济学、社会科学、自然科学和工程等领域。
一、概述线性回归分析是一个广泛使用的统计工具,用于建立变量间的线性关系模型。
该模型假设自变量(独立变量)与因变量(依赖变量)之间存在线性关系,并通过最小化观测值与模型预测值之间的误差来确定模型的参数。
二、基本原理线性回归分析基于最小二乘法,通过最小化观测值与模型预测值之间的残差平方和来确定模型的参数。
具体来说,线性回归模型可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε,其中Y是因变量,X1到Xn是自变量,β0到βn是回归系数,ε是误差项。
回归系数表示自变量对因变量的影响程度。
三、应用步骤进行线性回归分析时,通常需要以下几个步骤:1. 收集数据:获取自变量和因变量的样本数据。
2. 建立模型:根据数据建立线性回归模型。
3. 评估模型的准确性:通过计算残差、决定系数等指标来评估模型的准确性。
4. 进行预测和推断:利用模型对未知数据进行预测和推断。
四、模型评价指标在线性回归分析中,有几个常用的指标用于评价模型的准确性:1. R平方值:R平方值表示因变量的变异性能够被模型解释的比例,数值范围为0到1。
R平方值越接近1,表示模型对数据的拟合程度越好。
2. 残差分析:进行残差分析可以帮助我们判断模型是否符合线性回归的基本假设。
一般来说,残差应该满足正态分布、独立性和等方差性的假设。
五、优缺点线性回归分析有以下几个优点:1. 简单易懂:线性回归模型的建立和解释相对较为简单,无需复杂的数学知识。
2. 实用性强:线性回归模型适用于很多实际问题,可以解决很多预测和推断的需求。
然而,线性回归分析也存在以下几个缺点:1. 假设限制:线性回归模型对于变量间关系的假设比较严格,不适用于非线性关系的建模。
总结:线性回归分析的基本步骤
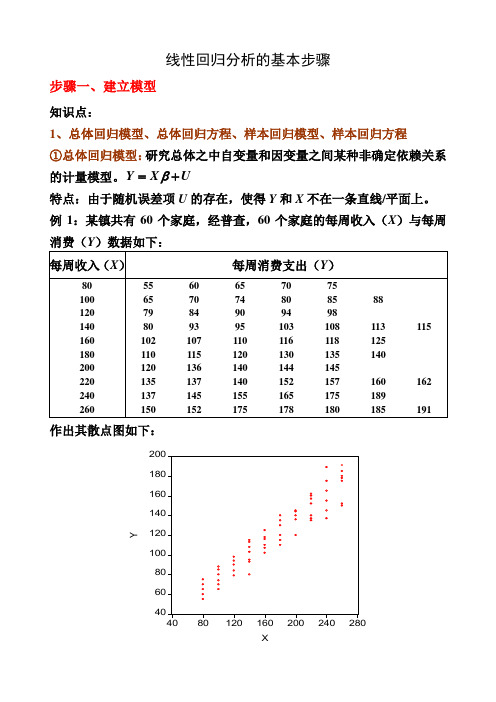
线性回归分析的基本步骤步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。
Y X U β=+特点:由于随机误差项U 的存在,使得Y 和X 不在一条直线/平面上。
例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X )与每周消费(Y )数据如下:作出其散点图如下:②总体回归方程(线):由于假定0EU =,因此因变量的均值与自变量总处于一条直线上,这条直线()|E Y X X β=就称为总体回归线(方程)。
总体回归方程的求法:以例1的数据为例,求出E (Y |X 由于01|i i i E Y X X ββ=+,因此任意带入两个X i 和其对应的E (Y |X i )值,即可求出01ββ和,并进而得到总体回归方程。
如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得:01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系,即所求的总体回归方程为:()|170.6i i i E Y X X =+,其图形为:③样本回归模型:总体通常难以得到,因此只能通过抽样得到样本数据。
如在例1中,通过抽样考察,我们得到了20个家庭的样本数据:那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。
④样本回归方程(线):通过样本数据估计出ˆβ,得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。
如下图所示:⑤四者之间的关系:ⅰ:总体回归模型建立在总体数据之上,它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系;样本回归模型建立在抽样数据基础之上,它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。
线性回归分析

线性回归分析线性回归分析是一种常见的统计分析方法,主要用于探索两个或多个变量之间的线性关系,并预测因变量的值。
在现代运营和管理中,线性回归分析被广泛应用于市场营销、财务分析、生产预测、风险评估等领域。
本文将介绍线性回归分析的基本原理、应用场景、建模流程及常见误区。
一、基本原理线性回归分析基于自变量和因变量之间存在一定的线性关系,即当自变量发生变化时,因变量也会随之发生变化。
例如,销售额与广告投入之间存在一定的线性关系,当广告投入增加时,销售额也会随之增加。
线性回归分析的目标是找到这种线性关系的最佳拟合线,并利用该线性方程来预测因变量的值。
二、应用场景线性回归分析可以应用于许多不同的领域,例如:1.市场营销。
通过分析销售额和广告投入之间的关系,企业可以确定最佳的广告投入量,从而提高销售额。
2.财务分析。
线性回归分析可以用于预测公司的收入、费用和利润等财务指标,并帮助企业制定有效的财务战略。
3.生产预测。
通过分析生产量和生产成本之间的关系,企业可以确定最佳的生产计划,从而提高生产效率。
4.风险评估。
通过分析不同变量之间的关系,企业可以评估各种风险并采取相应的措施,从而减少损失。
三、建模流程线性回归分析的建模流程包括以下步骤:1.确定自变量和因变量。
自变量是用来预测因变量的变量,而因变量是需要预测的变量。
2.收集数据。
收集与自变量和因变量相关的数据,并进行初步的数据处理和清理工作。
3.拟合最佳拟合线。
利用最小二乘法拟合最佳拟合线,并计算相关的统计指标(如拟合优度、标准误等)。
4.判断线性关系的签ificance。
利用t检验或F检验来判断线性关系的签ificance,并进行推断分析。
5.进行预测。
利用已知的自变量的值,通过线性方程来预测因变量的值。
四、常见误区在进行线性回归分析时,有一些常见的误区需要注意:1.线性假设误区。
线性回归分析建立在自变量和因变量之间存在线性关系的基础之上,如果这种关系不是线性的,则建立的回归模型将失效。
线性回归分析的基本步骤
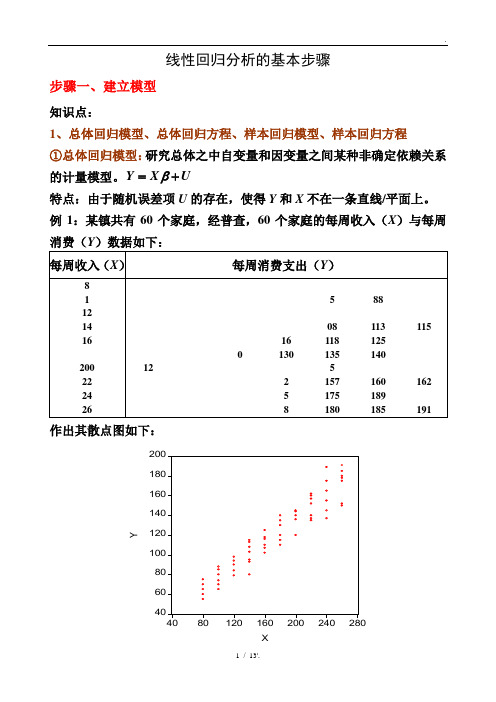
线性回归分析的基本步骤步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。
Y X U β=+特点:由于随机误差项U 的存在,使得Y 和X 不在一条直线/平面上。
例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X )与每周消费(Y )数据如下:作出其散点图如下:②总体回归方程(线):由于假定0EU =,因此因变量的均值与自变量总处于一条直线上,这条直线()|E Y X X β=就称为总体回归线(方程)。
总体回归方程的求法:以例1的数据为例 由于01|i i i E Y X X ββ=+,因此任意带入两个X i 和其对应的E (Y |X i )值,即可求出01ββ和,并进而得到总体回归方程。
如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得:01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系,即所求的总体回归方程为:()|170.6i i i E Y X X =+,其图形为:③样本回归模型:总体通常难以得到,因此只能通过抽样得到样本数据。
如在例1中,通过抽样考察,我们得到了20个家庭的样本数据:那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。
④样本回归方程(线):通过样本数据估计出ˆβ,得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。
如下图所示:⑤四者之间的关系:ⅰ:总体回归模型建立在总体数据之上,它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系;样本回归模型建立在抽样数据基础之上,它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。
线性回归分析实验报告

实验一:线性回归分析实验目的:通过本次试验掌握回归分析的基本思想和基本方法,理解最小二乘法的计算步骤,理解模型的设定T检验,并能够根据检验结果对模型的合理性进行判断,进而改进模型。
理解残差分析的意义和重要性,会对模型的回归残差进行正态型和独立性检验,从而能够判断模型是否符合回归分析的基本假设。
实验内容:用线性回归分析建立以高血压作为被解释变量,其他变量作为解释变量的线性回归模型。
分析高血压与其他变量之间的关系。
实验步骤:1、选择File | Open | Data 命令,打开gaoxueya.sav图1-1 数据集gaoxueya 的部分数据2、选择Analyze | Regression | Linear…命令,弹出Linear Regression (线性回归) 对话框,如图1-2所示。
将左侧的血压(y)选入右侧上方的Dependent(因变量) 框中,作为被解释变量。
再分别把年龄(x1)、体重(x2)、吸烟指数(x3)选入Independent (自变量)框中,作为解释变量。
在Method(方法)下拉菜单中,指定自变量进入分析的方法。
图1-2 线性回归分析对话框3、单击Statistics按钮,弹出Linear Regression : Statistics(线性回归分析:统计量)对话框,如图1-3所示。
1-3线性回归分析统计量对话框4、单击 Continue 回到线性回归分析对话框。
单击Plots ,打开Linear Regression:Plots (线性回归分析:图形)对话框,如图1-4所示。
完成如下操作。
图1-4 线性回归分析:图形对话框5、单击Continue ,回到线性回归分析对话框,单击Save按钮,打开Linear Regression;Save 对话框,如图1-5所示。
完成如图操作。
图1-5 线性回归分析:保存对话框6、单击Continue ,回到线性回归分析对话框,单击Options 按钮,打开Linear Regression ;Options 对话框,如图1-6所示。
线性回归分析步骤

线性回归分析步骤线性回归分析是一种统计学方法,用于确定两个变量之间的线性关系。
它可以用于预测特定的变量,并估计它们之间的关系。
它也可以用于识别影响变量的其他因素,以验证假设。
线性回归是定量分析的一个重要方面,可以帮助研究人员更好地理解数据,并从中得出有意义的结论。
本文将介绍线性回归分析的基本步骤,包括数据收集、数据分析、回归分析和结果解释。
首先,在进行线性回归分析之前,需要收集数据。
这可通过实验、观察、实地考察或从其他人获得这些资料。
通常,数据收集者需要有清晰的研究目的,确定有关数据的变量类型和范围,以及所涉及的样本大小。
收集的数据需要记录,以便进行数据分析的第二步。
接下来,需要对收集的数据进行分析。
其核心方法是计算两个变量之间的相关系数,以确定它们之间的线性关系。
如果两个变量之间呈线性关系,那么可以使用线性回归分析,以估计它们之间的相关性。
同时,在样本内可以应用其他技术,比如回归的分类、因变量的探索和多变量的线性回归分析,以帮助调查人员更好地理解数据。
第三步是实施回归分析,以估计变量之间的关系。
回归分析的过程包括选择回归模型、计算参数、检验模型好坏和比较模型之间的区别。
需要注意的是,计算参数时,应该考虑到所采用的统计方法,以确保结果的准确性。
最后,还需要解释结果,以获得有意义的结论。
结果解释可以采用模型诊断和参数检验的结果,以识别模型的弱点,并根据结果对结论进行调整。
另外,也可以检查预期的变量之间的联系,以及其他变量对模型结果的影响。
最后,可以利用结果改善和解释过程中的假设,以验证研究的可行性。
综上所述,线性回归分析是一种重要的定量分析技术,可以帮助研究人员更好地理解数据,以及从中得出有意义的结论。
它的基本步骤包括数据收集、数据分析、回归分析和结果解释。
在收集数据时,应记录所涉及的变量类型、范围和样本大小的信息;在进行数据分析时,要计算变量之间的相关系数;在运行回归分析时,应考虑回归模型、计算参数和检验模型的好坏;在解释结果时,应诊断模型弱点、检查预期变量及其他变量对模型结果的影响,以及利用结果改善和验证假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。
Y X U β=+特点:由于随机误差项U 的存在,使得Y 和X 不在一条直线/平面上。
例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X )与每周作出其散点图如下:②总体回归方程(线):由于假定0EU =,因此因变量的均值与自变量总处于一条直线上,这条直线()|E Y X X β=就称为总体回归线(方程)。
总体回归方程的求法:以例1的数据为例实用标准文案由于()01|i i i E Y X X ββ=+,因此任意带入两个X i 和其对应的E (Y |X i )值,即可求出01ββ和,并进而得到总体回归方程。
如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得:01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系,即所求的总体回归方程为:()|170.6i i i E Y X X =+,其图形为:③样本回归模型:总体通常难以得到,因此只能通过抽样得到样本数据。
如在例1中,通过抽样考察,我们得到了20个家庭的样本数据:那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。
④样本回归方程(线):通过样本数据估计出ˆβ,得到样本观测值的拟合值与解释变量之间的关系方程ˆˆYX β=称为样本回归方程。
如下图所示:⑤四者之间的关系:ⅰ:总体回归模型建立在总体数据之上,它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系;样本回归模型建立在抽样数据基础之上,它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。
这种近似表现在两个方面:一是结构参数ˆβ是其真实值β的一种近似估计;二是残差e 是随机误差项U 的一个近似估计;ⅱ:总体回归方程是根据总体数据得到的,它描述的是因变量的条件均值E (Y |X )与自变量X 之间的线性关系;样本回归方程是根据抽样数据得到的,它描述的是因变量Y 样本预测值的拟合值ˆY与自变量X 之间的线性关系。
ⅲ:回归分析的目的是试图通过样本数据得到真实结构参数β的估计值,并要求估计结果ˆβ足够接近真实值β。
由于抽样数据有多种可能,每一次抽样所得到的估计值ˆβ都不会相同,即β的估计量ˆβ是一个随机变量。
因此必须选择合适的参数估计方法,使其具有良好的统计性质。
2、随机误差项U 存在的原因: ①非重要解释变量的省略 ②人的随机行为 ③数学模型形式欠妥④归并误差(如一国GDP 的计算) ⑤测量误差等3、多元回归模型的基本假定 ①随机误差项的期望值为零()0i E U =②随机误差项具有同方差性2() 1,2,,i Var u i n σ==L③随机误差项彼此之间不相关(,)0 ; ,1,2,,i j Cov u u i j i j n =≠=L ④解释就变量X 1,X 2,·,X k 为确定型变量,与随机误差项彼此不相关。
(,)0 1,2,, 1,2,,ij j Cov X u i k j n ===L L⑤解释就变量X 1,X 2,·,X k 之间不存在精确的(完全的)线性关系,即解释变量的样本观测值矩阵X 为满秩矩阵:rank (X )=k +1<n ⑥随机误差项服从正态分布,即:u i ~N (0,σ2),i =1,2,·,n步骤二、参数估计知识点:1、最小二乘估计的基本原理:残差平方和最小化。
2、参数估计量:① 一元回归:1201ˆˆˆi i i x y x Y Xβββ⎧=⎪⎨⎪=-⎩∑∑ ② 多元回归:()1ˆT X X X Y β-'= 3、最小二乘估计量的性质(Gauss-Markov 定理):在满足基本假设的情况下,最小二乘估计量ˆβ是β的最优线性无偏估计量(BLUE 估计量)步骤三、模型检验1、经济计量检验(后三章内容)2、统计检验 ①拟合优度检验 知识点:ⅰ:拟合优度检验的作用:检验回归方程对样本点的拟合程度 ⅱ:拟合优度的检验方法:计算(调整的)样本可决系数22/R R21RSS ESSR TSS TSS==-,2/11/1ESS n k R TSS n --=--注意掌握离差平方和、回归平方和、残差平方和之间的关系以及它们的自由度。
计算方法:通过方差分析表计算例2:下表列出了三变量(二元)模型的回归结果:1) 样本容量为多少?解:由于TSS 的自由度为n -1,由上表知n -1=14,因此样本容量n =15。
2) 求ESS解:由于TSS =ESS +RSS ,故ESS =TSS -RSS =77 3) ESS 和RSS 的自由度各为多少?解:对三变量模型而言,k =2,故ESS 的自由度为n -k -1=12 RSS 的自由度为k =2 4) 求22R R 和解:2659650.998866042RSS R TSS ===,2/110.9986/1ESS n k R TSS n --=-=-②回归方程的显著性检验(F 检验)目的:检验模型中的因变量与自变量之间是否存在显著的线性关系 步骤:1、提出假设:0121:...0:0 , 1,2,...,k j H H j kββββ====≠=至少有一2、构造统计量:/~(,1)/1RSS kF F k n k ESS n k =----3、给定显著性水平α,确定拒绝域(),1F F k n k α>--4、计算统计量值,并判断是否拒绝原假设例3:就例2中的数据,给定显著性水平1%α=,对回归方程进行显著性检验。
解:由于统计量值/65965/25140.13/177/12RSS k F ESS n k ===--,又()0.012,12 6.93F =,而()0.015140.132,12 6.93F F =>=故拒绝原假设,即在1%的显著性水平下可以认为回归方程存在显著的线性关系。
附:2R F 与检验的关系:由于()()22222/1/1/1/1RSS RSS R R RSS ESS R k TSS ESS RSS R F RSS k R n k F ESS n k ⎫==⇒=⎪⎪+-⇒=⎬---⎪=⎪--⎭又 ③解释变量的显著性检验(t 检验)目的:检验模型中的自变量是否对因变量存在显著影响。
知识点:多元回归:ˆiS β=1,1i i C ++为()1X X -'中位于第i +1行和i +1列的元素;一元回归:1ˆˆS S ββ==变量显著性检验的基本步骤:1、提出假设:01:0 :0i i H H ββ=≠2、构造统计量:ˆˆ~(1)ii t t n k S ββ=--3、给定显著性水平α,确定拒绝域/2(1)tt n k α>--4、计算统计量值,并判断是否拒绝原假设 例4:根据19个样本数据得到某一回归方程如下:12ˆ58.90.20.1 (0.0092) (0.084)Y X X se =-+-试在5%的显著性水平下对变量12X X 和的显著性进行检验。
解:由于/20.025(1)(16) 2.12t n k t α--==,故t 检验的拒绝域为 2.12t>。
对自变量1X 而言,其t 统计量值为11ˆˆ0.221.74 2.120.0092t S ββ===>,落入 拒绝域,故拒绝10β=的原假设,即在5%的显著性水平下,可以认为自变量1X 对因变量有显著影响;对自变量2X 而言,其t 统计量值为22ˆˆ0.11.192.120.084t S ββ===<,未落入拒绝域,故不能拒绝20β=的原假设,即在5%的显著性水平下,可以认为自变量2X 对因变量Y 的影响并不显著。
④回归系数的置信区间目的:给定某一置信水平1α-,构造某一回归参数i β的一个置信区间,使i β落在该区间内的概率为1α-基本步骤:1、构造统计量ˆˆ~(1)ii i t t n k S βββ-=--2、给定置信水平1α-,查表求出α水平的双侧分位数/2(1)t n k α--3、求出i β的置信度为1α-的置信区间()ˆˆ/2/2ˆˆ,iii i t S t S ααββββ-⨯+⨯ 例5:根据例4的数据,求出1β的置信度为95%的置信区间。
解:由于0.025(16) 2.12t =,故1β的置信度为95%的置信区间为:()()0.2 2.120.0092,0.2 2.120.00920.18,0.22-⨯+⨯=3、经济意义检验目的:检验回归参数的符号及数值是否与经济理论的预期相符。
例6:根据26个样本数据建立了以下回归方程用于解释美国居民的个人消费支出:122ˆ10.960.93 2.09 ( 3.33) (249.06) ( 3.09)0.9996Y X X t R =-+---= 其中:Y 为个人消费支出(亿元);X 1为居民可支配收入(亿元);X 2为利率(%)1) 先验估计12ˆˆββ和的符号; 解:由于居民可支配收入越高,其个人消费水平也会越高,因此预期自变量X 1回归系数的符号为正;而利率越高,居民储蓄意愿越强,消费意愿相应越低,因此个从消费支出与利率应该存在负相关关系,即2ˆβ应为负。
2) 解释两个自变量回归系数的经济含义;解:1ˆ0.93β=表示,居民可支配收入每增加1亿元,其个人消费支出相应会增加0.93亿元,即居民的边际消费倾向MPC =0.93;2ˆ 2.09β=-表示,利率提高1个百分点,个人消费支出将减少2.09亿元。
截距项表示居民可支配收入和利率为零时的个人消费支出为-10.96亿元,它没有明确的经济含义。
3) 检验1β是否显著不为1;(5%α=) 解:1)提出假设:0111: 1 :1H H ββ=≠2)构造统计量:111ˆˆ~(1)t t n k S βββ-=--3)给定显著性水平5%α=,查表得/20.025(1)(23) 2.07t n k t α--==,故拒绝域为 2.07t>4)计算统计量值:由于1111ˆ1ˆ1ˆˆ0.93ˆ()0.003734ˆ249.06()t S S t ββββββ=⇒=== 则111ˆˆ0.0718.75 2.070.003734t S βββ-===>,落入拒绝域。
故拒绝1 1 β=的原假设。
即在5%的显著性水平下,可认为边际消费倾向MPC 显著不为1。
4) 检验2β显否显著不为零;(5%α=) 解:1)提出假设:0212:0 :0H H ββ=≠2)构造统计量:22ˆˆ~(1)t t n k S ββ=--3)给定显著性水平5%α=,查表得/20.025(1)(23) 2.07t n k t α--==,故拒绝域为 2.07t>4)计算统计量值:由于2ˆ() 3.09 2.07t β=>,落入拒绝域,故拒绝原假设。
