清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
理论力学课后习题第三章解答
理论力学课后习题第三章解答3.1解 如题3.1.1图。
均质棒受到碗的弹力分别为，棒自身重力为。
棒与水平方向的夹角为。
设棒的长度为。
由于棒处于平衡状态，所以棒沿轴和轴的和外力为零。
沿过点且与轴平行的合力矩为0。
即：①②③ 由①②③式得：④ 又由于即⑤ 将⑤代入④得：图题1.3.11N ,2N G θl x y A z 0sin 2cos 21=-=∑θθN N F x0cos 2sin 21=-+=∑G N N Fyθθ0cos 22=-=∑θlG c N M i ()θθ22cos 1cos 22-=c l ,cos 2c r =θrc 2cos =θ3.2解 如题3.2.1图所示，均质棒分别受到光滑墙的弹力，光滑棱角的弹力，及重力。
由于棒处于平衡状态，所以沿方向的合力矩为零。
即①由①②式得：所以()cr c l 2224-=o图题1.3.21N 2N G y 0cos 2=-=∑G N Fyθ0cos 22cos 2=-=∑θθlG d N M z ld=θ3cos 31arccos ⎪⎭⎫ ⎝⎛=l d θ3.3解 如题3.3.1图所示。
棒受到重力。
棒受到的重力。
设均质棒的线密度为。
由题意可知，整个均质棒沿轴方向的合力矩为零。
3.4解 如题3.4.1图。
轴竖直向下，相同的球、、互切，、切于点。
设球的重力大小图题1.3.32AB i G ag ρ=1i G bgρ=2ρz ()BH BF G OD G M z --⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a ga aba b 2tan 22+=θ图题1.3.4Ox A B C B C D为，半径为，则对、、三个球构成的系统来说，在轴方向的合力应为零。
即：①对于球，它相对于过点与轴平行的轴的合力矩等于零。
即：②由式得：3.5解 如题3.5.1图。
梯子受到地面和墙的弹力分别为，，受地面和墙的摩擦力分别为，。
工程力学第3章 静力学平衡问题答案
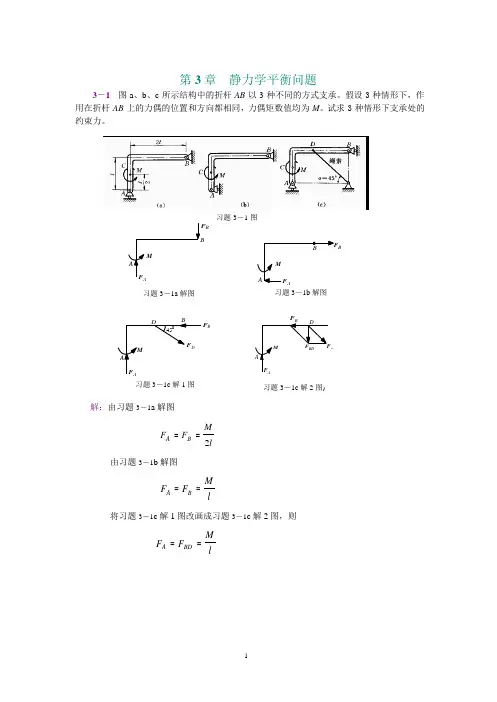
第 3 章 静力学平衡问题3－1 图 a 、b 、c 所示结构中的折杆 AB 以 3 种不同的方式支承。
假设 3 种情形下，作用在折杆 AB 上的力偶的位置和方向都相同，力偶矩数值均为 M 。
试求 3 种情形下支承处的 约束力。
习题 3－1 图BB习题 3－1a 解图习题 3－1b 解图BD习题 3－1c 解 1 图习题 3－1c 解 2 图)解：由习题 3－1a 解图M F A = F B = 2l由习题 3－1b 解图MF A = F B = l将习题 3－1c 解 1 图改画成习题 3－1c 解 2 图，则MF A = F BD =l∴ F B M= F BD = l，F D =2 M2 F BD =l3－2 图示的结构中，各构件的自重都略去不计。
在构件 AB 上作用一力偶，其力偶矩 数 值 M ＝800 N·m 。
试求支承 A 和 C 处的约束力。
FCAB '习题 3－2 图习题 3－2 解 1 图习题 3－2 解 2 图解：BC 为二力构件，其受力图如习题 3－2 解 1 图所示。
考虑 AB 平衡，由习题 3－2 解图，A 、B 二处的形成力偶与外加力偶平衡。
F = F ′ = M = 800 = 269.4 N A BBD 1.2 × 1.83－3 图示的提升机构中，物体放在小台车 C 上，小台车上装有 A 、B 轮，可沿垂导轨 ED 上下运动。
已知物体重 2 kN 。
试求导轨对 A 、B 轮的约束力。
F A F B习题 3－3 图解：W = 2kN ，T = W ΣF x = 0， F A = F B习题 3－3 解图ΣM i = 0， W × 300 − F A × 800 = 0 ，方向如图示。
F = 3 W = 0.75kN A 8，F B = 0.75 kN ，3－4 结构的受力和尺寸如图所示，求：结构中杆 1、2、3 杆所受的力。
工程力学习题讲义(清华大学)第3章作业.docx
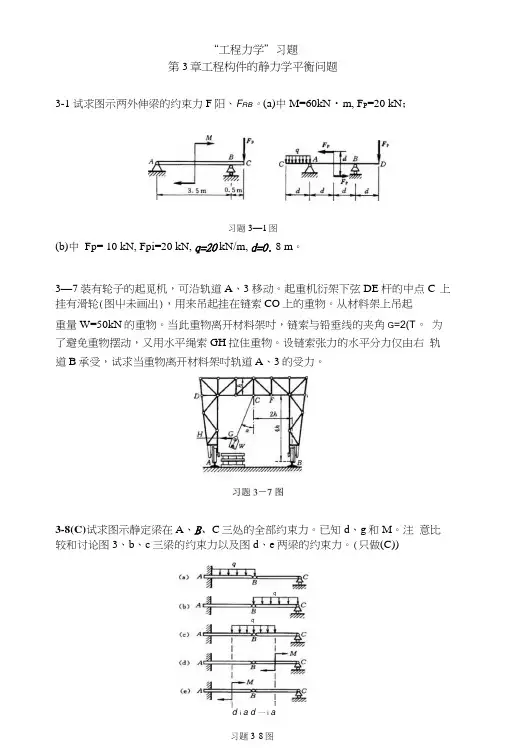
“工程力学”习题第3章工程构件的静力学平衡问题3-1试求图示两外伸梁的约束力F阳、F RB。
(a)中M=60kN・m, F P=20 kN；习题3—1图(b)中Fp= 10 kN, Fpi=20 kN, q=20 kN/m, d=0. 8 m。
3—7装有轮子的起觅机，可沿轨道A、3移动。
起重机衍架下弦DE杆的中点C 上挂有滑轮(图屮未画出)，用来吊起挂在链索CO上的重物。
从材料架上吊起重量W=50kN的重物。
当此重物离开材料架吋，链索与铅垂线的夹角G=2(T。
为了避免重物摆动，又用水平绳索GH拉住重物。
设链索张力的水平分力仅由右轨道B承受，试求当重物离开材料架吋轨道A、3的受力。
3-8(C)试求图示静定梁在A、B、C三处的全部约束力。
已知d、g和M。
注意比较和讨论图3、b、c三梁的约束力以及图d、e两梁的约束力。
(只做(C))qq| Id i a d一i a习题3-8图3-11飞机起落架由弹簧液压杆4D和油缸D以及连杆OB和CB组成，0、A、B、C处均为較链。
假设：飞机起飞或降落时以匀速沿着跑道运动。
轮子所支承的载荷为24 k乂试求A处销钉所受的力。
习题3-11图3-13图示为汽车台秤简图，BCF为整体台面，杠杆AB可绕轴0转动，B、C、D三处均为較链，杆DC处于水平位置。
假设法码和汽车的重量分别为皿和临。
试求平衡时M和M之间的关系。
习题3—13图3-14体重为W的体操运动员在吊环上做十字支撑。
图屮d为两肩关节间的距离。
皿为两臂总重量。
已知/、0、d、阳和假设手臂为均质杆，试求肩关节受力.习题3-14图3-16尖劈起重装置如图所示。
尖劈A的顶角为物块B上受力F Q的作用。
尖劈A与物块B之间的静摩擦因数为/s （有滚珠处摩擦力忽略不计）。
如不计尖劈A和物块B的重量，试求保持平衡时，施加在尖劈A上的力Fp的范围。
习题3-16图3-17砖夹的宽度为250 mm,杆件AGB和GCED在G点较接。
已知：砖的重量为W；提砖的合力为F P,作用在砖夹的对称中心线上；尺寸如图所示；砖夹与砖之间的静摩擦因数；s = 0. 5。
理论力学课后习题与答案解析
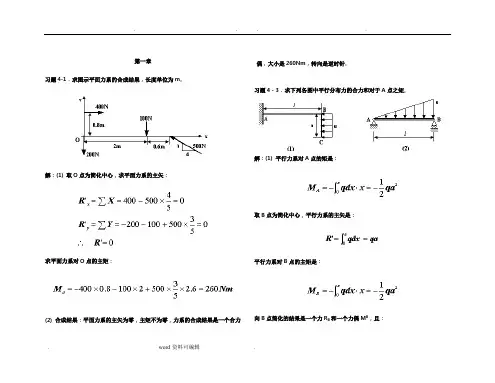
第一章习题4-1．求图示平面力系的合成结果，长度单位为m。
解：(1) 取O点为简化中心，求平面力系的主矢：求平面力系对O点的主矩：(2) 合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力偶，大小是260Nm，转向是逆时针。
习题4－3．求下列各图中平行分布力的合力和对于A点之矩。
解：(1) 平行力系对A点的矩是：取B点为简化中心，平行力系的主矢是：平行力系对B点的主矩是：向B点简化的结果是一个力R B和一个力偶M B，且：如图所示；将R B向下平移一段距离d，使满足：最后简化为一个力R，大小等于R B。
其几何意义是：R的大小等于载荷分布的矩形面积，作用点通过矩形的形心。
(2) 取A点为简化中心，平行力系的主矢是：平行力系对A点的主矩是：向A点简化的结果是一个力R A和一个力偶M A，且：如图所示；将R A向右平移一段距离d，使满足：最后简化为一个力R，大小等于R A。
其几何意义是：R的大小等于载荷分布的三角形面积，作用点通过三角形的形心。
习题4-4．求下列各梁和刚架的支座反力，长度单位为m。
解：(1) 研究AB杆，受力分析，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(2) 研究AB杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(3) 研究ABC，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
习题4-5．重物悬挂如图，已知G=1.8kN，其他重量不计；求铰链A的约束反力和杆BC所受的力。
解：(1) 研究整体，受力分析（BC是二力杆），画受力图：列平衡方程：解方程组：反力的实际方向如图示。
习题4-8．图示钻井架，G=177kN，铅垂荷载P=1350kN，风荷载q=1.5kN/m，水平力F=50kN；求支座A的约束反力和撑杆CD所受的力。
理论力学习题及答案(全)
第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。
（）2．在理论力学中只研究力的外效应。
（）3．两端用光滑铰链连接的构件是二力构件。
（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。
（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。
（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。
（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。
则其合力可以表示为。
①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。
①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。
3．三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。
4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。
①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。
5．在下述原理、法则、定理中，只适用于刚体的有。
①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。
三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。
2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。
理论力学解答(清华版)
第一章 静力学基本概念1-1 考虑力对物体作用的运动效应，力是（ A ）。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示，作用在物体A 上的两个大小不等的力1F 和2F ，沿同一直线但方向相反，则其合力可表为（ C ）。
A.1F –2FB.2F - 1FC.1F +2F图1－18 图1－191-3 F =100N ，方向如图1-19所示。
若将F 沿图示x ，y 方向分解，则x 方向分力的大小x F = C N ，y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体；B. 变形体；C. 刚体和变形体。
1-6 如图1-20所示，已知一正方体，各边长a ，沿对角线BH 作用一个力F ，则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.－F/31-7如图1-20所示，已知F=100N ，则其在三个坐标轴上的投影分别为： Fx = －402N ，Fy = 302N ，Fz = 502 N 。
图1－20 图1－21第二章力系的简化2-1．通过A（3，0，0），B（0，4，5）两点（长度单位为米），且由A指向B的力F，在z轴上投影为，对z轴的矩的大小为。
答：F/2；62F/5。
2-2．已知力F的大小，角度φ和θ，以及长方体的边长a，b，c，则力F在轴z和y上的投影：Fz= ；Fy= ；F对轴x的矩M x(F)= 。
答：Fz=F·sinφ；Fy=－F·cosφ·cosφ；Mx（F）=F（b·sinφ+c·cosφ·cosθ）图2－40 图2－412-3．力通过A（3，4、0），B（0，4，4）两点（长度单位为米），若F=100N，则该力在x轴上的投影为，对x轴的矩为。
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
F DBCBDBF '习题3－3图第3章 静力学平衡问题3－1 图示两种正方形结构所受荷载F 均已知。
试求其中1，2，3各杆受力。
解：图（a ）：045cos 23=-︒F FF F 223=（拉） F 1 = F 3（拉） 045cos 232=︒-F F F 2 = F （受压） 图（b ）：033='=F F F 1 = 0F 2 = F （受拉）3－2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上，点B 与拴在桩A 上的绳索AB 连接，在点D 加一铅垂向下的力F ，AB 可视为铅垂，DB 可视为水平。
已知α= 0.1rad.，力F = 800N 。
试求绳AB 中产生的拔桩力（当α很小时，tan α≈α）。
解：0=∑y F ，F F ED =αsin αs i nFF ED = 0=∑x F ，DB ED F F =αcos F FF DB 10tan ==α由图（a ）计算结果，可推出图（b ）中：F AB = 10F DB = 100F = 80 kN 。
3－3 起重机由固定塔AC 与活动桁架BC 组成，绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ，并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上，链索绕过点B 的滑轮，并沿直线BC 引向绞盘。
长度AC = BC ，不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3－1图(a-1)(a-2)'3(b-2)习题3－2图F习题3-5图习题3－4图 解：图（a ）：0=∑x F ，0sin 2cos=-ϕϕW F AB ，2sin2ϕW F AB =0=∑y F ，02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3－4 杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。
清华大学版理论力学课后习题答案大全
第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解：ϕc o s )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解：RvR v A A ==ωR v R v B B 22==ωB A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。
设杆BC 在水平位置时，滚子的角速度ω＝12 rad/s ，θ＝30︒，ϕ＝60︒，BC ＝270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
理论力学课后答案3
魏
泳
涛
m
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
ww
w.
kh
解：由于 BC 刚体是二力构件， AB 受力图如上，其中 N A 和 N B 构成一对力 偶。 M 5 N A NB 1 N AB 3 以整体为研究对象，受力图如上， A 、 D 处约束反力应构成力偶。因此 N D 也在水平方向上。 1 M D 0 ， N A ( AB CD sin 30 ) M1 M 2 0 ， M 2 3 N m
W
x
Ax
Bx
Ax
y
Ay
x
W
Bz
kh
Bz
da
w.
co
静力学习题及解答—力系的平衡
3.12 三脚圆桌的半径 r 500mm ，重 FW 600 N 。圆桌的三脚 A 、 B 和 C 成一等 边三角形。若在中线 CD 上距圆心为 a 的点 E 作用一铅垂力 F 1500N ，如图所 示。试求使圆桌不致翻到的最大距离。
kh
da
w.
co
kh
da
w.
(b)
co
q 2 2 0 ， N Bl sin 30 l l 0 ； N B ql 2 3 3 3 Fx 0 ， N Ax N B cos 30 3 ql 1 1 Fy 0 ， N Ay 2 ql N B sin 30 6 ql
静力学习题及解答—力系的平衡
3.1 在下列各图中，已知载荷集度 q 和长度 l ，试求梁长度所受的约束力。 (a)
理论力学解答(清华版)
第一章 静力学基本概念1-1 考虑力对物体作用的运动效应，力是（ A ）。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示，作用在物体A 上的两个大小不等的力1F 和2F ，沿同一直线但方向相反，则其合力可表为（ C ）。
A.1F –2FB.2F - 1FC.1F +2F图1－18 图1－191-3 F =100N ，方向如图1-19所示。
若将F 沿图示x ，y 方向分解，则x 方向分力的大小x F = C N ，y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体；B. 变形体；C. 刚体和变形体。
1-6 如图1-20所示，已知一正方体，各边长a ，沿对角线BH 作用一个力F ，则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.－F/31-7如图1-20所示，已知F=100N ，则其在三个坐标轴上的投影分别为： Fx = －402N ，Fy = 302N ，Fz = 502 N 。
图1－20 图1－21第二章力系的简化2-1．通过A（3，0，0），B（0，4，5）两点（长度单位为米），且由A指向B的力F，在z轴上投影为，对z轴的矩的大小为。
答：F/2；62F/5。
2-2．已知力F的大小，角度φ和θ，以及长方体的边长a，b，c，则力F在轴z和y上的投影：Fz= ；Fy= ；F对轴x的矩M x(F)= 。
答：Fz=F·sinφ；Fy=－F·cosφ·cosφ；Mx（F）=F（b·sinφ+c·cosφ·cosθ）图2－40 图2－412-3．力通过A（3，4、0），B（0，4，4）两点（长度单位为米），若F=100N，则该力在x轴上的投影为，对x轴的矩为。
理论力学静力学第三章习题答案
FBx F (与假设方向相反)
FAx F (与假设方向相反)
FCy
FCx FD
解：取整体为研究对象，受力如图所示，列平衡方程：
MC 0
FD b F x 0
FD
x F b
取杆 AB 为研究对象，受力如图所示，列平衡方程：
M A 0
FB b F x 0
线方向的夹角都是 ，因此只要接触面的摩擦角大于 ，不论 F 多大，圆柱不
2
2
会挤出，而处于自锁状态。
FAy o FAx
法 2（解析法） ： 首先取整体为研究对象，受力如图所示。列平衡方程：
FSD FND
MA 0
FND a F l 0
l FND F a
再取杆 AB 为研究对象，受力如图所示。列平衡方程：
F1 14.58(kN ) (受拉) F3 31.3 (受拉) F2 18.3 (受压)
Fx 0
Fy 0
3-38
F1 sin F3 FH 0 F2 F1 cos FG 0
解：假设各杆均受压。取三角形 BCG 为研究对象，受力如图所示。列平衡方程：
MA 0
FNC a F l 0
l FNC F FND a
取圆柱为研究对象，受力如图所示。假设圆柱半径为 R，列平衡方程：
MO 0
FSC R FSD R 0
FSC FSD
Fx 0
FNC sin FSC cos FSD 0
N1 6.93( N )
Fx 0
Fy 0
FAx N1 sin 60 0 0
FAy N 1 cos 60 0 P 0
理论力学解答(清华版)
第一章 静力学基本概念1-1 考虑力对物体作用的运动效应，力是（ A ）。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示，作用在物体A 上的两个大小不等的力1F 和2F ，沿同一直线但方向相反，则其合力可表为（ C ）。
A.1F –2FB.2F - 1FC.1F +2F图1－18 图1－191-3 F =100N ，方向如图1-19所示。
若将F 沿图示x ，y 方向分解，则x 方向分力的大小x F = C N ，y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体；B. 变形体；C. 刚体和变形体。
1-6 如图1-20所示，已知一正方体，各边长a ，沿对角线BH 作用一个力F ，则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.－F/31-7如图1-20所示，已知F=100N ，则其在三个坐标轴上的投影分别为： Fx = －402N ，Fy = 302N ，Fz = 502 N 。
图1－20 图1－21第二章力系的简化2-1．通过A（3，0，0），B（0，4，5）两点（长度单位为米），且由A指向B的力F，在z轴上投影为，对z轴的矩的大小为。
答：F/2；62F/5。
2-2．已知力F的大小，角度φ和θ，以及长方体的边长a，b，c，则力F在轴z和y上的投影：Fz= ；Fy= ；F对轴x的矩M x(F)= 。
答：Fz=F·sinφ；Fy=－F·cosφ·cosφ；Mx（F）=F（b·sinφ+c·cosφ·cosθ）图2－40 图2－412-3．力通过A（3，4、0），B（0，4，4）两点（长度单位为米），若F=100N，则该力在x轴上的投影为，对x轴的矩为。
清华出版社工程力学答案-第3章 力系的平衡条件与平衡方程
ln
=
l n
3－11 厂房构架为三铰拱架，由两片拱架在 C 处铰接而成。桥式吊车沿着垂直于纸面
方向的轨道行驶，吊车梁的重量 W1＝20 kN，其重心在梁的中点。梁上的小车和起吊重物的
重量 W2＝60 kN。两个拱架的重量均为 W3＝60 kN，二者的重心分别在 D、E 二点，正好与
吊车梁的轨道在同一铅垂线上。风的合力为 10 kN，方向水平。试求：当小车位于离左边轨
ΣFy = 0， FAy = FB′y = qd （↑）； （c） 题解：
图（c1）：
ΣFx = 0， FBx = 0
ΣMB
=
0，
−
qd
⋅
d 2
+ FRC
⋅ 2d
= 0 ， FRC
=
qd 4
（↑）
ΣFy = 0， FBy + FRC − qd = 0 ，
FBy
=
3 4
qd
（↑）
图（c2）：
ΣFx = 0，FAx = 0
ΣFy
=
0，
FAy
=
qd
+
FB′y
=
7 4
qd
（↑）
ΣMA
=
0， M A
−
FB′y
⋅ 2d
− qd
⋅
3d 2
=0
（d） 题解：
∴ MA = 3qd 2（逆时针）；
图（d1）：
ΣMB
=
0， FRC
=
M 2d
（↑）
ΣFy
=
0，
FBy
=
M 2d
（↓）
8
(c)
A
q
B
《理论力学》第三章力系的平衡习题解
第三章力系的平衡习题解[习题3- 1]三铰拱受铅直力F作用，如拱的重量不计, 求A、B处支座反力。
［解］：(1)画受力图如图所示。
(2)因为BC平衡，所以①' F ix = 0R C cos45°-R B sin : =0sin :-二,9 丄22 l2 -+—4110 31cos 2-.4 4 _ 3.10R C"2R B sin：5 R B②二F iy = 0R C sin 45°R B cos ： - F P = 0 R C -^+』R B下2 ,10A B I、”邱R「主F P"79F P4R c 10.79F P=0.35F P-.5BF PCCa45012lR B(3)由AC的平衡可知：R A二R C 二10.79F P =0.35F P<5［习题3-2］弧形闸门自重W= 150 kN,试求提起闸门所需的拉力F和铰支座处的反力。
-Fcos60°2-Fsi n 60°8 W 6=0-F -0.866F 8 150 6 =07.928F =900F =113.522(kN)、F ix "F cos60°- R Ax = 0R AX -113.522 0.5 =56.761(kN) O)、F, -0Fsin 60°R Ay-W = 0R AX二W-Fsin60°=150 -113.522 0.866 = 51.690(kN) (f)R A二‘56.761251.692= 76.77(kN)丄51.69--arctan 42.32356.761［习题3-3］已知F= 10kN,杆AC B(及滑轮重均不计，试用作图法求杆AC BC寸轮的约束力。
解：作力三角形图如图所示。
R B = =14.142(kN) , R A =0［习题3 — 4］直径相等的两均质混凝土圆柱放在斜面与之间，柱重解：(1)以上柱为研究对象，其受力图与力三角形图如图所示。
理论力学课后习题答案_清华大学出版社_2004年版_范钦珊,刘燕,王琪 编著
习题 1－1 图
y
y2
F
F y1
F y1
F y2 F y2
F
Fx1 Fx1
（c）
x
F x2
Fx 2
x2
（d）
解： （a）图（c） ： F F cos i1 F sin j1 分力： F x1 F cos i1 投影： Fx1 F cos ， ，
F y1 F sin j1 Fy1 F sin
讨论： = 90°时，投影与分力的模相等；分力是矢量，投影是代数量。 （b）图（d） ： 分力： F x 2 ( F cos F sin cot ) i 2 投影： Fx 2 F cos ， 讨论： ≠90°时，投影与分量的模不等。
1－2 试画出图 a 和 b 两种情形下各物体的受力图，并进行比较。
F Ax
， Fy 2
F sin j2 sin
Fy 2 F cos( )
FAy
A
C
F
B
D
习题 1－2 图
FRD
FAy
F Ax
A
C
F
C
FC
F Ax
FAy
(a-1)
F
C
B
A
B
D
' FC
(a-2)
FRD
(a-3)
FRD
D
(b-1)
比较：图（a-1）与图（b-1）不同，因两者之 FRD 值大小也不同。
解： 图（a） ： 2F3 cos 45 F 0
F3 2 F （拉） 2
F1 = F3（拉）
F2 2 F3 cos 45 0
F2 = F（受压） 图（b） ： F3 F3 0 F1 = 0 F2 = F（受拉）
理论力学答案完整版(清华大学出版社)3
之差称为静不定次数。这类问题需要补充与静不定次数相同数量的变形协调方程才能求解。 未知约束力分量的数目小于独立平衡方程的数目，这类平衡问题是不存在的。 解题要领：
（2）AD 梁上，固定铰链 A 处有 2 个约束力，辊轴铰链 B、C 和 D 各有 1 个约束力， 共有 5 个约束力，这 5 个约束力组成平面一般力系，可以列出 3 个独立的平衡方程。所以， AD 梁是 2 次静不定。
（3）曲梁 AB 两端都是固定端约束，各有 3 个共 6 个约束力组成平面一般力系，而独 立的平衡方程只有 3 个。所以是 3 次静不定。
2 要区分物体维持平衡时的摩擦力与能够产生的最大静摩擦力，两者不可混淆。 3 有摩擦时的平衡问题往往还伴随物体的翻倒问题，要全面考虑，择其合理解。 4 自锁问题通常利用摩擦角概念和二力平衡条件或三力平衡汇交定理解题，具有几何直观、 概念清楚和便于理解的特点。关键是要确定临界平衡时的摩擦角。 5 滚动摩擦问题的考虑类似于滑动摩擦问题。
FA = 63.22 kN . ∑ Fy = 0, FA + FC sin 60o + FB − F1 sin 60o − F2 − q × 3 = 0 ,
FB = 88.74 kN .
题 3-3(a)图
（b）解：以 AB 以梁为研究对象，画受力图，列平衡方程
∑ Fx = 0 ， FD cos 45o − FB cos 45o − F2 cos30o = 0 ， ∑ mC = 0, FD sin 45o × 4 + FB sin 45o × 8 − M − F1 × 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F DBCBDBF '习题3－3图第3章 静力学平衡问题3－1 图示两种正方形结构所受荷载F 均已知。
试求其中1，2，3各杆受力。
解：图（a ）：045cos 23=-︒F FF F 223=（拉） F 1 = F 3（拉） 045cos 232=︒-F F F 2 = F （受压） 图（b ）：033='=F F F 1 = 0F 2 = F （受拉）3－2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上，点B 与拴在桩A 上的绳索AB 连接，在点D 加一铅垂向下的力F ，AB 可视为铅垂，DB 可视为水平。
已知α= 0.1rad.，力F = 800N 。
试求绳AB 中产生的拔桩力（当α很小时，tan α≈α）。
解：0=∑y F ，F F ED =αsin αs i nFF ED = 0=∑x F ，DB ED F F =αcos F FF DB 10tan ==α由图（a ）计算结果，可推出图（b ）中：F AB = 10F DB = 100F = 80 kN 。
3－3 起重机由固定塔AC 与活动桁架BC 组成，绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ，并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上，链索绕过点B 的滑轮，并沿直线BC 引向绞盘。
长度AC = BC ，不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3－1图(a-1)(a-2)'3(b-2)习题3－2图F习题3-5图习题3－4图 解：图（a ）：0=∑x F ，0sin 2cos=-ϕϕW F AB ，2sin2ϕW F AB =0=∑y F ，02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3－4 杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。
对于给定的θ角，试求平衡时的β角。
解：AB 为三力汇交平衡，如图（a ）所示ΔAOG 中： βs i n l AO =， θ-︒=∠90AOG β-︒=∠90OAG ，βθ+=∠AGO由正弦定理：)90sin(3)sin(sin θβθβ-︒=+ll ，)cos 31)sin(sin θβθβ=+l 即 βθβθθβs i n c o s c o s s i n c o s s i n 3+=即 θβt a n t a n 2=)t a n21a r c t a n (θβ= 注：在学完本书第3章后，可用下法求解： 0=∑x F ，0sin R =-θG F A （1） 0=∑y F ，0cos R =-θG F B（2） 0)(=∑F A M ，0sin )sin(3R =++-ββθl F l G B（3）解（1）、（2）、（3）联立，得 )t a n 21a r c t a n (θβ=3–5 起重架可借绕过滑轮A 的绳索将重力的大小G =20kN 的物体吊起，滑轮A 用不计自重的杆AB 和AC 支承，不计滑轮的自重和轴承处的摩擦。
求系统平衡时杆AB 、AC 所受力（忽略滑轮的尺寸）。
解：以A 为研究对象，受力如图（a ） 所示，其中：F T = G 。
0=∑AB F ，030sin 30cos T =︒+︒-G F F ABkN 32.7)30sin 30(cos =︒-︒=G F AB 0=∑AC F ，030sin 30cos T =︒-︒-F G F C AkN 32.27)30sin 30(cos =︒+︒=G F AB3–6图示液压夹紧机构中，D 为固定铰链，B 、C 、E 为铰链。
已知力F ，机构平衡时角度如图所示，求此时工件H 所受的压紧力。
BF （a ）F F ECF N H F H 习题3-6图（a ） （b ）（c ）B(a)B(c)(b)(d)F F CyF AxF AyF B 习题3-7图 （a ）（b ）解：以铰B 为研究对象，受力如图（a ）。
0=∑y F ，0sin =-F F BC α；αsin FF BC =（1） 以铰C 为研究对象，受力如图（b ）。
0=∑x F ，02sin =-αCE CB F F ；α2sin CBCE F F =（2）以铰E 为研究对象，受力如图（c ）。
0=∑y F ，0cos =-αEC H F F ；αcos EC H F F = （3）由于CB BC F F =；CE EC F F =，联立式（1）、（2）、（3）解得：α2sin 2FF H =3–7三个半拱相互铰接，其尺寸、支承和受力情况如图所示。
设各拱自重均不计，试计算支座B 的约束力。
解：先分析半拱BED ，B 、E 、D 三处的约束力应汇交于点E ，所以铰D 处的约束力为水平方向，取CDO 为研究对象，受力如图（a ）所示。
0)(=∑F C M ，0=-Fa a F D ；F F D =以AEBD 为研究对象，受力如图（b ）。
0)(=∑F A M ，033='--DB F a aF 3aF ；F F B 2=3－8 折杆AB 的三种支承方式如图所示，设有一力偶矩数值为M 的力偶作用在折杆AB 上。
试求支承处的约束力。
习题3—8图A(a)F AF CF B习题3-11图 （a ）解：图（a ）：l M F F B A 2== 图（b ）：lMF F B A ==由图（c ）改画成图（d ），则 l M F F BD A == ∴ lM F F BDB == lMF F BD D 22==3－9 齿轮箱两个外伸轴上作用的力偶如图所示。
为保持齿轮箱平衡，试求螺栓A 、B 处所提供的约束力的铅垂分力。
解：ΣM i = 0，05.0125500=⨯++-Ay FF Ay = 750N （↓）， F By = 750N （↑）（本题中F Ax ，F Bx 等值反向，对力偶系合成结果无贡献。
）3－10 试求图示结构中杆1、2、3所受的力。
解：杆3为二力杆图（a ）： ΣM i = 0 03=-⋅M d FdM F =3 F = F 3（压）图（b ）： ΣF x = 0 F 2 = 0 ΣF y = 0dMF F ==1（拉）3–11图示空间构架由三根不计自重的有杆组成，在D 端用球铰链连接，A 、B 和C 端则用球铰链固定在水平地板上，若拴在D 端的重物P = 10 kN ，试求铰链A 、B 、C 的反力。
解：(a)F ByFAy习题3－9图2F(b)习题3－10图FAF CF B习题3-12图 （a ）xyzF F CF AF BF BF D（c ）（d ） O取铰D 为研究对象，受力如图（a ）。
0=∑xF ，045cos 45cos =︒-︒A B F F ；A B F F = （1）0=∑yF，030cos 45sin 215cos =︒︒-︒-A C F F （2）0=∑zF，030sin 45sin 215sin =-︒︒-︒-P F F A C （3）联立式（1）、（2）、（3）解得：39.26-==A B F F kN ，46.33=C F kN3–12 图示空间构架由三根不计自重的有杆组成，在O 端用球铰链连接，A 、B 和C 端则用球铰链固定在水平地板上，若拴在O 端的重物P =10kN ，试求铰链A 、B 、C 的反力。
解：取铰O 为研究对象，受力如图（a ）。
0=∑xF，045cos 45cos =︒-︒C B F F ；C B F F =0=∑zF ，045cos =-︒-P F A ；kN 14.142-=-=P F A 0=∑y F ，045sin 245sin =︒-︒-B A F F ；07.7==C B F F kN3–13 梁AB 用三根杆支承，如图所示。
已知F 1=30kN ，F 2 = 40kN ，M =30kN ·m, q = 20N/m ，试求三杆的约束力。
解：0=∑x F ，060cos 60cos 1=︒+︒-F F C ；kN 301==F F C0)(=∑F BM，035.160sin 3460sin 8821=⨯+︒++-︒+q F F M F F C A ；kN 22.63-=A F0)(=∑F AM ，035.660sin 5482=⨯+︒+++q F F M F C B ；kN 74.88-=A F （2）图（b ）中梁的受力如图（d ）所示。
0)(=∑F O M ，030cos 24621=︒--+F M F F C ；kN 45.3-=C F 0)(=∑F B M ，030sin 245sin 46821=︒+︒+-+F F M F F D C ；kN 41.57-=D F 0)(=∑F DM，045sin 430sin 22421=︒-︒-+-B C F F F M F ；kN 42.8-=B F3－14 一便桥自由放置在支座C 和D 上，支座间的距离CD = 2d = 6m 。
桥面重321kN/m 。
试求当汽车从桥上面驶过而不致使桥面翻转时桥的悬臂部分的最大长度l 。
设汽车的前后轮的负重分别为20kN 和40kN ，两轮间的距离为3m 。
解：图（a ）中，321=q kN/mF = 40 kN （后轮负重） ΣM D = 003)26(=-⨯+Fl l q0403)26(35=-⨯+⨯l ll = 1m 即 l max = 1m3－15 图示构架由杆AB 、CD 、EF 和滑轮、绳索等组成，H ，G ，E 处为铰链连接，固连在杆EF 上的销钉K 放在杆CD 的光滑直槽上。
已知物块M 重力P 和水平力Q ，尺寸如图所示，若不计其余构件的自重和摩擦，试求固定铰支座A 和C 的反力以及杆E F 上销钉K 的约束力。
解：取系统整体为研究对象，其受力如图（a ）所示。
习题3－14图Ax F Cx F Ay F Cy习题3－15图 （a ） HyDy Cx （b ）习题3－17图（a ）（b ）F AxF GxF GyAyF 0)(=∑F A M ，0463=-+Cy aF aQ aP ；4)2(3Q P F Cy +=0=∑y F ，0=--Cy Ay F P F ；4)67Q P F Ay += 0=∑xF，0=++Cx Ax F F Q （1）取轮E 和杆EF 为研究对象，其受力如图（b ）所示。
0)(=∑F HM，045cos 23T =︒--K aF aF aP （F T = P ）；P F K 2=（F T = P ） 取杆CD 为研究对象，其受力如图（c ）所示。