反比例函数中K的几何意义的变式练习
反比例函数k的几何意义专项训练及答案

反比例函数K 的几何意义专项训练及答案(中考复习)1、如图(1)所示,已知反比例函数 y =x k 和 y =x 1分别过点 A 和点 B ,且 AB // x 轴, S ABC △ =23,点C 是 x 轴上任意一点,则 k =____________. 2、如图(2)所示,矩形ABOC 的顶点B ,C 分别在x 轴,y 轴上,顶点A 在第二象限,点B 的坐标为(-2,0),将线段OC 绕点O 逆时针旋转60°至线段0D,若反比例函数y=xk (k ≠0)的图像经过A ,D 两点,则k 的值为_____________. 3、如图(3)所示,面积为25的Rt △OAB 的斜边OB 在x 轴上,∠ABO=30°,反比例函数y=xk 的图象恰好经过点A ,则k 的值为______________.4、如图(4)所示,A ⎪⎭⎫ ⎝⎛1y 21,,B ()2y 2,为反比例数y=x 2图象上的两点,动点P(x,0)在x 轴上运动,当|AP-BPI 的值最大时,连接OA ,则△AOP 的面积为_________.5、如图(5)所示,反比例函数y=x12在第一象限内的分支经过菱形OACB 的顶点A,B,且点A,B 的横纵坐标都为正整数,则点C 的坐标为__________________.6、如图(6)所示,在反比例函数y=xk 的图象上有A,B 两点,过点A 作AC ⊥x 轴,交x 轴于点C ,连接BC 并延长交y 轴于点D,连接AB,AD,若BD=4CD,ABD S △=8,则k 的值为__________________.(1)(2) (3)7、如图(7)所示,直线y=3x-6分别交x ,y 轴于点A ,B ,M 是反比例函数y=xa (x>0)的图象上位于直线AB 上方的一点,MC//x 轴交AB 于点C,MD ⊥MC 交AB 于点D,若AC ·BD=43则a 的值为__________.8如图(8)所示,正方形ABCD 的顶点A.B 分别在x ,y 轴上,tan ABO=3,正方形的面积为10,反比例函数y=xk 的图象经过点D,则k 的值是_______________. 9如图(9)所示,在平面直角坐标系中,△OAB 的顶点A 在反比例函数y=x 1上,顶点B 在反比例函数y=xk 上,AB ∥x 轴,△OAB 的面积是3,则k 的值为____________. 10、如图(10)所示,在平面直角坐标系中,等边三角形的顶点 A 在反比例函数y=x 1(x>0)上,顶点B,C 在反比例函数y=xk (x>0)上,且点B,C 关于直线y=x 对称.若等边三角形的边长为62,则k 的值为________________.(4) (5) (6) (7) (8) (9) (10)参考答案1、-22、3316-3、5-4、55、(13,13)或(8,8)或(7,7)6、-47、-38、-69、7 10、13。
专题1 反比例函数K的几何意义——初中几何与代数必考模型+例题+变式

8.如图,A,B两点在双曲线y= 上,分别经过A,B两点向轴作垂线段,已知阴影小矩形的面积为1,则空白两小矩形面积的和S1+S2=______.
【答案】4
【解析】
【分析】欲求S1+S2,只要求出过A、B两点向x轴、y轴作垂线段求出与坐标轴所形成的矩形的面积即可,而矩形面积为双曲线y= 的系数k,由此即可求出S1+S2.
【详解】解:作AE⊥BC于E,如图,
∵四边形ABCD为平行四边形,
∴AD//x轴,∴四边形ADOE为矩形,
∴ ,而 =|−k|,
∴|−k|=6,而−k<0,即k>0,∴k=6.
故选C.
【点睛】本题考查了反比例函数 (k≠0)系数k的几何意义:从反比例函数 (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
【解析】
【分析】根据反比例函数的性质对A、B、D进行判断;根据反比例函数系数k的几何意义对C进行判断.
【详解】解:A、反比例函数图象分布在第二、四象限,则k<0,所以A选项错误;
B、在每一象限,y随x的增大而增大,所以B选项错误;
C、矩形OABC面积为2,则|k|=2,而k<0,所以k=﹣2,所以C选项正确;
A.1B.3C.6D.-6
【答案】C
【解析】
【分析】作AE⊥BC于E,由四边形ABCD为平行四边形得AD//x轴,则可判断四边形ADOE为矩形,所以平行四边形ABCD的面积=矩形ADOE的面积,根据反比例函数k的几何意义得到矩形ADOE的面积=|−k|,则|−k|=6,利用反比例函数图象得到−k<0,即k>0,于是有k=6.
【点睛】考查了反比例函数的图象的知识,解题的关键是了解系数k的几何意义.
反比例函数K的几何意义

反比例函数K 的几何意义知识引入反比例函数)0(≠=k x k y 中k 的几何意义:双曲线)0(≠=k xky 上任意一点向两坐标轴作垂线,两垂线与坐标轴围成的矩形面积为k 。
理由:如下图,过双曲线上任意一点P 作x 轴、y 轴的垂线PM PN 、所得的矩形PMON 的面积PMON S PM PN y x xy =⋅=⋅=矩形;ky x=,xy k ∴=即S k =,即过双曲线上任意一点作x 轴、y 轴的垂线,所得的矩形面积均为k 。
下面两个结论是上述结论的拓展: 如下图,则有k xy S S AOB OPA 2121===∆∆ (1)如图①,OPA OCD OPC ADCP S S S S ∆∆∆==梯形;图①图②(2)如图②,BPE ACE OAPB OBCA S S S S ∆∆==梯形梯形;典型例题题型一:K 意义的直接运用【例1】(2013•宜昌)如图,点B 在反比例函数()02>=x xy 的图象上,横坐标为1,过点B 分别向x 轴,y 轴作垂线,垂足分别为A C 、,则矩形OABC 的面积为_______2、(2013•淄博)如图,矩形AOBC 的面积为4,反比例函数xky =的图象的一支经过矩形对角线的交点P ,则该反比例函数的解析式是__________【变式练习】:1、如图,A 是反比例函数图象上一点,过点A 作AB y ⊥轴于点B ,点P 在x 轴上:ABP∆的面积为2,则这个反比例函数的解析式为______________.2、如图,A B 、为双曲线xy 12-=上的点,AD x ⊥轴于D ,BC y ⊥轴于点C ,则四边形ABCD 的面积为。
题型二:知K 求面积【例2】①双曲线xy 4=在第一象限内的图像如图所示,作一条平行于x 轴的直线分别交双曲线于A 点,交y 轴于B 点,点C 为x 轴上一点,连结AC 交y 轴于D 点,连结BC ,若DBC ∆的面积为3,则ABD ∆的面积为。
反比例函数中k的几何意义 (3)

教学目标: (一)知识与技能1.理解和掌握反比例函数 (k ≠0)中k 的几何意义2.能灵活运用函数图象和性质解决一些较综合的问题 (二)过程与方法1.让学生自己尝试在 的图象上任取一点P(x 、y),过P 点分别向X 轴、Y 轴作垂线,从而探究求出两垂线与坐标轴形成的矩形的面积及三角形的面积,从而探究所形成的矩形与三角形的面积与k 的关系。
2.深刻领会函数解析式与函数图象之间的联系,体会数形结合及转化的思想方法。
(三)情感态度与价值观培养学生自主探究,合作交流的精神。
学情分析:知识基础:本节课学习前,学生已经具有了函数概念的知识积累,在上一节课的学习中,学生已经掌握了反比例函数的概念。
学习方法:学生已经积累的学习函数的方法有:画图象,观察图像归纳函数性质,了解函数变化规律和函数的变换趋势等。
学生喜欢用探究式的学习方式,通过自己的分析来体验知识间的内在联系。
能力水平:处在这个年龄段的学生多数可以熟练的进行抽象逻辑思维,但其辩证逻辑思维的能力水平还较低。
另外,学生参与活动的积极性高,但仍然缺乏合作交流等方面的能力。
教学重点、难点:1.重点:理解并掌握反比例函数 (k ≠0)中k 的几何意义;并能利用它们解决一些综合问题2.难点:学会从图象上分析、解决问题 教学过程:(一)创设情境、导入新课1、反比例函数的解析式是什么?如何确定比例系数K 的值?2、反比例函数的比例系数K 能决定什么?反比例函数的比例系数K 除了能确定图像位置和增减性外还能确定什么呢?xy 6=xk y xky =1.如图,点P 是反比例函数图象上的一点,过点P 分别向x 轴、y 轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是.xyoMNp3-=∴k .3||k |,|k S 矩形P m O n =∴=,,四象限图像在二又 .3xy -=∴解析式为由题意得:本节课我们来探究反比例函数的比例系数K 的几何意义。
(二)新课探究 活动1:议一议如图,已知点P 是反比例函数 的图象上任意一点,过P 点分别向X 轴、Y 轴作垂线,垂足分别为M 、N ,那么四边形OMPN 的面积是多 少?△OMP 的面积是多少?1、学生讨论时出现的问题是OM 应如何表示,教师给予及时点拔,使问题得以解决。
反比例K的几何意义专题训练
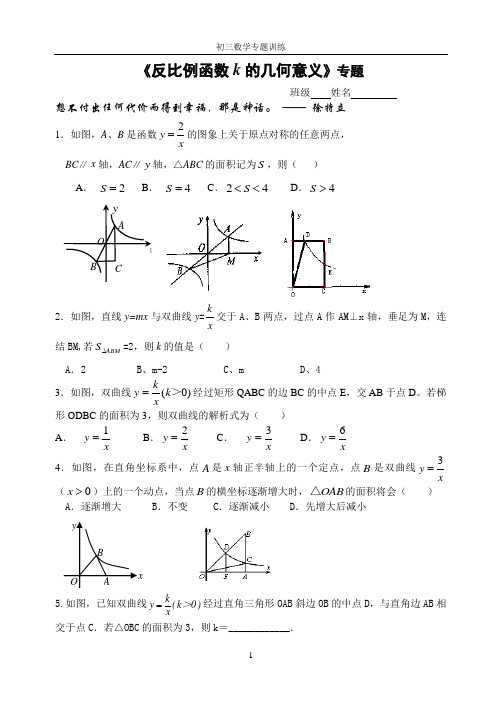
《反比例函数k 的几何意义》专题班级 姓名想不付出任何代价而得到幸福,那是神话。
—— 徐特立1.如图,A 、B 是函数2y x=的图象上关于原点对称的任意两点, BC ∥x 轴,AC ∥y 轴,△ABC 的面积记为S ,则( ) A . 2S = B . 4S = C .24S << D .4S >2.如图,直线y=mx 与双曲线y =xk交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM,若ABM S ∆=2,则k 的值是( ) A .2B 、m-2C 、mD 、43.如图,双曲线)0(>k xky =经过矩形QABC 的边BC 的中点E ,交AB 于点D 。
若梯形ODBC 的面积为3,则双曲线的解析式为( ) A .x y 1=B .x y 2=C . x y 3=D .xy 6= 4.如图,在直角坐标系中,点A 是x 轴正半轴上的一个定点,点B 是双曲线3y x=(0x >)上的一个动点,当点B 的横坐标逐渐增大时,OAB △的面积将会( ) A .逐渐增大 B .不变 C .逐渐减小 D .先增大后减小5.如图,已知双曲线)0k (xk y >=经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =____________.6.如图,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,若1S =阴影,则12S S += .7.如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数1y x=的图象上,则图中阴影部分的面积等于 .8.如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、,得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、,并设其面积分别为12345S S S S S 、、、、,则5S 的值为 ..9.如图,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 1y x=(0x >)的图象上,则点E 的坐标是( , ).10.如图, 123,,P P P 是反比例函数(0)ky k x=≠的图象上的三个点.经过这三个点分别作y 轴的垂线,垂足分别为123,,A A A 设112233,,,P AO P A O P A O ∆∆∆的面积分别为123,,S S S ,试比较这三个三角形面积的大小如图,已知点A 在反比例函数4y=x 图象上,点B 在反比例函数k y=x(k ≠0)的图象上,AB ∥x 轴,分别过点A 、B 向x 轴作垂线,垂足分别为C 、D ,若OC =13OD ,则k 的值为【 】A 、10B 、12C 、14D 、16如右图是y kx b =+与my x=在同一坐标系中的图象 请判断: k 0,b 0,m 0。
反比例函数K的几何意义求面积

例3:反比例函数
y1
m x
与一次函数
y2
kx
b
交于
点A(1,8 ) 和B (4,n),
求:⑴这两个函数的解析式;
⑵三角形⊿AOB的面积。 S△AOB=S△AOD-S△BOD
S AOB S MOB S AOM
S△AOB=S△MOD-S△AOM-S△BOD
y
MA
B o E FDx
SAOB S梯形AEFB
变式练习1:如图C是AB的中点,反比例函数 y 6 (x 0)
x
在第一象限的图象经过A( 2,3)、C(6,1)两点,
求:△OAB面积
C是A B的中点。
SAOC SCOB
SAOC SCOE
D
E
SAOC S梯形ADE(C 等量代换)
SAOB 2S梯形ADEC
直击中考 ☞
如图,直线AB过点A(m, 0)、B(0, n)(其中 m>0, n>0).反比例函数 y p(p>0)
x
的图象与直线AB交于C、D两点,连结OC、OD. (1)已知m+n=10,△AOB的面积为S, 问:当n何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC、 △COD、△DOB的面积都相等 时,求p的值。
——成都明成学校、王莉
-
回顾与思考
图中的这些矩形面积有什么特点? y
y k x
O
x
回顾与思考
反比例函数中“k”的几何意义
结论1: S矩形 = k
k 结论2: S直角三角形 = 2
面积与P在反比例函数图像上的位置无关
y P(x,y)
y
反比例函数中k的几何意义
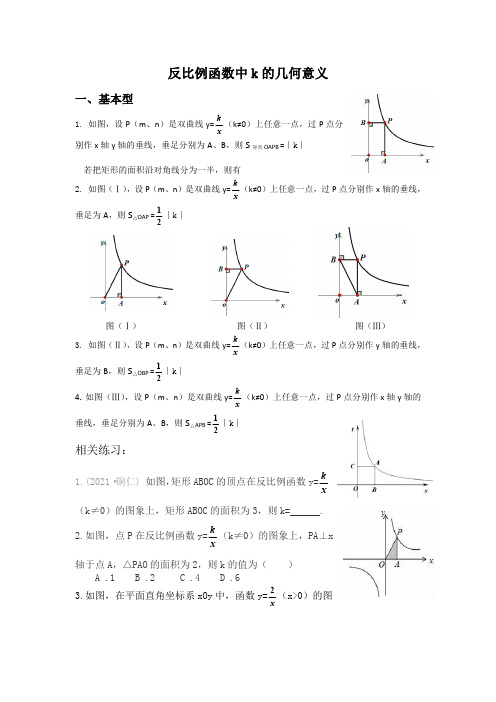
过 P 点作 x 轴的垂线,过 B 点作 y 轴的垂线,两直线相交于 C,则 S△PBC =2∣k∣
容易看出,此变式是基本型的综合情况,△PBC 可以分解成两个小的三角形(△PAO 与 △P’BO)和一个矩形 OABC。
x
垂足为 B,A 是 x 轴上任意一点,则 S△APB = 1 ∣k∣
2
图(Ⅴ)
图(Ⅵ)
相关练习
6.如图,点 A 是反比例函数 y= k (k≠0)的图象上的一点,
x
过点 A 作 AB⊥x 轴,垂足为 B.点 C 为 y 轴上的一点,连接 AC,
BC.若△ABC 的面积为 4,则 k 的值是
.
7.如图,A 是反比例函数图象上一点,过点 A 作 AB⊥y 轴于点 B,
x
k 的值为( )
A.32 B.20 C.24 D.12
13.如图,两个反比例函数 y= 2 和 y= 4 在第一象限内的图像分别是 C1 和 C2,设点
x
x
P 在 C1 上,PA⊥x 轴于点 A,交 C2 于点 B,则△POB 的面积为
.
(第 5 题)
(第 6 题)
(第 7 题)
14.如图,直线 l⊥x 轴于点 P,且与反比例函数 y1= k1 (x>0)及 y2= k2 (x>0)
三、变式二
1.如图(Ⅴ),设 P(m、n)是双曲线 y= k (k≠0)上任意一点,过 P 点分别作 x 轴的垂线, x
垂足为 A,B 是 y 轴上任意一点,则 S△APB = 1 ∣k∣
2 2..如图(Ⅵ),设 P(m、n)是双曲线 y= k (k≠0)上任意一点,过 P 点分别作 y 轴的垂线,
反比例函数K的几何意义试题与答案

反比例函数K的几何意义试题一.选择题(共30小题)1.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC ﹣S△BAD为()A.36B.12C.6D.32.如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S △AOB=2,则k的值为()A.2B.3C.4D.53.如图,点A、C为反比例函数y=图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为时,k的值为()A.4B.6C.﹣4D.﹣64.如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为()A.﹣4B.4C.﹣2D.25.如图,反比例函数y=的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为()A.2B.4C.5D.86.如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积()A.减小B.增大C.先减小后增大D.先增大后减小7.如图,P,Q分别是双曲线y=在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC 的面积为S3,则有()A.S1=S2≠S3B.S1=S3≠S2C.S2=S3≠S1D.S1=S2=S38.如图,矩形ABCD的顶点D在反比例函数y=(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为()A.﹣6B.﹣8C.﹣9D.﹣129.如图,A,B,C为反比例函数图象上的三个点,分别从A,B,C向xy轴作垂线,构成三个矩形,它们的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是()A.S1=S2>S3B.S1<S2<S3C.S1>S2>S3D.S1=S2=S310.如图,A、B是双曲线上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=9.则k的值是()A.9B.6C.5D.411.如图,直线l和双曲线(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1,△BOD面积是S2,△POE面积是S3,则()A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S312.如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE 的面积分别是1和2,则k的值为()A.B.+1C.D.213.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=()A.B.C.D.1214.如图,双曲线y=(k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为()A.1B.2C.3D.415.如图,过反比例函数(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得()A.S1>S2B.S1=S2C.S1<S2D.大小关系不能确定16.如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C 为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是()A.3B.﹣3C.6D.﹣617.如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数y=经过另一条直=3,则k=()角边AC的中点D,S△AOCA.2B.4C.6D.318.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,则S平行四边形ABCD 为()A.2B.3C.4D.519.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴并反比例函数y=﹣的图象于点B,以AB为边作▱ABCD,其中点C,D在x轴上,则▱ABCD的面积为()A.3B.5C.7D.920.如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=A n﹣1A n(n为正整数),过点A1、A2、A3、…、A n分别作x轴的垂线,与反比例函数y=(x>0)交于点P1、P2、P3、…、P n,连接P1P2、P2P3、…、P n﹣1P n,过点P2、P3、…、P n分别向P1A1、P2A2、…、P n﹣1A n﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是()A.B.C.D.21.在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个动点,过A点作y轴的平行线交反比例函数y=(x>0)的图象于B点,当点A的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.逐渐减小C.不变D.先增大后减小22.如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.先减后增C.逐渐减小D.先增后减23.如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=的图象经过点A,若△ABO的面积为2,则k的值为()A.1B.2C.4D.24.如图,两个反比例函数y1=(其中k1>0)和y2=在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为()A.﹕1B.2﹕C.2﹕1D.29﹕1425.如图,已知矩形OABC面积为,它的对角线OB与双曲线相交于D且OB:OD=5:3,则k=()A.6B.12C.24D.3626.如图,▱OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=的图象经过点A与点D,则▱OABC的面积为()A.30B.24C.20D.1627.如图,A、C分别是x轴、y轴上的点,双曲线y=(x>0)与矩形OABC的边BC、AB分别交于E、F,若AF:BF=1:2,则△OEF的面积为()A.2B.C.3D.28.如图,过原点O的直线与双曲线y=交于A、B两点,过点B作BC⊥x轴,垂足为C,=5,则k的值是()连接AC,若S△ABCA.B.C.5D.1029.如图,已知A(﹣3,0),B(0,﹣4),P为反比例函数y=(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为()A.12B.13C.24D.2630.如图,点A在双曲线上,点B在双曲线上,且AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为()A.0.5B.1C.1.5D.2反比例函数K 的几何意义试题答案一.选择题(共30小题)1.(菏泽)如图,△OAC 和△BAD 都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B ,则△OAC 与△BAD 的面积之差S △OAC ﹣S △BAD 为()A .36B .12C .6D .3【分析】设△OAC 和△BAD 的直角边长分别为a 、b ,结合等腰直角三角形的性质及图象可得出点B 的坐标,根据三角形的面积公式结合反比例函数系数k 的几何意义以及点B 的坐标即可得出结论.【解答】解:设△OAC 和△BAD 的直角边长分别为a 、b ,则点B 的坐标为(a +b ,a ﹣b ).∵点B 在反比例函数y=的第一象限图象上,∴(a +b )×(a ﹣b )=a 2﹣b 2=6.∴S △OAC ﹣S △BAD =a 2﹣b 2=(a 2﹣b 2)=×6=3.故选D .【点评】本题考查了反比例函数系数k 的几何意义、等腰三角形的性质以及面积公式,解题的关键是找出a 2﹣b 2的值.本题属于基础题,难度不大,解决该题型题目时,设出等腰直角三角形的直角边,用其表示出反比例函数上点的坐标是关键.2.(河南)如图,过反比例函数y=(x >0)的图象上一点A 作AB ⊥x 轴于点B ,连接AO ,若S △AOB =2,则k 的值为()A .2B .3C .4D .5【分析】根据点A 在反比例函数图象上结合反比例函数系数k 的几何意义,即可得出关于k 的含绝对值符号的一元一次方程,解方程求出k 值,再结合反比例函数在第一象限内有图象即可确定k 值.【解答】解:∵点A 是反比例函数y=图象上一点,且AB ⊥x 轴于点B ,∴S=|k|=2,△AOB解得:k=±4.∵反比例函数在第一象限有图象,∴k=4.故选C.【点评】本题考查了反比例函数的性质以及反比例函数系数k的几何意义,解题的关键是找出关于k的含绝对值符号的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义找出关于k的含绝对值符号的一元一次方程是关键.3.(本溪)如图,点A、C为反比例函数y=图象上的点,过点A、C分别作AB ⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E 恰好为OC的中点,当△AEC的面积为时,k的值为()A.4B.6C.﹣4D.﹣6【分析】设点C的坐标为(m,),则点E(m,),A(m,),根据三角形的面积公式可得出S=﹣k=,由此即可求出k值.△AEC【解答】解:设点C的坐标为(m,),则点E(m,),A(m,),=BD•AE=(m﹣m)•(﹣)=﹣k=,∵S△AEC∴k=﹣4.故选C.【点评】本题考查了反比例函数图象上点的坐标特征,解题的关键是设出点C的坐标,利用点C的横坐标表示出A、E点的坐标.本题属于基础题,难度不大,解决该题型题目时,利用反比例函数图象上点的坐标特征表示出点的坐标是关键.4.(毕节市)如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为()A.﹣4B.4C.﹣2D.2【分析】根据反比例函数系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变,可计算出答案.【解答】解:△ABO的面积为:×|﹣4|=2,故选D.【点评】本题考查了反比例函数系数k的几何意义,关键是掌握比例系数k的几何意义:①在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.②在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.5.(黔西南州)如图,反比例函数y=的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为()A.2B.4C.5D.8【分析】由反比例函数的系数k的几何意义可知:OA•AD=2,然后可求得OA•AB的值,从而可求得矩形OABC的面积.【解答】解:∵y=,∴OA•AD=2.∵D是AB的中点,∴AB=2AD.∴矩形的面积=OA•AB=2AD•OA=2×2=4.故选:B.【点评】本题主要考查的是反比例函数k的几何意义,掌握反比例函数系数k的几何意义是解题的关键.6.(长春)如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x 轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积()A.减小B.增大C.先减小后增大D.先增大后减小【分析】首先利用m和n表示出AC和AQ的长,则四边形ACQE的面积即可利用m、n表示,然后根据函数的性质判断.【解答】解:AC=m﹣1,CQ=n,则S=AC•CQ=(m﹣1)n=mn﹣n.四边形ACQE∵P(1,4)、Q(m,n)在函数y=(x>0)的图象上,∴mn=k=4(常数).=AC•CQ=4﹣n,∴S四边形ACQE∵当m>1时,n随m的增大而减小,=4﹣n随m的增大而增大.∴S四边形ACQE故选B.【点评】本题考查了反比例函数的性质以及矩形的面积的计算,利用n表示出四边形ACQE 的面积是关键.7.(三明)如图,P,Q分别是双曲线y=在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有()A.S1=S2≠S3B.S1=S3≠S2C.S2=S3≠S1D.S1=S2=S3【分析】根据题意可以证明△DBA和△DQP相似,从而可以求出S1,S2,S3的关系,本题得以解决.【解答】解:延长QB与PA的延长线交于点D,如右图所示,设点P的坐标为(a,b),点Q的坐标为(c,d),∴DB=a,DQ=a﹣c,DA=﹣d,DP=b﹣d,∵DB•DP=a•(b﹣d)=ab﹣ad=k﹣ad,DA•DQ=﹣d(a﹣c)=﹣ad+cd=﹣ad+k=k﹣ad,∴DB•DP=DA•DQ,即,∵∠ADB=∠PDQ,∴△DBA∽△DQP,∴AB∥PQ,∴点B到PQ的距离等于点A到PQ的距离,∴△PAB的面积等于△QAB的面积,∵AB∥QC,AC∥BQ,∴四边形ABQC是平行四边形,∴AC=BQ,∴△QAB的面积等于△QAC,∴S1=S2=S3,故选D.【点评】本题考查反比例函数系数k的几何意义、反比例函数的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.8.(抚顺)如图,矩形ABCD的顶点D在反比例函数y=(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为()A.﹣6B.﹣8C.﹣9D.﹣12【分析】先设D(a,b),得出CO=﹣a,CD=AB=b,k=ab,再根据△BCE的面积是6,得出BC×OE=12,最后根据AB∥OE,得出=,即BC•EO=AB•CO,求得ab的值即可.【解答】解:设D(a,b),则CO=﹣a,CD=AB=b,∵矩形ABCD的顶点D在反比例函数y=(x<0)的图象上,∴k=ab,∵△BCE的面积是6,∴×BC×OE=6,即BC×OE=12,∵AB∥OE,∴=,即BC•EO=AB•CO,∴12=b×(﹣a),即ab=﹣12,∴k=﹣12,故选(D).【点评】本题主要考查了反比例函数系数k的几何意义,矩形的性质以及平行线分线段成比例定理的综合应用,能很好地考核学生分析问题,解决问题的能力.解题的关键是将△BCE 的面积与点D的坐标联系在一起,体现了数形结合的思想方法.9.(钦州校级自主招生)如图,A,B,C为反比例函数图象上的三个点,分别从A,B,C 向xy轴作垂线,构成三个矩形,它们的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是()A.S1=S2>S3B.S1<S2<S3C.S1>S2>S3D.S1=S2=S3【分析】过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值,即S=|k|.【解答】解:设点A坐标为(x1,y1)点B坐标(x2,y2)点C坐标(x3,y3),∵S1=x1•y1=k,S2=x2•y2=k,S3=x3•y3=k,∴S1=S2=S3.故选D.【点评】主要考查了反比例函数中k 的几何意义,即过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积为|k |,是经常考查的一个知识点.10.(邯郸校级自主招生)如图,A 、B 是双曲线上的点,A 、B 两点的横坐标分别是a 、2a ,线段AB 的延长线交x 轴于点C ,若S △AOC =9.则k 的值是()A .9B .6C .5D .4【分析】作AD ⊥x 轴于D ,BE ⊥x 轴于E ,设反比例函数解析式为y=(k >0),根据反比例函数图象上点的坐标特征得A 、B 两点的纵坐标分别是、,再证明△CEB ∽△CDA ,利用相似比得到===,则DE=CE ,由OD :OE=a :2a=1:2,则OD=DE ,所以OD=OC ,根据三角形面积公式得到S △AOD =S △AOC =×9=3,然后利用反比例函数y=(k ≠0)系数k 的几何意义得|k |=3,易得k=6.【解答】解:作AD ⊥x 轴于D ,BE ⊥x 轴于E ,如图,设反比例函数解析式为y=(k >0),∵A 、B 两点的横坐标分别是a 、2a ,∴A 、B 两点的纵坐标分别是、,∵AD ∥BE ,∴△CEB ∽△CDA ,∴===,∴DE=CE ,∵OD :OE=a :2a=1:2,∴OD=DE ,∴OD=OC ,∴S △AOD =S △AOC =×9=3,而k>0,∴k=6.故选B.【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.也考查了三角形相似的判定与性质.11.(福州校级二模)如图,直线l和双曲线(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1,△BOD面积是S2,△POE面积是S3,则()A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3【分析】由于点A在y=上,可知S△AOC =k,又由于点P在双曲线的上方,可知S△POE>k,而点B在y=上,可知S△BOD=k,进而可比较三个三角形面积的大小【解答】解:如右图,∵点A在y=上,∴S△AOC=k,∵点P在双曲线的上方,∴S△POE>k,∵点B在y=上,△BOD∴S1=S2<S3.故选;D.【点评】本题考查了反比例函数与一次函数的交点问题,解题的关键是观察当x不变时,双曲线上y的值与直线AB上y的值大小.12.(盐都区模拟)如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF 和矩形HDBE的面积分别是1和2,则k的值为()A.B.+1C.D.2【分析】设D(t,),由矩形OGHF的面积为1得到HF=,于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,),接着利用矩形面积公式得到(kt﹣t)•(﹣)=2,然后解关于k的方程即可得到满足条件的k的值.【解答】解:设D(t,),∵矩形OGHF的面积为1,DF⊥x轴于点F,∴HF=,而EG⊥y轴于点G,∴E点的纵坐标为,当y=时,=,解得x=kt,∵矩形HDBE的面积为2,∴(kt﹣t)•(﹣)=2,整理得(k﹣1)2=2,而k>0,∴k=+1.故选B.【点评】本题考查了反比例函数比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.13.(昆山市一模)如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=()A.B.C.D.12【分析】所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B 的横纵坐标的积即是反比例函数的比例系数.【解答】解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b),∵点D,E在反比例函数的图象上,∴=k,∴E(a,),∵S △ODE =S 矩形OCBA ﹣S △AOD ﹣S △OCE ﹣S △BDE =ab ﹣﹣﹣•(b ﹣)=9,∴k=,故选C .【点评】此题考查了反比例函数的综合知识,利用了:①过某个点,这个点的坐标应适合这个函数解析式;②所给的面积应整理为和反比例函数上的点的坐标有关的形式.14.(蒙阴县一模)如图,双曲线y=(k >0)与⊙O 在第一象限内交于P 、Q 两点,分别过P 、Q 两点向x 轴和y 轴作垂线,已知点P 坐标为(1,3),则图中阴影部分的面积为()A .1B .2C .3D .4【分析】根据反比例函数图象和圆的性质得到点P 与点Q 关于直线y=x 对称,Q 点的坐标为(3,1),则图中阴影部分为两个边长分别为1和2的矩形,然后根据矩形的面积公式求解.【解答】解:∵双曲线y=(k >0)与⊙O 在第一象限内交于P 、Q 两点,∴点P 与点Q 关于直线y=x 对称,∴Q 点的坐标为(3,1),∴图中阴影部分的面积=2×(3﹣1)=4.故选D .【点评】本题考查了反比例函数y=(k ≠0)系数k 的几何意义:从反比例函数y=(k ≠0)图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为|k |.15.(呼伦贝尔校级一模)如图,过反比例函数(x >0)的图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,比较它们的大小,可得()A .S 1>S 2B .S 1=S 2C .S 1<S 2D .大小关系不能确定【分析】根据反比例函数的几何意义,直接求出S 1、S 2的值即可进行比较.【解答】解:由于A 、B 均在反比例函数y=的图象上,且AC ⊥x 轴,BD ⊥x 轴,则S 1=;S 2=.故S 1=S 2.故选B .【点评】此题考查了反比例函数k 的几何意义,找到相关三角形,求出k 的一半即为三角形的面积.16.(许昌二模)如图,点A 是反比例函数y=的图象上的一点,过点A 作AB ⊥x 轴,垂足为B .点C 为y 轴上的一点,连接AC ,BC .若△ABC 的面积为3,则k 的值是()A .3B .﹣3C .6D .﹣6【分析】连结OA ,如图,利用三角形面积公式得到S △OAB =S △CAB =3,再根据反比例函数的比例系数k 的几何意义得到|k |=3,然后去绝对值即可得到满足条件的k 的值.【解答】解:连结OA ,如图,∵AB ⊥x 轴,∴OC ∥AB ,∴S △OAB =S △CAB =3,而S △OAB =|k |,∴|k |=3,∵k <0,∴k=﹣6.故选D .【点评】本题考查了反比例函数的比例系数k 的几何意义:在反比例函数y=图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k |.17.(港南区二模)如图,Rt △AOC 的直角边OC 在x 轴上,∠ACO=90°,反比例函数y=经过另一条直角边AC 的中点D ,S △AOC =3,则k=()A .2B .4C .6D .3【分析】由直角边AC 的中点是D ,S △AOC =3,于是得到S △CDO =S △AOC =,由于反比例函数y=经过另一条直角边AC 的中点D ,CD ⊥x 轴,即可得到结论.【解答】解:∵直角边AC 的中点是D ,S △AOC =3,∴S △CDO =S △AOC =,∵反比例函数y=经过另一条直角边AC 的中点D ,CD ⊥x 轴,∴k=2S △CDO =3,故选D .【点评】本题考查了反比例函数系数k 的几何意义,求得D 点的坐标是解题的关键.18.(同安区一模)如图,点A 是反比例函数y=(x >0)的图象上任意一点,AB ∥x 轴交反比例函数y=﹣的图象于点B ,以AB 为边作平行四边形ABCD ,其中C 、D 在x 轴上,则S 平行四边形ABCD 为()A .2B .3C .4D .5【分析】连结OA 、OB ,AB 交y 轴于E ,由于AB ⊥y 轴,根据反比例函数y=(k ≠0)系数k 的几何意义得到S △OEA 与S △OBE ,则四边形ABCD 为平行四边形,然后根据平行四边形的性质得到S 平行四边形ABCD =2S △OAB =5.【解答】解:连结OA 、OB ,AB 交y 轴于E ,如图,∵AB ∥x 轴,∴AB ⊥y 轴,∴S △OEA =×3=,S △OBE =×2=1,∴S △OAB =1+=,∵四边形ABCD 为平行四边形,∴S 平行四边形ABCD =2S △OAB =5.故选:D .【点评】本题考查反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k |.本知识点是中考的重要考点,同学们应高度关注.19.(肥城市校级模拟)如图,点A 是反比例函数y=(x >0)的图象上任意一点,AB ∥x轴并反比例函数y=﹣的图象于点B ,以AB 为边作▱ABCD ,其中点C ,D 在x 轴上,则▱ABCD 的面积为()A.3B.5C.7D.9【分析】连结OA、OB,如图,AB交y轴于E,根据反比例函数k的几何意义得到S△OAE=1,S△OBE=,则S△OAB=,然后根据平行四边形的面积公式求解.【解答】解:连结OA、OB,如图,AB交y轴于E,∵AB∥x轴,∴S△OAE =×|2|=1,S△OBE=×|﹣3|=,∴S△OAB=,∵四边形ABCD为平行四边形,∴▱ABCD的面积=2S△OAB=5.故选B.【点评】本题考查了反比例函数系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.20.(启东市一模)如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=A n﹣1A n(n为正整数),过点A1、A2、A3、…、A n分别作x轴的垂线,与反比例函数y=(x>0)交于点P1、P2、P3、…、P n,连接P1P2、P2P3、…、P n﹣1P n,过点P2、P3、…、P n分别向P1A1、P2A2、…、P n﹣1A n﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是()A.B.C.D.【分析】由OA1=A1A2=A2A3=…=A n﹣1A n=1可知P1点的坐标为(1,y1),P2点的坐标为(2,y2),P3点的坐标为(3,y3)…P n点的坐标为(n,y n),把x=1,x=2,x=3代入反比例函数的解析式即可求出y1、y2、y3的值,再由三角形的面积公式可得出S1、S2、S3…S n﹣1的值,故可得出结论.【解答】解:(1)设OA1=A1A2=A2A3=…=A n﹣1A n=1,∴设P1(1,y1),P2(2,y2),P3(3,y3),…P4(n,y n),∵P1,P2,P3…Bn在反比例函数y=(x>0)的图象上,∴y1=2,y2=1,y3=…y n=,∴S1=×1×(y1﹣y2)=×1×1=;∴S1=;(3)∵S1=×1×(y1﹣y2)=×1×(2﹣)=1﹣;∴S2=×1×(y2﹣y3)=﹣;S3=×1×(y3﹣y4)=×(﹣)=﹣;…∴S n=﹣,﹣1∴S1+S2+S3+…+S n﹣1==1﹣+﹣+﹣+…﹣=.故选A.【点评】本题考查的是反比例函数综合题,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.21.(平房区模拟)在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个动点,过A点作y轴的平行线交反比例函数y=(x>0)的图象于B点,当点A的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.逐渐减小C.不变D.先增大后减小【分析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=|k|,所以当点A的横坐标逐渐增大时,△OAB的面积将不变.【解答】解:依题意,△OAB的面积=|k|=1,所以当点A的横坐标逐渐增大时,△OAB的面积将不变.故选:C.【点评】此题主要考查了反比例函数y=中k的几何意义,即过双曲线上任意一点引x轴、y轴的垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.22.(临沂模拟)如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.先减后增C.逐渐减小D.先增后减【分析】由双曲线y=﹣(x>0)设出点P的坐标,运用坐标表示出四边形OAPB的面积函数关系式即可判定.【解答】解:设点P的坐标为(x,﹣),∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,∴四边形OAPB是个直角梯形,∴四边形OAPB的面积=(PB+AO)•BO=(﹣x+AO)•﹣=2﹣,∵AO是定值,∴四边形OAPB的面积是个增函数,即点P的横坐标逐渐增大时四边形OAPB的面积逐渐增大.故选A.【点评】本题主要考查了反比例函数系数k的几何意义,解题的关键是运用点的坐标求出四边形OAPB的面积的函数关系式.23.(兴化市校级三模)如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=的图象经过点A,若△ABO的面积为2,则k的值为()A.1B.2C.4D.【分析】如图,过点A作AD⊥y轴于点D,结合等腰三角形的性质得到△ADO的面积为1,根据反比例函数系数k的几何意义求得k的值.【解答】解:如图,过点A作AD⊥y轴于点D,∵AB=AO,△ABO的面积为2,∴S=|k|=1,△ADO又反比例函数的图象位于第一象限,k>0,则k=2.故选:B.【点评】本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.24.(深圳二模)如图,两个反比例函数y1=(其中k1>0)和y2=在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为()A .﹕1B .2﹕C .2﹕1D .29﹕14【分析】首先根据反比例函数y 2=的解析式可得到S △ODB =S △OAC =×3=,再由阴影部分面积为6可得到S 矩形PDOC =9,从而得到图象C 1的函数关系式为y=,再算出△EOF 的面积,可以得到△AOC 与△EOF 的面积比,然后证明△EOF ∽△AOC ,根据对应边之比等于面积比的平方可得到EF ﹕AC 的值.【解答】解:∵B 、C 反比例函数y 2=的图象上,∴S △ODB =S △OAC =×3=,∵P 在反比例函数y 1=的图象上,∴S 矩形PDOC =k 1=6++=9,∴图象C 1的函数关系式为y=,∵E 点在图象C 1上,∴S △EOF =×9=,∴==3,∵AC ⊥x 轴,EF ⊥x 轴,∴AC ∥EF ,∴△EOF ∽△AOC ,∴=,故选:A .【点评】此题主要考查了反比例函数系数k 的几何意义,以及相似三角形的性质,关键是掌握在反比例函数y=图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k |;在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k |,且保持不变.25.(富顺县校级一模)如图,已知矩形OABC面积为,它的对角线OB与双曲线相交于D且OB:OD=5:3,则k=()A.6B.12C.24D.36【分析】先找到点的坐标,然后再利用矩形面积公式计算,确定k的值.【解答】解:由题意,设点D的坐标为(x D,y D),则点B的坐标为(x D,y D),矩形OABC的面积=|x D×y D|=,∵图象在第一象限,∴k=x D•y D=12.故选B.【点评】本题考查了反比例函数与几何图形的结合,综合性较强,同学们应重点掌握.26.(重庆模拟)如图,▱OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=的图象经过点A与点D,则▱OABC的面积为()A.30B.24C.20D.16【分析】根据平行四边形的性质的性质及反比例函数k的几何意义,判断出OE=EF,再由△AOD的面积,即可求出结果.【解答】解:过点A作AE⊥OC于E,过点D作DF⊥OC于F,∵反比例函数y=的图象经过点A,且点A的横坐标为2,∴y==5,∴A(2,5),∴AE=5,∵四边形OABC是平行四边形,∴AD=CD,∴DF=AE=,OF=4,∵反比例函数y=的图象经过点A 与点D ,∴S △AOD =S 四边形AEFD =(+5)×2=,∴▱OABC 的面积=4×S △AOD =4×=30.故选A .【点评】本题考查了平行四边形的性质及反比例函数k 的几何意义,涉及的知识点较多,注意理清解题思路,分步求解.27.(河南模拟)如图,A 、C 分别是x 轴、y 轴上的点,双曲线y=(x >0)与矩形OABC 的边BC 、AB 分别交于E 、F ,若AF :BF=1:2,则△OEF 的面积为()A .2B .C .3D .【分析】设F 点的坐标为(t ,),由AF :BF=1:2得到AB=3AF ,则B 点坐标可表示为(t ,),再利用反比例函数解析式确定E 点坐标为(,),然后利用△OEF 的面积=S 矩形ABCO ﹣S △OEC ﹣S △OAF ﹣S △BEF 和三角形的面积公式进行计算.【解答】解:设F 点的坐标为(t ,),∵AF :BF=1:2,∴AB=3AF ,∴B 点坐标为(t ,),把y=代入y=得x=,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点与坐标轴围成的矩形面积= /K/
例题:
如图13,A为反比例函数 y 4图象上的任意一点,
x
AB⊥x轴于B,AC ⊥y
轴于C,
y
A
C
OB
x
则矩形ACOB的面积=( 4 )
图13
变式一、
如图13,矩形AOBC的面积为16,反比例函数
yk x
的图象的一
支经过矩形对角线的交点P,则该反比例函数的解析式是( C )
D C
C.6 D.4
O
EBx
图9
变式十、
如图10,直线L与双曲线
y
k x
相交于A、B两
点,与x轴交于点C,B为线段AC的中点,过点B作BM⊥x轴
于M,连结OA.若OM=2MC,S △OAC=6.则k的值为( 4 ).
在上题中,若连接OB, y
则S △OAB=( 3 )
L A
B
OH
Mc
x
图10
变式十一:如图12,反比例函数
A作AB ⊥x轴于点B,若△AOB的面积为2,则K的值
是( -4 )
(2)A是双曲线
yk x
上任意一点,过A作AB ⊥x
轴于点B,若△AOB的面积为2,则K的值是(±4 )
(3)A为双曲线
y
k
x(K>0)上的任意一点,过A
作AB⊥x轴于点B,若△AOB的面积为2,则下面各点
中也在这个反比例函数图象上的点是( A )
拓展:若连接OP、OQ, 则S△OPM、S△OPN、S△OQE、
S△OQF有什么关系?
得出结论:反比例函数图象∣上∣
任意一点与坐标轴围成的矩形面
y
积= /K/ ,反比例函数图象上任意 一点与坐标轴围成的三角形形面
P
M
积= / k / 。 2
oF
x N
E
Q
内容一:考察反比例函数图象上的任意一
点与坐标轴围成的三角形面积= 1 /K/
x
在上题的基础上,点 C在双曲线
y
12 x
上,且AC‖x轴交y轴于点B,
y
则△PAC 的面积为 ( 4 )
B
AA
C
PO
x
图7
变式八、
如图8, A是双曲线 y 4 上的任意一点,若B在X x
轴上,且OA=AB,则△ OAB的面积=( 4 )
若四边形ABCO是菱形,则菱形面积是 ( 8 )
若上题改为:如图8,菱形ABCO
课题:
反比例函数中K的几何意义的变式练习
题目的出处: 九年级上册P151页想一想的中的(1)问
考查的知识点: 反比例函数中K的几何意义
原题:在一个反比例函数图象上任取两点P、Q,过点P分别
作x轴、y的平行线,与坐标轴围成的矩形面积为S1,过点Q分 别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,则S1 与S2有什么关系?为什么?
CD⊥x轴于点D.若△BOC的面积是2,则这个反比例函数的解
析式为(
y4 x
)若△BCD的面积是4,则这个反比例函数的解
析式为( y 4 )若口ABCD的面积是8,则这个反比例函数的解
x
析式为( y 4 )
x
图6
变式七:(2010山西)如图7,A是反比例函数图象上一点,
过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则 这个反比例函数的解析式为( y 4 ).
C. S1< SD3< S2 D. S1=S2=S3
图3
变式四、
如图4:A是反
AB⊥X轴于点B,D是X轴上的一点,若OD=OB,则
S△AOD=( 2 ),S△ABD = ( 4 )y
A
DO B
x
图4
变式五、
如图5:正比例函数y=kx ( k≠0 )与反比例函数
y 4的 x
y
4 x (x>0)的图象与
矩形OABC的边AB、BC分别交于点E、F,且 AE=BE,则
△OEF的面积的值为( 3 )
上题也可变为:双曲线经过矩形OABC的边AB、BC的中点
E、F,且四边形OEBF的面积为4,则K=( 4 ),△BEF的 面积为( 1 )
图12
内容二:考察反比例函数图象上的任意一
y
的顶点O是原点,顶点B在x轴上,
A
若菱形的面积是8,且反比例函 数 y k 的图象经过点A,
x
则k的值为( 4 )
O
DB x
C
图8
变式九、
如图9,已知双曲线 y k 经过Rt △OAB斜边OA的中点D, x
且与直角边AB相交于点C.若点A坐标为(4,4)则△AOC的
面积为( ) C
y
A
A.12 B.9
图象交于A、 C两点,过A作AB⊥x 轴于B,则S△ABC =( 4 )
若再过点C作CD⊥x轴于D,连接AD,则 S口ABCD=( D)
A.2 B.4 C.6 D.8
y
A
D
OB
x
cC
图5
变式六、
将上题的条件和结论交换:如图6,反比例函数与正比例函数
的图象相交于A、C两点,过点A作AB⊥x轴于点B.过点C作
2
例题:
如图1,A为反比例函数 y 4 x
图象上的任意一点,
y A
AB⊥x轴于B, 则△AOB的面积=( 2 )
OB
x
图1
变式一、
如图2, A是双曲线
y
k x
上的任意一点,过A作
AB ⊥x轴于点B,若△AOB的面积为2,则K的值是
(4 )
y
A
OB
x
图2
变式二、
(1) A是双曲线
y
k x
(K<0)上任意一点,过
x
图15
变式四:如图16,点A是双曲线 y k(x>0)上的一动
x 点,过A作AC⊥y轴于点C,作AC的垂直平分线交双曲线于点
B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形
ABCD的面积( D )
A(1,4) B(1,2) C(-2,2) D(2,-2)
变式三、如图3所示,P1、P2、P3是双曲线
y
k上 x
的三个点,过这三点分别作y轴的垂线,得三个三角
形 △OP1A1、△OP2A2、△OP3A3,设它们的面积分 别为S1、S2、S3,
则下列选项正确的是( D )
A. S1<S2<S3 B. S2 <S1< S3
x
图14
变式三:
如图15,
A、B是双曲线
y
4 x
上任意两点,过A作
AC⊥x轴于点C,AD ⊥y轴于点D,过B作BE⊥x轴于点E,作
BF⊥y轴于点F,设AC与BF交于点G,若设S 矩形ADFG=S1 ,
S 矩形BGCE=S2,且S1 +S2=5, y
则四边形OCGF
D
A
的面积 =(1.5)
F
B G
O CE
(A)y 8 x
(B) y 2 x
(C) y 4 x
(D)y
1 x
y
A
E
P
O
F
图13
C Bx
变式二、如图14:A是反比例函数 y 4 (x<0)的图
x 象上的一点,过点A作口ABCD,使点B、C在x轴上,点D
在y轴上,则口ABCD的面积是( B )
A、2 B、4 C、6 D、8
y
A
D
B E CO
