正弦余弦的诱导公式专题训练
02三角函数诱导公式(含经典例题+答案)
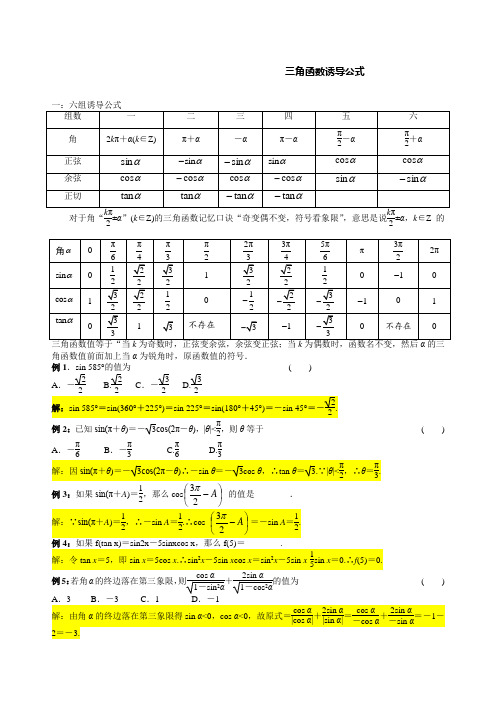
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
高一数学 知识点 三角函数 诱导公式 常考题 经典题 50道 含答案和解析

高一数学三角函数诱导公式50道常考题经典题一、单选题1.若角的终边上有一点(-4,a),则a的值是()A. B. C. D.【答案】A【考点】任意角的三角函数的定义,诱导公式一【解析】【解答】由三角函数的定义知:,所以,因为角的终边在第三象限,所以<0,所以的值是。
【分析】三角函数是用终边上一点的坐标来定义的,和点的位置没有关系。
属于基础题型。
================================================================================2.若,则的值是( )A. B. C. D.【答案】C【解析】【解答】即,所以,,=,故选C。
【分析】简单题,此类题解的思路是:先化简已知条件,再将所求用已知表示。
================================================================================3.若,则()A. B. C. D.【答案】C【考点】诱导公式一,同角三角函数间的基本关系【解析】【解答】,故选C.================================================================================4.函数图像的一条对称轴方程是()A. B. C. D.【答案】A【考点】诱导公式一,余弦函数的图象,余弦函数的对称性【解析】【分析】,由y=cosx的对称轴可知,所求函数图像的对称轴满足即,当k=-1时,,故选A.================================================================================5.已知,则()A. B. C. D.【答案】C【考点】诱导公式一,同角三角函数间的基本关系,弦切互化【解析】【解答】因为,所以,可得,故C符合题意.故答案为:C .【分析】利用诱导公式将已知条件化简可求出tan,将中分子分母同时除以cos.================================================================================6.函数()A. 是奇函数B. 是偶函数C. 既是奇函数,又是偶函数D. 是非奇非偶函数【答案】A【考点】奇函数,诱导公式一【解析】【解答】∵,∴,∴是奇函数.故答案为:A【分析】首先利用诱导公式整理化简f(x) 的解析式,再根据奇函数的定义即可得证出结果。
正弦、余弦的诱导公式经典练习题

正弦、余弦的诱导公式基础练习1.求下列三角函数值:(1)sin (-120°); (2)cos (-240°); (3)tan (-135°);(4))4π7sin(-; (5))6π11cos(- (6))3π4tan(-. 2.求下列三角函数值: (1)sin (-2460°); (2)cos840°; (3)tan (-2025°) (4))3π17sin(-; (5))3π50cos(-; (6))6π415tan(-. 3.将下列各值化为锐角的三角函数值: (1)sin4321°; (2))π9368cos(-; (3))π7117sin(; (4)cos2001°. 4.下列各式的值等于-sin A 的是( ).A .sin (-A )B .sin (k ·360°-A ),k ∈ZC .sin (k ·360°+A ),k ∈ZD .-sin (-A )5.如果+=180°,那么下列等式中成立的是( ).A .sin =-sinB .cos =cosC .sin =sinD .cos (+)=16.函数式)1-πcos()1-πsin(21-化简的结果是( ). A .sin1-cos1 B .sin1+cos1C .±(sin1-cos1)D .cos1-sin17.已知31)πsin(=+x ,求)π(cos 1)-πsin(2x x ++的值. 8.若(-4,3)是角 终边上一点,则)π(sin )2π-tan( ) π3cos(2αα-⋅-a 的值为_______.综合练习1.求下列三角函数值:(1))π665cos(-; (2)sin (-1590°); (3)cos (-1260°); (4)π331sin ; (5)sin (-542°); (6))π724cos(-.2.设A 、B 、C 是某三角形的三个内角,给出下列四个命题:(1)sin (A +B )=sin C ;(2)cos (B +C )=cos A ;(3)tan (A +C )=tan B ;(4)A +B +C =.其中正确的命题是( ).A .(1)(2)B .(2)(3)C .(3)(4)D .(1)(4)3.是第三象限的角,则下列各式中其值恒正的是( ).A .sin -cos (-)B .-tan -cos (+)C .tan (-2)+sin (2-)D .-tan (4+)+sin4.)4π3tan(6π25cos 3π4sin-⋅⋅的值是( ). A .43- B .43 C .43- D .435.当31tan =α时,求cos (――5)tan (3+)sin (-)-1的值.6.已知f (x )=2cos x ,则下列等式成立的是( ).A .)()π2(x f x f -=+B .)()(x f x f =-C .)()(x f x f -=-D .)()π2(x f x f =+ 7.化简:(1)[][])-π)1(cos π)1(sin )cos()-πsin(αααπα+⋅+++⋅k k k k (k ∈Z ); (2)790cos 200cos 110cos 470sin 21+⋅+. 8.化sin (75+)(为钝角)为锐角的三角函数为________.9.已知3)2001cos()π2001sin(=+++βπαb a ,(其中、、a 、b 都是常数),则a sin (2002+)+b cos (2002+)的值为________.10.已知33)6πcos(=-α,则)6π(sin )6π5cos(2--+αα的值为________.拓展练习 1.)cos )](sin πcos()sin(1[cos )-2sin(2π-) πcos(sin 1αααααααα++---⋅--+. 2.计算: 1sin 2+ 2sin 2+…+ 89sin 2+ 90sin 2+ 91cos 2+ 92cos 2+…+ 179cos 2+180cos 2.3.化简:)πsin(α++)π2sin(α++)π3sin(α++…+)π2sin(α+k ,k ∈Z .4.已知是锐角,sin (-)和cos (-)是方程022=+-m x x (m 是常数)的两个根,求sin +cos 的值.5.设A 、B 、C 、D 是圆内接四边形ABCD 的四个内角,求证:(1)sin A =sin C ;(2)cos (A +B )=cos (C +D );(3)tan (A +B +C )=-tan D . 6.设⎪⎪⎩⎪⎪⎨⎧≥+-<=⎩⎨⎧≥+-<=).21(1)1(),21(πcos )();0(1)1(),0)(πsin()(x x g x x x g x x f x x x f 求)65()41()43()31(g g f f +++的值.参考答案基础练习1.(1)23-;(2)21-;(3)1;(4)22;(5)23;(6)3-. 2.(1)23;(2)21;(3)-1;(4)23;(5)21-;(6)33-. 3.(1)sin1°;(2)9πcos -;(3)π72sin ;(4)-cos21°. 4.B 5.C 6.B .7.173-.由已知得31sin -=x ,x x x x 22cos 1sin )π(cos 1)-πsin(+=++. 8.原式可化为ααααsin 1sin tan cos 2-=⋅-,由条件53sin =α,故所求值为35-. 综合练习1.(1)23-;(2)21-;(3)-1;(4)23;(5)0.0349;(6)-0.2225. 2.D 3.C 4.A5.109-.化简 cos (--5)tan (3+)sin (-7)-1=-cos 2. 6.B .7.(1)当k =2n (n ∈Z )时,有原式1)cos (sin cos sin -=-⋅-⋅-=αααα;当k =2n +1(n ∈Z )时,原式1cos sin )cos (sin -=-=αααα. (2)原式=︒+︒-︒⋅︒+70cos 20cos 110cos 110sin 21=︒-︒︒⋅︒-70sin 70cos 70cos 70sin 21= ︒-︒︒-︒70sin 70cos )70cos 70sin (2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1. 8.-sin (-).9.-3.a sin (2001+)+b cos (2001+)=-a sin a -b cos.∴a sin (2002+)+b cos (2002+)=a sin +b cos =-3. 10.33)6πcos(])-6π(-πcos[)6πcos(332-=--==+⋅+-ααα. 32311)6π(cos 1)6π(sin )6π(sin 222=-=---=-ααα. 拓展练习1.原式)cos )(sin cos sin 1(cos sin )cos (sin )cos )(sin cos sin 1(cos sin 2cos sin 12αααααααααααααααα++++++=+++⋅+++= 1)cos )(sin cos sin 1()cos sin 1)(cos (sin =++++++=αααααααα. 2.原式=9111cos 88cos 89cos 189sin 2sin 1sin 222222=+︒++︒+︒++︒++︒+︒ .3.原式=(-sin +sin )+(-sin +sin)+…+(-sin +sin )=0. 4.由已知21)cos()sin(=-+-θθ,即21sin cos =-θθ,∴ 41cos sin 21=-θθ,于是83cos sin =θθ.47cos sin 21)cos (sin 2=+=+θθθθ,又为锐角.∴θθcos sin +=27. 5.由已知A +C =,A +B +C +D =2得A =-C ,则sin A =sin (-C )=sin C ,又A +B =2-(C +D ),故cos (A +B )=cos[2-(C +D )]=cos (C +D ).tan (A +B +C )=tan (2-D )=-tan D .6.由已知231)31(-=f ,221)43(-=f ,22)41(=g ,231)65(+=g .故原式=3.0。
三角函数诱导公式练习题集附答案解析

三角函数诱导公式练习题一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数2、点P(cos2009°,sin2009°)落在()A、第一象限B、第二象限C、第三象限D、第四象限3、已知,则=()A、B、C、D、4、若tan160°=a,则sin2000°等于()A、B、C、D、﹣5、已知cos(+α)=﹣,则sin(﹣α)=()A、﹣B、C、﹣D、6、函数的最小值等于()A、﹣3B、﹣2C、D、﹣17、本式的值是()A、1B、﹣1C、D、8、已知且α是第三象限的角,则cos(2π﹣α)的值是()A、B、C、D、9、已知f(cosx)=cos2x,则f(sin30°)的值等于()A、B、﹣C、0 D、110、已知sin(a+)=,则cos(2a﹣)的值是()A、B、C、﹣D、﹣11、若,,则的值为()A、B、C、D、12、已知,则的值是()A、B、C、D、13、已知cos(x﹣)=m,则cosx+cos(x﹣)=()A、2mB、±2mC、D、14、设a=sin(sin20080),b=sin(cos20080),c=cos(sin20080),d=cos(cos20080),则a,b,c,d的大小关系是()A、a<b<c<dB、b<a<d<cC、c<d<b<aD、d<c<a<b15、在△ABC中,①sin(A+B)+sinC;②cos(B+C)+cosA;③tan tan;④,其中恒为定值的是()A、②③B、①②C、②④D、③④16、已知tan28°=a,则sin2008°=()A、B、C、D、17、设,则值是()A、﹣1B、1C、D、18、已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2007)=5,则f(2008)=()A、3B、5C、1D、不能确定19、给定函数①y=xcos(+x),②y=1+sin2(π+x),③y=cos(cos(+x))中,偶函数的个数是()A、3B、2C、1D、020、设角的值等于()A、B、﹣C、D、﹣21、在程序框图中,输入f0(x)=cosx,则输出的是f4(x)=﹣csx()A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题(共9小题)22、若(﹣4,3)是角终边上一点,则Z的值为.23、△ABC的三个内角为A、B、C,当A为°时,取得最大值,且这个最大值为.24、化简:=25、化简:= .26、已知,则f(1)+f(2)+f(3)+…+f(2009)= .27、已知tanθ=3,则(π﹣θ)= .28、sin(π+)sin(2π+)sin(3π+)…sin(2010π+)的值等于.29、f(x)=,则f(1°)+f(2°)+…+f(58°)+f(59°)= .30、若,且,则cos(2π﹣α)的值是.答案与评分标准一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
三角函数诱导公式练习题非常经典含有--答案

一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A.-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k πC . 2π+2k π≤x ≤2π3+2k πD .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z )2.sin (-6π19)的值是( )A . 21 B .-21C .23 D .-233.下列三角函数:①sin (n π+3π4);②cos(2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π];⑤sin [(2n +1)π-3π](n ∈Z ).其中函数值与sinπ的值3相同的是()A.①②B.①③④C.②③⑤D.①③⑤4.若cos(π+α)=-10,5且α∈(-π,0),则tan(2π3+α)2的值为()A.-6B.363C.-6D.2625.设A、B、C是三角形的三个内角,下列关系恒成立的是()A.cos(A+B)=cos C B.sin(A+B)=sin C C.tan (A+B)=tan C D.sin2B A =sin2C 6.函数f(x)=cos3πx(x ∈Z)的值域为()A.{-1,-1,0,21,21} B .{-1,-21,21,1}C .{-1,-23,0,23,1} D .{-1,-23,23,1}二、填空题7.若α是第三象限角,则)πcos()πsin(21αα---=_________.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).10.证明:1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ.11.已知cos α=31,cos(α+β)=1,求证:cos (2α+β)=31.12. 化简:︒+︒︒︒+790cos 250sin 430cos 290sin 21.13、求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ.14. 求证:(1)sin (2π3-α)=-cos α;(2)cos (2π3+α)=sin α.参考答案1一、选择题1.C 2.A 3.C 4.B 5.B 6.B二、填空题7.-sin α-cos α 8.289三、解答题 9.43+1.10.证明:左边=θθθθ22sin cos cos sin 2-1--=-θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++, 右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--,左边=右边,∴原等式成立. 11.证明:∵cos (α+β)=1,∴α+β=2k π.∴cos (2α+β)=cos (α+α+β)=cos (α+2k π)=cos α=31.12.解:︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21 =︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1.13.证明:左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tan θ=右边,∴原等式成立.14证明:(1)sin(π3-α)2=sin[π+(π-α)]=-sin(2π-2α)=-cosα.(2)cos(π3+α)=cos[π+2(π+α)]=-cos(2π+α)=sinα.2三角函数的诱导公式2一、选择题:1.已知sin(π+α)=23,则4sin(3π-α)值为()4A.1 B. —21 C.223 D. —232.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( )A. 23 B. 21 C.23±D. —233.化简:)2cos()2sin(21-∙-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sin α=sin βB.sin(α-π2) =sin βC.cos α=cos βD. cos(π2-α) =-cos β5.设tan θ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ),A. 51(4+5) B. 51(4-5)C. 51(4±5) D. 51(5-4)二、填空题:6.cos(π-x)= 23,x ∈(-π,π),则x 的值为 .7.tan α=m ,则=+-+++)c o s(-s i n ()c o s(3s i n (απα)απ)απ .8.|sin α|=sin (-π+α),则α的取值范围是 .三、解答题: 9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin3π4·cos6π25·tan4π5;(2)sin[(2n+1)π-3π2].13.设f(θ)=)cos()π(2cos23)2πsin()π2(sin cos2223θθθθθ-+++-++-+,求f(3π)的值.参考答案21.C 2.A 3.C 4.C 5.A6.±65π7.11-+m m8.[(2k-1) π,2kπ]9.原式=)cos(·sin()cos()ns(sinαα)παπα--+--αi=)cos?(sin)cos(sin2αααα--=sin α 10.161111.解:(1)sin 3π7=sin(2π+3π)=sin 3π=23.(2)cos 4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23.(4)sin (-765°)=sin [360°×(-2)-45°]=sin(-45°)=-sin45°=-2.2注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.12.解:(1)sinπ4·cos6π25·tan4π5=sin3(π+π)·cos(4π+6π)·tan(π+4π)3=(-sinπ)·cos6π·tan4π=(-323)·23·1=-43.(2)sin [(2n +1)π-3π2]=sin (π-3π2)=sin 3π=23.13.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++--- =θθθθθcos cos 22)1(cos cos )1(cos 223++---=θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cosθ-1,∴f(3π)=cos3π-1=21-1=-1.2三角函数公式1.同角三角函数基本关系式sin2α+cos2α=1sinα=tanαcosαtanαcotα=12.诱导公式(奇变偶不变,符号看象限)(一)sin(π-α)=sinαsin(π+α)=-sinαcos(π-α)=-cosαcos(π+α)=-cosαtan(π-α)=-tanαtan(π+α)=tanαsin(2π-α)=-sinαsin(2π+α)=sinαcos(2π-α)=cosαcos(2π+α)=cosαtan(2π-α)=-tanαtan(2π+α)=tanα(二)sin(π2-α)=cosαsin(π2+α)=cosαcos(π2-α)=sin αcos(π2+α)=- sin αtan(π2-α)=cot αtan(π2+α)=-cot αsin(3π2-α)=-cos αsin(3π2+α)=-cos αcos(3π2-α)=-sin αcos(3π2+α)=sin αtan(3π2-α)=cot αtan(3π2+α)=-cot αsin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα3.两角和与差的三角函数cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin (α+β)=sinαcosβ+cosαsinβsin (α-β)=sinαcosβ-cosαsinβtan(α+β)=tanα+tanβ1-tanαtanβtan(α-β)= tanα-tanβ1+tanαtanβ4.二倍角公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2αtan2α=2tanα1-tan2α5.公式的变形(1)升幂公式:1+cos2α=2cos2α1—cos2α=2sin2α(2)降幂公式:cos2α=1+cos2αsin2α=21-cos2α2(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tan αtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)(4)万能公式(用tanα表示其他三角函数值)sin2α=2tanα1+tan2αcos2α=1-tan2α1+tan2αtan2α=2tanα1-tan2α6.插入辅助角公式asinx+bcosx=a2+b2sin(x+φ) (tanφ= b a )特殊地:sinx±cosx= 2sin(x±π4 )7.熟悉形式的变形(如何变形)1±sinx±cosx 1±sinx 1±cosxtanx+cotx若A、B是锐角,A+B=π4,则(1+tanA)(1+tanB)=2 8.在三角形中的结论若:A+B+C=π,A+B+C2=π2则有tanA+tanB+tanC=tanAtanBtanCtan A2tanB2+tanB2tan C2+tanC2tanA2=1。
诱导公式练习题

诱导公式练习题一、基本概念题1. 写出三角函数的诱导公式:正弦、余弦、正切函数的周期性公式。
2. 利用诱导公式,将sin(π α)转换为基本三角函数的形式。
3. 将cos(3π/2 + β)用基本三角函数表示。
4. 利用诱导公式,将tan(2π + γ)简化。
5. 已知sinθ = 1/2,求cos(π/2 θ)的值。
二、化简题6. 化简表达式:sin(π + α) cos(π/2 α)。
7. 化简表达式:tan(2π β) + tan(π + β)。
8. 化简表达式:sin^2(π/2 γ) + cos^2(π/2 γ)。
9. 化简表达式:cos(2π 2θ) sin(2π + 2θ)。
10. 化简表达式:tan(π 3α) tan(π + 3α)。
三、应用题11. 已知sinα = 3/5,求cos(π/2 α)的值。
12. 已知cosβ = 4/5,求sin(π β)的值。
13. 已知tanγ = 1,求tan(π + γ)的值。
14. 已知sinθ = √3/2,求cos(2π + θ)的值。
15. 已知cosφ = √2/2,求sin(π/2 φ)的值。
四、综合题16. 已知sinα + cosα = 1,求sin(π/2 α)的值。
17. 已知sinβ cosβ = 0,求cos(π β)的值。
18. 已知tanγ = tan(π/4 γ),求sin(2π + γ)的值。
19. 已知sinθ = cos(π/2 θ),求tan(2π θ)的值。
20. 已知cosφ = sin(π/2 φ),求sin(π + φ)的值。
五、拓展题21. 利用诱导公式证明:sin^2α + cos^2α = 1。
22. 利用诱导公式证明:tan(π + α) = tanα。
23. 利用诱导公式证明:sin(π 2α) = sin2α。
24. 利用诱导公式证明:cos(2π 2β) = cos2β。
25. 利用诱导公式证明:tan(π/2 γ) = cotγ。
(完整版)诱导公式练习

诱导公式Ⅰ习题2一、判断题(每道小题1分共2分)( )2. 当α在第三象限时,180°+α在第一象限,其正弦值为正,所以有:sin(180°+α)=sinα( )二、单选题(每道小题3分共9分)1. 下列各函数值中与-cos130°的值相同的是[ ]A.cos50°.B.sin50°.C.-cos50°.D.cos(-130°).[ ][ ]三、填空题(1-2每题2分,第3小题3分,4-5每题4分,共15分)1. △ABC中,若A∶B∶C=3∶4∶5,则最小角的余弦值是____________.4. tan(-210°)-tan420°+tan(-840°)=________.5. 适合sin | x | =sin(π+x)的x的集合是______.四、解答题( 7分)求适合4cos2(3π+x)-3=0的x的集合.诱导公式Ⅱ习题1一、单选题(1-9每题3分,10-12每题4分,共39分)[ ][ ]3. 如果α+β=180°,那么下列等式中成立的是[ ] A.sinα=-sinβ B.cosα=cosβ C.tanα=tanβ D.sinα=sinβ[ ] [ ] [ ] [ ] [ ] [ ] [ ][ ] 二、填空题(第1小题3分,第2小题4分,共7分)诱导公式Ⅰ习题2答案一、判断题1. ×2. ×二、单选题1. A2. C3. D三、填空题5. {x | x≤0,x ∈R} 或{x | x=kπ,k∈z}四、解答题1D 2. D3. D4. C5. A6. C7. D8. A9. A10. C11. B. 4。
三角函数诱导公式经典例题

三角函数诱导公式练习题及答案1.2cos(−θ)+sin(π−θ)cos(π2−θ)+sin(3π2−θ)=4,求tanθ的值 2.已知f(α)=sin(α−3π)⋅cos(2π−α)⋅sin(−α+32π)cos(−π−α)⋅sin(−π−α)(1)化简f(α);(2)若α为第四象限角且sinα=−35,求f(α)的值;(3)若α=−313π,求f(α)。
3.已知sin(α+2022π)−6sin(α−3π2)2cos(α−π)−sinα=−tan 3π4. (1)求tanα的值;(2)求sinα−cosα的值。
4.已知sinα=−35,且α为第三象限角.(1)求cosα和tanα的值;(2)已知f(α)=2sin(π+α)+cos(2π+α)cos(α−π2)+sin(π2+α),求f(α)的值。
5.已知关于x 的方程25x 2−ax +12=0的两根为sinθ和cosθ,其中θ∈(π4,3π4),(1)求a 的值;(2)求2sin(θ+π2)−cos(θ−π2)+sin(θ−π)cos(π+θ)4cos(θ+π2)−1的值。
6.已知f(α)=cos(π−α)sin(−α−π)sin(α−π2)cos(3π2+α)tan(π−α). (1)化简f(α);(2)若角α为第二象限角,且sinα=13,求f(α)的值。
7.已知tanα=2,求cos(π2+α)sin(−α)+cos(2π−α)的值。
8.已知α∈(0,π2),cosα=35,求sin(π2−α)+cos(3π2−α)sin(3π+α)+cos(π−α)的值。
9.(1)化简sin(π−α)sin(π2−α)cos(π+α)cos(π2+α).(2)已知:tanα=2,求sinα+2cosα5cosα−sinα的值.10.化简f(α)=sin(π−α)cos(3π2−α)tan(−π−α)cos(−π2−α)tan(2π+α)11.已知cosα=−√55,α是第三象限角,求: (1)tanα的值;(2)sin(3π2−α)cos(π+α)tan(−α−π)cos(2π−α)sin(π−α)tan(−α)的值. 12.已知tanα=12,求13cos(−α)−2cos(π2−α)sin(π2+α)+3sin(π+α)的值. 13.已知cosα=−45,且tanα>0.(1)求tanα的值;(2)求2sin(π−α)+sin(π2+α)cos(2π−α)+cos(−α)的值. 14.已知3cosα−2sinαsinα+2cosα=−14,cos(π+α)cos(π2+α)sin(3π2−α)cos(3π2−α)sin(3π−α)sin(5π2+α)的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正、余弦函数的图象和性质检测题
10.函数y = J —cosx+Jcotx 的定义域是
( )
总分15 0分
、选择题(每小题5分,共50分,请将正确答案填在题后的括号内)
y =2si n(2x +*) 的图象
关于原点对称 B.关于点(一三,0)对称
6
C. 关于y 轴对称
D .关于直线 x=2L 对称
6
2•函数 ;r y =2si n(— -2x)(xW[0, 6 刃) 为增函数的区间是 3
3
A . [k^+;r,kH+ — ;r]
B . [2k 花 + ;r ,2^ +
- ;r ]
2 2
3 T 3 C . (2kH +;T ,2心+ —TT ]或x = 2kH+— D . (2kH + TT ,2负+ —7!]
2
2
2
二、填空题(每小题5分,共25分,答案填在横线上)
1 X +
11 .已知函数 y= —sin ---- (A > 0)的最小正周期为 3応,贝U A= ______
2 A
TT 2 2
12 .在0w xw —条件下,则 y= cos X — sinxcosx — 3sinx 的最大值为
2
13 .已知方程cos 2
x+4sin x_a = 0有解,那么a 的取值范围是 _____________ A . r c n _ [0, B . [ L 7:]
C / C .[彳石]
D .
3 12 12 6
3.设a 为常数,且 a :>1,0 <x <2;r ,则函数 f(X)=cos 2 X+2asinx-1 的最大值为( )
A . 2a+1
B . 2a-1
C . -2a-1
D . 2 a
4.函数 y =si n (2x +5;r)的图象的一条对称轴方程是 (
) A . ;r X =—— B . x=-- C . X =— D . 5
X =—TT
2 4 8 4
f(X)=sin(申)的图象(部分)如图所示,则
co 和W 的取值是
5.若函数
( )
14 .函数y=些og 的值域是 cos X + 2 15 .定义在R 上的函数f(x)既是偶函数又是周期函数, 若f (X)的最小正周期是;r ,且当X 迂[0,弓]
时,f(x) = sinx ,则 仃竺)的值为 3
三、解答题(本大题共75分,16 —19题每题12分,20题13分,21题14分)
,—
2
5 L _
f(x) = 5sin X cosx — 5、'3 cos x + —A /3(X D R)
2
16.已知函数 (1 )求 f(x)的最小正周期;(2)求f(X)的单调区间;
=1 申=-
,
3 "6 71
(3 )求
f(X)图象的对称轴,对称中心
2,
6.下列函数中,以 3 T
T -3
2;T
n 为周期的偶函数是 A. y =|sin X I B. y =sin | x| C.
(
TT
:T
y = sin(2x + 5)D. y = sin(x +
—)
7.如果函数y=sin2x+ a cos2x 的图象关于直线 X=——对称, 8
那么 a 的值为
A. &函数 v2
B. - <2 2
y=2cos x+1(x € R )的最小正周期为
C.
C. D. 4n
9.已知函数f(X)=si 门(致—3)T ,则下列命题正确的是 A . f(x)是周期为1的奇函数 B . f(x)是周期为 C . f (X)是周期为1的非奇非偶函数 D . f(x)是周期为
2的偶函数 2的非奇非偶函数
2
、 2 2
18.已知函数 y= sin x + 2sinxcosx + 3cosx.x € R. (1)求函数的最小正周期.
⑵ 函数的图象可由函数 y={2sin2x 的图象经过怎样的变换得出?
21.已知函数f (x ) =2a s in (2x —- ) +b 的定义域为[0, 3 ],值域为[—5,1 ],求a 和b 的
3
2
值.
19.已知函数y = a — b sin (4x — — ) (b >0)的最大值是5,最小值是1,求a , b 的值.
3
17.如图,某地一天从 6时至14时的温度变化曲线近似满足函数 y = Asin(©x +半)+b .
(I)求这段时间的最大温差; (n)写出这段曲线的函数解析式. 30 20
10—"
20.函数 f(x) = 1 — 2acosx — 2a — 2sin x 的最小值为 g(a), (a€ R).求: (1)g(a);
1
⑵ 若g(a) =2求a 及此时f(x)的最大值.
答案 一、 选择题 1. B 2 . C3. B 4 . C 5 . C6. 二、 填空题 A7 . D 8 . B 9. B10. C 18. y = sin2x + cos2x + 2=^sin(2x +寸)+ 2. (1)T =
n ,
n
(2)将y = V 2sin2x 的图象向左平移个长度单位,再向上平移
2个单位长度即得. 11. 2312. 2 三、解答题
16.解析: 3 13.- 4 4 14. [44) 15.— 2 < yw — 3 19.解析: 由y= a — bsin (4x ——)的最大值是5,最小值是1
3
及b>0知:
T= n ; TT . 5
12 12 5 11 ["+ —匚"+—;!]为f(x)的单减区间;
12 12 (3)对称轴为x=」+ = ,kwz. 2 6 17.解析:(I)由图示知,这段时间的最大温差是 (1) 1;豐 5 解得 b :3
(2) [kH- — ,k H+二盯为f(x)的单增区间, 2
2
a 2 a
20 .解:f(x) = 2cos x — 2acosx — 2a — 1 = 2(cosx —三)—三—
2a — 1.
a (1)当-<-1 即 av — 2 时.g(a) = 1 .(此时 cosx=— 1).
30 -10 =20 ( C ) 2
当一1 w|w 1 即—2W aw 2 时.g(a)=—号—2a — 1. (此时
当 a> 2 时,g(a) = 2— 2a — 2a — 1 = 1 — 4a.
a
cosx
="2).
(此时 COSX = 1).
(n)图中从6时到14时的图象是函数 y=Asi n( «x +W )+b 的半个周期的图象,
1 2
乂
2⑷
= 14-6,解得 0 =- I 1. (a< — 2)
I 2
•-g(a)= —专一2a — 1 (—2w aw 2).
L 1 — 4a (a> 2). 5分
由图示,
⑵•/ g(a)= 1.显然a<— 2和a>2不成立.
- 2 .
.[—号一2a —1=1 十 A
••f
2
2
=a = — 1 或一3(舍).
丨一2 w aw 2. 2 1 2 1 ••• f(x) = 2cos x+ 2cosx + 1 = 2(cosx+?)十?. ••当 cosx= 1 时,f(x) max = 5 .
b =1(30+10) =20
这时心吨宀+20
21 .解析:•/ 0w xw —
2
;r yr ••• — 一 w 2x — — w
3
3
•―逅 7t
TT 2 _ — 3=3 Tt .
将X =6, y =10代入上式,可取 10分
综上,所求的解析式为
TT 3乂 _
y =10sin(—x+——)+20 , x 迂[6,14].
8 4
;r
w sin (2x ——)w 1.
2
3
「2a+b=1
当a>0时,则彳 一
I —V3a + b = —5.
解得〔心2
一出厂
lb = -23 + 12J3.
12分
I2a + b = —5
当a <0时,则彳厂
:一吋 3a + b =
1,
解得尸
b = 19—12丁
3.。
