八年级上册思维导图
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
八年级上册数学第十三章 轴对称思维导图 脑图
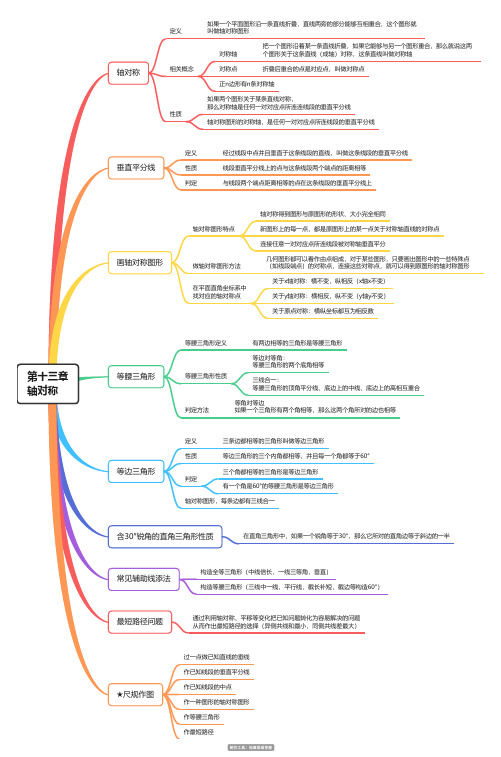
第十三章轴对称轴对称定义如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形相关概念对称轴把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴对称点折叠后重合的点是对应点,叫做对称点正n边形有n条对称轴性质如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连连线段的垂直平分线轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线垂直平分线定义经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线性质线段垂直平分线上的点与这条线段两个端点的距离相等判定与线段两个端点距离相等的点在这条线段的垂直平分线上画轴对称图形轴对称图形特点轴对称得到图形与原图形的形状、大小完全相同新图形上的每一点,都是原图形上的某一点关于对称轴直线的对称点连接任意一对对应点所连线段被对称轴垂直平分做轴对称图形方法几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形在平面直角坐标系中找对应的轴对称点关于x轴对称:横不变,纵相反(x轴x不变)关于y轴对称:横相反,纵不变(y轴y不变)关于原点对称:横纵坐标都互为相反数等腰三角形等腰三角形定义有两边相等的三角形是等腰三角形等腰三角形性质等边对等角:等腰三角形的两个底角相等三线合一:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合判定方法等角对等边如果一个三角形有两个角相等,那么这两个角所对的边也相等等边三角形定义三条边都相等的三角形叫做等边三角形性质等边三角形的三个内角都相等,并且每一个角都等于60°判定三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形轴对称图形,每条边都有三线合一含30°锐角的直角三角形性质在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半常见辅助线添法构造全等三角形(中线倍长,一线三等角,垂直)构造等腰三角形(三线中一线,平行线,截长补短,截边等构造60°)最短路径问题通过利用轴对称、平移等变化把已知问题转化为容易解决的问题从而作出最短路径的选择(异侧共线和最小,同侧共线差最大)★尺规作图过一点做已知直线的垂线作已知线段的垂直平分线作已知线段的中点作一种图形的轴对称图形作等腰三角形作最短路径。
八年级上册数学第14章思维导图

八年级上册数学第14章思维导图引言本文档是八年级上册数学第14章的思维导图,通过思维导图的形式,对该章节的知识点进行整理和归纳,帮助学生更好地理解和掌握这一章的内容。
思维导图概述思维导图是一种以图形化的方式表达和展示知识结构的工具。
它通过主题、分支、关键词等元素的组织和连接,使复杂的知识体系变得简洁、逻辑清晰。
本文档的思维导图以主题为节点,分支为关联的知识点,结构分层明确,帮助读者更好地理解和记忆。
第14章思维导图主题1:代数基础• 1.1 代数运算符– 1.1.1 加法和减法– 1.1.2 乘法和除法• 1.2 代数式– 1.2.1 代数式的定义– 1.2.2 代数式的计算• 1.3 代数方程– 1.3.1 代数方程的定义– 1.3.2 解代数方程的方法主题2:一元一次方程• 2.1 一元一次方程的概念– 2.1.1 一元一次方程的定义– 2.1.2 一元一次方程的例子• 2.2 一元一次方程的解法– 2.2.1 一元一次方程的解法步骤– 2.2.2 一元一次方程的解法示例• 3.1 一元一次不等式的概念– 3.1.1 一元一次不等式的定义– 3.1.2 一元一次不等式的例子• 3.2 一元一次不等式的解法– 3.2.1 一元一次不等式的解法步骤– 3.2.2 一元一次不等式的解法示例主题4:利用一元一次方程和不等式解实际问题• 4.1 实际问题的转化– 4.1.1 实际问题的描述– 4.1.2 实际问题的转化为方程或不等式• 4.2 解实际问题的步骤和方法– 4.2.1 解实际问题的步骤– 4.2.2 解实际问题的方法示例• 5.1 一元一次方程组的概念– 5.1.1 一元一次方程组的定义– 5.1.2 一元一次方程组的例子• 5.2 一元一次方程组的解法– 5.2.1 一元一次方程组的解法步骤– 5.2.2 一元一次方程组的解法示例主题6:平方根与算术平方根• 6.1 平方根的概念– 6.1.1 平方根的定义– 6.1.2 平方根的例子• 6.2 平方根的性质– 6.2.1 平方根的基本性质– 6.2.2 平方根的运算法则• 6.3 算术平方根的计算– 6.3.1 算术平方根的定义– 6.3.2 算术平方根的计算方法总结本文档通过思维导图的形式概括了八年级上册数学第14章的重要知识点。
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作√a和√a。
0的平方根是0。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
立方根只有一个。
3. 算术平方根:正数a的正的平方根,记作√a,称为a的算术平方根。
4. 立方根的性质:①正数的立方根是正数;②负数的立方根是负数;③0的立方根是0。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:①正实数;②负实数;③零。
3. 实数的运算:实数的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
三、二次根式1. 二次根式的概念:形如√a的式子,其中a≥0,称为二次根式。
2. 二次根式的性质:①√a²=a(a≥0);②(√a)²=a(a≥0);③√ab=√a√b(a≥0,b≥0);④√a²+b²=√a²+√b²(a≥0,b≥0)。
3. 二次根式的运算:二次根式的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
四、一元二次方程1. 一元二次方程的概念:形如ax²+bx+c=0(a≠0)的方程,称为一元二次方程。
2. 一元二次方程的解法:①配方法;②求根公式法;③因式分解法。
3. 一元二次方程的根的判别式:判别式△=b²4ac,当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根。
五、不等式1. 不等式的概念:表示不相等关系的式子称为不等式。
2. 不等式的性质:①两边同时加上或减去同一个数,不等号方向不变;②两边同时乘以或除以同一个正数,不等号方向不变;③两边同时乘以或除以同一个负数,不等号方向改变。
人教版八年级上册 中国近代史思维导图
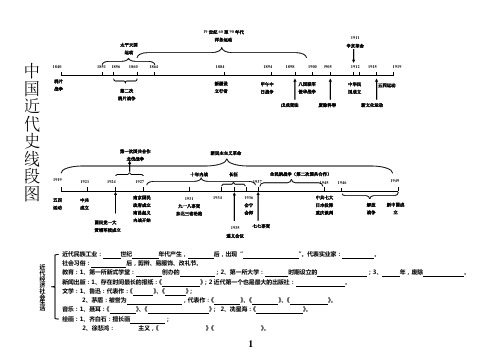
1919第二次 鸦片战争八国联军 侵华战争1905十年内战1919五四 运动1949新中国成立1921国民党一大 黄埔军校成立新民主主义革命中共 成立19241927第一次国共合作北伐战争南京国民 政府成立 南昌起义 内战开始19371931 九一八事变 东北三省沦陷1934 1935 遵义会议1936 会宁 会师1945 长征全民族战争(第二次国共合作)七七事变中共七大 日本投降 重庆谈判1946解放 战争1840 18941860甲午中 日战争鸦片 战争1856190019世纪60至90年代洋务运动戊戌变法18981884新疆设 立行省废除科举五四运动中华民 国成立1915新文化运动18511864太平天国 运动1911 辛亥革命1912中国近代史线段图近代民族工业: 世纪 年代产生, 后,出现“ ”。
代表实业家: 。
社会习俗: 后,剪辫、易服饰、改礼节。
教育:1、第一所新式学堂: 创办的 ;2、第一所大学: 时期设立的 ;3、 年,废除 。
新闻出版:1、存在时间最长的报纸:《 》;2近代第一个也是最大的出版社: 。
文学:1、鲁迅:代表作:《 》、《 》;2、茅盾:被誉为 ,代表作:《 》、《 》、《 》。
音乐:1、聂耳:《 》、《 》; 2、冼星海:《 》。
绘画:1、齐白石:擅长画 ;2、徐悲鸿: 主义,《 》《 》。
近代经济社会生活列强侵华史一览表★中国近代化进程一览表(探索史一览表)★新文化运动(学习)宣传与《》宣传马克思主义五四运动︑中共成立︑北伐战争五四运动中共成立时间:年;导火索:;主力:;中心:;口号:、、。
第二阶段:6月5日以后,主力:;中心:;成果:初步胜利(撤曹、陆、章;释放学生;拒绝在合约签字)性质:的爱国运动。
五四精神的内涵:忧国忧民、热爱祖国、积极创新、探索科学的爱国主义精神。
意义:登上历史舞台;的开端;推动了的传播。
成立的条件:①干部条件、思想基础:后的传播;先驱:;成立的标志:年月日,的召开。
数学八年级上册第一章思维导图
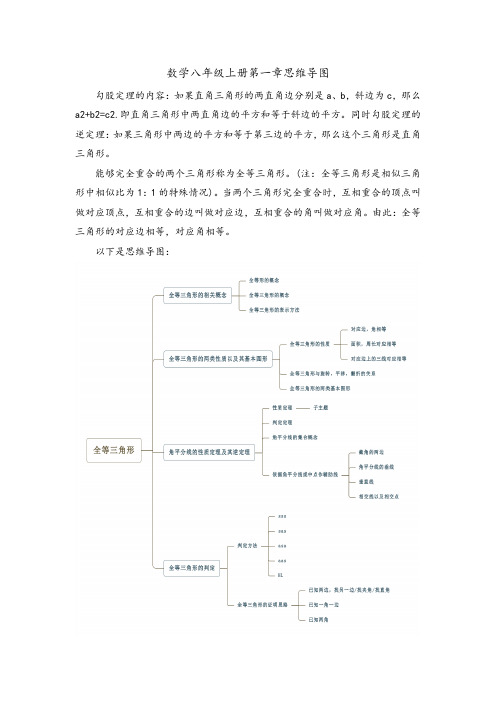
数学八年级上册第一章思维导图
勾股定理的内容:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方。
同时勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
能够完全重合的两个三角形称为全等三角形。
(注:全等三角形是相似三角形中相似比为1:1的特殊情况)。
当两个三角形完全重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
由此:全等三角形的对应边相等,对应角相等。
以下是思维导图:
全等三角形的判定定理:
⑴边边边:三边对应相等的两个三角形全等。
⑵边角边:两边和它们的夹角对应相等的两个三角形全等。
⑶角边角:两角和它们的夹边对应相等的两个三角形全等。
⑷角角边:两角和其中一个角的对边对应相等的两个三角形全等。
⑸斜边、直角边:斜边和一条直角边对应相等的两个直角三角形全等
1、其中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3、当图中出现两个以上等边三角形时,应首先考虑用SAS找全等三角形。
4、用在实际中,一般我们用全等三角形测相等的距离。
以及相等的角,可以用于工业和军事。
八年级地理上册思维导图-第四章中国的经济发展-知犀思维导图

中国的经济发展交通运输交通运输方式的选择公路运输方便、机动灵活、速度快运费较贵、运量较小铁路运输速度快、运费低、运量大、连续性好灵活性较差、短途运输成本高航空运输速度最快、舒适、安全运量最小、运费最高水路运输运费最低、运量最大速度最慢、受天气影响较大管道运输方便、速度快运量大、运费低、损耗小、安全可靠、连续性强、管理方便灵活性差选择合适得交通运输客运根据旅客的出行目的和交通运输方式的特点进行选择货运贵重或急需的货物且数量不大的,多由航空运送易死亡变质的活物、鲜货,短程可由公路运送,远程而又数量大的可用铁路上的专用车大宗笨重的货物,远距离运输,尽可能利用水运或铁路运输我国铁路干线的分布我国交通运输分布特点:分布不均,东部密集,西部稀疏,密度相差很大最重要的运输方式:铁路运输主要铁路线“三横五纵”南北向的铁路线京沪线京九线京哈——京广线焦柳线宝成——成昆线东西向的铁路线京包——包兰线陇海——兰新线沪杭线——浙赣线——湘黔线——贵昆线在若干条交通运输线交叉的地方,形成了重要的交通运输枢纽,分为单一型和综合型农业农业及其重要性农业的主要部门依据劳动对象的不同,分为种植业、林业、畜牧业、渔业、副业五个部门我国农业的地区分布主要表现为东西、南北和垂直三个方面的差异,大致以400毫米等降水量线为界,把我国分为东部农耕区和西部牧业区东部地区农业分布种植业东部半湿润和湿润的平原地区林业东北和西南的天然林区,以及东南部的人工林区渔业东部沿海地区是我国海洋捕捞和海洋养殖的基地长江中下游地区是我国淡水渔业最发达的地区西部地区农业分布天然草场广布,以畜牧业为主,种植业只分布在有灌溉水源的平源、河谷和绿洲我国四大牧区:内蒙古牧区、新疆牧区、青海牧区、西藏牧区南北差异:以秦岭——淮河一线为界北方地区旱地东北平原:一年一熟华北平原:两年三熟或一年两熟南方地区水田长江中下游平原:一年两熟华南及海南岛:一年三熟我国三大产棉区:新疆南部、黄河流域、长江流域发展农业要因地制宜宜林则林地形陡峭,水土容易流失,但是发展林业可以保持水土宜粮则粮地形平坦,土壤肥沃,水源丰富,利于耕作的地方,适宜种粮宜牧则牧降水较少,但是牧草生长良好,适宜发展畜牧业宜渔则渔河湖较多的地方和沿海地区,适宜发展渔业走科技强农之路改革开放以来,我国走科技强农之路,机械化和专业化水平,生产效率不断提高依靠科技优势,大力发展高产、优质、高效、生态、安全农业,加快我国从农业大国向农业强国迈进的步伐工业工业及其重要性工业生产包括开采自然资源以及对原材料进行加工和再加工;工业是基本的物质生产部门重工业以生产生产数据为主的工业采矿、冶金、电力、机械、化学工业、核工业等轻工业以生产生活数据为主的工业纺织、食品、皮革、造纸、钟表、家用电器等我国工业的分布空间分布沿铁路线京广、京沪、哈大等铁路沿线形成许多工业基地沿河黄河流域是能源开发的重要工业带长江沿线形成了以上海、南京、武汉、重庆等城市为中心的沿江经济发达地带沿海集中了4个工业基地、5个经济特区、14个沿海开放城市等工业最发达的经济核心区四大工业基地辽中南地区大连、沈阳、鞍山我国著名的重工业基地京津唐地区北京、天津、唐山我国北方最大的综合性工业基地沪宁杭地区上海、南京、杭州我国最大的综合性工业基地珠江三角洲广州、深圳、珠海以轻工业为主得综合性工业基地蓬勃发展的高新技术产业涵义以新的科学技术为基础,电子和信息为龙头,产品科技含量高的新兴产业特点科技人员比例大、研究开发费用高、产品更新换代快布局多依附于大城市,呈现出大分散、小集中的分布特点我国高新技术产业的地区发展方向的差导沿海——科技园区型沿边——贸易导向型内陆——国防军工型。
