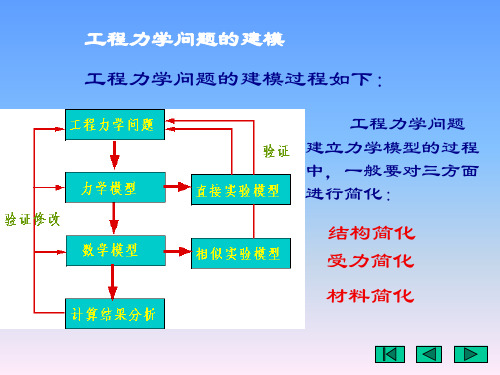
第一篇1力学模型的建立

m1 m1l m sin j m2l sin j m3 0 2 l sin j m1 y1 m2 y2 m3 y3 2 yC 2 m1 m2 m3 m1 m2 m3 m1 m2 m3
2.转动惯量
仅用质心的概念还不能完全反映质点系内部质量 分布的情况。引入转动惯量的概念就能够全面描述质 点系的质量分布情况。 通常使用质点系对轴的转动惯量。质点系内每个 质点的质量与它们到某一轴线（如z轴）的距离的平 方的乘积之和定义为质点系对该轴的转动惯量，用Jz 表示：
分布）；以及便于描述物体运动状态的量：形状与 大小。 力学中使用的物体模型有： 质点：忽略物体形状与大小，视为一个有质量的点。 自由度：确定物体在空间位置的独立坐标数目。 一个自由的质点有三个自由度。
质点系：由有限个或无限个有着一定联系的质点组成。
刚体：各质点的距离保持不变的质点系。 刚体的形状大小是不会发生改变的，它是会发生 变形的实际物体在理论力学中的理想化模型。 一个自由刚体有六个自由度
常用均质直杆、圆盘、圆环对质心轴的转动惯量。
1 2 ml 12
例2–3 如图所示，已知质量为m、半径为R的均质薄圆 环对于中心轴的转动惯量是mR2；质量为m、长度为l的 均质细直杆对于质心轴的转动惯量是
J z mR
2
1 2 J z ml 12
分别计算质量为m、半径为R的均质圆板对中心轴（过 圆心且垂直于圆板的轴）的转动惯量和此圆板对于任一 直径的转动惯量。
第2章 力学模型的建立
2.1 物体的模型
品牌、价格、 色彩、大小、 形状、耗油、 重量（质量）、 速度、保养、 材料、舒适 性、 …... 物体的诸多属性中，哪些是研究机械运动所需要的呢？
2.1.1 质点 质点系 刚体
对于研究物体机械运动的理论力学，关注的只
是物体自身与运动状态改变有关的量：质量(大小与
2


2
2
17 13 17 2
2
例2–2 图示的曲柄滑杆机构中，曲柄OA的长度OA=l,
质量为m1，质心在OA中点；滑块A的质量为m2；滑杆
BD的质量为m3，质心在E点。试求在图示位置时机构 的质心位置。 解：此机构由曲柄OA，
A O
滑块A与滑杆BD三个
j
B a
E D
物体组成，在图示坐
R 3
y
x O x
均质圆板对于同样过圆心的不同方向的轴的 转动惯量不同。
dy
刚体的转动惯量与轴的位置有关，一般工程手册中只 给出刚体对过质心的轴的转动惯量。如果需要刚体对 其它轴的转动惯量必须通过平行轴定理计算。
平行轴定理
刚体对于任一轴的转动惯量等于刚体
对于通过质心并与该轴平行的轴的转动惯量加上刚体
滚动支座与光滑接触面的约束类似
2.减少二个自由度的约束(平面约束）
y
x
光滑圆柱铰链（简称为柱铰）使受到约束的研究对象 失去了沿x、y方向移动的自由度。 在柱铰约束中，如果其中一个构件是支座，就成为 固定柱铰支座的约束模型。 向心轴承也可以简化为固定柱铰支座。
3． 减少三个自由度的约束
z
y x
光滑球铰链（简称为球铰）使受到约束的研究对象失 去了沿x、y、z三个方向移动的自由度。 止推轴承也是机器中常用的轴的支承之一，它比向心轴 承增加了一个对轴沿轴线方向移动的限制
2.1.2 质心 转动惯量
质点系的运动特性不但与它的总质量有关，还与 它的质量分布情况有关。质点系的质量分布特点用两 个基本特征量表示：质心与转动惯量。
1.质心 设有n个质点组成的质点系，其中任一个质点的质量 是mi，坐标是 xi , yi , zi 。于是定义这个质点系的质量中 心（简称质心）C的坐标 xC , yC , zC
解：（1）计算均质圆板对中心轴的转动惯量 把圆板分为无数同心的薄圆环，则薄圆环的质量为：
dm A 2rdr
圆板单位面积的质量
m A 2 R
薄圆环对中心轴的转动惯量是 2m 3 2 3 dJ O dmr 2Ar dr 2 r dr R
均质圆板对中心轴的转动惯量是
如果这有限个物体的密度相同，其中任一形体的体 积为Vi，则组成物体或物系的质心（形心）按下式计算：
Vi xi xC , V i Vi yi yC , V i Vi zi zC V i
当每一个物体是密度相同的等厚度的均质平板时，其 中任一形体的面积为Ai，则组成物体或物系的质心（形 心）可以按下式计算：
轮毂
JO2 1 2 1 2 1 2 2 r h1 r r1 h1 r1 h1 r 4 r14 0.069kg m2 2 2 2
轮辐对转轴的转动惯量要用平行轴定理计算：
JO3 1 ab 2 ab R1 r R r R r R r 1 1 1 12 4 4 2
门
手腕关节
行车梁（简支梁）
桁架
桁架由若干直杆在两端按一定的方式相互连接组 成。杆件的相互连接处称为节点。 如果连接于同一个节点处的各杆轴线汇交于一点， 节点对转动的限制很小。因此就可以把桁架的节点简 化成光滑铰链。桁架的理想模型就是若干直杆用光滑 铰链连接而成的结构。
件称为约束。约束一般是与研究对象接触的周围物体
形成的，因此常常就把这些周围的物体也叫做约束。 约束限制了物体的自由度，可以按限制自由度 的多少对约束进行分类。
2.2.2
约束模型的分类
1.减少一个自由度的约束
柔索减少研究对象沿柔索伸长方向移动的一个自由度。 光滑接触面减少研究对象沿接触面的法线方向向约束 内部移动的一个自由度。
b
在图示坐标系中，由于对称性，必有
xC 0
设y1，y2，y3分别是A1，A2，A3质心的坐标，查表可得
4R 400 y1 mm, 3 3 4(r b) 40 y2 mm, 3 y3 0
由（2–3）式，偏心块质心的坐标yC为

A1 y1 A2 y2 A3 y3 2 yC A1 A2 A3 40.01(mm) 1002 400 40 2 17 13 17 2 0 3 2 100
4.减少四个自由度的约束
z z
x
y x
y
导向轴承
万向接头
5． 减少五个自由度的约束
z z
y x
y x
带柱销夹板
导轨
6． 减少六个自由度的约束
z z
y x x y
固定端
2.2.3 建立约束模型举例 在建立约束模型时，要抓住主要因素，忽略次要 因素，进行合理的简化。主要因素是约束对研究对象 的运动限制的种类与方向，以及限制的强度。
mi xi xC , M mi yi yC , M mi zi zC M
M mi 是整个质点系的质量。
质量元的体积是dV密度是，则质量元的质量 dm dV
密度是常数时物体的质量
xdV
V ,
M V （V是物体的体积）
ydV
V ,
由上式得到物体形心的坐标计算公式：
J z mi ri 2
式中mi与ri分别是第i个质点的质量与该质点到z轴的 距离。在国际单位制中转动惯量的单位是 kg m2 。
在工程中常将转动惯量写成：
ቤተ መጻሕፍቲ ባይዱJ z m
或惯性半径。
2 z
式中m是刚体的总质量，z称为刚体对z轴的回转半径
工程中对于几何形状复杂的物体或非均质物体常用实 验方法确定其转动惯量。
2m 3 1 J O 2 r dr mR 2 2 0 R
R
dr r
O
R
（2）计算均质圆板对于任一直径的转动惯量
圆板外圆周的方程是
x y R
2 2 2
y
把圆板分为无数长度是2x，宽度是dy 的细长条，质量是
2m dm A 2xdy 2 R2 y 2 dy R
x O x
轮缘 b 轮辐
轮毂 h
a
d1 d D1 D
h1
解：把飞轮分解成轮缘、轮辐和 轮毂三个组成部分。轮缘和轮毂 可视为空心圆柱，轮辐可视为六 根细直杆。分别计算它们对转轴 的转动惯量。
轮缘 b 轮辐 a 轮毂
轮缘
1 2 1 2 1 2 2 J O1 R h R R1 h R1 h R4 R14 45.211kg m2 2 2 2
xC V yC V zC V
zdV
V
对于质量均匀的物体，其质心与形心是重合的。 当物体是密度为常数的等厚度的均质平板时，质心在 板平面上的位置与平面图形的形心一致（设平板是Oxy 面上的平面图形），有
xC
A
xdA
A ,
yC
A
ydA
A
对于由几个常见形体组成的物体的质心，或者物系 的质心，可以把每一个组成物体视为质点，用质心公 式计算。
2
R1 r 2 R1 r 2 0.193kg m2 R1 r 12 4 4
ab
整个飞轮对转轴的转动惯量为
轮缘 b 轮辐 a 轮毂
J O J O1 J O 2 6 J O 3 46.44kg m2
x
标系中分别计算它们 的质心坐标。 再由质心公式计算机 构质心坐标。
曲柄OA： 滑块A： 滑杆BD：
l x1 cos j, 2
l y1 sinj 2
x2 l cos j , x3 l cos j a,
A O
y2 l sinj y3 0
j
B a
E D
x
机构质心的坐标为