11勾股定理
勾股定理

第1讲勾股定理第一部分知识梳理1.勾股定理:直角三角形的两直角边的平方和等于斜边的平方。
若直角三角形的两条直角边为a、b,斜边为c,则a²+b²=c²。
2.勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a²+b²=c²,那么这个三角形是直角三角形。
3.满足a²+b²=c²的三个正整数,称为勾股数。
若a,b,c是一组勾股数,则ak,bk,ck(k为正整数)也必然是一组勾股数。
常用的几组勾股数有3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41等。
4.勾股定理的应用:①圆柱形物体表面上的两点间的最短距离;②长方体或正方体表面上两点间的最短距离问题。
5.直角三角形的判别:①定义,判断一个三角形中有一个角是直角;②根据勾股定理的逆定理,三角形一边的平方等于另外两边的平方和,则该三角形是直角三角形。
6.勾股定理中的方程思想:勾股定理三角形有一个直角的“形”的特征,转化为三边“数”的关系,因此它是数形结合的一个典范.对于一些几何问题,往往借助于勾股定理,利用代数方法来解决.把一条边的长设为未知数,根据勾股定理列出方程,解方程求出未知数的值,即使有时出现了二次方程,大多可通过抵消而去掉二次项。
7.勾股定理中的转化思想:在利用勾股定理计算时,常先利用转化的数学思想构造出直角三角形,比如立体图形上两点之间的最短距离的求解,解答时先把立体图形转化为平面图形,在平面图形中构造直角三角形求解。
8.拓展:特殊角的直角三角形相关性质定理。
第二部分精讲点拨考点1. 勾股定理【例1】在Rt△ABC中,已知两边长为3、4,则第三边的长为变式1 等腰三角形的两边长为10和12,则周长为______,底边上的高是________,面积是_________。
变式2 等边三角形的边长为6,则它的高是________变式3 在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边,(1)已知c=4,b=3,求a;(2)若a:b=3:4,c=10cm,求a、b。
勾股定理十种证明

勾股定理十种证明欧几里德是古典数学的代表人物,他提出的勾股定理被认为是数学史上最重要的定理之一。
勾股定理,即给定直角三角形的两条直角边a,b,其斜边的平方等于两边的平方和,即:a2+b2=c2。
今天,我们将为读者介绍十种证明勾股定理的方法。
第一种是利用重心法证明。
当定义等腰三角形ABC时,在线段AB上定义重心G。
将线段AG视为一直角三角形,AG和BG就构成直角三角形。
易知三角形AGC也是直角三角形,三角形ABC也就是一个等腰直角三角形,AG和BC就是一组等腰三角形。
易得:a2+b2=AC2+BC2,即:a2+b2=c2。
第二种是利用反证法证明。
假设勾股定理不成立,即a2+b2≠c2,那么,就会得到一条不等式:a2+b2>c2或a2+b2<c2。
因为a、b都是非负的,再加上c也是非负的,所以,有:a2>0、b2>0、c2>0,从而:a2+b2>0,由此可以得出矛盾:a2+b2>c2,但是c2>0。
这与原假设矛盾,则勾股定理成立。
第三是利用余弦定理证明。
设等腰三角形ABC的角A,B,C的对边分别为a,b,c,则有:a2=b2+c2-2bc cosA,b2=a2+c2-2ac cosB,c2=a2+b2-2ab cosC,将三式相加,可得到:2a2+2b2=2c2,从而证明勾股定理。
第四是利用边缘法证明。
由边缘定理可知,在等腰三角形ABC 中:a2=b2=c2=2S2,其中S为ABC的面积。
令α、β、γ分别为三角形ABC的内角,及对应的外接圆的半径,令ΔO为三角形ABC的外切圆,则有:α+β+γ=180°,易知:a2+b2+c2=2(α2+β2+γ2)=2R2=c2,可以证明出勾股定理。
第五种是利用角和弧法证明。
在等腰三角形ABC中,用圆弧a 表示两边a和b的连接的圆弧,一条弧的长度是直径乘以圆心角的度数,即可推得:c2=a2+2aR-b2,将c2的左边加上b2,右边减去b2,即可得到:c2=a2+b2,从而证明出勾股定理。
勾股定理常用11个公式

勾股定理常用11个公式勾股定理也叫毕达哥拉斯定理,指的是直角三角形中,任意一条直角边的平方等于另外两条边的平方之和。
勾股定理是数学中非常重要的一条定理,广泛应用于各个领域。
以下是勾股定理常用的11个公式:1. 勾股定理的一般形式在直角三角形 ABC 中,设 AB、AC 为直角边,BC 为斜边,则有:BC² = AB² + AC²2. 勾股定理的两个常见形式a. 已知直角边和斜边设直角边 AB = a,AC = b,BC = c,则有:c² = a² + b²b. 已知两条直角边设直角边 AB = a,BC = b,AC = c,则有:c² = a² + b²3. 勾股定理的逆定理如果在一个三角形中,某一边的平方等于另外两边的平方之和,那么这个三角形肯定是直角三角形,即有:若 c² = a² + b²,则三角形 ABC 是直角三角形。
4. 勾股数指满足勾股定理的整数三元组 (a, b, c),其中 a、b、c 都是正整数,称为勾股数。
例如:(3, 4, 5)、(5, 12, 13)。
5. 勾股数的生成公式生成勾股数的公式称为勾股数生成公式。
其中,m 和 n 是正整数,且 m > n,gcd(m, n) = 1,k 是任意正整数,则有:a = k × (m² - n²),b = k × (2mn),c = k × (m² + n²)6. 勾股数的性质a. 勾股数只存在于原始勾股数列中。
b. 勾股数之间不存在公因数。
c. 每个奇数都可以表示为两个勾股数之和。
d. 每个正整数都可以表示为不超过四个勾股数之和。
7. 勾股数的应用a. 构造直角三角形。
b. 计算斜线长度。
c. 解决一些证明问题。
d. 在几何光学中,勾股数用于计算光路长度。
勾股定理20种证明方法

勾股定理20种证明方法1. 最常见的勾股定理证明是基于三角形面积公式的。
利用三角形的底边与高的关系,可以将直角三角形分成两个三角形,然后应用面积公式进行计算得出勾股定理。
2. 通过向直角三角形内部引入一个圆形,利用圆的性质可以得到勾股定理。
3. 将直角三角形中的一条直角边平移到非直角边上,形成一个平行四边形,再利用平行四边形对角线的关系即可得到勾股定理。
4. 利用正弦定理和余弦定理进行推导,可以得出勾股定理。
5. 通过三角形内部的相似三角形进行推导得出勾股定理。
将直角三角形分成两个相似三角形,利用相似三角形的性质进行推导得出勾股定理。
6. 通过归纳法进行证明,即证明勾股定理对于所有自然数n都成立。
7. 利用勾股定理推导其他几何定理,例如正弦定理、余弦定理等,进而证明勾股定理。
8. 利用数学归纳法,可证勾股定理对于所有正整数n都成立。
9. 利用勾股定理证明勾股三角形的存在性,也就是存在一组自然数a、b、c,使得a²+b²=c²。
这可以通过暴力算法或递推算法来实现。
10. 利用反证法证明勾股定理。
假设勾股定理不成立,即假设存在一个直角三角形,其两条直角边的平方和不等于斜边的平方。
通过假设的前提,推导出矛盾的结论,从而证明勾股定理成立。
11. 利用勾股定理证明三角形的周长和面积公式。
将直角三角形分成两个直角三角形,利用勾股定理计算出直角边的长度,然后应用周长和面积公式。
12. 利用勾股定理证明三角形的内心与垂心之间的关系。
将直角三角形分成两个相似三角形,利用勾股定理计算出内心与垂心之间的距离。
13. 利用勾股定理证明三角形的外心与垂心之间的关系。
通过三角形的外接圆,证明外心与垂心之间的距离等于直角边之间距离的一半。
14. 利用圆的性质证明勾股定理。
将三角形中的一条直角边作为直径,表示成圆上的弦长,利用圆的定理得到勾股定理。
15. 通过三角形的相似性质,证明勾股定理。
将直角三角形分成两个与之相似的三角形,利用相似三角形的性质得到勾股定理。
勾股定理常用个公式

勾股定理常用个公式勾股定理是数学中一个非常重要的定理,它是平面几何中的基础定理,常用来求解直角三角形的边长和角度。
根据勾股定理,我们可以推导出多个相关的公式来解决各种问题。
在本篇文章中,我将介绍11个常用的勾股定理公式,每个公式都会附带一个解析和一个示例。
1.三角形斜边的长度(已知两边长度):c=√(a²+b²),其中a和b分别是直角三角形的两条直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的两条直角边的长度分别为3和4,求斜边的长度。
解析:根据公式,c=√(3²+4²)=√(9+16)=√25=5、因此,斜边的长度为52.直角三角形的直角边长度(已知斜边长度和另一直角边长度):a=√(c²-b²),其中b是已知直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的斜边长度为5,另一直角边的长度为4,求第二个直角边的长度。
解析:根据公式,a=√(5²-4²)=√(25-16)=√9=3、因此,第二个直角边的长度为33.直角三角形的直角边长度(已知斜边长度和另一直角边长度):b=√(c²-a²),其中a是已知直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的斜边长度为5,另一直角边的长度为3,求第二个直角边的长度。
解析:根据公式,b=√(5²-3²)=√(25-9)=√16=4、因此,第二个直角边的长度为44.直角三角形的面积(已知两个直角边的长度):A=1/2*a*b,其中a和b为直角三角形的两个直角边的长度。
示例:已知一个直角三角形的两个直角边的长度分别为3和4,求其面积。
解析:根据公式,A=1/2*3*4=6、因此,直角三角形的面积为65.直角三角形的周长(已知两个直角边的长度):P=a+b+c,其中a和b分别为直角三角形的两个直角边的长度,c为斜边的长度。
[数学]-专题11 勾股定理中的蕴含数学思想的典型试题(原版)
![[数学]-专题11 勾股定理中的蕴含数学思想的典型试题(原版)](https://img.taocdn.com/s3/m/96f95c62905f804d2b160b4e767f5acfa1c783d4.png)
专题11 勾股定理中的蕴含数学思想的典型试题(原卷版)第一部分典例剖析类型一方程思想(1)单勾股列方程1.(2022秋•泰兴市期末)如图,某渡船从点B处沿着与河岸垂直的路线AB横渡,由于受水流的影响,实际沿着BC航行,上岸地点C与欲到达地点A相距70米,结果发现BC比河宽AB多10米,求该河的宽度AB.(两岸可近似看作平行)2.(2021春•全南县期中)小明将一副三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知CD=3,求AC的长.3.(2022秋•运城期末)如图,∠AOB=90°,OA=18cm,OB=6cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C 处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?二、双勾股方程4.(2022秋•仪征市期中)我们规定:三角形任意一条边的“线高差”等于这条边与这条边上高的差.如图1,△ABC中,CD为BA边上高,边BA的“线高差”等于BA﹣CD,记为h(BA).(1)如图2,若△ABC中AB=AC,AD⊥BC垂足为D,AD=6,BD=4,则h(BC)=;(2)若△ABC中,∠B=90°,AB=6,BC=8,则h(AC)=;(3)如图3,△ABC中,AB=21,AC=20,BC=13,求h(AB)的值.5.(2020秋•金台区校级期末)如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE 翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,(1)求∠ECF的度数;(2)若CE=4,B′F=1,求线段BC的长和△ABC的面积.6.如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.(1)填空:△ADC是三角形;(2)若AB=15,AC=13,BC=14,求BC边上的高AE的长;(3)如图②,若∠DAC=90°,试猜想:BC、BD、AE之间的数量关系,并加以证明.类型二数形结合思想7.(2022•锡山区)如图,数轴上点A,B分别对应2,4,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C;以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是()A.4√2B.2√5C.5D.3√28.(2022春•雁塔区校级期末)为比较√13+√6与√13+6的大小,小亮进行了如下分析后作一个直角三角形,使其两直角边的长分别为√13与√6,则由勾股定理可求得其斜边长为√(√13)2+(√6)2=√13+6.根据“三角形三边关系”,可得√13+√6>√13+6.小亮的这一做法体现的数学思想是()A.分类讨论思想B.方程思想C.类比思想D.数形结合思想9.(2019秋•海州区校级月考)数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.(1)探究√x2+y2的几何意义:如图①,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,则MO=√OP2+PM2=√|x|2+|y|2=√x2+y2,因此,√x2+y2的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离OM.①√(−2)2+32的几何意义可以理解为点N1(填写坐标)与点O(0,0)之间的距离N1O;②点N2(5,﹣1)与点O(0,0)之间的距离ON2为.(2)探究√(x−1)2+(y−5)2的几何意义:如图②,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究(1)可知,A′O=√(x−1)2+(y−5)2,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB=√(x−1)2+(y−5)2,因此√(x−1)2+(y−5)2的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离.(3)探究√(x+2)2+(y−3)2的几何意义:请仿照探究二(2)的方法,在图③中画出图形,那么√(x+2)2+(y−3)2的几何意义可以理解为点C(填写坐标)与点D(x,y)之间的距离.(4)拓展应用:①√(x−1)2+(y+4)2+√(x+2)2+(y+3)2的几何意义可以理解为:点A(x,y)与点E(1,﹣4)的距离与点A(x,y)与点F(填写坐标)的距离之和.②√(x−1)2+(y+4)2+√(x+2)2+(y+3)2的最小值为(直接写出结果)类型三分类讨论思想10.(2019春•自贡期末)如图,在四边形ABCD中,AB=BC=2√2,AD=2,AB⊥BC,CD⊥AD,连接AC,点P是在四边形ABCD边上的一点;若点P到AC的距离为√3,这样的点P有()A.0个B.1个C.2个D.3个11.(如皋市期末)已知∠MAN=30°,点B在射线AN上,点C在射线AM上,且AB=12.(1)若△ABC是直角三角形,求AC的长;(2)若BC=8,求AC的长;(3)要使满足条件的△ABC唯一确定,直接写出BC的长度x的取值范围.12.(2022秋•南关区校级期末)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A出发,沿A→B方向运动,速度为每秒2cm;点Q从点B出发,沿B→C→A方向运动,速度为每秒4cm;两点同时开始运动,设运动时间为t秒.(1)①Rt△ABC斜边AC上的高为;②当t=3时,PQ的长为;(2)当点Q在边BC上运动时,出发几秒钟后,△BPQ是等腰三角形?(3)当点Q在边AC上运动时,直接写出所有能使△BCQ成为等腰三角形的t的值.类型四转化思想13.(2022秋•卧龙区校级期末)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=4,则AB2+CD2=.14.(2019•柯桥区模拟)如图,已知在Rt△ABC中,E,F分别是边AB,AC上的点,AE=13AB,AF=13AC,分别以BE、EF、FC为直径作半圆,面积分别为S1,S2,S3,则S1,S2,S3之间的关系是()A.S1+S3=2S2 B.S1+S3=4S2C.S1=S3=S2 D.S2=13(S1+S3)第二部分专题提升训练1.(2020春•长春期末)如图,四边形ABCD和四边形AEFG都是正方形,点B在EF上,S1=140,S2=124,EB的长为.2.(2021春•东昌府区期末)如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,且B′D=6,则BN的长是.3.如图,已知等腰△ABC的底边BC=25cm,D是腰AB上一点,连接CD,且CD=24cm,BD=7cm.(1)求证:△BDC是直角三角形;(2)求AB的长.4.如图,在长方形ABCD中,AB=3,BC=2√6,点E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.(1)求证:DF=GF;(2)求DF的长度.5.(2022•岳池县模拟)在劳技课上,老师请同学们在一张长为9cm,宽为8cm的长方形纸板上,剪下一个腰长为5cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边长上).请你帮助同学们画出图形并计算出剪下的等腰三角形的面积.(求出所有可能的情况)6.设计师要用四条线段CA,AB,BD,DC首尾相接组成如图所示的两个直角三角形图案,∠C与∠D为直角,已知其中三条线段的长度分别为1cm,9cm,5cm,第四条长为xcm,试求出所有符合条件的x的值.7.(2022秋•南关区校级期末)如图,在△ABC中,∠ACB=90°,AB=10,AC=8,点P从点A出发,以每秒2个单位长度的速度沿折线A﹣C﹣B﹣A运动,设点P的运动时间为t秒(t>0).(1)求BC的长.(2)斜边AB上的高是.(3)若点P在∠BAC的角平分线上,则t的值为.(4)在整个运动过程中,直接写出△PBC是等腰三角形时t的值.。
(完整版)勾股定理知识点+对应类型
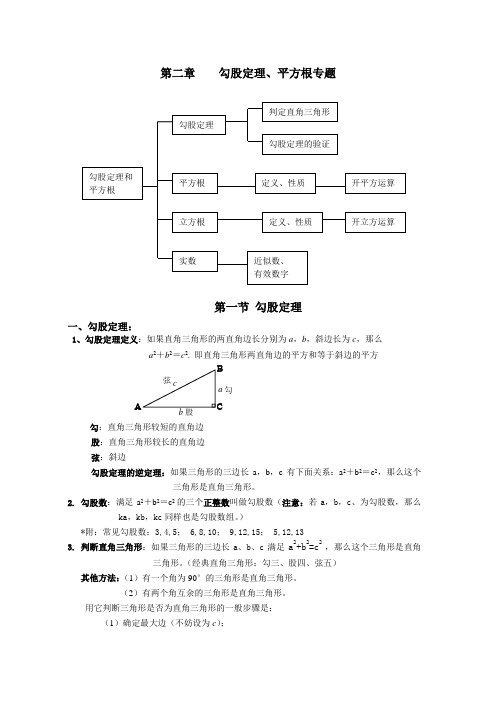
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
专题11 勾股定理的实际应用模型(原卷版)

专题11勾股定理的实际应用模型勾股定理将图形与数量关系有机结合起来,在解决实际问题和几何应用中有着广泛的应用。
运用勾股定理解决实际问题的一般步骤:(1)从实际问题中抽象出几何图形(建模);(2)确定要求的线段所在的直角三角形;(3)确定三边,找准直角边和斜边:①若已知两边,则根据勾股定理直接计算第3边;②若已知一边,则根据勾股定理列方程间接求解。
(挖掘两个未知边之间的数量关系,设出一边为未知数,把另一边用含有未知数的式子表示出来)。
模型1、梯子滑动模型相关模型背景:梯子滑动、绳子移动等。
解题关键:梯子的长度为不变量、墙与地面垂直。
梯子滑动模型解题步骤:1)运用勾股定理求出梯子滑动之前在墙上或者地面上的距离;2)运用勾股定理求出梯子滑动之后在墙上或者地面上的距离;3)两者相减即可求出梯子在墙上或者地面上滑动的距离。
例1.(2023春·安徽亳州·八年级校考期中)风华中学八年级(2班)小明同学和他的好朋友小亮一起利用所学知识完成下面的操作,如图,梯子AB斜靠在墙角MON处,4mAB=,梯子底端离墙角的距离 2.4mBO=.(1)求这个梯子顶端A距地面有多高;(2)上下移动梯子的过程中,小明发现梯子上总有一个定点到墙角O的距离始终是不变,你能说出这个点并说明其中的道理吗?(3)若梯子顶端A下滑的距离为m a,底端B向左滑b,小亮认为a与b的值始终相等,小明认为b可能比a的值大,也可能比a的值小,也有可动的距离为m能相等.你认为他们两个谁说的正确,请说明理由.A.2m B.2.5m例3.(2023秋·河南郑州·八年级校考期末)图中的两个滑块平的滑道上滑动.开始时,滑块A时,滑块B滑动了厘米.例4.(2023春·重庆·八年级专题练习)位于沈阳周边的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A子拉船移动,开始时绳子AC的长为D的位置,问此时游船移动的距离模型2、轮船航行模型相关模型背景:轮船航行等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理
一、勾股定理
在直角三角形中,三边长为a、b、c,其中c为斜边,则a2+b2=c2.
如:已知Rt△ABC中,三边长为a、b、c,其中a=3,b=4,则c=__________.
答案:.
二、直角三角形的性质
(1)两锐角互余;
(2)Rt△ABC中,c为斜边,则a2+b2=c2.
(3)如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半,三边长为a,,2a.(4)等腰直角三角形三边长分别为a,a,.
例1、如图,在△ABC中,CD⊥AB于D,若AB=5,,∠BCD=30°,求AC的长.
解:
设BD=x,∵CD⊥AB,∠BCD=30°.
∴BC=2BD=2x.
在Rt△BCD中,根据勾股定理得BD2+CD2=BC2.
即.
解得x=2.
∴BD=2,∵AB=5,∴AD=3.
在Rt△ACD中,由勾股定理有
例2、如图,在△ABC中,∠C=90°,AD、BE是中线,,AD=5,求AB的长.
解:
设CE=x,CD=y,则AC=2x,BC=2y.
在Rt△ACD和Rt△BCE中,由勾股定理得
例3、如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,求MN.
解:
连接AM,
∵AB=AC,M为BC的中点.
∴AM⊥BC.BM=MC=BC=3.
在Rt△AMB中,由勾股定理得.
设CN=x,则AN=5-x
在Rt△ANM中,MN2=AM2-AN2=42-(5-x)2.
在Rt△CNM中,MN2=MC2-CN2=32-x2.
∴32-x2=42-(5-x)2,解得.
.
方法2:由面积法得:AM·MC=MN·AC.
例4、如图,在△ABC中,∠A=90°,P是AC的中点,PD⊥BC于D,BC=9,DC=3,求AB的长.
解:
连结PB,BD=BC-DC=6.
在Rt△BDP和Rt△PDC中
PD2=BP2-BD2,PD2=PC2-DC2.
∴BP2-BD2=PC2-DC2.
∴BP2-PC2=BD2-DC2=36-9=27.
在Rt△ABP中,AB2=BP2-AP2.
∵AP=PC.
∴AB2=BP2-PC2=27.
.
例5、如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.
解:
如图,延长AD、BC交于点E.
∵∠B=90°,∠A=60°,∴∠E=30°.
∴AE=2AB=4.
在Rt△ABE中,由勾股定理得.
同步测试
一、选择题
1、如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿直线AC折叠,点B落在点E
处,AE交DC于点F,若,则AD的长为()
A.4cm B.5cm
C.6cm D.7cm
二、填空题
2、在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对应的边分别是a、b、c.
(1)若a=3cm,b=5cm,则c=__________.
(2)若a=8cm,c=17cm,则b=__________.
(3)若a︰b=3︰4,c=10cm,则a=__________,b=__________.
3、分别以直角三角形的三边为边向形外作正方形,如图中所示的正方形A的面积
是__________,B的面积是__________.
4、在Rt△ABC中,斜边AB=2cm,则AB2+BC2+CA2=__________cm2.
5、一个直角三角形的两边长分别为3cm和4cm,则它的第三边长为__________.
6、已知:直角三角形的两条直角边长分别为6cm、8cm,那么斜边上的高为
__________.
7、矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B和点D重合,
折痕为EF,则DE=__________cm.
8、如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,
AD、BC是母线.若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是__________(结果保留根式).
三、解答题
9、如图所示,铁路上有A、B两点(看做直线上两点)相距40千米,C、D为两村
庄(看做两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,现在要在铁路旁修建一个煤栈E,使得C、D两村到煤栈的距离相等,问煤栈应建在距A点多少千米处?
10、如图所示,地面上有一个长方体,一只蜘蛛在这个长方体的顶点A处,一滴
水珠在这个长方体的顶点C′处,已知长方体的长为6m,宽为5m,高为3m,蜘蛛
要沿着长方体的表面从A处爬到C′处,沿着怎样的路线爬行的距离最短?你能求
出这个最短距离吗?
答案:1、C 2、(1);(2)15cm;(3)6cm,8cm 3、25;256 4、8 5、5cm或
6、4.8cm 点拨:设斜边上的高为h,.
7、点拨:设DE=BE=x cm,则AE=(10-x)cm,∴(10-x)2+42=x2. 8、
9、AE2+242=(40-AE)2+162,解得AE=16(千米) 10、将长方体上面展开并和前面在同一平面上,则蜘蛛沿对角线AC′爬行距离最短,最短距离是
课外拓展
例、国家电力总公司为了改善农村用电电费过高的现状,目前正在全国各地农村进
行电网改造,莲花村六组有四个村庄,A、B、C、D正好位于一个正方形的四个顶点,
现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图中的实线部
分.请你帮助计算一下,哪种架设方案最省电线.(以下数据可供参考:
)
解:
不妨设正方形的边长为1(也可以设为a),则图(1)、(2)中的总线路长分别为
AD+AB+BC=3,AB+BC+CD=3.
图(3)中,总线路长为AC+BD==2.828.
图(4)中,延长EF交BC于点H,则FH⊥BC,BH=HC.
由∠FBH=30°,BH=及勾股定理,得
EA=ED=FB=FC=,FH=.
∴EF=1-2FH=1-.
此时,总线路长为4EA+EF=.
显然,3>2.828>2.732,
∴图(4)的连结线路最短,即图(4)的架设方案最省电线.
点评:
这里是逐一计算四条线路的长度,并加以比较,选出最短的方案.在方案(4)中注意作铺助线,构成直角三角形,再运用勾股定理.
中考分析
例1、如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
分析:
方法一、(1)如图①
(2)证明:大正方形的面积表示为,
大正方形的面积也可表示为,
,,
.即直角三角形两直角边的平方和等于斜边的平方.
方法二、(1)如图②
(2)证明:大正方形的面积表示为:,
又可以表示为:,
,,
.即直角三角形两直角边的平方和等于斜边的平方.
例2、有一块直角三角形的绿地,量得两直角边长分别为现在要将绿地扩充成等腰三角形,且扩充部分是以为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
分析:
在中,
由勾股定理有:,扩充部分为扩充成等腰应分以下三种情况.
①如图1,当时,可求
得的周长为32m.
②如图2,当时,可求
由勾股定理得:,得的周长为
③如图3,当为底时,设则由勾股定理得:,得的周长为。
