2020年人教版七年级数学上册 课时作业本12 整式的加减-代数式(含答案)
人教版-七年级上册-数学-第二章-整式-的加减知识点-例题-练习题-(含答案)

七年级上册第二章整式知识点例题(含答案)第一部分:知识点与例题一.整式1.单项式:都是数字或者字母的积(单独一个数字或字母也是单项式)①单项式中的数字因数叫做这个单项式的系数②一个单项式中,所有字母的指数的和叫做这个单项式的指数。
如:10x2y3z4的指数为9,叫做九次单项式2.多项式:几个单项式的和叫做多项式,其中每个单项式叫做多项式的项,不含字母的叫做常数项;多项式里最高项的次数叫做这个多项式的项。
(这个要与单项式区分开)如:x2+x+3这个多项式有三个项,分别为x2,x和常数项3,最高次是2,所以它是一个二次三项式。
3.单项式与多项式统称整数、二.整式的加减1.同类项:所含字母相同,并且相同字母的指数也相同的项,如2xy2与3 xy2是同类项练习:2xy n-2与4x m+3y2是同类项,则n=,m=2.把多项式中的同类项合并成一项,叫做合并同类项。
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变。
3.去括号后要注意的点:①如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同②如果括号外面的因数是负数,去括号后原括号内各项的符号与原来的符号相反4.一般地,几个整式相加减,如果有括号的要先去括号,然后再合并同类项例:(1)合并下面各式的同类项① x+y-4(x-y)② 5ab+3a2-4b2-(6b2+a2-3ab)(2)①求多项式(-x2+5+4x)-(5x-4+2x2)的值,其中x=3②求多项式13x-4(x2-12y2)+(-23x+y2)的值,其中x=-1,y=125. 设方程解决问题:(重点,难点)(1)一条河流的水流速度是2.5km/h,如果已知船在静水中的速度,则船在这条河流中顺水行驶和逆水行驶的速度分别要怎么表示?如果甲,乙两船在静水中的速度分别为20 km/h和35 km/h时,则它们在这条河流中顺水的速度和逆水的速度分别是多少km/h?练习:一种商品每件成本a元,按成本增加20%定出价格,每件售价多少元?后来因库存积压减价,按原价的85%出售,现售价多少钱?每件还能盈利多少元?(2)某村小麦种植的面积是a公顷,水稻种植面积是小麦种植面积的3倍,玉米种植面积比小麦种植面积少5公顷,列式表示水稻,玉米种植面积,并计算水稻种植面积比玉米种植面积大多少?(3)一架飞机无风时的航速为a km/h,风速为20 km/h,从甲地飞到乙地用了3小时,从乙地飞往甲地用了4小时,求飞机的航速a?(4)礼堂第一排有a个座位,后面每排都比前一排多一个座位,第二排有多少个座位?第三排呢?用m表示n排的座位数,m是多少?当a=20,n=19时,m是多少?第二部分:练习题教师用卷:一、精心选一选1、如果与823x y 是同类项,则代数式的值为(C )A 、0B 、-1C 、+1D 、±12、如果2222324,45M x xy y N x xy y =--=+-,则2281315x xy y --等于(D )A 、2M-NB 、2M-3NC 、3M-2ND 、4M-N3、如果22x x -+的值为7,则的值为(A )A 、52B 、32C 、152D 、答案不惟一4、如果2a b -=,3c a -=,则()()234b c b c ---+的值为(C )A 、14B 、2C 、44D 、不能确定5、的值是(C )A 、±3B 、±1C 、±1或±3D 、不能确定6、商场七月份售出一种新款书包a 只,每只b 元,营业额c 元,八月份采取促销活动,优惠广大学子,售出该款书包3a 只,每只打八折,则八月份该款书包的营业额比七月份增加(B )A 、1.4c 元B 、2.4c 元C 、3.4c 元D 、4.4c 元7、一件工作,甲单独做x 天完成,乙单独做y 天完成。
2020年人教版数学七年级上册单元测试《整式的加减》 (含答案)

单元测试《整式的加减》一、选择题1.当a=﹣2时,代数式1﹣3a2的值是( )A.﹣2B.11C.﹣11D.22.单项式的系数是( )A. B.π C.2 D.3.对于式子:,,,3x2+5x-2,abc,0,,m,下列说法正确的是( )A.有5个单项式,1个多项式B.有3个单项式,2个多项式C.有4个单项式,2个多项式D.有7个整式4.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )A.这个多项式是五次四项式B.四次项的系数是7C.常数项是1D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+15.若关于x的多项式(a-4)x3-x b+x-ab为二次三项式,则当x=-1时,这个二次三项式的值是( )A.-8B.-10C.-12D.-146.给出下列判断:①单项式5×103x2的系数是5;②x﹣2xy+y是二次三项式;③多项式﹣3a2b+7a2b2﹣2ab+1的次数是9;④a是相反数是-a;⑤几个有理数相乘,当负因数有奇数个时,积为负.其中判断正确的是( )A.1个B.2个C.3个D.4个7.用代数式表示“a与b的平方和”,正确的是( )A.a+b2B.a2+bC.(a+b)2D.a2+b28.多项式3x3﹣2x2y2+x+3是( )A.三次四项式B.四次四项式C.三次三项式D.四次三项式9.如果多项式是关于的三次三项式,则ab的值是( )10.已知m,n为常数,代数式2x4y+mx|5-n|y+xy化简之后为单项式,则m n的值共有( )A.1个B.2个C.3个D.4个11.x2+ax﹣y﹣(bx2﹣x+9y+3)的值与x的取值无关,则﹣a+b的值为( )A.0B.﹣1C.﹣2D.212.“数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4,乙烷的化学式是C2H6,丙烷的化学式是C3H8,…,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )A.C n H2n+2B.C n H2nC.C n H2n﹣2D.C n H n+3二、填空题13.已知“a比b大2”,则a﹣b= ,代数式2a﹣2b﹣3的值为.14.若﹣2x6y2m与﹣5x n+9y6是同类项,那么n m的值为_________.15.单项式的系数是___________,次数是___________.16.若关于x,y的多项式4xy3–2ax2–3xy+2x2–1不含x2项,则a=__________.17.-xy的次数是,2ab+3a2b+4a2b2+1是次项式.18.若多项式3x n+2﹣x2﹣n+4是三次三项式,则代数式3n2﹣[7n﹣(4n﹣3)﹣2n2]= .三、解答题19.化简:3(m﹣5n+4mn)﹣2(2m﹣4n+6mn)20.化简:2x2﹣[7x﹣(4x﹣3)﹣3x2]21.化简:3(2x2-y2)-2(3y2-2x2)22.化简:﹣(3x2﹣3xy)+2(﹣2xy+2x2)23.初一年级学生在7名教师的带领下去公园秋游,公园的门票为每人20元.现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.(1)若有m名学生,用代数式表示两种优惠方案各需多少元?(2)当m=50时,采用哪种方案优惠?(3)当m=400时,采用哪种方案优惠?24.今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环保意识,节约用水,某校数学教师编制了一道应用题:为保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:(1)若某用户六月份用水量为18吨,求其应缴纳的水费;(2)记该用户六月份用水量为吨,试用含的代数式表示其所需缴纳水费y(单位:元).25.已知A=2x2+3xy+2x﹣1,B=x2+xy+3x﹣2.(1)当x=y=﹣2时,求A﹣2B的值;(2)若A﹣2B的值与x无关,求y的值.26.某商场销售一种西装和领带,西装每套定价800元,领带每条定价200元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一套西装送一条领带;方案二:西装和领带都按定价的90%付款.现某客户要到该商场购买西装2套,领带x条(x>2).(1)若该客户按方式一购买,需付款元(用含x的式子表示);若该客户按方式二购买,需付款元.(用含x的式子表示)(2)若x=5,通过计算说明此时按哪种方案购买较为合算?(3)当x=5时,你能给出一种更为省钱的购买方案吗?请直接写出你的购买方案,并算出所需费用.27.已知A=2x2-3xy+y2+2x+2y,B=4x2-6xy+2y2-3x-y.(1)当x=2,y=-0.2时,求B-2A的值.(2)若∣x-2a∣+(y-3)2=0,且B-2A=0,求a的值.参考答案1.答案为:C.2.答案为:D3.答案为:C4.答案为:B5.答案为:B6.答案为:B7.答案为:D.8.答案为:B9.答案为:B10.答案为:C11.答案为:D12.答案为:A13.答案为:2,1.14.答案为:-2715.答案为:,六.16.答案为:117.答案为:2、4、四;18.答案为:四;五19.原式=3m﹣15n+12mn﹣4m+8n﹣12mn=﹣m﹣7n.20.原式=2x2﹣(7x﹣4x+3﹣3x2)=2x2﹣7x+4x﹣3+3x2=(2x2+3x2)+(﹣7x+4x)﹣3=5x2﹣3x﹣3.21.原式=6x2-3y2-6y2+4x2 =10x2-9y2.22.原式=﹣3x2+3xy﹣4xy+4x2=x2﹣xy;23.解:(1)甲方案需要的钱数为:,乙方案需要的钱数为:;(2)当m=50时,乙方案:855(元),甲方案:800(元),∵800<855,∴甲方案优惠;(3)当m=400时,乙方案:6105(元),甲方案:8400(元),∵6105<8400,∴乙方案优惠.24.解:(1)∵10<18<50,∴应缴纳水费为31元;(2)x≤10吨时,y=1.5x,10<x≤m时,y=2x-5,x>m时,y=2x-m-5.25.解:A﹣2B=(2x2+3xy+2x﹣1)﹣2(x2+xy+3x﹣2)=xy﹣4x+3,(1)当x=y=﹣2时,A﹣2B=(﹣2)×(﹣2)﹣4×(﹣2)+3=15;(2)A﹣2B=xy﹣4x+3=(y﹣4)x+3∵A﹣2B的值与x无关,∴y﹣4=0,解得:y=4.26.解:(1)客户要到该商场购买西装2套,领带x条(x>2).方案一费用:200(x-2)+1600=200x+1200;方案二费用:(200x+1600)×90%=180x+1440;(2)当x=5时,方案一:200×5+1200=2200(元)方案二:180×5+1440=2340(元)所以,按方案一购买较合算.(3)先按方案一购买2套西装获赠送2条领带,再按方案二购买3条领带. 所需费用为1600+200×3×90%=2140(元),是最省钱的购买方案.27.解:(1)∵A=2x2-3xy+y2+2x+2y,B=4x2-6xy+2y2-3x-y,∴B-2A=-7x-5y当x=2,y=0.2时,B-2A=-13.(2)∵|x﹣2a|+(y﹣3)2=0,∴x-2a=0,y-3=0,∴x=2a,y=3,∵B-2A=a,∴-14a-15=a,解得a=-1.。
2020人教版七年级数学上册 课时作业本《整式的加减-合并同类项》(含答案)

2020人教版七年级数学上册课时作业本《整式的加减-合并同类项》一、选择题1.π2与下列哪一个是同类项()A.ab B.ab2 C.22 D.m2.当x=﹣4时,代数式﹣x3﹣4x2﹣2与x3+5x2+3x﹣4的和是()A.0 B.4 C.-4 D.-23.下列计算正确的是( )A.2x+3y=5xyB.2a2+2a3=2a5C.4a2﹣3a2=1D.﹣2ba2+a2b=﹣a2b4.把(x﹣3)2﹣2(x﹣3)﹣5(x﹣3)2+(x﹣3)中的(x﹣3)看成一个因式合并同类项,结果应是()A.﹣4(x﹣3)2﹣(x﹣3)B.4(x﹣3)2﹣x(x﹣3)C.4(x﹣3)2﹣(x﹣3)D.﹣4(x﹣3)2+(x﹣3)5.代数式7a3﹣6a3b+3a2b+3a2+6a3b﹣3a2b﹣10a3的值()A.与字母a,b都有关B.只与a有关C.只与b有关D.与字母a,b都无关6.下面四个整式中,不能表示图中阴影部分面积的是( )A.(x+3)(x+2)﹣2xB.x(x+3)+6C.3(x+2)+x2D.x2+5x7.下面的计算正确的是()A.6a﹣5a=1B.a+2a2=3a3C.﹣(a﹣b)=﹣a+bD.2(a+b)=2a+b8.计算2xy2+3xy2的结果是()A.5xy2 B.xy2 C.2x2y4 D.x2y4二、填空题9.若单项式mx2y与单项式5x n y的和是﹣3x2y,则m+n .10.若﹣4x a y+x2y b=﹣3x2y,则a+b= .11.若2005x n+7与2006x2m+3是同类项,则(2m﹣n)2= .12.已知代数式2x2+ax﹣y+6﹣2bx2+3x﹣5y﹣1的值与字母x的取值无关,则的值为.三、解答题13.已知代数式﹣3x2+2y﹣mx+5﹣3nx2+6x﹣20y的值与字母x的取值无关,求的值.参考答案1.答案为:C.2.答案为:D.3.D4.答案为:A.5.答案为:B.6.答案为:D.7.C8.答案为:A.9.答案为:﹣610.答案为:3.11.答案为:16.12.答案为:-.13.解:代数式﹣3x2+2y﹣mx+5﹣3nx2+6x﹣20y=(﹣3﹣3n)x2+(6﹣m)x﹣18y+5,∵结果与字母x的取值无关,∴﹣3﹣3n=0,6﹣m=0,解得n=﹣1,m=6,则m2﹣2mn﹣n5=×36﹣2×6×(﹣1)﹣×(﹣1)5=12+12+=24.。
人教版初中七年级数学上册第二章《整式的加减》经典习题(含答案解析)

1.如果,A B 两个整式进行加法运算的结果为3724x x -+-,则,A B 这两个整式不可能是( )A .3251x x +-和3933x x ---B .358x x ++和31212x x -+-C .335x x -++和341x x -+-D .3732x x -+-和2x -- C解析:C【分析】由整式的加法运算,把每个选项进行计算,再进行判断,即可得到答案.【详解】解:A 选项、333251933724x x x x x x +----=-+-,不符合题意;B 选项、333581212724x x x x x x ++-+-=-+-,不符合题意;C 选项、333541x x x x -++-+-=3724x x -++,符合题意;D 选项、337322724x x x x x -+---=-+-,不符合题意.故选:C .【点睛】本题考查了整式的加法运算,解题的关键是熟练掌握整式加法的运算法则进行解题. 2.若2312a b x y +与653a b x y -的和是单项式,则+a b =( ) A .3-B .0C .3D .6C 解析:C【分析】 要使2312a b x y +与653a b x y -的和是单项式,则2312a b x y +与653a b x y -为同类项; 根据同类项的定义:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项,即可得到关于a 、b 的方程组;结合上述提示,解出a 、b 的值便不难计算出a+b 的值.【详解】解:根据题意可得:26{3a b a b +=-=, 解得:3{0a b ==, 所以303a b +=+=,故选:C .【点睛】本题考查了同类项的定义,掌握同类项的定义是解题的关键.3.某公司今年2月份的利润为x万元,3月份比2月份减少8%,4月份比3月份增加了10%,则该公司4月份的利润为(单位:万元)()A.(x﹣8%)(x+10%)B.(x﹣8%+10%)C.(1﹣8%+10%)x D.(1﹣8%)(1+10%)x D解析:D【分析】首先利用减小率的意义表示出3月份的利润,然后利用增长率的意义表示出4月份的利润.【详解】解:由题意得3月份的产值为(1﹣8%)x,4月份的产值为(1﹣8%)(1+10%)x.故选:D.【点睛】本题考查了列代数式,正确理解增长率以及下降率的定义是关键.4.某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为x,则该文具店五月份销售铅笔的支数是()A.100(1+x)B.100(1+x)2C.100(1+x2)D.100(1+2x)B解析:B【解析】试题分析:设出四、五月份的平均增长率,则四月份的市场需求量是100(1+x),五月份的产量是100(1+x)2.故答案选B.考点:列代数式.5.如图,用若干大小相同的黑白两种颜色的长方形瓷砖,按下列规律铺成一列图案,则第7个图案中黑色瓷砖的个数是()A.19 B.20 C.21 D.22D解析:D【分析】观察图形,发现:黑色纸片在4的基础上,依次多3个;根据其中的规律,用字母表示即可.【详解】第个图案中有黑色纸片3×1+1=4张第2个图案中有黑色纸片3×2+1=7张,第3图案中有黑色纸片3×3+1=10张,…第n个图案中有黑色纸片=3n+1张.当n=7时,3n+1=3×7+1=22.故选D.【点睛】此题考查规律型:图形的变化类,解题关键在于观察图形找到规律.6.下列计算正确的是( )A .﹣1﹣1=0B .2(a ﹣3b )=2a ﹣3bC .a 3﹣a=a 2D .﹣32=﹣9D 解析:D【分析】根据有理数的减法、去括号、同底数幂的乘方即可解答.【详解】解:A .﹣1﹣1=﹣2,故本选项错误;B .2(a ﹣3b )=2a ﹣6b ,故本选项错误;C .a 3÷a =a 2,故本选项错误;D .﹣32=﹣9,正确;故选:D .【点睛】本题考查了去括号和简单的提取公因式,掌握去括号时符号改变规律是解决此题的关键. 7.如图,阴影部分的面积为( )A .228ab a π-B .222ab a π-C .22ab a π-D .224ab a π- C解析:C【分析】 本题首先求解矩形面积,继而求解空白部分的圆形面积,最后作差求解阴影面积.【详解】由已知得:矩形面积为2ab ,空白圆形半径为a ,故圆形面积为2a π,则阴影部分的面积为22ab a π-.故选:C .【点睛】本题考查几何图形阴影面积的求法,涉及矩形面积公式以及圆形面积公式运用,求解不规则图形面积时通常利用割补法.8.1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察图中的数字排列规律,则,,a b c 的值分别为( )1111211464115101051331151161a b c A .1,6,15a b c === B .6,15,20a b c ===C .15,20,15a b c ===D .20,15,6a b c === B 解析:B【分析】由数字排列规律可得:除去每行两端的数字外,每个数字都等于上一行的左右两个数字之和,据此解答即可.【详解】解:根据图形得:除去每行两端的数字外,每个数字都等于上一行的左右两个数字之和, 所以156a =+=,51015,101020b c =+==+=.故选:B .【点睛】本题以“杨辉三角”为载体,主要考查了与整式有关的数字类规律探索,找准规律是关键. 9.如图,填在下面各正方形中的4个数之间都有相同的规律,根据此规律,m 的值是( )A .38B .52C .74D .66 C 解析:C【分析】 分析前三个正方形可知,规律为右上和左下两个数的积减左上的数等于右下的数,且左上,左下,右上三个数是相邻的偶数.因此,图中阴影部分的两个数分别是左下是8,右上是10.【详解】解:8×10−6=74,故选:C .【点睛】本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解决本题的难点在于找出阴影部分的数.10.一个多项式与²21x x -+的和是32x -,则这个多项式为( )A .253x x -+B .21x x -+-C .253x x -+-D .2513x x -- C解析:C【分析】 根据题意列出关系式,去括号合并即可得到结果.【详解】∵一个多项式与x 2-2x+1的和是3x-2,∴这个多项式=(3x-2)-(x 2-2x+1)=3x-2-x 2+2x-1=253x x -+-.故选:C .【点睛】本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键. 11.下列变形中,正确的是( )A .()x z y x z y --=--B .如果22x y -=-,那么x y =C .()x y z x y z -+=+-D .如果||||x y =,那么x y = B 解析:B【分析】根据去括号法则、等式的基本性质以及绝对值的性质逐一判断即可.【详解】A :()x z y x z y --=-+,选项错误;B :如果22x y -=-,那么x y =,选项正确;C :()x y z x y z -+=--,选项错误;D :如果||||x y =,那么x 与y 互为相反数或二者相等,选项错误;故选:B.【点睛】本题主要考查了去括号法则、等式的基本性质与绝对值性质,熟练掌握相关概念是解题关键.12.若关于x ,y 的多项式2237654x y mxy xy -++化简后不含二次项,则m =( ) A .17 B .67 C .-67D .0B 解析:B【分析】将原式合并同类项,可得知二次项系数为6-7m ,令其等于0,即可解决问题.【详解】解:∵原式=()2236754x y m xy +-+, ∵不含二次项,∴6﹣7m =0,解得m =67. 故选:B .【点睛】 本题考查了多项式的系数,解题的关键是若不含二次项,则二次项系数6-7m=0. 13.﹣(a ﹣b +c )变形后的结果是( )A .﹣a +b +cB .﹣a +b ﹣cC .﹣a ﹣b +cD .﹣a ﹣b ﹣c B 解析:B【分析】根据去括号法则解题即可.【详解】解:﹣(a ﹣b +c )=﹣a +b ﹣c故选B .【点睛】本题考查去括号法则:括号前是“+”,去括号后,括号里的各项都不改变符号,括号前是“-”,去括号后,括号里的各项都改变符号.运用这一法则去掉括号.14.下列说法:①在数轴上表示a -的点一定在原点的左边;②有理数a 的倒数是1a ;③一个数的相反数一定小于或等于这个数;④如果a b >,那么22a b >;⑤235x y 的次数是2;⑥有理数可以分为整数、正分数、负分数和0;⑦27m ba -与2abm 是同类项.其中正确的个数为( )A .1个B .2个C .3个D .4个A解析:A【分析】根据字母可以表示任意数可判断①,根据特殊例子0没有倒数可判断②,根据负数的相反数可判断③,根据特殊例子a=1,b=-2,可判断④,根据单项式次数的定义可判断⑤,根据有理数的分类判断⑥,根据同类项的概念判断⑦.【详解】字母可以表示任意数,当a <0时,-a >0,故①错误;0没有倒数,故②错误;负数的相反数是正数,正数大于负数,故③错误;若a=1,b=-2,a b >,但是22a b <,故④错误; 235x y 的次数是3,故⑤错误; 0属于整数,故⑥这种分类不正确;27m ba -与2abm 是同类项,⑦正确,故选A.【点睛】本题考查有理数和代数式的相关概念,熟记这类知识点是解题的关键.15.已知3a b -=-,2c d +=,则()()a d b c --+的值为( )A .﹣5B .1C .5D .﹣1A解析:A【分析】先把所求代数式去掉括号,再化为已知形式把已知代入求解即可.【详解】解:根据题意:(a-d )-(b+c )=(a-b )-(c+d )=-3-2=-5,故选:A .【点睛】本题考查去括号、添括号的应用.先将其去括号化简后再重新组合,得出答案. 1.如图是用棋子摆成的“上”字:如果按照以下规律继续摆下去,第n 个“上”字需用______枚棋子. (4n+2)【分析】先数出前三个上字各所需棋子数然后规律即可解答【详解】解:∵第一个上字需用6枚棋子第二个上字需用10枚棋子第三个上字需用14枚棋子∴依次多4个∴第n 个上字需用(4n+2)枚棋子故答解析:(4n+2).【分析】先数出前三个“上”字各所需棋子数,然后规律即可解答.【详解】解:∵第一个“上”字需用6枚棋子,第二个“上”字需用10枚棋子,第三个“上”字需用14枚棋子,∴依次多4个∴第n 个“上”字需用(4n+2)枚棋子.故答案为:(4n+2).【点睛】本题主要考查了图形的变化规律,观察出哪些部分发生了变化、是按照什么规律变化的是解答本题的关键.2.请观察下列等式的规律:111=11323⎛⎫- ⎪⨯⎝⎭,1111=-35235⎛⎫ ⎪⨯⎝⎭, 1111=-57257⎛⎫ ⎪⨯⎝⎭,1111=-79279⎛⎫ ⎪⨯⎝⎭, …则1111...=133********++++⨯⨯⨯⨯______.【解析】试题 解析:50101 【解析】试题1111++++13355799101⨯⨯⨯⨯ =111111111111)()()()23235257299101-+-+-++-(=111111111++)23355799101---++-( =111)2101-( =11002101⨯ =50101. 3.某数学老师在课外活动中做了一个有趣的游戏:首先发给A 、B 、C 三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤: 第一步,A 同学拿出二张扑克牌给B 同学;第二步,C 同学拿出三张扑克牌给B 同学;第三步,A 同学手中此时有多少张扑克牌,B 同学就拿出多少张扑克牌给A 同学. 请你确定,最终B 同学手中剩余的扑克牌的张数为______.7【分析】本题是整式加减法的综合运用设每人有牌x 张解答时依题意列出算式求出答案【详解】设每人有牌x 张B 同学从A 同学处拿来二张扑克牌又从C 同学处拿来三张扑克牌后则B 同学有张牌A 同学有张牌那么给A 同学后解析:7【分析】本题是整式加减法的综合运用,设每人有牌x 张,解答时依题意列出算式,求出答案.【详解】设每人有牌x 张,B 同学从A 同学处拿来二张扑克牌,又从C 同学处拿来三张扑克牌后, 则B 同学有()x 23++张牌,A 同学有()x 2-张牌,那么给A 同学后B 同学手中剩余的扑克牌的张数为:()x 23x 2x 5x 27++--=+-+=.故答案为:7.【点睛】本题考查列代数式以及整式的加减,解题关键根据题目中所给的数量关系,建立数学模型,根据运算提示,找出相应的等量关系.4.如图,是由一些点组成的图形,按此规律,在第n个图形中,点的个数为_____.n2+2【详解】解:第1个图形中点的个数为3;第2个图形中点的个数为3+3;第3个图形中点的个数为3+3+5;第4个图形中点的个数为3+3+5+7;…第n个图形中小圆的个数为3+3+5+7+…+(2解析:n2+2【详解】解:第1个图形中点的个数为3;第2个图形中点的个数为3+3;第3个图形中点的个数为3+3+5;第4个图形中点的个数为3+3+5+7;…第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1)=n2+2.故答案为:n2+2.【点睛】本题考查规律型:图形的变化类.5.已知轮船在静水中的速度为(a+b)千米/时,逆流速度为(2a-b)千米/时,则顺流速度为_____千米/时3b【分析】顺流速度静水速度(静水速度逆流速度)依此列出代数式计算即可求解【详解】解:依题意有(千米时)故顺流速度为千米时故答案为:【点睛】本题主要考查了整式加减的应用整式的加减步骤及注意问题:1整解析:3b【分析】顺流速度=静水速度+(静水速度-逆流速度),依此列出代数式+++--计算即可求解.()[()(2)]a b a b a b【详解】解:依题意有+++--a b a b a b()[()(2)]=+++-+a b a b a b[2]=+++-+2a b a b a b=(千米/时).3b故顺流速度为3b千米/时.故答案为:3b.【点睛】本题主要考查了整式加减的应用,整式的加减步骤及注意问题:1.整式的加减的实质就是去括号、合并同类项.一般步骤是:先去括号,然后合并同类项.2.去括号时,要注意两个方面:一是括号外的数字因数要乘括号内的每一项;二是当括号外是“-”时,去括号后括号内的各项都要改变符号.6.有一列数:12,1,54,75,…,依照此规律,则第n个数表示为____.【分析】根据分母是从2开始连续的自然数分子是从1开始连续的奇数解答即可【详解】这列数可以写为因此分母为从2开始的连续正整数分子为从1开始的奇数故第n个数为故答案为:【点睛】本题考查了数字的变化规律找解析:211nn-+.【分析】根据分母是从2开始连续的自然数,分子是从1开始连续的奇数解答即可.【详解】这列数可以写为12,33,54,75,因此,分母为从2开始的连续正整数,分子为从1开始的奇数,故第n个数为211nn-+.故答案为:211nn-+.【点睛】本题考查了数字的变化规律,找出分子分母的联系,得出运算规律是解决问题的关键.7.观察下列各等式中的数字特征:53-58=53×58,92-911=92×911,107-1017=107×1017,…将所发现的规律用含字母a,b的等式表示出来是_____.-=×【分析】从大的方面看两个数的差等于两个数的积从小的方面看所有的分子都相同可设两个分母分别为ab分子用ab表示即可【详解】观察发现都是两个分数的差等于两个分数的积设第一个分式为则第二个分式的分子解析:ab-aa b+=ab×aa b+【分析】从大的方面看,两个数的差等于两个数的积.从小的方面看,所有的分子都相同,可设两个分母分别为a,b,分子用a,b表示即可.【详解】观察发现,都是两个分数的差等于两个分数的积.设第一个分式为a b,则第二个分式的分子与第一个分式的分子相同,而分母恰好是a b +,∴用含字母a b ,的等式表示出来是a b -a a b +=a b ×a a b +. 故答案为:a b -a a b +=a b ×a a b +. 【点睛】本题考查了数字类规律的探索,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.8.在括号内填上恰当的项:22222x xy y -+-=-(_____________________).【分析】根据添括号的法则解答【详解】解:故答案是:【点睛】本题考查了去括号与添括号添括号法则:添括号时如果括号前面是正号括到括号里的各项都不变号如果括号前面是负号括号括号里的各项都改变符号添括号与去解析:222x xy y -+【分析】根据添括号的法则解答.【详解】解:222222(2)x xy y x xy y -+-=--+.故答案是:222x xy y -+.【点睛】本题考查了去括号与添括号,添括号法则:添括号时,如果括号前面是正号,括到括号里的各项都不变号,如果括号前面是负号,括号括号里的各项都改变符号.添括号与去括号可互相检验.9.求值:(1)()()22232223a a a a a -++-=______,其中2a =-;(2)()()222291257127a ab ba ab b -+-++=______,其中12a =,12b =-; (3)()()222222122a b ab a b ab +----=______,其中2a =-,2b =.60【分析】先根据去括号合并同类项法则进行化简然后再代入求值即可【详解】(1)原式=当时原式=;(2)原式=当时原式=;(3)原式=【点睛】本题考查整式的化简求值掌握去括号合并同类项法则是解题的关键解析:6 0【分析】先根据去括号、合并同类项法则进行化简,然后再代入求值即可.【详解】(1)原式= 2222342268a a a a a a a --+-=-,当2a =-时,原式=()()228241620--⨯-=+=;(2)原式=222222912571272242a ab b a ab b a ab b -+---=--, 当12a =,12b =-时,原式=22111111224266222222⎛⎫⎛⎫⎛⎫⨯-⨯⨯--⨯-=+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; (3)原式=22222222220a b ab a b ab +-+--=.【点睛】本题考查整式的化简求值,掌握去括号、合并同类项法则是解题的关键.10.图中阴影部分的面积为______. 【分析】图中阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积进行计算即可【详解】解:【点睛】本题考查圆的面积计算公式熟记公式并根据题意找出阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积解析:21π4R【分析】图中阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积,进行计算即可.【详解】解:2221=()224R R S R πππ-=阴影 【点睛】本题考查圆的面积计算公式,熟记公式并根据题意找出阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积是解题关键.11.请根据给出的x ,-2,y 2组成一个单项式和一个多项式________________-2xy2;-2x+y2;【分析】根据单项式的定义和多项式的定义即可得出答案单项式的定义:数或字母的积组成的式子叫做单项式单独的一个数或字母也是单项式几个单项式的和叫做多项式每个单项式叫做多项式的项解析:-2xy 2;-2x+y 2;【分析】根据单项式的定义和多项式的定义即可得出答案.单项式的定义:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数.【详解】由x 、-2、y 2组成一个单项式,这个单项式可以为-2xy 2,由x 、-2、y 2组成一个二项式,这个二次项式可以为-2x+y 2.故答案为:-2xy 2;-2x+y 2;【点睛】此题考查单项式,多项式,解题关键在于掌握其定义.1.已知222242,325A ab b a B b a ab =--=-+,当11.5,2a b ==-时,求34B A -的值. 解析:12【分析】根据题意,先根据整式的混合运算法则化简34B A -,再将a ,b 的值代入即可.【详解】()()2222222234332544296151684B A b a ab ab b a b a ab ab b a -=-+---=-+-++=22172b a ab --, 当11.5,2a b ==-时,原式22111931172 1.5 1.517224242⎛⎫⎛⎫=⨯--⨯-⨯-=⨯-+= ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题主要考查了整式的化简求值,熟练掌握整式的混合运算法则以及有理数的运算是解决本题的关键.2.当0.2x =-时,求代数式22235735x x x x -+-+-的值。
【最新】人教版七年级数学上册第2章 整式的加减 _(第1课时)含答案.doc
用运算符号,如;+、—、×、÷、乘方等,将数或表示数的字母联结起来,所得的式子叫做代数式。
单独的一个数或一个字母,如3、a 、21也叫做代数式。
(2)分式:在代数式中,不但有除法,而且除式(或分母)中含有字母。
像这样的代数式叫做分式。
(3)单项式:不含有加减运算的整式,叫做单项式。
单独一个数或一个字母,也叫单项式。
单项式的系数:单项式里的数字因数,叫做单项式的系数。
它通常写在字母的前面。
单式的次数:一个单项式中所有字母的指数的和叫做单项式的次数。
(4)多项式:几个单项式的和叫做多项式。
)多项式里每个单项式叫做多项式的项。
多项式中不含字母的项,叫做常数项。
多项式中,次数最高的项的次数,叫做多项式的次数。
多项式里含有几项,这个多项式就叫做几项式。
多项式的次数是几,就叫做几次多项式。
3、同类项及合并同类项的法则:(1)同类项:所含字母相同,并且相同字母的指数也分别相同的项,叫做同类项。
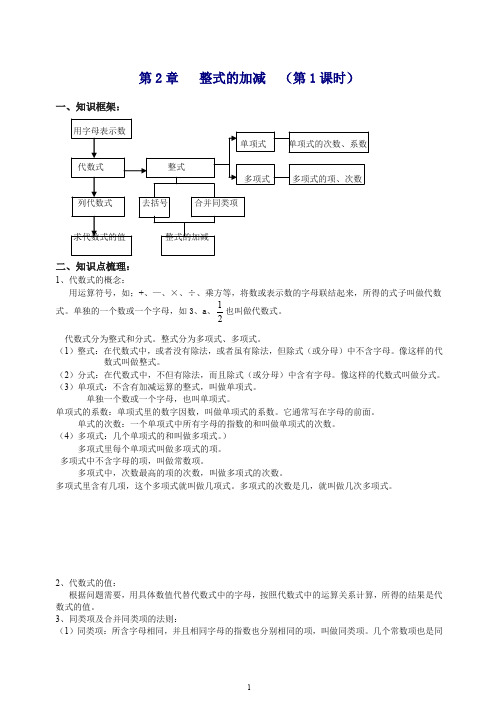
几个常数项也是同第2章 整式的加减 (第1课时)一、知识框架:二、知识点梳理:1、代数式的概念:代数式分为整式和分式。
整式分为多项式、多项式。
(1)整式:在代数式中,或者没有除法,或者虽有除法,但除式(或分母)中不含字母。
像这样的代数式叫做整式。
2、代数式的值:根据问题需要,用具体数值代替代数式中的字母,按照代数式中的运算关系计算,所得的结果是代数式的值。
类项。
(2)合并同类项:根据乘法对加法的分配律把同类项合并成一项叫做合并同类项。
(3)合并同类项的法则:同类项的系数相加,所得的结果作为系数,字母与字母的指数不变。
4、去括号:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不变号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变。
5、整式的加减:进行整式的加减运算时,如果有括号先去括号,再合并同类项。
人教版七年级上册第二章整式的加减单元作业及答案

第二章整式的加减2.1 整式知识要点1.单项式:只含有数和字母的乘积的代数式叫做单项式.•单独的一个数或一个字母也是单项式.它的本质特征在于:(1)不含加减运算;(2)可以含乘、除、乘方运算,但分母中不能含有字母.2.单项式的次数、系数:一个单项式中,•所有字母的指数和叫做这个单项式的次数.单项式中的数字因数叫做这个单项式的系数.3.多项式:几个单项式的和叫做多项式.多项式中,•每个单项式叫做多项式的项,其中不含字母的项叫常数项.一个多项式中,次数最高的项的次数,叫做这个多项式的次数.4.整式:单项和多项式统称整式.5.升幂排列:按照某个字母的次幂从高次幂到低次幂排列。
(不含该字母则是该字母的0次幂。
次幂即指该字母的次方数。
)6.降幂排列:按照某个字母的次幂从低次幂到高次幂排列。
典型例题例1.填空:(1)单项式-a2b2c3的系数是________,次数是___________.(2)单项式-245x yπ的系数是__________,次数是__________.(3)多项式5a3b2c-12abc2+4ab3-6ab-9•的次数是______,•常数项是_____,•它是____次____项式.分析:单项式的系数是指其数字因数,次数是其所含的所有字母的指数和;•多项式的次数是其中次数最高的项的次数.例2把多项式2πxy4-1+3πx3y-π2x2按x升幂排列。
说明:π是数字,不是字母,题目中一次项、二次项、三次项系数分别为2π、-π2、3π。
例3把多项式1+a3-b3-3a2b+3ab2重新排列。
(1)按a升幂排列;(2)按a降幂排列。
例4把多项式-1+2πx2-x-x3y用适当的方式排列。
分析:题中含有2个字母x和y,而各项中关于x的指数层次较全,因此,选择关于x的升(降)幂排列较为合理。
例5把多项式x4-y4+3x3y-2xy2-5x2y3用适当的方式排列。
(1)按字母x的升幂排列得:;(2)按字母y的升幂排列得:。
【最新】人教版七年级上册整式的加减含答案.doc

七年级上册整式的加减一、选择题(每小题3分,共24分)1、下列各组中,不是同类项的是()A 、2235.0abb a 与B 、yx y x 2222与C 、315与D 、mmxx 32与2、若七个连续整数中间的一个数为n ,则这七个数的和为()A 、0B 、7nC 、-7nD 、无法确定3、若a 3与52a 互为相反数,则a 等于()A 、5B 、-1C 、1D 、-54、下列去括号错误的共有()①c ab c b a )(;②d c b a d c ba)(;③c b a c b a 2)(2;④baa b a ab a a222)]([A 、1个B 、2个C 、3个D 、4个5、计算:)](2[n mmnm 等于()A 、n2B 、m 2C 、nm24D 、mn226、式子223b a 与22b a 的差是()A 、22a B 、2222b a C 、24a D 、2224ba7、c b a 的相反数是()A 、c b a B 、c b a C 、cb a D 、cb a 8、减去m 3等于5352m m 的式子是()A 、)1(52mB 、5652m mC 、)1(52m D 、)565(2m m二、填空题(每小题3分,共24分)1、若4243b a b a m n与是同类项,则m =____,n =____。
2、在x xx x6214722中,27x 与___同类项,x 6与___是同类项,-2与__是同类项。
3、单项式ab b a ab ab b a 3,4,3,2,3222的和为____。
4、把多项式3223535y x y x xy 按字母x 的指数从大到小排列是:____5、若4)13(22aaAaa,则A =_____。
6、化简:_______77_______,653121_________,5722bab a a aaxx 7、去括号:__________)(32________;)2(2d cbay x 8、已知:_______2,3,2cbacbca则三、解答题(52分)1、去括号并合并同类项①)22(a a ;②)32(3)5(y x y x ;③)(2)(2b ab aa;④)32(2[)3(1yz xx xy2、计算①22222323xy xyyx yx ;②)32(3)23(4)(5b a b a b a ;③)377()5(322222a babb abaa3、化简求值①2),45()54(3223x x x x x 其中②43,32),12121()3232(yxxyx y xy其中4、试用含x 的多项式表示如图所示中阴影部分的面积。
人教版七年级数学上册课时练 第二章 整式的加减 2.2整式的加减

人教版七年级数学上册课时练 第二章 整式的加减 2.2整式的加减一、选择题1.若 3x m y 3 与﹣2x 2y n 是同类项,则( )A .m=1,n=1B .m=2,n=3C .m=﹣2,n=3D .m=3,n=22.下列计算正确的是( )A .224x x x +=B .2352x x x +=C .3x ﹣2x=1D .2222x y x y x y -=-3.如果,A B 两个整式进行加法运算的结果为3724x x -+-,则,A B 这两个整式不可能是( )A .3251x x +-和3933x x ---B .358x x ++和31212x x -+-C .335x x -++和341x x -+-D .3732x x -+-和2x --4.已知有理数1a ≠,我们把11a-称为a 的差倒数,如:2的差倒数是1112=--,1-的差倒数是()11112=--.如果12a =-,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数…依此类推,那么2020a 的值是( )A .2-B .13C .23D .325.萱萱的妈妈下岗了,在国家政策的扶持下开了一家商店,全家每个人都要出一份力,妈妈告诉萱萱说,她第一次进货时以每件a 元的价格购进了35件牛奶;每件b 元的价格购进了50件洗发水,萱萱建议将这两种商品都以2a b +元的价格出售,则按萱萱的建议商品卖出后,商店( )A .赚钱B .赔钱C .不嫌不赔D .无法确定赚与赔6.某天数学课上老师讲了整式的加减运算,小颖回家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:5(2a 2+3ab-b 2)-(-3+ab+5a 2+b 2)=5a 2■-6b 2+3被墨水弄脏了,请问被墨水遮盖住的一项是()A .+14abB .+3abC .+16abD .+2ab 7.有两桶水,甲桶装有a 升水,乙桶中的水比甲桶中的水多3升.现将甲桶中倒一半到乙桶中,然后再将此时乙桶中总水量的13倒给甲桶,假定桶足够大,水不会溢岀.我们将上述两个步骤称为一次操作,进行重复操作,则( ) A .每操作一次,甲桶中的水量都会减小,最后甲桶中的水会全部倒入乙桶B .每操作一次,甲桶中的水量都会减小,但永远倒不完C .每操作一次,甲桶中的水量都会增加,反复操作,最后甲桶中的水会比乙桶多D .每操作一次,甲桶中的水量都会增加,但永远比乙桶中的水量要少8.已知m)n 为常数,代数式2x 4y)mx |5-n|y)xy 化简之后为单项式,则m n 的值共有( )A .1个B .2个C .3个D .4个9.代数式4x 3–3x 3y +8x 2y +3x 3+3x 3y –8x 2y –7x 3的值A .与x )y 有关B .与x 有关C .与y 有关D .与x )y 无关10.有理数m)n 在数轴上的位置如图所示,则化简│n│-│m -n│的结果是( )A .mB .2n -mC .-mD .m -2n 二、填空题11.给定一列按规律排列的数:32-,1,710-,917,…,根据前4个数的规律,第2020个数是_____. 12.若(x -1)4(x+2)5=a 0+a 1x+a 2x 2+…+ a 9x 9,求:a 1+a 3+a 5+a 7+a 9=________.13.观察下列单项式:0,23x -,38x ,415x -,524x ⋯按规律写出第n 个单项式是________.14.若3132m a b -与52114n a b +的和仍是单项式,则56m n +的值为______ ) 15.若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12)16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3)5)7)8)9)11)12)13)15)16)17)19)20)21)23)24)25)…则第2 013个“智慧数”是______.三、解答题16.已知关于,x y 的多项式212x my +-与多项式36nx y -+的差中不含有关于,x y 的一次项,求m n mn ++的值. 17.有这样一道题“计算:(2m 4-4m 3n -2m 2n 2)-)m 4-2m 2n 2)+)-m 4+4m 3n -n 3)的值,其中14m =)n=-1.”小强不小心把14m =错抄成了14m =-,但他的计算结果却也是正确的,你能说出这是为什么吗? 18.某商场销售一种西装和领带,西装每套定价800元,领带每条定价200元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一套西装送一条领带;方案二:西装和领带都按定价的90%付款.现某客户要到该商场购买西装2套,领带x 条(x >2).(1)若该客户按方式一购买,需付款 元(用含x 的式子表示);若该客户按方式二购买,需付款 元.(用含x 的式子表示)(2)若x=5,通过计算说明此时按哪种方案购买较为合算?(3)当x=5时,你能给出一种更为省钱的购买方案吗?请直接写出你的购买方案,并算出所需费用.19.如图,数轴上有三个点A ,B ,C ,表示的数分别是﹣4,﹣2,3.(1)若使C 、B 两点的距离是A 、B 两点的距离的2倍,则需将点C 向左移动 个单位;(2)点A 、B 、C 开始在数轴上运动,若点A 以每秒a 个单位长度的速度向左运动,同时,点B 和点C 分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t 秒:①点A 、B 、C 表示的数分别是 、 、 (用含a 、t 的代数式表示);②若点B 与点C 之间的距离表示为d 1,点A 与点B 之间的距离表示为d 2,当a 为何值时,5d 1﹣3d 2的值不会随着时间t 的变化而改变,并求此时5d 1﹣3d 2的值.20.已知210x x +-=,求322002200120032007x x x +--的值.21.老师在黑板上写了一个正确的演算过程,然后用手掌捂住了一个多项式,形式如下:(1)求被捂住的多项式;(2)当1,1a b ==-时,求被捂住的多项式的值.22.有一道题目,是一个多项式减去2146x x +-,小强误当成了加法计算,结果得到223x x -+,正确的结果应该是多少?23.在数学中,有许多关系都是在不经意间被发现的.当然,没有敏锐的观察力是做不到的.数学家们往往是这样来研究问题的:特值探究–猜想归纳–逻辑证明–总结应用.下面我们也来像数学家们那样分四步找出这两个代数式的关系:对于代数式()()a b a b +-与22a b -)()1特值探究)当2a =)0b =时,()()a b a b +-=________)22a b -=________当5a =-)3b =时,()()a b a b +-=________)22a b -=________()2猜想归纳:观察()1的结果,写出()()a b a b +-与22a b -的关系:________)()3逻辑证明:如图,边长为a 的正方形纸片剪出一个边长为b 的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出()2中的关系?()4总结应用:利用你发现的关系,求:①若226a b -=,且2a b +=,则a b -=________)②()()()()()248162121212121+++++的值.(提示:你可能要用到公式()m n mn a a =) 【参考答案】1.B 2.D 3.C 4.A 5.D 6.A 7.D 8.C 9.D 10.C 11.4041408040112.-813.()()1(1)11n n n n x ---+14.1615.2 68716.-717.才会出现小强计算结果也是正确的18.(1)200x+1200;180x+1440;(2)按方案一购买较合算;(3)先按方案一购买2套西装获赠送2条领带,再按方案二购买3条领带. 所需费用为1600+200×3×90%=2140(元),是最省钱的购买方案.19.(1)1或9(2)①﹣4﹣at ;﹣2+2t ;3+5t ;②19.20.-2008.21.(1)8b 2+4ab ;(2)422.2915x -+)23.()14)4)16)16) ()2 ()()22a b a b a b +-=-)()3 略;()4①3)②3221-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.16
B.﹣14
C.14
D.﹣16
9.若 x2+x+1 的值是 8,则 4x2+4x+9 的值是( )
A.37
B.25
C.32
D.0
10.某服装店新开张,第一天销售服装 a 件,第二天比第一天少销售 14 件,第三天的销售量是
第二天的 2 倍多 10 件,则这三天销售了( )件.
A.3a﹣42 B.3a+42
18.已知:x﹣2y+3=0,则代数式(2y﹣x)2﹣2x+4y﹣1 的值为 .
19.参加农村合作医疗的王大伯住院,其手术费用 a 元,可以报销 80%;其它费用 b 元,可以报
销 60%,则王大伯此次住院可报销
元.
20.某 4 名工人 3 月份完成的总工作量比此月人均定额的 4 倍多 15 件,如果设此月人均定额是
)
A.11a-1
B.11a-10
C.11a+1
D.11a+10
5.某企业今年 3 月份产值为 a 万元,4 月份比 3 月份减少了 10%,5 月份比 4 月份增加了 15%,
则 5 月份的产值是(
)
A.(a-10%)(a+15%)万元
B.a(1-90%)(1+85%)万元
C.a(1-10%)(1+15%)万元
D.a(1-10%+15%)万元
6.若 x=-3,y=1,则代数式 2x-3y+1 的值为(
)
A.-10
B.-8
C.4
D.10
7.已知代数式 x+2y 的值是 3,则代数式 2x+4y+1 的值是( )
A.1
B.4
C.7
D.不能确定
8.已知代数式 x﹣2y 的值是 5,则代数式﹣3x+6y+1 的值是( )
13.原价为 a 元的书包,现按 8 折出售,则售价为 元.
14.某水果店销售 50 千克香蕉,第一天售价为 9 元/千克,第二天降价为 6 元/千克,第三天再
降为 3 元/千克.三天全部售完,共计所得 270 元.若该店第二天销售香蕉 t 千克,则第三
天销售香蕉
千克.(用含 t 的代数式表示)
x 件,那么这 4 名工人此月实际人均工作量为
件.(用含 x 的式子表示)
21.如图所示的运算程序中,若开始输入的x值为 10,我们发现第 1 次输出的结果为 5,第 2 次
输出的结果为 8,…,第 2016 次输出的结果为
.
22.观察下列算式:1×5+4=32,2×6+4=42,3×7+4=52,4×8+4=62,请你在观察规律之后,则
C.4a﹣32
D.3a+32
二、填空题 11.一种商品每件成本是 a 元,原来按成本增加 20%定出价格进销售,一段时间后,由于库存积 压减价,按原价的 9 折出售,则现在每件售价为 元.
12.把四张形状大小完全相同的小长方形卡片(如图①)不重叠无缝隙地放在一个底面为矩形(长 为 15cm,宽为 12cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图② 中两块阴影部分的周长和是 .
15.如图,从边长为(a+3)的正方形纸片中剪去一个边长为 3 的正方形,剩余部分沿虚线又剪
拼成一个如图所示的长方形(不重叠无缝 元,小明用 10 元钱买了 n 支铅笔后,还剩下
元.
17.一个两位数,个位数字是 a,十位数字比个位数字大 2,则这个两位数是 .
参考答案
2020 年人教版七年级数学上册 课时作业本 12
整式的加减-代数式
一、选择题
1.苹果原价是每斤 a 元,现在按 8 折出售,假如现在要买一斤,那么需要付费( )
A.0.8a 元
B.0.2a 元
C.1.8a 元
D.(a+0.8)元
2.一条河的水流速度是 2.5km/h,某船在静水中的速度是 vkm/h,则该船在这条河中逆流行驶
的速度是( )
A.(v+2.5)km/h B.(v﹣2.5)km/h
C.(v+5)km/h D.(v﹣5)km/h
3.若多项式 2x2﹣3y﹣4 的值为 2,则多项式 6x2﹣9y﹣10 的值是( )
A.6
B.8
C.10
D.12
4.一个两位数,个位数字为 a,十位数字比个位数字大 1,则这个两位数可表示为(
这第 n 个式子是
.
1.答案为:A 2.答案为:B. 3.答案为:B. 4.D 5.C 6.答案为:B
7.答案为:C. 8.答案为:B. 9.答案为:A. 10.C. 11.答案为:1.08a(元); 12.答案为:48cm.
13.答案为: a. 14.答案为:30-0.5t. 15.答案为:a+6. 16.答案为:(10-mn) ; 17.答案为:11a+20. 18.答案为:14. 19.答案为:0.8a+0.6b; 20.x+3.75; 21.答案为:4. 22.答案为:n(n+4)+4=(n+2)2.
