平面图形和立体图形.1多姿多彩的图形)
新人教版七年级上册立体图形与平面图形

赏作 品 欣
北京2008年奥运会会徽
北京申奥会徽
W
动动脑子哦?
你能设计出漂亮的图案吗
?
圆柱
圆锥
正方体
长方体
四棱柱 三棱柱
球
圆柱体
圆锥体
正方体
长方体
五棱柱
三棱锥
常见的平面图形
五边形 三角形
圆八边形梯形从这只 Nhomakorabea爱的小花猫
用
”构造图形
“
好朋友
吊环
落日余晖
眼镜
七巧板 (Tangram)起源于宋 代,是我国人民创造的 益智游戏,流传到世 界上不少国家. 由一 个正方形分割的七块 几何形状可以拼出千 变万化的几何图形,形 似各种自然事物.近代 围绕七巧板展开的科 学研究证明七巧板的 设计和人工智能、拓 扑学之间有密切的联 系.
4.1 多姿多彩的图 形
亲爱的同学们:
祝贺你步入了一个新的学习起点! 我们将一起走进丰富的图形世界,
你会觉得生活中处处都有图形的身影 你会发现许多令人惊喜的东西; 你还会感到自己变得越来越聪明,越来越有本领 想想,试试,说说,议议,相信你一定能学好 现在,就让我们携手一起走进神奇的图形世界吧!
常见的立体图形
几何图形初步认识
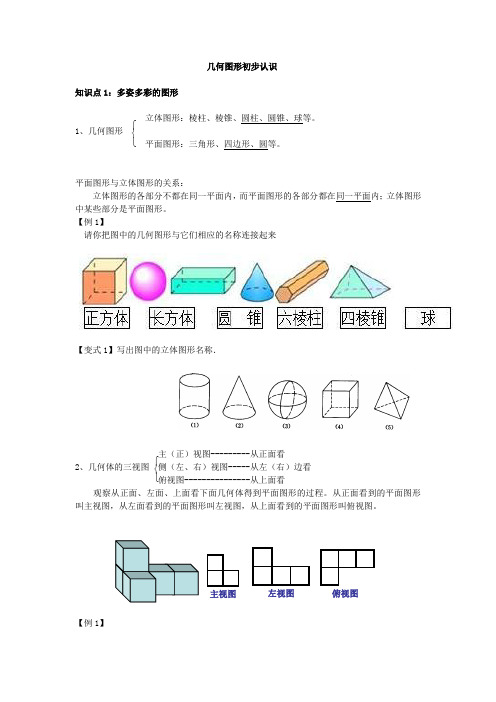
⎧⎨⎩⎧⎨⎩几何图形初步认识知识点1:多姿多彩的图形立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形平面图形:三角形、四边形、圆等。
平面图形与立体图形的关系:立体图形的各部分不都在同一平面内,而平面图形的各部分都在同一平面内;立体图形中某些部分是平面图形。
【例1】请你把图中的几何图形与它们相应的名称连接起来【变式1】写出图中的立体图形名称.主(正)视图---------从正面看2、几何体的三视图侧(左、右)视图-----从左(右)边看俯视图---------------从上面看观察从正面、左面、上面看下面几何体得到平面图形的过程。
从正面看到的平面图形叫主视图,从左面看到的平面图形叫左视图,从上面看到的平面图形叫俯视图。
【例1】主视图左视图俯视图如图,请把相应立体图形的平面展开图序号填在对应的立体图形下方.【变式1】画出下面三棱锥的三视图。
【变式2】从正面、上面、左面看圆锥得到的平面图形是()A.从正面、上面看得到的是三角形,从左面看得到的是圆B.从正面、左面看得到的是三角形,从上面看得到的是圆C.从正面、左面看得到的是三角形,从上面看得到的是圆和圆心D.从正面、上面看得到的是三角形,从左面看得到的是圆和圆心【变式3】如下图,是一个几何体正面、左面、上面看得到的平面图形,下列说法错误的是()A.这是一个棱锥B.这个几何体有4个面C.这个几何体有5个顶点D.这个几何体有8条棱【变式4】下图三个图是分别从正面,左面,上面看某立体图形得到的平面图形,你能画出这个主体图形吗?知识点2:立体图形的展开我们可能有这样的经验,把一些像墨水瓶盒、粉笔盒这样的纸盒沿它的表面适当剪开,可以展平成平面图形。
这样的平面图形叫做相应立体图形的展开图。
你知道长方体、圆柱、圆锥和三棱柱的展开图是什么样子的吗?想象一下。
【例1】下面是一些常见几何体的展开图,你能正确说出这些几何体的名字么?【变式1】如图,是一个正方体的展开图,每个面内部标注了字母,则展开前与面E相对的是()A.面D B.面B C.面C D.面A【例2】如图,是一个正方体的平面展开图,若把它折成正方体会是选项中的哪一个呢?【变式2】如图,是标有图案的正方体,若把它展开,平面展开图会是选项中的哪一个呢?()知识小结:同一立体图形,按不同的方式展开得到的平面展开图是不一样的.正方体的平面展开图有多少种呢?分析:正方体的六个面都是正方形,所以平面展开图也是由六个正方形构成,把一正方体的包装盒剪开铺开,观察各种平面展开图,找出异同点.解:(1)两个正方形连成一排(2)三个正方形连成一排(3)四个正方形连成一排说明:观察平面图形,没有一个图形中出现“”形的,也没有一个图形含有缺口的,下图中的平面图形虽然也是由六个正方形构成,但不能折成正方体.知识点3:点、线、面、体(1)几何图形的组成点:线和线相交的地方是点,它是几何图形最基本的图形。
《各种立方体集合》知识点及习题

一. 教学内容:多姿多彩的图形1. 通过实物观察,了解数学中的几何图形.2. 通过对立体图形的直观感知及动手操作题解决一些简单图形的展开图.3. 认识最基本的图形——点、线、面、体.二. 知识要点:1. 立体图形和平面图形(1)长方体、正方体、球、圆柱、圆锥、棱柱、棱锥等都是立体图形.(2)长方形、正方形、梯形、三角形、圆等都是平面图形(3)从不同的方向看一个立体图形,都只能看到立体图形的一部分,并且所看到的都不尽相同,从不同的方向看一个平面图形,看到的还是一个平面图形. 因此,常把立体图形的问题转化为平面图形来研究和处理.2. 点、线、面、体(1)几何图形都是由点、线、面、体组成的,点是构成图形的基本元素,点、线、面、体经过运动变化,能组合成各种各样的几何图形,形成多姿多彩的图形世界.(2)从运动的角度看,点动成线,线动成面,面动成体.(3)一个长方体有六个面(上面、下面、正面、背面、左面、右面),面和面相交的地方成了线,共有12条线,线和线相交的地方成了点,共有8个点.(4)立体图形可以展开,把立体图形的问题转化为平面图形来研究和处理.3. 如何识别几何体识别几何体,要注意识别它们的形状特征,几何体的表面可能是平的,也可能是曲的,根据几何体的形状数出平的面和曲的面的个数. 如常见的几种几何体:圆柱、圆锥、正方体、长方体、各类棱柱、球,这些几何体中,表面都是平的有正方体、长方体、棱柱,表面都是曲的有球;只有一个面的是球;表面有两个面的有圆锥;表面有三个面的有圆柱;表面有四个面的有三棱锥;表面有五个面的有三棱柱;表面有六个面的有正方体、长方体、四棱柱;表面有七个面的有五棱柱,从面的个数来识别不同类型的几何体.三. 重点难点:1. 重点:了解平面图形、立体图形、点、线、面、体等这些基本概念及其联系.2. 难点:(1)从不同方向观察立体图形会得到不同的平面图形. (2)几何体的展开图. 例1. 把下面几何体的标号写在相应的括号里.(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)长方体:{}棱柱体:{}圆柱体:{}球体:{}圆锥体:{}分析:本题的要求是按括号前给出的几何体的名称进行分类,属于哪类的图形就把这个图形的标号写在对应的括号中.解:长方体:{(2)(4)(10)}棱柱体:{(2)(4)(6)(10)}圆柱体:{(1)(3)(7)}球体:{(5)(8)}圆锥体:{(9)}评析:观察图形可以看到,(1)(3)(7)虽然大小不一样,摆放的角度也不一样,但都是圆柱体;另外,长方体、正方体都符合棱柱体的特征,所以也都是棱柱体.例2. (1)(湖北荆门)下左图是由若干个小正方形所搭成的几何体及从上面看这个几何体所看到的图形,那么从左边看这个几何体时,所看到的几何图形是()B C D(2)(希望杯初一第1试)如图所示的4个立体图形中,从左边看是长方形的有()个A. 0B. 1C. 2D. 3圆柱体 圆锥体 半球体 长方体分析:(1)从左边看,有两列,第一列有三行,第二列有一行,应选B. (2)圆柱体从左边看是长方形,圆锥体从左边看三角形,半球体从左边看是半圆,长方体从左边看是长方形,因此选C.解:(1)B(2)C评析:从不同方向看立体图形,看到的都是它的一个面,是平面图形,被遮去的部分看不到.例3. 如图所示的六个平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相等的三角形)的表面展开图,请把几何体与它的表面展开图用线连起来.(1)(2)(3)(4)(5)(6)分析:回答此类问题,首先要观察平面图形是否与所给出的几何体的特点相符,然后可折一折进行验证. 如圆柱的平面图形是由2个圆和一个长方形组成,应考虑(2)、(6),但(6)的两个底面在侧面的同侧,折叠后不能成圆柱,故选(2);圆锥的特点像锥子,有一个底面是圆,侧面展开图是扇形,应考虑(3)、(4),但(3)的底面圆的位置不对,不能折成圆锥,故选(4);三棱柱的特点是底面为三角形,故应考虑(1)、(5),但(5)的两个底面在侧面同侧,折叠后不能围成三棱柱,故应选(1).解:圆柱的表面展开图是(2);圆锥的表面展开图是(4);三棱柱的表面展开图是(1). 评析:解答此类问题要注意两点:①形状;②位置.例4. 下列选项中图形绕直线l旋转一周,哪一个能得到如下右图所示的立体图形()A B C D ll l l l分析:A与C图得圆锥,D图得球,B图得如图所示的立体图形. 解:B评析:本题考查了面与体之间的关系,面动成体,及几何体形成的一种方法.例5. 填空题(1)五棱柱共有__________个面,__________条棱,__________个顶点,(顶点数)+(面数)-(棱数)=__________;(2)一个棱柱共有10个面,那么它有__________条棱,__________个顶点,(顶点数)+(面数)-(棱数)=__________;(3)一个棱柱共有18条棱,那么它有__________个面,__________个顶点,(顶点数)+(面数)-(棱数)=__________.分析:本题考查棱柱的面、棱和顶点的概念,了解它们之间的数量关系,棱柱的棱不但包括上、下两个底面的边,还包括侧棱.解:(1)7,15,10,2;(2)24,16,2;(3)8,12,2评析:n棱柱的面数为n+2,顶点数为2n,棱数是3n.例6. (陕西)搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②、图③的方式串起来搭建,则串7顶这样的帐篷需要__________根钢管.①②……③分析:图①可以看做是一个正方体和一个三棱柱组合而成的,它共有17条棱. 两个这样的图形有17×2-6=28条棱,三个这样的图形有17×3-6×2=39条棱, (7)这样的图形有17×7-6×6=83条棱.解:83根评析:这是一道综合探究性问题,通过探究立体图形的棱的数量关系考查同学们用字母表示数及有理数的运算等知识.【方法总结】1. 从生活中存在的大量图形入手,体验立体图形与平面图形的相互转化,从而初步建立起空间观念.2. 注意多观察,多动手操作,在活动中体验图形的变化过程,发展空间观念和语言表达能力.3. 从运动的观点看,可以说点动成线,线动成面,面动成体.【模拟试题】(答题时间:70分钟)一. 选择题1. 与红砖、足球所类似的图形分别是()A. 长方体、圆B. 长方体、球C. 长方形、圆D. 长方形、球2. 下列说法不正确的是()A. 长方体与正方体都有六个面B. 圆锥的底面是圆C. 棱柱的上、下底面是两个完全相同的图形D. 三棱柱有三个面、三条棱3. (广州)下面四个图形中,是三棱柱的平面展开图的是()AB CD4. (武汉)一个无盖的正方体盒子的平面展开图可以是下列图形中的()①②③A. 只有图①B. 图①、图②C. 图②、图③D. 图①、图③5. (长沙)如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“迎”相对的面上的汉字是()A. 文B. 明C. 奥D. 运讲文奥迎明运6. (广州)下列立体图形中,是多面体的是()ABCD*7. (长春)一根单线从钮扣的4个孔中穿过(每个孔只穿过一次),其正面情形如图所示,下面4个图形中可能是其背面情形的是().**8. (吉林)把图①的纸片折成一个三棱柱,放在桌面上如图②所示,则从左侧看到的面为().A. QB. RC. SD. TP QRST34二. 填空题1. 包围着几何体的是________,面与面相交形成_________,线与线相交形成__________.2. 点动成__________,线动成__________,面动成__________.3. 举例说明生活中哪些实物类似于下面的几何体:球:____________________. 圆柱:____________________.圆锥:____________________.*4. 比较长方体和正方体的相同点和不同点:长方体和正方体的相同点:它们都有六个面,__________条棱,__________个顶点.长方体和正方体的不同点:长方体的六个面可能都是_________形,也可能有2个面是_________形,它的_________面完全相同;正方体的6个面都是_________形,6个面的面积_________;长方体的_________条相对的侧棱的长度相等,正方体的_________条棱长度相等.5. 请你把每个几何体的名称写在它的下面(如图所示).*6. 一个直棱柱共有12个顶点,所有的侧棱长的和是120cm,则每条侧棱长为__________.三. 解答题1. 如图所示,把下列图形与相应的实物连接起来.地球仪电视机箱水管瓦房顶2. 下图中的立体图形是由哪个平面图形旋转后得到的?请用线连起来.*3. 某厨师把一块棱长为10cm的正方体的豆腐切成棱长为2cm的小正方体. 一盘可装25个这样的小正方体豆腐,那么这块棱长为10cm的正方体豆腐可装多少盘?4. 想像一下,下面生活实例给我们以点动成线,线动成面,面动成体的印象的各是哪一个?(1)国庆节的夜晚,天安门广场上烟花绽放.(2)教室的门绕轴转动.(3)工人师傅用涂料刷向墙面上刷涂料.**5. 在手工课上,需要将一个四棱柱形的橡皮泥变成两块四棱柱的橡皮泥,你能做到吗?请说出两种以上的方法. 如果要把它变成一个四棱柱和一个三棱柱呢?说说你的方法.【试题答案】一. 选择题1. B2. D3. A4. D5. A6. B7. A8. B二. 填空题1. 面,线,点2. 线,面,体3. 足球,气球,太阳,地球等;易拉罐,圆木,门柱等;铅锤,冰激凌等4. 12,8;长方,正方,相对的两个;正方,相等;4,125. 长方体,球,圆柱,圆锥,三棱柱,正方体,四棱柱6. 20cm三. 解答题1. 如图所示:地球仪电视机箱水管瓦房顶2. ①-d,②-c,③-a,④-b3. 如图所示,这块豆腐可以切成5×5×5块棱长为2cm的小正方体豆腐,5×5×5÷25=5(盘),所以可以装5盘.4. (1)点动成线(2)面动成体(3)线动成面5. 如图(1)可以将一个四棱柱变成两个四棱柱,如图(2)可以将一个四棱柱变成一个棱柱和一个三棱柱.(1)(2)。
多姿多彩的图形

教案4.1 多姿多彩的图形几何图形教学目标:1、能从现实物体中抽象出几何图形,正确区分立体图形与平面图形;2、能把一些立体图形的问题,转化为平面图形进行研究和处理,探索平面图形与立体图形之间的关系;3、经历探索平面图形与立体图形之间的关系,发展空间观念,培养观察、分析、抽象、概括的能力和动手操作能力;4、通过所观察的现实情境和动手操作进行合作学习的过程,培养学生的学习积极性和主动性。
重、难点:重点:从现实物体中抽象出几何图形,把立体图形转化为平面图形。
难点:立体图形与平面图形之间的转化。
关键:从现实情境出发,通过动手操作进行实验和交流学习。
教具准备:长方体、正方体、球、圆柱、圆锥等几何体模型,墨水瓶包装盒(每个学生都准备一个),及多媒体教学设备。
教学过程:一、引入新课用收集的故宫建筑图片和一些实物图让学生观察并讲出其中有哪些是我们熟悉的图形,这些图形就是我们今天要学习的。
多姿多彩的图形几何图形二、新课1、请同学们想一想,生活中还有哪些实物形状是几何图形的?(请同学回答)2、观察图4.1—3,看这些实物形状接近于什么几何图形?它们的各个部分都在同一个平面内吗?这样的几何图形叫立体图形。
3、把图4.1—4中的实物形状与对应的立体图形用线连起来。
4、观察图4.1—5的各图中包含哪些几何图形?这些图形的各部分都在同一个平面中吗?(学生回答)这样的几何图形叫平面图形。
因此:平面图形几何图形分为立体图形这两种图形之间有联系吗?5、观察图4.1—6中各个立体图的表面中包含哪些平面图形?(学生回答)说明立体图形与平面图形之间有联系吗?6、观察图4.1—7,从下面、左面、上面看到的平面图形一样吗?请你们把所看到的平面图形画出来。
从正面看从左面看从上面看把你们画的和老师画的对比一下,一样吗?我们把从三个不同的方向观察得到的图形分别叫正(主)视图、左视图、俯视图,统称为三视图。
7、请同学们观察图4.1—8,你们能把它的三视图画出来吗?请动手画一画,并互相对比。
多姿多彩的图形教学设计

4.1多姿多彩的图形(第一课时几何图形)(一)、基础知识与基本技能1、基础知识:初步认识立体图形和平面图形的概念。
2、基本技能: 能从具体物体中抽象出立体图形,能举出类似于长方体、正方体、球、圆柱、圆锥、棱柱、棱锥的物体实例。
(二)、数学思考在探索实物与立体图形关系的活动过程中,对具体图形进行概括,发展几何直觉。
通过观察、动手操作、类比、推理等数学活动,积累数学活动经验,感受数学思考过程的条理性,发展形象思维。
(三)、解决问题能从具体实物中抽象出几何图形,并用几何图形描述一些现实生活中的物体。
(四)、情感与态度领域1.积极参与教学活动过程,形成主动探究的意识和自觉认真的学习态度,丰富学生数学活动的成功体验,培养敢于面对学习困难的精神,激发学生对几何图形的好奇心,感受几何图形的美感,发展学生的审美情趣。
2.在积极参与数学学习活动的过程中,形成实事求是的态度和独立思考的习惯;学会在解决问题时,与其他同学交流,培养互相合作精神。
教学重点:1、识别一些基本几何体(直棱柱,圆柱,圆锥,球)以及它们的简单组合得到的平面图形,从现实物体中抽象出几何图形。
2、把立体图形转化为平面图形。
教学难点:立体图形与平面图形之间的转化。
教学媒体:多媒体辅助教学教学过程设计(一)、创设情境,引入新课在献给爱丽丝的钢琴曲伴奏下,演示课件展示多姿多彩的图片,学生欣赏图片。
[设计意图]鞍山城市建筑物、北京奥林匹克公园中心、世界各地名胜、食物、交通标志、剪纸等这些学习内容都是具有现实意义的。
新课的引入联系学生的生活现实与数学现实(小学已学过部分立体图形),因为在学生原有的认知结构中,对生活中的立体图形已有所认识,所以这些活动是建立在学生的认识发展水平和已有的知识经验基础上,通过欣赏图片激发学生主动回忆联想,增强学生的审美意识,激发学习兴趣。
(二)实物中抽象、概括出立体图形,引导学生认识立体图形1、找一找(1)下图中的一些物体形状与我们学过的哪些图形相类似?把相应的物体和图形连接起来。
几何图形PPT教学课件

• 7.读图,回答下列问题。
• (1)图中A、B、C、D、E五处,属背斜的 是________。
• (2)从地形上看,C处是________,形成 原因是 ________________________________ ______。
• (3)泰山的成因类型与图中________处一 致;地震多发地带位于图中________处。
超过岩石的承受能力时,岩体断发裂生面 破裂,
并沿
发生明显的位移。
• (2)断层的位移类型
• ①水平方向:会错断原有的各种地貌, 或在断层附近派生出若干地貌。
压力
• 3.中央火喷山出口
• (1)成因:岩浆火在山巨口 大的
作用下,
沿着地壳的
或管道喷出。
• (2)组在成断:层包构造括地带,由于岩石和破火坏山,易锥受两风部化侵分蚀。,
”字或“8”字状( 建设成本;
线路尽量与等高线 ②降低技术
平行);
难度;③工
①同蒲铁路 沿汾河谷地 伸展;②陇 海铁路的西
线 ③避开陡坡和断层 程施工要安 段沿渭河谷
路 、滑坡、泥石流等 全;④降低 地伸展;③
走 地质灾害多发地段 运营成本和 襄渝铁路沿
向;
提高运营安 汉水谷地伸
影响 线网密度
山区交通 建设的一 般原则
D.砾岩
• 3.图示地段发生过的地质作用不能确定 的是( )
• A.水平拉伸作用 B.岩浆活动
• C.变质作用
D.堆积作用
• 【解析】 第1题,图中①处为断层地带, 因岩层破碎易遭侵蚀而形成河谷。第2题, 从断层左侧的岩层关系可以看出③处位 于砾岩的下方,而断层右侧显示砾岩的 下方是石灰岩,说明③处原为石灰岩, 后因接触高温岩浆而变质形成大理岩, 第3题,图中有岩浆活动形成的花岗岩, 变质作用形成的大理岩,堆积作用形成 的沉积物④,不能确定是否发生了水平 拉伸作用。
多姿多彩的图形:立体图形和平面图形

义务教育教科书
数学
七年级
上册
4.1.1 立体图形与平面图形 (第1课时)
课件说明
本课学习“立体图形”和“平面图形”两个概 念,是初中学段“图形与几何”领域的第一课.首 先通过前言中的实际问题和大量实物图片,展示现 实生活中多姿多彩的图形世界与几何知识间的密切 联系;接着从观察长方体形纸盒入手,引导我们初 次经历从具体物体的外形中抽象出几何图形,然后 通过观察、对比,归纳出立体图形和平面图形的概 念,并进一步认识常见的棱柱和棱锥等立体图形.
四棱锥 五棱锥 六棱锥
„„
图4.1- 4中实物的形状对应哪些立体图形?把相应 的实物与图形用线连接起来.正方体球六棱柱圆锥长方体
四棱锥
你看到了哪些立体图形?
三角形
长方形
正方形
平行四边形
梯形
圆形 探究3:这些 图形的各部 分都在同一 平面内吗?
平面图形:有些几何图形(如线段、 角、三角形、长方形、圆等)的各部 分都在同一平面内,它们是平面图 形.
从城市建筑到乡村 住宅,从立交桥到交通标 志,从剪纸艺术到城市雕 塑,从申奥标志到动物形 态„„图形世界是多姿多 彩的! 物体的形状、大小 和位置关系是几何研究 的内容.
观察这个纸盒,从中可以看出哪些你熟悉的图形?
.
长方体 ;看不同的侧 从整体上看,它的形状是______ 正方形 长方形 ;看棱得到的 面,得到的是______ 或 ______ 线段 点 是 ______ ;看顶点得到的是______ .
2.2008 年奥运会在我国举行,它的标志是五环,这 五环的每一个环的形状与下列哪个图形类似 ( C ) . A.三角形 C.圆 B.正方形 D.长方形
3. 如图 2,将下列图形与对应的图形名称用线 连接起来:
(精心整理)图形的基本认识

第三章图形认识初步§1.多姿多彩的图形1.几何图形:图形世界中蕴含着大量的几何图形,我们可以用几何图形知识来表示的解决有关图形的问题.2.立体图形:长方体、正方体、球、圆柱、圆锥、棱柱、棱锥等都是立体图形. 3.平面图形:三角形、四边形、多边形、圆等都是平面图形.4.三视图:从正面、上面、侧面(左面的右面)三个不同方向看一个物体,然后描绘出三张所看到的图,就是视图.从正面看到的图形称为正视图;从上面看到的图形称为俯视图;从侧面面看到的图形称为侧视图,根据观看方向不同,有左视图和右视图之分5.立体图形的平面展开图:许多立图形是由一些平面图形围成的,将它们适当的剪,就可以展开成平面图形,同一个立体图形按不同的方式展开,得到的平面展开图是不一样的.6.点、线、面、体点:线和线相交的地方是点线:面和面相交的地方是线面:包围着体的是面体:几何体也简称体注意:点动成线、线动成面、面动成体.例题与练习1.画出下列几何体的三视图2. 下列几何体的展开图是什么3.一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体. 试想(1)以长方形的一边为轴把长方形绕轴一周得到的立体图形是什么?你能画出示意图吗(2)把直角三角形以直角边为轴旋转一周得到的几何体又是什么?以斜边呢?你能画出示意图吗? (点拨:从运动的观点体会面动成体.)4.指出下列平面图形是什么几何体的展开图:5.推理猜测题(1)、三棱锥有____条棱,四棱锥有____条棱,十棱锥有____条棱._____棱锥有30条棱._____棱柱有60条棱.一个多面体的棱数是8,则这个多面体的面数是_____6.下列平面图形绕虚线旋转一周是什么几何体?7、填空题.(1)在立体图形中,面与面相交成,线与线相交成 .(2)圆柱体由个面围成,圆锥是个面围成,它们的底面都是,侧面都是 .(3)三棱柱有个顶点, 条棱.(4)圆锥的侧面与底面相交成条线,这条线是线.(填“曲”、“直”)8.一个三面带有标记的正方体:如果把它展开,应是下列展开图形中的()9.下列哪个图形经过折叠不能围成一个立方体是()10.如图,这是一个由小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请你画出它的主视图每与左视图11.一个多边形都可以按图甲的方法分割成若干个三角形.(图甲)(图乙)根据图甲的方法,图乙中的七边形能分割成个三角形,那么n边形能分割成个三角形.§2. 直线、射线和线段表示法长度作法叙述端点直线直线AB(BA)(字母无序)无长度过A点或B点作直线AB无端点射线射线AB(字母有序)无长度以A为端点作射线AB有一个端点线段线段AB(BA)(字母无序)可测量长度连接AB 有有两个端点A BC124 132.点的表示方法:常用英文大写字母表示,一个大写字母表示一点,不同的点要用不同的字母来表示3.直线的表示方法:①一条直线可以用在这条直线上的两个点来表示,如"直线AB”;②一条直线可以用一个小写字母来表示,如"直线a”4.射线的表示方法:①一条射线可用它的端点和射线上的另一点来表示,端点必须写在前面,如射线OA;②一条射线也可用一个小写字母来表示,如射线b.5.直线的性质:经过过两点有一条直线,并且只有一条直线.或者说两点确定一条直线.6.线段的表示方法:①一条线段可用它的的两个端点的两个大写字母表示,如线段AB或线段BA;②一条线段也可用一个小写字母来表示,如线段a注意:①表示直线、射线和线段时,都要在字母的前面写上直线、射线或线段;②用两个大写字母表示直线或线段时,两个字母的地位平等,可以交换位置;表示射线的两个字母不能交换位置,必须把端点字母放在前面7.线段的画法、连接AB的意义、线段的延长线①用直尺可以画出以A、B为端点线段,画时注意不要向任何一方延伸;②连接A、B的意义就是画出以A、B的线段;③线段的延长线:延长AB是指由A到B的方向延长,延BA是指由B到A的方向延长(也可说成反向延长AB),注意延长线应画成虚线.8.画一条线段等于已知线段:①度量法②尺规作图910B叫线段12例②A、B③点P例2例3AB=例42:(三)练习与作业1. 判断下列说法是否正确(1)直线AB 与直线BA 不是同一条直线膨胀 ( )(2)用刻度尺量出直线AB 的长度过 ( )(3)直线没有端点,且可以用直线上任意两个字母来表示( )(4)线段AB 中间的点叫做线段AB 的中点 ( )(5)取线段AB 的中点M,则AB-AM=BM ( )(6)连接两点间的直线的长度,叫做这两点间的距离 ( )(7)一条射线上只有一个点,一条线段上有两个点 ( )2.已知点A 、B 、C 三个点在同一条直线上,若线段AB=8,BC=5,则线段AC=_________3. 电筒发射出去的光线,给我们的形象似4.如图,四点A 、B 、C 、D 在一直线上,则图中有______条线段,有_______条射线;若AC=12cm,BD=8cm,且AD=3BC,则AB=______,BC=______,CD=_ ___5.已知点A 、B 、C 三个点在同一条直线上,若线段AB=8,BC=5,则线段AC=_________6.如图,若C 为线段AB 的中点,D 在线段CB 上,6=DA ,4=DB ,则CD=_____7.C 为线段AB 上的一点,点D 为CB 的中点,若AD=4,求AC+AB 的长.8.把一条长24cm 的线段分成三段,使中间一段的长为6cm,求第一段与第三段中点的距离.9.如图,同一直线上有A 、B 、C 、D 四点,已知,25,32CB AC AD DB ==CD=4cm,求AB 的长10.如图,点C 在线段AB 上,E 是AC 的中点,D 是BC 的中点,若ED=6,则AB 的长为( ).11.已知如图,点C 在线段AB 上,线段AC=6cm,BC=4cm,点M 、N 分别是AC 、BC 的中点,求线段MN 的长.. . .. B C. A CM N . . . . B. . . . ABC D A B C D C A B E D§3.角1. 角的概念:(1)有公共端点的两条射线组成的图形叫角.这个公共端点叫做角的顶点,这两条射线叫做角的两条边,(2)也可以看作由一条射线绕着它的端点旋转而成的图形.(3)射线旋转时经过的平面部分称为角的内部,平面的其余部分称为角的外部.(4)射线OA 绕点O 旋转,当终止位置OC 和起始位置OA 成一条直线时,所成的角叫做平角;继续旋转,回到起始位置OA 时,所成的角叫做周角.2. 角的表示方法:(1)用数字表示一个角,如∠1、∠2等.(2)用一个小写希腊字母表示一个角,如∠α、∠β、∠γ、∠θ等.(3)用一个大写英文字母表示一个独立的角(在一顶点处只有一个角),如∠A 、∠B 等.(4)用三个大写英文字母表示任意一个角,如∠ABC 等.3. 角的度量单位及换算:把一个周角等分成360份,一份就是1度的角;把1度的角等分成360份,每一份就是1分的角;把1分的角等分成360份,每一份是1秒的角;1度记作1º,1分记作1¹,1秒记作1¹¹.1º=60¹,1¹=60¹¹,1周角等于360º,1平角=180º4. 角的分类:平角的一半叫做直角;小于直角的角叫做锐角;大于直角而小于平角的角叫做钝角.所以小于平角的角分为锐角、直角、钝角三类.它们辶间的关系是: 1周角=2平角=4直角=360º1平角=2直角=180º 1直角=90º5. 角的简单性质:(1)角的大小与边的长短无关,只与构成角的边的两条射线张开的幅度大小有关; (2)角的大小可以度量,可以比较,也可以参与运算.6. 画角:①用量角器画一个角等于已知度数;②用三角板画特殊度数的角;③画一个角等于已知角;④画一个角的余角或补角7. 角的比较方法:(1)度量法 (2)叠合法:把一个角放在另一个角上,使它们的顶点重合,其中的一边也重合,并使这两个角的另一边都在这一边的同侧,即可比较大小. 8. 角的和差:如图 ∠AOC=∠AOB+∠ =∠ — ∠ ;∠BOC= 9. 角的平分线:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.10. 互余、互补:(1)如果两个角的和为90º,那么这两个角互为余角.其中一个角是另一个的余角,锐角α的余角是90º-∠α.(2)如果两个角的和为180º那么这两个角互为补角,其中一个角是另一个的补角,∠α的余角是180º-∠α.(3)互余互补的性质:同角(或等角)的余角(或补角)相等.11. 用角度表示方向:一般以正北、正南为基准,用向东或向西旋转的角度表示方向,如图所示,OA 方向可表示为北偏西60º .(二)、例题分析例1.填空(1)42.34º= 度 分 秒(2)56º25¹72¹¹= 度 例2.计算(1)180º—(39º18¹24¹¹+12º49¹48¹¹)(2)34º17¹⨯5 (3)49º28¹52¹¹÷4例3.如图,OC 平分∠AOD,OE 是∠BOD 的平分线,如果∠AOB=130º,那么∠O A B C D 北 南 西 东 60º E D CBO AECDBCOE 是多少度?例4.一个角的余角的补角比这个角的补角的一半大90º,求这个角. 例5.如图,O 是直线AB 上一点,∠AOE=∠分∠COD,图中与∠DOE 互余的角有哪些?与∠DOE 哪些?例6.如图,CB ⊥AB,∠CBA 与∠CBD 则∠DBA =________度,∠CBD 的补角是_________(三)、练习与作业1.填空:(1)如图:已知∠AOB=2∠BOC, 且OA ⊥OC,则∠AOB=_________0(2).已知有共公顶点的三条射线OA 、OB 、OC,∠AOC=_________(3).已知OA ⊥OB,直线CD 经过顶点O,若∠BOD :∠AOC=5:2,则∠AOC=_______∠(4)如图所示:已知OE ⊥OF 直线AB AOE=__________若∠AOF=2∠AOE,(5) 2点30分时,2.选择题:(1).如图,∠AOE =∠BOC,OD 等的角共有( ) A .1对 B .2对C .3对D .4对 (2).互为余角的两个角之差为35°, A .117.5° B .112.5° C .125° (3).如图,由A 到B 的方向是( A .南偏东30° B .南偏东60°C .北偏西30D .北偏西60° (4)旋转周,则结果指针的指向( ).(A )南偏东50º (B )西偏北50º (C )南偏3.解答题: (1)一个角的余角比它的补角29还多1°,(2)已知互余两角的差为20 ,(3)如图,∠AOB =600,OD 、OE 分别平分∠BOC 、∠AOC,那么∠EOD = 0.B A O CN M(4).老师要求同学们画一个750的角,右图是小红画出的图形.①检验小红画出的角是否等于750;②利用我们常用的画图工具,你有哪些检验方法?③画此角的平分线;④解释图中几个角之间的相互关系.(5)已知:如图,∠AOB=900,∠BOC=300,OM 平分∠AOC,ON 平分∠BOC,求∠MON 的度数.①如果∠AOB=α,其它条件不变,求∠MON 的度数.②如果∠BOC=β(β为锐角),其它条件不变,求∠MON 的度数(6)已知∠A 和∠B 互余,∠A 与∠C 互补∠B 和∠C 的和等于周角的31,求∠A+∠B+∠C 的度数.(7)已知∠AOC 与∠BOC 互补,∠AOC 比∠BOC 的余角的3倍大10°,求∠AOB 的度数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学设计
一、目的要求
1、通过观察生活中的大量图片或实物,体验、感受、认识以生活中的事物为原型的几何图形,认识一些简单几何体(长方体、正方体、棱柱、棱锥、圆柱、圆锥、球等)的基本特性,能识别这些几何体.
2、(1)经历探索平面图形与立体图形之间的关系,发展空间观念,•培养提高观察、分析、抽象、概括的能力,培养动手操作能力.(2)经历问题解决的过程,提高解决问题的能力.
3、从现实世界中抽象出几何图形的过程,感受图形世界的丰富多彩,激发对学习空间与图形的兴趣,通过与其他同学交流、活动,初步形成参与数学活动,主动与他人合作交流的意识。
二、内容分析
本节课从生活中存在的大量图形入手,引出了几何图形的概念,并在几何图形的基础上,引出了立体图形与平面图形的概念,结合从不同方向看立体图形,让学生体验立体图形与平面图形的相互转化,从而初步建立空间概念。
三、教学过程
(一)自主探究
展示丰富多彩的图形世界.
你能再举出一些常见的图形学生从周围的事物(如建筑物、
(二)尝试应用
3.图中的各立体图形的表面中包含哪些平面
(三)立体图形的分类及平面图形
(四)小结与作业。
