高考文科数学模拟题.doc
江西省宜春市2023届高三高考模拟文科数学试题(含解析)

江西省宜春市2023届高三高考模拟文科数学试题一、单选题1.(2023·江西宜春·统考模拟预测)设全集U =R ,{1A x x =<-或}2x ≥,{}2,1,0,1,2B =--,则()U B A ⋂=ð( )A .{}0,1B .{}1,0-C .{}0,1,2D .{}1,0,1-2.(2023·江西宜春·统考模拟预测)已知复数z 满足()1i 2z +=-,则z 等于( )A .1i--B .1i-C .1i+D .1i-+3.(2023·江西宜春·统考模拟预测)非零向量a r ,b r ,c r 满足()a cb ⊥-r r r ,a r 与b r 的夹角为π3,2b =r ,则c r 在a r 上的投影为( )A .-1B.C .1D4.(2023·江西宜春·统考模拟预测)已知实数,x y 满足约束条件0,30,1,x y x y y -≥⎧⎪+-≤⎨⎪≥⎩则23x yz -+=的最大值是( )A .3B .13CD .1275.(2023·江西宜春·统考模拟预测)从棱长为2的正方体内随机取一点,则取到的点到中心的距离不小于1的概率为( )A .π6B .π4C .π16-D .π14-6.(2023·江西宜春·统考模拟预测)若30.04,ln1.04,log 1.04a b c ===则( )A .c b a <<B .b a c <<C .c a b<<D .b<c<a7.(2023·江西宜春·统考模拟预测)在数学和许多分支中都能见到很多以瑞士数学家欧拉命名的常数,公式和定理,若正整数,m n 只有1为公约数,则称,m n 互质,对于正整数(),n n ϕ是小于或等于n 的正整数中与n 互质的数的个数,函数()n ϕ以其首名研究者欧拉命名,称为欧拉函数,例如:()()32,76ϕϕ==,()96ϕ=.记n S 为数列(){}3nϕ的前n 项和,则10S =( )A .9312-B .931-C .10312-D .1031-8.(2023·江西宜春·统考模拟预测)函数()πsin 6f x x ω⎛⎫=+ ⎪⎝⎭的图象(04)ω<<关于直线π6x =对称,将()f x 的图象向左平移π4个单位长度后与函数()y g x =图象重合,下列说法正确的是( )A .函数()g x 图象关于直线π6x =对称B .函数()g x 图象关于点π,06⎛⎫- ⎪⎝⎭对称C .函数()g x 在π0,3⎛⎫⎪⎝⎭单调递减D .函数()g x 最小正周期为π29.(2023·江西宜春·统考模拟预测)在Rt ABC V 中,1,2CA CB ==.以斜边AB 为旋转轴旋转一周得到一个几何体,则该几何体的内切球的体积为( )ABC .32π81D .4π8110.(2023·江西宜春·统考模拟预测)如图,设1F ,2F 是双曲线2222:1(0,0)x y C a b a b -=>>的左右焦点,点A ,B 分别在两条渐近线上,且满足22133OA OF OB =+u u u r u u u u r u u u r ,20OA BF ⋅=u u u r u u u u r,则双曲线C 的离心率为( )A .B .2CD11.(2023·江西宜春·统考模拟预测)已知数列{}n a 满足1321223n n a a a a n+++++=L ,若数列()21n n n a ⎧⎫+⎪⎪⎨⎬+⎪⎪⎩⎭的前n 项和n S ,对任意*N n ∈不等式n S λ<恒成立,则实数λ的取值范围是( )A .1λ>B .1λ≥C .58λ≥D .58λ>12.(2023·江西宜春·统考模拟预测)已知函数()()()ln 1,ln (0)1m xf x xg x x m x m =+-=+>+,且()()120f x g x ==,则()2111em xx -+的最大值为( )A .1B .eC .2eD .1e二、填空题13.(2023·江西宜春·统考模拟预测)已知)114d πa x x -=+⎰,则到点(),0M a 的距离为2的点的坐标可以是___________.(写出一个满足条件的点就可以)14.(2023·江西宜春·统考模拟预测)已知点()()1,1,1,1A B ---,若圆22()(24)1x a y a -+-+=上存在点M 满足3MA MB ⋅=u u u r u u u r,则实数a 的取值的范围是___________.15.(2023·江西宜春·统考模拟预测)已知某线路公交车从6:30首发,每5分钟一班,甲、乙两同学都从起点站坐车去学校,若甲每天到起点站的时间是在6:30--7:00任意时刻随机到达,乙每天到起点站的时间是在6:45-7:15任意时刻随机到达,那么甲、乙两人搭乘同一辆公交车的概率是___________________16.(2023·江西宜春·统考模拟预测)如图,多面体ABCDEF 中,面ABCD 为正方形,DE ⊥平面,ABCD CF DE ∥,且2,1,AB DE CF G ===为棱BC 的中点,H 为棱DE 上的动点,有下列结论:①当H 为DE 的中点时,GH P 平面ABE ;②存在点H ,使得GH AC ⊥;③直线GH 与BE ④三棱锥A BCF -的外接球的表面积为9π.其中正确的结论序号为___________.(填写所有正确结论的序号)三、解答题17.(2023·江西宜春·统考模拟预测)在ABC V 中,角,,A B C 所对的边分别为,,a b c ,且2cos a b c B +=.(1)求证:2C B =;(2)求3cos a bb B+的最小值.18.(2023·江西宜春·统考模拟预测)如图1,在直角梯形ABCD 中,//,90,224AB CD DAB CD AB AD ∠====o ,点E ,F 分别是边,BC CD 的中点,现将CEF △沿EF 边折起,使点C 到达点P 的位置(如图2所示),且2BP =.(1)求证:平面APE ⊥平面ABD ;(2)求点B 到平面ADP 的距离.19.(2023·江西宜春·统考模拟预测)为了缓解日益拥堵的交通状况,不少城市实施车牌竞价策略,以控制车辆数量.某地车牌竞价的基本规则是:①“盲拍”,即所有参与竞拍的人都是网络报价,每个人不知晓其他人的报价,也不知道参与当期竞拍的总人数;②竞价时间截止后,系统根据当期车牌配额,按照竞拍人的出价从高到低分配名额.某人拟参加2023年5月份的车牌竞拍,他为了预测最低成交价,根据竞拍网站的公告,统计了最近5个月参与竞拍的人数(见表):月份2022.122023.12023.22023.32023.4月份编号t12345竞拍人数y (万人)1.72.12.52.83.4(1)由收集数据的散点图发现可用线性回归模型拟合竞拍人数y (万人)与月份编号t 之间的相关关系.请用最小二乘法求y 关于t 的线性回归方程:ˆˆˆy bt a =+,并预测2023年5月份参与竞拍的人数.(2)某市场调研机构对200位拟参加2023年5月份车牌竞拍人员的报价进行抽样调查,得到如下一份频数表:报价区间(万元)[)1,2[)2,3[)3,4[)4,5[)5,6[]6,7频数206060302010(i )求这200位竞拍人员报价X 的平均数x 和样本方差2s (同一区间的报价可用该价格区间的中点值代替);(ii )假设所有参与竞价人员的报价X 可视为服从正态分布()2,N μσ,且μ与2σ可分别由(i )中所求的样本平均数x 及方差2s 估值.若2023年5月份实际发放车牌数是5000,请你合理预测(需说明理由)竞拍的最低成交价.附:()()()121ˆ 1.3niii nii x x y y bx x ==--=≈-∑∑,若()0,1Y N :,则( 1.11)0.8660<=P Y ,( 1.12)0.8686P Y <=.20.(2023·江西宜春·统考模拟预测)已知函数()ln 2f x x x =--.(1)求函数的最小值;(2)若方程()f x a =有两个不同的实数根1x ,2x 且12x x <,证明:1223x x +>.21.(2023·江西宜春·统考模拟预测)在平面直角坐标系xoy 中,已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12,左、右焦点分别是12,F F ,以1F 为圆心,6为半径的圆与以2F 为圆心,2为半径的圆相交,且交点在椭圆C 上.(1)求椭圆C 的方程;(2)设过椭圆C 的右焦点2F 的直线12,l l 的斜率分别为12,k k ,且122k k =-,直线1l 交椭圆C 于,M N 两点,直线2l 交椭圆C 于,G H 两点,线段,MN GH 的中点分别为,R S ,直线RS 与椭圆C 交于,P Q 两点,,A B 是椭圆C 的左、右顶点,记PQA △与PQB △的面积分别为12,S S ,证明:12S S 为定值.22.(2023·江西宜春·统考模拟预测)在平面直角坐标系xoy 中,曲线C 的参数方程11222122t t t t x y ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎪=-⎪⎩(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程cos 2sin 10m ρθρθ+-=.(1)求曲线C 的普通方程;(2)若直线l 与曲线C 有两个不同公共点,求m 的取值范围.23.(2023·江西宜春·统考模拟预测)已知函数()244f x x x =++-.(1)求不等式24410x x ++-≥的解集;(2)若()f x 的最小值为m ,正实数a ,b ,c 满足a b c m ++=,求证:11192a b b c c a m++≥+++.参考答案:1.D【分析】先计算得到U A ð,进而求出交集.【详解】{}12U A x x =-≤<ð,故(){}1,0,1U B A =-I ð故选:D 2.A【分析】利用复数的除法运算和共轭复数的定义求解.【详解】由题可得2(1i)1i 1iz -==--=-++,所以1i z =--,故选:A.3.C【分析】根据投影公式计算出正确答案.【详解】由于()a c b ⊥-r r r,所以()0,a c a b a c a a b b c ⋅-=⋅-⋅=⋅=⋅r r r r r r r r r r r ,由于a r 与b r 的夹角为π3,所以πcos 3a c a b a b a ⋅=⋅=⋅⋅=r r r r r r r,c r 在a r 上的投影为1a a c a a⋅==rr r r r .故选:C 4.B【分析】画出可行域,向上平移基准直线20x y -+=到可行域边界位置,由此求得23x y z -+=的最大值.【详解】画出可行域如下图所示,向上平移基准直线20x y -+=到可行域边界点()1,1B 的位置,此时z 取得最大值为1max 12111,3z z --⨯+=-==,.故选:B.5.C【分析】根据几何概型概率问题的计算公式求得正确答案.【详解】点到中心距离小于等于1的几何体是以中心为球心,1为半径的球体.所以,取到的点到中心的距离不小于1的概率为334π1π31126⨯-=-.故选:C 6.A【分析】构造函数()()ln 1f x x x =+-,利用导数判断函数单调性,再结合对数的性质即可判断大小关系.【详解】因为0.04a =,ln1.04b =,3log 1.04c =,当()0,1x ∈时,设()()ln 1f x x x =+-,则()11011xf x x x -'=-=<++,所以()f x 在()0,1上单调递减且()00f =,所以()()()0.04ln 10.040.0400f f =+-<=,即()0.04ln 10.04>+,所以a b >;又因为3e >,所以ln 3ln e 1>=,3ln1.04log 1.03ln1.04ln 3=<,即b c >,所以c b a <<.故选:A.7.D【分析】根据题意分析可得()1323nn ϕ-=⋅,结合等比数列求和公式运算求解.【详解】由题意可知:若正整数3nm ≤与3n不互质,则m 为3的倍数,共有1333n n -=个,故()1133332n n n n ϕ---=⋅=,∵()()113233233n n n n ϕϕ+-⋅==⋅,即数列(){}3n ϕ是以首项()32ϕ=,公比3q =的等比数列,故()1010102133113S -==--.故选:D.8.C【分析】由对称性求得ω,由图象平移变换求得()g x ,然后结合正弦函数的对称性,单调性,周期判断各选项.【详解】由已知ππππ662k ω+=+,62k ω=+,Z k ∈,又04ω<<,∴2ω=,ππ2π()sin[2()sin(2463g x x x =++=+,π2ππ2ππ,Z 632k k ⨯+=≠+∈,A 错;π2ππ2()π,Z 633k k ⨯-+=≠∈,B 错;π(0,3x ∈时,2π2π4ππ3π2(,)(,)33322x +∈⊆,C 正确;()g x 的最小正周期是2ππ2T ==,D 错.故选:C .9.C【分析】根据旋转体的概念得出该旋转体是两个共底面的圆锥的组合体,作出轴截面,得出内切球于心O 位于对称轴AB 上,由平行线性质求得球半径r 后可得球体积.【详解】由题意该几何体是两个共底面的圆锥的组合体,如图是其轴截面,由对称性知其内切球球心O 在AB 上,O 到,CA CB 的距离,OE OF 相等为球的半径,设其为r ,因为C 是直角,所以OECF 是正方形,即CF CE r ==,由//OF CA 得OF BF CA BC =,即212r r -=,解得23r =,球体积为3344232ππ(π33381V r ==⨯=.故选:C .10.C【分析】先求出AB 所在的直线方程,分别与两条渐近线联立方程组,求出,A B 两点的坐标,再根据22133OA OF OB =+u u u r u u u u r u u u r,求出,a c 之间的关系,从而可得双曲线的离心率【详解】由题意:OA b k a = ,20OA BF =u u u r u u u u r Q g ,2OA BF ∴⊥ ,2BF ak b ∴=-所以直线2BF 的方程为:()ay x c b=-- ①直线OA 的方程为:by x a =②直线OB 的方程为:by x a=-③联立①②可得:2a x cab y c⎧=⎪⎪⎨⎪=⎪⎩ ,即2(,)a ab A c c 联立①③可得22222a c x a babcy a b ⎧=⎪⎪-⎨-⎪=⎪-⎩,即22222(,a c abc B a b a b ---又22133OA OF OB =+u u u r u u u u r u u u r Q 22222221(,)(,0)(,)33a ab a c abcc c c a b a b-∴=+--可得222222233()3()a a c c c a b ab abcc a b ⎧=+⎪-⎪⎨-⎪=⎪-⎩ ,化简可得223a c = ,即2e 3=,e ∴= 故选:C 11.C【分析】根据1321223n n a a a a n+++++=L 求得 n a ,再因为对任意*N n ∈不等式n S λ<恒成立,()max n S λ>,求出实数λ的取值范围.【详解】1321223n n a a a a n+++++=L ①,31212231n n a a a a n -++++=-L ②,由①-②可得,当 2n ≥ 时,2n na n=,当211,2n a ==,当2n ≥,()()()122211222111n n n n n n n a n n n n +⎛⎫++==- ⎪ ⎪++⨯⨯+⨯⎝⎭,当1,n =()2318n n n a +=+,所以()()2312131111311228223221282212n n n n S n n n ++⎡⎤⎛⎫⎛⎫⎛⎫=+-++-=+-⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⨯⨯⨯+⨯⨯+⨯⎝⎭⎢⎥⎝⎭⎝⎭⎣⎦L ,对任意*N n ∈不等式n S λ<恒成立,所以 ()max n S λ>,()21332528882221181n n S n +⎛⎫=+<+=⎪ ⎪-⨯+⎝⎭⨯.所以58λ≥.故选:C.12.A【分析】根据题意表示出()()21121ln 1e ,x x x x m ++==从而推导出21e 1,xx =+将问题转化为()21111e em m x x m--+=,利用导数求得函数的最值.【详解】()()()()()ln 10,ln 10,1ln 1,11m mf x x x m x x x x =+-=+-==++++()ln0,e ,x xg x x m x m=+==由题意知,()()21121ln 1e ,x x x x m ++==即()()2221121ln 1e e ln e ,x x xx x x m ++===因为0m >,所以21e 1,11xx >+>,设()ln ,1p x x x x =>,则()1ln 0p x x '=+>,()()211e ,xp x p m +==所以211e x x +=,所以()22121111e e e e x m m m x x x m---+==,1(),0e m m t m m -=>,则11(),em mt m --'=当01m <<时,()0;t m '>当1m >时,()0;t m '<所以()t m 在()0,1时单调递增,在()1,+∞时单调递减,所以max ()(1)1,t m t ==故选:A.13.22(2)4x y -+=上的任意一点都可以【分析】根据定积分的几何意义先求出a ,再写出到点(),0M a 的距离为2的点表示一个圆.【详解】由于11d x -⎰表示以()0,0为圆心,1为半径且在第一、二象限的圆弧与坐标轴围成的面积,其面积是半径为1的圆的面积的一半,即为π2.所以)111144π4d d 202ππ2πa x x x x --==⨯+=+=⎰⎰,到点()2,0M 的距离为2的点是圆22(2)4x y -+=上的点.故答案为:22(2)4x y -+=上的任意一点.14.120,5⎡⎤⎢⎥⎣⎦【分析】设(,)M x y ,由数量积的坐标表示求得M 点轨迹是一个圆,然后由圆与圆的位置关系可得a 的范围.【详解】设(,)M x y ,则(1,1),(1,1)MA x y MB x y =----=---u u u r u u u r,2(1)(1)(1)3MA MB x x y ⋅=---+--=u u u r u u u r,即22(1)4x y ++=,M 在以(0,1)-为圆心,2为半径的圆上,由题意该圆与圆22()(24)1x a y a -+-+=有公共点,所以2121-≤≤+,解得1205a ≤≤.故答案为:12[0,]5.15.112【分析】由题意知本题是一个几何概型,设甲和乙到达的分别为6时x +分、6时y +分,则3060x ……,4575y ……,他们能搭乘同一班公交车,则4560x ……,4560y …….试验包含的所有区域是{(,)|3060x y x Ω=……,4575}y ……,他们能搭乘同一班公交车所表示的区域为A ,由此能求出结果.【详解】解:由题意知本题是一个几何概型,设甲和乙到达的分别为6时x +分、6时y +分,则3060x ……,4575y ……,则试验包含的所有区域是{(,)|3060x y x Ω=……,4575}y ……,他们能搭乘同一班公交车所表示的区域为4550{(,)|4550x A x y y ⎧=⎨⎩…………或50555055x y ⎧⎨⎩…………或5560}5560x y ⎧⎨⎩…………,则他们能搭乘同一班公交车的概率5531303012P ⨯⨯==⨯.故答案为:11216.①④【分析】根据线面平行的判定定理,以及线线垂直的判定,结合异面直线所成角,以及棱锥外接球半径的求解,对每一项进行逐一求解和分析即可.【详解】对①:当H 为DE 的中点时,取EA 中点为M ,连接,MH MB ,因为,H M 分别为,ED EA 的中点,故可得MH //AD ,12MH AD =,根据已知条件可知:BG //1,2AD BG AD =,故MH //,BG MH BG =,故四边形HMBG 为平行四边形,则H G //MB ,又MB ⊂平面,ABE HG ⊄平面ABE ,故H G //面ABE ,故①正确;对②:因为ED ⊥平面ABCD ,,⊂DA DC 平面ABCD ,故,DE DA DE DC ⊥⊥,又四边形ABCD 为矩形,故DA DC ⊥,则,,DE DA DC 两两垂直,以D 为坐标原点,建立空间直角坐标系如图所示:则()()()()()2,0,0,0,2,0,2,2,0,0,0,2,1,2,0A C B E G ,设()0,0,H m ,[]0,2m ∈,若GH AC ⊥,则()()1,2,2,2,020GH AC m ⋅=--⋅-=-≠u u u r u u u r,不满足题意,故②错误;对③:()1,2,GH m =--u u u r,()2,2,2BE =--u u u r ,()()()()1222262GH BE m m ⋅=-⨯-+-⨯-+=+u u u r u u u r,GH ==u u u r,BE =u u u r []0,2m ∈,,cos GH =u u u r u=[]0,2m ∈,令2325m y m +=+,设32t m =+,[]2,4t ∈,23t m -=,则29492453ty t t t==-⎛⎫+-+ ⎪⎝⎭,当[]2,4t ∈时,根据对勾函数的性质得4949454,42t t ⎡⎤+-∈⎢⎥⎣⎦,则236,549y ⎡⎤∈⎢⎥⎣⎦,当25y =时,cos ,GH BE u u u r u u u r有最小值,最小值为,故③错误;对④:由题可得CF ⊥平面ABCD ,又面ABCD 为正方形,∴,,AB BC CF AB BC CF C ⊥⊥⋂=,∴AB ⊥平面BCF ,则AB ,BC ,CF 两两垂直,∴AF 为三棱锥A BCF -的外接球的直径,又22222212219AF AB BC CF =++=++=,∴三棱锥A BCF -的外接球表面积为9π,故④正确.故答案为:①④.17.(1)证明见解析(2)最小值为【分析】(1)根据正弦定理边角互化和两角和差正弦化简即可证明.(2)将问题转化32cos 2cos cos a b c B b b B b B++=24cos cos B B =+,根据第一问解得π10,,cos ,132B B ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,然后结合不等式求解.【详解】(1)在ABC V 中,2cos a b c B +=,由正弦定理得sin sin 2sin cos A B C B +=,又()πA B C =-+,因为()sin sin 2sin cos B C B C B ++=⋅,所以sin cos sin cos sin C B B C B ⋅-⋅=,所以()sin sin C B B -=,又sin 0B >,所以0πC B C <-<<,且πB C B C +-=<,所以B C B =-,故2C B =.(2)由(1)2C B =得()30,πB C B +=∈,所以π10,,cos ,132B B ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,因为2cos ,2a b c B C B +==,所以32cos 2cos cos a b c B b b B b B++=2sin cos 2sin 2sin2cos 2sin sin cos sin cos C B B B B BB B B B⋅+⋅+==⋅⋅24cos cos B B=+≥当且仅当24cos cos B B =即cos B =π0,3B ⎛⎫∈ ⎪⎝⎭,即当且仅当π4B =时等号成立,所以当π4B =时,3cos a bb B +的最小值为18.(1)证明见解析【分析】(1)连接,BD BF ,由等腰三角形的性质和勾股定理,证明PE EF ⊥,PE BE ⊥,可证得PE ⊥平面ABD ,即可证得平面APE ⊥平面ABD .(2)取AD 的中点O ,连接,,OE DE PO ,由勾股定理求,,PD PA PO ,又B PAD P ABD V V --=,利用体积法求点B 到平面ADP 的距离.【详解】(1)证明:由题意,连接,BD BF ,因为224CD AB AD ===,//AB CD ,90,DAB F ∠=o 是边CD 的中点,所以2BF CF ==,则BC =又E 是边BC 的中点,则EF BC ⊥,在折起中PE EF ⊥.又222224BE PE BP +=+==,所以PE BE ⊥,又BE EF E =I ,BE ⊂平面ABD ,EF ⊂平面ABD ,故PE ⊥平面ABD ,又PE ⊂平面APE ,所以平面APE ⊥平面ABD .(2)由(1)中取AD 的中点O ,连接,,OE DE PO ,由(1)可知,PE ⊥平面ABD ,所以,,PE DE PE AE PE OE ⊥⊥⊥,而()132OE AB DC =+=,112OD AD ==,所以DE =同理AE =所以PD PA PO ======所以PAD V 是等腰三角形,所以1122PAD S AD PO =⋅=⨯=V 又B PAD P ABD V V --=,即1133PAD ABD S h S PE ⋅=⋅V V ,所以ABD PADS PE h S ⋅==VV =,即点B 到平面ADP19.(1)0.41.7ˆ12=+yt ,预测2023年5月份参与竞拍的人数为3.73万人(2)(i ) 3.5x =,2 1.7s =;(ii )预测竞拍的最低成交价为4.943万元【分析】(1)由已知公式求得线性回归方程,6t =代入回归方程可得预测值;(2)(i )由均值与方差公式计算出均值与方差;(ii )由预测值求得报价在最低成交价以上人数占总人数比例,然后由正态分布的性质求得预测竞拍的最低成交价.【详解】(1)11(12345)3,(1.7 2.1 2.5 2.8 3.4) 2.555t y =++++==++++=,55211149162555, 1.7 4.27.511.21741.6,ii i i i tt y ===++++==++++=∑∑,241.653 2.5ˆˆ0.41, 2.50.413 1.275553ba -⨯⨯∴===-⨯=-⨯,y 关于t 的线性回归方程0.41.7ˆ12=+y t 2023年5月份对应6t =,所以0.416 1.27 3.73ˆ=⨯+=y所以预测2023年5月份参与竞拍的人数为3.73万人.(2)(i )由题意可得:1.50.12.50.33.50.34.50.155.50.16.50.05 3.5x =⨯+⨯+⨯+⨯+⨯+⨯=22222(1.5 3.5)0.1(2.5 3.5)0.3(3.5 3.5)0.3(4.5 3.5)0.15s =-⨯+-⨯+-⨯+-⨯22(5.5 3.5)0.1(6.5 3.5)0.05 1.7+-⨯+-⨯=(ii )2023年5月份实际发放车牌数是5000,设预测竞拍的最低成交价为a 万元,根据竞价规则,报价在最低成交价以上人数占总人数比例为5000100%13.40%37300⨯≈根据假设报价X 可视为服从正态分布()22,, 3.5, 1.7, 1.3===≈N μσμσσ,令 3.51.3--==X X Y μσ,由于( 1.11)0.8660<=P Y ,1( 1.11)0.1340P Y ∴-<=,3.5() 1.110.86601.3a P Y a P Y -⎛⎫∴<=<== ⎪⎝⎭,所以 3.5 1.111.3a -=得 4.943=a ,所以预测竞拍的最低成交价为4.943万元.20.(1)1-(2)证明见解析【分析】(1)利用导数法求函数最值的步骤解求解;(2)根据题意构造函数()()()2F x f x f x =--,()0,1x ∈.对函数求导,利用导函数的正负判断函数的单调性,进而利用函数的最值得出()()212f x f x >-,再结合(1)中函数的单调性即可得证.【详解】(1)由题意可知:函数()ln 2f x x x =--的定义域为:()0,∞+.则()11f x x'=-,令()0f x '=,解得1x =.当()0,1x ∈,()0f x '<,函数()f x 单调递减;当()1,x ∈+∞,()0f x ¢>,函数()f x 单调递增.所以1x =为极小值点,且()()min 11f x f ==-.所以函数()f x 的最小值为1-.(2)根据题意可知:()()12f x f x =,根据(1)设101x <<,21x >,构造函数()()()2F x f x f x =--,()0,1x ∈.()()()()()221202x F x f x f x x x -'''=+-=<-,所以()F x 在()0,1上单调递减.则有()()10F x F <=,也即()()1120f x f x -->.因为()()12f x f x =,所以()()2120f x f x -->,也即()()212f x f x >-因为121x ->,21x >,由(1)可知()f x 在()1,+∞上单调递增,所以212x x >-,也即122x x +>.由已知21x >,所以1223x x +>.21.(1)2211612x y +=;(2)证明见解析.【分析】(1)根据离心率的定义和椭圆定义求得,a c ,再计算出b 后得椭圆方程;(2)设()()1122,,,M x y N x y ,直线方程代入椭圆方程,利用韦达定理求得中点,R S 的坐标,当直线PQ 斜率存在时,设直线:PQ y mx n =+,点,R S 在直线PQ 上,代入整理得12,k k 是一个一元二次方程的根,由韦达定理得12k k ,从而得出,m n 关系,得出直线PQ 过定点E ,再确定直线PQ 斜率不存在时也过这个定点E ,然后结合该定点得出三角形面积比.【详解】(1)依题意得12622c a a⎧=⎪⎨⎪+=⎩,则4,2,a c =⎧⎨=⎩则22212b a c =-=,所以椭圆C 的方程为2211612x y +=;(2)直线()11:2l y k x =-,设()()1122,,,M x y N x y ,由122(2)11612y k x x y =-⎧⎪⎨+=⎪⎩得()2222111341616480k x k x k +-+-=,所以2112211634k x x k +=+,211221164834k x x k -=+,且0∆>,则中点211221186,3434k k R k k ⎛⎫- ⎪++⎝⎭,同理可算222222286,3434k k S k k ⎛⎫- ⎪++⎝⎭①当直线斜率存在时,设直线:PQ y mx n =+,点,R S 在直线PQ 上,点,R S 坐标代入整理得()()21122284630,84630,m n k k n m n k k n ⎧+++=⎪⎨+++=⎪⎩易知12,k k 为方程()284630m n k k n +++=的两个根,则123284n k k m n==-+,所以1611n m =-,所以直线16:11PQ y mx m =-,则直线恒过点16,011E ⎛⎫⎪⎝⎭②当直线的斜率不存在时,由对称性可知12k k =-,由122k k =-,不妨设12k k ==,所以221222128816343411k k k k ==++,直线16:11PQ x =过16,011⎛⎫⎪⎝⎭,根据①②可知,直线PQ 恒过点16,011E ⎛⎫⎪⎝⎭,因为PQA △的面积11212S AE y y =⋅-,PQB △的面积21212S BE y y =⋅-,所以121641511167411AE S S BE +===-.【点睛】方法点睛:椭圆中的直线过定点问题的解决方法:斜率存在时,设出直线方程为y mx n =+,根据已知条件确定,m n 的关系后,由直线方程得出定点坐标.本题中,动直线PQ 是由点,R S 确定的,因此可由已知直线12,l l 确定,R S 的坐标,再把坐标代入所设直线方程,发现12,k k 是一个一元二次的两根,这样可由韦达定理求得,m n 的关系,得出结论.22.(1)()22441x y x -=≥(2)4m <<【分析】(1)在曲线C 的参数方程中消去参数t ,可得出曲线C 的普通方程,利用基本不等式求出x 的取值范围,即可得解;(2)求出直线l 的普通方程,分析可知直线l 与双曲线2214y x -=的右支有两个交点,将直线l 与双曲线2214y x -=方程联立,利用直线与双曲线的位置关系可得出关于m 的不等式组,即可解得实数m 的取值范围.【详解】(1)因为112122t t x ⎛⎫=+≥ ⎪⎝⎭()222222221422,2441122,2t t t t x x y x y ⎧=++⎪⎪-=≥⎨⎪=+-⎪⎩则则曲线的普通方程为()22441x y x -=≥(2)cos 2sin 10m ρθρθ+-=则210mx y +-=由得()22210,1,14mx y y x x +-=⎧⎪⎨-=≥⎪⎩得()22162170m x mx -+-=有两个不等正根()22222160,Δ468160,20,1617016m m m m m m ⎧-≠⎪=+->⎪⎪⎨->⎪-⎪⎪->-⎩则4m <<23.(1)[)10,2,3∞∞⎛⎤--⋃+ ⎥⎝⎦(2)证明见解析【分析】(1)利用零点分段法分类讨论,分别求出不等式的解集,即可得解;(2)利用绝对值三角不等式求出()f x 的最小值,即m 的值,再利用柯西不等式证明即可.【详解】(1)不等式24410x x ++-≥,所以224410x x x ≤-⎧⎨---+≥⎩,解得103x ≤-,或2424410x x x -<<⎧⎨+-+≥⎩,解得24x ≤<,或424410x x x ≥⎧⎨++-≥⎩,解得4x ≥,所以原不等式解集为[)10,2,3∞∞⎛⎤--⋃+ ⎥⎝⎦.(2)()244242f x x x x x x =++-=++-++()2406x x ≥+--+=,当且仅当2x =-时取得,即min ()6f x =,所以6a b c m ++==,因为()1112a b c a b b c a c ⎛⎫++⨯++ ⎪+++⎝⎭()111a b b c c a a b b c c a ⎛⎫=+++++++ ⎪+++⎝⎭()()()111a b b c c a a b b c c a ⎛⎫=+++++++⎡⎤ ⎪⎣⎦+++⎝⎭222222⎡⎤⎡⎤⎢⎥=++++⎢⎥⎣⎦⎢⎥⎣⎦2≥()21119=++=,当且仅当12a b c ===时取等号,所以()1119922a b b c c a a b c m ++≥=+++++成立.。
2023年高三420文科数学模拟考试(学生版)——统考

绝密★启用前赤峰市高三年级4·20模拟考试试题文科数学注意事项:1、答卷前,考生务必将自己的姓名,准考证号填写在答题卡上.2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效. 3、考试结束后,将本试卷和答题卡一并交回.一、 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设全集{}1,2,3,4,5,6,7,8U =,{}1,3U A B = ,(){}2,4U A B = ,则集合B 为( ) A .{}1,3,5,6,7,8 B .{}2,4,5,6,7,8 C .{}5,6,7,8 D .{}1,2,3,42、已知复数z z 对应向量的模长为2,则( )A .1z =B .1z =±+C .1z =±D .1z =−±3、在“万众创业”的大背景下,“直播电商”已经成为我国当前经济发展的新增长点,已知某电商平台的直播间经营化妆品和食品两大类商品,2022年前三个季度,该直播间每个季度的收入都比上一个季度的收入翻了一番,其前三季度的收入情况如图所示,则( )A .该直播间第三季度总收入是第一季度总收入的3倍;B .该直播间第三季度化妆品收入是第一季度化妆品收入的6倍;C .该直播间第三季度化妆品收入是第二季度化妆品收入的3倍;D .该直播间第三季度食品收入低于前两个季度的食品收入之和.4、函数()21sin f x x x x=−在()(),00,ππ− 上的图像大致为( ) A . B . C . D .5、九连环是中国杰出的益智游戏,九连环由9个相互连接的环组成,这9个环套在一个中空的长形柄中,九连环的玩法就是要将这9个环从柄上解下来(或套上),规则如下:如果要解下(或套上)第n 环,则第1n −号环必须解下(或套上),1n −往前的都要解下(或套上)才能实现.记解下n 连环所需的最少移动步数为n a ,已知()12121,2,213n n n a a a a a n −−===++≥,若要解下7环最少需要移动圆环步数为( ) A .42 B .85C .170D .3416、下列选项中,命题p 是命题q 的充要条件的是( ) A .在ABC 中,:p A B >,:sin sin q A B >.B .已知x ,y 是两个实数,2:230p x x −−≤,:02q x ≤≤.C .对于两个实数x ,y ,:8p x y +≠,:3q x ≠或5y ≠.D .两条直线方程分别是1:260l ax y ++=,()22:110l x a y a +−+−=,12:p l l ∥, :2q a =或1−.7、记函数()()sin 0,02f x x πωϕωϕ =+><< 的最小正周期为T .若()f T =,6x π=为()f x 的零点,则ω的最小值为( ) A .2 B .3 C .4 D .68、四叶草曲线是数学中的一种曲线,因形似花瓣,又被称为四叶玫瑰线(如右图),其方程为()322228xy x y +=,玫瑰线在几何学、数学、物理学等领域中有广泛应用。
高考文科数学模拟试题

高考文科数学模拟试题一、选择题:本大题共12小题,每小题5分,共60分.1.如图,点O 是正六边形ABCDEF 的中心,则以图中点A 、B 、C 、D 、E 、F 、O 中的任意一点为始点,与始点不 同的另一点为终点的所有向量中,除向量OA 外,与向量OA 共线的向量共有( )A .2个B . 3个C .6个D . 7个2.已知曲线C :y 2=2px 上一点P 的横坐标为4,P 到焦点的距离为5,则曲线C 的焦点到准线的距离为 ( ) A . 21B . 1C . 2D . 43.若(3a 2 -312a ) n 展开式中含有常数项,则正整数n 的最小值是 ( )A .4B .5C . 6D . 84. 从5名演员中选3人参加表演,其中甲在乙前表演的概率为 ( )A . 203B . 103C . 201D . 1015.抛物线y 2=a(x+1)的准线方程是x=-3,则这条抛物线的焦点坐标是( )A.(3,0)B.(2,0)C.(1,0)D.(-1,0)6.已知向量m=(a ,b ),向量n⊥m,且|n|=|m|,则n的坐标可以为( )A.(a ,-b )B.(-a ,b )C.(b ,-a )D.(-b ,-a )3.如果S ={x |x =2n +1,n ∈Z },T ={x |x =4n ±1,n ∈Z },那么A.S TB.T SC.S =TD.S ≠T7. 如果S ={x |x =2n +1,n ∈Z },T ={x |x =4n ±1,n ∈Z },那么 A.S T B.T S C.S=T D.S ≠T8.有6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有 ( )A .36种B .48种C .72种D .96种9.已知直线l 、m ,平面α、β,且l ⊥α,m ⊂β.给出四个命题:(1)若α∥β,则l ⊥m ;(2)若l ⊥m ,则α∥β;(3)若α⊥β,则l ∥m ;(4)若l ∥m ,则α⊥β,其中正确的命题个数是( )A.4B.1C.3D.210.已知函数f(x)=log 2(x 2-ax +3a)在区间[2,+∞)上递增,则实数a 的取值范围是( )A.(-∞,4)B.(-4,4]C.(-∞,-4)∪[2,+∞)D.[-4,2)11.4只笔与5本书的价格之和小于22元,而6只笔与3本书的价格之和大于24元,则2只笔与3本书的价格比较( )A .2只笔贵B .3本书贵C .二者相同D .无法确定12.若α是锐角,sin(α-6π)=31,则cos α的值等于 A.6162- B. 6162+ C. 4132+ D. 3132- E F DO C B A二、填空题:本大题共4小题,每小题4分,共16分.13.在等差数列{a n }中,a 1=251,第10项开始比1大,则公差d 的取值范围是___________. 14.已知正三棱柱ABC —A 1B 1C 1,底面边长与侧棱长的比为2∶1,则直线AB 1与CA 1所成的角为 。
潍坊一中高考模拟文科数学试题(3)

高考冲刺模拟训练(文科)(3)考试说明:本试卷分第I 卷(选择题)和第1I 卷(非选择题)两部分,满分1 50分,考试时间120分钟. 第I 卷(选择题,共50分)一、选择题(本大题共12小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题意要求的.)1.已知全集U=Z ,集合A={一1,0,1,2},B={x|x 2=x},则A C U B 为( )A .{一1,2)B .{一1,0}C .{0,1)D .{1,2)2.设i 为虚数单位,则复数31i z i=-在复平面内对应的点位于( )A .第一象限B .第_象限C .第三象限D .第四象限 3.若a=(一1,3),b=(x+1,一4),且(a+b )//b ,则实数x 为( )A .3B .13 C .一3 D .一134.执行如图所示的程序框图,若输入8,n S ==则输出的 ( ) A .49 B . 67 C .89 D .10115.已知a ,b ,l ,表示三条不同的直线,,,αβγ表示三个不同的平面,有下列四个命题:A .①②B .①④C .②③D .③④6.一动圆过点A (0,1),圆心在抛物线214y x =上,且恒与定直线,相切,则直线l 的方程为( )A .x=1B .132x =C .132y =- D .1y =-7.设第一象限内的点(,x y )满足2400x y x y --⎧⎨-⎩,,≤≥若目标函数(0,0)z ax by a b =+>>的最大值是4,则11a b+的最小值为 (A )3 (B )4 (C )8 (D )9 8.函数2()cos sin f x x x =+,那么下列命题中假命题的是( )A .()[,0]f x π-在上恰有一个零点B .f (x )既不是奇函数也不是偶函数C .f (x )是周期函数D .f (x )在区间(5,26ππ)上是增函数9.在△ABC 中,内角A,B,C 的对边长分别为a ,b ,c ,且22tan 2,3,tan A a c b C-==则b 等于 ( )A .3B .4C .6D .710.对实数a 和b ,定义运算“*”:a*b=,1,1a ab b a b -≤⎧⎨->⎩,设函数f (x )=(21x +)*(x+2),若函数y=f (x )一c 的图像与x 轴恰有两个公共点,则实数C 的取值范围是( )A .(2,4](5,+∞)B .(1,2] (4,5]C .(一∞,1)(4,5]D .[1,2]第II 卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.) 11.已知某三棱锥的三视图如图所示,则它的外接球的半径为 .12.平面坐标系中,O 为坐标原点,点A (3,1),点B (一1,3),若点C 满足,,1OC OA OB R αβαβαβ=+∈+=其中且,则点C 的轨迹方程为 .13.定义域为R 的函数()f x 满足(1)3f =,且()f x 的导函数1()3f x '>,则满足3()8f x x >+的x 的集合为 . 14.在区间0,1]上任取两个实数a ,b ,则函数f (x )=312x ax b +-在区间[—1,1]上有且仅有一个零点的概率为 .15.已知f (1,1)=1,f (m ,n )∈N *(m 、n∈N *),且对任意m 、n∈N *都有:① f(m ,n+1)= f (m ,n )+2; ② f(m +1,1)=2 f (m ,1).给出以下三个结论:(1)f (1,5)=9;(2)f (5,1)=16;(3)f (5,6)=26. 其中正确的个数为 .三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 16.(本小题满分12分)已知△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ,向量2(4,1),(cos ,cos2)2A A =-=,m n 7.2⋅=且m n (Ⅰ)求角A 的大小;(Ⅱ)若a =,试判断b·c 取得最大值时△ABC 形状.17.(本小题满分12分) 一多面体的三视图和直观图如下图所示,它的正视图为直角三角形,侧视图为矩形,俯视图为直角梯形(尺寸如图所示)直观图中的平面BEFC 水平放置.(1)求证:AE//平面DCF ; (2)当92AB =时,求该多面体的体积. 18.(本小题满分12分)一汽车厂生产A ,B ,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A ,B ,C 三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A 类轿车有10辆. (Ⅰ)求z 的值;(Ⅱ)用随机抽样的方法从B 类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看作一个总体,从中任取一个分数a .记这8辆轿车的得分的平均数为x ,定义事件E ={0.5a x -≤,且函数()22.31f x ax ax =-+没有零点},求事件E 发生的概率. 19.(本小题满分12分)已知数列{}n a 满足:1121222222,n n a a aan n N -+*++⋅⋅⋅++=-∈.(1)求数列{}n a 的通项公式; (2)设12n n n b a a +=,数列{}n b 的前n 项和为n T .若存在实数λ,使得n T λ≥,试求出实数λ的最小值. 20.(本小题满分1 3分) 己知函数()(2)xf x nx n e =-+⋅∈(其中n N*)(I )求f (x )在[0,2]上的最大值;(II )若函数g (x )=(nx+2)(nx 一15)(n ∈N*),求n 所能取到的最大正整数,使对任意x>0,都有2f’(x )>g (x )恒成立. 21.(本小题满分1 4分)已知抛物线22x py =上点()2,2处的切线经过椭圆()2222:10y x E a b a b+=>>的两个顶点.(1)求椭圆E 的方程;(2)过椭圆E 的上顶点A 的两条斜率之积为4-的直线与该椭圆交于B 、C 两点.请问:是否存在一点D ,使得直线BC 恒过该点?若存在,请求出定点D 的坐标;若不存在,请说明理由; (3)在(2)的条件下,过点A 作直线BC 的垂线,垂足为H ,求点H 的轨迹方程.。
2023届高考文科数学模拟试卷三十六(含参考答案)

2023届高考文科数学模拟试卷三十六(含参考答案)一.选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若全集{}{}0,1,2,32U U C A ==且,则集合A 的真子集共有 A .3个B .5个C .7个D .8个 2. sin 42sin 72cos 42cos 72+=A .B .12C .sin114 D .cos114 3.下列各组命题中的假命题是A .1,20x x R -∀∈>B .2,(1)0x N x +∀∈->C .,lg 1x R x ∃∈<D .,tan 2x R x ∃∈= 4.右图是函数sin()(0,0,)2y A x A πωφωφ=+>><在区间5[,]66ππ-上的图象,为了得到这个函数的图象,只要将sin ()y x x R =∈的图象上所有的点 A .向左平移3π个单位长度,再把所得各点的横坐标缩短 到原来的12倍,纵坐标不变B .向左平移3π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变D .向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变5.已知等比数列{}n a 中,公比1q >,且168a a +=,3412a a =,则116a a = A .2 B .3 C .6 D .3或66.若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间A. 和内B. 和内C. 和内D. 和内7.设a ,b ,c 均为正数,且122log aa =, 121log 2bb ⎛⎫= ⎪⎝⎭,21log 2cc ⎛⎫= ⎪⎝⎭则 A .a <b <cB .c <b <aC .c <a <bD .b <a <c8.P 是ABC ∆所在平面上的一点,满足20PA PB PC ++=,若ABC ∆的面积为1,则(),a b (),b c (),a -∞(),a b (),b c (),c +∞(),a -∞(),c +∞6π-56πABP ∆的面积为 A. 1 B. 2 C. 21D. 319.从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为A .2097B .2264C .2111D .201210.函数,正实数满足且.若实数是方程的一个解,那么下列四个判断:① ② ③ ④ 中有可能成立的个数为A .1B .2C .3D .4二.填空题:本大题共5小题,每小题5分,满分25分.把答案填在答题卡的横线上. 11.函数y =的值域是 ▲ . 12.已知tan()35πα-=-,则22sin cos 3cos 2sin αααα-= ▲ . 13.如右图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ,测得15BCD ︒∠=,30BDC ︒∠=,30CD =米,并在点C 测得塔顶A 的仰角为60︒,则塔高AB = ▲ 米.14. 已知向量=(1,3)OA ,=(2,1)OB - ,(1,2)OC m m =+-,若点A 、B 、C 能构成三角形,则实数m 满足的条件是 ▲ . 15.已知函数f (x )=|x +11x-|,则关于x 的方程2()6()0f x f x c -+= (c ∈R )有6个不同实数解的充要条件是 ▲ .三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)已知集合231{|1,[,2]},{|||1}22A y y x x xB x x m ==-+∈-=-≥;命题:p x A ∈,命题:q x B ∈,并且命题p 是命题q 的充分条件,求实数m 的取值范围.x x f x2log )31()(-=c b a ,,c b a <<d 0)(=x f a d <a d >c d >c d < 1 23 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 343536 37 383940…17.(本小题满分12分) 已知 (1)求的最大值及取得最大值时x 的取值的集合;(2)在△ABC 中,a b c 、、分别是角A ,B ,C所对的边,若a =,且对()f x 的定义域内的每一个x ,都有()()f x f A ≤恒成立,求AB AC ⋅的最大值.18.(本小题满分12分)叙述两角差的余弦公式,并用向量的数量积证明.19.(本小题满分12分)已知数列{}n a 满足:121,(0).a a a a ==>数列{}n b 满足1(*)n n n b a a n N +=∈. (1)若{}n a 是等差数列,且312b =,求a 的值及{}n a 的通项公式; (2)若{}n a 是等比数列,求{}n b 的前项和n S ;(3)当{}n b 是公比为1a -的等比数列时,{}n a 能否为等比数列?若能,求出a 的值;若不能,请说明理由.20.(本小题满分13分)某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数与听课时间之间的关系满足如图所示的曲线.当时,曲线是二次函数图象的一部分,当时,曲线是函数(且)图象的一部分.根据专家研究,当注意力指数≥80时,听课效果最佳.(1) 试求的函数关系式;(2) 老师在什么时段内安排核心内容能使得学生听课效果最佳?请说明理由.sin 2().sin xf x x x=+()f x p t ]14,0(∈t ]40,14[∈t ()835log +-=x y a 0a >1a ≠p ()p f t =。
高考文科数学模拟试题
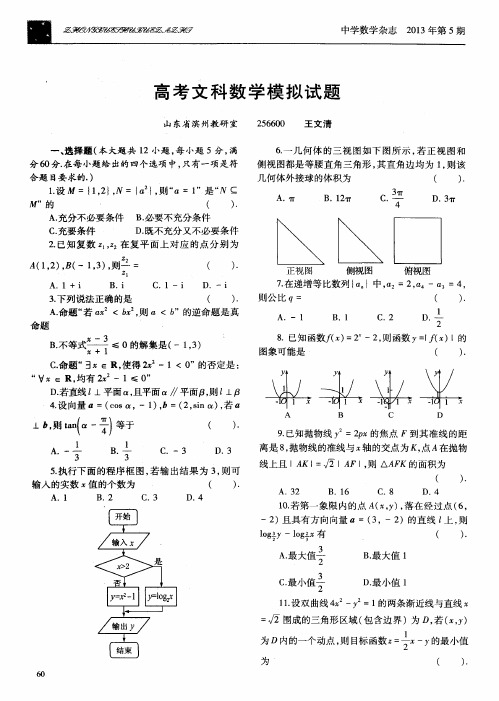
一
(
) .
A . 命题“ 若口 <b x , 则 口<b ”的逆命题是真
B . 不 等式
≤ 0的解 集是 ( 一1 , 3 )
8 .已知 函数厂 ( ) =2 一2 , 则 函数 Y= l _ 厂 ( ) l的
图象可 能是 ( ) .
c . 命 题 “j ∈R, 使得 2 一1<0 ”的否定是 : “V ∈ R, 均有 2 一 1≤ 0 ”
E B j - 平面A B C, F是 B C的中 1 4 . 已知 圆 C: +Y 一6 x+8=0 , 则 圆心 C的坐 标为
— —
点, = A C=B E=2 , C D=1 .
; 若 直线 Y= k x与 圆 C相 切 , 且 切点 在第
.
四象 限 , 则 k=
D . 若直线 z 上平面 a , 且平面 ∥ 平面 , 则f j . 卢 4 . 设 向量 a=( 0 o s ,一1 ) , b=( 2 , s i n . ) , 若a
A B C D
上 , 则 t a n ( a 一 号 ) 等 于
1 1
( ) .
l o g f y—l o g  ̄ x 有
A. 最 大值 c . 最小 值
1 1 . 设双 曲线
=
(
B . 最 大值 1 D. 最小值 1
) .
一 Y 。 =1 的两条 渐 近线与 直线
围成 的三角形 区域 ( 包 含 边界 )为 D, 若( , y ) 一, , 的最小 值
(
C.8 D.4
5 . 执行下 面 的程 序框 图 , 若输 出结 果 为 3 , 则可 输 人 的实数 值 的个数 为
备战高考 高中数学文科 试卷习题 仿真模拟冲刺卷(一)

仿真模拟冲刺卷(一)时间:120分钟 满分:150分一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A =⎩⎨⎧⎭⎬⎫x |y =x 12 ,集合B =⎩⎨⎧⎭⎬⎫y ⎪⎪y =⎝⎛⎭⎫12x ,则A ∩B =( ) A .[1,+∞) B .(1,+∞) C .(0,+∞) D .[0,+∞)2.设复数z 满足z ·i =1+2i ,其中i 为虚数单位,则|z |=( ) A .2+i B .1 C .5 D .53.如图所示的图形中,每一个小正方形的边长均为1,则(AC → -AD → )·AB →=( ) A .0 B .-1 C .-2 D .14.如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m ,平均值为x -,则下列正确的是( )A.m 甲=m 乙,x 甲>x 乙 B .m 甲=m 乙,x 甲<x 乙 C .m 甲>m 乙,x 甲>x 乙 D .m 甲<m 乙,x 甲<x 乙5.设x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +3≥02x +y -3≤0y ≥1 ,则z =x +y -1的最大值是( )A .-1B .0C .1D .26.抛物线y =6x 2的准线方程为( )A .y =-124B .y =-112C .y =-6D .y =-37.如图程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a ,b 分别为35、28,则输出的a =( )A .1B .14C .7D .28 8.函数f (x )=cos x -x 2x的图象大致为( )9.正四棱锥S ABCD 的所有边长都相等,E 为SC 的中点,则BE 与SA 所成角的余弦值为( )A .13B .12C .33D .3210.十二平均律是我国明代音乐理论家和数学家朱载堉发明的.明万历十二年(公元1584年),他写成《律学新说》,提出了十二平均律的理论,这一成果被意大利传教士利玛窦通过丝绸之路带到了西方,对西方音乐产生了深远的影响.十二平均律的数学意义是:在1和2之间插入11个正数,使包含1和2的这13个数依次成递增的等比数列,依此规则,新插入的第4个数应为( )A .214B .213C .2313D .241311.已知函数f (x )=23 sin 2x -m cos 2x ,若对任意的x ≠k π2 ,k ∈Z ,f (x )=2m 有解,则m 的取值范围是( )A .[2,+∞)B .(0,2]C .(-∞,-2]∪[2,+∞)D .[-2,0)∪(0,2]12.截角八面体是由正四面体经过适当的截角,即截去正四面体的四个顶点处的小棱锥所得的八面体. 如图所示,有一个所有棱长均为a 的截角八面体石材,现将此石材切削、打磨、加工成球,则加工后球的最大表面积为( )A .πa 2B .32 πa 2C .53 πa 2D .83πa 2二、填空题:本大题共4小题,每小题5分,共20分.13.{a n }为等差数列,a 1+a 4+a 7=39,a 3+a 6+a 9=33,则S 9=________. 14.“青山”饮料厂推出一款新产品——“绿水”,该厂开展促销活动,将6罐“绿水”装成一箱,且每箱均有2罐可以中奖.若从一箱中随机抽取2罐,则能中奖的概率为________.15.写出一个同时满足下列条件①②的圆的标准方程:________. ①圆心在直线y =x +1上,②与y 轴相切.16.已知函数f (x )是定义在R 上的奇函数,对于任意x 1≠x 2,必有f (x 1)≠f (x 2),若函数F (x )=f (x 2-m )+f (3-2x )只有一个零点,则当x <2时,函数g (x )=mx 2-62-x的最小值为________. 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知2cos (π+A )+sin (π2 +2A )+32=0. (1)求角A ; (2)若c -b =33a ,求证:△ABC 是直角三角形. 18.(12分)党的十九大明确把精准扶贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为了坚决打赢脱贫攻坚战,某帮扶单位要开展精准扶贫,此帮扶单位为了了解某地区贫困户对其所提供帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:现用系统抽样法从40个贫困户满意度评分中抽取容量为10的样本,且在第一段内随机抽到的样本数据为92.(1)请你列出抽到的10个样本数据;(2)计算所抽到的10个样本数据的均值x -和方差s 2;(3)在(2)条件下,若贫困户的满意度评分在(x - -s ,x -+s )之间,则满意度等级为“A 级”.试应用样本估计总体的思想,现从(1)中抽到的10个样本为“A 级”的贫困户中随机地抽取2户,求所抽到2户的满意度评分均“超过80”的概率(参考数据:30 ≈5.48,33 ≈5.74,35 ≈5.92).19.(12分)如图,在四棱锥B ACED 中,AD ∥CE ,且AD =23 CE ,F 是棱BE 上一点,且满足BF=2FE .(1)证明:DF ∥平面ABC ;(2)若三棱锥B ADF 的体积是4,△ABC 的面积是22 ,求点F 到平面ABC 的距离.20.(12分)已知抛物线C :y 2=2px (p >0)的焦点为F ,且点F 与圆M :(x +4)2+y 2=1上点的距离的最小值为4.(1)求C 的方程;(2)设点T (1,1),过点T 且斜率存在的两条直线分别交曲线C 于A ,B 两点和P ,Q 两点,且|TA |·|TB |=|TP |·|TQ |,求直线AB 的斜率与直线PQ 的斜率之和.21.(12分)已知函数f (x )=x (ax -a ln x +1). (1)若x =1是f (x )的极值点,求a 的值; (2)若a ≤e -1,证明:f (x )≤e x .(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,曲线C 的参数方程是⎩⎪⎨⎪⎧x =2+cos θy =sin θ (θ为参数),正方形ABCD的顶点均在C 上,且A ,B ,C ,D 依逆时针次序排列,点A (3,0).(1)求C 的普通方程及点B ,C ,D 的坐标;(2)设P 为C 内(包含边界)任意一点,求|P A |2+|PB |2+|PC |2+|PD |2的最小值.23.[选修4-5:不等式选讲](10分)已知函数f(x)=2|x|+|2x-1|,集合A={x|f(x)<3}.(1)求A;(2)若s,t∈A,求证|1-ts|<|t-1 s|.。
2023届高考文科数学模拟试卷五十五(含参考答案)

2023届高考文科数学模拟试卷五十五(含参考答案)一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中。
只有一项是符合题目要求的。
1.设集合A=2{|21},{|ln(1)}x x B x y x -<==-,则A B 为A .{|2}x x <B .{|12}x x <<C .{|1}x x <D .{|1}x x ≤2.若cos isin z θθ=-(i 为虚数单位),则使21z =-的θ值可能是A .0B .πC .2πD .2π3.下列函数中,在区间02π⎛⎫⎪⎝⎭,上为增函数且以π为周期的函数是A .sin2xy = B . sin y x = C . tan y x =- D . cos 2y x =- 4.命题“0x R ∃∈,3210x x -+>”的否定是A .x R ∀∈,3210x x -+≤ B .0x R ∃∈,3210x x -+< C .0x R ∃∈,3210x x -+≤ D .不存在x R ∈,3210x x -+> 5. 设α表示平面,b a ,表示直线,给定下列四个命题:①αα⊥⇒⊥b b a a ,//;②αα⊥⇒⊥b a b a ,//; ③αα//,b b a a ⇒⊥⊥;④b a b a //,⇒⊥⊥αα. 其中正确命题的个数有A.1个B.2个C.3个D.4个 6.在等比数列{}n a 中,5113133,4,a a a a ⋅=+=则155a a = A .3 B .13 C .3或13 D .3-或13- 7.圆224450x y x y +--+=上的点到直线90x y +-=的最大距离与最小距离的差为A.B.C. D.6频率706050408.一个算法的程序框图如下图所示,若该程序输出的结果为56,则判断框中应填入的条件是A.4i <B.5i <C. 5i ≥D. 6i < 9.在面积为S 的△ABC 的边AB 上任取一点P ,则△PBC 的面积不小于3S的概率是A .32 B .13C .43 D .41 10.若不等式组0024x y y x s y x ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩表示的平面区域是一个三角形,则s 的取值范围是A.s ≥4 B.0s <≤2 C.2≤s ≤4D.0s <≤2或s ≥4二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分. 11. 统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如右图示,规定不低于60分为 及格,不低于80分为优秀,则及格人数是 ; 优秀率为 。
