图论考试
图论习题课——精选推荐

图论习题课⼀、填空题1、对下列图,试填下表(是??类图的打〝√ 〞,否则打〝?〞)。
①②③2、若图G=中具有⼀条汉密尔顿回路,则对于结点集V 的每个⾮空⼦集S ,在 G 中删除S 中的所有结点得到的连通分⽀数为W ,则S 中结点数|S|与W 满⾜的关系式为。
3、设有向图D 为欧拉图,则图D 中每个结点的⼊度.4、数组{1,2,3,4,4}是⼀个能构成⽆向简单图的度数序列,此命题的真值是 .5、“3,3K 是欧拉图也是哈密顿图”这句话是_______。
(填对或错)6、极⼤可平⾯图的每⼀个⾯的次数都是_________.7、5阶完全图的边连通度是.8、图G是2-⾊的当且仅当G是.⼆、选择题1、下列⽆向图可能不是偶图的是( )(A) ⾮平凡的树(B)⽆奇圈的⾮平凡图(C) n(1)n ⽅体图(D) 平⾯图2、关于平⾯图,下列说法错误的是( )(A) 简单连通平⾯图中⾄少有⼀个度数不超过5的顶点;(B)极⼤外平⾯图的内部⾯是三⾓形,外部⾯也是三⾓形;(C) 存在⼀种⽅法,总可以把平⾯图的任意⼀个内部⾯转化为外部⾯;(D) 平⾯图的对偶图也是平⾯图。
3、已知图G的邻接矩阵为,则G有().A.5点,8边B.6点,7边C.6点,8边D.5点,7边4、设图G=,则下列结论成⽴的是( ).A.deg(V)=2∣E∣B.deg(V)=∣E∣C.EvVv2)deg(=∑∈D.Vv=∑∈)deg(5、设完全图K n有n个结点(n≥2),m条边,当()时,K n中存在欧拉回路.A.m为奇数B.n为偶数C.n为奇数D.m为偶数6、设G是连通平⾯图,有v个结点,e条边,r个⾯,则r= ( ).A.e-v+2 B.v+e-2 C.e-v-2 D.e+v+27、下列定义正确的是( ).A含平⾏边或环的图称为多重B不含平⾏边或环的图称为简单图C含平⾏边和环的图称为多重D不含平⾏边和环的图称为简单图8、以下结论正确是( ).A仅有⼀个孤⽴结点构成的图是零图B⽆向完全图Kn每个结点的度数是nC有n(n>1)个孤⽴结点构成的图是平凡图D图中的基本回路都是简单回路9、下列数组能构成简单图的是( ).(A) (0,1,2,3) (B) (2,3,3,3) (C) (3,3,3,3) (D) (4,2,3,3)10、n阶⽆向完全图Kn中的边数为().(A) 2)1(+nn(B) 2)1(-nn(C) n (D)n(n+1)11、以下命题正确的是( ).(A) n(n≥1)阶完全图Kn都是欧拉图(B) n(n≥1)阶完全图Kn都是哈密顿图(C) 连通且满⾜m=n-1的图(∣V∣=n,∣E∣=m)是树(D) n(n≥5)阶完全图Kn都是平⾯图12、下列结论不正确是( ).(A) ⽆向连通图G是欧拉图的充分必要条件是G不含奇数度结点(B) ⽆向连通图G有欧拉路的充分必要条件是G最多有两个奇数度结点(C) 有向连通图D是欧拉图的充分必要条件是D的每个结点的⼊度等于出度(D) 有向连通图D有有向欧拉路的充分必要条件是除两个结点外,每个结点的⼊度等于出度13、⽆向完全图K4是().(A)欧拉图(B)哈密顿图(C)树(D)平⾯图14、在如下各图中()欧拉图。
电子科大研究生图论06-14年图论期末试题

条边,但不是哈密尔顿图。
七、(10 分)今有赵、钱、孙、李、周五位教师,要承担语文、数学、 物理、化学、英语五门课程。已知赵熟悉数学、物理、化学三门课程, 钱熟悉语文、数学、物理、英语四门课程,孙、李、周都只熟悉数学 和物理两门课程。 问能否安排他们 5 人每人只上一门自己所熟悉的课 程,使得每门课程都有人教,说明理由
(C)
(B)
(D)
5、下列优化问题中,存在好算法的是( ) (A) 最短路问题;(B) 最小生成树问题;(C) TSP 问题;(D) 最优匹配问题. 三、作图题(10 分) 1、分别作出满足下列条件的图 (1)、E 图但非 H 图;(2) H 图但非 E 图;(3) 既非 H 图又非 E 图;(4) 既是 H 图又是 E 图 2、画出度序列为(3,2,2,1,1,1)的两个非同构的简单图。 四、求下图的最小生成树,并给出它的权值之和(10 分)。
一.填空题(每题 2 分,共 12 分) 1. 简单图 G=(n,m)中所有不同的生成子图(包括 G 和空图)的个数 是_____个; 2. 设无向图 G=(n,m)中各顶点度数均为 3, 且 2n=m+3,则 n=_____; m=_____; 3.一棵树有 ni 个度数为 i 的结点,i=2,3,…,k,则它有____个度 数为 1 的结点; 4.下边赋权图中,最小生成树的权值之和为_______;
问能否安排他们5人每人只上一门自己所熟悉的课程使得每门课程都有人教说明理由八10分设g是具有n个顶点m条边p个连通分支的平面图g的每个面至少由k十10分1在一个只有2个奇度点的边赋权图中如何构造一个最优欧拉环游
电子科技大学图论作业

图论作业3一、填空题1. 完全图K2n共有个不同的完美匹配。
2. 超方体Q6的最小覆盖包含的点数为。
3. 图K m,n (m≤n)的最小覆盖包含的点数为。
4. 完全图K60能分解为个边不重的一因子之并。
5. 完全图K61能分解为个边不重的二因子之并。
6. 假设G是具有n个点、m条边、k个连通分支的无圈图,则G的荫度为。
7. 图G是由3个连通分支K1, K2, K4组成的平面图,则其共有个面。
8. 设图G与K5同胚,则至少从G中删掉条边才可能使其成为可平面图。
9. 设连通平面图G具有5个顶点,9条边,则其面数为。
10. 若图G是10阶极大平面图,则其面数等于。
11. 若图G是10阶极大外平面图,其内部面共有个。
二、不定项选择题1. 关于非平凡树T,下面说法错误的是( )(A) T至少包含一个完美匹配;(B) T至多包含一个完美匹配;(C) T的荫度大于1;(D) T是只有一个面的平面图;(E) T的对偶图是简单图。
2. 下列说法正确的是( )(A) 三正则的偶图存在完美匹配;(B) 无割边的三正则图一定存在完美匹配;(C) 有割边的三正则图一定没有完美匹配;(D) 有完美匹配的三正则图一定没有割边;(E) 三正则哈密尔顿图存在完美匹配。
3. 下列说法正确的是( )(A) 在偶图中,最大匹配包含的边数等于最小覆盖包含的点数;(B) 任一非平凡正则偶图包含完美匹配;(C) 任一非平凡正则偶图可以1-因子分解;(D) 偶度正则偶图可以2-因子分解;(E) 非平凡偶图的最大匹配是唯一的。
4. 下列说法中错误的是( )(A) 完全图K101包含1-因子;(B) 完全图K101包含2-因子;(C) 完全图K102包含1-因子;(D) 完全图K102包含2-因子;(E) 图G的一个完美匹配实际上就是它的一个1因子;(F) 图G的一个2-因子实际上就是它的一个哈密尔顿圈。
5. 下列说法正确的是( )(A) 方体Q n可以1-因子分解;(B) 非平凡树可以1-因子分解;(C) 无割边的3正则图可以1-因子分解;(D) 有割边的3正则图一定不可以1-因子分解;(E) 可1-因子分解的3正则图一定是哈密尔顿图。
图论期末考试整理复习资料

目录第一章图的基本概念 (1)二路和连通性 (3)第二章树 (3)第三章图的连通度 (4)第四章欧拉图与哈密尔顿图 (5)一,欧拉图 (5)二.哈密尔顿图 (6)第五章匹配与因子分解 (9)一.匹配 (9)二.偶图的覆盖于匹配 (10)三.因子分解 (11)第六章平面图 (14)二.对偶图 (16)三.平面图的判定 (17)四.平面性算法 (20)第七章图的着色 (24)一.边着色 (24)二.顶点着色 (25)第九章有向图 (30)二有向树 (30)第一章图的基本概念1.点集与边集均为有限集合的图称为有限图。
2.只有一个顶点而无边的图称为平凡图。
3.边集为空的图称为空图。
4.既没有环也没有重边的图称为简单图。
5.其他所有的图都称为复合图。
6.具有二分类(X, Y)的偶图(或二部图):是指该图的点集可以分解为两个(非空)子集X 和Y ,使得每条边的一个端点在X 中,另一个端点在Y 中。
7.完全偶图:是指具有二分类(X, Y)的简单偶图,其中X的每个顶点与Y 的每个顶点相连,若|X|=m,|Y|=n,则这样的偶图记为Km,n8. 定理1 若n 阶图G 是自补的(即),则n = 0, 1(mod 4)9. 图G 的顶点的最小度。
10. 图G 的顶点的最大度。
11. k-正则图: 每个点的度均为 k 的简单图。
例如,完全图和完全偶图Kn,n 均是正则图。
12. 推论1 任意图中,奇点的个数为偶数。
13.14. 频序列:定理4 一个简单图G 的n 个点的度数不能互不相同。
15. 定理5 一个n 阶图G 相和它的补图有相同的频序列。
16.17.18. 对称差:G1△G2 = (G1∪G2) - (G1∩G2) = (G1-G2)∪(G2-G1)19. 定义: 联图 在不相交的G1和G2的并图G1+G2中,把G1的每个顶点和G2的每个顶点连接起来所得到的图称为G1和G2的联图,记为G1∨G220. 积图:积图 设G1= (V1, E1),G2 = (V2, E2),对点集V = V1×V2中的任意两个点u =(u1,u2)和v = (v1,v2),当(u1 = v1和 u2 adj v2) 或 (u2 = v2 和 u1 adj v1) 时就把 u 和 v 连接起来所得到的图G 称为G1和G2积图。
2020-2021《图论》期末课程考试试卷(含答案)

2020-2021《图论》期末课程考试试卷适用专业:信计本科生考试日期:年月考试时间:120分钟;考试方式:闭卷;总分100分一、填空题. (6小题,每小题3分,共18分)1 树中所有度大于1的顶点都是。
2 称为欧拉图。
3 若G是连通的(),p q图,则它的一棵生成树有条边。
4 求一个连通图的生成树的两种方法:和。
5 使图G为n-着色的n最小数值称为G的。
6 如果M中任意两条边在G中均不邻接,则称M是G的一个。
二解答题(5小题,共38分)1 假设A,B……G是7个哨所,监视着11条路段(如下图所示),为节省人力,问至少需要在几个哨所派人站岗,就可以监视全部路段,写出具体的一个可行方案?(6分)2 试作出下列二图作的并,交与环和。
(8分)3写出下图的关联集,并由此求出图的全部断集。
(10分)4 写出下图的完全关联矩阵。
(8分)5 画出下图的对偶图(在原图上用另一种颜色的笔画出来)。
(6分)三 应用题 (3小题,共34分)6 如下图,现准备在g f e d c b a ,,,,,,七个居民点设置一银行,各点之间距离由图给出,则银行设在哪个点可使最大服务距离最小?若要设置两个银行,则设在哪两个点?(12分)7 在通信中,0、1、2、…、7出现的频率如下:0:30%,1:20%,2:15%,3:10%,4:10%,5:5%,6:5%,7:5% 求传输它们的最佳前缀码。
(12分)8 求下述网络的最大流。
(10分)四 证明题 (1小题,每小题10分,共10分)9、若图(,)G V E =不是哈密顿图(3)V ≥,证明至少有一个顶点的度适合deg()2v V <。
2020-2021《图论》期末课程考试试卷答案一填空题(共6小题,每小题3分,共18分)1 割点。
2 顶点的度均为偶数的图。
3 p-1 ;4 破圈法和避圈法。
5 色数;6 匹配。
二解答题(共5小题,共38分)(题5图)(题2图)1 解:{A,D,G,E }和{A,D,G,B }都是最小点覆盖, 所以至少需要在4个哨所派人站岗来监视全部路段.3 解:S(1)={a,d,f},S(2)={a,b,e},S(3)={b,c,d}然后作出它们所有的环和S(1)✞ S(2)={b,d,e,f}, S(1)✞ S(3)={a,b,c,f}S(2)✞ S(3)={a,c,e,d},S(1)✞ S(2) ✞ S(3)={e,c,f}4 解:0000011000011000001010111⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦三、应用题(3小题,共34分)6 解:求出任意两点间的距离,得出每行的最大值,在最大值中取最小值4.8,故一个银行应设在c,此时最大服务距离为4.86254524636233513336395365436393643651333684525154518184364333633813396363936843..............................gfedcbagfedcba最大值如取两个银行,在上表7列中任取两列,从两列序号的分量中选出最小数,再在这7个最小数中选出最大者,最后在21个数字中选出最小者3,所以设两个银行应设在fa,或fb,7 解::(1) 求带权5,5,5,10,10,15,20,30的最优二叉树;(2) 求T所对应的前缀码;(3) 通过权把传输符号同前缀码的二进制位对应起来:用11表示1, 01表示0, 101表示3, 100表示4, 001表示2, 0000表示F, 0001表示5,00001表示6,00000表示7。
电子科大研究生图论考试 附答案

1电子科技大学研究生试卷(考试时间: 至 ,共__2_小时)课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2013__年_6__月__20__日 成绩 考核方式: (学生填写)一.填空题(每空2分,共20分)1. n 阶k 正则图G 的边数m =_____。
2.4个顶点的不同构单图的个数为________。
3.完全偶图,r s K (,2r s ≥且为偶数),则在其欧拉环游中共含____条边。
4.高为h 的完全2元树至少有_______片树叶。
5. G 由3个连通分支124,,K K K 组成的平面图,则其共有_______个面。
6. 设图G 与5K 同胚,则至少从G 中删掉_______条边,才可能使其成为可平面图。
7. 设G 为偶图,其最小点覆盖数为α,则其最大匹配包含的边数为________。
8. 完全图6K 能分解为________个边不重合的一因子之并。
9. 奇圈的边色数为______。
10. 彼得森图的点色数为_______。
二.单项选择(每题3分,共15分) 1.下面说法错误的是( )学 号 姓 名 学 院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集,在其补图中的点导出子图必为一个完全子图;(B) 若图G 连通,则其补图必连通; (C) 存在5阶的自补图; (D) 4阶图的补图全是可平面图. 2.下列说法错误的是( ) (A) 非平凡树是偶图;(B) 超立方体图(n 方体,1n ≥)是偶图; (C) 存在完美匹配的圈是偶图; (D) 偶图至少包含一条边。
3.下面说法正确的是( )(A) 2连通图一定没有割点(假定可以有自环); (B) 没有割点的图一定没有割边;(C) 如果3阶及其以上的图G 是块,则G 中无环,且任意两点均位于同一圈上;(D) 有环的图一定不是块。
图论习题课
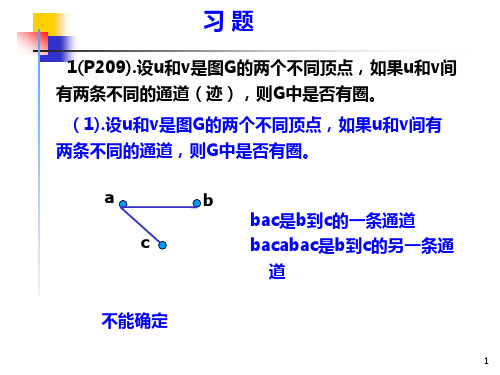
1(P209).设u和v是图G的两个不同顶点,如果u和v间 有两条不同的通道(迹),则G中是否有圈。
(1).设u和v是图G的两个不同顶点,如果u和v间有 两条不同的通道,则G中是否有圈。
a c
b bac是b到c的一条通道 bacabac是b到c的另一条通
道
不能确定
1
习题
(2).设u和v是图G的两个不同顶点,如果u和v间有 两条不同的迹,则G中是否有圈。 有
6. 树最多有 个中心。
7. n个顶点的最大连通度是: 。
8. 集合X的特征函数的个数是:
。
9. 对称关系的关系矩阵A的特征是: 。
10. 20个顶点的平面图最多有 条边。
19
二、判断题(每小题2分,共10分)
(1)简单图要求两个顶点之间最多有一条边是因为:多 边没有意义。
(2)关系是特殊的映射。 (3)区间[10,100]中的实数可以从大到小排成
*10
习题
2(P209).证明:一个连通的(p, q)图中q p-1。
11
习题
8(P209).设G是图,证明:若(G)2, 则G包含至少 是(G)+1的圈。
与第6题同
12
习题
4(P228).完全偶图Km,n是哈密顿图的充分必要条件是什 么?
是 m=
10(P228n).证明具有奇数个顶点的偶图不是哈密顿 图?
25
四、证明题(每小题10分,共20分) 2. 用归纳法证明:只有两个一度顶点的一棵树是
一条路。
26
五、计算题(每小题5分,共10分)
1. A,B,C,D,E,F,G共7个学生排队,请计算 不能出现“AB”,“CD”,“EF”的方案 数。
离散数学考试题及答案

离散数学考试题及答案一、选择题1. 关于图论的基本概念,以下哪个说法是正确的?A. 无向图中的边无方向性,有向图中的边有方向性。
B. 有向图中的边无方向性,无向图中的边有方向性。
C. 无向图和有向图都是由顶点和边组成的。
D. 无向图和有向图都只由边组成。
答案:A2. “若顶点集合为V,边集合为E,那么图G可以表示为G(V, E)”是关于图的哪个基本概念的描述?A. 图的顶点B. 图的边C. 图的邻接D. 图的表示方法答案:D3. 以下哪个命题是正确的?A. 若集合A和B互相包含,则A和B相等。
B. 若集合A和B相交为空集,则A和B相等。
C. 若集合A和B相等,则A和B互相包含。
D. 若集合A和B相等,则A和B相交为空集。
答案:C二、填空题1. 有一个集合A = {1, 2, 3, 4},则集合A的幂集的元素个数为__________。
答案:162. 设A = {a, b, c},B = {c, d, e},则集合A和B的笛卡尔积为__________。
答案:{(a, c), (a, d), (a, e), (b, c), (b, d), (b, e), (c, c), (c, d), (c, e)}3. 若p为真命题,q、r为假命题,则合取范式(p ∨ q ∨ r)的值为__________。
答案:真三、计算题1. 计算集合A = {1, 2, 3, 4}和集合B = {3, 4, 5, 6}的交集、并集和差集。
答案:交集:{3, 4}并集:{1, 2, 3, 4, 5, 6}差集:{1, 2}2. 计算下列命题的真值:(~p ∨ q) ∧ (p ∨ ~q),其中p为真命题,q为假命题。
答案:真四、证明题证明:对于任意集合A和B,如果A和B互相包含,则A和B相等。
证明过程:假设A和B互相包含,即A包含于B且B包含于A。
设x为集合A中的任意元素,则x也必然存在于集合B中,即x属于B。
同理,对于集合B中的任意元素y,y也属于集合A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论考试
————————————————————————————————作者:————————————————————————————————日期:
2
3
电子科技大学研究生试卷
(考试时间:至,共__2_小时)
课程名称图论及其应用教师学时60 学分
教学方式讲授考核日期_2012__年___月____日成绩 考核方式:(学生填写)
一、填空题(填表题每空1分,其余每题2分,共30分)
1.n 阶k 正则图G 的边数()m G =___
___2
nk
; 2.3个顶点的不同构的简单图共有___4___个;
3.边数为m 的简单图G 的不同生成子图的个数有__2___m 个;
4. 图111(,)G n m =与图222(,)G n m =的积图12G G ⨯的边数为1221____n m n m +;
5. 在下图1G 中,点a 到点b 的最短路长度为__13__;
6. 设简单图G 的邻接矩阵为A ,且2311201
21111
13022102001202A ⎛⎫
⎪
⎪
⎪= ⎪
⎪ ⎪⎝
⎭
,则图G 的边数
为
__6__;
学号姓名学院
……………………密……………封……………线……………以……………
4 5
6
6 4
1 1
2
7 2
4
3
a
b G 1
4
7. 设G 是n 阶简单图,且不含完全子图3K ,则其边数一定不会超过
2___4n ⎢⎥
⎢⎥⎣⎦
; 8.3K 的生成树的棵数为__3__;
9. 任意图G 的点连通度()k G 、边连通度()G λ、最小度()G δ之间的关系为
__()()()____k G G G λδ≤≤;
10. 对下列图,试填下表(是⨯⨯类图的打〝√ 〞,否则打〝⨯〞)。
① ② ③
能一笔画的图 Hamilton 图 偶图 可平面图
① ⨯ √ ⨯ √
② ⨯ ⨯ ⨯ √
③ ⨯ √ √ √
二、单项选择(每题2分,共10分)
1.下面命题正确的是(B )
对于序列(7,5,4,3,3,2),下列说法正确的是: (A) 是简单图的度序列;
(B) 是非简单图的度序列; (C) 不是任意图的度序列; (D)是图的唯一度序列.
2.对于有向图,下列说法不正确的是(D)
(A) 有向图D 中任意一顶点v 只能处于D 的某一个强连通分支中; (B) 有向图D 中顶点v 可能处于D 的不同的单向分支中;
(C) 强连通图中的所有顶点必然处于强连通图的某一有向回路中; (D)有向连通图中顶点间的单向连通关系是等价关系。
3.下列无向图可能不是偶图的是( D )
5
(A) 非平凡的树;
(B)无奇圈的非平凡图; (C) n (1)n ≥方体; (D) 平面图。
4.下列说法中正确的是( C )
(A)连通3正则图必存在完美匹配;
(B)有割边的连通3正则图一定不存在完美匹配; (C)存在哈密尔顿圈的3正则图必能1因子分解; (D)所有完全图都能作2因子分解。
5. 关于平面图,下列说法错误的是( B )
(A) 简单连通平面图中至少有一个度数不超过5的顶点; (B)极大外平面图的内部面是三角形,外部面也是三角形;
(C) 存在一种方法,总可以把平面图的任意一个内部面转化为外部面; (D) 平面图的对偶图也是平面图。
三、 (10分)设G 与其补图G 的边数分别为12,m m ,求G 的阶数。
解:设G 的阶数为n 。
因12(1)
2n n m m -+=…………………………………4分
所以:212220n n m m ---=……………………..2分 得:12118()
2
m m n +++=
………………………..4分
四、(10分)求下图的最小生成树(不要求中间过程,只要求画出最
小生成树, 并给出T 的权和)。
()16w T =
V v
v v v v v
v v 6 5
4 3
5 16
24 1 2 3
V v
v
v v v v
v v 6 5
4 3
5 16
24 1 2 3
6
五、(10分) (1). 求下图G 的k 色多项式;(2). 求出G 的点色数χ;
(3). 给出一种使用χ种颜色的着色方法。
G
解:(1)图G 的补图为:(2分)
1(,)h H x x =………………………………………………..1分
对于2H :12340,2,4,1r r r r ====,所以,其伴随多项式为: 2342(,)24h H x x x x =++……………………………………..1分 所以:345(,)24h G x x x x =++………………………………1分 于是色多项式[][][]345()24G P x k k k =++
2(1)(2)4(1)(2)(3)(1)(2)(3)(4)
k k k k k k k k k k k k =--+---+----
= k (k -1) (k-2)[2+4(k -3) +(k-3) (k-4)] = k (k -1)2 (k-2)2
解法2()(1)k P G k =- 2分
H 1
H 2
7
=(k -1) 3分
=(k -1)[ k (k -1) (k-2)2] = k (k -1)2 (k-2)2 2分
(2)由于123()()0,()12P G P G P G ===,所以,点色数χ=3; 2分 (3)χ点着色: 1分
六、(10分)5个人,,,,A B C D E 被邀请参加桥牌比赛。
桥牌比赛规则是每一场比赛由两个2人组进行对决。
要求每个2人组{},X Y 都要与其它2人组{},W Z (W ,Z ∉{X ,Y })进行对决。
若每个人都要与其他任意一个人组成一个2人组,且每个组在同一天不
能有多余一次的比赛,则最少安排多少天比赛(每一天可以有多场比赛)?请给出相应的一个时间安排表。
(用图论方法求解)
解:(1)、建模:5个人能够组成10个2人组:AB, AC, AD, AE, BD, BC, BE, CD , CE, DE 。
以每个2人组作为顶点,因要求每个2人组{},X Y 都与其它2人组{},W Z 比赛,所以,得到比赛状态图如下:
AB AC
AD BC
BD BE
CD
CE DE AE
(2)、最少安排多少天比赛转化为求状态图的边色数χ'。
G
1 1
1
2
3
⎝⎛ ⎪
⎪⎪⎪
⎪⎭⎫+
8
因为彼得森图不可1因子分解,于是可推出4χ'≥,又可用4种色对其正常边着色(见下图),所以:4χ'≤。
(3)、安排时间表:
第一天:AB---DE, AE---BC, AC---BE, AD---CE;
第二天:AB---CE, AC---DE, AE---BD, AD---BC, BE---CD; 第三天:AB---CD, BC---DE, BD---CE;
第四天:AC---BD, AD---BE, AE---CD 。
4分
七、(10分) 由于在考试中获得好成绩,6名学生,,,,,A B C D E F 将获得下列书籍的奖励,分别是:代数学(a),微积分(c),微分方程(d),几何学(g),数学史(h),规划学(p),拓扑学(t)。
每门科目只有1本书,而每名学生对书的喜好是:
A :d, h, t ;
B : h, t ;
C :d, h ;
D :d, t ;
E :a, c, d ; F::c, d, p, g 。
每名学生是否都可以得到他喜欢的书?为什么?(用图论方法求解)
解:由题意,得模型图:(4分)
B C D E F
a c d g h p t
A
问题转化为是否存在饱和A,B,C,D,E,F 的匹配存在。
2分 取顶点子集合{},,,S A B C D =,因{}(),,N S d h t =,所以()N S S < 由霍尔定理知:不存在饱和A,B,C,D,E,F 的匹配。
AB AC AD BC BD
BE CD
CE
DE AE
1 1 1
2
2 2 1 2 2
3 3 3
4 4 4
9
故每名学生不能都得到他喜欢的书。
4分
八、(10分)若n 为偶数,且单图G 满足:()12
n
G δ≥
+,求证:G 中有3因子。
证明:因单图G 满足:()12
n
G δ≥+,所以G 中存在哈密尔顿圈n C 。
2分
又因n 为偶数,所以,n C 可分解为两个1因子12,H H ,它们显然也是图G
的两个1因子。
3分
考虑11G G H =-,则1()2
n
G δ≥,于是,1G 中存在哈密尔顿圈n
C '。
2分 作1n H H C '=U ,则H 为G 的一个3因子。
3分。
