东南大学计算力学习题及答案汇总(2011版)汇总
考研专业课复习 东南大学结构力学习题集及答案
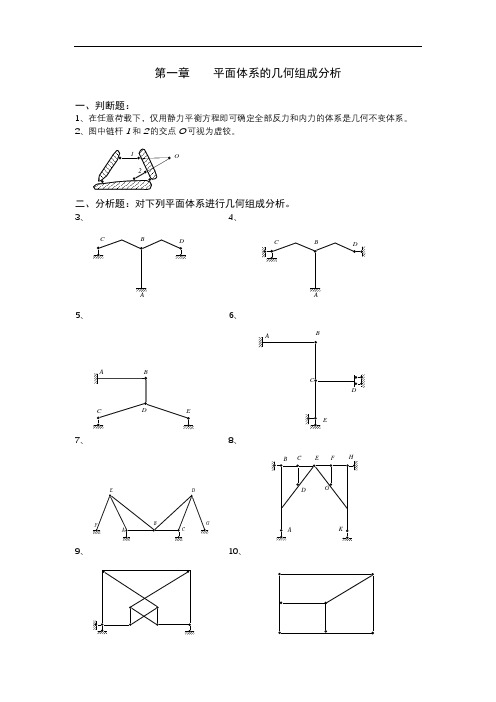
第一章 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBACDB5、 6、A CD BEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、123456781234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、BA CFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二章 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
aa(a)BCa aAϕ2a2(b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0, R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2()↑。
(d)9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:N1=N2=N3= 0。
13、图(h)所示桁架DE杆的内力为零。
a a(h)(i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
15、图(j)所示桁架共有三根零杆。
东南大学结构力学习题(附答案)

M /8
M图
11、 X = ql (←) (有侧支座水平反力) 1 28 13、
P
12、 M CB
= 2.06kN ⋅ m (上侧受拉)
X1
X2
—— 8 ——
15、
17、
P l
X1
Pl 2Pl
Pl
Pl Pl 2 MP 图 Pl 2 M图
M1 图
δ 11 =
2l Pl , Δ1P = − , 3EI EI
Pa
52、
53、
N=4.5qa 117 81 36 1.5 qa 24 9 0 M 图 0 5 qa2 36 _ N= 9qa 4.5qa2 4.5qa
54、
4 54 54
55、
4 N =-28.8 kN 36 36 4 M 图 ( kN . m ) 4
4
56、
2 qa 2 2 qa 2
M 图
57、
第二部分 静定结构内力计算(参考答案)
1、 (O) 6、 (O) 11、 (O) 16、 (O) 19、
3 Pa+1.5 m 0 4 3m 4 0
2、 (X) 7、 (X) 12、 (O) 17、 (X)
3、 (O) 8、 (X) 13、 (O) 18、 (O)
4、 (O) 9、 (O) 14、 (X) 20、
3 30、 Δ DV = 8 Pa / EI + 125 Pa / 4 EA( ↓ )
4 2 31、 Δ DV = 11qa / 24 EI + 15qa / 8 EA( ↓ )
32、 φ SR = 33、 Δ DV
3Pa 2 EI
(
)
(完整版)计算力学复习题答案

计算力学试题答案1. 有限单元法和经典Ritz 法的主要区别是什么?答:经典Ritz 法是在整个区域内假设未知函数,适用于边界几何形状简单的情形;有限单元法是将整个区域离散,分散成若干个单元,在单元上假设未知函数。
有限单元法是单元一级的Ritz 法。
2、单元刚度矩阵和整体刚度矩阵各有什么特征?刚度矩阵[K ]奇异有何物理意义?在 求解问题时如何消除奇异性?答:单元刚度矩阵的特征:⑴对称性⑵奇异性⑶主元恒正⑷平面图形相似、弹性矩阵D 、厚度t 相同的单元,e K 相同⑸e K 的分块子矩阵按结点号排列,每一子矩阵代表一个结点,占两行两列,其位置与结点位置对应。
整体刚度矩阵的特征:⑴对称性⑵奇异性⑶主元恒正⑷稀疏性⑸非零元素呈带状分布。
[]K 的物理意义是任意给定结构的结点位移所得到的结构结点力总体上满足力和力矩的平衡。
为消除[]K 的奇异性,需要引入边界条件,至少需给出能限制刚体位移的约束条件。
3. 列式说明乘大数法引入给定位移边界条件的原理?答:设:j j a a =,则将 jj jj k k α=j jj j P k a α=即:修改后的第j 个方程为112222j j jj j j n n jj j k a k a k a k a k a αα+++++=由于得 jj j jj j k a k a αα≈ 所以 j j a a ≈对于多个给定位移()12,,,l j c c c =时,则按序将每个给定位移都作上述修正,得到全部进行修正后的K 和P ,然后解方程即可得到包括给定位移在内的全部结点位移值。
4. 何为等参数单元?为什么要引入等参数单元?答:等参变换是对单元的几何形状和单元内的场函数采用相同数目的结点参数及相同的插值函数进行变换,采用等参变换的单元称之为等参数单元。
借助于等参数单元可以对于一般的任意几何形状的工程问题和物理问题方便地进行有限元离散,其优点有:对单元形状的适应性强;单元特性矩阵的积分求解方便(积分限标准化);便于编制通用化程序。
计算力学大作

以下确定 Q(y),和 R(x); 将 u,V 代入 exy 表达式得
PLx PLx 2 dQ( y) vPy 2 dR( x) (1 v) P h 2 ( y2 ) EJ 2 EJ dy 2 EJ dx EJ 4
再分别对 x 和 y 求导并积分有
Q( y )
vPy 3 (1 v) Py 3 (1 v) Pyh 2 Ay B 6 EJ 3EJ 4 EJ PLx 2 Px3 R( x) Ax C 2 EJ 6 EJ
{
联立解得:
c1 2P h3
c2 0
c3
3P 2h
c4
P 2
故: 有上式求解应力:
A
P y y3 ( L x)(1 3 4 3 ) 2 h h
X
2 A P( L x) y y 2 J
{ 利用广义 Hooked 定律
eij
2 A y 0 x 2 2 A P h2 xy ( y2 ) yx 2J 4
目录
计算力学大作业 ......................................................................................................... 1 一. 解析部分 ................................................................................................... 1 二. 数值计算结果 ............................................................................................ 4 第一组: ..................................................................................................... 4 第二组 ......................................................................................................... 8 第三组 ......................................................................................................... 9 第四组 ....................................................................................................... 10 三. COMSOL 计算 .......................................................................................... 11 1x16 网格................................................................................................... 11 1x20 网格................................................................................................... 13 Finer 网格(由 COMSOL 自动生成) ....................................................... 14 较短梁讨论 ....................................................................................................... 15
计算物理学课后答案(第一章、第二章)

第1章:绪论【1.2】设准确值为* 3.78694x =,*10y =,取它们的近似值分【1.1】按有效数字的定义,从两个方面说出1.0,1.00,1.000的不同含义【解】1.0,1.00,1.000的有效数字分别是两位,三位和四位;绝对误差限分别是0.05,0.005和0.0005别为123.7869, 3.780x x ==及129.9999, 10.1y y ==,试分析1212,,,x x y y 分别具有几位有效数字。
【解】*10.000040.00005x x -=<,1x 有5位有效数字;*20.006940.005x x -=>,2x 有2位有效数字;*10.000010.0005y y -=<,1y 有4位有效数字*2||0.10.5y y -=<,2y 有2位有效数字【1.3】(1)设p 的近似数有4位有效数字,求其相对误差限。
(2)用22/7和355/113作为 3.14159265p =L 的近似值,问它们各有几位有效数字?【解】(1)其绝对误差限是0.0005,则相对误差限为0.0005/3.1420.01591%r E ==(2)22/7 3.142857...=,有3位有效数字;355/113 3.14159292...=,有7位有效数字。
【1.4】试给出一种算法计算多项式32216180x a x a x a ++的函数值,使得运算次数尽可能少。
【解】24816328163281632012012,,,,x x x x x a x a x a x a x a x a x Þ++=++,总共8次乘法,两次加法【1.5】测量一木条长为542cm ,若其绝对误差不超过0.5cm ,问测量的相对误差是多少?【解】相对误差为0.5/5420.09%Î==【1.6】已知 2.71828e =L ,试问其近似值1232.7, 2.71, 2.718x x x ===各有几位有效数字?并给出他们的相对误差限。
东南大学土木工程弹性力学试卷

A 试卷1、 基本概念解释(24分,6小题)(1) 弹性力学的基本假定(2) 平面应变问题(3) 平面应力问题(4) 圣维南原理(5) 逆解法(6) 最小势能原理2、 简单题(40分,4题)(1) 列出图示全部边界条件。
(2) 求出下列应力函数的应力分量,并考察该应力函数是否满足相容方程A : )43(222243y h y x hF +=Φ B :)2(10)134(4332332h y hy qy h y h y qx -+--=Φ 注:由于此题目融合两个知识点,出两个小题,因此每个小题10分。
(3) 根据圣维南原理,比较图示中OA 边的面力是否等效,b h >>。
3、 综合题(36分)(1) 设单位厚度的悬臂梁在左端受到集中力和力矩作用(如图),体力不计,h l >>,试用应力函数332Dxy Cy By Axy +++=Φ求解应力分量。
(2) 矩形截面的长柱,密度为ρ,在一边侧面上受均布正应力q ,试求应力分量,体力不计。
A 试卷1、 基本概念解释(1) 连续性,完全弹性,均匀性,各向同性,位移和形变是微小的。
(2) 0=z ε,0=zx γ,0=zy γ,只存在平面应变分量x ε,y ε,xy γ,且不沿z 方向变化,仅为x ,y 的函数。
(3) 0=z σ,0=zx τ,0=zy τ,只存在平面应力分量x σ,y σ,xy τ,且不沿z 方向变化,仅为x ,y 的函数。
(4) 如果把物体的一小部分边界上的面力,变换为分布不同但静力等效的面力,那么,近处的应力分布将有显著的改变,但是远处所受的影响可以不计。
(5) 先设定各种形式的、满足相容方程的应力函数Φ;并求得应力分量;然后再根据应力边界条件和弹性体的边界形状,看这些应力分量对应于边界上什么样的面力,从而得知所选取的应力函数可以解决的问题。
(6) 在所有几何可能位移中,真实位移使得总势能取最小值。
2、 简单题(1) A :0)(2/==b x x σ,q b x xy ==2/)(τ;0)(2/=-=b x x σ,q b x xy 2)(2/-=-=τ;⎰-==2/2/00)(b b y y dx σ,⎰-==2/2/00)(b b y yx dx τ,⎰-==2/2/00)(b b y y xdx σ;0)(==h y u ,0)(==h y vB :0)(2/=-=h y y σ,q h y yx 2)(2/=-=τ;q h y y -==2/)(σ,0)(2/==h y yx τ;⎰-==2/2/00)(h h x x dy σ,⎰-==2/2/00)(h h x xy dy τ,⎰-=-=2/2/0)(h h x x M ydy σ;0)(==l x u ,0)(==l x v(2) A : )43(222243y h y x hF +=Φ B :)2(10)134(4332332h y hy qy h y h y qx -+--=Φ (3) ⎰--=-=-2/2/23)23(b b F qb dx q x b q ,⎰-==-2/2/212)23(b b qb M xdx q x b q3、 综合题(1) Dxy Cy B x 662++=σ,0=y σ,23Dy A xy --=τ⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-==⇒⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+-=-==+⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-==⎰⎰⎰-=-=-=±=022*********)()()(0)(32322/2/02/2/02/2/02/D h MC h F B A Dh A M Ch F Bh Dh A dy M ydy F dy s s h h x xy h h x x h h s x x h y xy τσστ 312hMy h F s x --=σ,0=y σ,0=xy τ (2) )()(2)()(2x h y x g y x f x f x ++=Φ⇒=σ 由相容方程可得234523232610)()(2Kx Hx x B x A Gx Fx Ex y D Cx Bx Ax y ++--++++++=Φ K Hx Bx Ax F Ex y B Ax y y 2622)26()26(2232++--+++=σD Cx Bx Ax x +++=23σ)23()23(22G Fx Ex C Bx Ax y xy ++-++-=τ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-+-=++-=⇒⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧=-=======-=⇒⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧=======⎰⎰⎰-=-=-=-=-===)236(53462232010000223020)(0)(0)(0)(0)(0)()(2333233332/2/02/2/02/2/02/2/2/2/b q x b q y x b q x b q xy b q q x b q x b q K b qH G F E q D b q C B b q A xdx dx dx q xy y x b b y y b b y yx b b y y b x xy b x x b x xy b x x τσσστστστσ。
2017-东南大学计算力学习题讲解

8 l
9
可以使用线性单元的 简化方法
东南大学土木工程学院
q
1 2 3
单元①荷载作用在1-2边上,故等 效结点力只与1、2号结点有关, 形函数
①
4 5
②
6
N1 (1 )
N 2
7 l
8 l
9
0 线性分布面力 q q
{FS } [ N ] {qS }hds
l
η
1 η=1 2
ξ=1
1 4 5
ξ
东南大学土木工程学院
单元②形函数
2 2 s 3
s N2 l
N3 1
s l
N6 0
6
s 0 1 l T Fs N qs ds s l l 0 1 l
0 q s s q l
7
3
三角形单元族插值 函数构造及变节点 数法联合运用
东南大学土木工程学院
1
1 x y xy x2y x3y x2y2 xy2 xy3 y2
完全一次 完全二次
9
4 5 10
x2
8
x3
3
y3 完全三次 y4
2
x4
6
7
•Pascal三角形
u 1 2 x 3 y 4 x 2 5 xy 6 y 2 7 x 3 8 x 2 y 9 xy 2 10 y 3 2 2 3 2 2 3 v x y x xy y x x y xy y 11 12 13 14 15 16 17 18 19 20
1
2
3
4
东南大学结构力学练习题(附答案)详解

第一部分 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBAC DB5、 6、A CDBEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、124567831234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、ACBDEF三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二部分 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
(a)BCa aA ϕ2a2 (b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0,R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2(。
)↑9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
—— 1 ——11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:=== 0。
N 1N 2N 313、图(h)所示桁架DE 杆的内力为零。
a a(h)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章1如图所示一三角形钢板,两个结点固定,对第三个结点施以单位水平位移,测出所施加的力,从而得出相应的刚度系数。
其他点依此类推,这样测得的刚度系数所组成的刚度矩阵,是否与按照常规三角形单元刚度矩阵计算公式所得结果一样?用这样实测所得的刚度矩阵能否进行有限元分析?为什么?解:不一样。
单元刚度矩阵中每个元素的物理意义:ij k 表示单元第j 个自由度产生单位位移,其它自由度固定时,第i 个自由度产生的节点力。
单元刚度矩阵是在单元处于平衡状态的前提下得出的,单元作为分离体看待,作用在它上面的外力(单元力)必是平衡力系,然而研究单元平衡时没有引入约束承受平衡力系作用的无约束单元,其变形是确定,但位移是不能确定的,即单元可发生任意的刚体位移。
不能。
因为与有限元中单元与单元之间的约束情况不一样,不能进行有限元分析。
2以位移为基本未知量的有限元法其解具有下限性质,试证明之。
解:系统总位能的离散形式{}{}{}{}12T Tp a K a a P ∏=- 将求解的方程[]{}{}K a P =带入可得{}[]{}{}[]{}{}[]{}1122T T Tp a K a a K a a K a U ∏=-=-=- 在平衡情况下,系统总位能等于负的应变能。
在有限元解中,由于假定的近似位移模式一般来说总与精确解有差别的。
设近似解为p ∏、U 、[]K 、{}a 、{}{}K a P ⎡⎤=⎣⎦,真实解为p ∏、U 、[]K 、{}a 、[]{}{}K a P = 且根据最小势能原理,得到的系统的总位能总会比真正的总位能要大,故p p ∏≥∏则U U ≤{}{}{}[]{}{}{}{}{}TT TTa K a a K a a P a P ⎡⎤≤⇒≤⎣⎦则近似解的位移总体上小于精确解的位移解释如下:单元原是连续体的一部分,具有无限多个自由度,在假定了单元的位移函数后,自由度限制为只有以结点位移表示的有限自由度,引入了更多的约束和限制,使得单元刚度较实际连续体加强了,连续体的整体刚度随之增加,所以有限元解整体上较真实解偏小。
3 请分别阐述单元刚度矩阵和整体刚度矩阵中任一元素的物理意义。
解:在单刚[]eK 中,eij k 表示单元第j 个位移产生一单位位移,其它位移为零时,第i 个位移方向上引起的节点力。
在整体刚度中,ij K 表示第j 个自由度产生一单位位移,其它自由度为零时,第i 个自由度上引起的节点力。
4 简述虚功原理,且使用虚功原理导出外荷载与节点荷载的等效关系式。
解:虚功原理:变形体中任意满足平衡的力系在任意满足协调条件的变形状态上作的虚功等于零,即体系外力的虚功与内力的虚功之和等于零。
设{}eq 为外荷载(此处为体力),{}ep 为节点荷载,{}ew 为单元内位移场,{}eδ为结点位移场 根据虚功原理{}{}{}{}{}{}TTe ee eVp w q dV δ=⎰由于{}{}[]e ew N δ=故{}{}{}{}{}{}{}{}{}[][]TTTe ee ee eTTVVVw q dV N q dV N q dV δδ==⎰⎰⎰则{}{}{}{}{}{}{}{}[][]TTe ee eeeT T VVp N q dV p N q dV δδ=⇒=⎰⎰5 试述弹性力学中按位移求解与有限单元法中按位移求解之间的异同点。
解:6 如果三节点三角形单元绕其中某一个节点作小的刚体转动,其转角为,证明单元内所有的应力均为零。
解:在三角形单元中{}[][]{}D B σδ=[]0000001100000022ij m j m m ii ji j m j m m i i j i ijjmm j m j mm im ii ji j b b b y y y y y y B c c c x x x x x x AAc b c b c b x x y y x x y y x x y y ⎡⎤⎡⎤---⎢⎥⎢⎥==-+-+-+⎢⎥⎢⎥⎢⎥⎢⎥-+--+--+-⎣⎦⎣⎦ 由于三角形单元绕其中某一个节点作小的刚体转动,各节点的位移可表示为:00u u yv v x θθ=-⎧⎨=+⎩则可知节点位移向量{}{}0,0,,,,TTj j m my x y x δθθθθ=--故应变{}[]{}000000110000220i m m i i j j j m m i i j j j m i mm im ii ji j mm y y y y y y y B x x x x x x x AA x x y y x x y y x x y y y x θεδθθθ⎧⎫⎪⎪⎪⎪⎡⎤---⎧⎫⎪⎪-⎢⎥⎪⎪⎪⎪==-+-+-+=⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥-+--+--+-⎩⎭⎣⎦⎪⎪-⎪⎪⎪⎪⎩⎭由于弹性矩阵[]D 为常量矩阵,应变向量{}ε为零向量,故{}[]{}D σε=为零向量,即单元内所有的应力为零。
7 二维单元在,x y 坐标内平面平移到不同位置,单元刚度矩阵相同吗?在平面内旋转时又怎样?试证明之。
解:二维单元在,x y 坐标内平面移到不同位置时,刚度矩阵相同。
在平面内旋转时,刚度矩阵也相同。
刚度矩阵[][][][]21122114(1)22r s r sr s r s T rs r s r s r s r s r s b b c c b c c b EhA k B D B hA c b b c c c b b μμμμμμμ--⎡⎤++⎢⎥==⎢⎥---⎢⎥++⎢⎥⎣⎦单元平移或旋转时,,i i b c 不变,故单元刚度矩阵不变。
8 判断有限元网格离散合理性a) 对图1(a)所示的有限元网格,评论网格的优劣性,指出模型中的错误,并加以改正。
b) 评论图1(b)的网格划分合理吗?为什么?请加以改正。
图1 解:(a )网格划分不合理。
1)无过渡单元 2)无边界条件3)夹角区应力集中,应适当加密风格 4)对称结构网格应对称划分 (b )不合理。
1)左部网格应适当加密2)由于三角形单元会造成局部精度不够,过渡区可采用其它单元划分 3)右部单元的长宽比较大,就进行适当调整。
9 如图2所示,平面三角形构件以x-y 坐标系表示的刚度矩阵方程如下:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------2211221145.25.25.25.25.25.25.45.25.20.55.283.15.283.15.21010y x y x y x y x P P P P v u v u试建立以1x u ,1y u ,,2x u (与图中,2x P 同向的位移)及1x P ,1y P ,'2x P来表示的刚度矩阵方程。
解:用坐标变换{}[]{}'T δδ=则[]111111''222''222cos sin x x x y y y x x x y x x u u u v v v T u u u v u u αα⎧⎫⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎩⎭其中[]100001000cos 000sin 0T αα⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦, 由[]{}{}[][]{}{}'K P K T P δδ=⇒=[][]100010 2.5 1.83 2.510 2.5 2.964001001.83 2.5 5.0 2.5 1.83 2.5 2.5040002.5 4.5 2.5 2.5 2.5 4.50.5052.5 2.5 2.5 2.53 2.5 2.50.50005K T ⎡⎤⎢⎥--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥----⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦11411''2210 2.5 2.96410 1.83 2.5 2.5020x x y y x x u P v P u P -⎡⎤⎧⎫⎧⎫⎪⎪⎪⎪⎢⎥=⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎣⎦⎩⎭⎩⎭10 某平面结构采用四节点矩形单元和三节点三角形单元建立有限元计算模型,其如图3所示。
试求结点2的等效荷载列阵{}2R 。
荷载作用于12-边上,故等效节点力只与12、号节点有关解:单元①,形函数12,(1)N N ξηηξ==-,在1η=边上,121,1N Nξξ∂∂==-∂∂ 12120,0N N N N x y l l m m ξξξξξξ∂∂∂∂∂∂=+==+=∂∂∂∂∂∂则ds ld ξξ== 线性分布面力{}0q q ξ⎧⎫=⎨⎬⎩⎭则121103y y lqlP N q ds qld ξξ===⎰⎰图5形函数1231,,0s s N N N l l =-== 在1-2边上,{}0s q s q l ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭单元③,{}{}010000[]01000120000233TTS S l l Tss l l F N q ds ds s s sq l l l ql ⎡⎤-⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦⎧⎫=⎨⎬⎩⎭⎰⎰故节点2的等效荷载列阵{}2023R ql ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭11 试求如图4所示的有限元网格的整体刚度矩阵,假设每个节点的自由度数为1,且设eK 表示第e 个单元的单元 刚度矩阵(注意:结果应该用eij k 表示)。
解:单元刚度矩阵{}(1)(1)(1)(1)11121415(1)(1)(1)(1)(1)21222425(1)(1)(1)(1)41424445(1)(1)(1)(1)51525455k k k k k k k k K k k k k k k k k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,{}(2)(2)(2)(2)22232625(2)(2)(2)(2)(2)32333635(2)(2)(2)(2)52636665(2)(2)(2)(2)62535655k k k k k k k k K k k k k k k k k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦{}(3)(3)(3)555758(3)(3)(3)(3)757778(3)(3)(3)858788k k k K k k k k k k ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,{}(4)(4)(4)555658(4)(4)(4)(4)656668(4)(4)(4)858688k k k K k k k k k k ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦整体刚度矩阵:[](1)(1)(1)(1)11121415(1)(1)(2)(2)(1)(1)(2)(2)2122222324252526(2)(2)(2)(2)32333536(1)(1)(1)(1)41424445(1)(1)(2)(2)(1)(1)(2)(3)(4)(515252535455555555560000000000000k k k k k k k k k k k k k k k k kk k k K k k k k k k k k k k ++=++++2)(4)(3)(3)(4)56575858(2)(2)(2)(4)(2)(4)(4)62636565666668(3)(3)(3)757778(3)(4)(4)(3)(3)(4)858586878888000000000k k k k k k k k k k k k k k k k k k k k ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎢⎥++⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦12 图5中两个三角形单元组成平行四边形,已知单元①按局部编码,,i j m 的单元刚度矩阵K ①和应力矩阵S ①是(1)806626166126413.597.5313.53 1.59.535.5K ---⎛⎫ ⎪--- ⎪ ⎪--= ⎪-- ⎪ ⎪- ⎪ ⎪⎝⎭对称(1)00303004030120 1.5-1.5-0.5 1.5S ⎛⎫ ⎪= ⎪ ⎪-⎝⎭---按图5示单元②的局部编码写出K ②,S ②。
