机械振动基础第2章习题
【单元练】高中物理选修1第二章【机械振动】经典练习题(2)
一、选择题1．如图甲所示，在一条张紧的绳子上挂几个摆。
当a 摆振动的时候，其余各摆在a 摆的驱动下也逐步振动起来，不计空气阻力，达到稳定时，b 摆的振动图像如图乙。
下列说法正确的是（ ）A ．稳定时b 摆的振幅最大B ．稳定时b 摆的周期最大C ．由图乙可以估算出b 摆的摆长D ．由图乙可以估算出c 摆的摆长D 解析：DA ．a 与c 的摆长接近，它们的固有频率接近，在a 摆的驱动下，稳定时c 摆的振幅最大，所以A 错误；B ．bc 摆是在a 摆的驱动下振动起来的，则b 的周期等于外力周期，稳定时abc 摆的周期都相同，所以B 错误； CD ．根据单摆的周期公式2l T g=解得224T gl π= 由图像可得a 摆周期，则可以算出a 摆的摆长，估算出c 摆的摆长，所以C 错误；D 正确； 故选D 。
2．下列说法中 不正确 的是( )A ．将单摆从地球赤道移到南(北)极,振动频率将变大B ．将单摆从地面移至距地面高度为地球半径的高度时,则其振动周期将变到原来的2倍C ．将单摆移至绕地球运转的人造卫星中,其振动频率将不变D ．在摆角很小的情况下,将单摆的振幅增大或减小,单摆的振动周期保持不变C 解析：CA 、将单摆从地球赤道移到南（北）极，重力加速度增加，根据2LT gπ=，振动的周期变小，故振动频率将变大，故A 正确；B 、重力等于万有引力，故：2Mm mg Gr =，解得：2GMg r =，将单摆从地面移至距地面高度为地球半径的高度时，r 增加为2倍，故g 减小为14；根据2T π=2倍，故B 正确； C 、将单摆移至绕地球运转的人造卫星中，处于完全失重状态，不能工作，故C 错误；D 、根据2T =，振动的周期与振幅无关；在摆角很小的情况下，将单摆的振幅增大或减小，单摆的振动周期保持不变，故D 正确． 【点睛】本题关键是根据单摆的周期公2T =和重力加速度公式2GM g r =分析，注意周期与振幅无关．3．关于简谐运动，下列说法正确的是（ ）A ．做简谐运动物体所受的回复力方向不变，始终指向平衡位置B ．在恒力的作用下，物体可能做简谐运动C ．做简谐运动物体速度越来越大时，加速度一定越来越小D ．做简谐运动物体的加速度方向始终与速度方向相反C 解析：CA ．回复力是使做简谐运动的物体返回平衡位置并总指向平衡位置的力，所以物体在远离和靠近平衡位置时的方向不同，A 错误；B ．物体做简谐运动中回复力满足F x κ=-即回复力大小与位移大小成正比，方向与位移方向相反，所以在恒力的作用下，物体不可能做简谐运动，B 错误；C ．做简谐运动物体速度越来越大，说明物体向着平衡位置运动，物体受回复力越来越小，加速度一定越来越小，C 正确；D ．做简谐运动物体的加速度方向始终指向平衡位置，速度方向与物体运动方向相同，物体做简谐运动过程中，加速度方向和速度方向有时相同，有时相反，D 错误。
2020--2021学年人教版(新教材)物理选择性必修第一册第2章：机械振动练习含答案
2020--2021人教（新教材）物理选择性必修第一册第2章：机械振动练习含答案人教（新教材）选择性必修第一册第2章：机械振动1、关于简谐运动的位移、速度和加速度的关系，下列哪些说法正确()A．位移减小时，加速度增大，速度增大B．位移方向总跟加速度的方向相反，跟速度方向相同C．物体运动方向指向平衡位置时，速度方向跟位移方向相反；背向平衡位置时，速度方向跟位移方向相同D．物体向平衡位置运动时，做减速运动，背离平衡位置时，做加速运动2、关于机械振动的位移和平衡位置，以下说法中正确的是()A．平衡位置就是物体振动范围的中心位置B．机械振动的位移是以平衡位置为起点的位移C．机械振动的物体运动的路程越大，发生的位移也就越大D．机械振动的位移是指振动物体偏离平衡位置最远时的位移3、如图所示，弹簧振子在BC间振动，O为平衡位置，BO＝OC＝5 cm，若振子从B到C的运动时间为1 s，则下列说法正确的是()A．振子从B经O到C完成一次全振动B．振动周期是1 s，振幅是10 cmC．经过两次全振动，振子通过的路程是20 cmD．从B开始经过3 s，振子通过的路程是30 cm4、一个做简谐运动的物体，每次具有相同的动能时，下列说法正确的是()A．一定具有相同的势能B．一定具有相同的速度C．一定具有相同的加速度D．一定具有相同的位移5、关于单摆，下列认识中正确的是()A．一根线系着一个球悬挂起来，这样的装置就是单摆B．可以看成单摆的装置中，细线的伸缩和质量忽略不计，线长比小球直径大得多C．单摆的振动总是简谐运动D．两个单摆只要结构相同，它们的振动步调便相同6、在洗衣机把衣服脱水完毕后，电动机还要转动一会才能停下来，此时发现洗衣机先振动得比较小，然后有一阵子振动得很剧烈，然后振动慢慢减小直至停下来，其间振动剧烈的原因是()A．洗衣机没放平衡B．电动机有一阵子转快了C．电动机转动的频率和洗衣机的固有频率相近或相等D．这只是一种偶然现象7、弹簧振子以O点为平衡位置，在水平方向上的A、B两点间做简谐运动，以下说法正确的是()A．振子在A、B两点时的速度和位移均为零B．振子在通过O点时速度的方向将发生改变C．振子所受的弹力方向总跟速度方向相反D．振子离开O点的运动总是减速运动，靠近O点的运动总是加速运动8、一个做简谐运动的质点，它的振幅是4 cm，频率是2.5 Hz，该质点从平衡位置开始经过2.5 s后，位移的大小和经过的路程为()A．4 cm10 cm B．4 cm100 cmC．024 cm D．0100 cm9、做简谐运动的弹簧振子，其质量为m，最大速率为v0，若从某时刻算起，在半个周期内，合外力()A．做功一定为0B．做功一定不为0C．做功一定是12m v2D．做功可能是0到12m v2之间的某一个值10、单摆在振动过程中，当摆球的重力势能增大时，摆球的()A．位移一定减小B．回复力一定减小C．速度一定减小D．加速度一定减小11、在飞机的发展史中有一个阶段，飞机上天后不久，飞机的机翼(翅膀)很快就抖动起来，而且越抖越厉害，后来经过人们的探索，利用在飞机机翼前装一个配重杆的方法，解决了这一问题，在飞机机翼前装配重杆的目的主要是()A．加大飞机的惯性B．使机体更加平衡C．使机翼更加牢固D．改变机翼的固有频率12、如图所示是某质点做简谐运动的振动图像．根据图像中的信息，回答下列问题．(1)质点离开平衡位置的最大距离有多大？(2)质点在10 s末和20 s末的位移各是多少？(3)质点在15 s和25 s时各向什么方向运动？(4)质点在前30 s内运动的路程是多少？13、如图所示，一个轻弹簧与一个质量为m＝0.5 kg的小球所构成的弹簧振子放在光滑金属杆上，已知该弹簧的劲度系数k＝200 N/m，O点是弹簧振子静止时的位置，今将振子向右拉10 cm到A点，此时外力对弹簧振子做功为1 J，然后由静止释放，则它在A、B之间运动，不计其他阻力，求：(1)振子在哪点的速度最大？最大速度为多少？(2)振子在A点的位移．(3)振子在B点的加速度．2020--2021人教（新教材）选择性必修第一册第2章：机械振动练习含答案人教（新教材）选择性必修第一册第2章：机械振动1、关于简谐运动的位移、速度和加速度的关系，下列哪些说法正确()A．位移减小时，加速度增大，速度增大B．位移方向总跟加速度的方向相反，跟速度方向相同C．物体运动方向指向平衡位置时，速度方向跟位移方向相反；背向平衡位置时，速度方向跟位移方向相同D．物体向平衡位置运动时，做减速运动，背离平衡位置时，做加速运动解析：位移增大时，加速度a ＝－kx m 增大，但物体做减速运动，速度减小，故A错误；加速度a ＝－kx m ，负号表示加速度方向与位移方向总相反，靠近平衡位置时加速，位移方向与速度方向相反，故B 错误，C 正确；物体向平衡位置运动时回复力的方向与运动方向相同，做加速运动，背离平衡位置时，回复力的方向与运动方向相反，物体做减速运动，故D 错误．答案：C2、关于机械振动的位移和平衡位置，以下说法中正确的是( )A ．平衡位置就是物体振动范围的中心位置B ．机械振动的位移是以平衡位置为起点的位移C ．机械振动的物体运动的路程越大，发生的位移也就越大D ．机械振动的位移是指振动物体偏离平衡位置最远时的位移解析：平衡位置是物体可以静止的位置，所以应与受力有关，与是否为振动范围的中心位置无关，A 错误；振动位移是以平衡位置为初始点，到振动物体所在位置的有向线段，振动位移随时间而变化，振动物体偏离平衡位置最远时，振动位移最大，B 正确，D 错误；振动物体的位移与运动的路程没有关系，C 错误．答案：B3、如图所示，弹簧振子在BC 间振动，O 为平衡位置，BO ＝OC ＝5 cm ，若振子从B 到C 的运动时间为1 s ，则下列说法正确的是( )A ．振子从B 经O 到C 完成一次全振动B．振动周期是1 s，振幅是10 cmC．经过两次全振动，振子通过的路程是20 cmD．从B开始经过3 s，振子通过的路程是30 cm解析：振子从B→O→C仅完成了半次全振动，所以周期T＝2×1 s＝2 s，振幅A＝BO＝5 cm，A、B错误；振子在一次全振动中通过的路程为4A＝20 cm，所以两次全振动振子通过的路程为40 cm，C错误；3 s的时间为1.5T，所以振子通过的路程为30 cm，D正确．答案：D4、一个做简谐运动的物体，每次具有相同的动能时，下列说法正确的是() A．一定具有相同的势能B．一定具有相同的速度C．一定具有相同的加速度D．一定具有相同的位移答案：A5、关于单摆，下列认识中正确的是()A．一根线系着一个球悬挂起来，这样的装置就是单摆B．可以看成单摆的装置中，细线的伸缩和质量忽略不计，线长比小球直径大得多C．单摆的振动总是简谐运动D．两个单摆只要结构相同，它们的振动步调便相同解析：单摆是实际摆的理想化模型，实际摆只有在不计绳的伸缩、质量和阻力以及小球可以看作质点时才能看作单摆，A错，B正确．单摆的运动只有在摆角很小时才能看作简谐运动，C错．两单摆结构相同时，振动步调不一定相同，D错．答案：B6、在洗衣机把衣服脱水完毕后，电动机还要转动一会才能停下来，此时发现洗衣机先振动得比较小，然后有一阵子振动得很剧烈，然后振动慢慢减小直至停下来，其间振动剧烈的原因是()A．洗衣机没放平衡B．电动机有一阵子转快了C．电动机转动的频率和洗衣机的固有频率相近或相等D．这只是一种偶然现象解析：洗衣机脱水时，电动机转速很快，频率很大，可以说远大于洗衣机的固有频率，不能发生共振现象．当脱水终止时，随着电动机转速的减小，频率也在减小，肯定有一段时间，频率接近或等于洗衣机的固有频率，从而发生共振现象，洗衣机振动剧烈．答案：C7、弹簧振子以O点为平衡位置，在水平方向上的A、B两点间做简谐运动，以下说法正确的是()A．振子在A、B两点时的速度和位移均为零B．振子在通过O点时速度的方向将发生改变C．振子所受的弹力方向总跟速度方向相反D．振子离开O点的运动总是减速运动，靠近O点的运动总是加速运动答案：D8、一个做简谐运动的质点，它的振幅是4 cm，频率是2.5 Hz，该质点从平衡位置开始经过2.5 s后，位移的大小和经过的路程为()A．4 cm10 cm B．4 cm100 cmC．024 cm D．0100 cm答案：B9、做简谐运动的弹簧振子，其质量为m，最大速率为v0，若从某时刻算起，在半个周期内，合外力()A．做功一定为0B．做功一定不为0C．做功一定是12m v2D．做功可能是0到12m v2之间的某一个值解析：弹簧振子过半个周期一定运动到关于平衡位置对称的位置处，两处速度大小相等，由动能定理知合外力做功为0，A正确．答案：A10、单摆在振动过程中，当摆球的重力势能增大时，摆球的()A．位移一定减小B．回复力一定减小C．速度一定减小D．加速度一定减小解析：单摆在振动过程中，当摆球的重力势能增大时，摆球的位移变大，回复力变大，加速度变大，速度减小，C对．答案：C11、在飞机的发展史中有一个阶段，飞机上天后不久，飞机的机翼(翅膀)很快就抖动起来，而且越抖越厉害，后来经过人们的探索，利用在飞机机翼前装一个配重杆的方法，解决了这一问题，在飞机机翼前装配重杆的目的主要是()A．加大飞机的惯性B．使机体更加平衡C．使机翼更加牢固D．改变机翼的固有频率解析：飞机的机翼(翅膀)很快抖动起来，是因为驱动力的频率接近机翼的固有频率，机翼发生共振，在飞机机翼前装配重杆，是为了改变机翼的固有频率，使驱动力的频率远离机翼的固有频率，选项D正确．答案：D12、如图所示是某质点做简谐运动的振动图像．根据图像中的信息，回答下列问题．(1)质点离开平衡位置的最大距离有多大？(2)质点在10 s末和20 s末的位移各是多少？(3)质点在15 s和25 s时各向什么方向运动？(4)质点在前30 s内运动的路程是多少？解析：(1)质点离开平衡位置的最大距离等于质点的最大位移的大小，由题图看出，此距离为20 cm.(2)质点在10 s末的位移x1＝20 cm,20 s末的位移x2＝0.(3)15 s末质点位移为正，15 s后的一段时间，位移逐渐减小，故质点在15 s末向负方向运动，同理可知，25 s末质点也向负方向运动．(4)前30 s质点先是由平衡位置沿正方向振动了20 cm，又返回平衡位置，最后又到达负方向20 cm处，故30 s内运动的总路程为60 cm.答案：(1)20 cm(2)20 cm0(3)负方向负方向(4)60 cm13、如图所示，一个轻弹簧与一个质量为m＝0.5 kg的小球所构成的弹簧振子放在光滑金属杆上，已知该弹簧的劲度系数k＝200 N/m，O点是弹簧振子静止时的位置，今将振子向右拉10 cm到A点，此时外力对弹簧振子做功为1 J，然后由静止释放，则它在A、B之间运动，不计其他阻力，求：(1)振子在哪点的速度最大？最大速度为多少？(2)振子在A 点的位移．(3)振子在B 点的加速度． 解析：(1)由于弹簧振子在运动过程中满足机械能守恒，故在平衡位置O 点的速度最大，由题意知：外力做的功转化为系统的弹性势能，该势能又全部转化成振子的动能，即W ＝12m v 2解得：v ＝2Wm ＝2×10.5 m/s ＝2 m/s. (2)振子在A 点的位移大小为x ＝10 cm ，方向由O 指向A.(3)由于振动的振幅为10 cm ，故在B 点的位移大小是10 cm ，即弹簧压缩10 cm ，此时回复力的大小F ＝kx ＝200×0.1 N ＝20 N ，即振子所受到的合外力大小为20 N ，由牛顿第二定律得：a ＝F m ＝200.5 m/s 2＝40 m/s 2，方向由B 指向O.答案：(1)O 点 2 m/s(2)10 cm ，方向由O 指向A(3)40 m/s 2，方向由B 指向O。
初中《物理》第2章机械振动单元练习题
初中《物理》第2章机械振动单元练习题一、单选题1.弹簧振子做简谐运动，振幅为0.4cm，周期为0.5s，计时开始时具有正向最大加速度，则它的位移公式是()) mA. x=8×10−3sin(4πt+π2) mB. x=4×10−3sin(4πt−π2) mC. x=8×10−3sin(2 πt+π2) mD. x=4×10−3sin(2 πt−π22.蜘蛛捕食是依靠昆虫落在丝网上引起的振动准确判断昆虫的方位。
已知丝网固有频率为f0，某昆虫掉落在丝网上挣扎时振动频率为f，则该昆虫落在丝网上时()A. f增大，则丝网振幅增大B. f减小，则丝网振幅减小C. 昆虫引起丝网振动的频率为f0D. 丝网和昆虫挣扎振动周期相同3.如图甲所示，弹簧振子以O点为平衡位置，在M、N两点之间做简谐运动。
振子的位移x随时间t的变化图像如图乙所示。
下列判断正确的是()A. 0.4s时振子的加速度为零B. 0.8s时振子的速度最大C. 0.4s和1.2s时振子的加速度相同D. 0.8s和1.6s时振子的速度相同4.如图甲所示，一弹簧振子在竖直方向上做简谐运动，以竖直向上为正方向，弹簧振子的振动图像如图乙所示，则弹簧振子()A. 频率为2.0HzB. 振幅为0.4mC. 0～0.5s内，动能逐渐减小D. t=0.5s与t=1.5s时，振子的位移相同5.甲、乙两单摆的振动图像如图所示，由图像可知()A. 甲、乙两单摆的周期之比是3:2B. 甲、乙两单摆的摆长之比是2:3C. t b时刻甲、乙两单摆的摆球速度相同D. t a时刻甲、乙两单摆的摆角不相等6.如图所示为两个单摆做受迫振动的共振曲线，则下列说法正确的是()A. 两个单摆的固有周期之比为TⅠ:TⅡ=5:2B. 若两个受迫振动在地球上同一地点进行，则两单摆摆长之比为LⅠ:LⅡ=4:25C. 图线Ⅱ对应的单摆若是在地面上振动，则该摆摆长约为2mD. 若两个受迫振动分别在月球上和地球上进行，且摆长相等，则图线Ⅱ是月球上的单摆的共振曲线7.“单摆”是一种理想化模型，如图所示，长为l的轻绳下端拴着一个可视为质点的小球，上端固定在倾角为θ的光滑斜面上，这个装置也可以等效为“单摆”。
《机械振动基础》第二章
已知 A = ( aij ) n× n , Aij 为 aij的代数余子式 , 则
A11 A adjA = 12 ⋮ A1n
A21 A22 ⋮ A2 n
⋯ ⋯ ⋯
An1 An 2 ⋮ Ann
预备知识－线性代数与矩阵理论 预备知识－
【矩阵乘积的逆】 矩阵乘积的逆】
d 21 k2 (d11 − d 21 )
F2 = 0
k 2 + k3 d11 = k1k2 + k1k3 + k2 k3
k3d 21
m2
k2 (d11 − d 21 ) − k3d 21 = 0
k2 d 21 = k1k2 + k1k3 + k2 k3
2.2:建立系统运动微分方程的方法 2.2:建立系统运动微分方程的方法
ɺɺ ɺ ɺ ɺ mu1 = −k1u1 + k2 (u2 − u1 ) − c1u1 + c2 (u2 − u1 ) + f1 (t ) 1 ɺɺ ɺ ɺ ɺ m2u2 = −k2 (u2 − u1 ) − k3u2 − c2 (u2 − u1 ) − c3u2 + f2 (t )
方程之间存在耦合 方程之间存在耦合
ɺɺ Mu + Ku = f ɺɺ Ku = −Mu + f ɺɺ u = D(−Mu + f )
ɺɺ u = −DMu + Df
EI
A M 0 cos t
l
EI
l u2
m
u1
(1)利用Castigliano第二定理计算刚架端点的柔度系数得到柔 (1)利用Castigliano第二定理计算刚架端点的柔度系数得到柔 利用Castigliano第二定理 度矩阵D 度矩阵D Castigliano定理 定理： Castigliano 定理 ： 系统的势能对力的偏导数等于此力的作用点 沿力的方向的位移。 沿力的方向的位移。 (2)计算外力矩作用下刚架端部的动位移 (2)计算外力矩作用下刚架端部的动位移
(好题)高中物理选修一第二章《机械振动》测试题(含答案解析)(3)
一、选择题1．(0分)[ID ：127387]如图所示，曲轴上挂一个弹簧振子，转动摇把，曲轴可带动弹簧振子上下振动。
开始时不转动摇把，让振子自由振动，测得其频率为2Hz 。
现匀速转摇把，转速为240r/min 。
则（ ）A ．当振子稳定振动时，它的振动周期是0.5sB ．当振子稳定振动时，它的振动频率是4HzC ．当转速增大时，弹簧振子的振幅增大D ．振幅增大的过程中，外界对弹簧振子做负功2．(0分)[ID ：127386]如图所示，一根用绝缘材料制成的劲度系数为k 的轻弹簧左端固定，右端与质量为m 、带电荷量为+q 的小球相连，静止在光滑绝缘的水平面上，在施加一个场强为E 、方向水平向右的匀强电场后，小球开始做简谐运动，那么（ ）A ．小球完成一次全振动的过程电场力冲量等于零B ．小球到达最右端时，弹簧的形变量为2qE kC ．小球做简谐运动的振幅为2qE kD ．运动过程中小球的电势能和弹簧的弹性势能的总量不变3．(0分)[ID ：127376]如图甲所示，弹簧振子以O 点为平衡位置，在光滑水平面上的A 、B 两点之间做简谐运动，A 、B 分居O 点的左右两侧的对称点。
取水平向右为正方向，振子的位移x 随时间t 的变化如图乙所示的正弦曲线，下列说法正确的是（ ）A ．0.6s t =时，振子在O 点右侧6cm 处B ．振子0.2s t =和 1.0s t =时的速度相同C ． 1.2s t =时，振子的加速度大小为223πm/s 16，方向水平向右 D ． 1.0s t =到 1.4s t =的时间内，振子的加速度和速度都逐渐增大4．(0分)[ID ：127371]如图是甲、乙两个单摆做简谐运动的图象，以向右的方向作为摆球偏离平衡位置位移的正方向，从t ＝0时刻起，当甲第一次到达右方最大位移处时，乙在平衡位置的（ ）A ．左方，向右运动B ．左方，向左运动C ．右方，向右运动D ．右方，向左运动 5．(0分)[ID ：127369]如图所示，弹簧振子在A 、B 之间做简谐运动．以平衡位置O 为原点，建立Ox 轴．向右为x 轴的正方向．若振子位于B 点时开始计时，则其振动图像为（ ）A ．B ．C ．D ．6．(0分)[ID ：127365]如图所示，两长方体木块A 和B 叠放在光滑水平面上，质量分别为m 和M ，A 与B 之间的最大静摩擦力为0f ，B 与劲度系数为k 的水平轻质弹簧连接构成弹簧振子。
机械振动第2章(习题)
1 / 21第二章 单自由度系统习题2.1 弹簧下悬挂一物体，弹簧静伸长为δ。
设将物体向下拉，使弹簧有静伸长3δ，然后无初速度地释放，求此后的运动方程。
解：2n=g/δ运动微分方程（式2.5）：x +2nx=0初始条件：x (0)=3δ,x(0)=0 由式2.8有：A=2020)(ωnxx +=3δ=arctgnx xω00 =0由式2.7有： 响应：x =3δcos(δg t)2.2 弹簧不受力时长度为65cm ，下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放，试求物体的运动方程、振幅、周期及弹簧力的最大值。
解：ω2n =g/δ=9.8/0.2=49运动微分方程（式2.5）：x +ω2n x=0 初始条件：x (0)=-0.2,x(0)=0 由式2.8有：振幅：A=2020)(ωnxx +=0.2ϕ=arctgnx xω00 =0由式2.7有： 响应：x=0.2cos(7t) 周期：T=2/ωn弹簧刚度：k=mg/δ=19.8/0.2=49(N/m)最大弹簧力：F Smax =-kA=-490.2=9.8(N)2.3 重物m l 悬挂在刚度为k 的弹簧上并处于静平衡位置，另一重物m 2从高度为h 处自由落到m l 上而无弹跳，如图T —2.3所示，求其后的运动。
图 T —2.3解：ω2n =k/(m 1+m 2)运动微分方程（式2.5）：x+2nx=0初始条件：x (0)=- m 2g/km 2gh=21(m 1+m 2)x2(0)⇒ x (0) (以下略)2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆3 / 21心受到一弹簧k 约束，如图T —2.4所示，求系统的固有频率。
图 T —2.4解：系统的势能：U=21kr 2θ2系统的动能：E t =21I •θ2+21mr2•θ2由d(U+E t )=0得：（I+ mr 2）••θ+kr 2θ=0ω2n =22m r I kr +2.5 均质杆长L 、重G ，用两根长h 的铅垂线挂成水平位置，如图T —2.5所示，试求此杆相对铅垂轴OO 微幅振动的周期。
机械振动基础课后习题解答_第2章习题
0.5
1
1
1
1 1/ 3
u1 (t ) u2 (t)
8 4
/ /
9 9
cos(
k 2m
)t
1/9 1/ 9
cos(
2k )t m
(3) 求结构的稳态响应
m1u1(t) k1(u1(t) u2 (t)) m2u2 (t) k1(u1(t) u2 (t)) k2 (u2 (t) v(t))
0 0
(K 2M)φ 0
1
1
2 2
k J
,
2
1
2k 2 J
1 1
φ1
1/
2
,
φ2
1/
2
P88,2-6: 不计刚杆质量，按图示坐标建立运动微分方程，并求出固有频率和固有振型。
系统动能：T
1 2
mu12
1 2
2mu22
系统势能：U
1 2
k (2u1
u2 )2
1 2
k (2u2
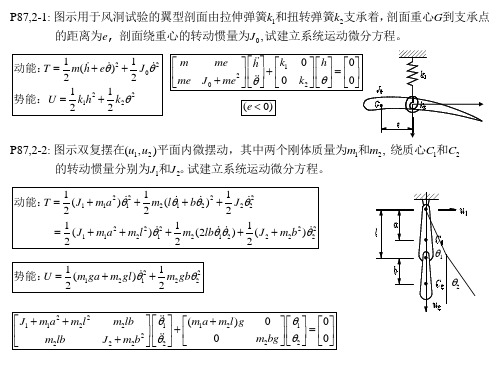
P87,2-1: 图示用于风洞试验的翼型剖面由拉伸弹簧k1和扭转弹簧k2支承着，剖面重心G到支承点 的距离为e, 剖面绕重心的转动惯量为J0,试建立系统运动微分方程。
动能：T
1 2
m(h e )2
1 2
J0 2
势能：U
1 2
k1h2
1 2
k2 2
m me
J0
me me2
h
k1
0
(e 0)
)
Re
2k k
k k
2
m
0
0 m
－1
i
f1
f2
eit
u* (t )
1
广西专版新教材高中物理第2章机械振动2简谐运动的描述课后习题新人教版选择性必修第一册
2简谐运动的描述课后·训练提升基础巩固一、选择题(第1~3题为单选题,第4~6题为多选题)1.一个质点以O为中心做简谐运动,位移随时间变化的图像如图所示,a、b、c、d表示质点在不同时刻的相应位置,下列说法正确的是()A.质点在位置b比位置d时相位超前π4B.质点通过位置b时,相对平衡位置的位移为A2C.质点从位置a到c和从位置b到d所用时间相等D.质点从位置a到b和从b到c的平均速度相等b比位置d时相位超前π,选项A错误;质点通过位置b时,相对平衡位置的2,选项B错误;质点从位置a到c和从位置b到d所用时间相等,都是2s,选项C正位移大于A2确;质点从位置a到b和从b到c的时间相等,位移不等,所以平均速度不相等,选项D错误。
2.有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放让它振动,第二次把弹簧压缩2x后释放让它振动,则先后两次振动的周期之比和振幅之比分别为() A.1∶11∶1 B.1∶11∶2C.1∶41∶4D.1∶21∶2,即振幅,故振幅之比为1∶2;而对同一振动系统,其周期与振幅无关,则周期之比为1∶1。
3.下图为一质点做简谐运动的位移—时间图像。
由图可知,下列说法正确的是()A.质点的运动轨迹为正弦曲线B.t=0时,质点正通过平衡位置向正方向运动C.t=0.25 s时,质点的速度方向与位移的正方向相反D.质点运动过程中,两端点间的距离为0.1 m,运动轨迹是一条直线,离开平衡位置的位移与时间的关系图像才是正弦曲线(余弦曲线),选项A错误;由题图可知,t=0时,质点正通过正向最大位移处向负方向运动,选项B错误;由题图可知,t=0.25s时,质点的速度方向沿x轴正方向,与位移的正方向相同,选项C错误;质点运动过程中,两端点间的距离d=0.05m+0.05m=0.1m,选项D正确。
4.如图所示,弹簧振子以O为平衡位置,在BC间振动,则()A.B→O→C→O→B为一次全振动B.O→B→O→C→B为一次全振动C.C→O→B→O→C为一次全振动D.OB的大小不一定等于OC为平衡位置,B、C为两侧最远点,则从B起始经O、C、O、B路程为振幅的4倍,选项A正确;若从O起始经B、O、C、B路程为振幅的5倍,超过一次全振动,选项B错误;若从C 起始经O、B、O、C路程为振幅的4倍,选项C正确;因弹簧振子系统不考虑摩擦,所以振幅一定,选项D错误。
机械振动 课后习题和答案 第二章 习题和答案
2.1 弹簧下悬挂一物体，弹簧静伸长为δ。
设将物体向下拉，使弹簧有静伸长3δ，然后无初速度地释放，求此后的运动方程。
解：设物体质量为m ，弹簧刚度为k ，则：mg k δ=，即：n ω==取系统静平衡位置为原点0x =，系统运动方程为： δ⎧+=⎪=⎨⎪=⎩00020mx kx x x （参考教材P14）解得：δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ，下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放，试求物体的运动方程、振幅、周期及弹簧力的最大值。
解：由题可知：弹簧的静伸长0.850.650.2()m =-= 所以：9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点，得到：系统的运动微分方程为：20n x x ω+=其中，初始条件：(0)0.2(0)0x x =-⎧⎨=⎩ （参考教材P14） 所以系统的响应为：()0.2cos ()n x t t m ω=-弹簧力为：()()cos ()k n mg F kx t x t t N ω===-因此：振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置，另一重物2m 从高度为h 处自由落到1m 上而无弹跳，如图所示，求其后的运动。
解：取系统的上下运动x 为坐标，向上为正，静平衡位置为原点0x =，则当m 有x 位移时，系统有： 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知：12()0m m x kx ++= 即：12/()n k m m ω=+系统的初始条件为：⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m （能量守恒得：221201()2m gh m m x =+） 因此系统的响应为：01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即：ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆心受到一弹簧k 约束，如图所示，求系统的固有频率。
人教版(2019)物理选择性必修一第2章机械振动含答案
人教（新教材）选择性必修第一册第2章：机械振动1、一质点做简谐运动，其振动图像如图所示，在0.3～0.4 s时间内质点的运动情况是()A．沿x轴负方向运动，位移不断增大B．沿x轴正方向运动，速度不断减小C．动能不断增大，势能不断减小D．动能不断减小，加速度不断减小2、（双选）如图所示为某物体做简谐运动的图像，下列说法中正确的是()A．由P→Q位移在增大B．由P→Q速度在增大C．由M→N位移是先减小后增大D．由M→N位移始终减小3、（双选）把一弹簧振子的弹簧拉长一些，然后由静止释放，0.5 s后振子经过平衡位置，则此弹簧振子的周期可能是()A．1 s B．2 s C．0.55 s D．0.4 s4、做简谐运动的弹簧振子，其质量为m，最大速率为v0，若从某时刻算起，在半个周期内，合外力()A．做功一定为0B．做功一定不为0C．做功一定是12m v2D．做功可能是0到12m v2之间的某一个值5、如图所示，MN为半径较大的光滑圆弧轨道的一部分，把小球A放在MN 的圆心处，再把另一小球B放在MN上离最低点C很近的M处，今使两球同时自由释放，则在不计空气阻力时有()A．A球先到达C点B．B球先到达C点C．两球同时到达C点D．无法确定哪一个球先到达C点6、在洗衣机把衣服脱水完毕后，电动机还要转动一会才能停下来，此时发现洗衣机先振动得比较小，然后有一阵子振动得很剧烈，然后振动慢慢减小直至停下来，其间振动剧烈的原因是()A．洗衣机没放平衡B．电动机有一阵子转快了C．电动机转动的频率和洗衣机的固有频率相近或相等D．这只是一种偶然现象7、如图所示是某振子做简谐运动的图像，以下说法中正确的是()A．因为振动图像可由实验直接得到，所以图像就是振子实际运动的轨迹B．振动图像反映的是振子位移随时间变化的规律，并不是振子运动的实际轨迹C．振子在B位置的位移就是曲线BC的长度D．振子运动到B点时的速度方向即为该点的切线方向（双选）某弹簧振子沿x轴的简谐运动图像如图所示，下列描述正确的是() 8、A．t＝0 s时，振子的速度为零，位移为零B．t＝1 s时，振子的速度为正向最大C．t＝2 s时，振子的速度为负的最大值D．t＝3 s时，振子的位移为负向最大9、如图所示，弹簧振子在BC间振动，O为平衡位置，BO＝OC＝5 cm，若振子从B到C的运动时间为1 s，则下列说法正确的是()A．振子从B经O到C完成一次全振动B．振动周期是1 s，振幅是10 cmC．经过两次全振动，振子通过的路程是20 cmD．从B开始经过3 s，振子通过的路程是30 cm10、如图所示为某个弹簧振子做简谐运动的振动图像，由图像可知()A．在0.1 s时，由于位移为零，所以振动能量为零B．在0.2 s时，振子具有最大势能C．在0.35 s时，振子具有的能量尚未达到最大值D．在0.4 s时，振子的动能最大11、（双选）如图所示为一单摆的振动图像，则()A．t1和t3时刻摆线的拉力等大B．t1和t3时刻摆球速度相等C．t3时刻摆球速度正在减小D．t4时刻摆线的拉力正在减小12、在飞机的发展史中有一个阶段，飞机上天后不久，飞机的机翼(翅膀)很快就抖动起来，而且越抖越厉害，后来经过人们的探索，利用在飞机机翼前装一个配重杆的方法，解决了这一问题，在飞机机翼前装配重杆的目的主要是() A．加大飞机的惯性B．使机体更加平衡13、甲同学想在家里做用单摆测定重力加速度的实验，但没有合适的摆球，他找到了一块长为3 cm左右，外形不规则的大理石块代替小球．他设计的实验步骤是：A．将石块用细线系好，结点为M，将细线的上端固定于O点(如图所示) B．用刻度尺测量OM间细线的长度l作为摆长C．将石块拉开一个大约α＝30°的角度，然后由静止释放D．从石块摆到最高点时开始计时，测出30次全振动的总时间t，由T＝t30得出周期(1)则该同学以上实验步骤中有错误的是________．(2)若该同学用OM的长作为摆长，这样做引起的系统误差将使重力加速度的测量值比真实值______(选填“偏大”或“偏小”)．(3)如果该同学改正了错误，改变OM间细线的长度做了2次实验，记下每次相应的细线长度l1、l2和周期T1、T2，则由上述四个量得到重力加速度g的表达式是________．14、一物体沿x轴做简谐运动，振幅为8 cm，频率为0.5 Hz，在t＝0时，位移是4 cm，且向x轴负方向运动．(1)试写出用正弦函数表示的振动方程．(2)求10 s内通过的路程是多少．15、有一单摆，其摆长l＝1.02 m，摆球的质量m＝0.10 kg，已知单摆做简谐运动，单摆完成30次全振动所用的时间t＝60.8 s，试问：(1)当地的重力加速度是多大？(2)如果将这个摆改为秒摆，摆长应怎样改变？改变多少？（新教材）人教物理选择性第一册第2章机械振动含答案1、一质点做简谐运动，其振动图像如图所示，在0.3～0.4 s时间内质点的运动情况是()A．沿x轴负方向运动，位移不断增大B．沿x轴正方向运动，速度不断减小C．动能不断增大，势能不断减小D．动能不断减小，加速度不断减小【答案】B2、（双选）如图所示为某物体做简谐运动的图像，下列说法中正确的是()A．由P→Q位移在增大B．由P→Q速度在增大C．由M→N位移是先减小后增大D．由M→N位移始终减小【答案】AC3、（双选）把一弹簧振子的弹簧拉长一些，然后由静止释放，0.5 s后振子经过平衡位置，则此弹簧振子的周期可能是()A．1 s B．2 s C．0.55 s D．0.4 s【答案】BD4、做简谐运动的弹簧振子，其质量为m，最大速率为v0，若从某时刻算起，在半个周期内，合外力()A．做功一定为0B．做功一定不为0C．做功一定是12m v2D．做功可能是0到12m v2之间的某一个值【答案】A5、如图所示，MN为半径较大的光滑圆弧轨道的一部分，把小球A放在MN 的圆心处，再把另一小球B放在MN上离最低点C很近的M处，今使两球同时自由释放，则在不计空气阻力时有()A．A球先到达C点B．B球先到达C点C．两球同时到达C点D．无法确定哪一个球先到达C点【答案】A6、在洗衣机把衣服脱水完毕后，电动机还要转动一会才能停下来，此时发现洗衣机先振动得比较小，然后有一阵子振动得很剧烈，然后振动慢慢减小直至停下来，其间振动剧烈的原因是()A．洗衣机没放平衡B．电动机有一阵子转快了C．电动机转动的频率和洗衣机的固有频率相近或相等D．这只是一种偶然现象【答案】C7、如图所示是某振子做简谐运动的图像，以下说法中正确的是()A．因为振动图像可由实验直接得到，所以图像就是振子实际运动的轨迹B．振动图像反映的是振子位移随时间变化的规律，并不是振子运动的实际轨迹C．振子在B位置的位移就是曲线BC的长度D．振子运动到B点时的速度方向即为该点的切线方向【答案】B（双选）某弹簧振子沿x轴的简谐运动图像如图所示，下列描述正确的是() 8、A．t＝0 s时，振子的速度为零，位移为零B．t＝1 s时，振子的速度为正向最大C．t＝2 s时，振子的速度为负的最大值D．t＝3 s时，振子的位移为负向最大【答案】CD9、如图所示，弹簧振子在BC间振动，O为平衡位置，BO＝OC＝5 cm，若振子从B到C的运动时间为1 s，则下列说法正确的是()A．振子从B经O到C完成一次全振动B．振动周期是1 s，振幅是10 cmC．经过两次全振动，振子通过的路程是20 cmD．从B开始经过3 s，振子通过的路程是30 cm【答案】D10、如图所示为某个弹簧振子做简谐运动的振动图像，由图像可知()A．在0.1 s时，由于位移为零，所以振动能量为零B．在0.2 s时，振子具有最大势能C．在0.35 s时，振子具有的能量尚未达到最大值D．在0.4 s时，振子的动能最大【答案】B11、（双选）如图所示为一单摆的振动图像，则()A．t1和t3时刻摆线的拉力等大B．t1和t3时刻摆球速度相等C．t3时刻摆球速度正在减小D．t4时刻摆线的拉力正在减小【答案】AD12、在飞机的发展史中有一个阶段，飞机上天后不久，飞机的机翼(翅膀)很快就抖动起来，而且越抖越厉害，后来经过人们的探索，利用在飞机机翼前装一个配重杆的方法，解决了这一问题，在飞机机翼前装配重杆的目的主要是() A．加大飞机的惯性B．使机体更加平衡【答案】D13、甲同学想在家里做用单摆测定重力加速度的实验，但没有合适的摆球，他找到了一块长为3 cm左右，外形不规则的大理石块代替小球．他设计的实验步骤是：A．将石块用细线系好，结点为M，将细线的上端固定于O点(如图所示) B．用刻度尺测量OM间细线的长度l作为摆长C．将石块拉开一个大约α＝30°的角度，然后由静止释放D．从石块摆到最高点时开始计时，测出30次全振动的总时间t，由T＝t30得出周期(1)则该同学以上实验步骤中有错误的是________．(2)若该同学用OM的长作为摆长，这样做引起的系统误差将使重力加速度的测量值比真实值______(选填“偏大”或“偏小”)．(3)如果该同学改正了错误，改变OM间细线的长度做了2次实验，记下每次相应的细线长度l1、l2和周期T1、T2，则由上述四个量得到重力加速度g的表达式是________．答案：(1)BCD(2)偏小(3)g＝21T22－T2114、一物体沿x轴做简谐运动，振幅为8 cm，频率为0.5 Hz，在t＝0时，位移是4 cm，且向x轴负方向运动．(1)试写出用正弦函数表示的振动方程．(2)求10 s内通过的路程是多少．【答案】(1)x＝0.08sinπt＋56πm(2)1.6 m15、有一单摆，其摆长l＝1.02 m，摆球的质量m＝0.10 kg，已知单摆做简谐运动，单摆完成30次全振动所用的时间t＝60.8 s，试问：(1)当地的重力加速度是多大？(2)如果将这个摆改为秒摆，摆长应怎样改变？改变多少？【答案】(1)9.79 m/s2(2)其摆长要缩短缩短0.027 m。
第二章 机械振动练习—— 高二上学期物理人教版(2019)选择性必修第一册
机械振动练习一、选择题1．如图所示，物体系在两弹簧之间，弹簧的劲度系数分别为1k 和2k ，且1k k =，22k k =，两弹簧均处于自然状态。
现在向右拉动物体，然后释放，物体在B 、C 间振动，O 为平衡位置（不计阻力），设向右为正方向，物体相对O 点的位移为x ，则下列判断正确的是（ ）A ．物体做简谐运动，OC OB =B ．物体做简谐运动，OC OB ≠ C ．物体所受合力F kx =-D ．物体所受合力3F kx =-2.一简谐振子沿x 轴振动,平衡位置在坐标原点,t=0时刻振子的位移x=-0.1m ；t=4/3 s 时刻x=0.1m ； t=4s 时刻x=0.1m.该振子的振幅和周期可能为( )A.0.1m,8/3sB.0.1m,8sC.0.2m,8sD.0.2m,8 sE.0.3m,10s3．如图1所示，弹簧振子以点O 为平衡位置，在A 、B 两点之间做简谐运动。
取向右为正方向，振子的位移x 随时间t 的变化如图2所示，下列说法正确的是（ ）A ．0t =时，振子经过O 点向左运动B ．0.5s t =时，振子在O 点右侧2.5cm 处C ． 1.5s t =和 3.5s t =时，振子的速度相同D ．10s t =时，振子的动能最大4．如图所示，A 球振动后，通过水平细绳迫使B 、C 振动，振动达到稳定时，下列说法中正确的是A ．只有A 、C 的振动周期相等B ．C 的振幅比B 的振幅小C ．C 的振幅比B 的振幅大D ．B 球的固有周期等于A 球的固有周期5．一钩码和一轻弹簧构成弹簧振子，可用如图甲所示的装置研究该弹簧振子的受迫振动。
匀速转动把手时，曲杆给弹簧振子以驱动力，使振子做受迫振动。
若保持把手不动，给钩码一向下的初速度，钩码便做简谐运动，振动图像如图乙所示当把手以某一速度匀速转动，受迫振动达到稳定时，钩码的振动图像如图丙所示。
下列说法正确的是（）A．弹簧振子的固有周期为8sB．驱动力的周期为4sC．减小驱动力的周期，弹簧振子的振幅一定减小D．增大驱动力的周期，弹簧振子的振幅一定减小6．把一个筛子用四根弹簧支起来，筛子上装一个电动偏心轮，它每转一周，给筛子一个驱动力，这就做成了一个共振筛，如图所示。
人教版高中物理选择性必修第1册基础过关练 第二章 机械振动 2 简谐运动的描述
第二章机械振动2 简谐运动的描述基础过关练题组一描述简谐运动的物理量1.关于简谐运动的频率,下列说法正确的是( )A.频率越高,振动物体运动的速度越大B.频率越高,单位时间内振动物体速度的方向变化的次数越多C.频率是50Hz时,1s内振动物体速度方向改变50次D.弹簧振子的固有频率与振动物体通过平衡位置时的速度大小有关2.(多选)下列关于简谐运动的振幅、周期和频率的说法中正确的是( )A.振幅是矢量,方向从平衡位置指向最大位移处B.周期和频率的乘积是一个常数C.振幅增加,周期必然增加,而频率减小D.做简谐运动的物体,其频率固定,与振幅无关3.(2019山东济宁实验中学高二上月考)一个做简谐运动的质点,它的振幅是4cm,频率是2.5Hz,该质点从平衡位置开始经过2.9s后,位移的大小和经过的路程分别为( )A.0 10cmB.4cm 100cmC.0 28cmD.4cm 116cm4.(2019吉林松原乾安七中高二下质检)如图所示,弹簧振子在B、C间振动,O为平衡位置,BO=OC=5cm。
若小球从B到C的运动时间为1s,则下列说法正确的是( )A.小球从B经O到C完成一次全振动B.振动周期是2s,振幅是5cmC.经过两次全振动,小球通过的路程是20cmD.从B开始经过3s,小球通过的路程是20cm题组二对简谐运动表达式的理解5.某振子做简谐运动的表达式为x=2sin(2πt+)cm,则该振子振动的振幅和周期为( )A.2cm 1sB.2cm 2πsC.1cm sD.以上全错6.(2020福建泉州永春第一中学月考)有一个弹簧振子,振幅为0.8cm,周期为0.5s,初始时具有负方向的最大加速度,则它的振动方程是( )A.x=8×10-3sin(4πt+)mB.x=8×10-3sin(4πt-)mC.x=8×10-3sin(4πt+)mD.x=8×10-3sin(t+)m7.(多选)如图所示,A、B为两个简谐运动的振动图像,下列说法正确的是( )A.A、B之间的相位差是B.A、B之间的相位差是πC.B比A超前D.A比B超前8.某质点做简谐运动,其位移随时间变化的关系式为x=3sin(t+)cm,则( )A.质点的振幅为3mB.质点的振动周期为sC.t=0.75s时,质点到达距平衡位置最远处D.质点前2s内的位移为-4.5cm题组三简谐运动的周期性与对称性9.一质点做简谐运动,它从最大位移处经0.3s第一次到达点M处,再经0.2s第二次到达M点,则其振动频率为( )A.0.4HzB.0.8HzC.2.5HzD.1.25Hz10.(2019河北廊坊高二下期中,改编)如图所示,弹簧振子的平衡位置为O点,在d、c间振动,振动物体从a到b历时0.2s,振动物体经a、b两点时速度相同。
【单元练】2021年高中物理选修1第二章【机械振动】经典复习题(答案解析)
一、选择题1．如图甲所示为以O 点为平衡位置。
在A 、B 两点间做简谐运动的弹簧振子，图乙为这个弹簧振子的振动图像，由图可知下列说法中正确的是（ ）A ．在0.2s t =时，弹簧振子一定运动到B 位置B ．在0.3s t =与0.7s t =两个时刻，弹簧振子的速度相同C ．从0到0.2s t =的时间内，弹簧振子的动能持续地减少D ．在0.2s t =与0.6s t =两个时刻，弹簧振子的加速度相同C解析：CA ．在t =0.2s 时，弹簧振子位移最大，但没有规定正方向，故可能在A 点，也可能在B 点，故A 错误；B ．x -t 图象的切线斜率表示速度，在t =0.3s 与t =0.7s 两个时刻，弹簧振子的速度大小相等，方向相反，故B 错误；C ．从t =0到t =0.2s 的时间内，位移增加，远离平衡位置，故动能减小，故C 正确；D ．在t =0.2s 与t =0.6s 两个时刻，位移相反，根据kx a m=-可知，加速度大小相等，方向相反，故D 错误。
故选C 。
2．如图所示，水平方向的弹簧振子振动过程中，振子先后经过a 、b 两点时的速度相同，且从a 到b 历时0.2s ，从b 再回到a 的最短时间为0.4s ，aO bO =，c 、d 为振子最大位移处，则该振子的振动频率为（ ）A ．1HzB ．1.25HzC ．2HzD ．2.5Hz B解析：B由题可知，a 、b 两点关于平衡位置对称，从a 到b 历时 10.2s t =从b 再回到a 的最短时间为0.4s ，即从b 到c 所用时间为20.40.2s 0.1s 2t -==所以弹簧振子振动的周期为12240.8s T t t =+=则振动频率为 1 1.25Hz f T== 故B 正确，ACD 错误。
故选B 。
3．如图所示，一块涂有炭黑的玻璃板在拉力F 的作用下，竖直向上运动.一个装有水平振针的固定电动音叉在玻璃板上画出了图示曲线，下列判断正确的是A ．音叉的振动周期在增大B ．音叉的振动周期不变C ．玻璃板在向上做减速运动D ．玻璃板在向上做匀速直线运动B解析：B AB.固定电动音叉的周期不变，故A 错误，B 正确；CD.从固定电动音叉在玻璃上画出的曲线看出OA 、AB 、BC 、间对应的时间均为半个周期，且距离越来越大，说明玻璃杯运动的速度越来越大，即玻璃板在向上做加速运动，故CD 错误。
机械动力学第二章作业(答案)
机械动力学第二章作业(答案)-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第二章习题2- 1如图2-1所示，长度为L 、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住，求杆绕O 点微幅振动的微分方程。
222...2..011T J 2231V 2(sin )(1cos )222()0m 0322ml L Lk mg dT V dtmg k L θθθθθθθ==⋅=⋅+-+=⎛⎫++= ⎪⎝⎭解：设系统处于静平衡位置时势能为，当杆顺时针偏转角时动能：势能：由能量守恒原理，得化简得：2- 2如图2-2所示，质量为m 、半径为r 的圆柱体，可沿水平面作纯滚动，它的圆心O 用刚度为k 弹簧相连,求系统的振动微分方程。
22 (2)2..0111T J ,2221V ()2()03m 02m r J mr k r dT V dtk θθθθθθ⎛⎫=+= ⎪⎝⎭=+=+=解：设系统处于静平衡位置时势能为，当杆顺时针偏转角时动能：势能：由能量守恒原理，得化简得：2- 3如图2-3所示，质量为m 、半径为R 的圆柱体,可沿水平面作纯滚动，与圆心O 距离为a 处用两根刚度为k 的弹簧相连，求系统作微振动的微分方程。
图2- 1 图2- 22.222..220111T J ,2221V (2)[()]2()032()02m R J mR k R a dT V dt mR k R a θθθθθ⎛⎫=+= ⎪⎝⎭=⋅++=++=解：设系统处于静平衡位置时势能为动能：势能：由能量守恒原理，得化简得： 2- 4求图2-4所示弹簧-质量-滑轮系统的振动微分方程(假设滑轮与绳索间无滑动)。
2.222....0111T J ,2221V ()2()0()02m r J Mr k r dT V dt x r x r M m x kx θθθθθ⎛⎫=+= ⎪⎝⎭=⋅+===++=解：设系统处于静平衡位置时势能为动能：势能：由能量守恒原理，得其中，，化简得： 2- 5质量可忽略的刚性杆-质量-弹簧-阻尼器系统参数如图2-5所示，2L 杆处于铅垂位置时系统静平衡，求系统作微振动的微分方程。
胡海岩主编机械振动基础课后习题解答第2章习题
胡海岩主编---机械振动基础课后习题解答_第2章习题第2章习题含答案习题2-1 定常力作用下的单自由度系统1. 一个单自由度系统的质量m=2kg，刚度k=1000N/m，阻尼系数c=10N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解：根据公式，该系统的固有频率可计算为：ωn = √(k/m) = √(1000/2) ≈ 22.36 rad/s阻尼比可计算为：ξ = c/(2√(mk)) = 10/(2√(2×1000)) ≈ 0.158振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时，系统为欠阻尼；当ξ=1时，系统为临界阻尼；当ξ>1时，系统为过阻尼。
2. 一个单自由度系统的质量m=5kg，刚度k=500N/m，阻尼系数c=20N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解：根据公式，该系统的固有频率可计算为：ωn = √(k/m) = √(500/5) = 10 rad/s阻尼比可计算为：ξ = c/(2√(mk)) = 20/(2√(5×500)) ≈ 0.141振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时，系统为欠阻尼；当ξ=1时，系统为临界阻尼；当ξ>1时，系统为过阻尼。
习题2-2 强迫振动的幅值和相位1. 一个单自由度系统的质量m=3kg，刚度k=2000N/m，阻尼系数c=30N·s/m。
给定的外力F(t) = 10sin(5t)N。
试求该系统在稳态时的振动幅值和相位。
解：首先求解系统的强迫响应，即对外力F(t)进行拉氏变换：F(s) = L{F(t)} = L{10sin(5t)} = 10L{sin(5t)} = 10×(5/(s^2+25))根据公式，系统的强迫响应可计算为：X(s) = F(s)/((s^2+ωn^2)+2ξωns)其中，ωn=√(k/m)为系统的固有频率，ξ=c/(2√(mk))为系统的阻尼比。
(必考题)高中物理选修一第二章《机械振动》测试题(答案解析)(1)
一、选择题1．一弹簧振子做简谱运动，它所受的回复力F随时间t变化的图象为正弦曲线，如图所示，下列说法正确的是（）A．在t从0到2s时间内，弹簧振子做加速运动B．在t1=3s和t2=5s时，弹簧振子的速度大小相等，方向相同C．在t2=5s和t3=7s时，弹簧振子的位移大小相等，方向相同D．在t从0到4s时间内，t=2s时刻弹簧振子所受回复力做功瞬时功率最大2．如图所示，曲轴上挂一个弹簧振子，转动摇把，曲轴可带动弹簧振子上下振动。
开始时不转动摇把，让振子自由振动，测得其频率为2Hz。
现匀速转摇把，转速为240r/min。
则（）A．当振子稳定振动时，它的振动周期是0.5sB．当振子稳定振动时，它的振动频率是4HzC．当转速增大时，弹簧振子的振幅增大D．振幅增大的过程中，外界对弹簧振子做负功3．弹簧振子的质量为M，弹簧劲度系数为k，在振子上放一质量为m的木块，使两者一起振动，如图。
木块的回复力F是振子对木块的摩擦力，F也满足F k x=-'，x是弹簧的伸长（或压缩）量，那么kk'为（）A．mMB．mM m+C．MM m+D．Mm4．劲度系数为20N/cm的弹簧振子，它的振动图象如图所示，在图中A点对应的时刻（）A．振子所受的弹力大小为5N，方向指向x轴的负方向B．振子的速度方向指向x轴的负方向C．在0~4s内振子作了1.75次全振动D．在0~4s内振子通过的路程为0.35cm，位移为05．如图所示，轻弹簧上端固定，下端连接一小物块，物块沿竖直方向做简谐运动。
以竖直向上为正方向，物块做简谐运动的表达式为y=0.1sin5πt(m)。
t=0时刻，一小球从距物块h 高处自由落下，t=0.3s时，小球恰好与物块处于同一高度，重力加速度g取10m/s2，空气阻力不计，以下判断正确的是（）A．h=0.35 mB．简谐运动的周期是 0.2 sC．0.3 s 内物块运动的路程是 0.1 mD．t=0.35s 时，物块与小球运动方向相同6．摆球质量相等的甲、乙两单摆悬挂点高度相同，其振动图象如图所示，选悬挂点所在水平面为重力势能的参考面，由图可知（）A．甲、乙两单摆的摆长之比是4 9B．t a时刻甲、乙两单摆的摆角相等C．t b时刻甲、乙两单摆的势能差最小D．t c时刻甲、乙两单摆的速率相等7．有一星球其半径为地球半径的2倍，平均密度与地球相同，今把一台在地球表面走时准确的摆钟移到该星球表面，摆钟的秒针走一圈的实际时间变为A ．0.5minB ．0.7minC ．1.4minD ．2min8．如图所示的单摆，摆球a 向右摆动到最低点时，恰好与一沿水平方向向左运动的粘性小球b 发生碰撞，并粘在一起，且摆动平面不便．已知碰撞前a 球摆动的最高点与最低点的高度差为h ，摆动的周期为T ，a 球质量是b 球质量的5倍，碰撞前a 球在最低点的速度是b 球速度的一半．则碰撞后A ．摆动的周期为56T B ．摆动的周期为65T C ．摆球最高点与最低点的高度差为0.3hD ．摆球最高点与最低点的高度差为0.25h9．图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子，图(乙)为这个弹簧振子的振动图象，由图可知下列说法中正确的是( )A ．在t =0.2s 时，弹簧振子可能运动到B 位置B ．在t =0.1s 与t =0.3s 两个时刻，弹簧振子的速度相同C ．从t =0到t =0.2s 的时间内，弹簧振子的动能持续地增加D ．在t =0.2s 与t =0.6s 两个时刻，弹簧振子的加速度相同10．某质点做简谐运动,其位移随时间变化的关系式为5sin 4x t π=(cm) ,则下列关于质点运动的说法中正确的是( )A ．质点做简谐运动的振幅为 10cmB ．质点做简谐运动的周期为 4sC ．在 t=4s 时质点的加速度最大D ．在 t=4s 时质点的速度最大11．一个做简谐运动的质点,它的振幅是5 cm,频率是2.5 Hz,该质点从平衡位置开始经过2.5 s后,位移的大小和经过的路程为( )A．5 cm、12.5 cmB．5 cm、125cmC．0、30cmD．0、125 cm12．一水平弹簧振子做简谐运动的振动图像如图所示，已知弹簧的劲度系数为20 N/cm，则 ( )A．图中A点对应的时刻振子所受的回复力大小为5 N，方向指向x轴的负方向B．图中A点对应的时刻振子的速度方向指向x轴的负方向C．在0～4 s内振子做了1.75次全振动D．在0～4 s内振子通过的路程为3.5 cm13．一根自由长度为10cm的轻弹簧，下端固定，上端连一个质量为m的物块P．在P上再放一个质量也是m的物块Q．系统静止后，系统静止后，弹簧长度为6cm，如图所示．如果迅速向上移去Q．物块P将在竖直方向做简谐运动．此后，弹簧的最大长度是（）A．8cm B．9cm C．10cm D．11cm14．一单摆做小角度摆动，其振动图象如图，以下说法正确的是（）A．1t时刻摆球速度为零，悬线对它的拉力为零B．2t时刻摆球速度最大，悬线对它的拉力最大C．3t时刻摆球速度最大，悬线对它的拉力最小D．4t时刻摆球速度最小，悬线对它的拉力最大15．如图，O点为弹簧振子的平衡位置，小球在B、C间做无摩擦的往复运动．若小球从C点第一次运动到O点历时0.1s，则小球振动的周期为（）A．0.1s B．0.2s C．0.3s D．0.4s二、填空题16．如图为一单摆的共振曲线。
高中物理选修一第二章《机械振动》测试卷(有答案解析)
一、选择题1．(0分)[ID ：127376]如图甲所示，弹簧振子以O 点为平衡位置，在光滑水平面上的A 、B 两点之间做简谐运动，A 、B 分居O 点的左右两侧的对称点。
取水平向右为正方向，振子的位移x 随时间t 的变化如图乙所示的正弦曲线，下列说法正确的是（ ）A ．0.6s t =时，振子在O 点右侧6cm 处B ．振子0.2s t =和 1.0s t =时的速度相同C ． 1.2s t =时，振子的加速度大小为223πm/s 16，方向水平向右D ． 1.0s t =到 1.4s t =的时间内，振子的加速度和速度都逐渐增大2．(0分)[ID ：127369]如图所示，弹簧振子在A 、B 之间做简谐运动．以平衡位置O 为原点，建立Ox 轴．向右为x 轴的正方向．若振子位于B 点时开始计时，则其振动图像为（ ）A ．B ．C ．D ．3．(0分)[ID ：127367]在科学研究中，科学家常将未知现象同已知现象进行比较，找出其共同点，进一步推测未知现象的特性和规律．法国物理学家库仑在研究异种电荷的吸引力问题时，曾将扭秤的振动周期与电荷间距离的关系类比单摆的振动周期与摆球到地心距离的关系．已知单摆摆长为l ，引力常量为G ，地球质量为M ，摆球到地心的距离为r ，则单摆振动周期T 与距离r 的关系式为( ) A ．T =2GMlB ．T =2l GMC ．T 2πGMr lD ．T =2r GM4．(0分)[ID ：127361]如图所示，质量为1m 的物体A 放置在质量为2m 的物体B 上，B 与弹簧相连，它们一起在光滑水平面上做简谐运动，振动过程中A 、B 之间无相对运动，设弹簧劲度系数为k ，当物体离开平衡位置的位移为x 时，A 受到的回复力的大小等于（ ）A ．0B ．kxC ．121m kx m m + D ．12m kx m 5．(0分)[ID ：127357]如图所示为单摆在两次受迫振动中的共振曲线，下列说法正确的是（ ）A ．若两次受迫振动分别在月球上和地球上进行，且摆长相等，则图线II 是月球上的单摆共振曲线B ．图线II 若是在地球表面上完成的，则该摆摆长约为2mC ．若摆长约为1m ，则图线I 是在地球表面上完成的D ．若两次受迫振动均在地球上同一地点进行的，则两次摆长之比为l 1：l 2= 25：4 6．(0分)[ID ：127352]两个弹簧振子甲的固有频率为f ，乙的固有频率为10f 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3
8l d 22 = 3EI
Hale Waihona Puke 3l3 1 柔度矩阵:D = 3 E I 2 .5
2 .5 8
刚 度 矩 阵 :K =
6E I 16 7l 3 5
5 2
m 运动方程: 1 0
0 u1 6 EI u + 7l 3 m2 2
16 5 u1 f1 sin ωt 5 2 u = 0 2
系 统 的 固 有 频 率 : ω 1 = 1 8 9 (rad /s), ω 2 = 9 7 3 .7 7 (rad /s)
H 1 1 ( ω )的 分 子 :
12 EI ω 2m2 = 0 3 7l
反 共 振 频 率: ω = 12 EI = 4 4 3 .6 (rad /s) 7l 3m 2
30 EI H 2 1 (ω )的 分 子 : 7l 3
P89,2-15: 双层建筑结构简化模型如图所示, 其中m1 = m, m2 = 2m, 剪切刚度k1 = k , k2 = 2k. (1) 求结构的固有频率和固有振型 (2) 若在m1上作用力产生单位位移,然后无初速度释放,求其自由响应; (3) 由于地震,基础产生水平方向运动v = v sin ωt , 求结构稳态响应.
P88,2-3: 求图示系统的固有频率和固有振型.
m 0 u1 4k 0 2m u + 3k 2 3k u1 0 = 5k u 2 0
( K ω 2 M )φ = 0
ω1 = k / m , ω2 = 11k / 2m
1 1 φ1 = , φ2 = 1 0.5
0.946 1 φ1 = , φ2 = 1 0.757
ω1 = 7.3384(rad/s), ω2 = 48.1783(rad/s)
P88,2-9: 图示均匀刚杆质量为m,求系统的固有模态.
1 2 ma θ = k1b2θ k2 (aθ u) a 3 mu = k2 (u aθ )
1
1 u (t ) θ (t ) = 0.618 l
1 1 u (t ) k k = 0.618 0.07236l cos(0.437 )t + 1.618 0.02764l cos(1.144 )t θ (t ) m m l l
P89,2-14: 图示悬臂梁宽b = 0.036m, 厚h = 2.5 × 103 m, 长2l = 0.14m, 材料弹性模量E = 2.1×102 GPa. 梁上安装有两个重块m1 = 0.5kg和m1 = 0.25kg, 梁的质量可以忽略. (1) 求系统的固有频率 (2) 当简谐力 f1 sin ωt 作用于 m1 时, 不计阻尼,求反共振频率f a.
P88,2-4: 图示电车由两节质量均为2.28 ×104 kg的车厢组成, 中间连接器的刚度为 2.86 ×106 N/m. 求电车振动的固有频率和固有振型.
m 0 u1 k 0 m u + k 2
k u1 0 u = 0 k 2
( K ω 2 M )φ = 0
Φ = [φ1
φ2 ]
0.707 0.707 φ1 = , φ2 = 1 1
ω1 = 0.7654
g g , ω2 = 1.8478 l l
θ Θ0 = 0 0
θ (t ) 0.707 0.707 g g Θ (t ) = 1 = 0.707θ 0 cos(0.7654 )t 0.707θ 0 cos(1.8478 )t θ 2 (t ) 1 1 l l
1 2 1 ml 2 2 系统势能:U = 1 k(u lθ )2 + 1 k(u + lθ )2 系统动能:T = mu + θ 2 2 2 4 2 2 12
0 u 2k kl / 4 u 0 m + 运动方程: 0 ml 2 /12 θ kl / 4 5kl 2 /16 θ = 0
m1 (2l )2θ1 = k1lθ1 l k2 (2lθ1 2lθ2 ) 2l m (2l )2θ = k (2lθ 2lθ ) 2l
2 2 2 2 1
m 运动方程: 1 0
0 θ1 k1 / 4 + k2 + k m2 θ 2 2
k2 θ1 0 θ = 0 k2 2
P89,2-13: 图示刚杆质量不计,并求系统的固有频率和固有振型.如果将杆向下平移0.1l , 求 突然释放后的自由振动.
2 mu (t ) = ku (t ) k (u (t ) lθ (t )) 2 ml 2θ (t ) = kl (u (t ) lθ (t ))
0 u 2k 2m 运动方程: 0 2ml 2 θ + kl
ω1 = 0, ω2 = 2k / m = 15.84 (rad/s)
1 1 φ1 = , φ2 = 1 1
P88,2-5: 求图示扭转振动系统的固有频率和固有振型.
J 0 0 u1 k + 2 J u2 k k u1 0 = 2k u2 0
P87,2-1: 图示用于风洞试验的翼型剖面由拉伸弹簧k1和扭转弹簧k2支承着, 剖面重心G到支承点 的距离为e, 剖面绕重心的转动惯量为J 0 , 试建立系统运动微分方程.
1 1 动能: = m(h + eθ ) 2 + J 0θ 2 T 2 2 1 1 势能:U = k1h 2 + k2θ 2 2 2
k u1 0 u = 2kv sin ωt 3k 2
a 设稳态解为: * (t ) = 1 sin ωt u a2
k m 0 a1 0 ω2 a = 2kv 3k 0 2m 2
k m 0 0 ω2 3k 0 2m 2kv
k k , ω2 = 1.144 m m
1 cos ω1t 1.618 0 l
kl u 0 = kl 2 θ 0
ω1 = 0.437
1 1 φ1 = 0.618 , φ2 = 1.618 l l
1 0 0.618 cos ω 2t l 1 0.1l 1.618 0 l
(1) 求结构的固有频率和固有振型
m 0 u1 k 运动方程: 0 2m u + k 2 k u1 0 = 3k u2 0
k 2k ω1 = , ω2 = 2m m
1 1 φ1 = , φ2 = 0.5 1
(2) 求结构的自由响应
(3) 求结构的稳态响应
m1u1 (t ) = k1 (u1 (t ) u2 (t )) m2u2 (t ) = k1 (u1 (t ) u2 (t )) k2 (u2 (t ) v(t ))
m 0 u1 k 运动方程: 0 2m u + k 2 k k
悬臂梁在单位力作用下的挠度公式为
x2 δ= (3 a x ), 0 ≤ x ≤ a 6EI a2 δ= (3 x a ), a ≤ x ≤ 2 l 6EI
bh3 截 面 惯 性 矩 :I = 12
2l 悬臂梁总长; a 力作用点到固定端的距离 计算柔度系数: = l d11
3
3EI
5l d 12 = 6EI
( K ω 2 M )φ = 0
2k 2k ω1 = 1 , ω2 = 1 + 2 J 2 J
1 1 φ1 = , φ2 = 1/ 2 1/ 2
P88,2-6: 不计刚杆质量,按图示坐标建立运动微分方程,并求出固有频率和固有振型.
系统动能:T = 系统势能:U = 1 1 2 mu12 + 2mu2 2 2 1 1 k (2u1 u2 ) 2 + k (2u2 u1 ) 2 2 2
2 2 2
θ θ θ 系统势能:U = mgl (1 cos θ1 ) + mgl (2 cos θ1 cos θ 2 ) ≈ mgl 2 1 + mgl (2 1 + 2 2 ) 2 2 2
2 1 θ1 g 2 0 θ1 0 运动方程: 1 1 + l 0 1 θ = 0 θ 2 2
ma 2 / 3 0 θ k1b 2 + k2 a 2 运动方程: + 0 m u k2 a
k2 a θ 0 = k2 u 0
P89,2-10: 建立图示双单摆的微振动微分方程,并求固有频率和固有振型.
系 统动能 : T = 1 1 1 1 1 m (lθ1 ) 2 + m (lθ1 + lθ2 ) 2 = 2 ml 2θ12 + ml 2θ22 + 2 ml 2θ1θ2 2 2 2 2 2
k k ω1 = 1.282 , ω2 = 2.026 m m
1 1 φ1 = , φ2 = 1.43 / l 8.42 / l
P88,2-8: 图示刚杆质量不计, 1 = 4kg, m2 = 5kg, k1 = 2 ×103 N/m, k2 = 5 × 103 N/m, 求系统 m 的固有频率和固有振型.
m 0 u1 5k 运动方程: 0 2m u + 4k 2
k ω1 = 0.81 m k ω2 = 2.62 m
4k u1 0 = 5k u2 0
1 1 φ1 = , φ2 = 1.09 0.46
P88,2-7: 已知刚杆质量为m,按图示坐标建立运动微分方程,并求出固有频率和固有振型.
θ1 θ2
1 1 势能: = ( m1 ga + m2 gl )θ12 + m2 gbθ 22 U 2 2
J1 + m1a 2 + m2l 2 m2lb
m2lb θ1 (m1a + m2l ) g + 2 0 J 2 + m2b θ 2
0 θ1 0 θ = 0 m2bg 2
ω1 = 0.7654
g g , ω2 = 1.8478 l l
0.707 0.707 φ1 = , φ2 = 1 1